Effect of the Addition of Graphene Nanoplatelets on the Thermal Conductivity of Rocket Kerosene: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Methods
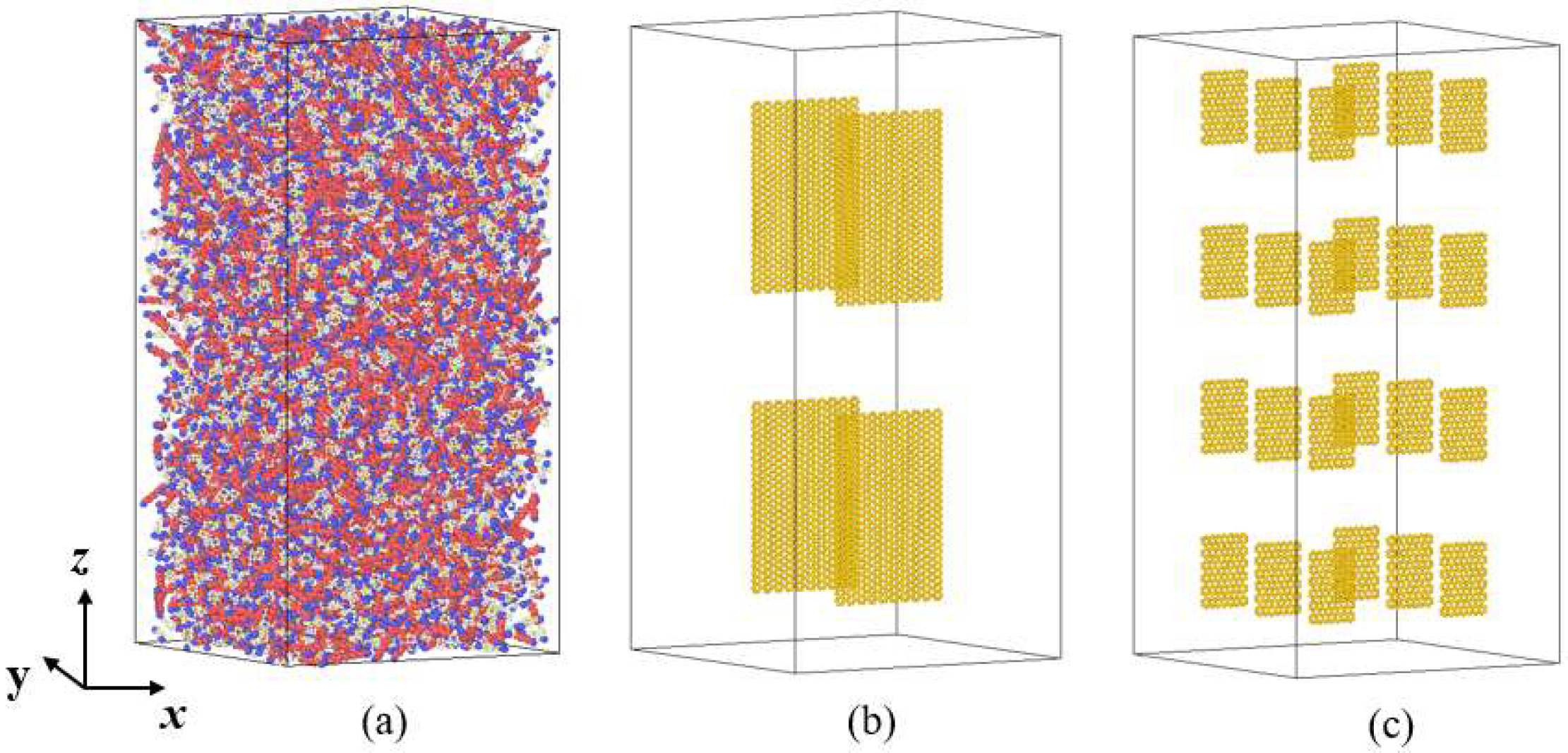
2.1. Construction of the Simulation System
2.2. Force Field
| Bond Type | Molecule | r0 (Å) | kr (kcal·mol·Å−2) | ||
| CHx-CHy [54] | Alkanes/Branched Alkanes | 1.54 | 899.52 | ||
| CHx(cyc)-CHy(cyc) [48] | Cycloalkanes | 1.54 | 536 | ||
| Bend type | Molecule | θ0 (°) | kθ/kB (K·rad−2) | ||
| CHx-CH2-CHy [46] | Alkanes/Branched Alkanes | 114 | 62,500 | ||
| CHx(cyc)-CH2(cyc)-CHy(cyc) [47] | Cycloalkanes | 114 | 62,500 | ||
| CHx(cyc)-CH(cyc)-any C [55] | Cycloalkanes | 112 | 62,500 | ||
| CHx(cyc)- CHx-CHy [46] | Branched Alkanes | 114 | 62,500 | ||
| Torsion type | Molecule | C0/kB (K) | C1/kB (K) | C2/kB (K) | C3/kB (K) |
| CHx- CH2-CH2 -CHy [46] | Alkanes/Branched Alkanes | 0 | 355.03 | −68.19 | 791.32 |
| CH2(cyc)-CH2(cyc)-CH2(cyc)-CH2(cyc) [48] | Cycloalkanes | 0 | 355.03 | −68.19 | 791.32 |
| CHx(cyc)-CH2(cyc)-CH(cyc)-any C [48] | Cycloalkanes | −251.06 | 428.73 | −111.85 | 441.27 |
| CHx(cyc)-CH(cyc)- CH2-CHy [48] | Cycloalkanes | −251.06 | 428.73 | −111.85 | 441.27 |
| CHx(cyc)-CH2- CH2 -CHy [46] | Branched Alkanes | 0 | 355.03 | −68.19 | 791.32 |
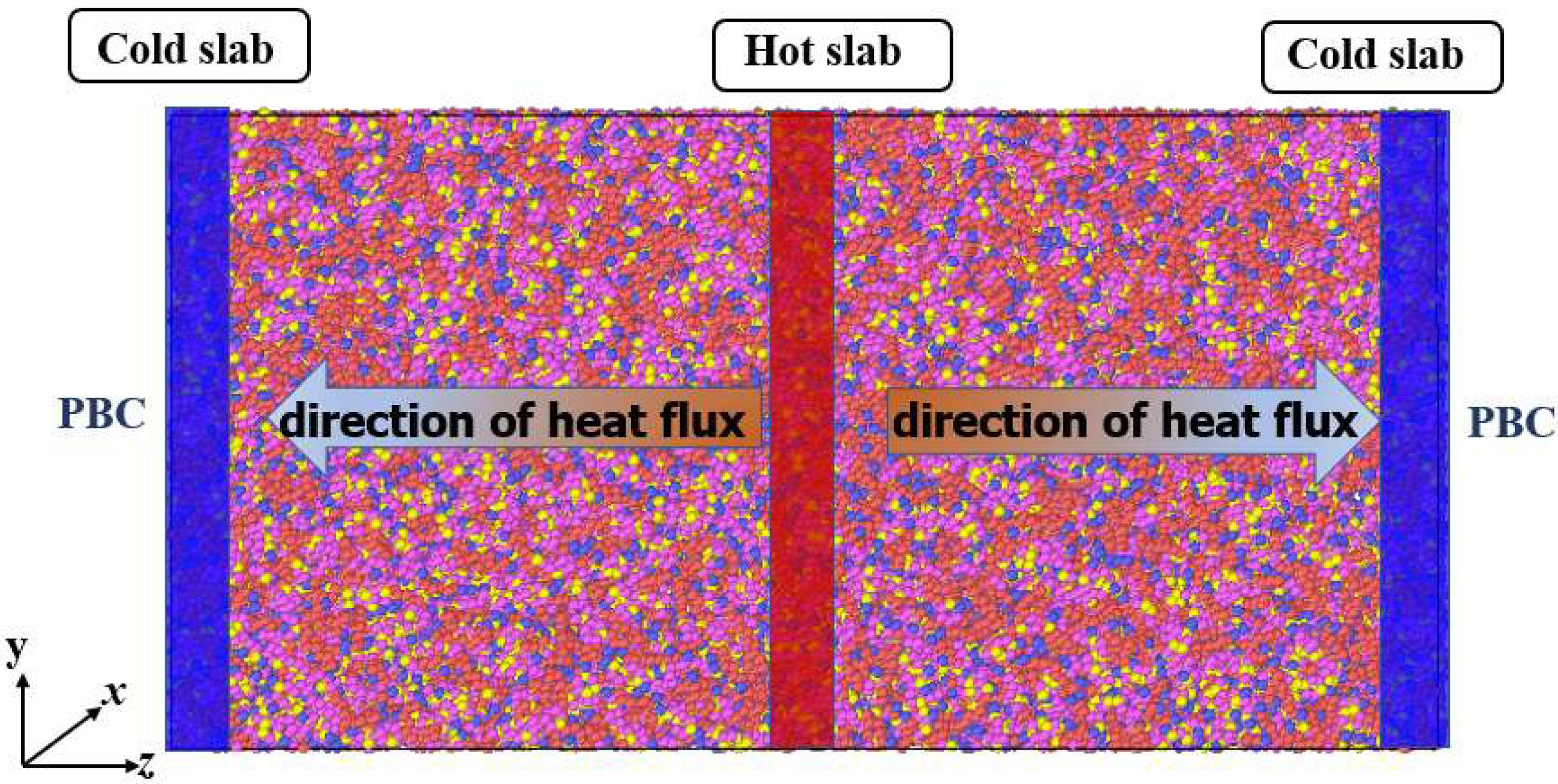
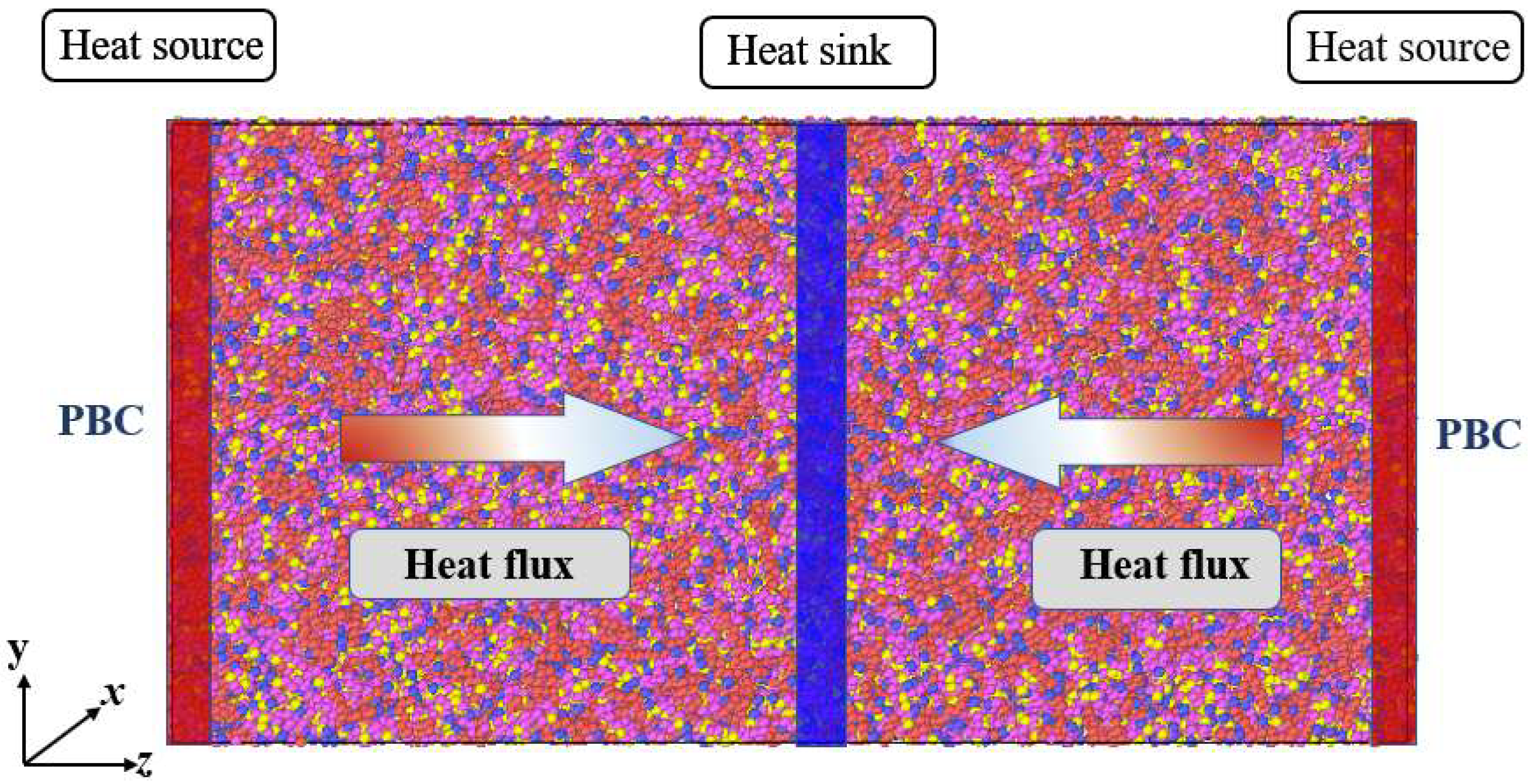
2.3. Simulation Details
3. Results and Discussions
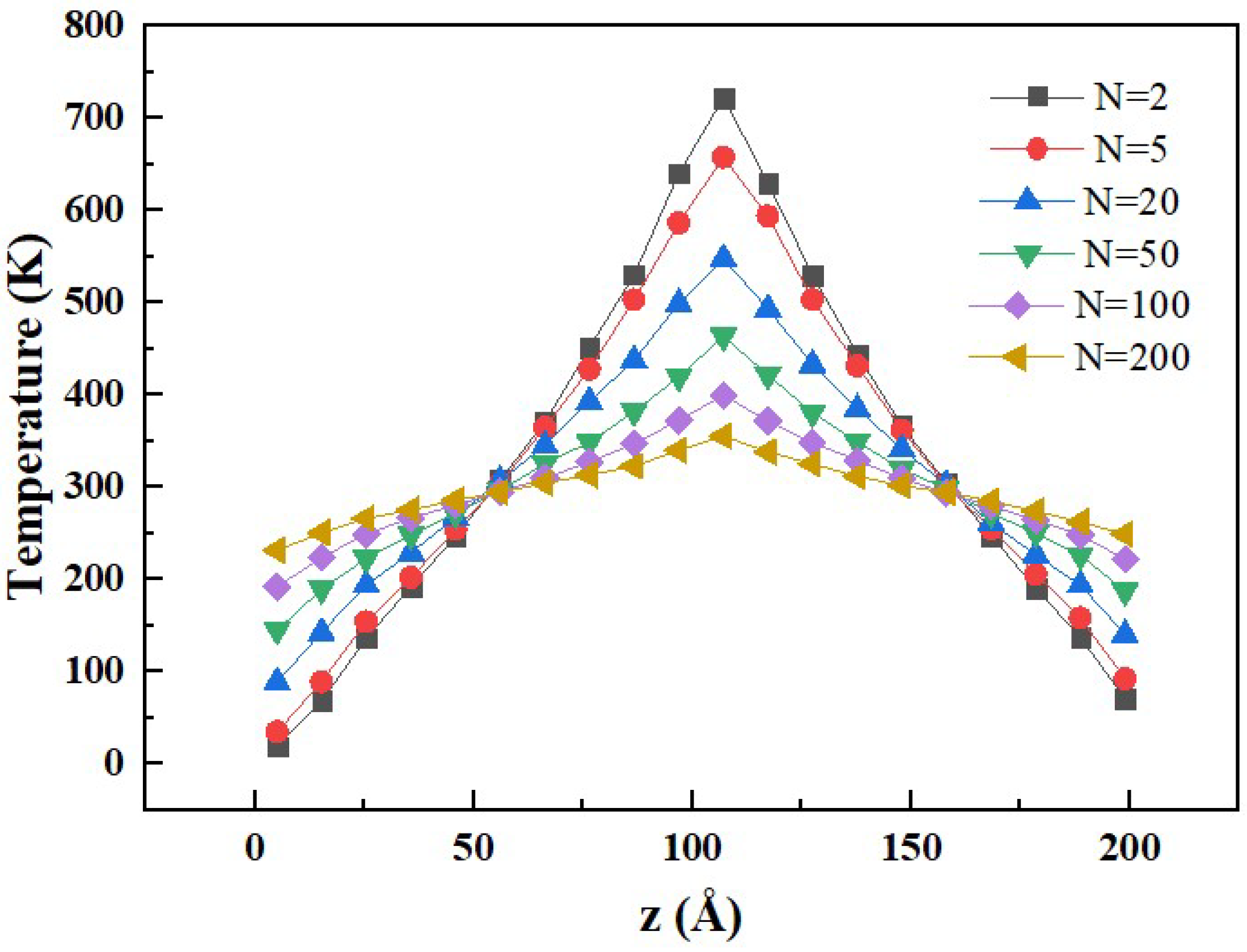
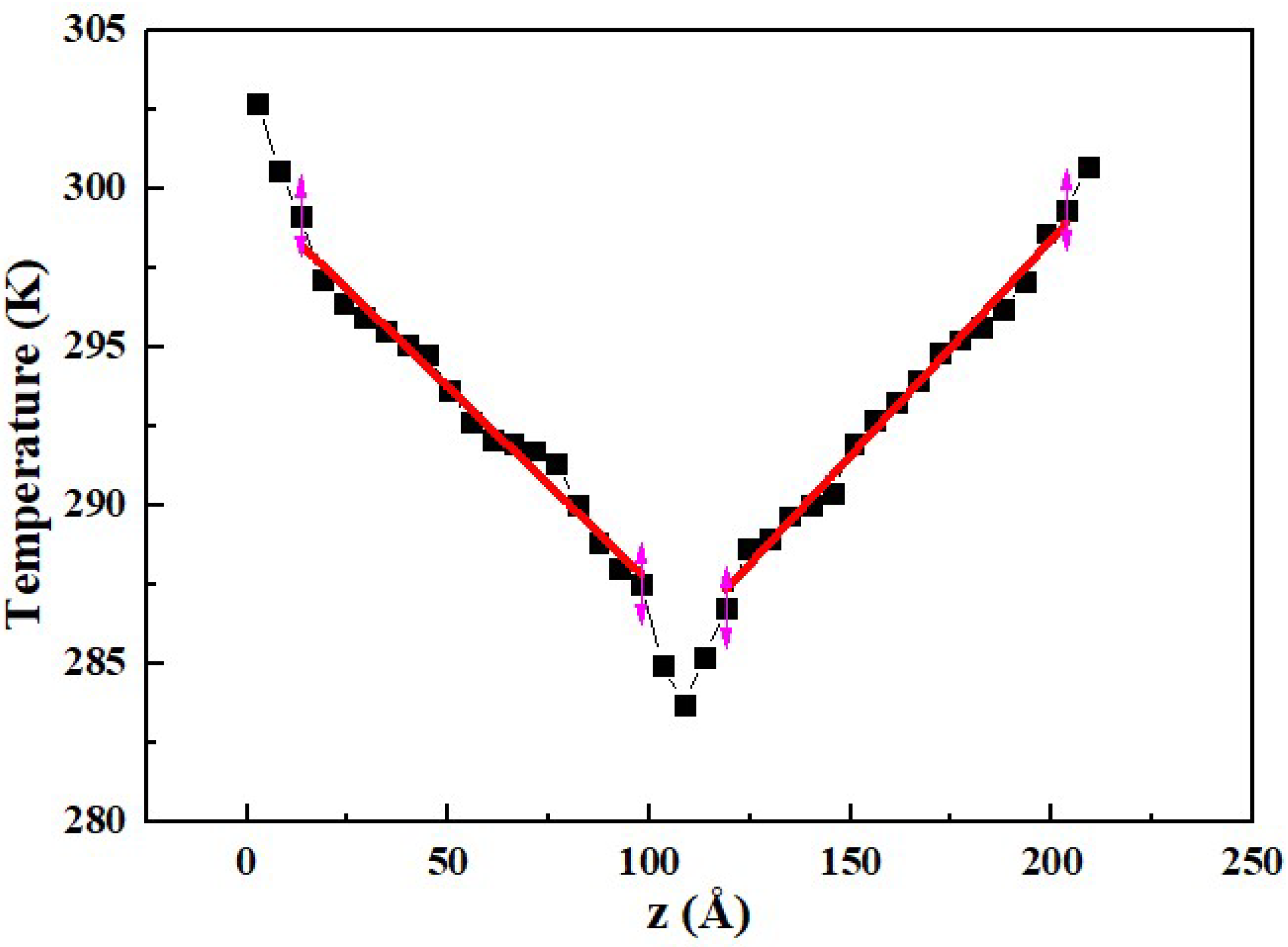
3.1. Comparison of Simulation Methods
3.2. Effect of the Mass Fraction of GNPs on Thermal Conductivity
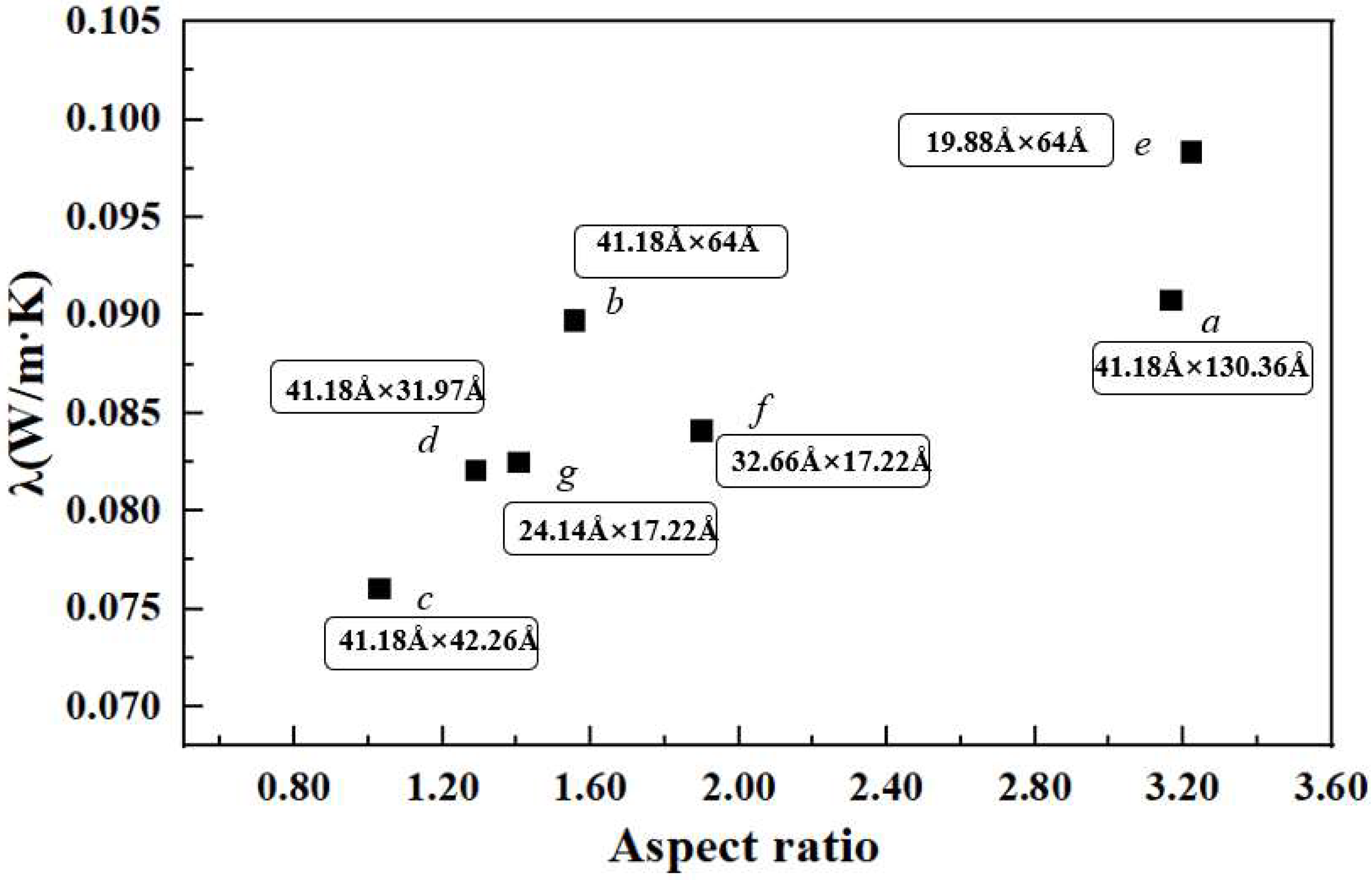
3.3. Effect of Graphene Size on Thermal Conductivity
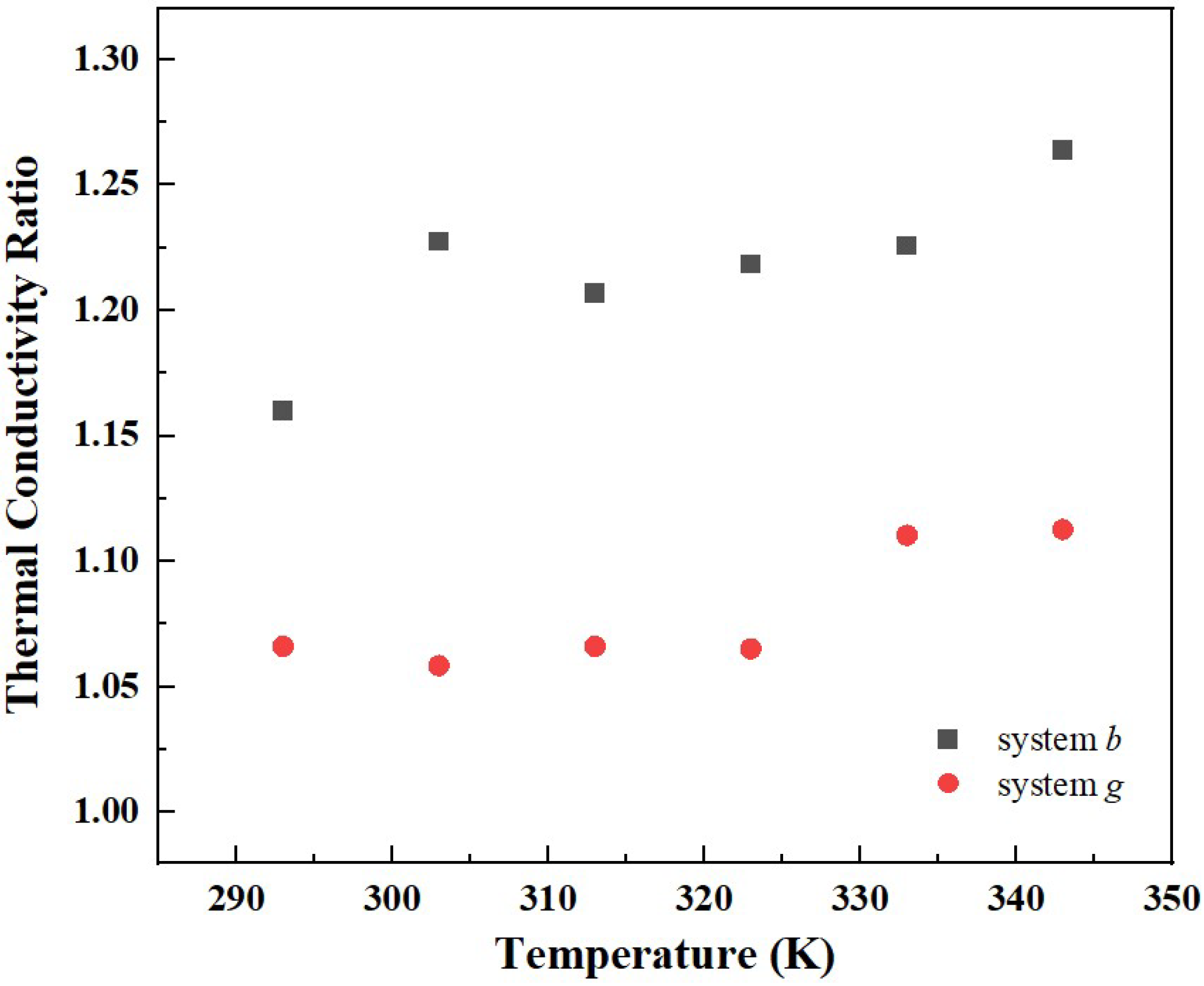
3.4. Effect of Temperature on Thermal Conductivity
4. Conclusions
- (1)
- The thermal conductivity of graphene-rocket kerosene composite systems is higher than that of the pure kerosene system, and it increases as the mass fraction of GNPs increases, which can be related to the enhancement of the percolation effect of heat transfer.
- (2)
- The thermal conductivity increases with the increase in the aspect ratio of GNPs, i.e., graphene with a higher aspect ratio is more conducive to the thermal transport, which indicates that the heat conduction mechanism of graphene in the nanofluid is controlled by both the percolation model and the Brownian motion of GNPs.
- (3)
- The effect of temperature on the thermal conductivity of graphene-rocket kerosene composite systems is found to be consistent with experimental results, i.e., the thermal conductivity decreases with the increase in temperature. Furthermore, the ratio of the thermal conductivity of composite systems to pure rocket kerosene systems increases as the temperature increases, which further proves that the Brownian motion of GNPs has non-negligible effects on the thermal conductivity of composite systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, S.-K.; Joh, M.; Choi, H.S.; Park, T.S. Multidisciplinary simulation of a regeneratively cooled thrust chamber of liquid rocket engine: Turbulent combustion and nozzle flow. Int. J. Heat Mass Transf. 2014, 70, 1066–1077. [Google Scholar] [CrossRef]
- Pizzarelli, M.; Nasuti, F.; Onofri, M. Analysis of Curved-Cooling-Channel Flow and Heat Transfer in Rocket Engines. J. Propuls. Power 2011, 27, 1045–1053. [Google Scholar] [CrossRef]
- Choudhuri, I.; Patra, N.; Mahata, A.; Ahuja, R.; Pathak, B. B–N@Graphene: Highly Sensitive and Selective Gas Sensor. J. Phys. Chem. C 2015, 119, 24827–24836. [Google Scholar] [CrossRef]
- Elsaid, K.; Abdelkareem, M.A.; Maghrabie, H.M.; Sayed, E.T.; Wilberforce, T.; Baroutaji, A.; Olabi, A.G. Thermophysical properties of graphene-based nanofluids. Int. J. Thermofluids 2021, 10, 100073. [Google Scholar] [CrossRef]
- Mbambo, M.C.; Khamlich, S.; Khamliche, T.; Moodley, M.K.; Kaviyarasu, K.; Madiba, I.G.; Madito, M.J.; Khenfouch, M.; Kennedy, J.; Henini, M.; et al. Remarkable thermal conductivity enhancement in Ag-decorated graphene nanocomposites based nanofluid by laser liquid solid interaction in ethylene glycol. Sci. Rep. 2020, 10, 10982. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.; Yu, W.; Pradeep, T. Nanofluids: Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Shi, J.-N.; Ger, M.-D.; Liu, Y.-M.; Fan, Y.-C.; Wen, N.-T.; Lin, C.-K.; Pu, N.-W. Improving the thermal conductivity and shape-stabilization of phase change materials using nanographite additives. Carbon 2013, 51, 365–372. [Google Scholar] [CrossRef]
- Yavari, F.; Fard, H.R.; Pashayi, K.; Rafiee, M.A.; Zamiri, A.; Yu, Z.; Ozisik, R.; Borca-Tasciuc, T.; Koratkar, N. Enhanced Thermal Conductivity in a Nanostructured Phase Change Composite due to Low Concentration Graphene Additives. J. Phys. Chem. C 2011, 115, 8753–8758. [Google Scholar] [CrossRef]
- Fang, X.; Fan, L.-W.; Ding, Q.; Wang, X.; Yao, X.-L.; Hou, J.-F.; Yu, Z.-T.; Cheng, G.-H.; Hu, Y.-C.; Cen, K.-F. Increased Thermal Conductivity of Eicosane-Based Composite Phase Change Materials in the Presence of Graphene Nanoplatelets. Energy Fuels 2013, 27, 4041–4047. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.; Choi, S.; Eastman, J. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Prasher, R.; Evans, W.; Meakin, P.; Fish, J.; Phelan, P.; Keblinski, P. Effect of aggregation on thermal conduction in colloidal nanofluids. Appl. Phys. Lett. 2006, 89, 143119. [Google Scholar] [CrossRef] [Green Version]
- Sastry, N.V.; Bhunia, A.; Sundararajan, T.; Das, S.K. Predicting the effective thermal conductivity of carbon nanotube based nanofluids. Nanotechnology 2008, 19, 055704. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.H.; Patel, H.E.; Kumar, V.R.; Sundararajan, T.; Pradeep, T.; Das, S.K. Model for heat conduction in nanofluids. Phys. Rev. Lett. 2004, 93, 144301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, H.E.; Anoop, K.; Sundararajan, T.; Das, S.K. A micro-convection model for thermal conductivity of nanofluids. In Proceedings of the International Heat Transfer Conference 13, Sydney, Australia, 13–18 August 2006; Begel House Inc.: Danbury, CT, USA, 2006. [Google Scholar]
- Liu, M.; Ding, C.; Wang, J. Modeling of thermal conductivity of nanofluids considering aggregation and interfacial thermal resistance. RSC Adv. 2016, 6, 3571–3577. [Google Scholar] [CrossRef]
- Prasher, R.; Phelan, P.E.; Bhattacharya, P. Effect of aggregation kinetics on the thermal conductivity of nanoscale colloidal solutions (nanofluid). Nano Lett. 2006, 6, 1529–1534. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.-Z. Model for effective thermal conductivity of nanofluids. Phys. Lett. A 2003, 307, 313–317. [Google Scholar] [CrossRef]
- Das, S.K.; Putra, N.; Thiesen, P.; Roetzel, W. Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat Transf. 2003, 125, 567–574. [Google Scholar] [CrossRef]
- Agarwal, D.K.; Vaidyanathan, A.; Kumar, S.S. Experimental investigation on thermal performance of kerosene–graphene nanofluid. Exp. Therm. Fluid Sci. 2016, 71, 126–137. [Google Scholar] [CrossRef]
- Yu, Z.-T.; Fang, X.; Fan, L.-W.; Wang, X.; Xiao, Y.-Q.; Zeng, Y.; Xu, X.; Hu, Y.-C.; Cen, K.-F. Increased thermal conductivity of liquid paraffin-based suspensions in the presence of carbon nano-additives of various sizes and shapes. Carbon 2013, 53, 277–285. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.; Zhang, L.; Fang, X.; Zhang, Z. Thermodynamic properties and thermal stability of ionic liquid-based nanofluids containing graphene as advanced heat transfer fluids for medium-to-high-temperature applications. Renew. Energy 2014, 63, 519–523. [Google Scholar] [CrossRef]
- Timofeeva, E.V.; Gavrilov, A.N.; McCloskey, J.M.; Tolmachev, Y.V.; Sprunt, S.; Lopatina, L.M.; Selinger, J.V. Thermal conductivity and particle agglomeration in alumina nanofluids: Experiment and theory. Phys. Rev. E 2007, 76, 061203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, W.; Xie, H.; Bao, D. Enhanced thermal conductivities of nanofluids containing graphene oxide nanosheets. Nanotechnology 2009, 21, 055705. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, D.K.; Vaidyanathan, A.; Kumar, S.S. Synthesis and characterization of kerosene–alumina nanofluids. Appl. Therm. Eng. 2013, 60, 275–284. [Google Scholar] [CrossRef]
- Ni, Z.; Bu, H.; Zou, M.; Yi, H.; Bi, K.; Chen, Y. Anisotropic mechanical properties of graphene sheets from molecular dynamics. Phys. B Condens. Matter 2010, 405, 1301–1306. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q.; Wang, S. A review on enhancement of mechanical and tribological properties of polymer composites reinforced by carbon nanotubes and graphene sheet: Molecular dynamics simulations. Compos. Part B Eng. 2019, 160, 348–361. [Google Scholar] [CrossRef]
- Mahdavi, M.; Rahmani, F.; Nouranian, S. Molecular simulation of pH-dependent diffusion, loading, and release of doxorubicin in graphene and graphene oxide drug delivery systems. J. Mater. Chem. B 2016, 4, 7441–7451. [Google Scholar] [CrossRef]
- Khoshoei, A.; Ghasemy, E.; Poustchi, F.; Shahbazi, M.A.; Maleki, R. Engineering the pH-Sensitivity of the Graphene and Carbon Nanotube Based Nanomedicines in Smart Cancer Therapy by Grafting Trimetyl Chitosan. Pharm. Res. 2020, 37, 160. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, F.; Hong, Y.; Xiong, Q.; Pan, J. A comprehensive review on the molecular dynamics simulation of the novel thermal properties of graphene. RSC Adv. 2015, 5, 89415–89426. [Google Scholar] [CrossRef]
- Jahromi, A.M.; Khedri, M.; Ghasemi, M.; Omrani, S.; Maleki, R.; Rezaei, N. Molecular insight into COF monolayers for urea sorption in artificial kidneys. Sci. Rep. 2021, 11, 12085. [Google Scholar] [CrossRef]
- Nicolai, A.; Zhu, P.; Sumpter, B.G.; Meunier, V. Molecular Dynamics Simulations of Graphene Oxide Frameworks. J. Chem. Theory Comput. 2013, 9, 4890–4900. [Google Scholar] [CrossRef]
- Babaei, H.; Keblinski, P.; Khodadadi, J.M. Thermal conductivity enhancement of paraffins by increasing the alignment of molecules through adding CNT/graphene. Int. J. Heat Mass Transf. 2013, 58, 209–216. [Google Scholar] [CrossRef]
- Huang, Y.-R.; Chuang, P.-H.; Chen, C.-L. Molecular-dynamics calculation of the thermal conduction in phase change materials of graphene paraffin nanocomposites. Int. J. Heat Mass Transf. 2015, 91, 45–51. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, C.; Luo, A.; Liu, Z.; Zhang, X. Molecular dynamics simulation on thermophysics of paraffin/EVA/graphene nanocomposites as phase change materials. Appl. Therm. Eng. 2020, 166, 114639. [Google Scholar] [CrossRef]
- Farmer, R.; Anderson, P.; Cheng, G.C. Propellant chemistry for CFD applications. In Proceedings of the Thirteenth Workshop for Computational Fluid Dynamic Applications in Rocket Propulsion and Launch Vehicle Technology, Huntsville, AL, USA, 25–27 April 1995; NASA: Huntsville, AL, USA, 1996. [Google Scholar]
- Huber, M.L.; Lemmon, E.W.; Bruno, T.J. Effect of RP-1 compositional variability on thermophysical properties. Energy Fuels 2009, 23, 5550–5555. [Google Scholar] [CrossRef]
- Kehimkar, B.; Hoggard, J.C.; Marney, L.C.; Billingsley, M.C.; Fraga, C.G.; Bruno, T.J.; Synovec, R.E. Correlation of rocket propulsion fuel properties with chemical composition using comprehensive two-dimensional gas chromatography with time-of-flight mass spectrometry followed by partial least squares regression analysis. J. Chromatogr. A 2014, 1327, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Errington, J.R.; Panagiotopoulos, A.Z. A new intermolecular potential model for the n-alkane homologous series. J. Phys. Chem. B 1999, 103, 6314–6322. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Jewett, A.I.; Stelter, D.; Lambert, J.; Saladi, S.M.; Roscioni, O.M.; Ricci, M.; Autin, L.; Maritan, M.; Bashusqeh, S.M.; Keyes, T.; et al. Moltemplate: A Tool for Coarse-Grained Modeling of Complex Biological Matter and Soft Condensed Matter Physics. J. Mol. Biol. 2021, 433, 166841. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Muller, E.A.; Mejia, A. Comparison of united-atom potentials for the simulation of vapor-liquid equilibria and interfacial properties of long-chain n-alkanes up to n-C100. J. Phys. Chem. B 2011, 115, 12822–12834. [Google Scholar] [CrossRef]
- Papavasileiou, K.D.; Peristeras, L.D.; Bick, A.; Economou, I.G. Molecular Dynamics Simulation of Pure n-Alkanes and Their Mixtures at Elevated Temperatures Using Atomistic and Coarse-Grained Force Fields. J. Phys. Chem. B 2019, 123, 6229–6243. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Keasler, S.J.; Charan, S.M.; Wick, C.D.; Economou, I.G.; Siepmann, J.I. Transferable potentials for phase equilibria–united atom description of five- and six-membered cyclic alkanes and ethers. J. Phys. Chem. B 2012, 116, 11234–11246. [Google Scholar] [CrossRef] [PubMed]
- Yiannourakou, M.; Ungerer, P.; Lachet, V.; Rousseau, B.; Teuler, J.-M. United atom forcefield for vapor-liquid equilibrium (VLE) properties of cyclic and polycyclic compounds from Monte Carlo simulations. Fluid Phase Equilibria 2019, 481, 28–43. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Cheng, Y.; Pei, Q.; Wang, C.; Xiang, Y. Thermal conductivity of defective graphene. Phys. Lett. A 2012, 376, 3668–3672. [Google Scholar] [CrossRef]
- Pei, Q.-X.; Sha, Z.-D.; Zhang, Y.-W. A theoretical analysis of the thermal conductivity of hydrogenated graphene. Carbon 2011, 49, 4752–4759. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Luo, T.; Lloyd, J.R. Enhancement of thermal energy transport across graphene/graphite and polymer interfaces: A molecular dynamics study. Adv. Funct. Mater. 2012, 22, 2495–2502. [Google Scholar] [CrossRef]
- Kioupis, L.I.; Maginn, E.J. Rheology, dynamics, and structure of hydrocarbon blends: A molecular dynamics study of n-hexane/n-hexadecane mixtures. Chem. Eng. J. 1999, 74, 129–146. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Novel configurational-bias Monte Carlo method for branched molecules. Transferable potentials for phase equilibria. 2. United-atom description of branched alkanes. J. Phys. Chem. B 1999, 103, 4508–4517. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Mori, H. Statistical-mechanical theory of transport in fluids. Phys. Rev. 1958, 112, 1829. [Google Scholar] [CrossRef]
- Heyes, D.M. Molecular dynamics simulations of liquid binary mixtures: Partial properties of mixing and transport coefficients. J. Chem. Phys. 1992, 96, 2217–2227. [Google Scholar] [CrossRef]
- Perronace, A.; Ciccotti, G.; Leroy, F.; Fuchs, A.; Rousseau, B. Soret coefficient for liquid argon-krypton mixtures via equilibrium and nonequilibrium molecular dynamics: A comparison with experiments. Phys. Rev. E 2002, 66, 031201. [Google Scholar] [CrossRef]
- Sindzingre, P.; Ciccotti, G.; Massobrio, C.; Frenkel, D. Partial enthalpies and related quantities in mixtures from computer simulation. Chem. Phys. Lett. 1987, 136, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Vogelsang, R.; Hoheisel, C.; Paolini, G.; Ciccotti, G. Soret coefficient of isotopic Lennard-Jones mixtures and the Ar-Kr system as determined by equilibrium molecular-dynamics calculations. Phys. Rev. A 1987, 36, 3964. [Google Scholar] [CrossRef]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Jund, P.; Jullien, R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica. Phys. Rev. B 1999, 59, 13707. [Google Scholar] [CrossRef] [Green Version]
- Wirnsberger, P.; Frenkel, D.; Dellago, C. An enhanced version of the heat exchange algorithm with excellent energy conservation properties. J. Chem. Phys. 2015, 143, 124104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dhar, P.; Sen Gupta, S.; Chakraborty, S.; Pattamatta, A.; Das, S.K. The role of percolation and sheet dynamics during heat conduction in poly-dispersed graphene nanofluids. Appl. Phys. Lett. 2013, 102, 163114. [Google Scholar] [CrossRef] [Green Version]
- Sen Gupta, S.; Manoj Siva, V.; Krishnan, S.; Sreeprasad, T.; Singh, P.K.; Pradeep, T.; Das, S.K. Thermal conductivity enhancement of nanofluids containing graphene nanosheets. J. Appl. Phys. 2011, 110, 084302. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.M.; Kumar, J.; Tamilarasan, R.; Sendhilnathan, S.; Suresh, S. Review on nanofluids theoretical thermal conductivity models. Eng. J. 2015, 19, 67–83. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, D.; Gong, X.-G. Thermal conductivity of graphene nanoribbons. Appl. Phys. Lett. 2009, 95, 163103. [Google Scholar] [CrossRef] [Green Version]
- Nika, D.L.; Askerov, A.S.; Balandin, A.A. Anomalous size dependence of the thermal conductivity of graphene ribbons. Nano Lett. 2012, 12, 3238–3244. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, S.; Kumar, H. Molecular dynamics simulations of two-dimensional materials. In Synthesis, Modeling, and Characterization of 2D Materials, and Their Heterostructures; Elsevier: Amsterdam, The Netherlands, 2020; pp. 125–148. [Google Scholar]
- Dočkal, J.; Moučka, F.; Lísal, M. Molecular Dynamics of Graphene–Electrolyte Interface: Interfacial Solution Structure and Molecular Diffusion. J. Phys. Chem. C 2019, 123, 26379–26396. [Google Scholar] [CrossRef]
- Maleki, R.; Khedri, M.; Malekahmadi, D.; Mohaghegh, S.; Jahromi, A.M.; Shahbazi, M.-A. Simultaneous doxorubicin encapsulation and in-situ microfluidic micellization of bio-targeted polymeric nanohybrids using dichalcogenide monolayers: A molecular in-silico study. Mater. Today Commun. 2021, 26, 101948. [Google Scholar] [CrossRef]
- Maleki, R.; Miri Jahromi, A.; Mohaghegh, S.; Rezvantalab, S.; Khedri, M.; Tayebi, L. A molecular investigation of urea and creatinine removal in the wearable dialysis device using Two-Dimensional materials. Appl. Surf. Sci. 2021, 566, 150629. [Google Scholar] [CrossRef]
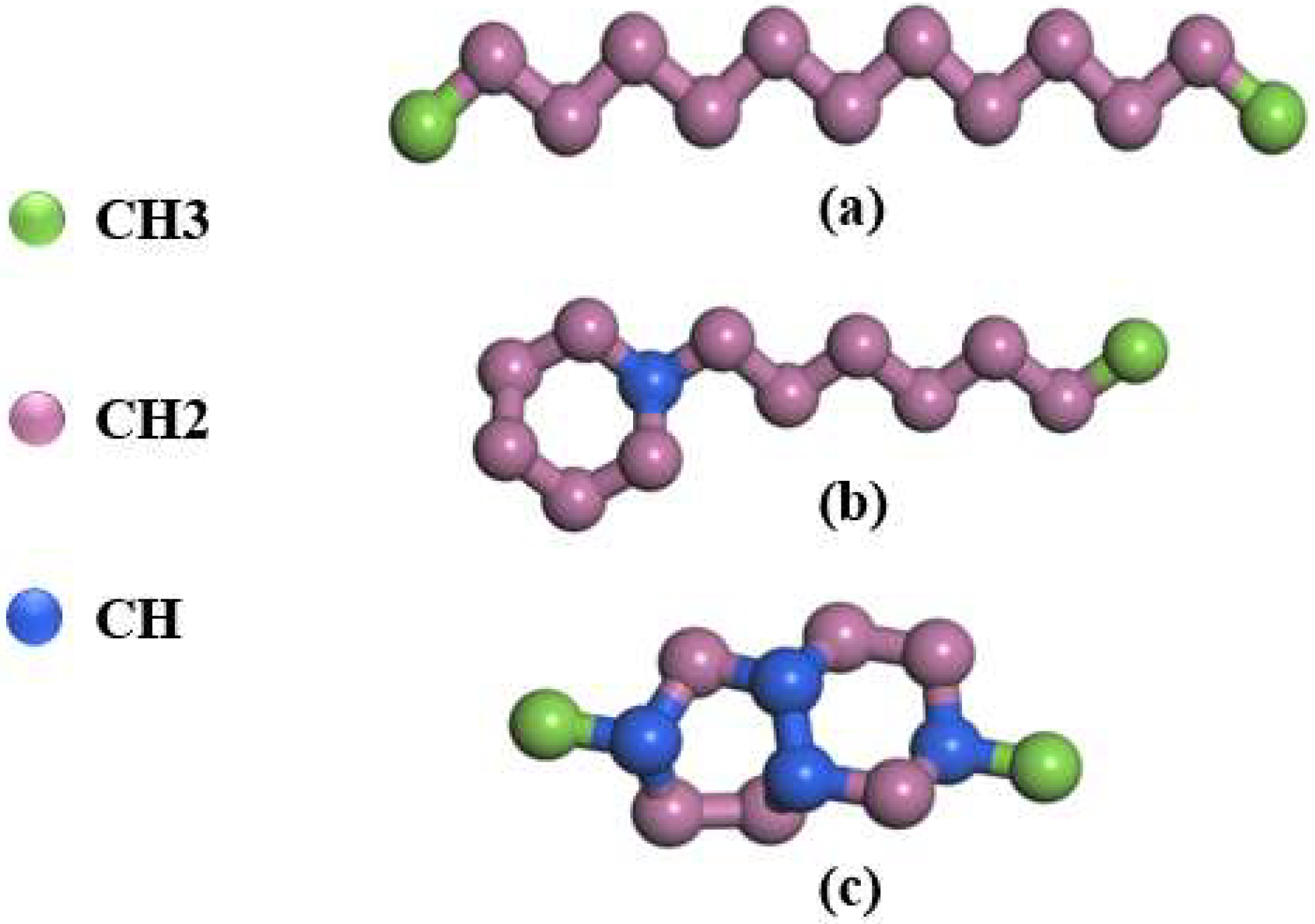
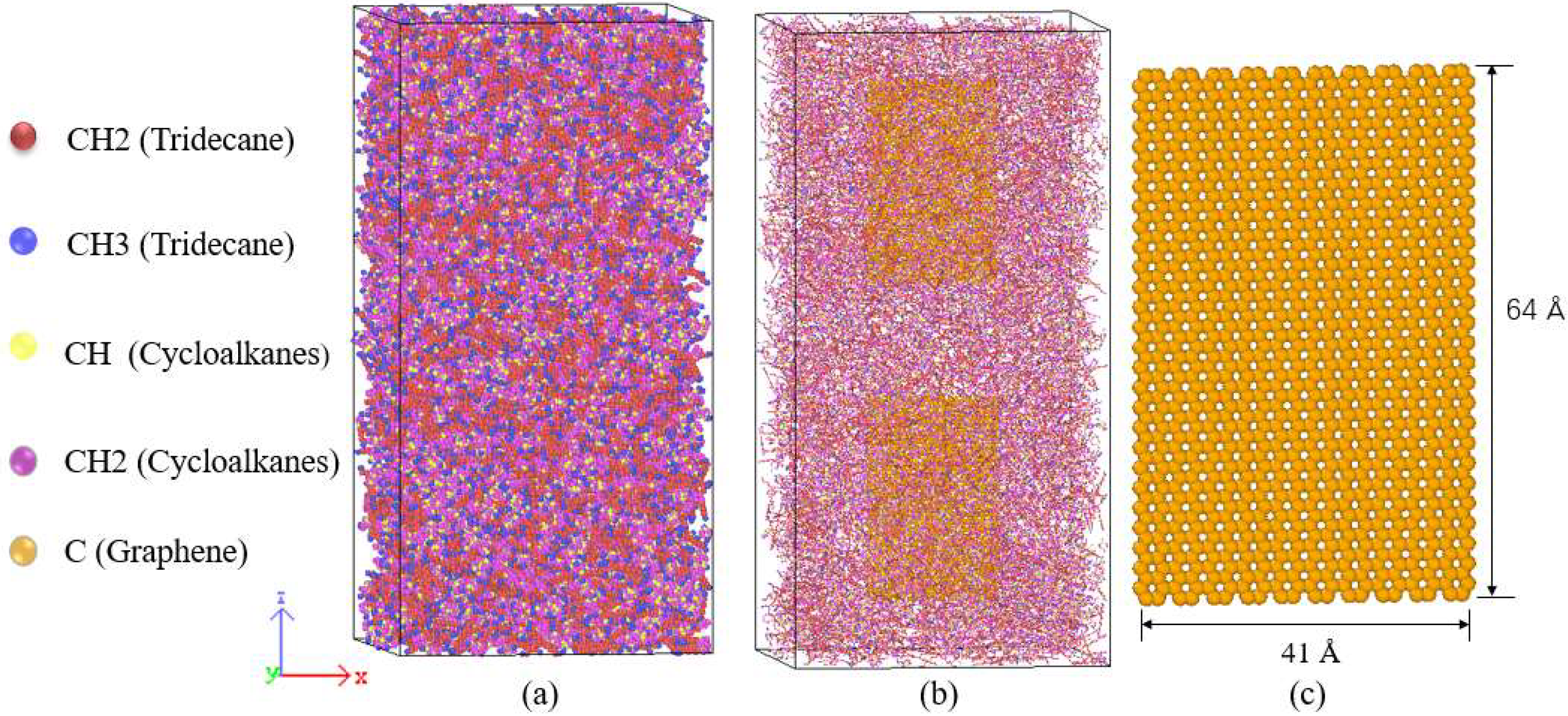



| Species | Components of Rocket Kerosene | Molecular Formula | Molecular Number | Atomic Number |
|---|---|---|---|---|
| n-alkanes | n-tridecane | C13H28 | 1210 | 15,730 |
| monocycloalkanes | n-heptylcyclohexane | C13H26 | 2244 | 29,172 |
| dicycloalkanes | Decahydro-2,6-dimethylnaphthalene | C12H22 | 2827 | 33,924 |
| sum | —— | 6281 | 78,826 |
| United Atom Type | Molecule | σii (Å) | εii/kB (K) |
|---|---|---|---|
| CH3 [46] | Alkanes/Branched Alkanes | 3.75 | 98 |
| CH2 [46] | Alkanes/Branched Alkanes | 3.95 | 46 |
| CH2(cyc) [47] | Cycloalkanes | 3.91 | 52.5 |
| CH(cyc) [48] | Cycloalkanes | 4.68 | 12 |
| Method | ∆T (K) | Model | λ (W/m·K) | Enhancement |
|---|---|---|---|---|
| MP | 125 | Rocket kerosene | 0.0767 | —— |
| Graphene-rocket kerosene | 0.0851 | 10.889% | ||
| NEMD | 20 | Rocket kerosene | 0.0770 | —— |
| Graphene-rocket kerosene | 0.0869 | 12.925% |
| Substance | Number | Size | Number of Atoms | Mass Fraction | λ (W/m·K) | Enhancement |
|---|---|---|---|---|---|---|
| Rocket kerosene | —— | —— | 78,826 | —— | 0.0774 | —— |
| Graphene sheets | 1 | 41.18 Å × 64 Å | 1060 | 1.14% | 0.0807 | 4.26% |
| 2 | 41.18 Å × 64 Å | 2120 | 2.27% | 0.0833 | 7.62% | |
| 4 | 41.18 Å × 64 Å | 4240 | 4.42% | 0.0892 | 15.25% | |
| 6 | 41.18 Å × 64 Å | 6360 | 6.49% | 0.0912 | 17.83% |
| System | Number of GNPs | Size (x × z) | Aspect Ratio (x/z) | λ (W/m·K) | Enhancement |
|---|---|---|---|---|---|
| Rocket kerosene | —— | —— | —— | 0.075 | —— |
| a | 2 | 41.18 Å × 130.36 Å | 3.166 | 0.091 | 20.29% |
| b | 4 | 41.18 Å × 64.00 Å | 1.554 | 0.090 | 18.93% |
| c | 6 | 41.18 Å × 42.26 Å | 1.026 | 0.076 | 0.78% |
| d | 8 | 41.18 Å × 31.97 Å | 1.288 | 0.082 | 8.76% |
| e | 8 | 19.88 Å × 64.00 Å | 3.219 | 0.098 | 30.32% |
| f | 18 | 32.66 Å × 17.22 Å | 1.897 | 0.084 | 11.47% |
| g | 24 | 24.14 Å × 17.22 Å | 1.402 | 0.083 | 9.32% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Chen, X.; Zhao, J.; Zhou, W.; Wei, J. Effect of the Addition of Graphene Nanoplatelets on the Thermal Conductivity of Rocket Kerosene: A Molecular Dynamics Study. Materials 2022, 15, 5511. https://doi.org/10.3390/ma15165511
Guo X, Chen X, Zhao J, Zhou W, Wei J. Effect of the Addition of Graphene Nanoplatelets on the Thermal Conductivity of Rocket Kerosene: A Molecular Dynamics Study. Materials. 2022; 15(16):5511. https://doi.org/10.3390/ma15165511
Chicago/Turabian StyleGuo, Xiaodie, Xuejiao Chen, Jinpeng Zhao, Wenjing Zhou, and Jinjia Wei. 2022. "Effect of the Addition of Graphene Nanoplatelets on the Thermal Conductivity of Rocket Kerosene: A Molecular Dynamics Study" Materials 15, no. 16: 5511. https://doi.org/10.3390/ma15165511
APA StyleGuo, X., Chen, X., Zhao, J., Zhou, W., & Wei, J. (2022). Effect of the Addition of Graphene Nanoplatelets on the Thermal Conductivity of Rocket Kerosene: A Molecular Dynamics Study. Materials, 15(16), 5511. https://doi.org/10.3390/ma15165511





