Experimental Characterization and Multi-Factor Modelling to Achieve Desired Flow, Set and Strength of N-A-S-H Geopolymers
Abstract
:1. Introduction
2. Experimental Program
2.1. Materials and Mix Proportions
2.2. Sample Preparation
2.3. Test Protocols
3. Experimental Results and Analyses
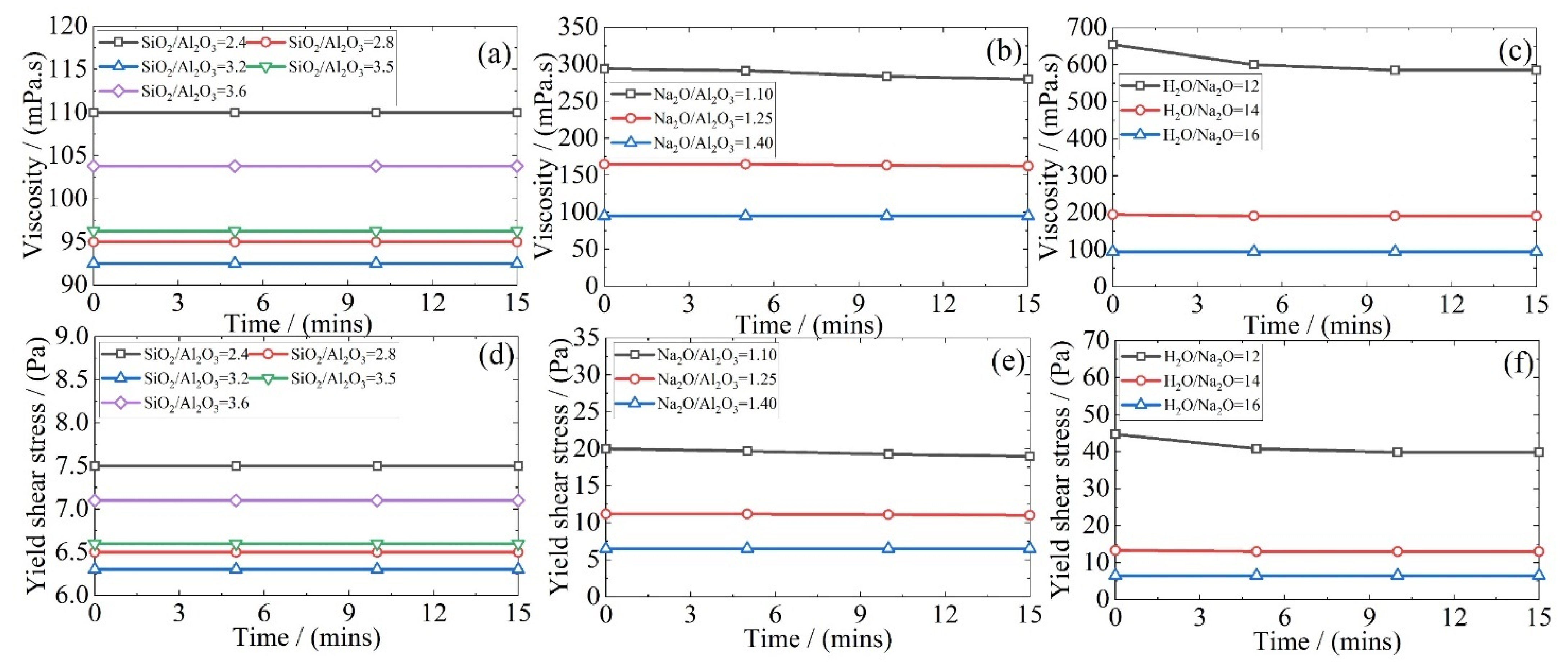
3.1. Rheology of Fresh Geopolymer Mixtures
3.2. Temperature Evolution during Setting Process
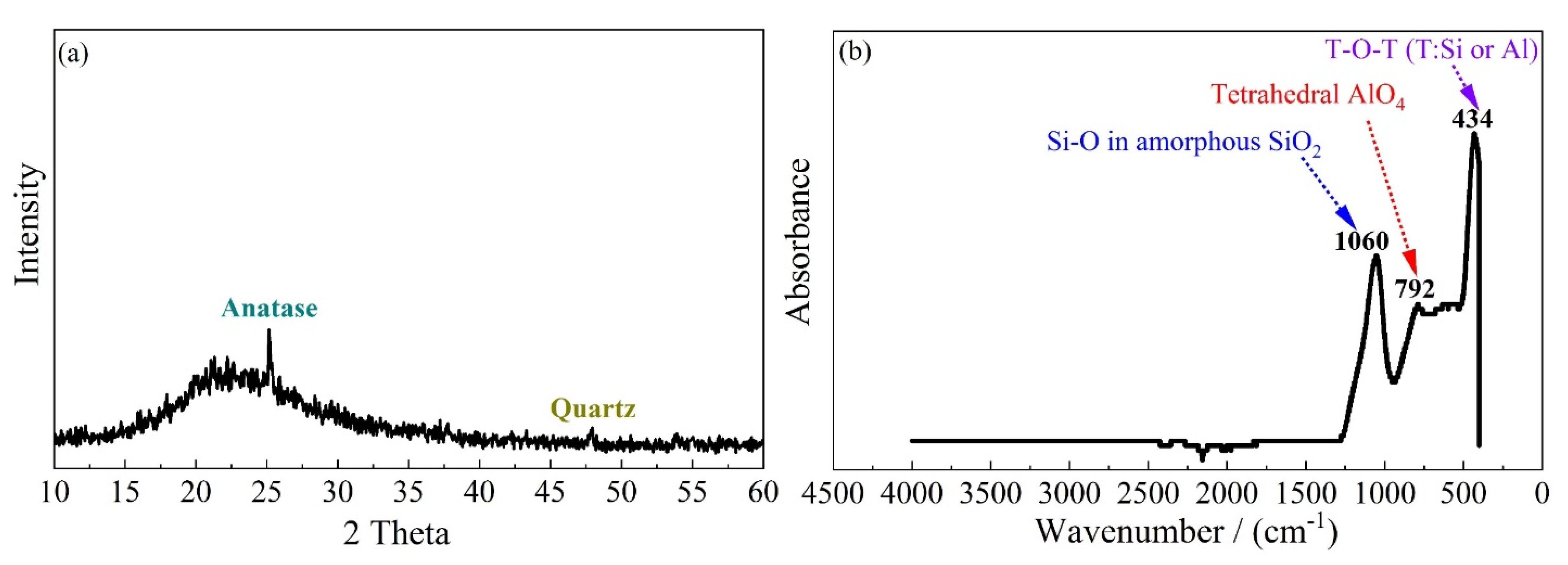
3.3. X-ray Diffraction (XRD) and Thermogravimetric Analysis (TGA)
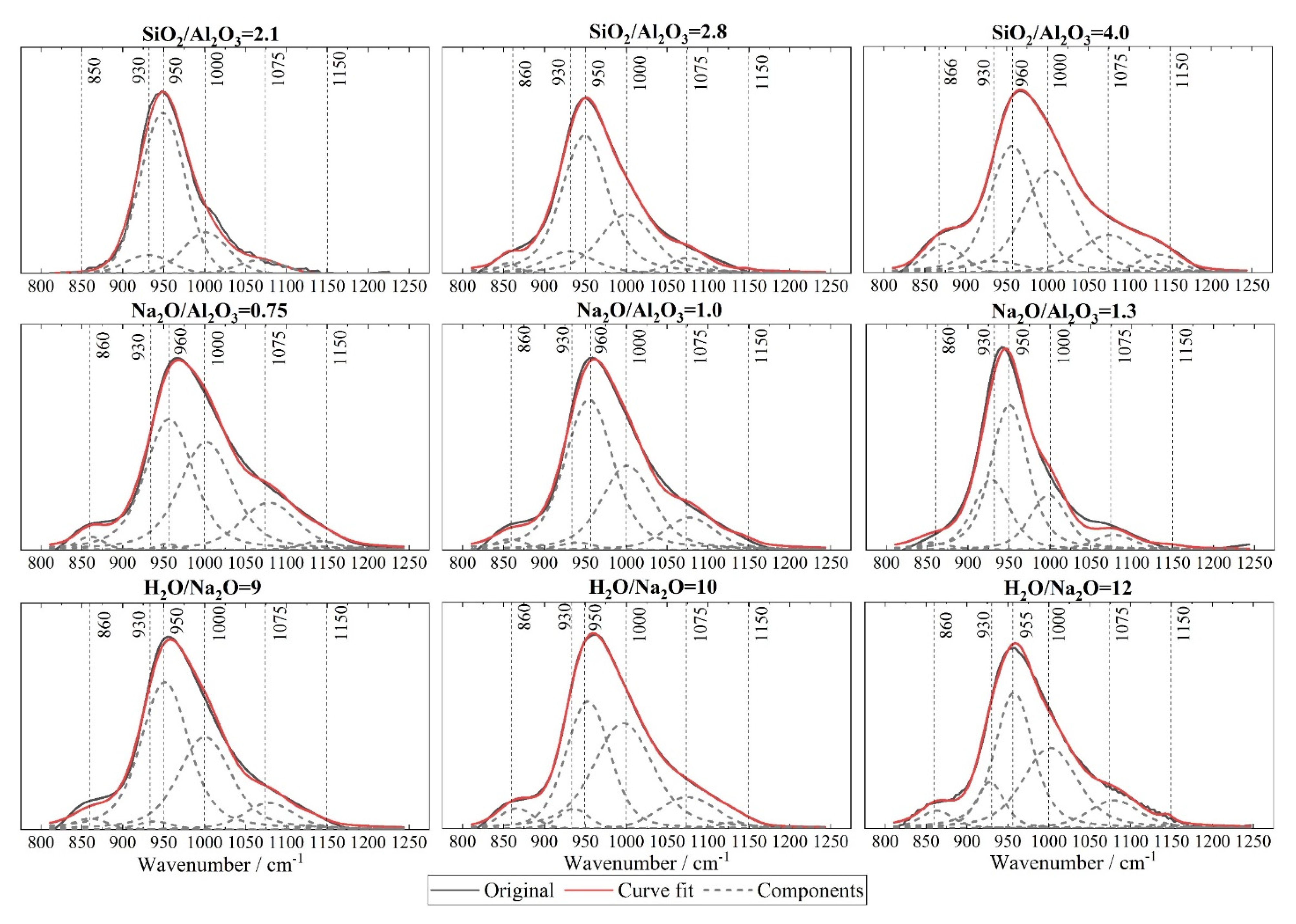
3.4. Fourier Transform Infrared Spectroscopy (FTIR)
3.5. Scanning Electron Micrographs
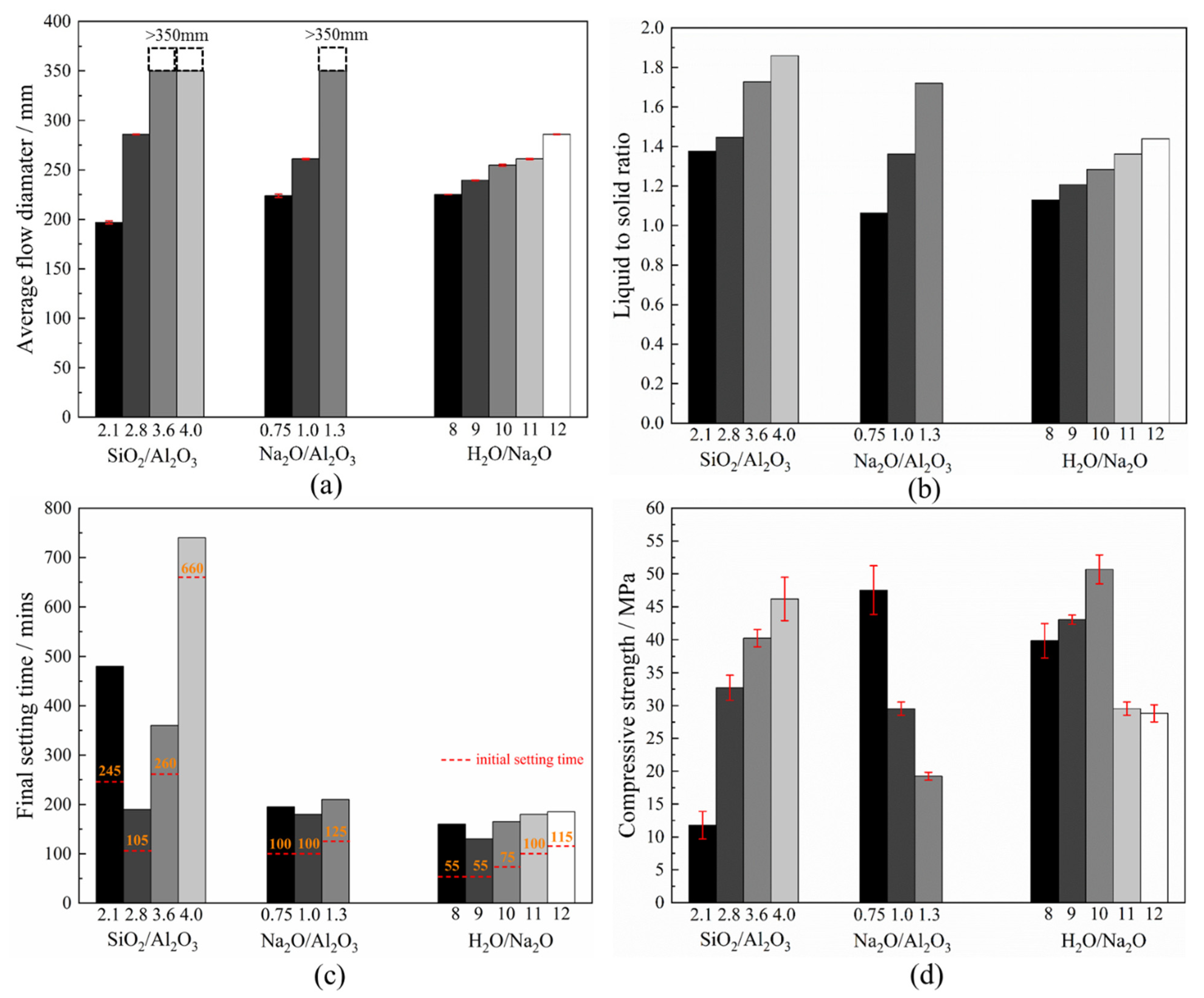
3.6. Workability, Final Setting Time and Compressive Strength
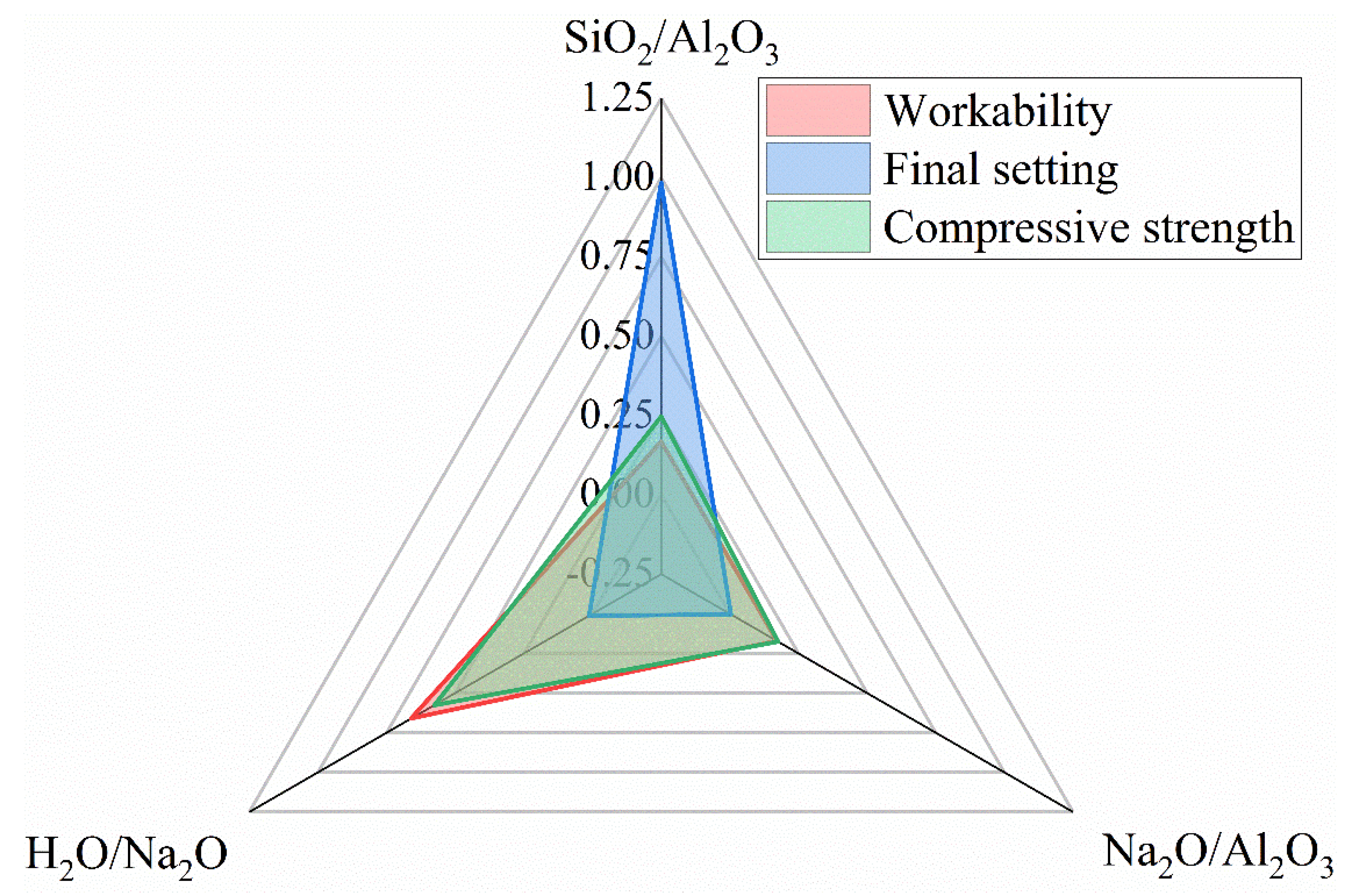
3.7. Sensitivity Analysis
4. Establishment of Multi-Factor Models
4.1. Find the Relationship between Variables and Predicted Outcomes
4.2. Determine Regression Coefficients for Multi-Factor Models
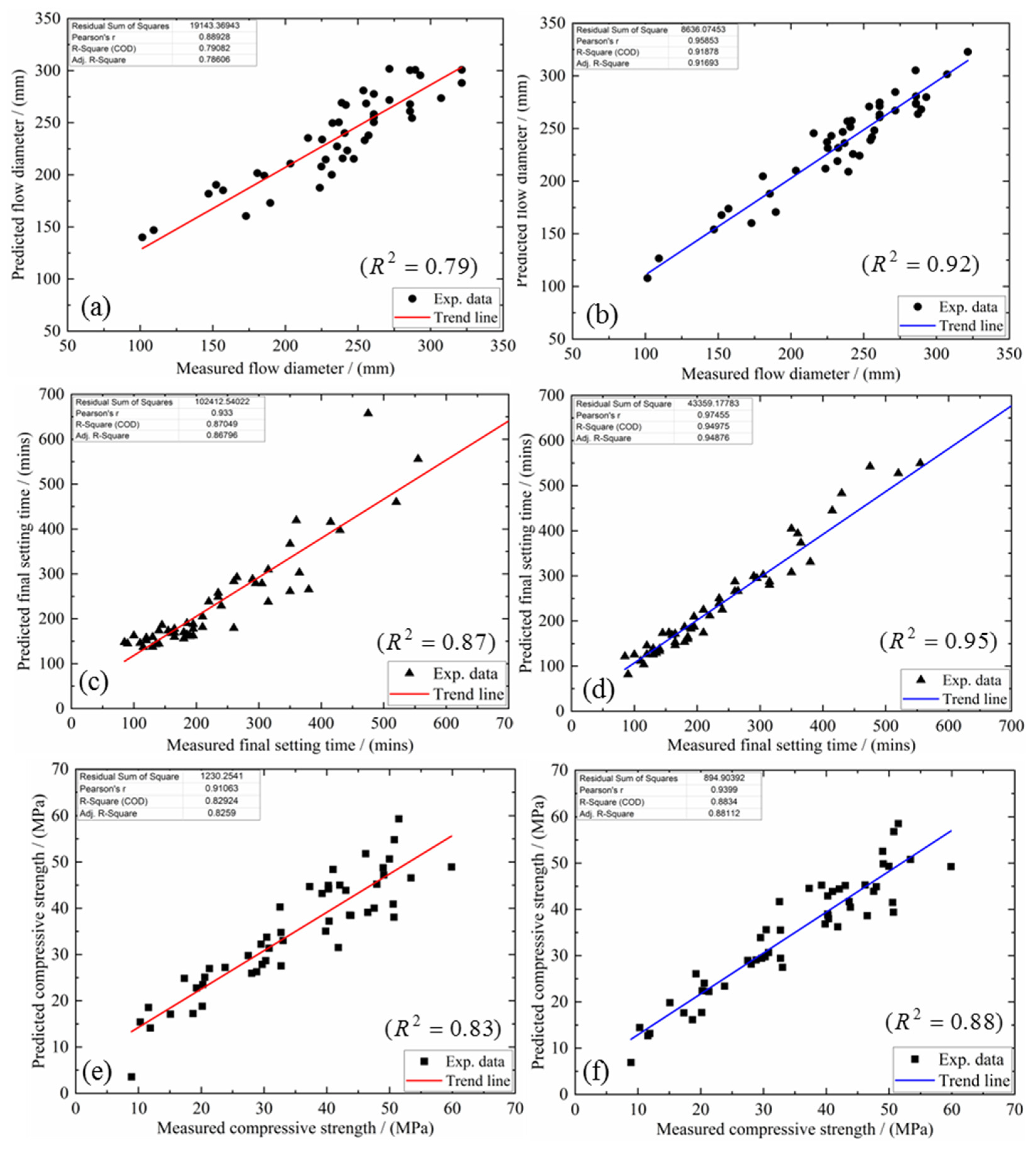
4.3. Model Justification
5. Further Discussion
6. Conclusions
- (1).
- An increase in the Na2O/Al2O3 or H2O/Na2O ratio reduces the viscosity of the fresh geopolymer mixture due to a corresponding increase in the liquid-to-solid ratio. There was an accompanying drop in the yield shear stress. Together, this leads to a greater flowability. However, there exists an optimum SiO2/Al2O3 ratio to obtain the lowest viscosity. Whereas, at lower values, the system is dominated by sodium silicate, once this ratio exceeds 3.2, the liquid-to-solid ratio dominates and eventually raises the flowability of the system;
- (2).
- In N-A-S-H geopolymers, the setting time is associated with the exothermicity during the geopolymerization, which was found most sensitive to the SiO2/Al2O3 ratio. The mixture made with a SiO2/Al2O3 ratio of about 2.8 registered the highest peak temperature and the fastest temperature rise, both of which coincide with its fastest setting time;
- (3).
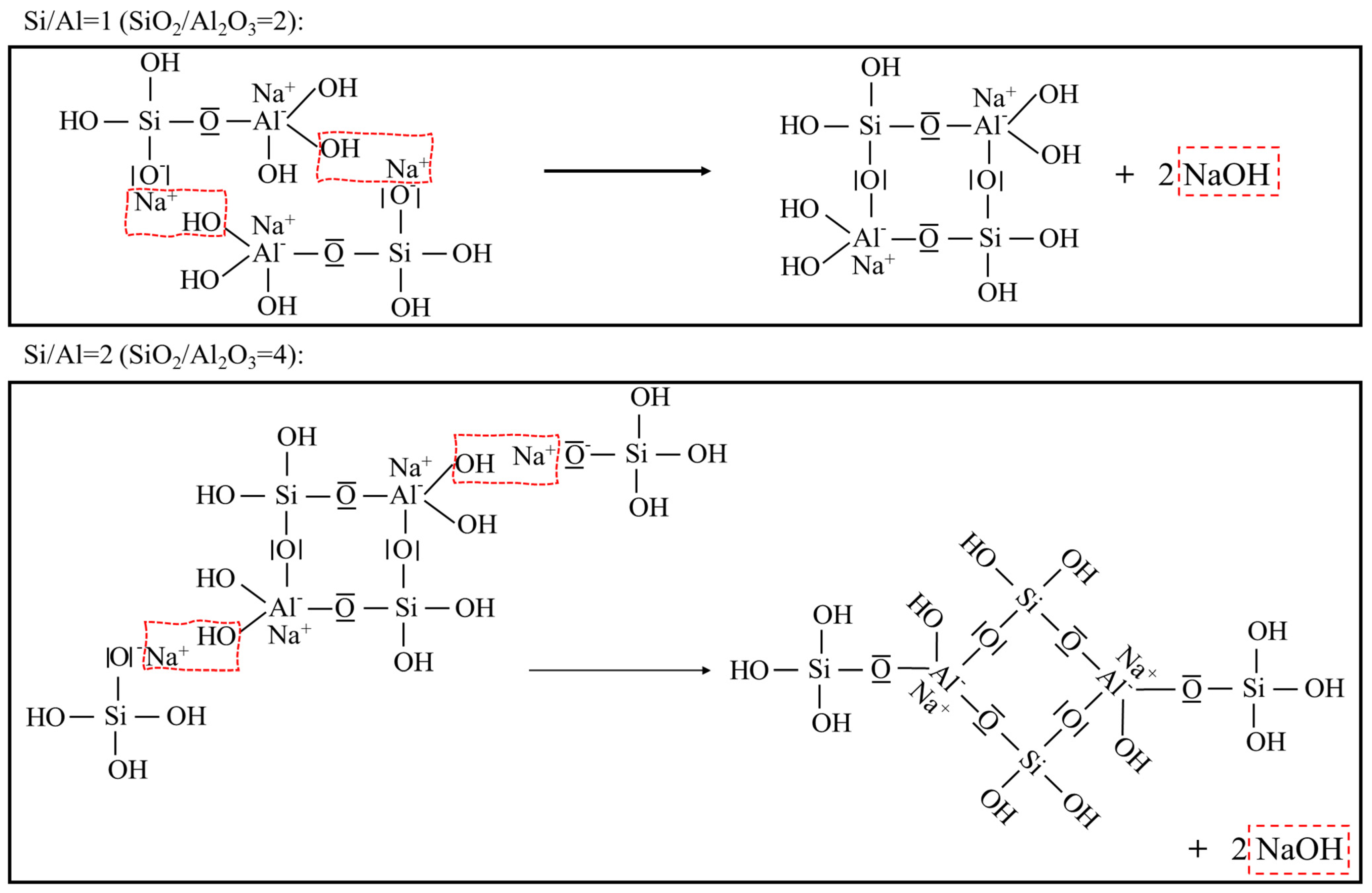
- A deficient SiO2/Al2O3 ratio and an excessive Na2O/Al2O3 ratio will, in either case, deter geopolymerization. Additionally, they promote significant zeolite formation. This was evident from the reduced amorphicity in XRD, a wider but much lower DTG peak assigned to depolymerization of N-A-S-H in TGA, and also a smaller peak area ascribed to the Si-O-T band in the N-A-S-H framework in FTIR. The H2O/Na2O ratio at its optimum value, found to be 9~10 here, led to the highest amorphicity and degree of polycondensation;
- (4).
- The proposed multi-factor models capture the effect of each oxide component in the mixture design upon the possible flow, final setting time and compressive strength. When the mutual interactions between the different oxide ratios are considered, the coefficient of determination for flow improved from 0.79 to 0.92, for setting time, from 0.87 to 0.95 and from 0.83 to 0.88 for the compressive strength. More importantly, these proposed models may serve as a predictive tool to conduct and validate mixture design for N-A-S-H geopolymers with varying priorities upon workability, final set and compressive strength;
- (5).
- A satisfactory combination of compositional ratios to simultaneously achieve the desired workability, final set and compressive strength may fall within SiO2/Al2O3 = 2.8~3.6, Na2O/Al2O3 = 0.75~1.0 and H2O/Na2O = 9~10. The workability of the fresh N-A-S-H mixture is most sensitive to the H2O/Na2O ratio, while the setting time is predominantly governed by the SiO2/Al2O3 ratio. The compressive strength is sensitive to the H2O/Na2O ratio and, to a lesser extent, the SiO2/Al2O3 ratio as well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gartner, E. Industrially interesting approaches to “low-CO2” cements. Cem. Concr. Res. 2004, 34, 1489–1498. [Google Scholar] [CrossRef]
- Damtoft, J.S.; Lukasik, J.; Herfort, D.; Sorrentino, D.; Gartner, E.M. Sustainable development and climate change initiatives. Cem. Concr. Res. 2008, 38, 115–127. [Google Scholar] [CrossRef]
- Ali, M.B.; Saidur, R.; Hossain, M.S. A review on emission analysis in cement industries. Renew. Sustain. Energy Rev. 2011, 15, 2252–2261. [Google Scholar] [CrossRef]
- US Geological Survey. Mineral Commodity Summaries; US Geological Survey: Reston, VA, USA, 2020. [Google Scholar]
- Hrabova, K.; Teply, B.; Vymazal, T. Sustainability assessment of concrete mixes. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Ostrava, Czech Republic, 2020; Volume 444, p. 012021. [Google Scholar]
- Horňáková, M.; Lehner, P. Analysis of measured parameters in relation to the amount of fibre in lightweight red ceramic waste aggregate concrete. Mathematics 2022, 10, 229. [Google Scholar] [CrossRef]
- Davidovits, J.; Comrie, D.C.; Paterson, J.H.; Ritcey, D.J. Geopolymeric concretes for environmental protection. Concr. Int. 1990, 12, 30–40. [Google Scholar]
- McLellan, B.C.; Williams, R.P.; Lay, J.; Van Riessen, A.; Corder, G.D. Costs and carbon emissions for geopolymer pastes in comparison to ordinary portland cement. J. Clean. Prod. 2011, 19, 1080–1090. [Google Scholar] [CrossRef]
- Duxson, P.S.; Mallicoat, S.W.; Lukey, G.C.; Kriven, W.M.; van Deventer, J.S. The effect of alkali and Si/Al ratio on the development of mechanical properties of metakaolin-based geopolymers. Colloids Surf. A 2007, 292, 8–20. [Google Scholar] [CrossRef]
- Kong, D.L.; Sanjayan, J.G.; Sagoe-Crentsil, K. Comparative performance of geopolymers made with metakaolin and fly ash after exposure to elevated temperatures. Cem. Concr. Res. 2007, 37, 1583–1589. [Google Scholar] [CrossRef]
- Yunsheng, Z.; Wei, S.; Zongjin, L. Composition design and microstructural characterization of calcined kaolin-based geopolymer cement. Appl. Clay Sci. 2010, 47, 271–275. [Google Scholar] [CrossRef]
- Wang, S.D.; Scrivener, K.L.; Pratt, P.L. Factors affecting the strength of alkali-activated slag. Cem. Concr. Res. 1994, 24, 1033–1043. [Google Scholar] [CrossRef]
- Cheng, T.W.; Chiu, J.P. Fire-resistant geopolymer produced by granulated blast furnace slag. Miner. Eng. 2003, 16, 205–210. [Google Scholar] [CrossRef]
- Wongsa, A.; Kunthawatwong, R.; Naenudon, S.; Sata, V.; Chindaprasirt, P. Natural fiber reinforced high calcium fly ash geopolymer mortar. Constr. Build. Mater. 2020, 241, 118143. [Google Scholar] [CrossRef]
- John, S.K.; Nadir, Y.; Girija, K. Effect of source materials, additives on the mechanical properties and durability of fly ash and fly ash-slag geopolymer mortar: A review. Constr. Build. Mater. 2021, 280, 122443. [Google Scholar] [CrossRef]
- Hu, W.; Nie, Q.; Huang, B.; Shu, X.; He, Q. Mechanical and microstructural characterization of geopolymers derived from red mud and fly ashes. J. Clean. Prod. 2018, 186, 799–806. [Google Scholar] [CrossRef]
- Villa, C.; Pecina, E.T.; Torres, R.; Gómez, L. Geopolymer synthesis using alkaline activation of natural zeolite. Constr. Build. Mater. 2010, 24, 2084–2090. [Google Scholar] [CrossRef]
- Font, A.; Soriano, L.; de Moraes Pinheiro, S.M.; Tashima, M.M.; Monzó, J.; Borrachero, M.V.; Payá, J. Design and properties of 100% waste-based ternary alkali-activated mortars: Blast furnace slag, olive-stone biomass ash and rice husk ash. J. Clean. Prod. 2020, 243, 118568. [Google Scholar] [CrossRef]
- Liew, Y.M.; Heah, C.Y.; Kamarudin, H. Structure and properties of clay-based geopolymer cements: A review. Prog. Mater. Sci. 2016, 83, 595–629. [Google Scholar] [CrossRef]
- Yi, C.; Boluk, Y.; Bindiganavile, V. Enhancing alkali-activation of metakaolin-based geopolymers using dry water. J. Clean. Prod. 2020, 258, 120676. [Google Scholar] [CrossRef]
- Noll, W. Chemistry and Technology of Silicones; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Barbosa, V.F.; MacKenzie, K.J.; Thaumaturgo, C. Synthesis and characterisation of materials based on inorganic polymers of alumina and silica: Sodium polysialate polymers. Int. J. Inorg. Mater. 2000, 2, 309–317. [Google Scholar] [CrossRef]
- Zakka, W.P.; Lim, N.H.A.S.; Khun, M.C. A scientometric review of geopolymer concrete. J. Clean. Prod. 2021, 280, 124353. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymers: Inorganic polymeric new materials. J. Therm. Anal. Calorim. 1991, 37, 1633–1656. [Google Scholar] [CrossRef]
- Van Jaarsveld, J.G.; Van Deventer, J.S.; Lorenzen, L. The potential use of geopolymeric materials to immobilise toxic metals: Part, I. Theory and applications. Miner. Eng. 1997, 10, 659–669. [Google Scholar] [CrossRef]
- Palomo, A.; Glasser, F.P. Chemically-bonded cementitious materials based on metakaolin. Br. Ceram. Trans. J. 1992, 91, 107–112. [Google Scholar]
- Davidovits, J.; Davidovits, M.; Davidovits, N. Process for Obtaining a Geopolymeric Alumino-Silicate and Products Thus Obtained. U.S. Patent 5342595, 30 August 1994. [Google Scholar]
- Davidovits, J. Geopolymer Chemistry and Applications, 4th ed.; Geopolymer Institute: Saint-Quentin, France, 2008. [Google Scholar]
- De Jong, B.H.; Brown, G.E., Jr. Polymerization of silicate and aluminate tetrahedra in glasses, melts, and aqueous solutions—I. Electronic structure of H6Si2O7, H6AlSiO71−, and H6Al2O72−. Geochim. Cosmochim. Acta 1980, 44, 491–511. [Google Scholar] [CrossRef]
- Panagiotopoulou, C.; Tsivilis, S.; Kakali, G. Application of the Taguchi approach for the composition optimization of alkali activated fly ash binders. Constr. Build. Mater. 2015, 91, 17–22. [Google Scholar] [CrossRef]
- Sadat, M.R.; Bringuier, S.; Muralidharan, K.; Runge, K.; Asaduzzaman, A.; Zhang, L. An atomistic characterization of the interplay between composition, structure and mechanical properties of amorphous geopolymer binders. J. Non-Cryst. Solids 2016, 434, 53–61. [Google Scholar] [CrossRef]
- Mozumder, R.A.; Laskar, A.I. Prediction of unconfined compressive strength of geopolymer stabilized clayey soil using artificial neural network. Comput. Geotech. 2015, 69, 291–300. [Google Scholar] [CrossRef]
- Rovnaník, P. Effect of curing temperature on the development of hard structure of metakaolin-based geopolymer. Constr. Build. Mater. 2010, 24, 1176–1183. [Google Scholar] [CrossRef]
- Kirschner, A.; Harmuth, H. Investigation of geopolymer binders with respect to their application for building materials. Ceram. Silik. 2004, 48, 7–20. [Google Scholar]
- Kamalloo, A.; Ganjkhanlou, Y.; Aboutalebi, S.H.; Nouranian, H. Modeling of compressive strength of metakaolin based geopolymers by the use of artificial neural network. Int. J. Eng. 2010, 23, 143–150. [Google Scholar]
- Nazari, A.; Torgal, F.P. Predicting compressive strength of different geopolymers by artificial neural networks. Ceram. Int. 2013, 39, 2247–2257. [Google Scholar] [CrossRef]
- Ghanbari, M.; Hadian, A.M.; Nourbakhsh, A.A.; MacKenzie, K.J.D. Modeling and optimization of compressive strength and bulk density of metakaolin-based geopolymer using central composite design: A numerical and experimental study. Ceram. Int. 2017, 43, 324–335. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Yazdani, M.; Ghanbari, S.; Bengar, H.A.; Jafari, A.; Ghatte, H.F. Artificial neural network model to predict the compressive strength of eco-friendly geopolymer concrete incorporating silica fume and natural zeolite. J. Clean. Prod. 2021, 279, 123697. [Google Scholar] [CrossRef]
- ASTM C230/C230M-08; Standard Specification for Flow Table for Use in Tests of Hydraulic Cement. ASTM International: West Conshohocken, PA, USA, 2008.
- ASTM C191-08; Standard Test Methods for Time of Setting of Hydraulic Cement by Vicat Needle. ASTM International: West Conshohocken, PA, USA, 2008.
- ASTM C39/C39M-18; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2018.
- Lei, D.Y.; Guo, L.P.; Sun, W.; Liu, J.; Shu, X.; Guo, X.L. A new dispersing method on silica fume and its influence on the performance of cement-based materials. Constr. Build. Mater. 2016, 115, 716–726. [Google Scholar] [CrossRef]
- Cundy, C.S.; Cox, P.A. The hydrothermal synthesis of zeolites: History and development from the earliest days to the present time. Chem. Rev. 2003, 103, 663–702. [Google Scholar] [CrossRef]
- Tchakouté, H.K.; Rüscher, C.H.; Kong, S.; Kamseu, E.; Leonelli, C. Thermal behavior of metakaolin-based geopolymer cements using sodium waterglass from rice husk ash and waste glass as alternative activators. Waste Biomass Valorization 2017, 8, 573–584. [Google Scholar] [CrossRef]
- Juengsuwattananon, K.; Winnefeld, F.; Chindaprasirt, P.; Pimraksa, K. Correlation between initial SiO2/Al2O3, Na2O/Al2O3, Na2O/SiO2 and H2O/Na2O ratios on phase and microstructure of reaction products of metakaolin-rice husk ash geopolymer. Constr. Build. Mater. 2019, 226, 406–417. [Google Scholar] [CrossRef]
- Yuan, J.; He, P.; Jia, D.; Yang, C.; Yan, S.; Yang, Z.; Duan, X.; Wang, S.; Zhou, Y. Effect of curing temperature and SiO2/K2O molar ratio on the performance of metakaolin-based geopolymers. Ceram. Int. 2016, 42, 16184–16190. [Google Scholar] [CrossRef]
- Moudio, A.M.; Tchakouté, H.K.; Ngnintedem, D.L.; Andreola, F.; Kamseu, E.; Nanseu-Njiki, C.P.; Leonelli, C.; Rüscher, C.H. Influence of the synthetic calcium aluminate hydrate and the mixture of calcium aluminate and silicate hydrates on the compressive strengths and the microstructure of metakaolin-based geopolymer cements. Mater. Chem. Phys. 2021, 264, 124459. [Google Scholar] [CrossRef]
- Zhang, Z.; Provis, J.L.; Wang, H.; Bullen, F.; Reid, A. Quantitative kinetic and structural analysis of geopolymers. Part 2. Thermodynamics of sodium silicate activation of metakaolin. Thermochim. Acta 2013, 565, 163–171. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Zhu, G.R.; Ding, S.; Zhang, H.Y.; Xia, F.Y. Mechanical Properties and Mechanisms of Polyacrylamide-Modified Granulated Blast Furnace Slag–Based Geopolymer. J. Mater. Civ. Eng. 2019, 31, 04018347. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S.; Zuo, Y.; Chen, W.; Ye, G. Chemical deformation of metakaolin based geopolymer. Cem. Concr. Res. 2019, 120, 108–118. [Google Scholar] [CrossRef]
- Cortes, P.P.; Luna, K.C.; Garcia, J.I. Alkali-activated limestone/metakaolin cements exposed to high temperatures: Structural changes. Cem. Concr. Compos. 2021, 122, 104147. [Google Scholar] [CrossRef]
- Hajimohammadi, A.; Provis, J.L.; Van Deventer, J.S. One-part geopolymer mixes from geothermal silica and sodium aluminate. Ind. Eng. Chem. Res. 2008, 47, 9396–9405. [Google Scholar] [CrossRef]
- Yi, C.; Chen, Z.; Bindiganavile, V. Crack growth prediction of cement-based systems subjected to two-dimensional sulphate attack. Constr. Build. Mater. 2019, 222, 814–828. [Google Scholar] [CrossRef]
- ASTM C150/C150M-19a; Standard Specification for Portland Cement. ASTM International: West Conshohocken, PA, USA, 2019.
- Ghosh, K.; Ghosh, P. Effect of Na2O/Al2O3, SiO2/Al2O3 and w/b ratio on setting time and workability of fly ash based geopolymer. Int. J. Eng. Res. Appl. 2012, 2, 2142–2147. [Google Scholar]






| SiO2 | Al2O3 | TiO2 | Fe2O3 | P2O5 | Na2O | K2O | CaO |
|---|---|---|---|---|---|---|---|
| 53.8% | 43.8% | 0.9% | 0.5% | 0.4% | 0.3% | 0.2% | 0.1% |
| SiO2/Al2O3 (Molar Ratio) | Na2O/Al2O3 (Molar Ratio) | H2O/Na2O (Molar Ratio) | Metakaolin (g) | Sodium Silicate (g) | NaOH Pellet (g) | Water (g) | Liquid-to-Solid |
|---|---|---|---|---|---|---|---|
| 2.1 | 1.15 | 11 | 500 | 6.63 | 196.86 | 484.96 | 1.377 |
| 2.8 | 1.15 | 11 | 500 | 320.98 | 160.76 | 400.76 | 1.540 |
| 3.6 | 1.15 | 11 | 500 | 680.23 | 119.50 | 63.96 | 1.727 |
| 4.0 | 1.15 | 11 | 500 | 837.41 | 104.89 | 0 | 1.885 |
| 2.8 | 0.75 | 11 | 500 | 320.98 | 92.02 | 118.37 | 1.063 |
| 2.8 | 1.00 | 11 | 500 | 320.98 | 134.98 | 224.70 | 1.361 |
| 2.8 | 1.30 | 11 | 500 | 320.98 | 186.54 | 352.29 | 1.720 |
| 2.8 | 1.00 | 8 | 500 | 320.98 | 134.98 | 108.71 | 1.129 |
| 2.8 | 1.00 | 9 | 500 | 320.98 | 134.98 | 147.37 | 1.207 |
| 2.8 | 1.00 | 10 | 500 | 320.98 | 134.98 | 186.04 | 1.284 |
| 2.8 | 1.00 | 11 | 500 | 320.98 | 134.98 | 224.70 | 1.361 |
| 2.8 | 1.00 | 12 | 500 | 320.98 | 134.98 | 263.37 | 1.439 |
| SiO2/Al2O3 (Molar Ratio) | Na2O/Al2O3 (Molar Ratio) | H2O/Na2O (Molar Ratio) | Metakaolin (g) | Sodium Silicate (g) | NaOH Pellet (g) | Water (g) | Liquid-to-Solid |
|---|---|---|---|---|---|---|---|
| 2.4 | 1.40 | 16 | 50 | 14.14 | 22.43 | 77.77 | 2.287 |
| 2.8 | 1.40 | 16 | 50 | 32.10 | 20.37 | 66.55 | 2.380 |
| 3.2 | 1.40 | 16 | 50 | 50.06 | 18.31 | 55.32 | 2.474 |
| 3.5 | 1.40 | 16 | 50 | 63.53 | 16.76 | 46.90 | 2.544 |
| 3.6 | 1.40 | 16 | 50 | 68.02 | 16.25 | 44.09 | 2.556 |
| 2.8 | 1.10 | 16 | 50 | 32.10 | 15.22 | 47.99 | 1.906 |
| 2.8 | 1.25 | 16 | 50 | 32.10 | 17.79 | 57.27 | 2.143 |
| 2.8 | 1.40 | 16 | 50 | 32.10 | 20.37 | 66.55 | 2.380 |
| 2.8 | 1.40 | 16 | 50 | 32.10 | 20.37 | 44.90 | 1.947 |
| 2.8 | 1.40 | 16 | 50 | 32.10 | 20.37 | 55.72 | 2.164 |
| 2.8 | 1.40 | 16 | 50 | 32.10 | 20.37 | 66.55 | 2.380 |
| SiO2/Al2O3 (Molar Ratio) | Na2O/Al2O3 (Molar Ratio) | H2O/Na2O (Molar Ratio) | Flow Diameter (mm) | Final Setting Time (min) | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| 2.1 | 0.95 | 11 | 152.3 | - | - |
| 2.4 * | 203.5 | - | - | ||
| 2.8 | 257.3 | - | - | ||
| 3.1 | 261.0 | - | - | ||
| 2.1 | 1.15 | 11 | - | 480 | 11.78 |
| 2.8 * | - | 190 | 32.71 | ||
| 3.6 | - | 360 | 40.23 | ||
| 4.0 | - | 740 | 46.19 | ||
| 2.1 | 0.75 | 11 | 101.5 | - | - |
| 0.95 * | 152.3 | - | - | ||
| 1.15 | 196.9 | - | - | ||
| 1.25 | 247.7 | - | - | ||
| 2.8 | 0.75 | 11 | - | 195 | 47.54 |
| 1.00 * | - | 180 | 29.53 | ||
| 1.15 | - | 190 | 32.71 | ||
| 1.30 | - | 210 | 19.24 | ||
| 2.8 | 1.00 | 8 | 225.1 | 160 | 39.83 |
| 9 * | 239.5 | 130 | 43.03 | ||
| 10 | 254.7 | 165 | 50.68 | ||
| 11 | 261.0 | 180 | 29.53 |
| SiO2/Al2O3 | Na2O/Al2O3 | H2O/Na2O | L/S | Tested Flow (mm) | Predicted Flow (mm) | Tested Set (min) | Predicted Set (min) | Tested Strength (MPa) | Predicted Strength (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 2.1 | 0.75 | 11 | 0.899 | 101.5 ± 1.2 | 107.8 | 140 | 144 | 17.3 ± 2.9 | 17.6 |
| 2.1 | 0.95 | 11 | 1.138 | 152.3 ± 1.7 | 167.8 | 185 | 172 | 11.6 ± 0.9 | 12.7 |
| 2.2 | 0.75 | 11 | 0.923 | 109.3 ± 0.7 | 126.6 | 100 | 131 | 21.3 ± 2.8 | 22.2 |
| 2.3 | 1.00 | 9 | 1.090 | 147.1 ± 1.0 | 154.1 | 115 | 124 | 33.0 ± 0.8 | 27.5 |
| 2.3 | 1.00 | 10 | 1.167 | 185.5 ± 0.8 | 188.0 | 130 | 131 | 23.8 ± 3.3 | 23.4 |
| 2.3 | 1.00 | 12 | 1.322 | 225.4 ± 0.2 | 231.3 | 160 | 179 | 10.3 ± 1.2 | 14.5 |
| 2.3 | 1.00 | 14 | 1.476 | 255.7 ± 0.5 | 241.7 | 220 | 269 | 8.9 ± 0.5 | 6.9 |
| 2.4 | 0.75 | 11 | 0.969 | 172.9 ± 0.2 | 160.1 | 120 | 123 | 30.8 ± 2.2 | 30.7 |
| 2.4 | 0.95 | 11 | 1.208 | 203.5 ± 0.4 | 210.0 | 135 | 129 | 20.6 ± 0.9 | 24.0 |
| 2.4 | 1.15 | 11 | 1.447 | 285.9 ± 0.5 | 280.6 | 180 | 184 | 20.2 ± 1.7 | 17.7 |
| 2.4 | 0.80 | 11 | 1.029 | 189.6 ± 1.8 | 170.7 | 85 | 120 | 27.5 ± 2.9 | 29.0 |
| 2.4 | 1.00 | 11 | 1.268 | 242.7 ± 0.2 | 225.7 | 140 | 139 | 20.3 ± 2.0 | 22.4 |
| 2.4 | 1.20 | 11 | 1.507 | 307.3 ± 0.1 | 301.5 | 195 | 205 | 18.7 ± 1.8 | 16.2 |
| 2.6 | 0.88 | 11.5 | 1.210 | 247.2 ± 1.8 | 224.2 | 120 | 136 | 30.3 ± 3.2 | 29.8 |
| 2.7 | 0.90 | 9 | 1.086 | 157.1 ± 1.9 | 173.9 | 90 | 128 | 39.2 ± 1.0 | 45.2 |
| 2.7 | 0.90 | 10 | 1.149 | 180.7 ± 1.0 | 204.6 | 110 | 126 | 43.8 ± 2.7 | 40.5 |
| 2.7 | 0.90 | 12 | 1.288 | 215.7 ± 1.0 | 245.5 | 165 | 155 | 29.7 ± 2.6 | 29.4 |
| 2.7 | 0.90 | 14 | 1.427 | 238.9 ± 0.7 | 256.9 | 235 | 227 | 15.1 ± 1.3 | 19.8 |
| 2.8 | 0.95 | 11 | 1.302 | 257.3 ± 0.7 | 248.2 | 165 | 149 | 30.4 ± 0.2 | 35.6 |
| 2.8 | 1.15 | 11 | 1.540 | 285.7 ± 0.2 | 305.2 | 190 | 171 | 32.7 ± 1.9 | 29.4 |
| 2.8 | 0.75 | 11 | 1.063 | 223.8 ± 1.6 | 211.9 | 195 | 172 | 47.5 ± 3.7 | 43.9 |
| 2.8 | 0.80 | 11 | 1.122 | 232.0 ± 0.8 | 219.0 | 155 | 162 | 43.6 ± 3.3 | 41.7 |
| 2.8 | 1.00 | 11 | 1.361 | 261.0 ± 0.5 | 260.6 | 180 | 150 | 29.5 ± 1.0 | 33.9 |
| 2.8 | 1.20 | 11 | 1.600 | 321.5 ± 0.8 | 322.7 | 195 | 184 | 28.0 ± 2.0 | 28.2 |
| 2.8 | 1.00 | 8 | 1.129 | 225.1 ± 0.2 | 170.8 | 160 | 182 | 39.8 ± 2.6 | 46.0 |
| 2.8 | 1.00 | 9 | 1.207 | 239.5 ± 0.3 | 209.0 | 130 | 162 | 43.0 ± 0.7 | 45.2 |
| 2.8 | 1.00 | 10 | 1.284 | 254.7 ± 0.9 | 238.9 | 165 | 151 | 50.7 ± 2.2 | 39.4 |
| 2.8 | 1.00 | 12 | 1.439 | 285.9 ± 0.2 | 274.0 | 185 | 160 | 28.8 ± 1.3 | 29.1 |
| 2.9 | 0.99 | 11 | 1.368 | 287.3 ± 0.1 | 263.7 | 145 | 167 | 39.8 ± 0.6 | 36.8 |
| 3.1 | 0.75 | 11 | 1.133 | 224.9 ± 0.6 | 237.1 | 315 | 267 | 53.4 ± 2.8 | 50.8 |
| 3.1 | 0.95 | 11 | 1.372 | 261.0 ± 0.7 | 263.3 | 240 | 221 | 32.5 ± 1.1 | 41.7 |
| 3.2 | 0.75 | 11 | 1.156 | 227.8 ± 1.2 | 243.0 | 380 | 310 | 49.0 ± 0.9 | 52.6 |
| 3.2 | 0.80 | 11 | 1.216 | 235.7 ± 0.9 | 246.7 | 350 | 293 | 49.1 ± 0.6 | 49.8 |
| 3.2 | 0.80 | 12.7 | 1.321 | 261.0 ± 1.7 | 271.2 | 365 | 343 | 46.5 ± 2.1 | 38.7 |
| 3.2 | 1.00 | 11 | 1.455 | 261.0 ± 1.1 | 274.7 | 235 | 249 | 50.6 ± 0.9 | 41.5 |
| 3.3 | 1.02 | 10.5 | 1.466 | 253.8 ± 0.7 | 270.8 | 260 | 296 | 48.0 ± 2.3 | 44.9 |
| 3.3 | 0.95 | 11 | 1.418 | 271.7 ± 0.2 | 267.1 | 290 | 297 | 37.3 ± 2.4 | 44.6 |
| 3.3 | 1.00 | 9 | 1.323 | 232.5 ± 2.1 | 231.6 | 305 | 339 | 50.8 ± 2.6 | 56.8 |
| 3.3 | 1.00 | 10 | 1.401 | 241.7 ± 1.7 | 257.4 | 295 | 309 | 59.9 ± 1.6 | 49.3 |
| 3.5 | 1.00 | 11 | 1.482 | 293.0 ± 0.4 | 279.8 | 350 | 383 | 50.0 ± 0.8 | 49.3 |
| 3.6 | 0.85 | 13 | 1.501 | 285.9 ± 0.5 | 273.3 | 520 | 527 | 40.2 ± 3.2 | 39.0 |
| 3.6 | 0.85 | 10 | 1.303 | 236.9 ± 0.7 | 236.2 | 430 | 485 | 51.5 ± 0.5 | 58.6 |
| 3.6 | 0.95 | 11.5 | 1.525 | 289.5 ± 0.5 | 268.2 | 415 | 445 | 41.0 ± 1.9 | 43.9 |
| 2.4 | 1.30 | 11 | 1.626 | / | / | 260 | 255 | 11.9 ± 0.3 | 13.2 |
| 2.8 | 1.30 | 11 | 1.720 | / | / | 210 | 218 | 19.2 ± 0.6 | 26.1 |
| 3.2 | 1.30 | 11 | 1.813 | / | / | 265 | 267 | 41.8 ± 1.7 | 36.2 |
| 3.6 | 1.15 | 11 | 1.727 | / | / | 360 | 407 | 40.2 ± 1.3 | 42.9 |
| 3.8 | 0.95 | 13 | 1.682 | / | / | 555 | 558 | 40.3 ± 3.5 | 38.7 |
| 4.0 | 1.20 | 12 | 1.973 | / | / | 475 | 533 | 42.1 ± 0.4 | 44.4 |
| 4.0 | 1.15 | 11 | 1.885 | / | / | 740 | 621 | 46.2 ± 3.3 | 45.3 |
| SiO2/Al2O3 | Na2O/Al2O3 | H2O/Na2O | L/S | Tested Flow (mm) | Predicted Flow (mm) | Tested Set (min) | Predicted Set (min) | Tested Strength (MPa) | Predicted Strength (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 2.2 | 0.85 | 11 | 1.042 | 143.53 ± 2.5 | 152.3 | 125 | 136 | 16.7 ± 1.3 | 19.6 |
| 2.6 | 0.90 | 10 | 1.126 | 201.40 ± 0.4 | 194.2 | 120 | 115 | 36.0 ± 3.2 | 37.4 |
| 2.7 | 1.00 | 11 | 1.275 | 240.87 ± 0.7 | 251.5 | 190 | 141 | 32.7 ± 2.4 | 35.5 |
| 3.0 | 0.85 | 11 | 1.229 | 240.54 ± 0.5 | 242.2 | 245 | 205 | 45.8 ± 3.3 | 44.0 |
| 3.4 | 0.90 | 10 | 1.312 | 243.13 ± 0.8 | 241.7 | 350 | 361 | 49.5 ± 1.7 | 54.6 |
| 3.4 | 0.80 | 10 | 1.201 | 214.90 ± 0.8 | 230.7 | 395 | 376 | 60.4 ± 4.3 | 59.5 |
| 3.4 | 1.00 | 10 | 1.424 | 263.03 ± 0.4 | 257.3 | 360 | 357 | 57.5 ± 2.7 | 50.5 |
| 3.4 | 1.20 | 10 | 1.648 | 335.14 ± 0.2 | 303.1 | 335 | 382 | 51.1 ± 2.1 | 45.6 |
| 3.4 | 0.85 | 12 | 1.388 | 271.13 ± 0.5 | 270.0 | 395 | 388 | 46.3 ± 1.2 | 43.2 |
| 3.6 | 0.85 | 11 | 1.369 | 259.02 ± 1.1 | 255.5 | 450 | 489 | 49.7 ± 1.5 | 51.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Boluk, Y.; Bindiganavile, V. Experimental Characterization and Multi-Factor Modelling to Achieve Desired Flow, Set and Strength of N-A-S-H Geopolymers. Materials 2022, 15, 5634. https://doi.org/10.3390/ma15165634
Yi C, Boluk Y, Bindiganavile V. Experimental Characterization and Multi-Factor Modelling to Achieve Desired Flow, Set and Strength of N-A-S-H Geopolymers. Materials. 2022; 15(16):5634. https://doi.org/10.3390/ma15165634
Chicago/Turabian StyleYi, Chaofan, Yaman Boluk, and Vivek Bindiganavile. 2022. "Experimental Characterization and Multi-Factor Modelling to Achieve Desired Flow, Set and Strength of N-A-S-H Geopolymers" Materials 15, no. 16: 5634. https://doi.org/10.3390/ma15165634






