Polarization-Dependent Scattering of Nanogratings in Femtosecond Laser Photowritten Waveguides in Fused Silica
Abstract
:1. Introduction
2. The Mechanism of PD Guiding
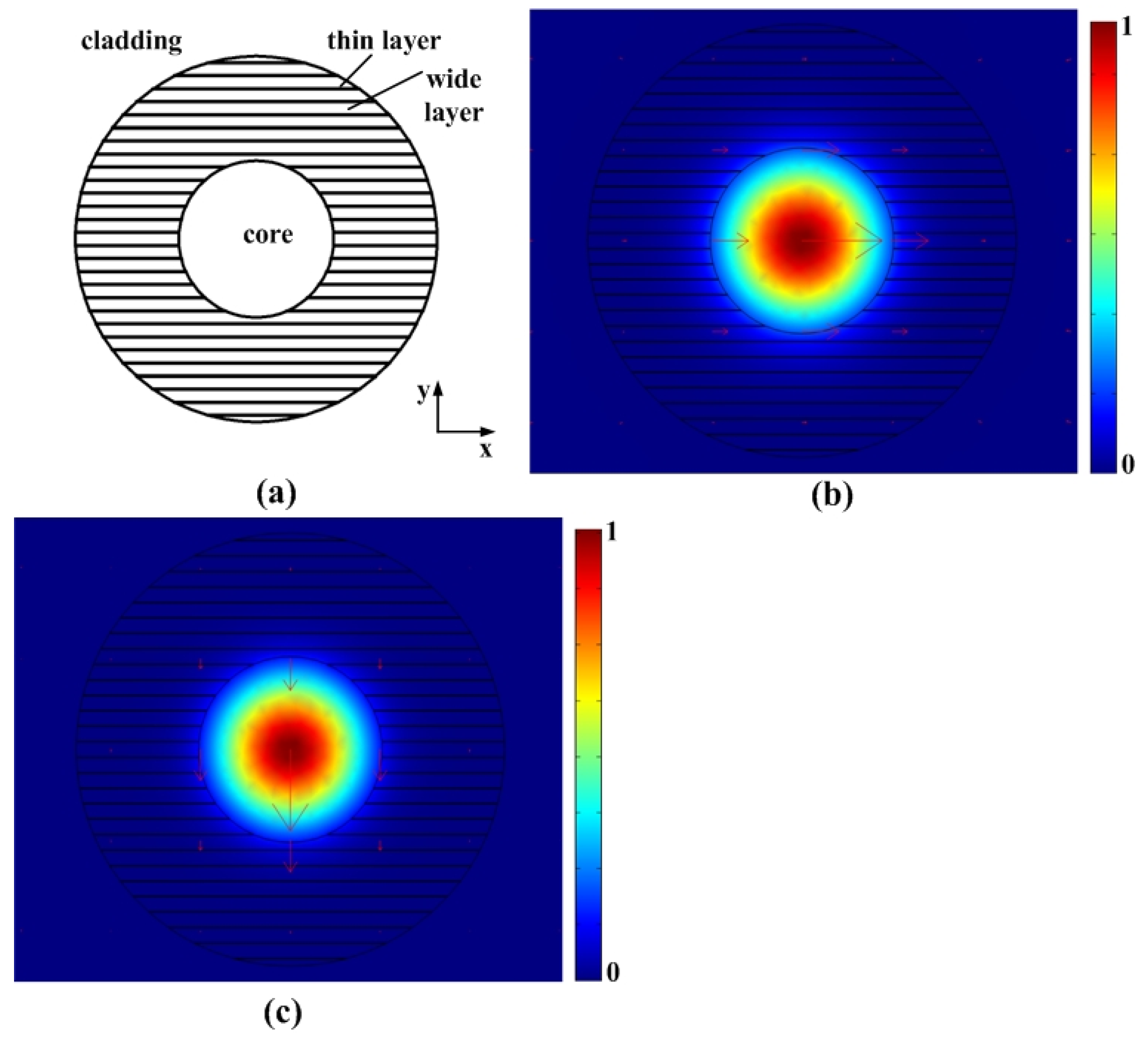
2.1. Mode Analysis
2.2. FDTD Simulation
2.3. Scattering Experiments
3. Application
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davis, K.M.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.W.; Huser, T.; Risbud, S.; Krol, D.M. Structural changes in fused silica after exposure to focused femtosecond laser pulses. Opt. Lett. 2001, 26, 1726–1728. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Mishchik, K.; Mauclair, C.; Audouard, E.; Stoian, R. Ultrafast laser photoinscription of polarization sensitive devices in bulk silica glass. Opt. Express 2009, 17, 9515–9525. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ramirez, L.P.R.; Heinrich, M.; Richter, S.; Dreisow, F.; Keil, R.; Korovin, A.V.; Peschel, U.; Nolte, S.; Tünnermann, A. Tuning the structural properties of femtosecond-laser-induced nanogratings. Appl. Phys. A 2010, 100, 1–6. [Google Scholar] [CrossRef]
- Beresna, M.; Gecevičius, M.; Kazansky, P.G. Polarization sensitive elements fabricated by femtosecond laser nanostructuring of glass. Opt. Mater. Express 2011, 1, 783–795. [Google Scholar] [CrossRef]
- Shimotsuma, Y.; Sakakura, M.; Kazansky, P.G.; Beresna, M.; Qiu, J.; Miura, K.; Hirao, K. Ultrafast manipulation of self-assembled form birefringence in glass. Adv. Mater. 2011, 22, 4039–4043. [Google Scholar] [CrossRef] [PubMed]
- Kazansky, P.G.; Bricchi, E.; Baumberg, J.J. Embedded anisotropic microreflectors by femtosecond-laser nanomachining. Appl. Phys. Lett. 2002, 81, 196–198. [Google Scholar] [CrossRef]
- Beresna, M.; Kazansky, P.G. Polarization diffraction grating produced by femtosecond laser nanostructuring in glass. Opt. Lett. 2010, 35, 1662–1664. [Google Scholar] [CrossRef]
- Taylor, R.; Hnatovsky, C.; Simova, E. Applications of femtosecond laser induced self-organized planar nanocracks inside fused silica glass. Laser Photonics Rev. 2008, 2, 26–46. [Google Scholar] [CrossRef]
- Mishchik, K.; Cheng, G.; Huo, G.; Burakov, I.M.; Mauclair, C.; Mermillod-Blondin, A.; Rosenfeld, A.; Ouerdane, Y.; Boukenter, A.; Parriaux, O.; et al. Nanosize structural modifications with polarization functions in ultrafast laser irradiated bulk fused silica. Opt. Express 2010, 18, 24809–24824. [Google Scholar] [CrossRef]
- Mauclair, C.; Zamfirescu, M.; Colombier, J.P.; Cheng, G.; Mishchik, K.; Audouard, E.; Stoian, R. Control of ultrafast laser-induced bulk nanogratings in fused silica via pulse time envelopes. Opt. Express 2012, 20, 12997–13005. [Google Scholar] [CrossRef]
- Chen, L.; Cao, K.; Li, Y.; Liu, J.; Zhang, S.; Feng, D.; Sun, Z.; Jia, T. Large-area straight, regular periodic surface structures produced on fused silica by the interference of two femtosecond laser beams through cylindrical lens. Opto-Electron. Adv. 2021, 4, 200036. [Google Scholar] [CrossRef]
- Geng, J.; Yan, W.; Shi, L.; Qiu, M. Surface plasmons interference nanogratings: Wafer-scale laser direct structuring in seconds. Light Sci. Appl. 2022, 11, 189. [Google Scholar] [CrossRef]
- Bai, J.; Cheng, G.; Long, X.; Wang, Y.; Zhao, W.; Chen, G.; Stoian, R.; Hui, R. Polarization behavior of femtosecond laser written optical waveguides in Ti:Sapphire. Opt. Express 2012, 20, 15035–15044. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Romero, C.; de Aldana, J.R.V.; Chen, F. Femtosecond laser irradiation on Nd:YAG crystal: Surface ablation and high-spatial-frequency nanograting. Appl. Surf. Sci. 2018, 441, 372–380. [Google Scholar] [CrossRef]
- Popescu, C.; Dorcioman, G.; Bita, B.; Besleaga, C.; Zgură, I.; Himcinschi, C.; Popescu, A. Fabrication of periodical surface structures by picosecond laser irradiation of carbon thin films: Transformation of amorphous carbon in nanographite. Appl. Surf. Sci. 2016, 390, 236–243. [Google Scholar] [CrossRef]
- Eickhoff, W. In-line fibre-optic polarizer. Electron. Lett. 1980, 16, 762–764. [Google Scholar] [CrossRef]
- Bergh, R.A.; Lefevre, H.C.; Shaw, H.J. Single-mode fiber-optic polarizer. Opt. Lett. 1980, 5, 479–481. [Google Scholar] [CrossRef]
- Zhou, K.; Simpson, G.; Chen, X.; Zhang, L.; Bennion, I. High extinction ratio in-fiber polarizers based on 45° tilted fiber Bragg gratings. Opt. Lett. 2005, 30, 1285–1287. [Google Scholar] [CrossRef]
- FDTD Solutions. Available online: www.lumerical.com (accessed on 15 July 2022).
- D’Amico, C.; Martin, G.; Troles, J.; Cheng, G.; Stoian, R. Multiscale Laser Written Photonic Structures in Bulk Chalcogenide Glasses for Infrared Light Transport and Extraction. Photonics 2021, 8, 211. [Google Scholar] [CrossRef]
- Lv, J.; Wang, K.; Cheng, G. 3D waveguide element fabrication in Gorilla glass by an ultrafast laser. Appl. Opt. 2020, 59, 8242–8246. [Google Scholar] [CrossRef] [PubMed]



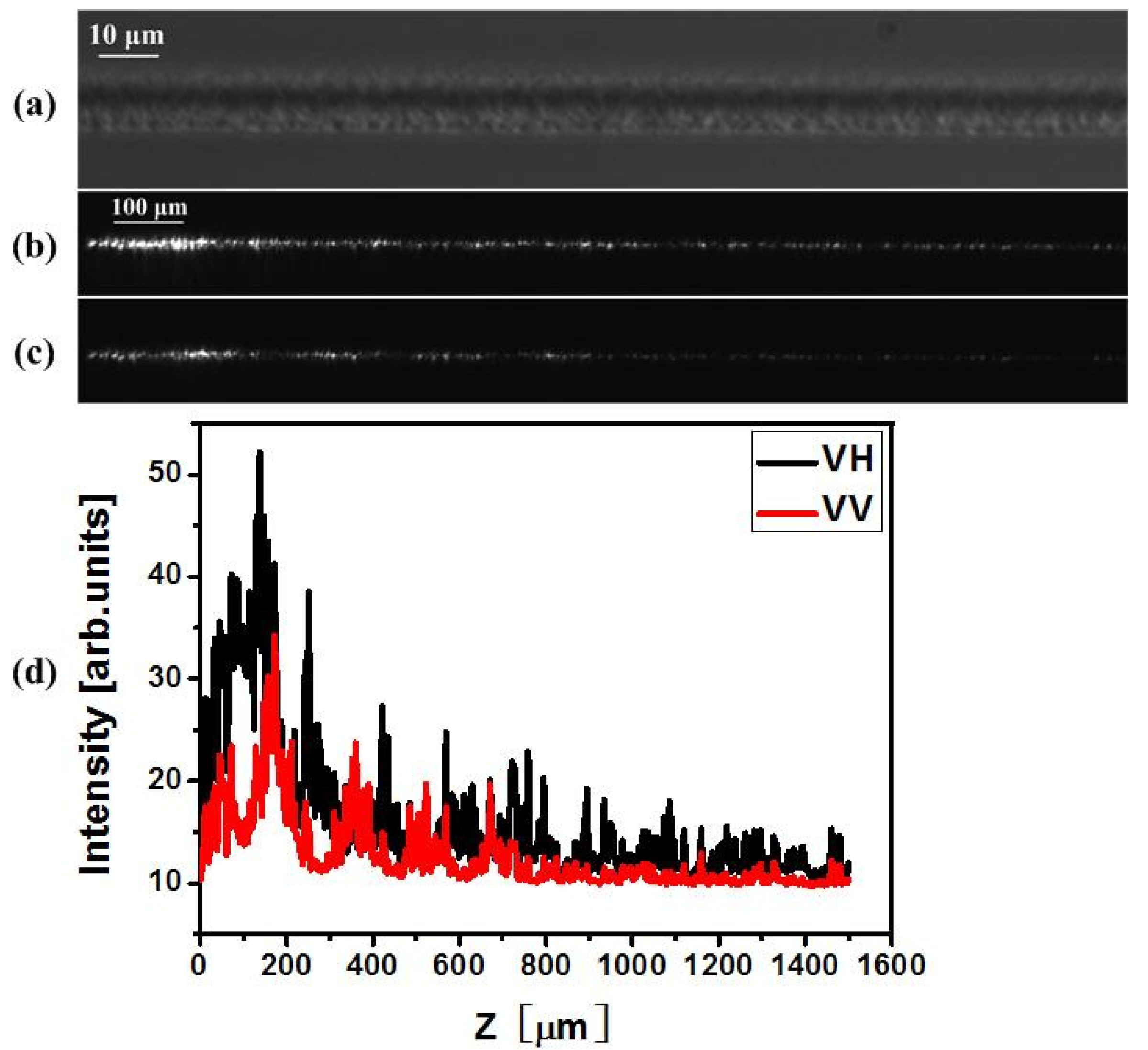
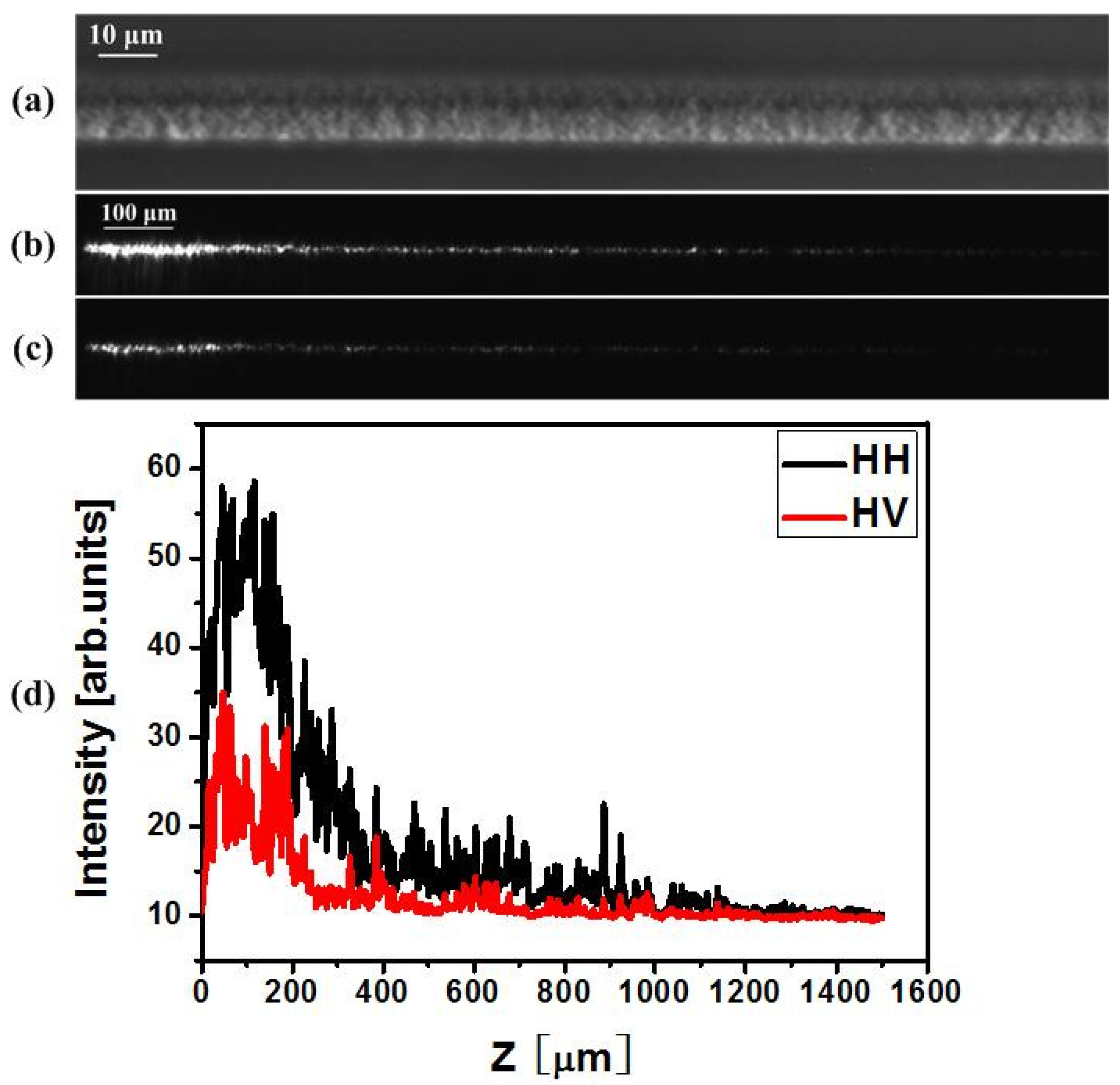


| Direction of Writing Polarization | Direction of Nanoplanes | Direction of Injection Polarization | Scattering in Vertical Direction | Main Scattering Direction |
|---|---|---|---|---|
| V | H | H | IH | V |
| V | IV (<IH) | H | ||
| H | V | H | IH * | V |
| V | IV * (<IH *) | H |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, G.; Lin, L.; Mishchik, K.; Stoian, R. Polarization-Dependent Scattering of Nanogratings in Femtosecond Laser Photowritten Waveguides in Fused Silica. Materials 2022, 15, 5698. https://doi.org/10.3390/ma15165698
Cheng G, Lin L, Mishchik K, Stoian R. Polarization-Dependent Scattering of Nanogratings in Femtosecond Laser Photowritten Waveguides in Fused Silica. Materials. 2022; 15(16):5698. https://doi.org/10.3390/ma15165698
Chicago/Turabian StyleCheng, Guanghua, Ling Lin, Konstantin Mishchik, and Razvan Stoian. 2022. "Polarization-Dependent Scattering of Nanogratings in Femtosecond Laser Photowritten Waveguides in Fused Silica" Materials 15, no. 16: 5698. https://doi.org/10.3390/ma15165698
APA StyleCheng, G., Lin, L., Mishchik, K., & Stoian, R. (2022). Polarization-Dependent Scattering of Nanogratings in Femtosecond Laser Photowritten Waveguides in Fused Silica. Materials, 15(16), 5698. https://doi.org/10.3390/ma15165698






