Study of the Dynamic Model and Vibration Performance of Pot-Shaped Metal Rubber
Abstract
:1. Introduction
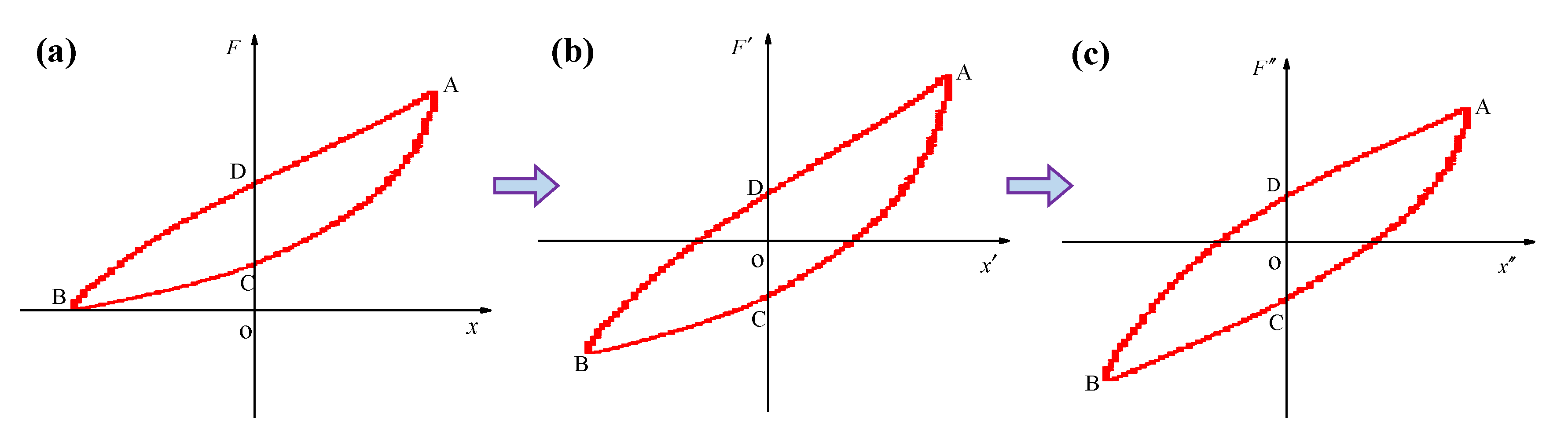
2. Asymmetric-Hysteresis Dynamic Model of Pot-Shaped Metal Rubber
3. Parameter Identification Method of the Model
3.1. Identification of the Parameters h and b
3.2. Identification of the Parameter b
3.3. Identification of the Parameters k1, k3, c, and α
4. Parameter Identification Results
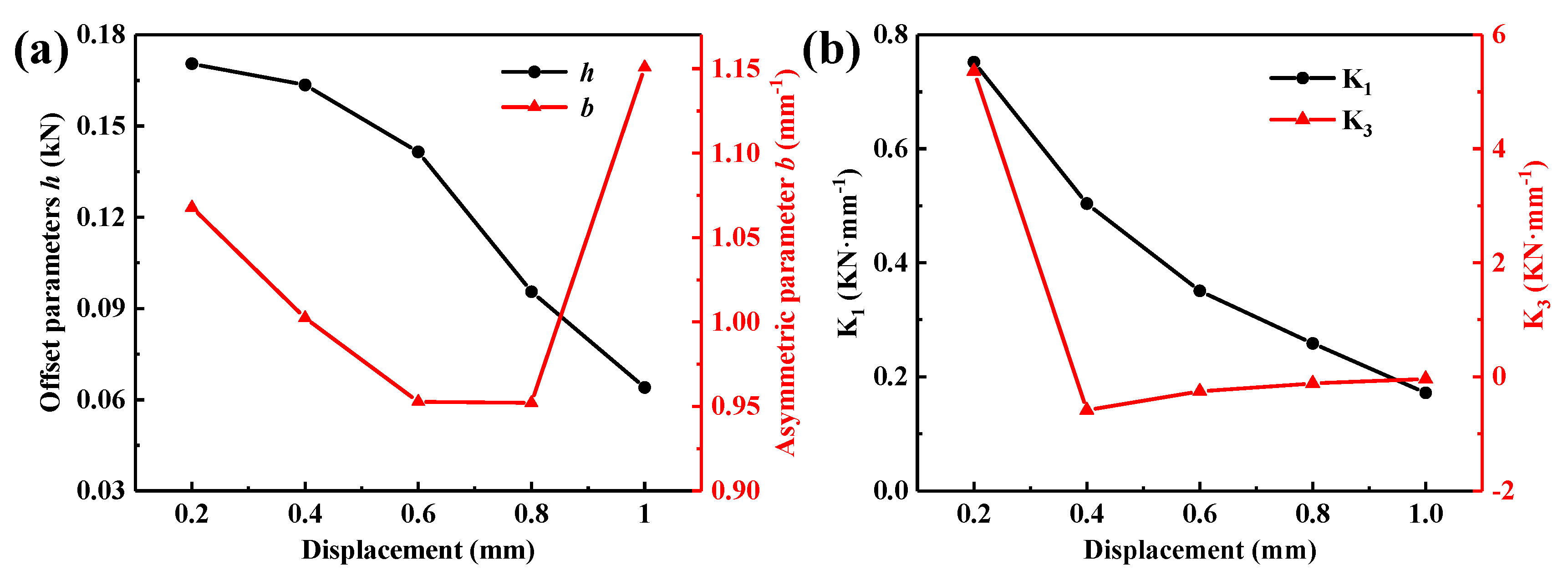
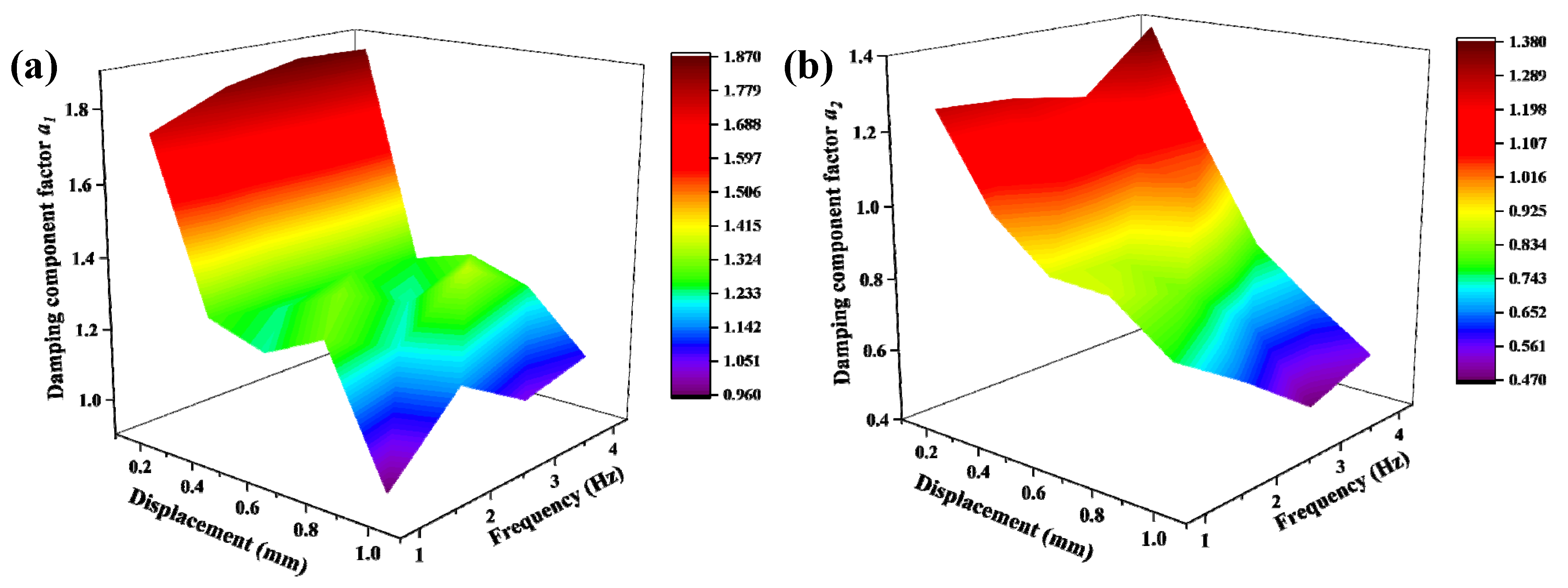
4.1. Identification Results of the Parameters h and b and the Stiffness Coefficient
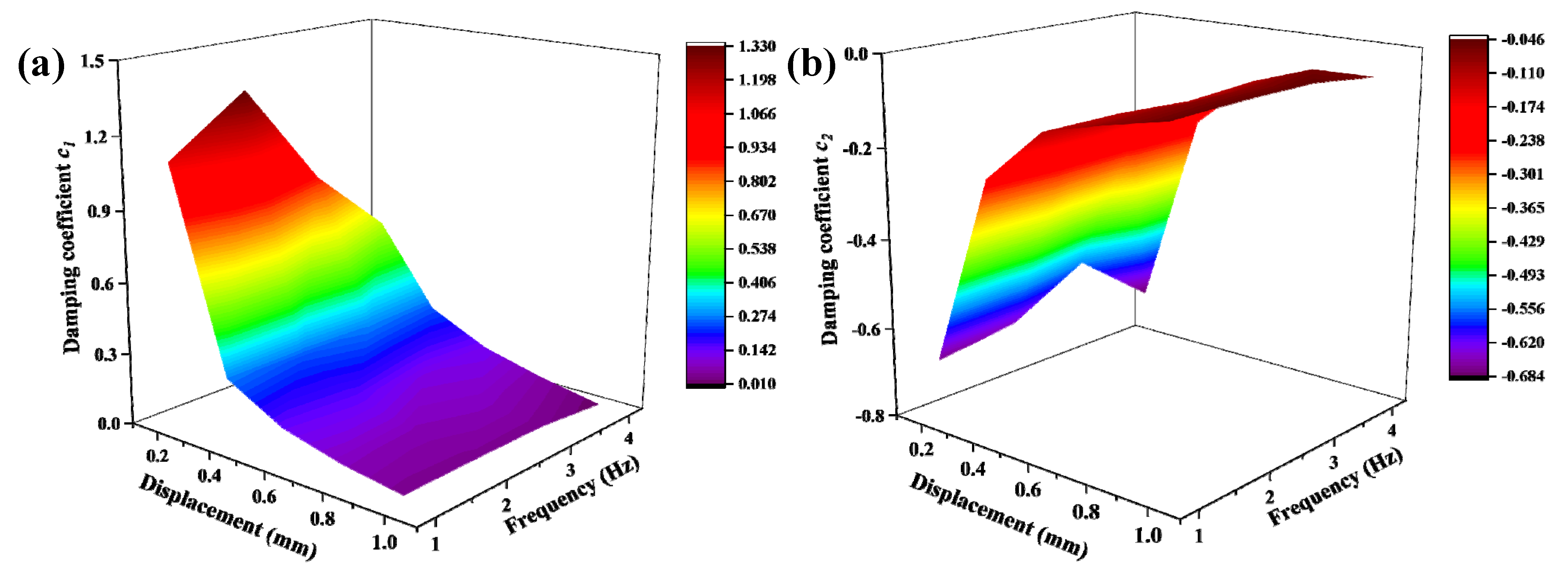
4.2. Identification Results of the Parameters c and α
4.2.1. Identification Results of the Parameter c
4.2.2. Identification Results of the Parameter a
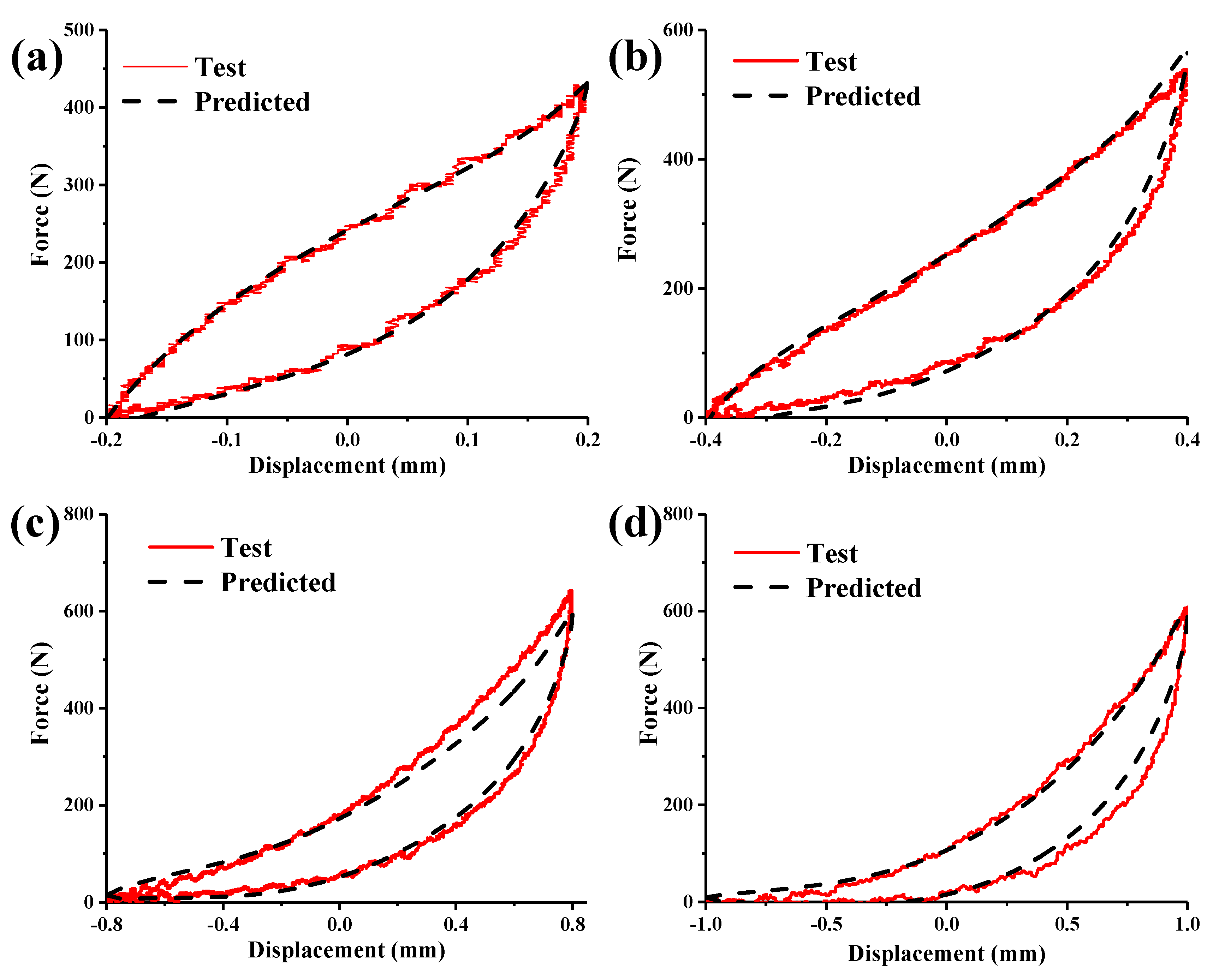
5. Experimental Verification of the Asymmetric Dynamic Model
6. Vibration Performance Test
6.1. Response Calculation of the Pot-Shaped Metal Rubber Damper
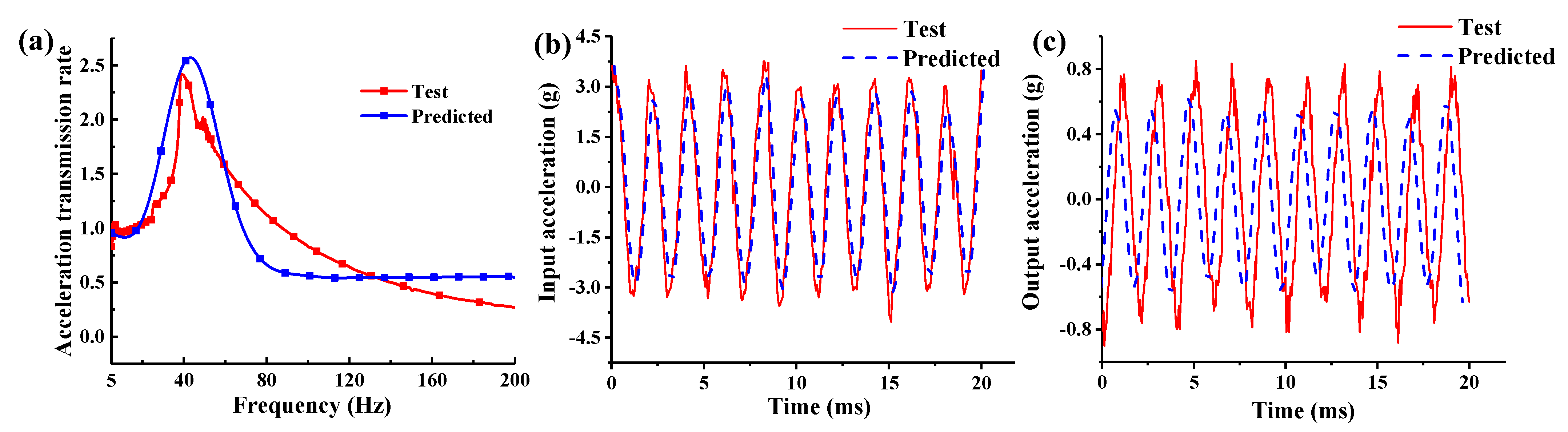
6.2. Verification of the Sinusoidal Sweep Test
7. Conclusions
- (1)
- Based on the parameter-separation concept, the hysteresis loop obtained from the dynamic test is accurately decomposed, and the nonlinear dynamic model of pot-shaped metal rubber is established. The specific expressions of the parameters of the model are obtained through parameter identification, and the accuracy of the model is verified.
- (2)
- The pot-shaped metal rubber damping system is analyzed theoretically. The experimental and theoretical acceleration transfer rate curves and the experimental and theoretical time-domain signals of the system under specific loading conditions, are compared. The results show that the theoretical curve is in good agreement with the experimental curve, which verifies the accuracy of the established model and the parameter identification method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, H.B.; Lu, C.H.; Cao, F.L. Metal Rubber Materials and Engineering Application; Science Press: Beijing, China, 2014; pp. 310–366. [Google Scholar]
- Alejandro, P.; Ferreño, D.; Carrascal, I.A. Metal cushion dampers for railway applications: A review. Constr. Build. Mater. 2020, 238, 117711. [Google Scholar]
- Zhang, D.Y.; Scarpa, F.; Ma, Y.H. Compression mechanics of nickel-based superalloy metal rubber. Mater. Sci. Eng. A 2013, 580, 305–312. [Google Scholar] [CrossRef]
- Ma, Y.H.; Zhang, Q.C.; Zhang, D.Y. The mechanics of shape memory alloy metal rubber. Acta Mater. 2015, 96, 89–100. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhang, Z.J.; Xue, X.M. Experimental investigation on enhanced mechanical and damping performance of corrugated structure with metal rubber. Thin-Walled Struct. 2020, 154, 106815. [Google Scholar] [CrossRef]
- Xiao, K.; Bai, H.; Xue, X. Damping characteristics of metal rubber in the pipeline coating system. Shock Vib. 2018, 15, 3974381. [Google Scholar] [CrossRef]
- Cao, X.; Wei, C.; Liang, J.; Wang, L. Design and dynamic analysis of metal rubber isolators between satellite and carrier rocket system. Mech. Sci. 2019, 10, 71–78. [Google Scholar] [CrossRef]
- Ma, Y.H.; Zhang, Q.C.; Wang, Y.F. Topology and mechanics of metal rubber via X-ray tomography. Mater. Des. 2019, 181, 108067. [Google Scholar] [CrossRef]
- Iwan, W.D. The Dynamic Response of Bilinear Hysteretic Systems; California Institute of Technology: Pasadena, CA, USA, 1961; pp. 66–70. [Google Scholar]
- Zhang, B.; Lang, Z.Q.; Billings, S.A. System identification methods for metal rubber devices. Mech. Syst. Signal Process 2013, 39, 207–226. [Google Scholar] [CrossRef]
- Bouc, R. Forced vibration of mechanical systems with hysteresis. In Proceedings of the Fourth Conference on Nonlinear Oscillations, Prague, Czech Republic, 5–9 September 1967. [Google Scholar]
- Yan, H.; Jiang, H.Y.; Liu, W.J. Identification of parameters for metal rubber isolator with hysteretic nonlinearity characteristics. Acta Phys. Sin. 2009, 58, 5238–5243. [Google Scholar] [CrossRef]
- Li, Y.L.; Bai, H.B.; Lu, C.H. Parameter identification of a new metal rubber damping system. J. Ordnance Eng. Coll. 2014, 26, 68–74. [Google Scholar]
- Xue, X.; Ruan, S.X.; Bai, H.B. Elasto-hysteresis model and experimental study of metal rubber based on equivalent damping theory. J. Exp. Mech. 2021, 36, 80–90. [Google Scholar]
- Li, T.; Bai, H.B.; Lu, C.H. Effects of sine displacement excitation on dynamic characteristics of vibration isolation system with knitted-dapped metal rubber. Mod. Manuf. Eng. 2014, 12, 97–101. [Google Scholar]
- Zi, B.; Ding, Z.Y.; Wu, Y.W. High temperature mechanical modeling and experimental research of metal rubber coated damping structure. China Mech. Eng. 2022, 33, 1294–1301. [Google Scholar]
- Zheng, X.Y.; Ren, Z.Y.; Bai, H.B. Mechanical Behavior of Entangled Metallic Wire Materials-Polyurethane Interpenetrating Composites. Def. Technol. 2022, 7. [Google Scholar] [CrossRef]
- Shen, G.J.; Li, M.; Xue, X. Damping Energy dissipation and parameter identification of the bellows structure covered with elastic-porous metal rubber. Shock Vib. 2021, 2021, 8813099. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Ko, J.M.; Wong, C.W. Modelling and identification of a wire-cable vibration isolator via a cyclic loading test. Proc. Inst. Mech. Eng. 1999, 213, 163–172. [Google Scholar]
- Zhou, X.R.; Wen, J.M. Parameter identification of quasi-static asymmetric hysteresis model for wire-rope isolators. Noise Vib. Control 2013, 5, 170–172. [Google Scholar]
- Wu, Y.S.; Zhu, S.J. Separated identification of asymmetric hysteretic model parameters for a wire-cable vibration isolator. J. Vib. Eng. Technol. 2007, 20, 614–617. [Google Scholar]
- Bai, H.B.; Huang, X.Q. Viscous damping bilinear hysteretic vibration isolation system with cubic nonlinearity. J. Vib. Shock 1998, 17, 5–8. [Google Scholar]
- Li, D.W.; Bai, H.B.; Yang, J.C. Modeling of a nonlinear system with hysteretic characteristics. Chin. J. Mech. Eng. 2005, 10, 205–209. [Google Scholar] [CrossRef]
- Wang, W.; Tang, Y.; Wu, Y.W. Experimental investigating on the tri-directional quasi-static of pot-shaped mental rubber. J. Mech. Strength 2022, 44, in press. [Google Scholar]
- Hu, H.B.; Jing, B.; Guo, X. Improved baseline correction method based on polynomial fitting for raman spectroscopy. Photonic Sens. 2018, 8, 332–340. [Google Scholar] [CrossRef]
- Lu, C.H. Experiment and Theoretical Study on the Metal Rubber/Rubber Composite Laminated Damper; Army Engineering University of PLA: Nanjing, China, 2008. [Google Scholar]
- Zhang, B.; Ren, Z.Y.; Bai, H.B. Experimental modeling and parameter identification of non-forming damping characteristics of metal rubber. J. Vib. Shock 2021, 40, 243–249. [Google Scholar]

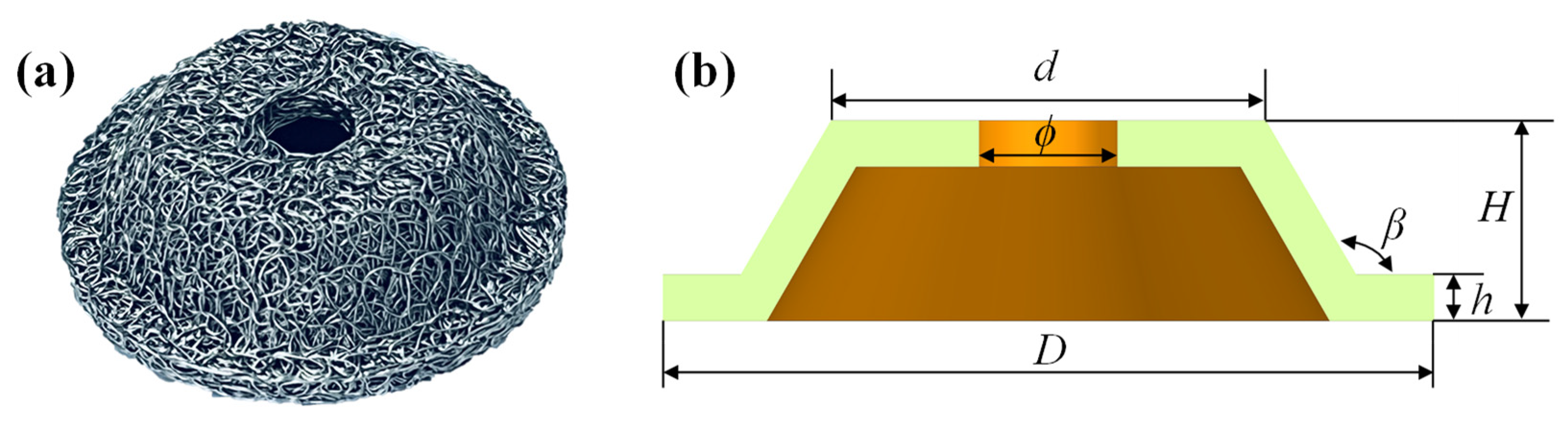


| β/o | D/mm | d/mm | ϕ/mm | H/mm | h/mm |
|---|---|---|---|---|---|
| 120 | 50 | 28.4 | 9 | 13 | 3 |
| Element | C | Si | Mn | P | S | Ni | Cr | Fe |
|---|---|---|---|---|---|---|---|---|
| Wt.% | 0.06 | 0.86 | 1.84 | 0.02 | 0.004 | 8.23 | 18.52 | Bal. |
| Parameter | a0 | a1 | a2 | a3 | b0 | b1 | b1 | b3 |
|---|---|---|---|---|---|---|---|---|
| Value | 0.134 | 0.306 | 0.685 | 0.307 | 1.022 | 0.626 | 2.410 | 1.911 |
| Parameter | d0 | d1 | d2 | d3 | e0 | e1 | e2 | e3 |
|---|---|---|---|---|---|---|---|---|
| Value | 1.147 | −2.412 | 2.374 | −0.938 | 18.780 | 92.920 | 140.100 | −66.050 |
| Parameter | p1 | p2 | p3 | p4 | p5 | p6 |
|---|---|---|---|---|---|---|
| Value | 0.043 | −0.111 | −0.103 | −0.055 | 0.116 | −0.063 |
| Parameter | p7 | p8 | p9 | p10 | p11 | |
| Value | 1.138 | 0.306 | −0.054 | 0.173 | −0.124 |
| Parameter | q1 | q2 | q3 | q4 | q5 | q6 |
|---|---|---|---|---|---|---|
| Value | −0.052 | 0.034 | 0.136 | 0.063 | −0.005 | 0.004 |
| Parameter | q7 | q8 | q9 | q10 | q11 | |
| Value | 1.556 | 0.589 | −0.019 | 0.057 | −0.032 |
| Parameter | m1 | m2 | m3 | m4 | m5 | m6 | m7 | m8 |
|---|---|---|---|---|---|---|---|---|
| Value | 83.298 | −13.673 | −166.229 | 29.842 | −0.697 | 116.474 | −27.175 | 1.550 |
| Parameter | m9 | m10 | m11 | m12 | m13 | m14 | m15 | |
| Value | −0.162 | −33.266 | 8.024 | −0.174 | −0.207 | 0.052 | 3.324 |
| Parameter | n1 | n2 | n3 | n4 | n5 | n6 | m7 | m8 |
|---|---|---|---|---|---|---|---|---|
| Value | −0.625 | −3.946 | 4.901 | 0.970 | 3.577 | −3.737 | 4.923 | −3.902 |
| Parameter | n9 | n10 | n11 | n12 | n13 | n14 | n15 | |
| Value | −0.628 | 1.091 | −2.962 | 0.688 | 0.537 | 0.001 | −0.108 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Wang, W.; Wu, Y.; Bai, H. Study of the Dynamic Model and Vibration Performance of Pot-Shaped Metal Rubber. Materials 2022, 15, 5878. https://doi.org/10.3390/ma15175878
Zheng X, Wang W, Wu Y, Bai H. Study of the Dynamic Model and Vibration Performance of Pot-Shaped Metal Rubber. Materials. 2022; 15(17):5878. https://doi.org/10.3390/ma15175878
Chicago/Turabian StyleZheng, Xiaoyuan, Wei Wang, Yiwan Wu, and Hongbai Bai. 2022. "Study of the Dynamic Model and Vibration Performance of Pot-Shaped Metal Rubber" Materials 15, no. 17: 5878. https://doi.org/10.3390/ma15175878






