The Mechanical Properties of Gangue Paste Material for Deep Mines: An Experimental and Model Study
Abstract
:1. Introduction
2. Material and Methods
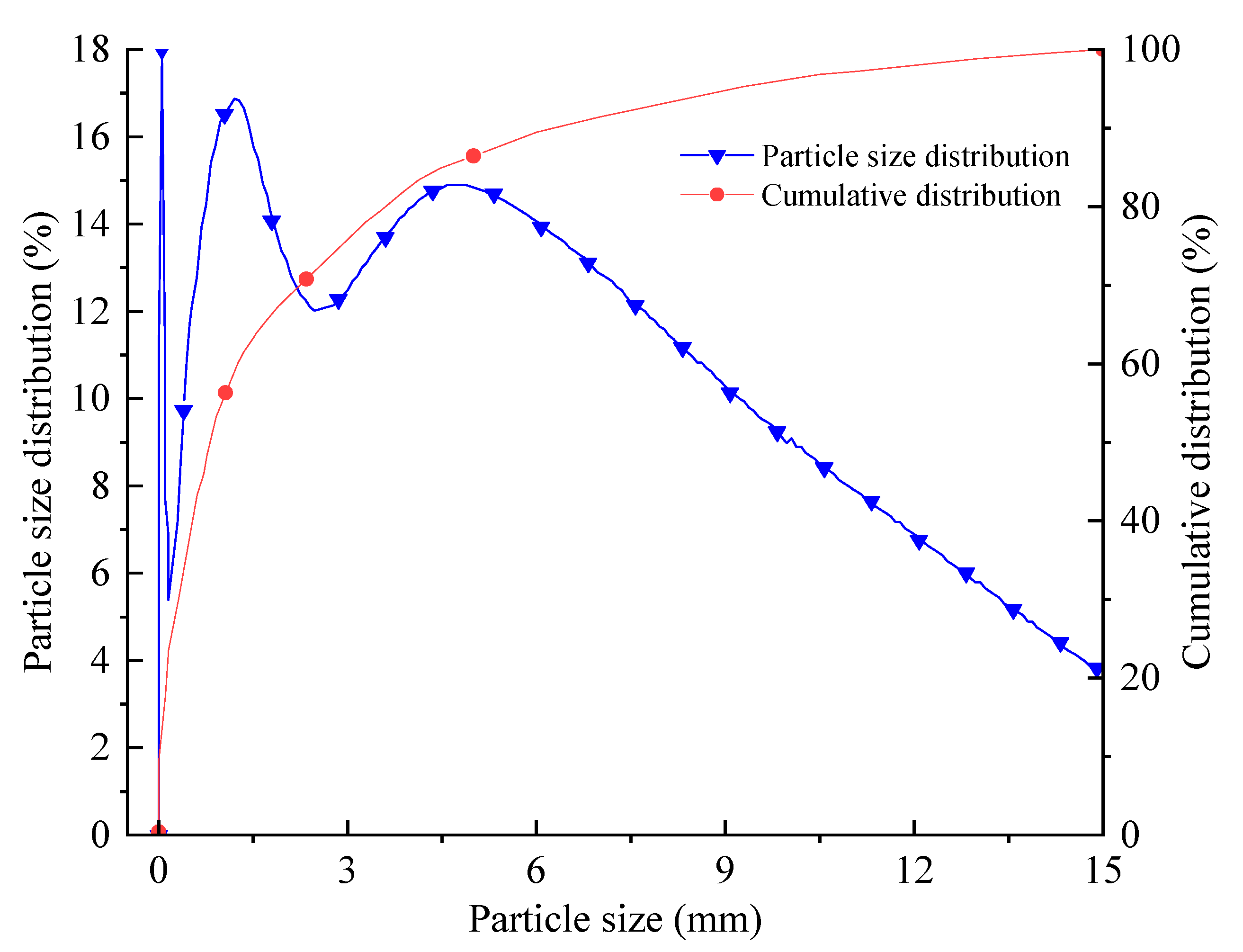
2.1. Materials
2.2. Experiments
3. Results and Discussion
3.1. Experimental Results
3.2. Range Analysis
3.3. Analysis of Variance
3.4. Conversion Relationship of Each Index
- (1)
- Relationship between splitting tensile strength and cube compressive strength.
- (2)
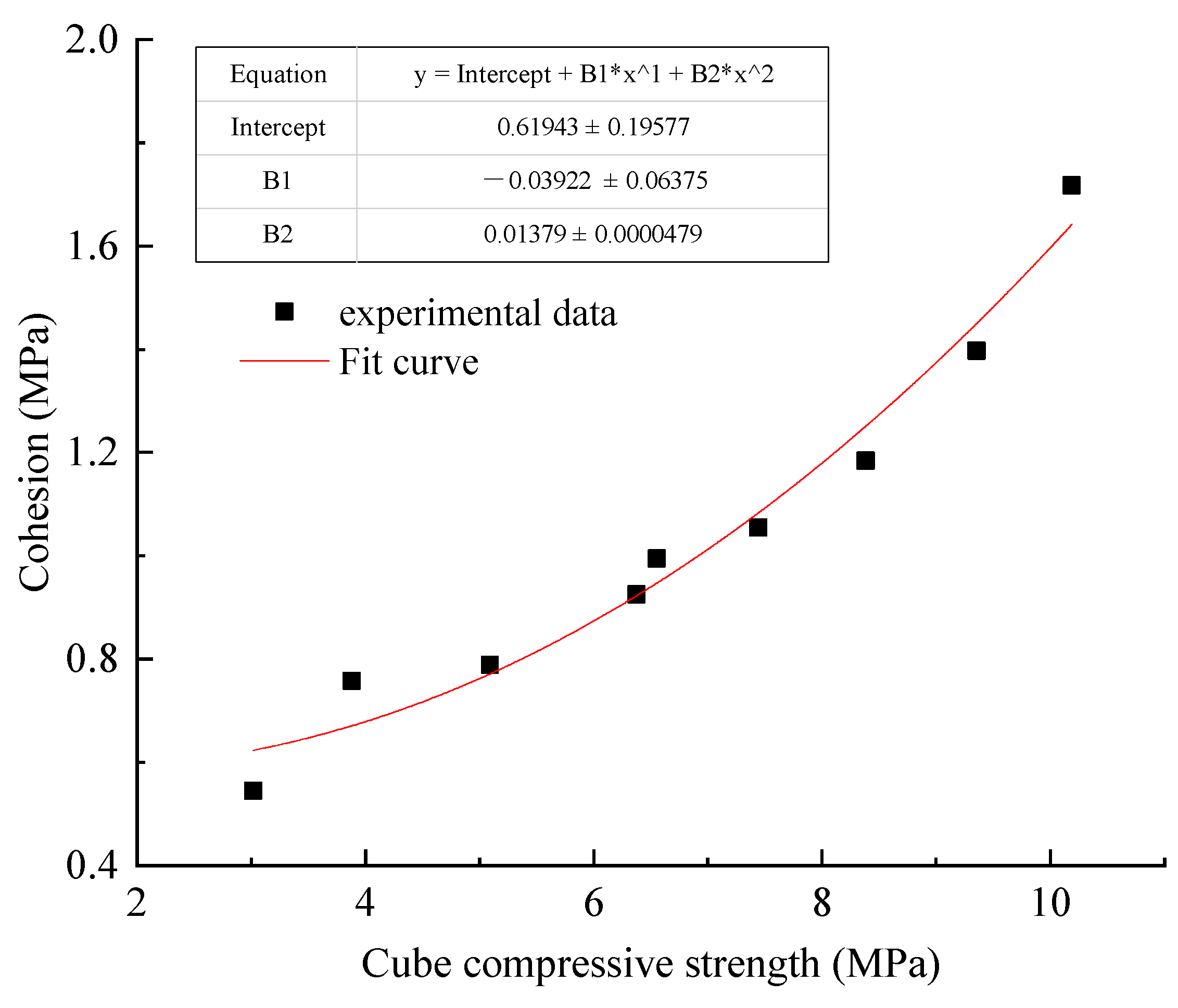
- Relationship between cohesion and cube compressive strength.
- (3)
- Relationship between elastic modulus and cube compressive strength.
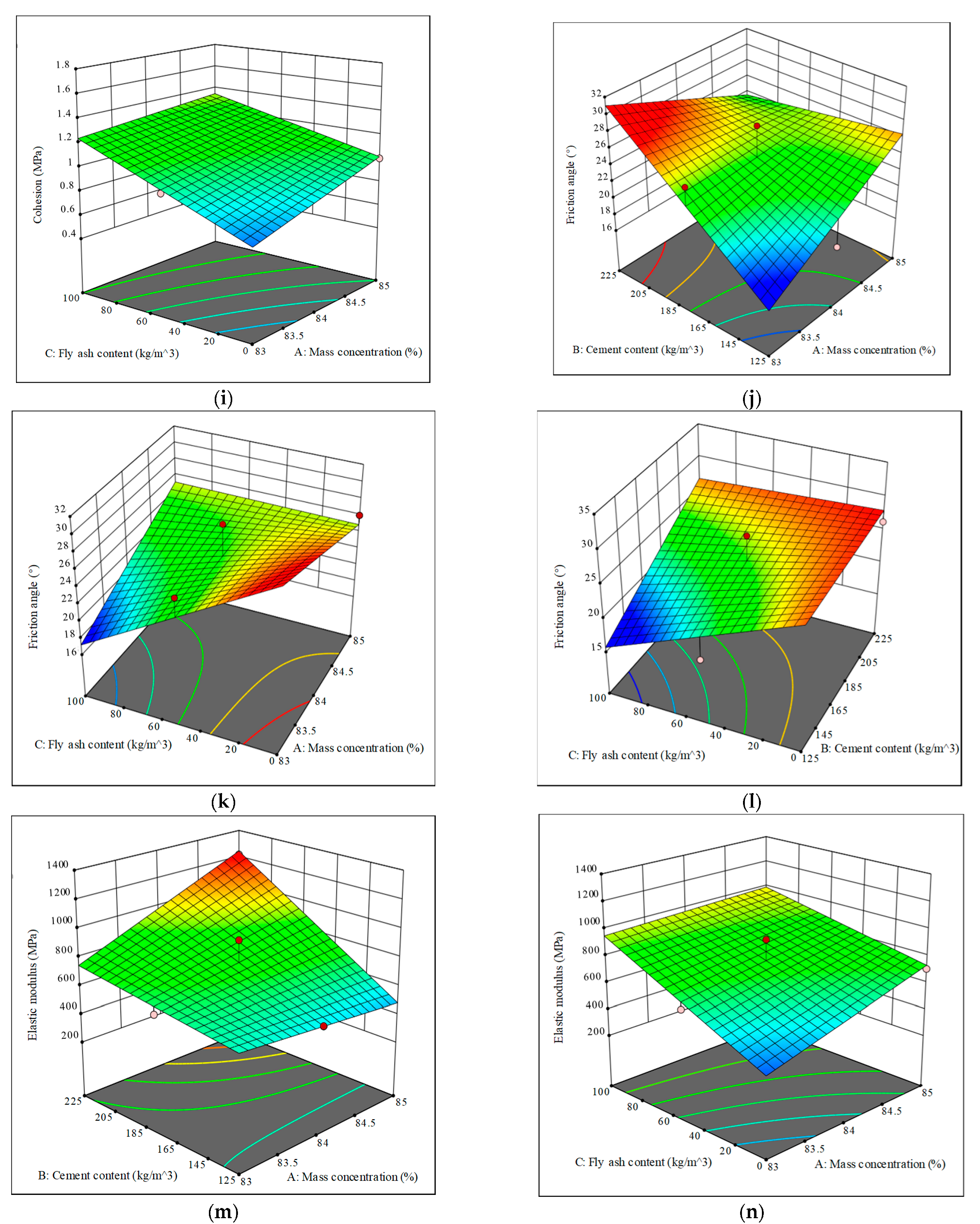
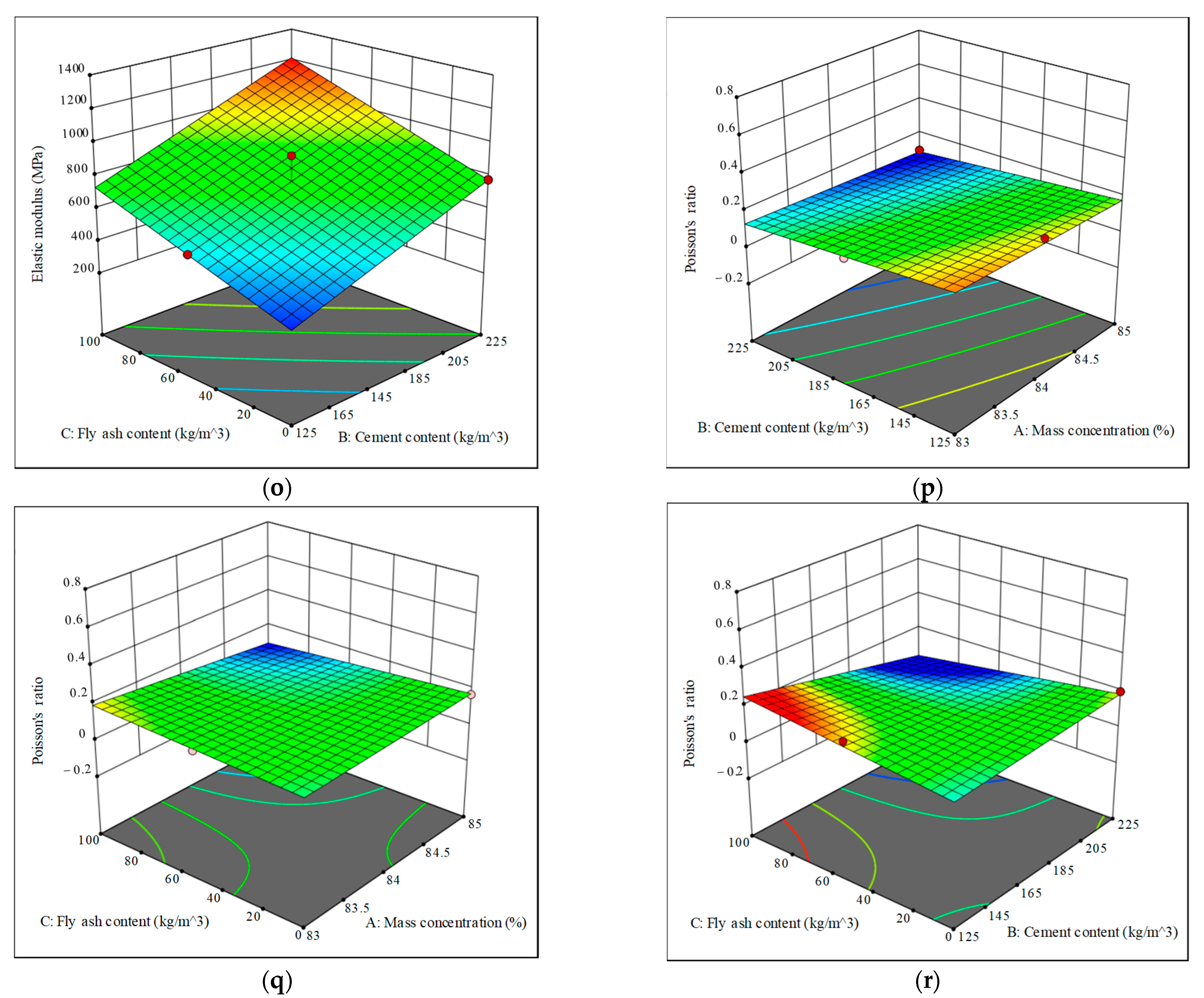
3.5. Prediction Model
4. Conclusions
- (1)
- According to the range analysis and variance analysis of the orthogonal experimental results of gangue paste filling material, it can be seen that the influence of single factor of cement content, fly ash content, and mass concentration on each performance index increases with the increase of the three-factor levels, and shows the primary and secondary relationship of cement content > fly ash content > mass concentration.
- (2)
- The uniaxial compressive strength, splitting tensile strength, cohesive force, and elastic modulus of gangue paste material can be fitted by origin, which has a good functional relationship, and this relationship is less affected by mass concentration, fly ash content, and cement content.
- (3)
- Through response surface analysis, the mathematical prediction model of the first-order interaction term between any two factors and the first-order interaction term of the influencing factors of the mechanical and deformation properties of gangue gypsum material is established, and it has high accuracy.
- (4)
- In this paper, the orthogonal experiment is selected in the experiment, and the number of experiments is reduced, which may lead to some shortcomings in the test results. Therefore, more experiments need to be carried out in the future, and the artificial intelligence prediction will be combined to acquire a better model.
- (5)
- The mechanical property prediction model of gangue gypsum body material is used to guide the determination of the proportion parameters of the filling body material in Gaohe coal mine. Through filling mining, a large amount of solid wastes in Gaohe coal mine are treated, and the problems of coal pressing under buildings are also solved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skrzypkowski, K. Comparative Analysis of the Mining Cribs Models Filled with Gangue. Energies 2020, 13, 5290. [Google Scholar] [CrossRef]
- Skrzypkowski, K. Decreasing Mining Losses for the Room and Pillar Method by Replacing the Inter-Room Pillars by the Construction of Wooden Cribs Filled with Waste Rocks. Energies 2020, 13, 3564. [Google Scholar] [CrossRef]
- Zhou, H.; Qu, Q.; Hou, C.; Zhao, C.; Chen, D.; Zhao, Q. Paste backfill study for none-village-relocation coal mining. In Mining Science and Technology; CRC Press: London, UK, 2004; pp. 91–94. [Google Scholar]
- Sun, Y.; Li, G.; Zhang, J. Investigation on jet grouting support strategy for controlling time-dependent deformation in the roadway. Energy Sci. Eng. 2020, 8, 2151–2158. [Google Scholar] [CrossRef]
- Keita, A.M.T.; Jahanbakhshzadeh, A.; Li, L. Numerical analysis of the stability of arched sill mats made of cemented backfill. Int. J. Rock Mech. Min. Sci. 2021, 140, 104667. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, H.; Sun, X.; Cao, Z.; Zhao, Q. Floor damage mechanism with cemented paste backfill mining method. Arab. J. Geosci. 2021, 14, 80. [Google Scholar] [CrossRef]
- Chang, Q.; Chang, X.S.Q.; Sun, X.; Dong, X.; Shao, S. Stability analysis of cemented paste backfill false roof in highwall mining: A case study. Desalination Water Treat. 2021, 219, 96–102. [Google Scholar] [CrossRef]
- Chang, Q.; Sun, Y.; Leng, Q.; Liu, Z.; Zhou, H.; Sun, Y. Stability Analysis of Paste Filling Roof by Cut and Fill Mining. Sustainability 2021, 13, 10899. [Google Scholar] [CrossRef]
- Sun, Y.; Bi, R.; Chang, Q.; Taherdangkoo, R.; Zhang, J.; Sun, J.; Huang, J.; Li, G. Stability Analysis of Roadway Groups under Multi-Mining Disturbances. Appl. Sci. 2021, 11, 7953. [Google Scholar] [CrossRef]
- Cavusoglu, I.; Yilmaz, E.; Yilmaz, A.O. Additivity effect on properties of cemented coal fly ash backfill containing water-reducing admixtures. Constr. Build. Mater. 2021, 267, 121021. [Google Scholar] [CrossRef]
- Sun, Y.T.; Li, G.C.; Basarir, H.; Karrech, A.; Azadi, M.R. Laboratory evaluation of shear strength properties for cement-based grouted coal mass. Arab. J. Geosci. 2019, 12, 690. [Google Scholar] [CrossRef]
- Sun, C.; Li, G.; Gomah, M.E.; Xu, J.; Rong, H. Experimental investigation on the nanoindentation viscoelastic constitutive model of quartz and kaolinite in mudstone. Int. J. Coal Sci. Technol. 2021, 8, 925–937. [Google Scholar] [CrossRef]
- Chang, Q.; Chen, J.; Zhou, H.; Bai, J. Implementation of Paste Backfill Mining Technology in Chinese Coal Mines. Sci. World J. 2014, 2014, 821025. [Google Scholar] [CrossRef] [PubMed]
- Valery, L.; Natalia, C.; Roman, F.; Amran, M. Optimization of fresh properties and durability of the green gypsum-cement paste. Constr. Build. Mater. 2021, 287, 123035. [Google Scholar]
- Nikoloutsopoulos, N.; Sotiropoulou, A.; Kakali, G.; Tsivilis, S. Physical and Mechanical Properties of Fly Ash Based Geopolymer Concrete Compared to Conventional Concrete. Buildings 2021, 11, 178. [Google Scholar] [CrossRef]
- Panuwat, J.; Nazam, A.; Qudeer, H. Performance of Hollow Bricks Made of Fly Ash, Cement and Sand. KMUTT Res. Dev. J. 2018, 8, 98–113. [Google Scholar]
- Zhang, B.; Zhou, H.; Chang, Q.; Zhao, X.; Sun, Y. The Stability Analysis of Roadway near Faults under Complex High Stress. Adv. Civ. Eng. 2020, 2020, 8893842. [Google Scholar] [CrossRef]
- Qi, C.; Guo, L.; Ly, H.-B.; Le, H.V.; Pham, B.T. Improving pressure drops estimation of fresh cemented paste backfill slurry using a hybrid machine learning method. Miner. Eng. 2021, 163, 106790. [Google Scholar] [CrossRef]
- Wu, K.; Shao, Z.; Sharifzadeh, M.; Hong, S.; Qin, S. Analytical computation of support characteristic curve for circumferential yielding lining in tunnel design. J. Rock Mech. Geotech. Eng. 2022, 14, 144–152. [Google Scholar] [CrossRef]
- Diao, S.; Hong, P.; Fu, Y.; Mao, X. Numerical Simulation Analysis of Surrounding Rock Deformation of Expansive Rock Roadway under Humidity Field. IOP Conf. Ser. Earth Environ. Sci. 2021, 719, 032034. [Google Scholar] [CrossRef]
- Pankratenko, A.; Isaev, A. The study of the influence of the rock mass heterogeneity on the stress-strain state of the shaft lining. MATEC Web Conf. 2019, 265, 04019. [Google Scholar] [CrossRef]
- Chang, Q.; Zhou, H.; Zhao, C. Application of Neural Network to Paste Backfill Quality Model. Min. Res. Dev. 2007, 5, 003. [Google Scholar]
- Sun, Y.; Li, G.; Zhang, N.; Chang, Q.; Xu, J.; Zhang, J. Development of ensemble learning models to evaluate the strength of coal-grout materials. Int. J. Min. Sci. Technol. 2021, 31, 153–162. [Google Scholar] [CrossRef]
- Mtarfi, N.H.; Rais, Z.; Taleba, M.; Kadab, K.M. Effect of fly ash and grading agent on the properties of mortar using response surface methodology. J. Build. Eng. 2017, 9, 109–116. [Google Scholar] [CrossRef]
- Le, Z.; Yu, Q.; Zhu, W.; Liu, H.; Yang, T. Experimental study on the effect of granular backfill with various gradations on the mechanical behavior of rock. Int. J. Min. Sci. Technol. 2021, 31, 889–899. [Google Scholar] [CrossRef]
- Chen, X.; Shi, X.; Zhou, J.; Li, E.; Qiu, P.; Gou, Y. High strain rate compressive strength behavior of cemented paste backfill using split Hopkinson pressure bar. Int. J. Min. Sci. Technol. 2021, 31, 387–399. [Google Scholar] [CrossRef]
- Ghirian, A.; Fall, M. Strength evolution and deformation behaviour of cemented paste backfill at early ages: Effect of curing stress, filling strategy and drainage. Int. J. Min. Sci. Technol. 2016, 26, 809–817. [Google Scholar] [CrossRef]
- Yin, S.; Yan, Z.; Chen, X.; Wang, L. Effect of fly-ash as fine aggregate on the workability and mechanical properties of cemented paste backfill. Case Stud. Constr. Mater. 2022, 16, e01039. [Google Scholar] [CrossRef]
- Liu, H.D.; Liu, S.; Xia, Z.G.; Liu, J.J.; Guo, H.; Yuan, Y.T. Study on mechanical properties and damage features of Rock-Coal-Rock combination models with defects and fillings. Geomech. Eng. 2021, 27, 239–251. [Google Scholar]
- Shao, X.; Sun, W.; Li, X.; Wang, L.; Fang, Z.; Zhao, B.; Sun, J.; Tian, C.; Xu, B. Experimental Study on the Mechanical Properties and Failure Characteristics of Layered Aeolian Sand Paste-Like Backfill-A Case Study from Shanghe Coal Mine. Minerals 2021, 11, 577. [Google Scholar] [CrossRef]
- Cong, M.; Zhang, S.; Sun, D.; Zhou, K. Optimization of Preparation of Foamed Concrete Based on Orthogonal Experiment and Range Analysis. Front. Mater. 2021, 8, 778173. [Google Scholar] [CrossRef]
- Jiang, B.; Xia, W.; Wu, T.; Liang, J. The optimum proportion of hygroscopic properties of modified soil composites based on orthogonal test method. J. Clean. Prod. 2021, 278, 123828. [Google Scholar] [CrossRef]
- Nunes, F.M.; Ferreira, C.C.; Pavan, F.A.; Guterres, M.X.; Quintana, L.M. Evaluation of Physical Parameters of a Clay with the Incorporation of Industrial Ash Waste by Means of Variance Analysis. Mater. Sci. Forum 2016, 881, 881. [Google Scholar] [CrossRef]








| Component | SiO2 | Al2O3 | CaO | Fe2O3 | C |
|---|---|---|---|---|---|
| Content | 48.8% | 20.3% | 2.2% | 6.2% | 9.9% |
| Consistency of Clean Pulp | Volume Stability | Fineness/% 0.08 mm Standard Sieve Residue | Setting Time/h:min | |
|---|---|---|---|---|
| Initial Setting | Final Coagulation | |||
| 23 | Stable | 4.00 | 2:00 | 5:00 |
| Flexural Strength/MPa | UCS/MPa | Flexural Compression Ratio | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 d | 7 d | 28 d | 3 d | 7 d | 28 d | 3 d | 7 d | 28 d |
| 6.76 | 6.85 | 7.03 | 37.3 | 40.9 | 43.1 | 0.10 | 0.17 | 0.16 |
| Level of Orthogonal | Influence Factor | ||
|---|---|---|---|
| Mass Concentration (%) | Cement Content (kg/m3) | Fly Ash (kg/m3) | |
| Level 1 | 83 | 125 | 0 |
| Level 2 | 84 | 175 | 50 |
| Level 3 | 85 | 225 | 100 |
| No. | Mass Concentration (%) | Cement Content (kg/m3) | Fly Ash (kg/m3) | PA (kg/m3) | HA (kg/m3) | Slump (mm) | Expansion Degree (mm) |
|---|---|---|---|---|---|---|---|
| GH-1 | 83 | 125 | 0 | 3 | 5 | 240 | 500 |
| GH-2 | 83 | 175 | 50 | 3 | 5 | 260 | 580 |
| GH-3 | 83 | 225 | 100 | 3 | 5 | 265 | 620 |
| GH-4 | 84 | 125 | 50 | 3 | 5 | 255 | 590 |
| GH-5 | 84 | 175 | 100 | 3 | 5 | 265 | 550 |
| GH-6 | 84 | 225 | 0 | 3 | 5 | 268 | 610 |
| GH-7 | 85 | 125 | 100 | 3 | 5 | 255 | 595 |
| GH-8 | 85 | 175 | 0 | 3 | 5 | 250 | 510 |
| GH-9 | 85 | 225 | 50 | 3 | 5 | 236 | 410 |
| Size | Quantity | Function |
|---|---|---|
| 100 mm × 100 mm × 100 mm | There are 6 for each ratio, and 54 specimens in total | 27 for cube compression test; 27 for splitting tensile test |
| 50 mm × 100 mm cylindrical | There are 3 for each ratio, and 27 specimens in total | Determination of elastic modulus and Poisson’s ratio |
| No. | UCS (MPa) | Splitting Tensile Strength (MPa) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| GH-1 | 3.00 | 0.60 | 0.55 | 25.1 | 318.20 | 0.12 |
| GH-2 | 6.37 | 1.18 | 0.93 | 25.9 | 618.64 | 0.16 |
| GH-3 | 9.33 | 1.51 | 1.40 | 25.9 | 1028.23 | 0.10 |
| GH-4 | 3.89 | 0.72 | 0.76 | 18.0 | 542.06 | 0.22 |
| GH-5 | 7.41 | 1.19 | 1.06 | 28.1 | 924.58 | 0.10 |
| GH-6 | 8.37 | 1.25 | 1.19 | 26.3 | 778.57 | 0.20 |
| GH-7 | 5.07 | 1.00 | 0.79 | 24.3 | 573.54 | 0.21 |
| GH-8 | 6.54 | 1.12 | 1.00 | 26.1 | 707.08 | 0.17 |
| GH-9 | 10.16 | 1.61 | 1.72 | 23.1 | 1218.87 | 0.10 |
| Index | UCS | Splitting Tensile Strength | Cohesion | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mass Concentration | Cement Content | Fly Ash Content | Mass Concentration | Cement Content | Fly Ash Content | Mass Concentration | Cement Content | Fly Ash Content | |
| K1j | 6.23 | 3.99 | 5.97 | 1.10 | 0.77 | 0.99 | 0.96 | 0.70 | 0.91 |
| K2j | 6.56 | 6.77 | 6.81 | 1.09 | 1.16 | 1.17 | 1.00 | 1.00 | 1.14 |
| K3j | 7.26 | 9.29 | 7.27 | 1.24 | 1.46 | 1.23 | 1.17 | 1.44 | 1.08 |
| R | 1.03 | 5.30 | 1.30 | 0.15 | 0.69 | 0.24 | 0.21 | 0.74 | 0.23 |
| Index | Friction Angle (°) | Elastic Modulus (MPa) | Poisson’s Ratio | ||||||
| Mass Concentration | Cement Content | Fly Ash Content | Mass Concentration | Cement Content | Fly Ash Content | Mass Concentration | Cement Content | Fly Ash Content | |
| K1j | 25.6 | 22.5 | 25.8 | 655.02 | 477.93 | 601.28 | 0.13 | 0.18 | 0.16 |
| K2j | 24.1 | 26.7 | 22.3 | 748.40 | 750.10 | 793.19 | 0.17 | 0.14 | 0.16 |
| K3j | 24.5 | 25.1 | 26.1 | 833.16 | 1008.56 | 842.12 | 0.16 | 0.13 | 0.14 |
| R | 1.5 | 4.2 | 3.8 | 178.14 | 530.63 | 240.84 | 0.04 | 0.05 | 0.02 |
| Sources of Volatility | UCS (MPa) | Splitting Tensile Strength (MPa) | Cohesion (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sum of Squares of Deviations (SS) | F Value | Critical Test Value (Fa) | Sum of Squares of Deviations (SS) | F Value | Critical Test Value (Fa) | Sum of Squares of Deviations (SS) | F Value | Critical Test Value (Fa) | |
| Mass concentration | 1.642 | 11.95 | F0.05 (2, 8) = 4.46 | 0.059 | 54.63 | F0.05 (2, 8) = 4.46 | 0.074 | 2.48 | F0.05 (2, 8) = 4.46 |
| Cement content | 42.172 | 307.03 | F0.01 (2, 8) = 8.65 | 0.705 | 647.53 | F0.01 (2, 8) = 8.65 | 0.824 | 27.70 | F0.01 (2, 8) = 8.65 |
| Fly ash content | 2.605 | 18.96 | F0.1 (2, 8) = 3.11 | 0.096 | 87.82 | F0.1 (2, 8) = 3.11 | 0.082 | 2.74 | F0.1 (2, 8) = 3.11 |
| Error, c | 0.137 | 0.011 | 0.030 | ||||||
| Sum | 46.556 | 0.861 | 1.010 | ||||||
| Sources of Volatility | Friction Angle (°) | Elastic Modulus (MPa) | Poisson’s Ratio | ||||||
| Sum of Squares of Deviations (SS) | F Value | Critical Test Value (Fa) | Sum of Squares of Deviations (SS) | F Value | Critical Test Value (Fa) | Sum of Squares of Deviations (SS) | F Value | Critical Test Value (Fa) | |
| Mass concentration | 3.669 | 0.40 | F0.05 (2, 8) = 4.46 | 47,638 | 1.16 | F0.05 (2, 8) = 4.46 | 0.003 | 0.32 | F0.05 (2, 8) = 4.46 |
| Cement content | 27.416 | 3.01 | F0.01 (2, 8) = 8.65 | 422,436 | 10.30 | F0.01 (2, 8) = 8.65 | 0.004 | 0.39 | F0.01 (2, 8) = 8.65 |
| Fly ash content | 26.509 | 2.91 | F0.1 (2, 8) = 3.11 | 97,223 | 2.37 | F0.1 (2, 8) = 3.11 | 0.001 | 0.12 | F0.1 (2, 8) = 3.11 |
| Error, c | 9.109 | 40,995 | 0.011 | ||||||
| Sum | 66.702 | 608,292 | 0.020 | ||||||
| Variation Source | UCS (MPa) | Splitting Tensile Strength (MPa) | Cohesion | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sum of Squares | p Value | R2 | Sum of Squares | p Value | R2 | Sum of Squares | p Value | R2 | |
| Model | 46.450 | 0.007 | 0.998 | 0.820 | 0.122 | 0.957 | 0.980 | 0.087 | 0.970 |
| x1 | 0.750 | 0.062 | 0.020 | 0.405 | 0.055 | 0.197 | |||
| x2 | 18.200 | 0.003 | 0.310 | 0.054 | 0.370 | 0.039 | |||
| x3 | 1.640 | 0.030 | 0.043 | 0.265 | 0.047 | 0.218 | |||
| x1x2 | 0.091 | 0.314 | 1.93 × 10−4 | 0.928 | 0.011 | 0.477 | |||
| x1x3 | 1.371 × 10−3 | 0.885 | 2.143 × 10−5 | 0.976 | 1.167 × 10−4 | 0.938 | |||
| x2x3 | 2.288 × 10−3 | 0.853 | 9.524 × 10−4 | 0.841 | 7.202 × 10−3 | 0.560 | |||
| Residual | 0.100 | 0.037 | 0.030 | ||||||
| Net error | 46.560 | 0.860 | 1.010 | ||||||
| Variation Source | Friction Angle (°) | Elastic Modulus (MPa) | Poisson’s Ratio | ||||||
| Sum of Squares | p Value | R2 | Sum of Squares | p Value | R2 | Sum of Squares | p Value | R2 | |
| Model | 65.150 | 0.604 | 0.735 | 6.062 × 105 | 0.011 | 0.997 | 0.017 | 0.329 | 0.875 |
| x1 | 3.460 | 0.642 | 27,749.060 | 0.036 | 2.881 × 10−4 | 0.677 | |||
| x2 | 30.520 | 0.249 | 1.448 × 105 | 0.007 | 3.086 × 10−3 | 0.255 | |||
| x3 | 50.270 | 0.175 | 91,202.260 | 0.012 | 1.61 × 10−3 | 0.372 | |||
| x1x2 | 37.720 | 0.215 | 20,315.680 | 0.049 | 6.095 × 10−4 | 0.555 | |||
| x1x3 | 20.440 | 0.318 | 4318.630 | 0.182 | 4.024 × 10−4 | 0.626 | |||
| x2x3 | 13.710 | 0.393 | 881.740 | 0.459 | 3.438 × 10−3 | 0.237 | |||
| Residual | 23.550 | 2127.330 | 2.467 × 10−3 | ||||||
| Net error | 88.700 | 6.083 × 105 | 0.020 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, Q.; Chang, Q.; Sun, Y.; Zhang, B.; Qin, J. The Mechanical Properties of Gangue Paste Material for Deep Mines: An Experimental and Model Study. Materials 2022, 15, 5904. https://doi.org/10.3390/ma15175904
Leng Q, Chang Q, Sun Y, Zhang B, Qin J. The Mechanical Properties of Gangue Paste Material for Deep Mines: An Experimental and Model Study. Materials. 2022; 15(17):5904. https://doi.org/10.3390/ma15175904
Chicago/Turabian StyleLeng, Qiang, Qingliang Chang, Yuantian Sun, Biao Zhang, and Jianzhuang Qin. 2022. "The Mechanical Properties of Gangue Paste Material for Deep Mines: An Experimental and Model Study" Materials 15, no. 17: 5904. https://doi.org/10.3390/ma15175904
APA StyleLeng, Q., Chang, Q., Sun, Y., Zhang, B., & Qin, J. (2022). The Mechanical Properties of Gangue Paste Material for Deep Mines: An Experimental and Model Study. Materials, 15(17), 5904. https://doi.org/10.3390/ma15175904







