In Situ Measurement of Cyclic Plastic Zone and Internal Strain Response of Q&P Steel near Fatigue Crack Tip Region Based on Micro-DIC
Abstract
:1. Introduction
- (1)
- The load–strain loop curves of the crack tip region are obtained by coupling the in situ strain field data with the related load data.
- (2)
- The boundary of the CPZ is obtained by the load–strain loop curve characteristic judgement algorithm.
- (3)
- In order to verify the accuracy of the measured results, the FCG test and micro-hardness experiment are performed with Compact Tension (CT) specimens of Q&P980 material, which is representative of the third generation of advanced high-strength steel (AHSS), proposed by Speer et al. in 2003 [30].
- (4)
- The evolution law of the shape and size of the measured CPZ are analyzed, and the strain response characteristics in the CPZ are discussed.
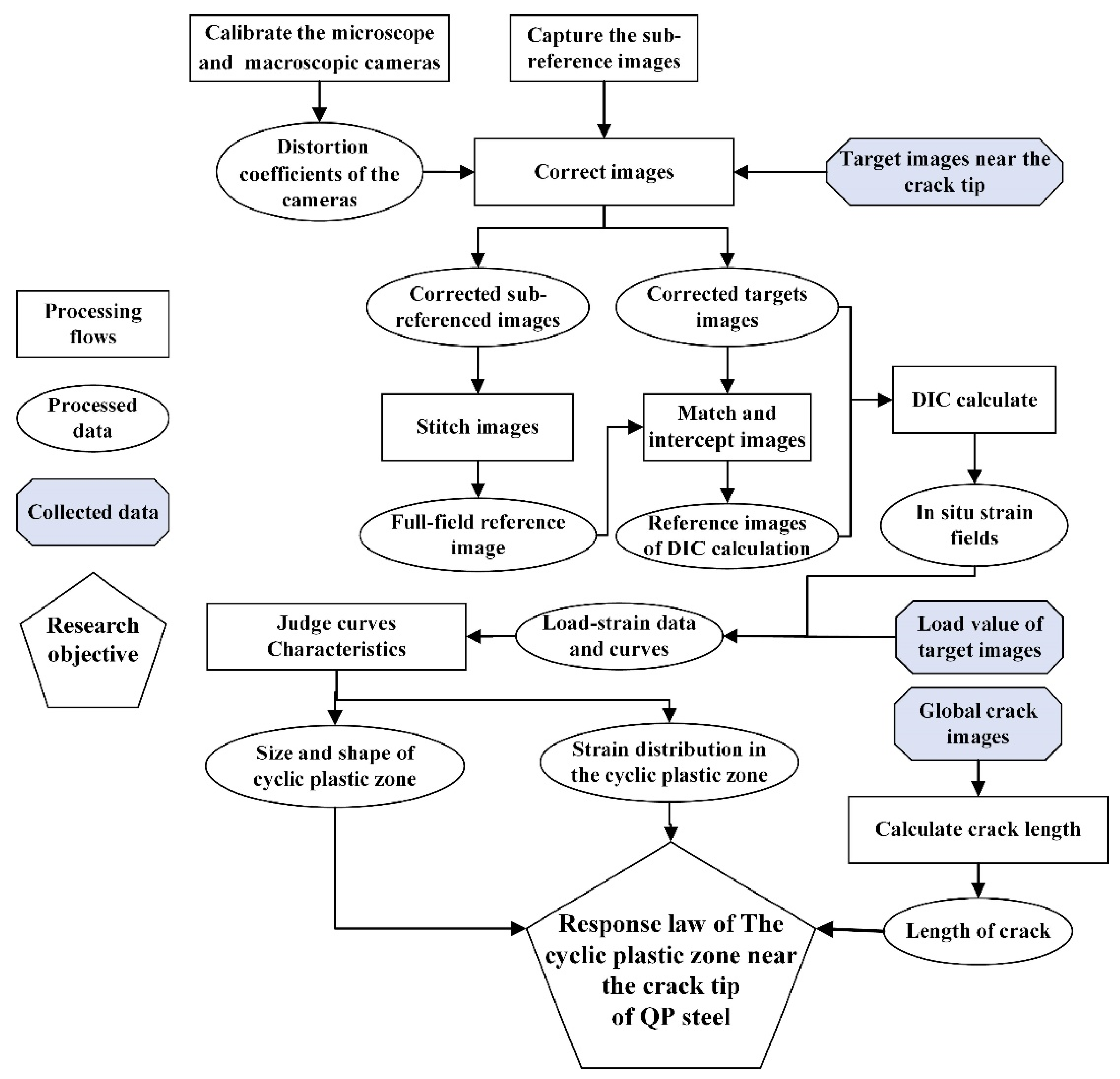
2. In Situ Crack Tip CPZ and Internal Strain Response Measurement System
2.1. Overall Measurement Method
2.2. Materials and Specimen
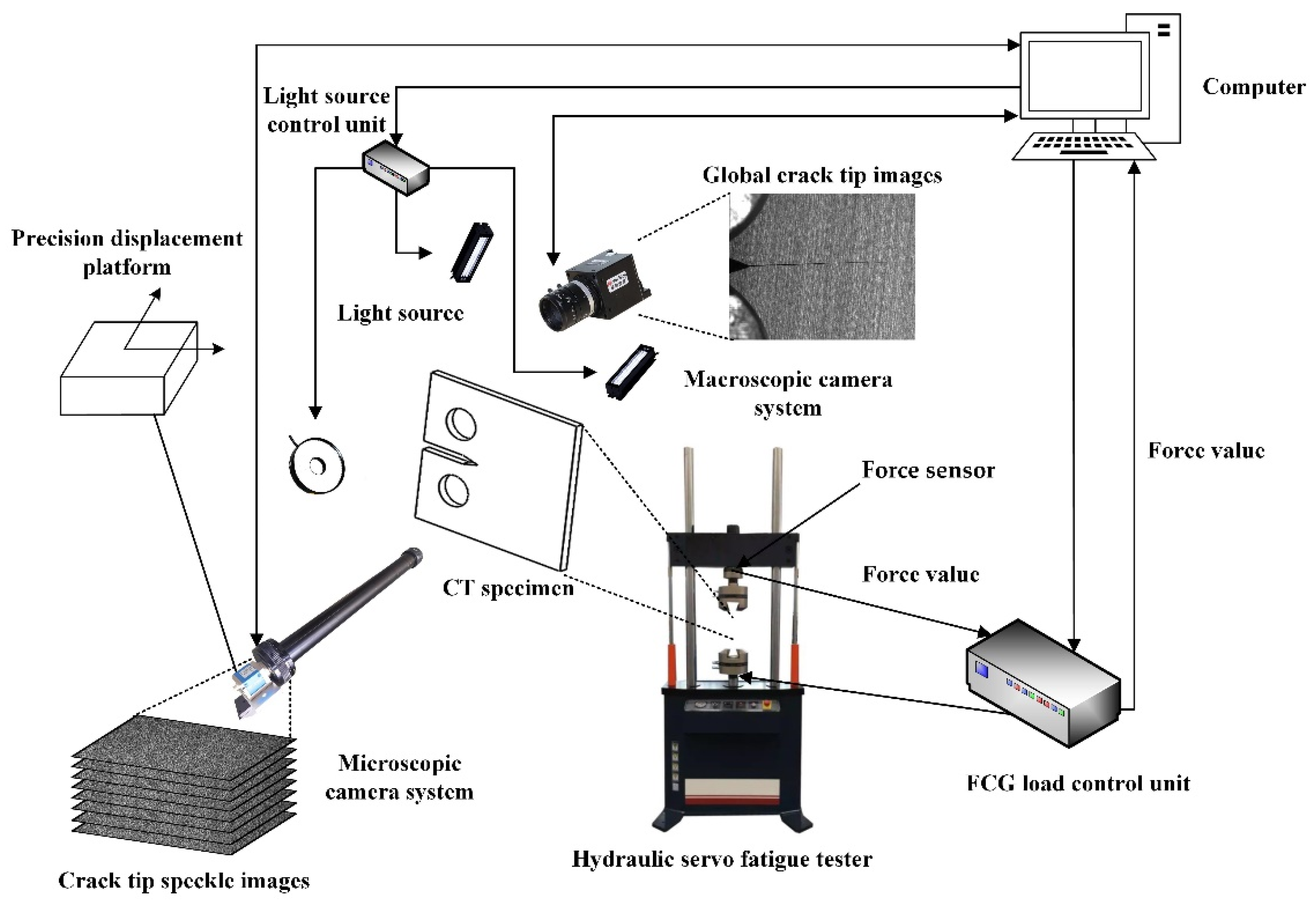
2.3. In Situ CPZ Measurement System Components and Multi-Scale Images Acquisition
- (1)
- Capturing sub-reference images before the FCG test: The microscopic camera moving step was set to be 2 mm, which is half of the horizontal field of view. The fatigue crack growth length was set to be 8 mm. Four sub-reference images, as shown in Figure 5, were collected by moving the microscopic camera shown in Figure 4. After the four speckle images were captured, the position of the microscopic camera needed to be reset to the initial position.
- (2)
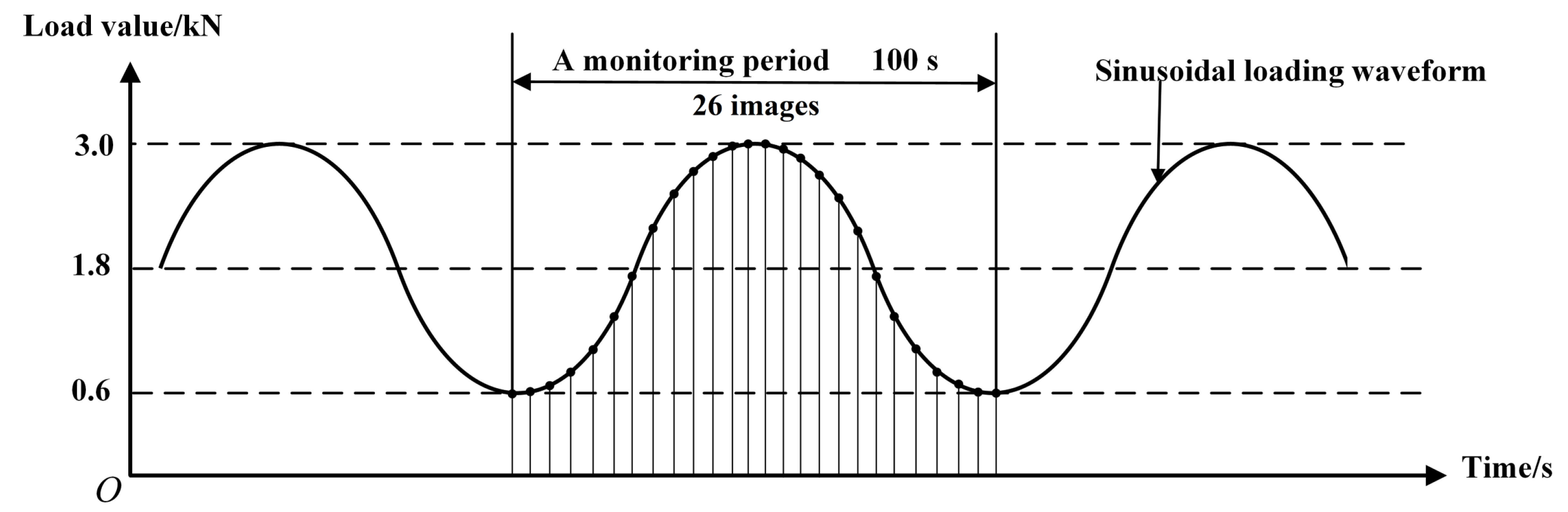
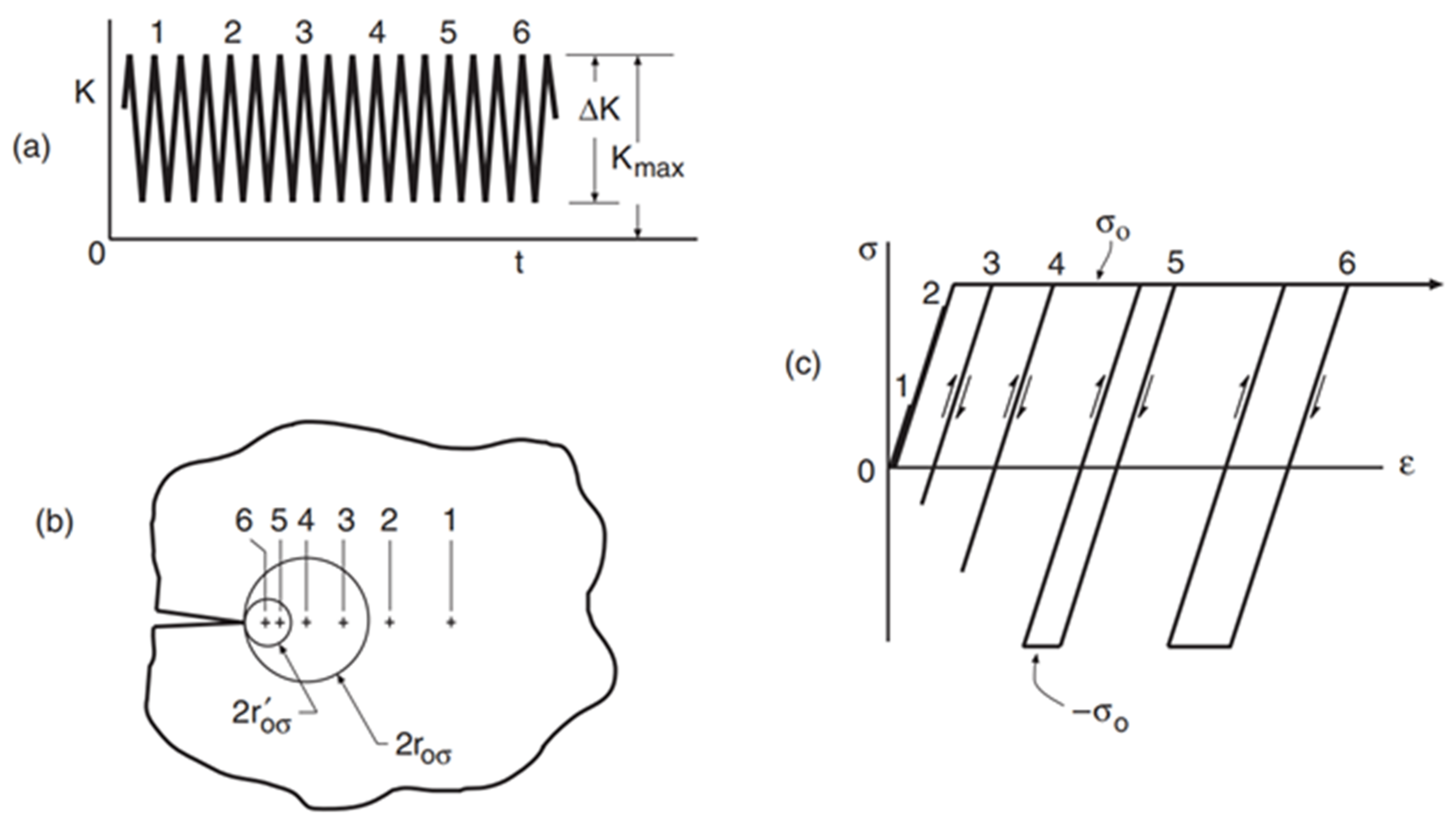
- Capturing target images during the FCG test: After setting test parameters, the FCG test was started. The FCG test load parameters are shown in Figure 6, and the fatigue testing frequency was 8 Hz. Under these test conditions, the fatigue crack could grow stably until the fatigue crack length was close to 15 mm according to previous experience. In order to ensure that the collected images could be used to calculate the strain field, when the position of the crack tip was close to 1/3 of the right edge of the microscopic field of view, the position of the microscopic camera needed to be adjusted. Finally, six groups of images with cycle numbers of 10,000, 15,000, 20,000, 22,500, 25,000, and 27,000 were collected. In the process of image acquisition, the test frequency needed to be reduced to 0.01Hz, and 1 macroscopic global crack image and 26 microscopic speckle images were collected in each monitoring period and saved on the computer in a defined order. The arrangement of acquisition points for 26 speckle images are shown in Figure 6.
3. In Situ Measurement Algorithms of CPZ and Internal Response at the Crack Tip
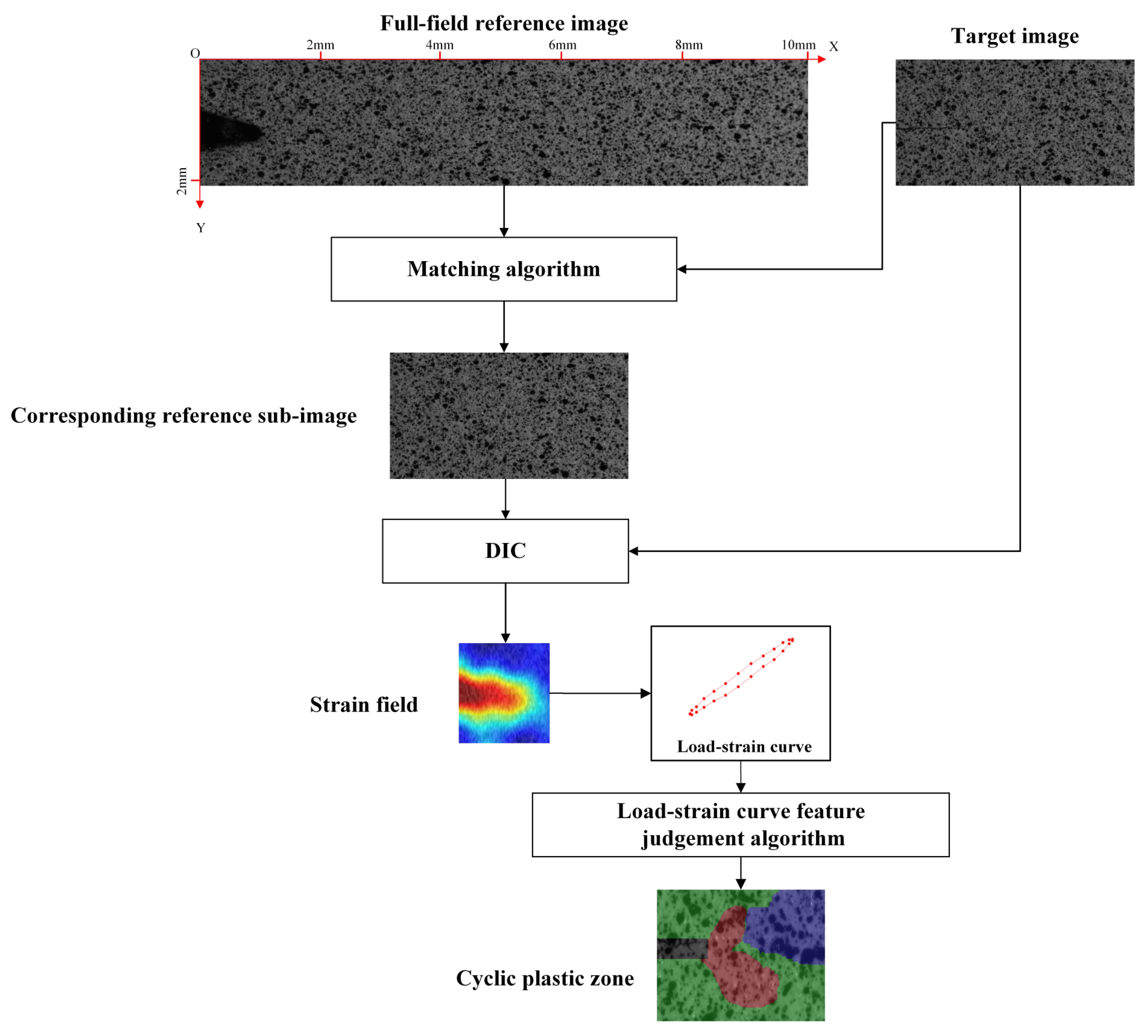
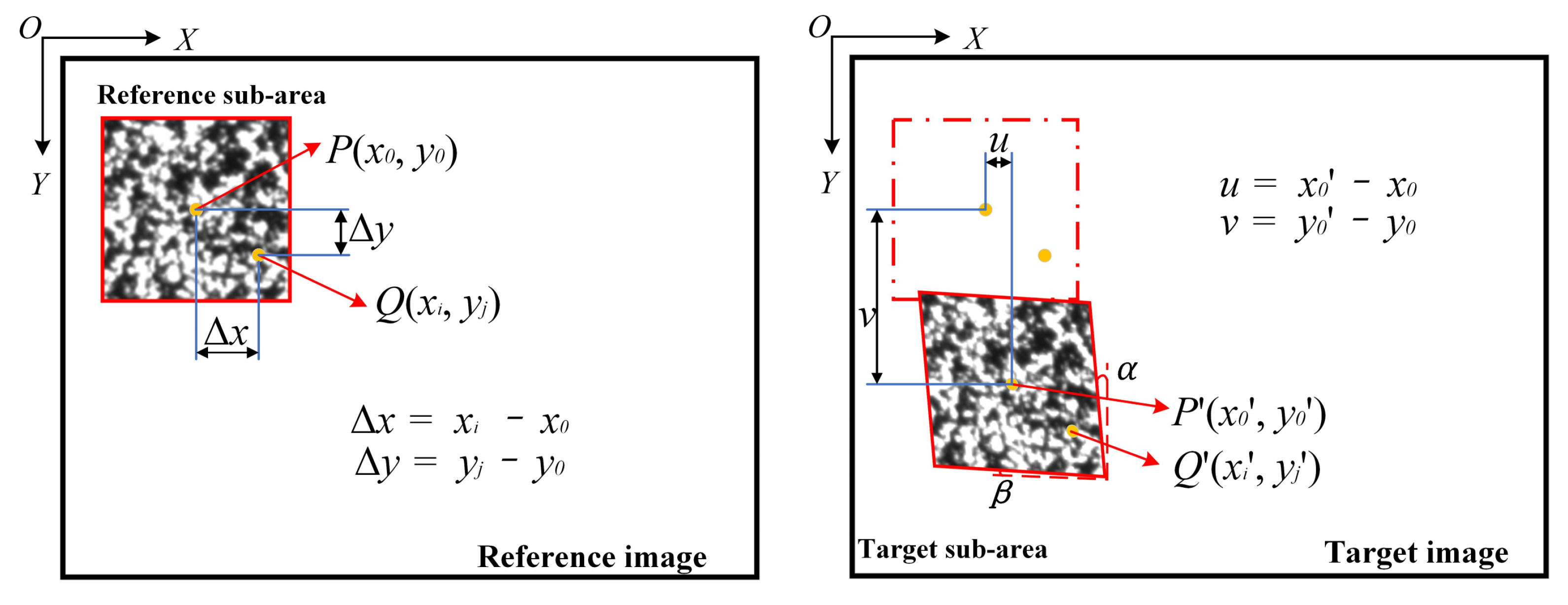
3.1. Measurement Algorithms of CPZ and Internal Response near the Crack Tip Based on DIC
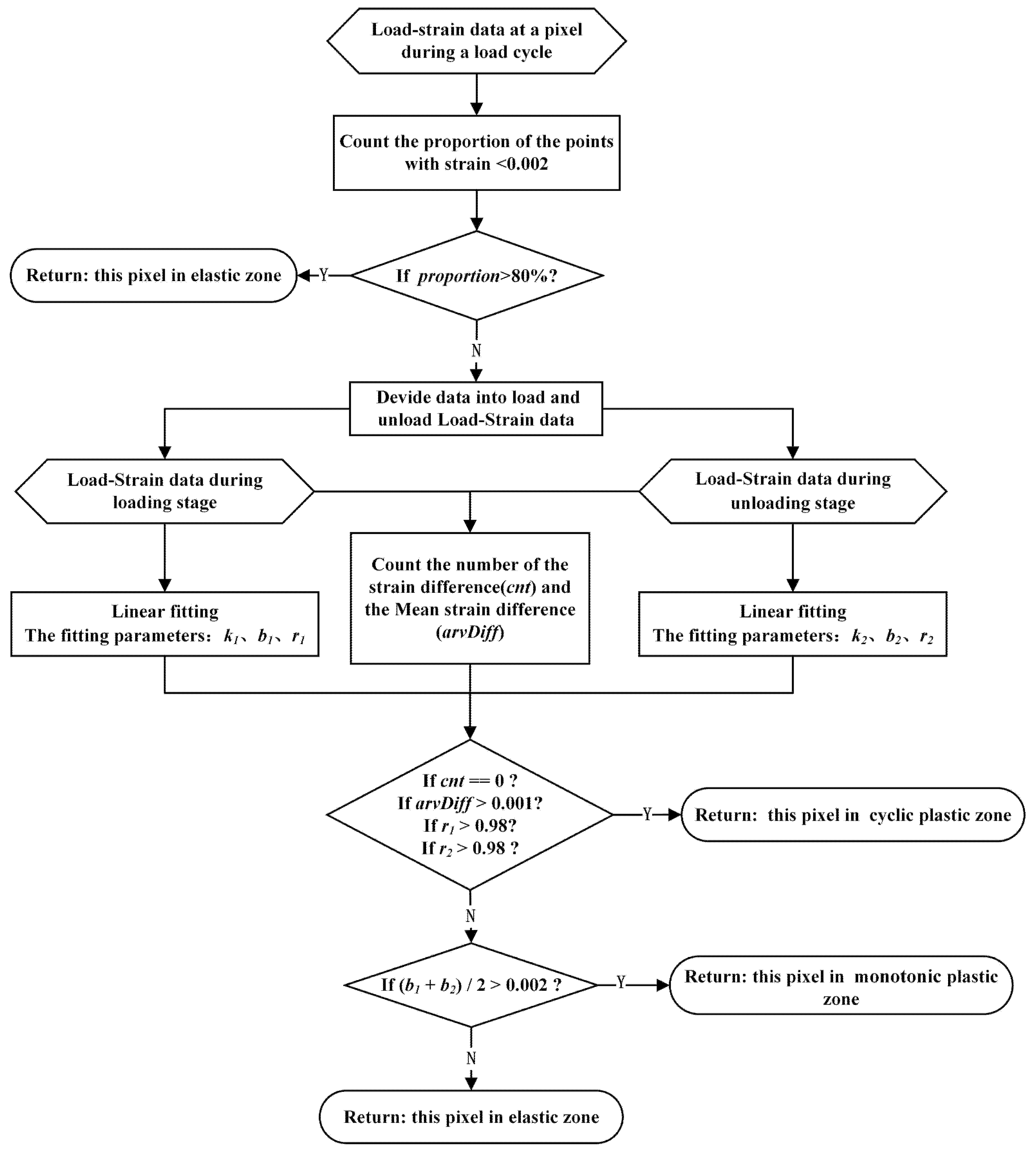
3.2. Load–Strain Loop Curve Characteristic Judgement Algorithm
4. Results and Discussion
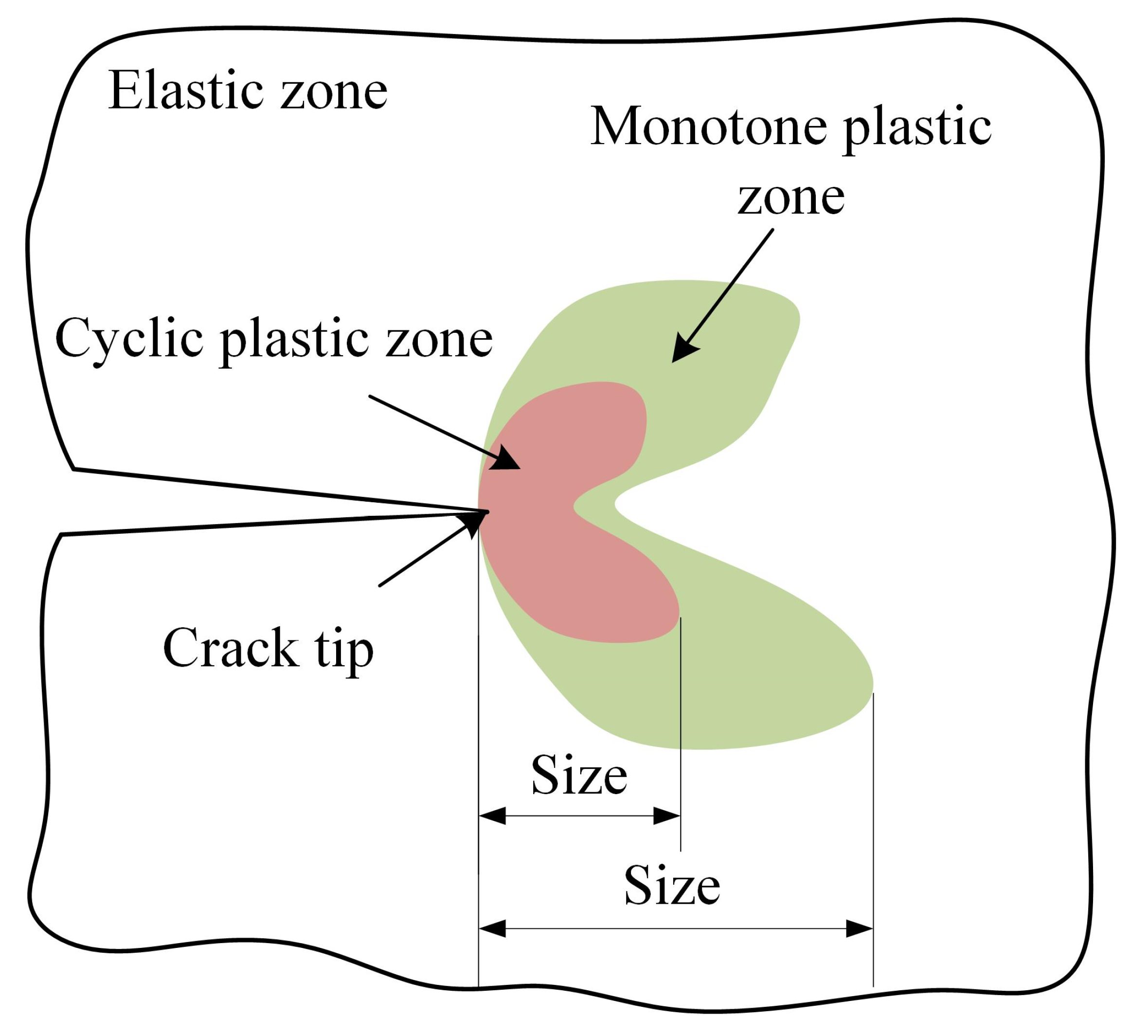
4.1. Measurement Result of the CPZ near the Fatigue Crack Tip in Q&P980 Steel
4.2. Measurement Results of the CPZ in Q&P980 Steel Verification and Analysis
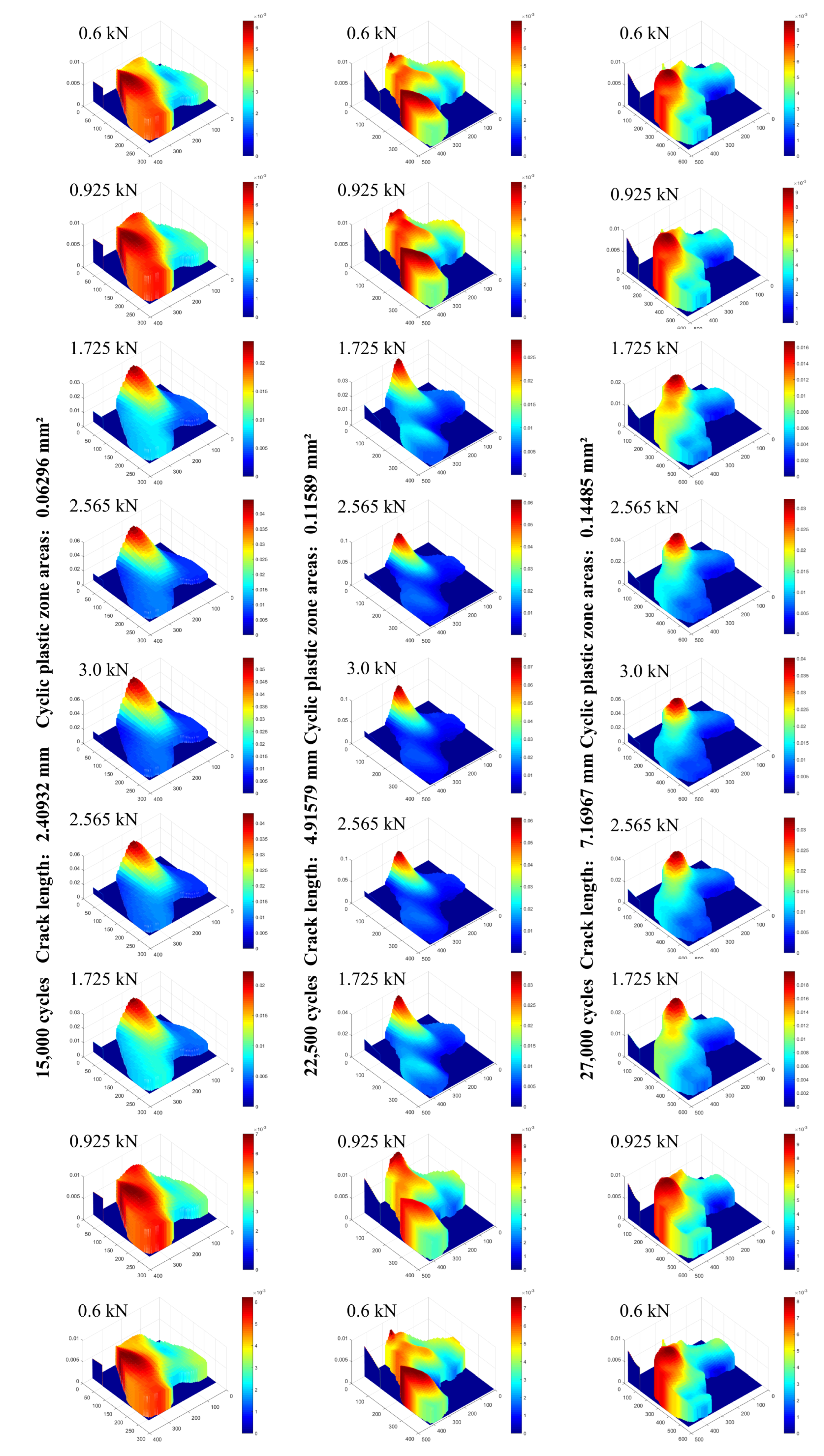
4.3. The Area Evolution Law of CPZ and the Dynamic Response in CPZ in Q&P980 Steel
4.3.1. The Area Evolution Law of CPZ in Q&P980 Steel
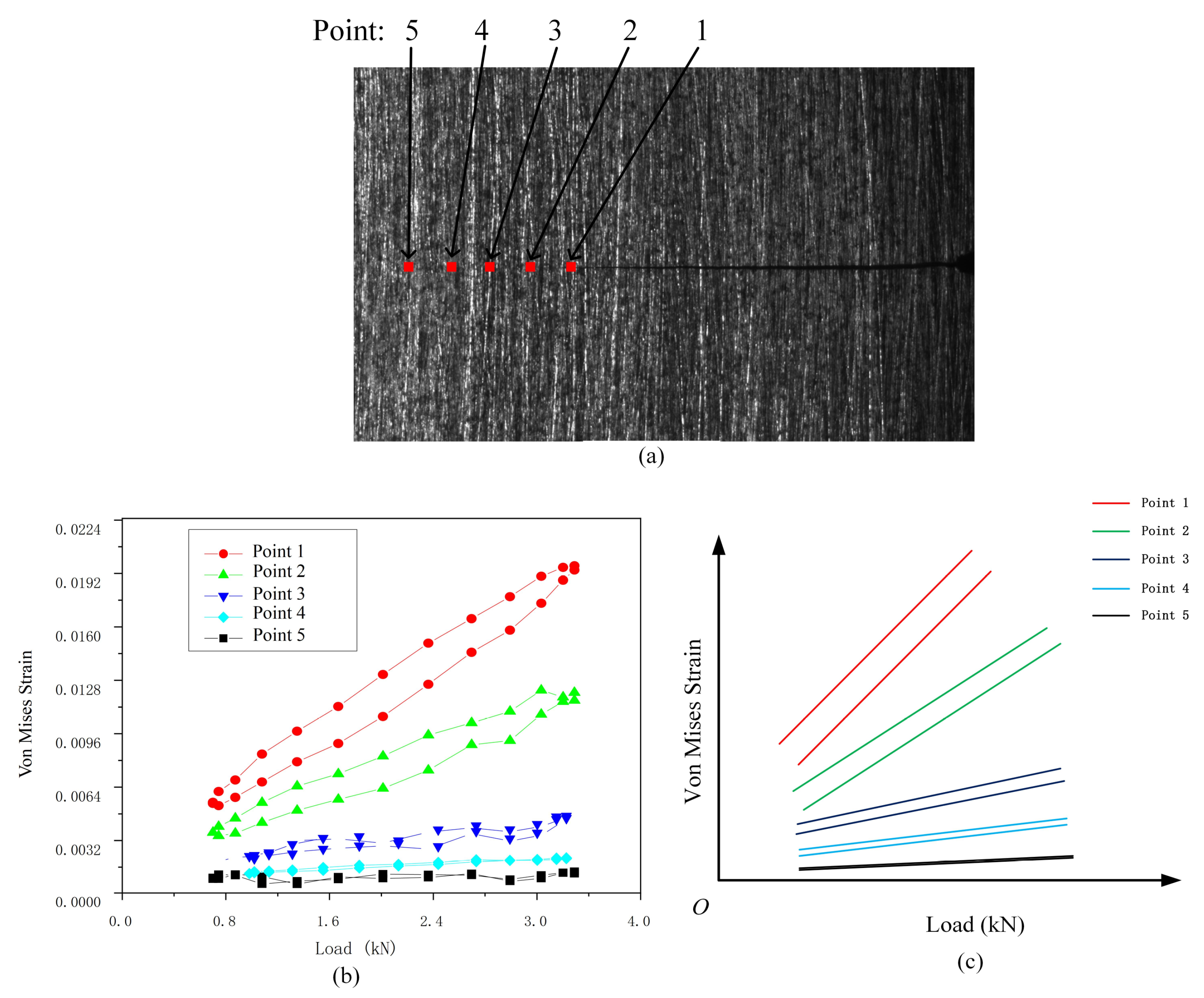
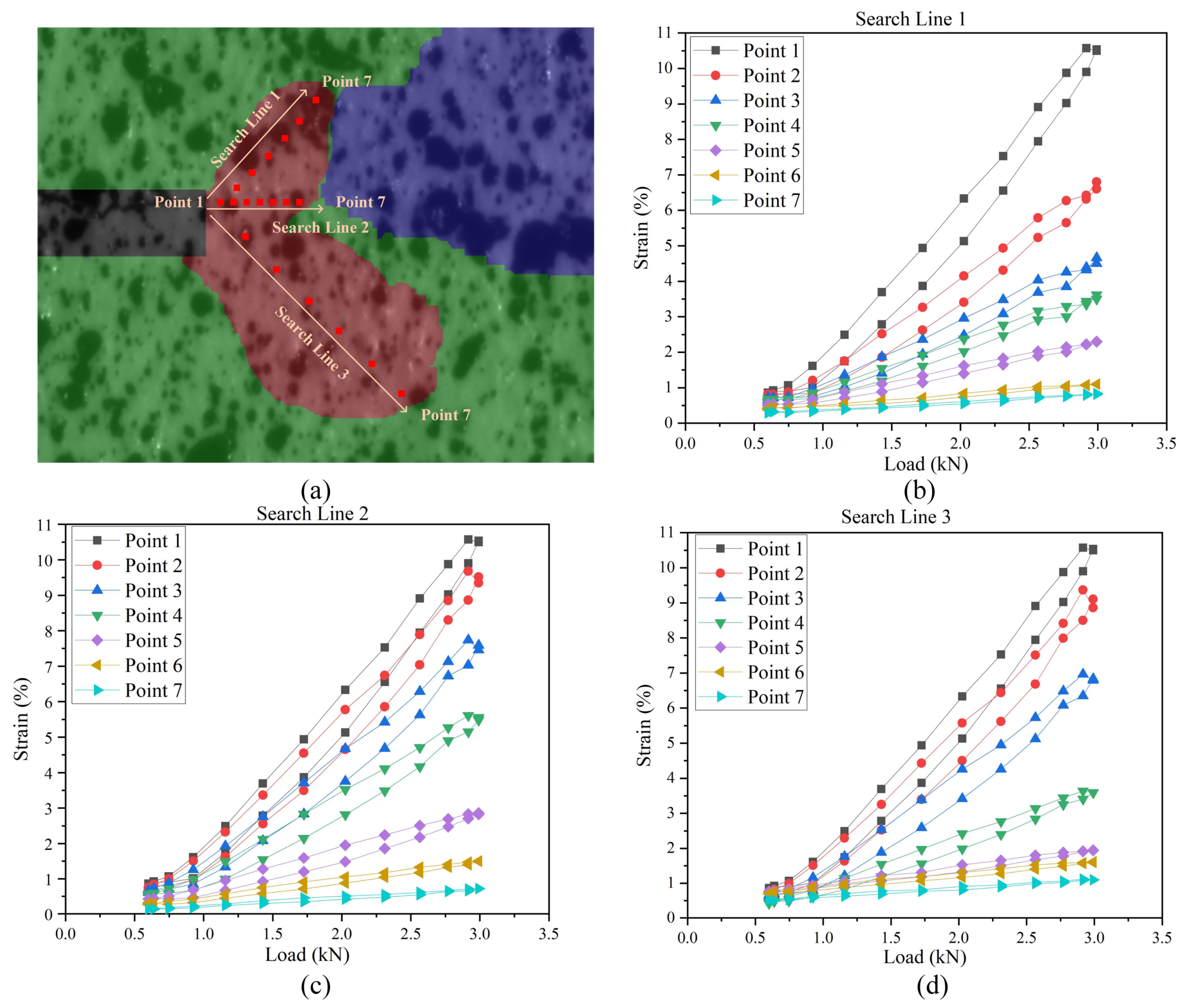
4.3.2. Strain Response in CPZ in a Load Cycle at Different Crack Lengths in Q&P980 Steel
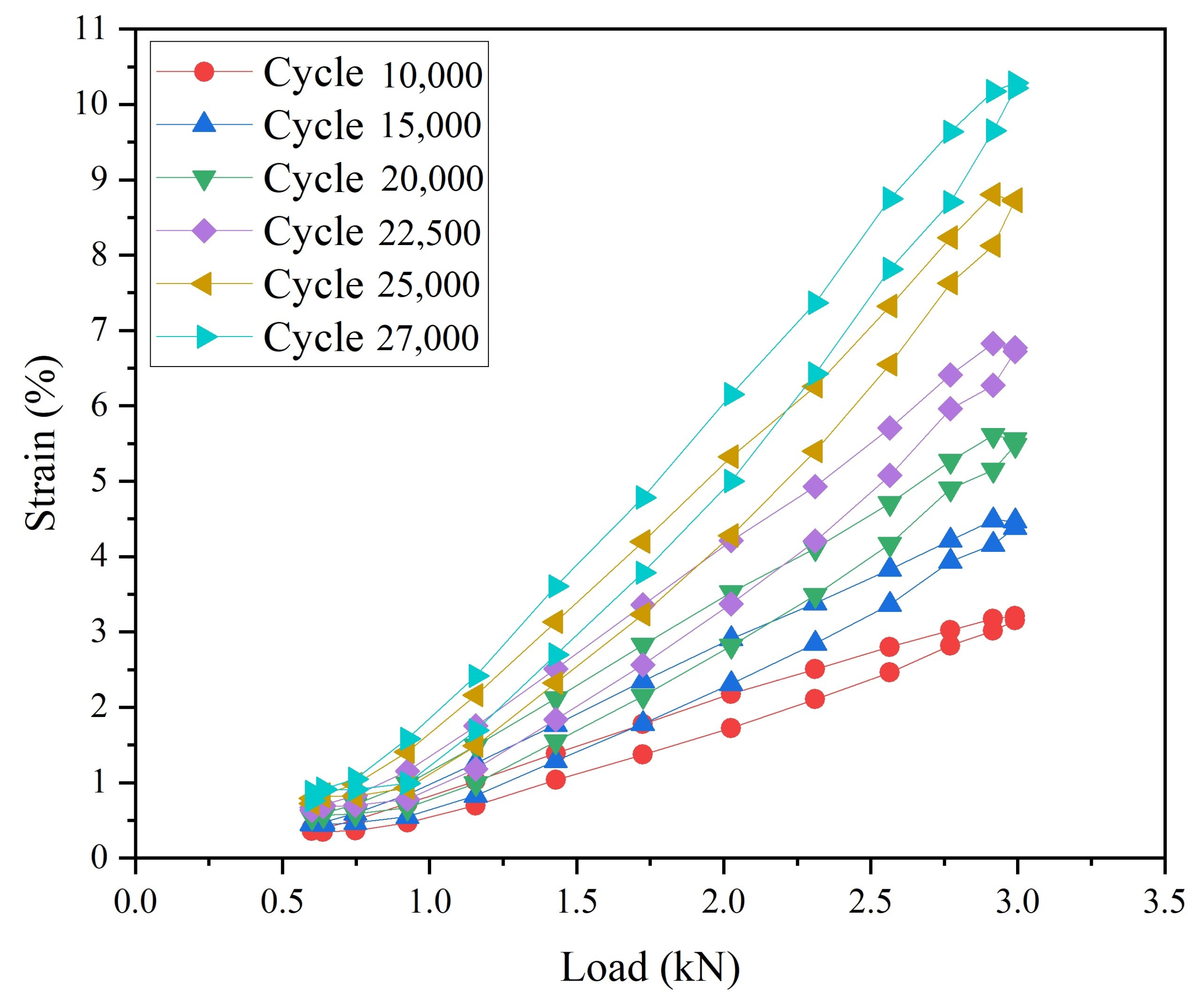
4.3.3. Load–Strain Response in CPZ during FCG Process in Q&P980 Steel
5. Conclusions
- (1)
- Comparing with the result of the micro-hardness experiment, the results of the CPZ measurements are reliable, and the measurement method proposed in this paper is available.
- (2)
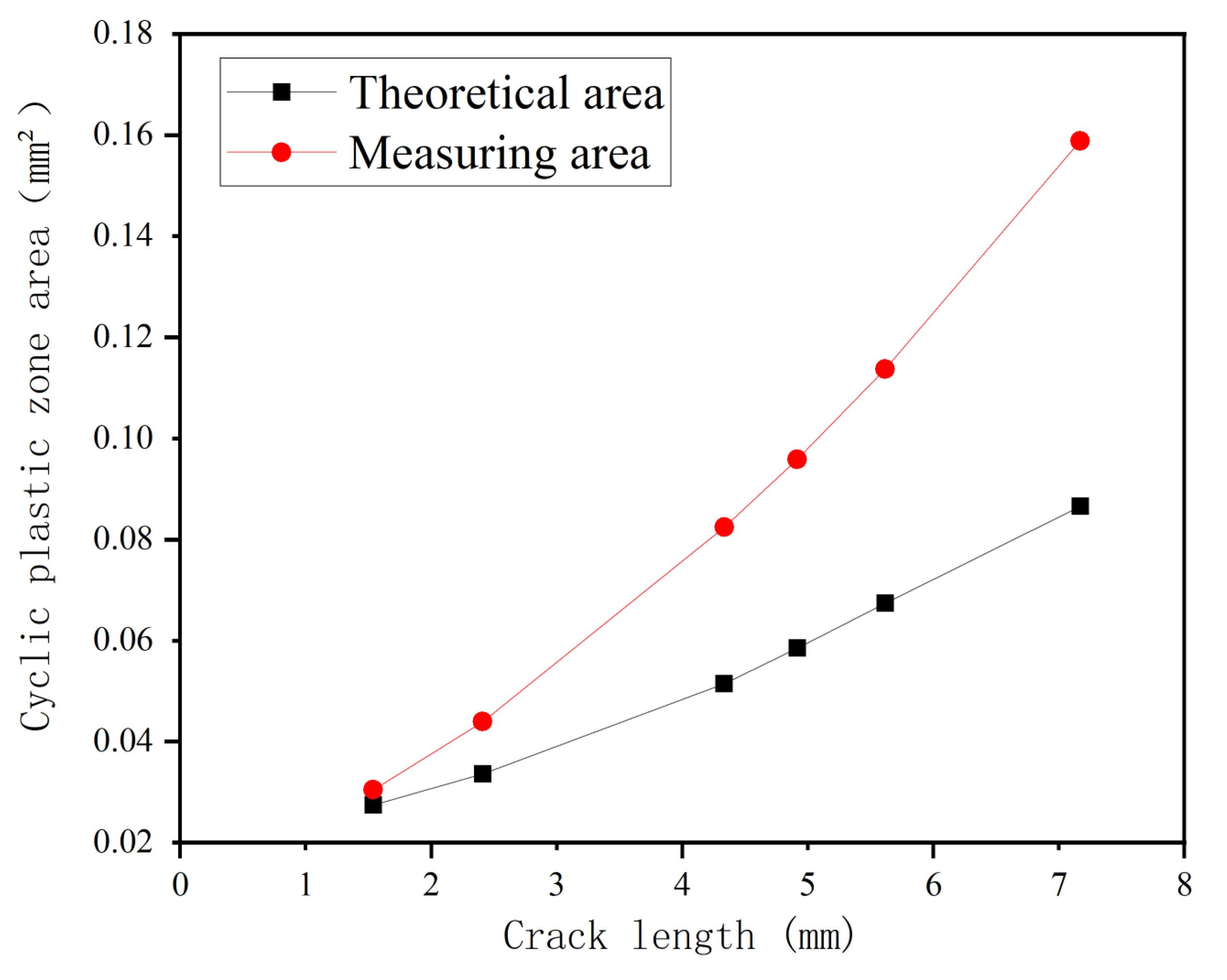
- It was observed that the CPZ near the crack tip showed a shape of butterfly wings, and the phenomenon of strain concentration was obvious near the crack tip in the CPZ. However, it is noted that the area of CPZ was greater than the theoretical value. This can be attributed to the hardening of the material.
- (3)
- The results and the analysis indicate that, with the crack propagation, the size of the CPZ, the degree of the strain concentration near the crack tip, and the area difference between theoretical and actual CPZ all increased. Moreover, within a load cycle, the strain concentration was strongest at the maximum load.
- (4)
- The results have also shown that the area of the load–strain loop at the crack tip at the maximum load gradually increased with the number of cycles. The closer to the crack tip, the larger the area of the load–strain loop.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lal, K.M.; Garg, S. On the evaluation of monotonic and CPZs. Eng. Fract. Mech. 1977, 9, 433–442. [Google Scholar] [CrossRef]
- Gonzáles, G.; González, J.; Castro, J.; Freire, J. Measuring elastoplastic strain loops in the near crack-tip region using a Stereo Microscope DIC system. Int. J. Fatigue 2019, 133, 105427. [Google Scholar] [CrossRef]
- González-Velázquez, J.L. Fatigue Fracture. In Fractography and Failure Analysis; Springer: Cham, Switzerland, 2018; pp. 71–95. [Google Scholar]
- Schijve, J. Fatigue of Structures and Materials; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Tavares, S.M.; De Castro, P.M. Damage Tolerance of Metallic Aircraft Structures; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Wasiluk, B.; Golos, K. Prediction of crack growth direction under plane stress for mixed-mode I and II loading. Fatigue Fract. Eng. Mater. Struct. 2010, 23, 381–386. [Google Scholar] [CrossRef]
- ASTM International. Fracture Toughness Testing and Its Applications; ASTM International: West Conshohocken, PA, USA, 1965. [Google Scholar]
- Vallellano, C.; Navarro, A.; Dominguez, J. Two-parameter fatigue crack growth driving force: Successive blocking of the monotonic and CPZs at microstructural barriers. Int. J. Fatigue 2013, 46, 27–34. [Google Scholar] [CrossRef]
- Uguz, A.; Martin, J.W. Plastic zone size measurement techniques for metallic materials. Mater. Charact. 1996, 37, 105–118. [Google Scholar] [CrossRef]
- McClung, R.C. Crack closure and plastic zone sizes in fatigue. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 455–468. [Google Scholar] [CrossRef]
- Xiong, Y.; Hu, X.X.; Katsuta, J.; Sakiyama, T.; Kawano, K. Influence of compressive plastic zone at the crack tip upon fatigue crack propagation. Int. J. Fatigue 2008, 30, 67–73. [Google Scholar] [CrossRef]
- Jingjie, C.; Yi, H.; Leilei, D.; Yugang, L. A new method for cyclic crack-tip plastic zone size determination under cyclic tensile load. Eng. Fract. Mech. 2014, 126, 141–154. [Google Scholar] [CrossRef]
- Paul, S.K.; Tarafder, S. Cyclic plastic deformation response at fatigue crack tips. Int. J. Press. Vessel. Pip. 2013, 101, 81–90. [Google Scholar] [CrossRef]
- Besel, M.; Breitbarth, E. Advanced analysis of crack tip plastic zone under cyclic loading. Int. J. Fatigue 2016, 93, 92–102. [Google Scholar] [CrossRef]
- Cicero, S. A Methodology to Determine the Effective Plastic Zone Size Around Blunt V-Notches under Mixed Mode I/II Loading and Plane-Stress Conditions. Metals 2021, 11, 1402. [Google Scholar]
- Torabi, A.R.; Shahbazian, B. Semi-analytical estimation of the effective plastic zone size at U-notch neighborhood in thin sheets under mixed mode I/II loading. Eng. Fract. Mech. 2020, 239, 107323. [Google Scholar] [CrossRef]
- Izumi, Y.; Fine, M.E. Role of plastic work in fatigue crack propagation in metals. Eng. Fract. Mech. 1979, 11, 791–804. [Google Scholar] [CrossRef]
- Kwun, S.I.; Fine, M.E. Dependence of cyclic plastic work of fatigue crack propagation on ΔK in MA87 A1 P/M alloy. Scr. Metall. 1980, 14, 155–158. [Google Scholar] [CrossRef]
- Hahn, G.T.; Hoagland, R.G.; Rosenfield, A.R. Local Yielding Attending Fatigue Crack Growth. Metall. Mater. Trans. B 1972, 3, 1189–1202. [Google Scholar] [CrossRef]
- Lopez-Crespo, C.; Cruces, A.S.; Seitl, S.; Moreno, B.; Lopez-Crespo, P. Estimation of the Plastic Zone in Fatigue via Micro-Indentation. Materials 2021, 14, 5885. [Google Scholar] [CrossRef]
- Tong, J. Full-field characterisation of crack tip deformation and fatigue crack growth using digital image correlation—A review. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1855–1869. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y. Plastic zone size estimation under cyclic loadings using in situ optical microscopy fatigue testing. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 717–727. [Google Scholar] [CrossRef]
- Vasco-Olmo, J.M.; James, M.N.; Christopher, C.J.; Patterson, E.A.; Díaz, F.A. Assessment of crack tip plastic zone size and shape and its influence on crack tip shielding. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 969–981. [Google Scholar] [CrossRef]
- Yang, B.; Wei, Z.; Díaz, F.; Liao, Z.; James, M.N. New algorithm for optimized fitting of DIC data to crack tip plastic zone using the CJP model. Theor. Appl. Fract. Mech. 2021, 113, 102950. [Google Scholar] [CrossRef]
- Park, H.B.; Kim, K.M.; Lee, B.W. Plastic zone size in fatigue cracking. Int. J. Press. Vessel. Pip. 1996, 68, 279–285. [Google Scholar] [CrossRef]
- Chikh, B.O.; Imad, A.; Benguediab, M. Influence of the CPZ size on the propagation of the fatigue crack in case of 12NC6 steel. Comput. Mater. Sci. 2008, 43, 1010–1017. [Google Scholar] [CrossRef]
- Bathias, C.; Pelloux, R.M. Fatigue crack propagation in martensitic and austenitic steels. Metall. Trans. 1973, 4, 1265–1273. [Google Scholar] [CrossRef]
- Gonzáles, G.; González, J.; Castro, J.; Freire, J. Using DIC techniques to measure strain ranges inside the CPZ ahead of a fatigue crack tip. Frat. Integrità Strutt. 2019, 13, 74–81. [Google Scholar] [CrossRef]
- Lin, Z.; Shang, H.; Gao, H.; Huang, X. In Situ Measurement of the Strain Field at the Fatigue Crack Tip Based on Sub-Image Stitching and Matching DIC. Materials 2022, 15, 5150. [Google Scholar] [CrossRef]
- Speer, J.; Matlock, D.K.; Cooman, B.; Schroth, J.G. Carbon partitioning into austenite after martensite transformation. Acta Mater. 2003, 51, 2611–2622. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Dowling, N.E. Mechanical Behavior of Materials—Engineering Methods for Deformation, Fracture, and Fatigue, 4th ed.; Pearson Education Limited: Edinburgh, UK, 2013; pp. 643–646. [Google Scholar]
- Jiang, H.; Du, H.; Xie, H.; Rong, L. Investigation on the micro-deformation characteristics of porous NiTi shape memory alloy using SEM Moiré method. Acta Metall. Sin. Chin. Ed. 2006, 42, 1153–1157. [Google Scholar]
- Fellows, L.J.; Nowell, D. Measurement of crack closure after the application of an overload cycle, using moiré interferometry. Int. J. Fatigue 2005, 27, 1453–1462. [Google Scholar] [CrossRef]
- Tang, M.; Xie, H.; Zhu, J.; Dan, W. The failure mechanisms of TBC structure by moiré interferometry. Mater. Sci. Eng. A 2013, 565, 142–147. [Google Scholar] [CrossRef]
- Murukeshan, V.M.; Sujatha, N. Digital speckle pattern interferometry for deformation analysis of inner surfaces of cylindrical specimens. Appl. Opt. 2004, 43, 2400–2408. [Google Scholar] [PubMed]
- Dai, X.; Qi, P.; Wang, L.; Hai, Y.; Wang, Y. Measurement on fracture process and prediction of the load capacity of steel fiber reinforced concrete by electronic speckle pattern interferometry. Compos. Part B Eng. 2011, 42, 1181–1188. [Google Scholar] [CrossRef]
- Broek, D. Elementary Engineering Fracture Mechanics. J. Appl. Mech. 1998, 42. [Google Scholar]
- Pan, B.; Qian, K.M.; Xie, H.M.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Paul, S.K. Numerical models of plastic zones and associated deformations for a stationary crack in a C(T) specimen loaded at different R-ratios. Theor. Appl. Fract. Mech. 2016, 84, 183–191. [Google Scholar] [CrossRef]
- Hui, Z.; Wei, L.; Yu, G.; Li, W.; Jin, X.J. Microstructure-based finite element modeling of effect of metastable austenite on mechanical properties of quenching and partitioning (Q&P) 980 steel. J. Iron Steel Res. Int. 2018, 25, 9. [Google Scholar]
- Hosseini, R.; Seifi, R. Influence of Hardening on the CPZ Around Crack Tip in Pure Copper CT Specimens. Bu-Ali Sina Univ. 2018, 2, 43–53. [Google Scholar]
- Bastun, V.N. On the influence of strain hardening on the length of a plastic zone near a crack tip in a transversely isotropic material. Rep. Natl. Acad. Sci. USA 2015, 11, 44–51. [Google Scholar] [CrossRef]
- Eringen, A.C.; Kim, B.S. Stress concentration at the tip of crack. Mech. Res. Commun. 1974, 1, 233–237. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Paddea, S.; Xiang, Z. Fatigue crack propagation behaviour in wire+arc additive manufactured Ti-6Al-4V: Effects of microstructure and residual stress. Mater. Des. 2016, 90, 551–561. [Google Scholar] [CrossRef]
- Tong, J.; Lin, B.; Lu, Y.W.; Madi, K.; Tai, Y.H.; Yates, J.R.; Doquet, V. Near-tip strain evolution under cyclic loading: In situ experimental observation and numerical modelling. Int. J. Fatigue 2015, 71, 45–52. [Google Scholar] [CrossRef]
- Lu, Y.W.; Lupton, C.; Zhu, M.L.; Tong, J. In Situ Experimental Study of Near-Tip Strain Evolution of Fatigue Cracks. Exp. Mech. 2015, 55, 1175–1185. [Google Scholar] [CrossRef]
- Reed, J.M.; Walter, M.E. Observations of serration characteristics and acoustic emission during serrated flow of an Al–Mg alloy. Mater. Sci. Eng. A 2003, 359, 1–10. [Google Scholar] [CrossRef]
- Abbadi, M.; Hähner, P.; Zeghloul, A. On the characteristics of Portevin–Le Chatelier bands in aluminum alloy 5182 under stress-controlled and strain-controlled tensile testing. Mater. Sci. Eng. A 2002, 337, 194–201. [Google Scholar] [CrossRef]








| (Young’s Modulus) E/GPa | (Yield Strength) σ/MPa | (Elongation) δ /% | (Strain Hardening Index) n |
|---|---|---|---|
| 197.20 | 776.48 | 21.33 | 0.17 |
| Parameters | Microscopic Camera | Macroscopic Camera |
|---|---|---|
| Focal length (mm) | 105 | 35 |
| Working distance (mm) | 115 | 232 |
| Field-of-view size (mm × mm) | 4 × 2.11 | 40 × 30 |
| Spatial resolution (μm/pixel) | 0.97 | 19.47 |
| Cycle Numbers | Crack Length/mm | Size of CPZ/mm | ||
|---|---|---|---|---|
| Theoretical Values | Measured Values | Errors/% | ||
| 10,000 | 1.53782 | 0.187 | 0.161 | 13.904 |
| 15,000 | 2.40932 | 0.207 | 0.188 | 9.179 |
| 20,000 | 4.33289 | 0.256 | 0.225 | 12.109 |
| 22,500 | 4.91579 | 0.273 | 0.245 | 10.256 |
| 25,000 | 5.61527 | 0.292 | 0.277 | 5.137 |
| 27,000 | 7.16967 | 0.332 | 0.318 | 4.217 |
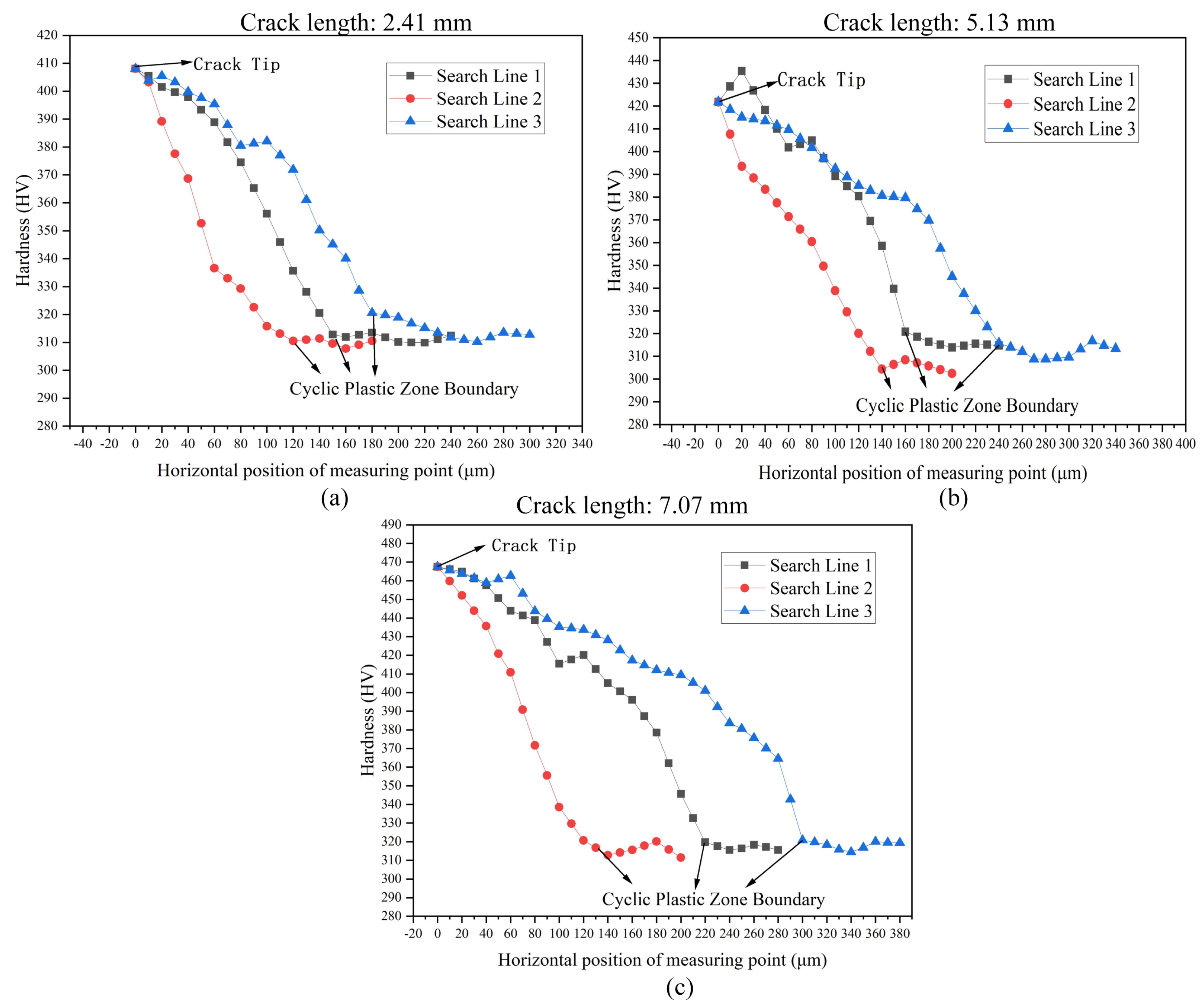
| Crack Length /mm | The Horizontal Distance from the Boundary of the CPZ to the Crack Tip/μm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Search Line 1 | Search Line 2 | Search Line 3 | |||||||
| Proposed Method | Hardness Method | Error % | Proposed Method | Hardness Method | Error /% | Proposed Method | Hardness Method | Error /% | |
| 2.41 | 156 | 150 | 4.00 | 124 | 120 | 3.23 | 189 | 180 | 5.00 |
| 4.93 | 168 | 160 | 1.25 | 145 | 140 | 3.57 | 250 | 240 | 4.00 |
| 7.07 | 231 | 220 | 5.00 | 133 | 130 | 2.31 | 308 | 300 | 3.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Lin, Z.; Huang, X.; Shang, H.; Zhan, J. In Situ Measurement of Cyclic Plastic Zone and Internal Strain Response of Q&P Steel near Fatigue Crack Tip Region Based on Micro-DIC. Materials 2022, 15, 6114. https://doi.org/10.3390/ma15176114
Gao H, Lin Z, Huang X, Shang H, Zhan J. In Situ Measurement of Cyclic Plastic Zone and Internal Strain Response of Q&P Steel near Fatigue Crack Tip Region Based on Micro-DIC. Materials. 2022; 15(17):6114. https://doi.org/10.3390/ma15176114
Chicago/Turabian StyleGao, Hongli, Zhiyuan Lin, Xinwei Huang, Hongbin Shang, and Jingsong Zhan. 2022. "In Situ Measurement of Cyclic Plastic Zone and Internal Strain Response of Q&P Steel near Fatigue Crack Tip Region Based on Micro-DIC" Materials 15, no. 17: 6114. https://doi.org/10.3390/ma15176114





