Free and Forced Vibration Analyses of Functionally Graded Graphene-Nanoplatelet-Reinforced Beams Based on the Finite Element Method
Abstract
:1. Introduction
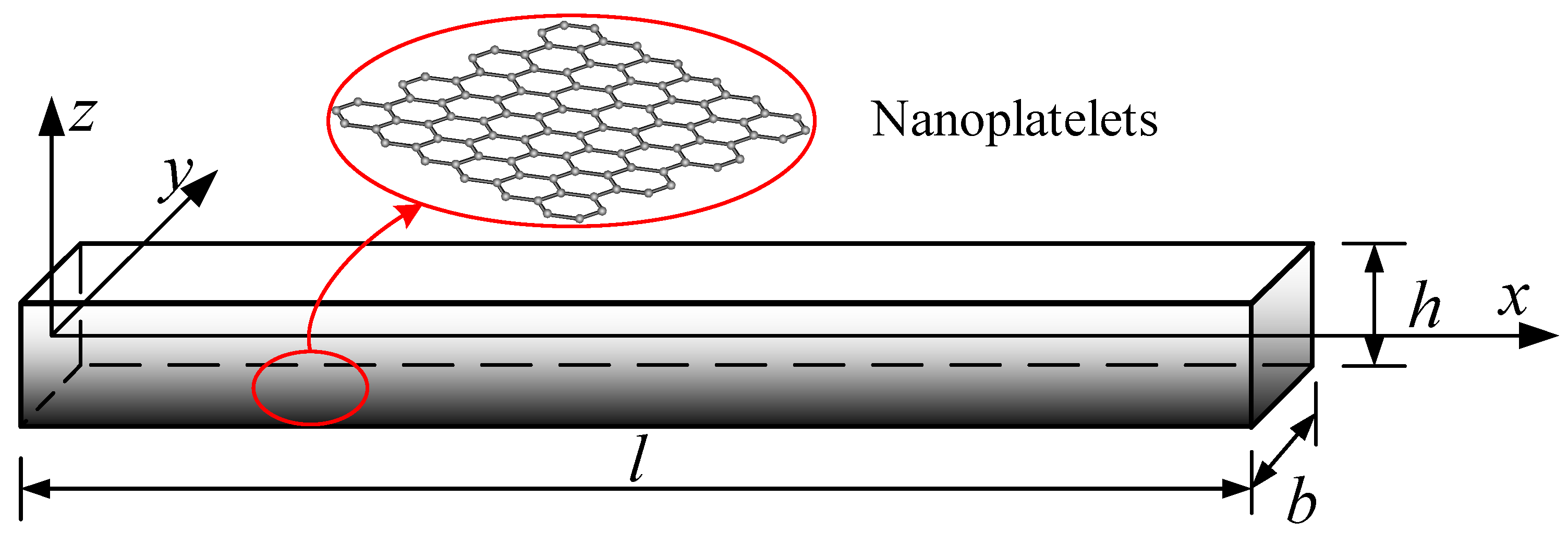
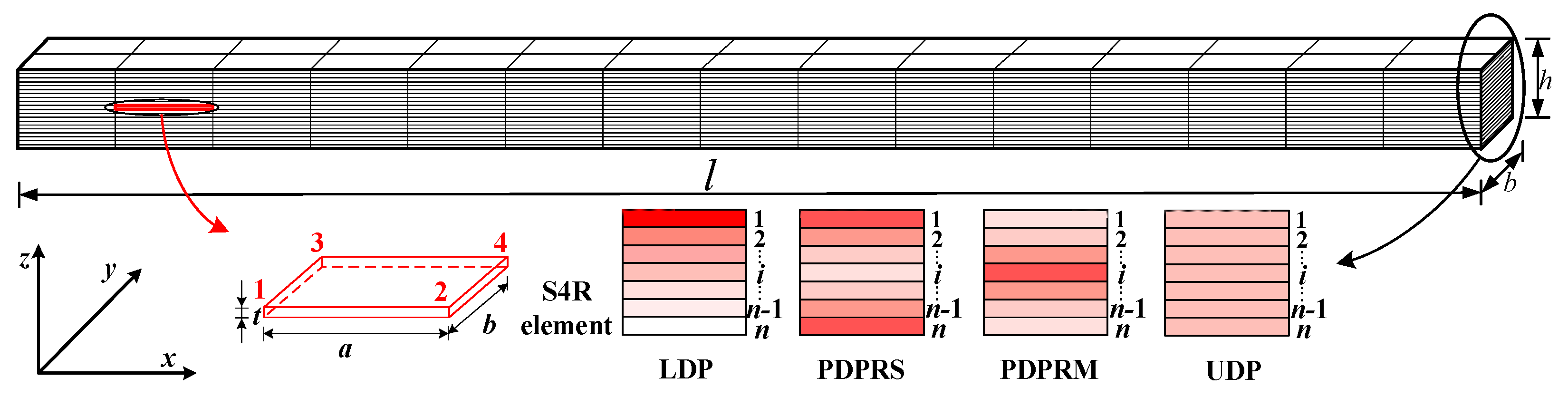
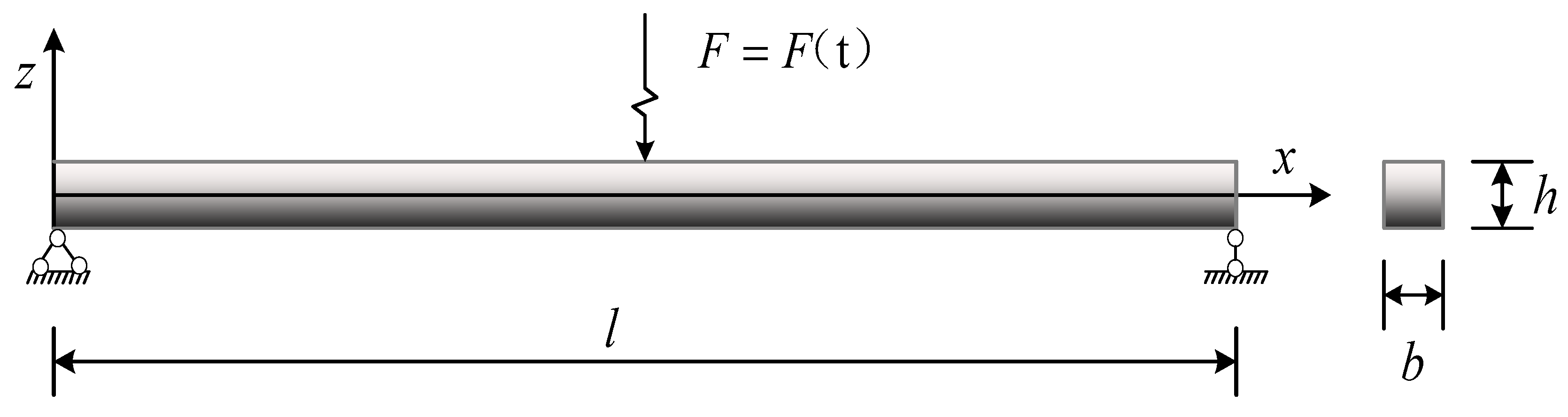
2. Functionally Graded Graphene-Nanoplatelet-Reinforced Beam
- (a)
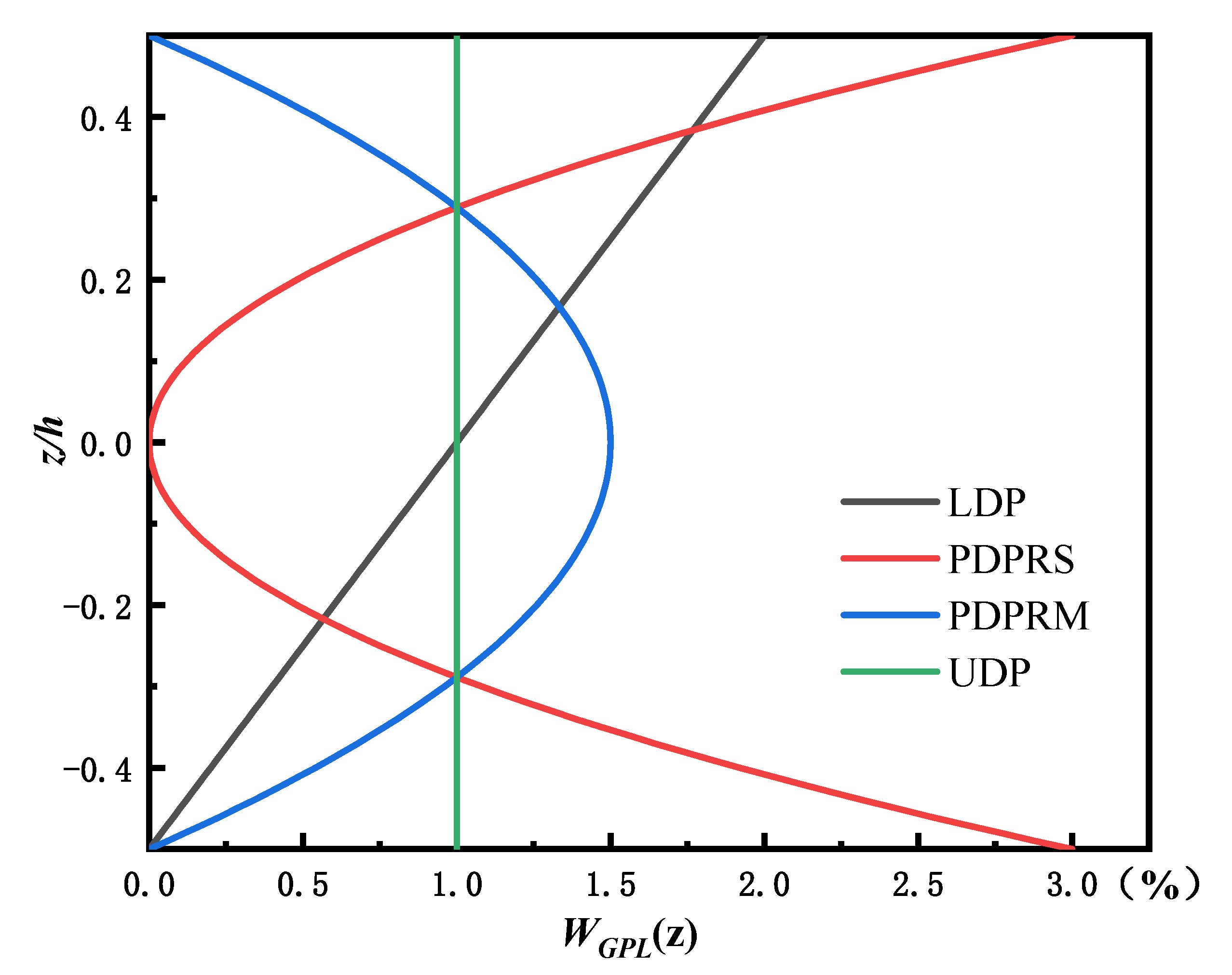
- Linear distribution pattern (LDP): The weight fraction of GPLs changes from the maximum value on the top surface to the minimum value on the bottom surface, along with the thickness, i.e.,
- (b)
- Parabolic distribution pattern with rich GPLs in the surface (PDPRS): The weight fraction of GPLs is the highest at the top and bottom, lowest in the middle plane, and symmetric about the neutral axis, i.e.,
- (c)
- Parabolic distribution pattern with rich GPLs in the middle plane (PDPRM): The weight fraction of GPLs is the lowest at the top and bottom, highest in the middle plane, and symmetric about the neutral axis, i.e.,
- (d)
- Uniform distribution pattern (UDP): The weight fraction of GPLs is evenly distributed in the beam, forming an isotropic, homogeneous beam, i.e.,where is a gradient indicator controlling the distribution of the weight fraction of GPLs along the thickness direction; and is a specific weight fraction, which is taken as in this paper.
3. Governing Equations
4. Finite Element Formulations
4.1. Dynamic Equations
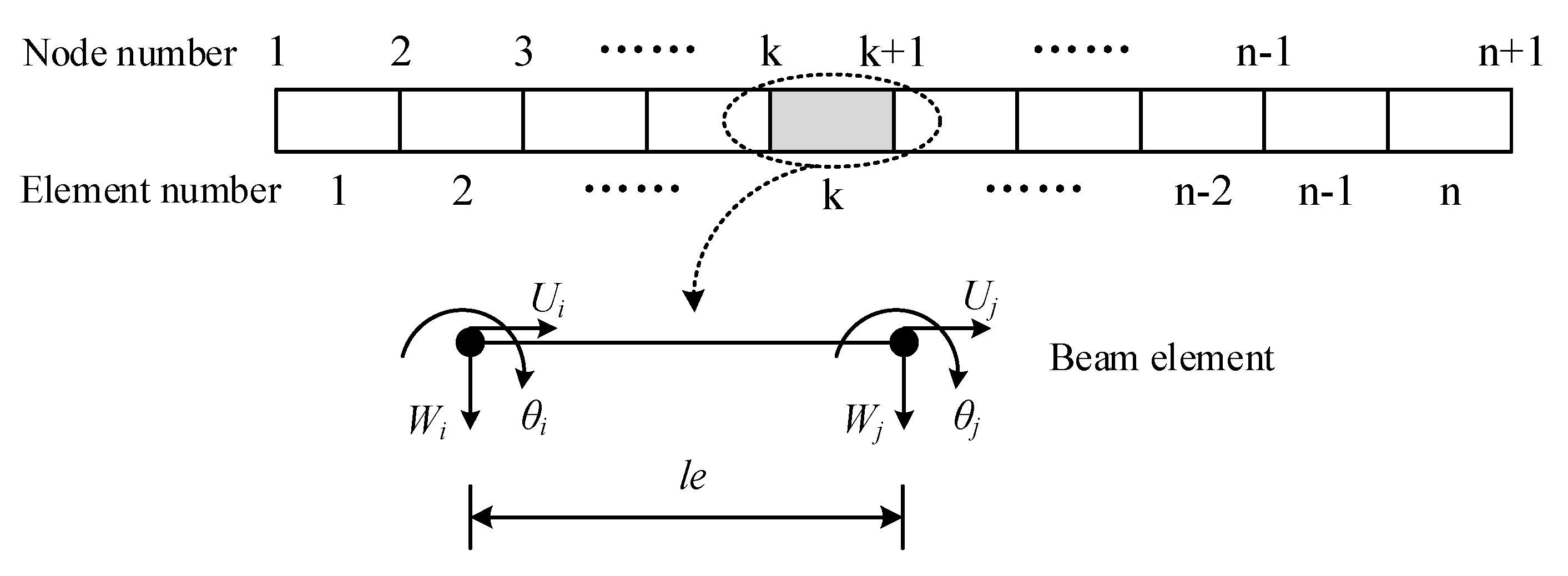
4.2. Beam Element for FG Beam Reinforced with GPLs
4.3. Free Vibration Analysis
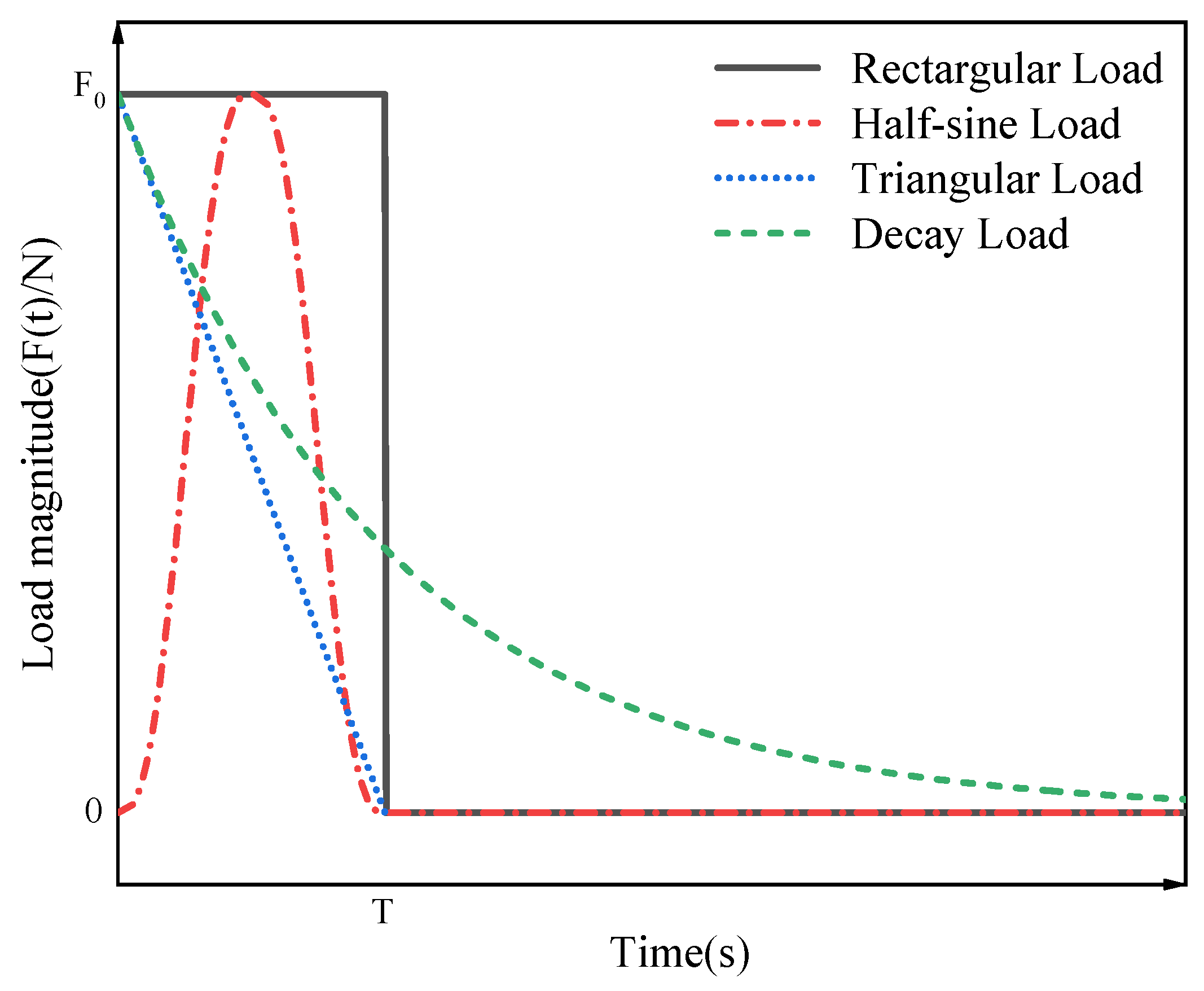
4.4. Transient Analysis
5. Numerical Results
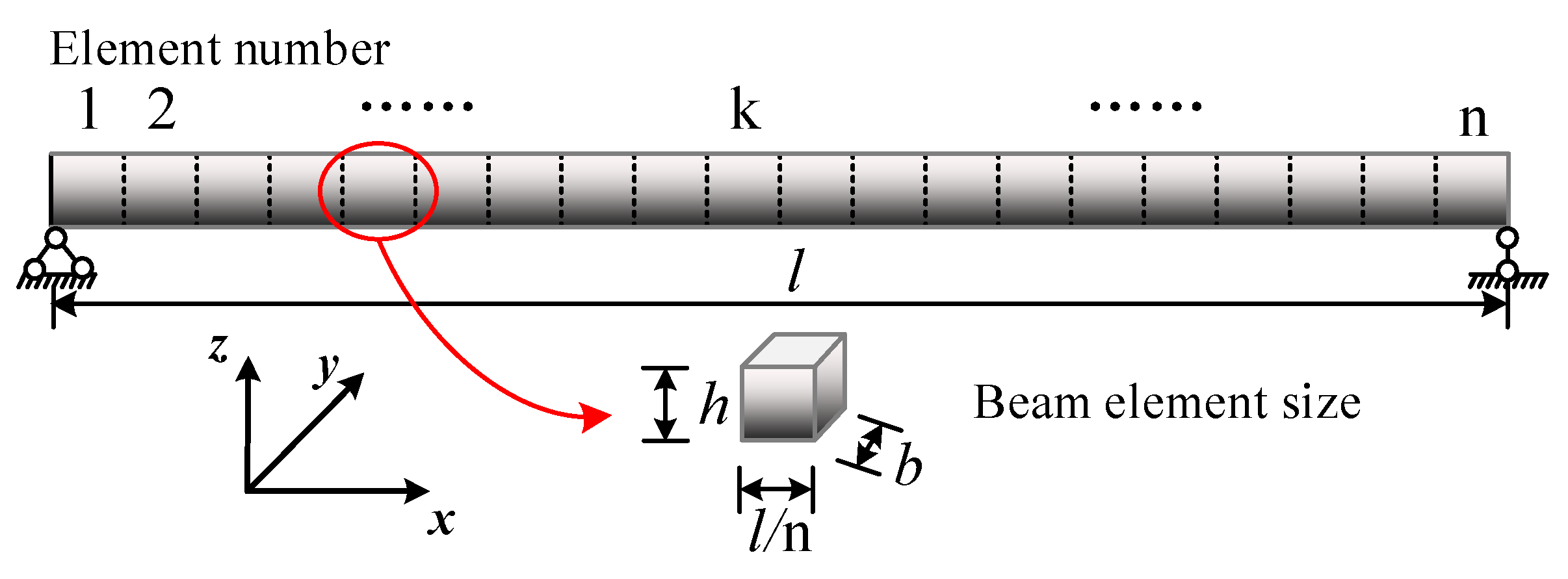
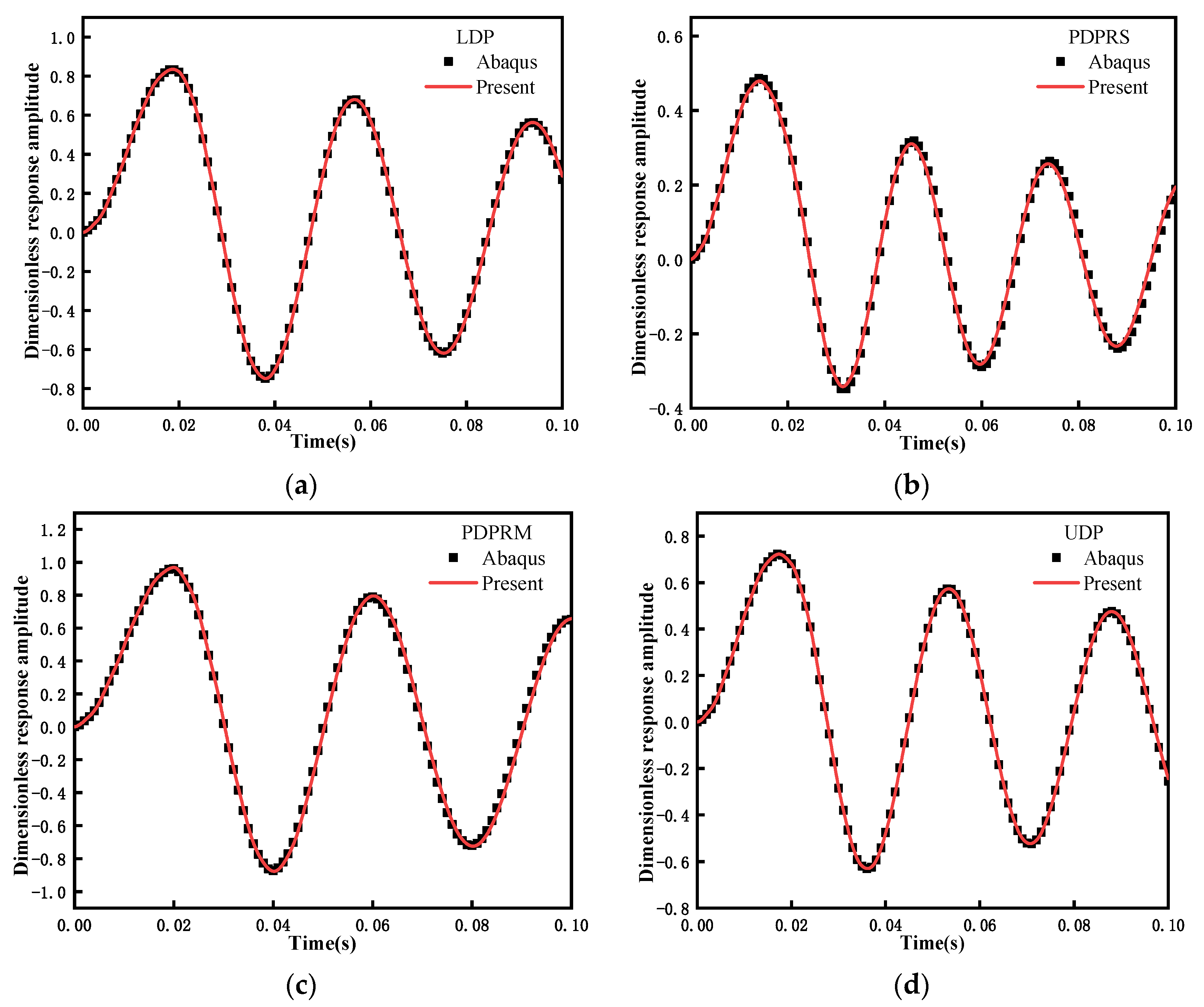
5.1. Convergence and Validation
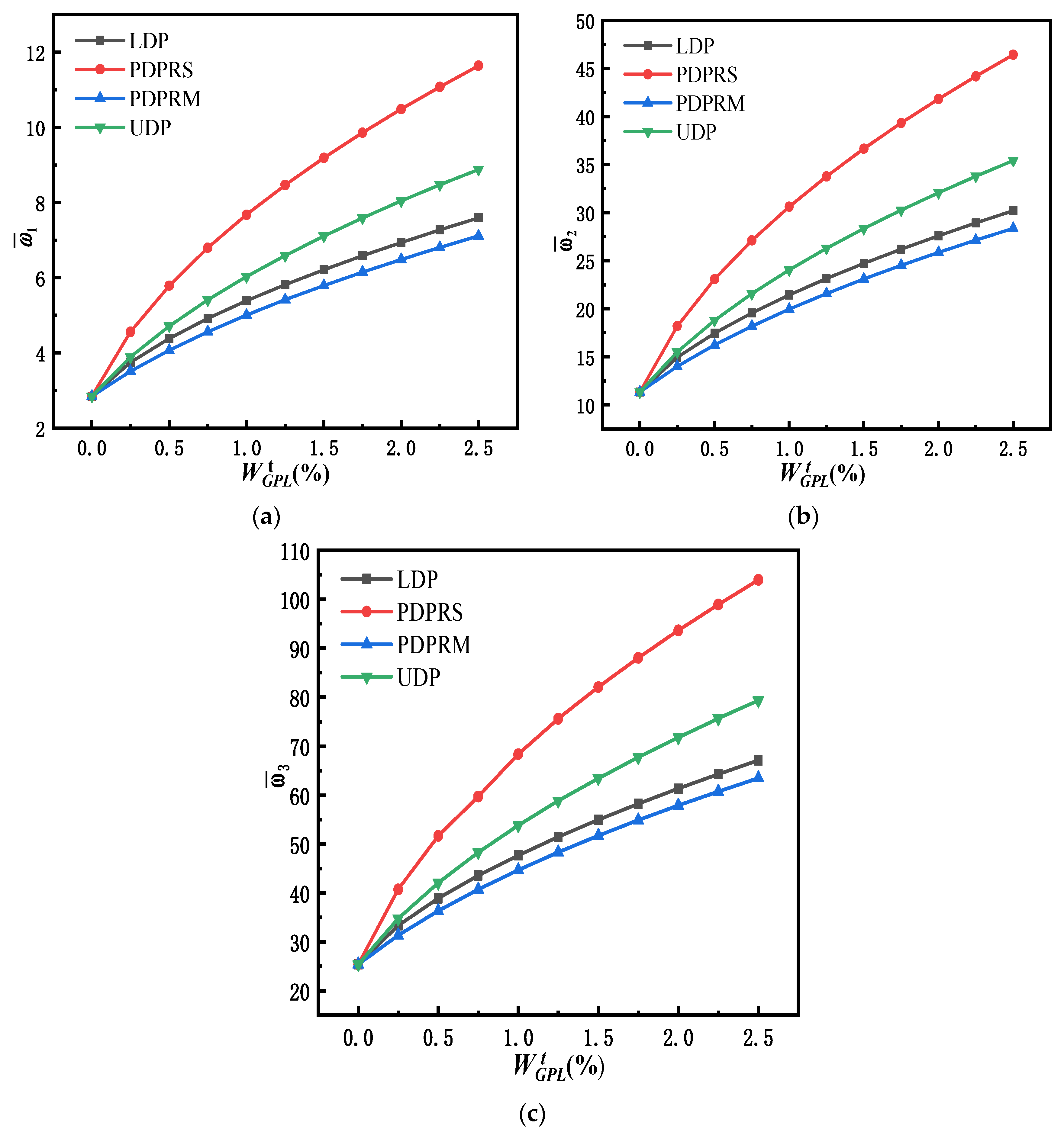
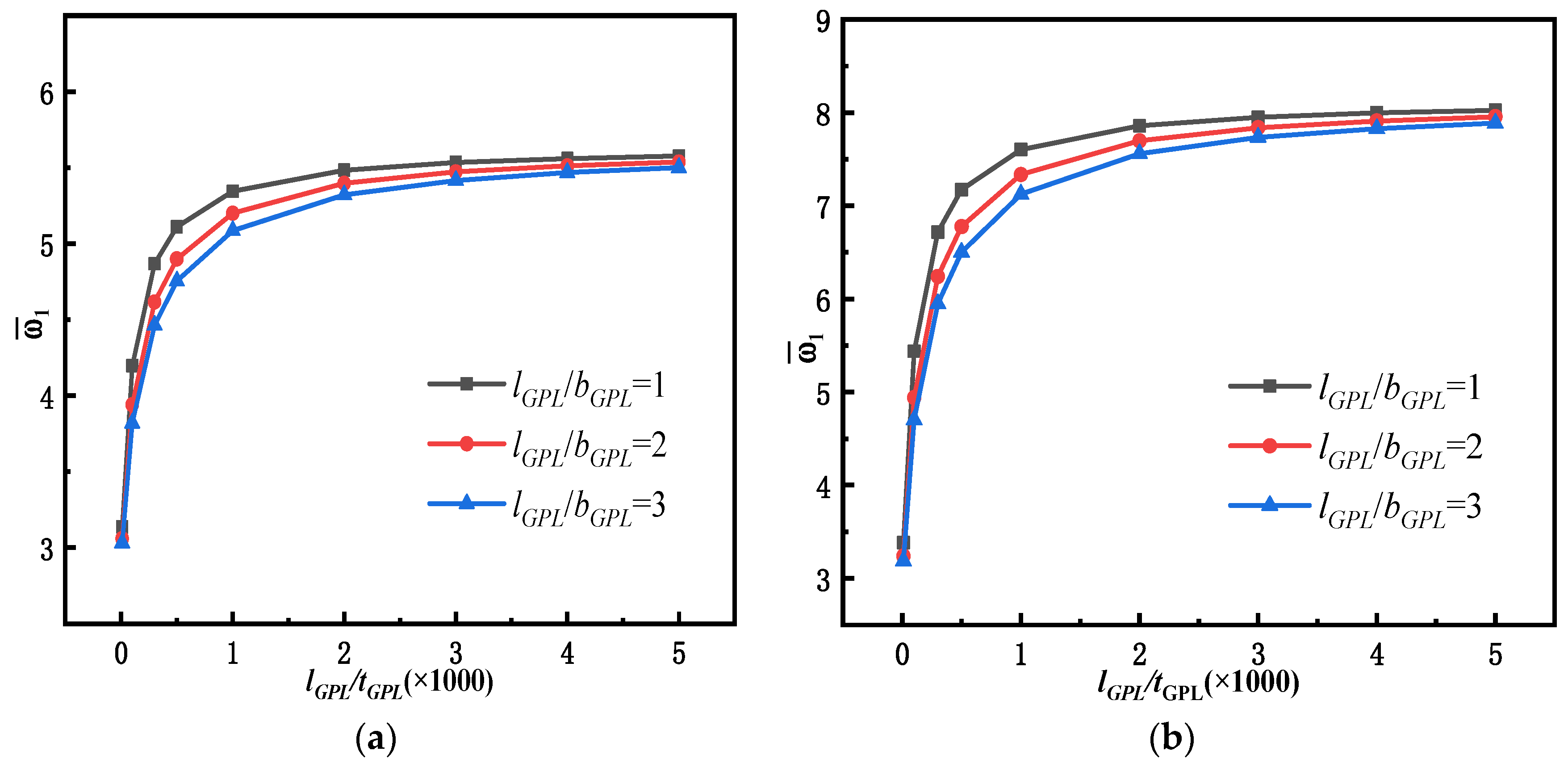
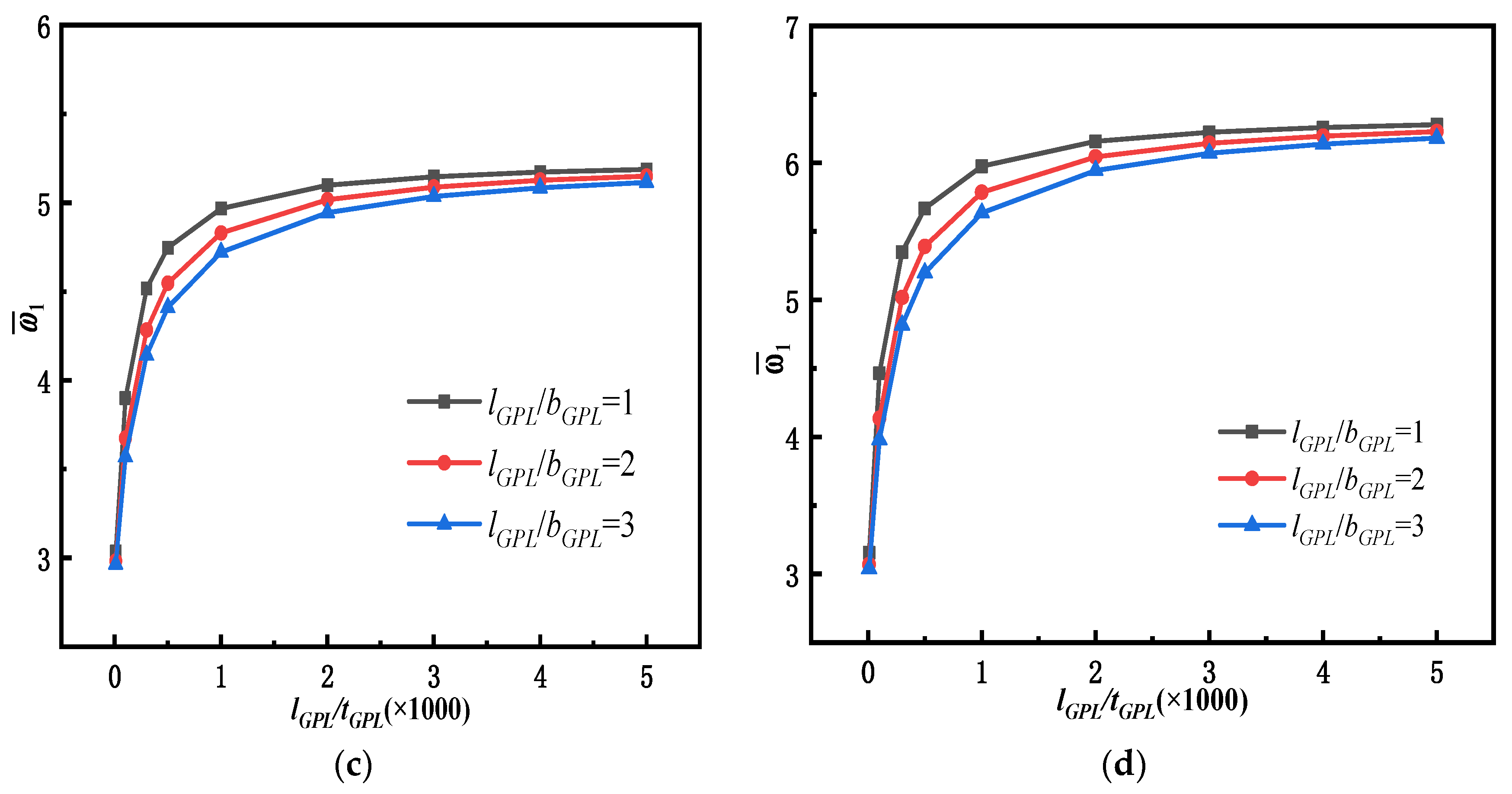
5.2. Free Vibration
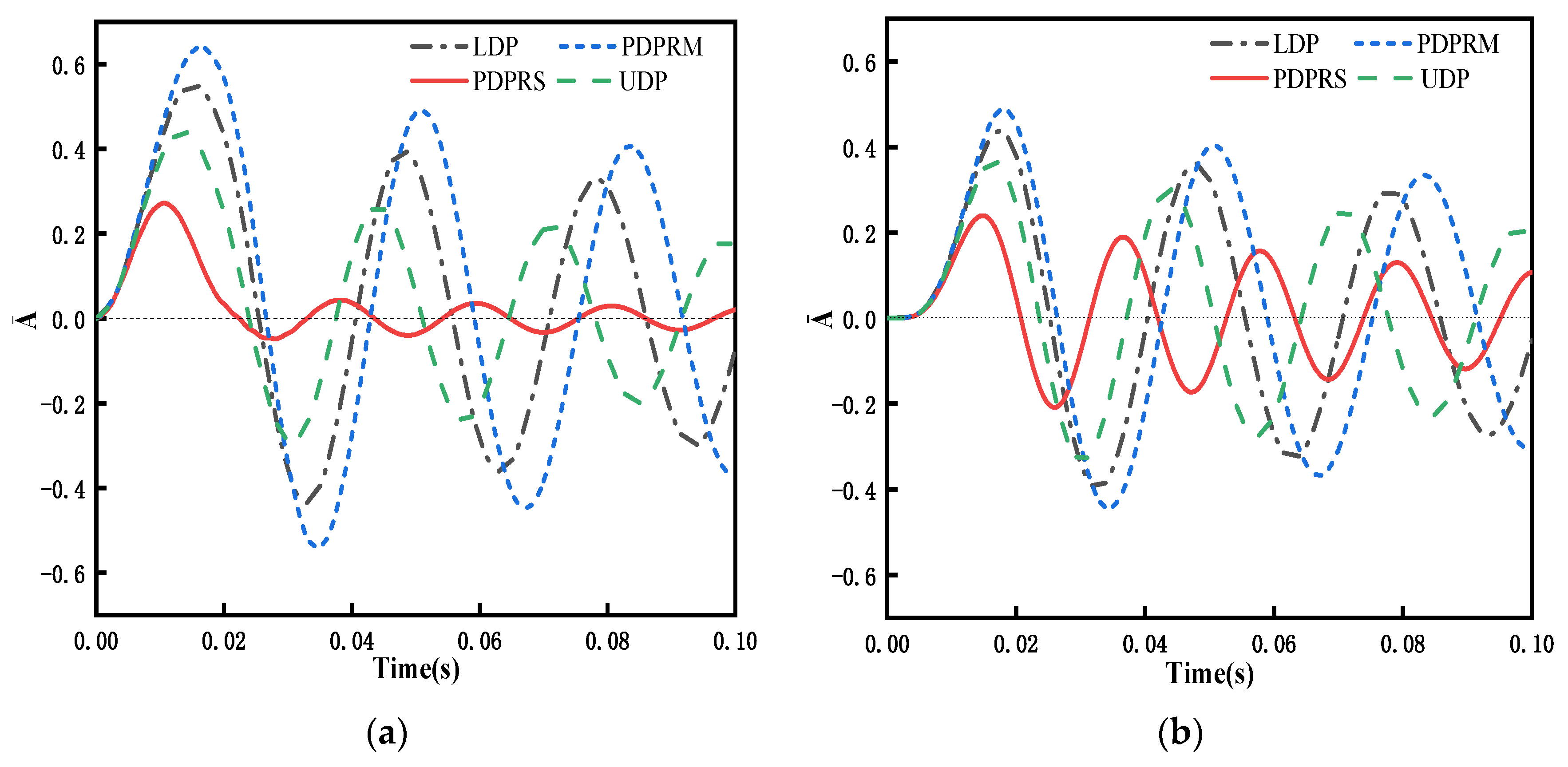
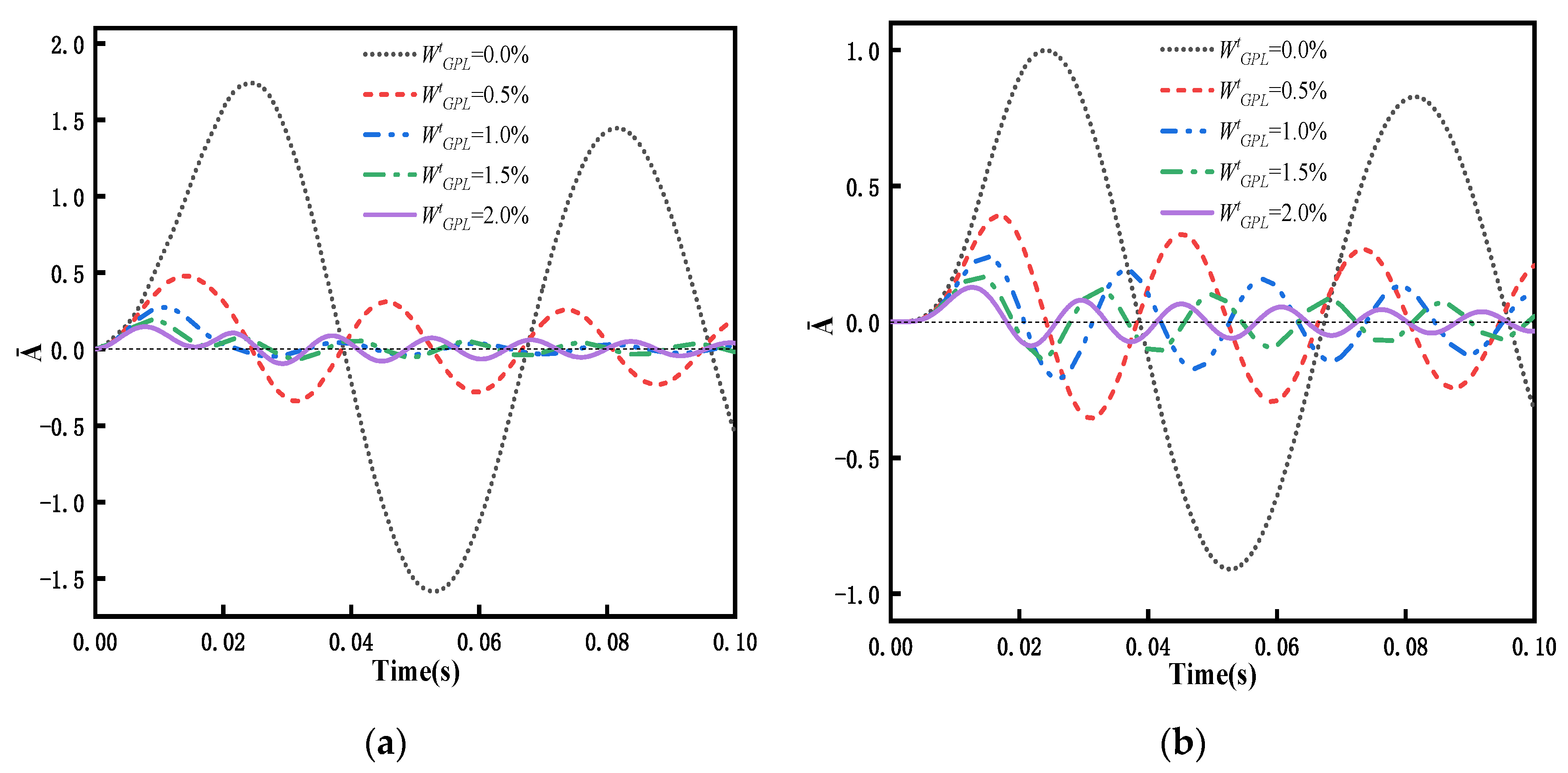
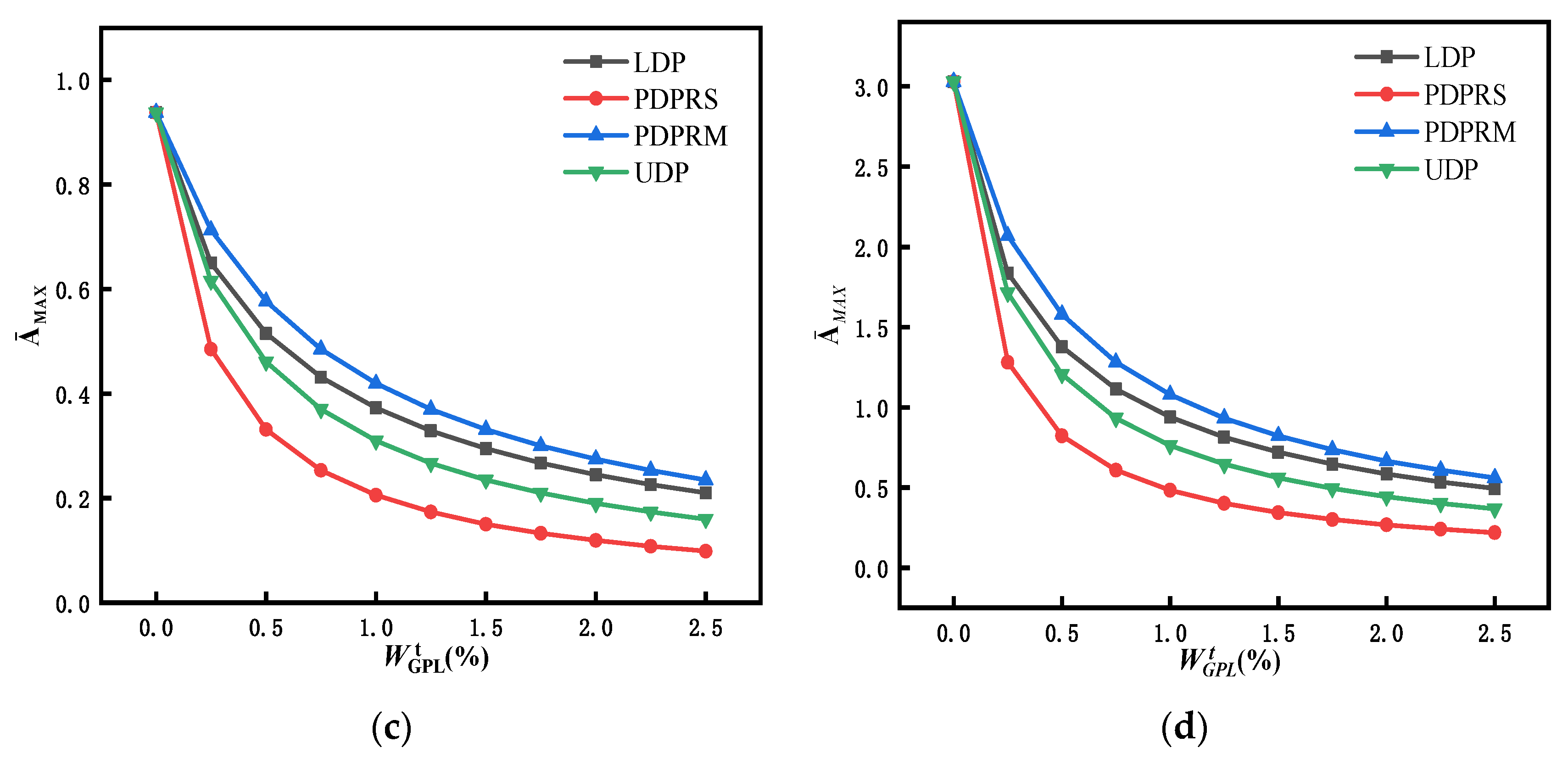
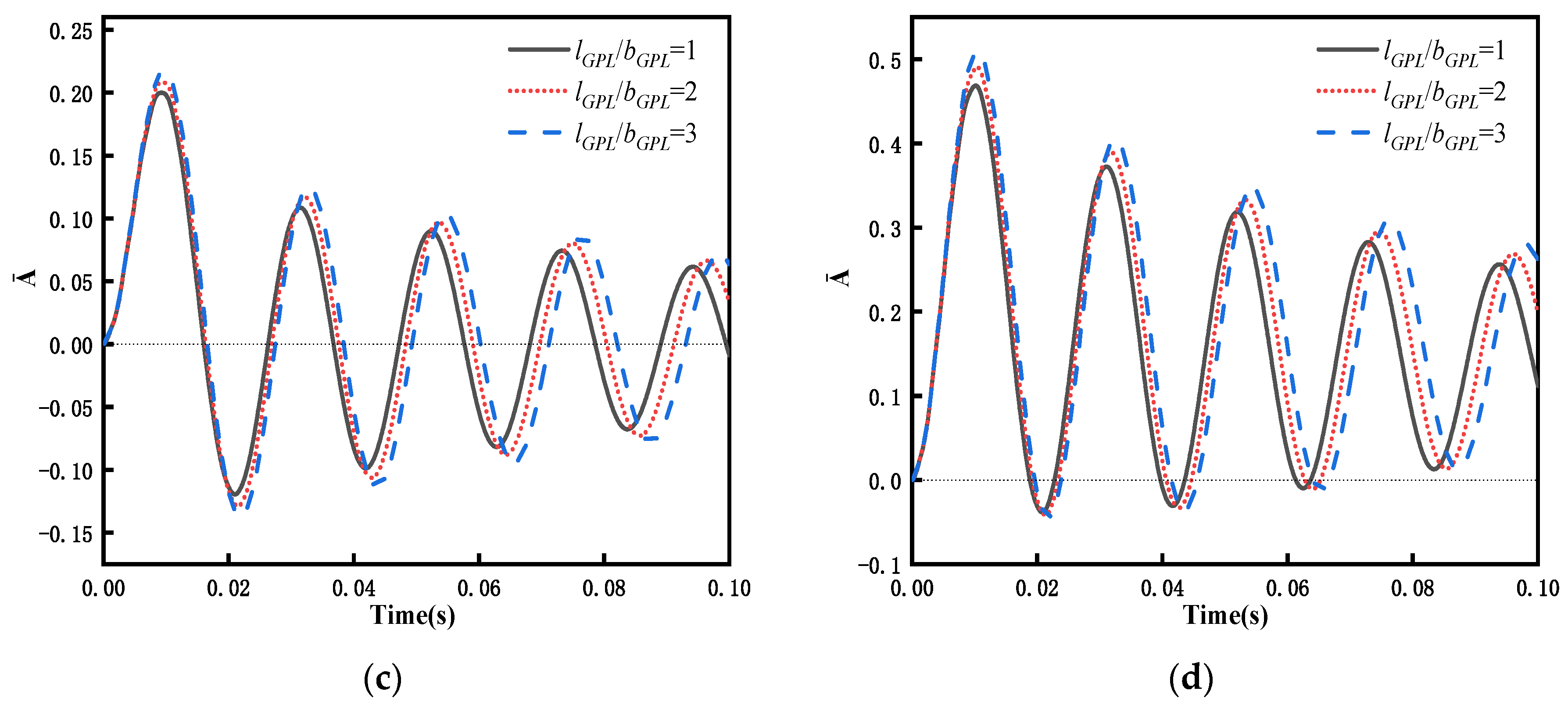
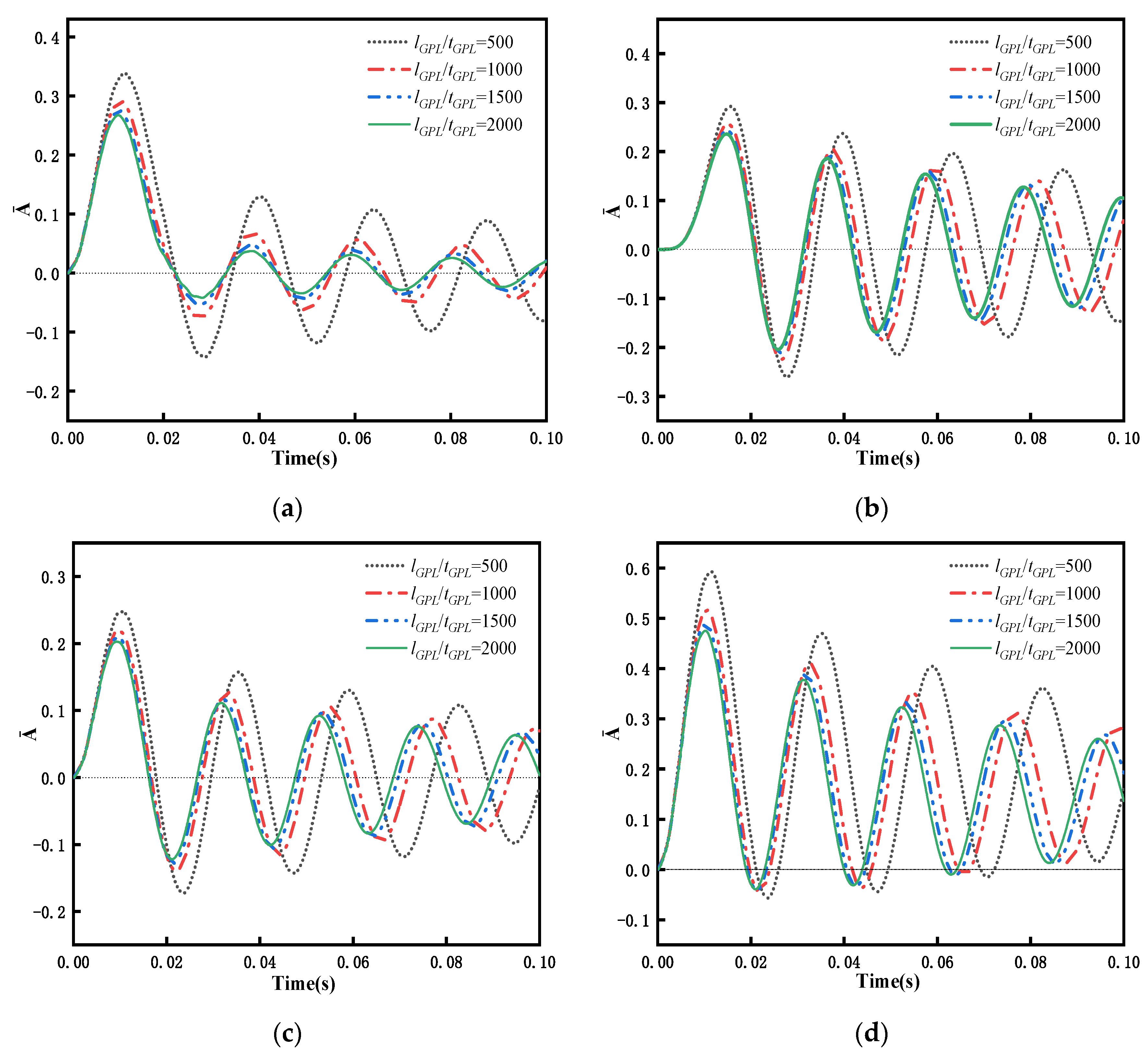
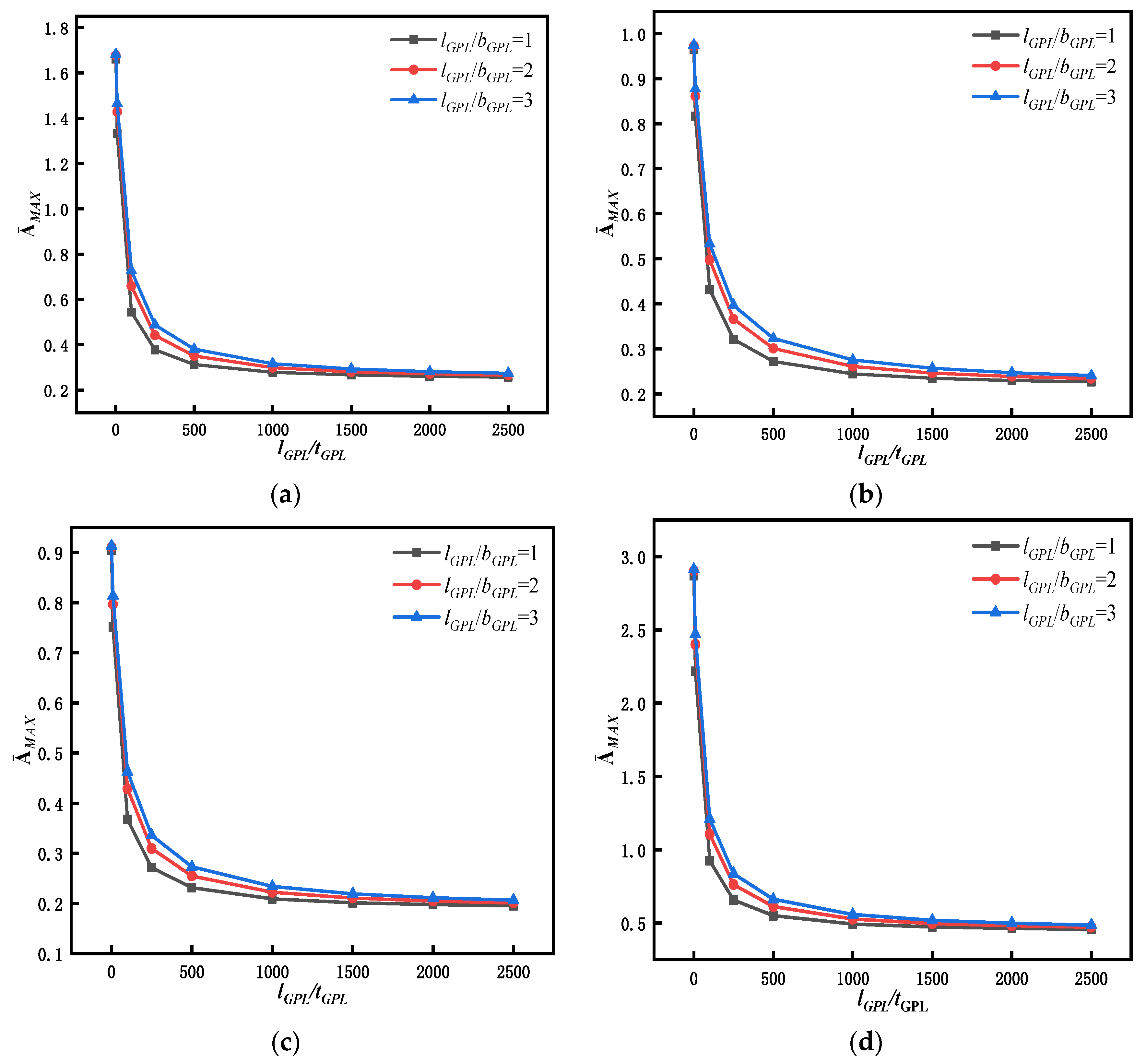
5.3. Transient Response
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The Explicit Forms of and (j = 1, 2, 3)
Appendix A.2. Explicit Forms of (j = 1, 2, 3)
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.G.; Wei, X.D.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and in-trinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.-Z.; Koratkar, N. Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content. ACS Nano. 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Fang, M.; Zhang, Z.; Li, J.; Zhang, H.; Lu, H.; Yang, Y. Constructing hierarchically structured interphases for strong and tough epoxy nanocomposites by amine-rich graphene surfaces. J. Mater. Chem. 2010, 20, 9635–9643. [Google Scholar] [CrossRef]
- Park, O.K.; Kim, S.G.; You, N.H.; Ku, B.-C.; Hui, D.; Lee, J.H. Synthesis and properties of iodo functionalized graphene oxide/polyimide nanocomposites. Compos. Part B Eng. 2014, 56, 364–371. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.H.; Chen, D.J.; Lu, P. Enhanced Mechanical Properties of Graphene-Based Poly(vinyl alcohol) Composites. Macromolecules 2010, 43, 2357–2363. [Google Scholar] [CrossRef]
- Liang, J.; Huang, Y.; Zhang, L.; Wang, Y.; Ma, Y.; Guo, T.; Chen, Y. Molecular-Level Dispersion of Graphene into Poly(vinyl alcohol) and Effective Reinforcement of their Nanocomposites. Adv. Funct. Mater. 2009, 19, 2297–2302. [Google Scholar] [CrossRef]
- Katsuyuki, W.; Cynthia, P.; Dmitriy, A.D.; Ruoff, R.S.; Ramanathan, T.; Brinson, L.C.; Torkelson, J.M. Polymer-Graphite Nanocomposites: Effective Dispersion and Major Property Enhancement via Solid-State Shear Pulverization. Macromolecules 2008, 2008, 1905–1908. [Google Scholar]
- Bever, M.B.; Duwez, P.E. Gradients in composite materials. Mater. Sci. Eng. 1972, 10, 1–8. [Google Scholar] [CrossRef]
- Shen, M.; Bever, M.B. Gradients in polymeric materials. J. Mater. Sci. 1972, 7, 741–746. [Google Scholar] [CrossRef]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.L.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.; Kitipornchai, S. Thermoelastic analysis of functionally graded graphene reinforced rectangular plates based on 3D elasticity. Meccanica 2017, 52, 2275–2292. [Google Scholar] [CrossRef]
- Yang, B.; Kitipornchai, S.; Yang, Y.F.; Yang, J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl. Math. Model. 2017, 49, 69–86. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part B Eng. 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Song, M.T.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef]
- Tam, M.F.; Yang, Z.C.; Zhao, S.Y.; Yang, J. Vibration and buckling characteristics of functionally graded graphene nanoplatelets reinforced composite beams with open edge cracks. Materials 2019, 12, 1412. [Google Scholar] [CrossRef]
- Song, M.T.; Gong, Y.H.; Yang, J.; Zhu, W.; Kitipornchai, S. Free vibration and buckling analyses of edge-cracked functionally graded multilayer graphene nanoplatelet-reinforced composite beams resting on an elastic foundation. J. Sound Vib. 2019, 458, 89–108. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Tornabene, F. Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 2018, 81, 108–117. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nano-platelets. Compos. Part B Eng. 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Baghbadorani, A.A.; Kiani, Y. Free vibration analysis of functionally graded cylindrical shells reinforced with graphene platelets. Compos. Struct. 2021, 276, 114546. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, W.; Guo, X.Y. Free vibration of rotating pretwisted functionally gradedcomposite cylindrical panel reinforced with graphene platelets. Eur. J. Mech. A Solids 2019, 77, 103798. [Google Scholar] [CrossRef]
- Li, X.Q.; Song, M.T.; Yang, J.; Kitipornchai, S. Primary and secondary resonances offunctionally graded graphene platelet-reinforced nanocomposite beams. Nonlinear Dyn. 2019, 95, 1807–1826. [Google Scholar] [CrossRef]
- Wang, A.W.; Chen, H.Y.; Zhang, W. Nonlinear transient response of doubly curved shallowshells reinforced with graphene nanoplatelets subjected to blast loads considering thermal effects. Compos. Struct. 2019, 225, 111063. [Google Scholar] [CrossRef]
- Şimşek, M.; Kocatürk, T. Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Compos. Struct. 2009, 90, 465–473. [Google Scholar] [CrossRef]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Bathe, K.-J. Finite Element Procedures in Engineering Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Alshorbagy, A.E.; Eltaher, M.A.; Mahmoud, F.F. Free vibration characteristics of a functionally graded beam by finite element method. Appl. Math. Model. 2011, 35, 412–425. [Google Scholar] [CrossRef]
- Aubad, M.J.; Khafaji, S.O.W.; Hussein, M.T.; Al-Shujairi, A.M. Modal analysis and transient response of axially functionally graded (AFG) beam using finite element method. Mater. Res. Express 2019, 6, 1065g4. [Google Scholar] [CrossRef]
- Bathe, K.J.; Wilson, E.L. Numerical Methods in Finite Element Analysis; Prentice-Hall of India: New Delhi, India, 1987. [Google Scholar]
- Wang, Y.W.; Xie, K.; Fu, T.R.; Shi, C.L. Vibration response of a functionally graded graphenenanoplatelet reinforced composite beam under two successive moving masses. Compos. Struct. 2019, 209, 928–939. [Google Scholar] [CrossRef]
- Liu, G.R.; Han, X.; Lam, K.Y. Stress waves in functionally gradient materials and its use for material characterization. Compos. Part B Eng. 1999, 30, 383–394. [Google Scholar] [CrossRef]
- Wang, Y.S.; Gross, D. Analysis of a crack in a functionally gradient interface layer under static and dynamic loading. Key Eng. Mater. 2000, 183–187, 331–336. [Google Scholar] [CrossRef]
- Wang, Y.S.; Huang, G.Y.; Gross, D. On the mechanical modeling of functionally graded interracial zone with a griffith crack: Anti-plane deformation. ASME J. Appl. Mech. 2003, 70, 676–680. [Google Scholar] [CrossRef]
- Fu, W.H.; Chung, D.D.L. Vibration reduction ability of polymers, particularly polymethylmethacrylate and polytetrafluoroethylene. Polym. Polym. Compos. 2001, 9, 423–426. [Google Scholar] [CrossRef]
- Fereidoon, A.; Kordani, N.; Ahangari, M.G.; Ashoory, M. Damping augmentation of epoxy using carbon nanotubes. Int. J. Polym. Mater. 2011, 60, 11–26. [Google Scholar] [CrossRef]






| 0 | 0 | 0 | 0 | 0 |
| 1 | 1.5 | 0.75 | 0.5 | 0.5 |
| 2 | 3 | 1.5 | 1 | 1 |
| 2x | 3x | 1.5x | x | x |
| lGPL/μm | bGPL/μm | tGPL/nm | νM | νGPL | ρM/kg/m3 | ρGPL/kg/m3 | EM/Gpa | EGPL/Gpa |
|---|---|---|---|---|---|---|---|---|
| 2.5 | 1.5 | 1.5 | 0.34 | 0.186 | 1.2 | 1.06 | 3.0 | 1010 |
| Number of Elements | LDP | PDPRS | PDPRS | UDP |
|---|---|---|---|---|
| 5 | 5.505 | 7.846 | 5.106 | 6.130 |
| 10 | 5.426 | 7.746 | 5.040 | 6.065 |
| 20 | 5.389 | 7.681 | 5.007 | 6.031 |
| 30 | 5.389 | 7.681 | 5.007 | 6.030 |
| 40 | 5.389 | 7.681 | 5.007 | 6.030 |
| 50 | 5.389 | 7.681 | 5.007 | 6.030 |
| 60 | 5.389 | 7.681 | 5.007 | 6.030 |
| Distribution Patterns | l/h = 20 | l/h = 25 | l/h = 100 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Present | ABAQUS | Present | ABAQUS | Ref. [28] | Present | ABAQUS | Ref. [28] | ||
| LDP | 0.0% | 2.846 | 2.851 | 2.847 | 2.850 | 2.841 | 2.849 | 2.849 | 2.849 |
| 0.5% | 4.383 | 4.394 | 4.386 | 4.393 | 4.379 | 4.390 | 4.391 | 4.389 | |
| 1.0% | 5.386 | 5.402 | 5.389 | 5.400 | 5.381 | 5.394 | 5.398 | 5.394 | |
| PDPRS | 0.0% | 2.846 | 2.851 | 2.847 | 2.850 | 2.841 | 2.849 | 2.849 | 2.849 |
| 0.5% | 5.789 | 5.756 | 5.791 | 5.765 | 5.764 | 5.794 | 5.788 | 5.793 | |
| 1.0% | 7.679 | 7.609 | 7.681 | 7.629 | 7.637 | 7.686 | 7.681 | 7.683 | |
| PDPRM | 0.0% | 2.846 | 2.851 | 2.847 | 2.850 | 2.841 | 2.849 | 2.849 | 2.849 |
| 0.5% | 4.071 | 4.092 | 4.073 | 4.089 | 4.067 | 4.075 | 4.076 | 4.075 | |
| 1.0% | 5.006 | 5.038 | 5.007 | 5.034 | 5.001 | 5.011 | 5.029 | 5.010 | |
| UDP | 0.0% | 2.846 | 2.851 | 2.847 | 2.850 | 2.841 | 2.849 | 2.849 | 2.849 |
| 0.5% | 4.714 | 4.721 | 4.715 | 4.720 | 4.705 | 4.718 | 4.719 | 4.718 | |
| 1.0% | 6.029 | 6.040 | 6.030 | 6.038 | 6.019 | 6.036 | 6.036 | 6.035 | |
| Distribution Pattern | Dimensionless Frequency | |||||
|---|---|---|---|---|---|---|
| Value | Value | Growth Rate | Value | Growth Rate | ||
| LDP | 2.846 | 4.383 | 54.006% | 5.386 | 89.248% | |
| 11.350 | 17.458 | 53.815% | 21.438 | 88.881% | ||
| 25.408 | 38.907 | 53.129% | 47.701 | 87.740% | ||
| PDPRS | 2.846 | 5.789 | 103.408% | 7.679 | 169.817% | |
| 11.350 | 23.084 | 103.383% | 30.620 | 169.780% | ||
| 25.408 | 51.677 | 103.389% | 68.377 | 169.116% | ||
| PDPRM | 2.846 | 4.071 | 43.043% | 5.006 | 75.896% | |
| 11.350 | 16.234 | 43.031% | 19.962 | 75.877% | ||
| 25.408 | 36.343 | 43.038% | 44.687 | 75.878% | ||
| UDP | 2.846 | 4.714 | 65.636% | 6.029 | 111.841% | |
| 11.350 | 18.797 | 65.612% | 24.044 | 111.841% | ||
| 25.408 | 42.079 | 65.613% | 53.826 | 111.847% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Teng, J.; Huang, J.; Zhou, K.; Huang, L. Free and Forced Vibration Analyses of Functionally Graded Graphene-Nanoplatelet-Reinforced Beams Based on the Finite Element Method. Materials 2022, 15, 6135. https://doi.org/10.3390/ma15176135
Zhang Y, Teng J, Huang J, Zhou K, Huang L. Free and Forced Vibration Analyses of Functionally Graded Graphene-Nanoplatelet-Reinforced Beams Based on the Finite Element Method. Materials. 2022; 15(17):6135. https://doi.org/10.3390/ma15176135
Chicago/Turabian StyleZhang, Yuanxiu, Jingmei Teng, Jun Huang, Kun Zhou, and Lixin Huang. 2022. "Free and Forced Vibration Analyses of Functionally Graded Graphene-Nanoplatelet-Reinforced Beams Based on the Finite Element Method" Materials 15, no. 17: 6135. https://doi.org/10.3390/ma15176135
APA StyleZhang, Y., Teng, J., Huang, J., Zhou, K., & Huang, L. (2022). Free and Forced Vibration Analyses of Functionally Graded Graphene-Nanoplatelet-Reinforced Beams Based on the Finite Element Method. Materials, 15(17), 6135. https://doi.org/10.3390/ma15176135





