Free Vibration Analysis of a Graphene-Platelet-Reinforced, Porous, Two-Cylindrical-Panel System
Abstract
:1. Introduction
2. Theoretical Formulations
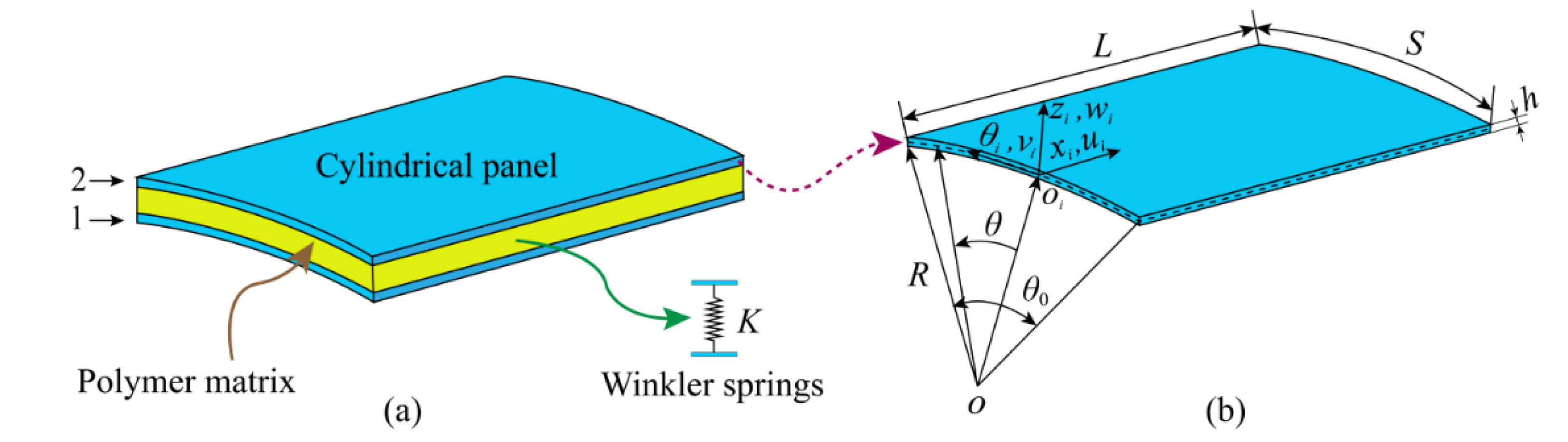
2.1. Description of the Model
2.2. Governing Equations and Solution
3. Model Validation and Convergence Analysis
4. Results and Discussion
5. Conclusions
- (1)
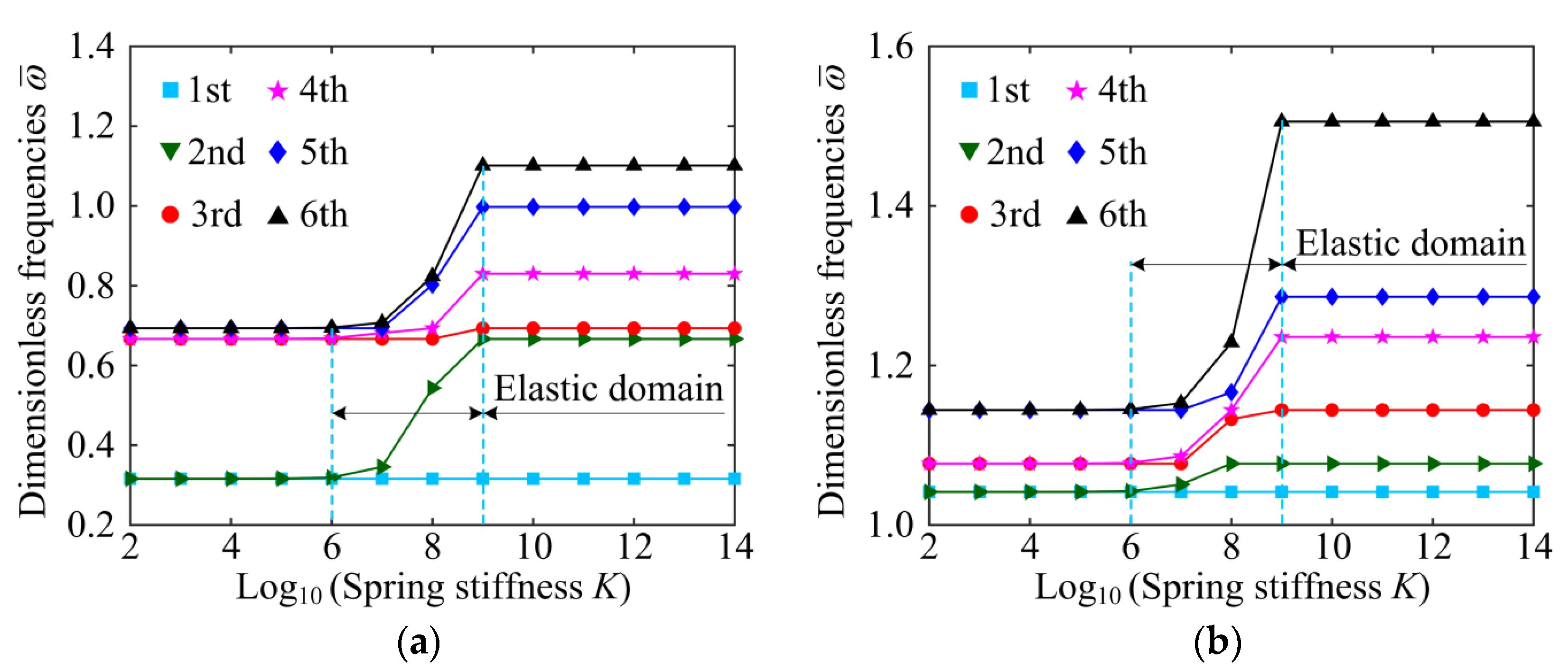
- The variation in the stiffness of the Winkler springs in the GPLRP, two-cylindrical-panel system has no effect on the first-order natural frequency, but other natural frequencies can be adjusted by controlling the value of the spring stiffness to obtain the desired natural frequency.
- (2)
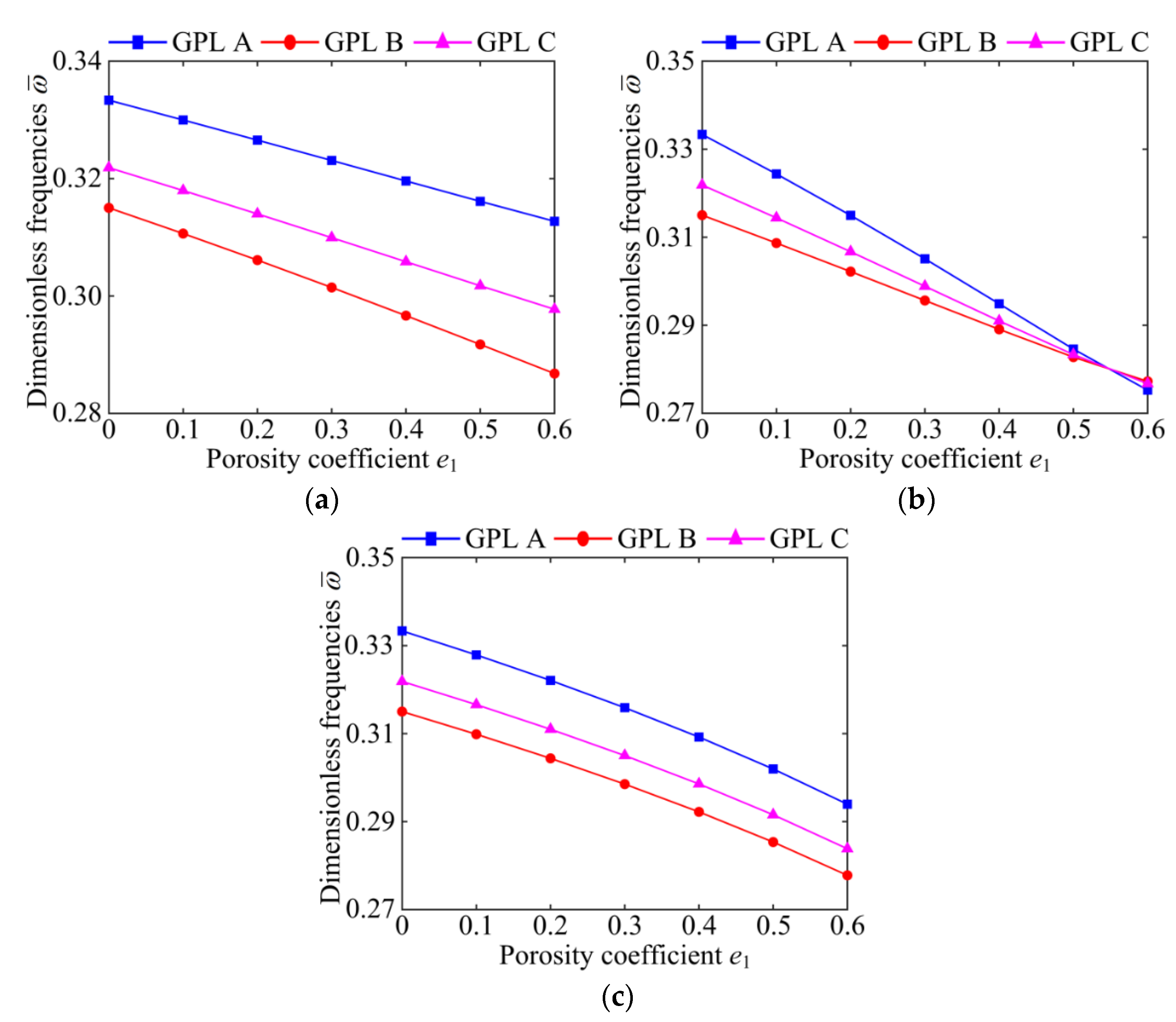
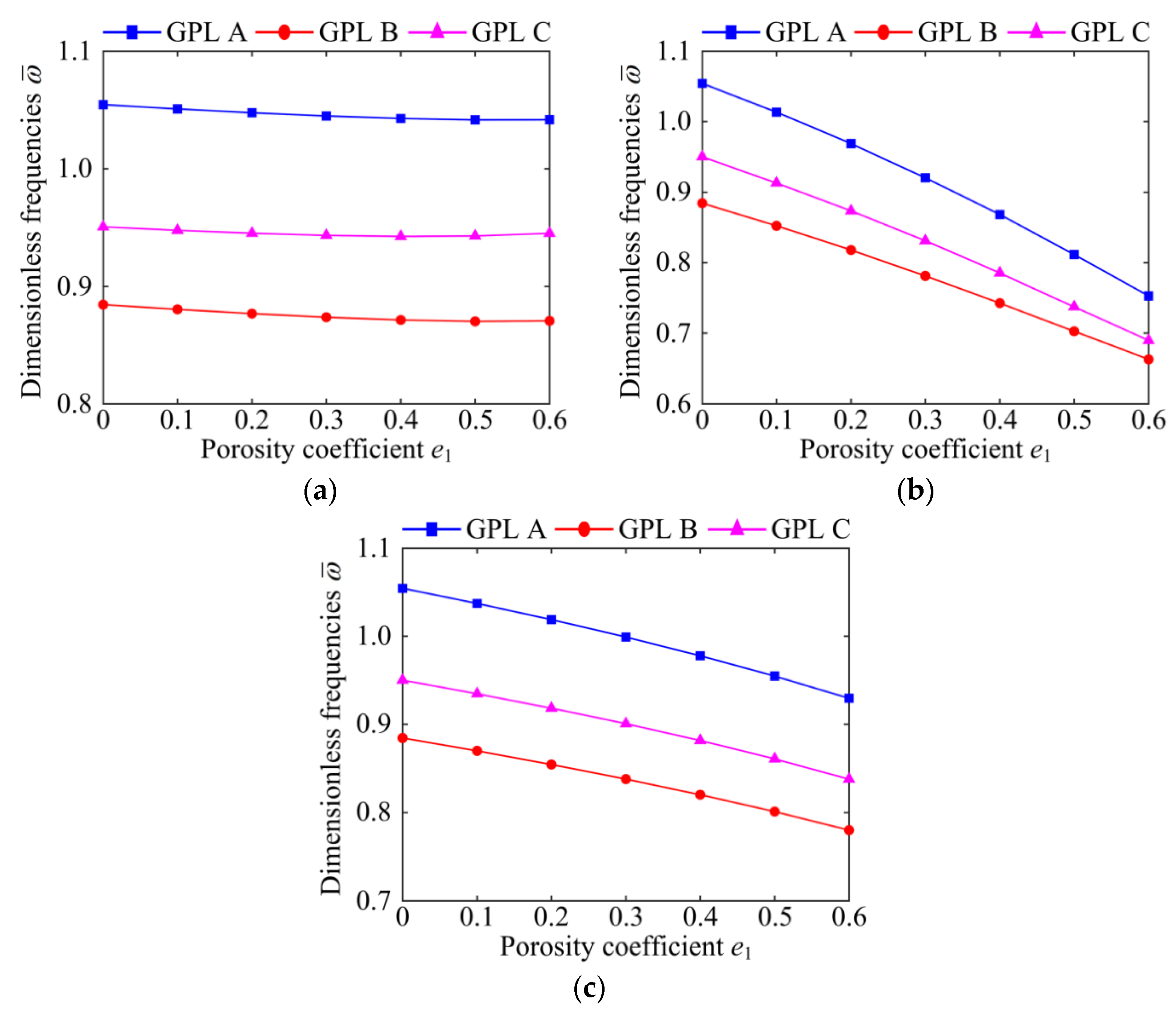
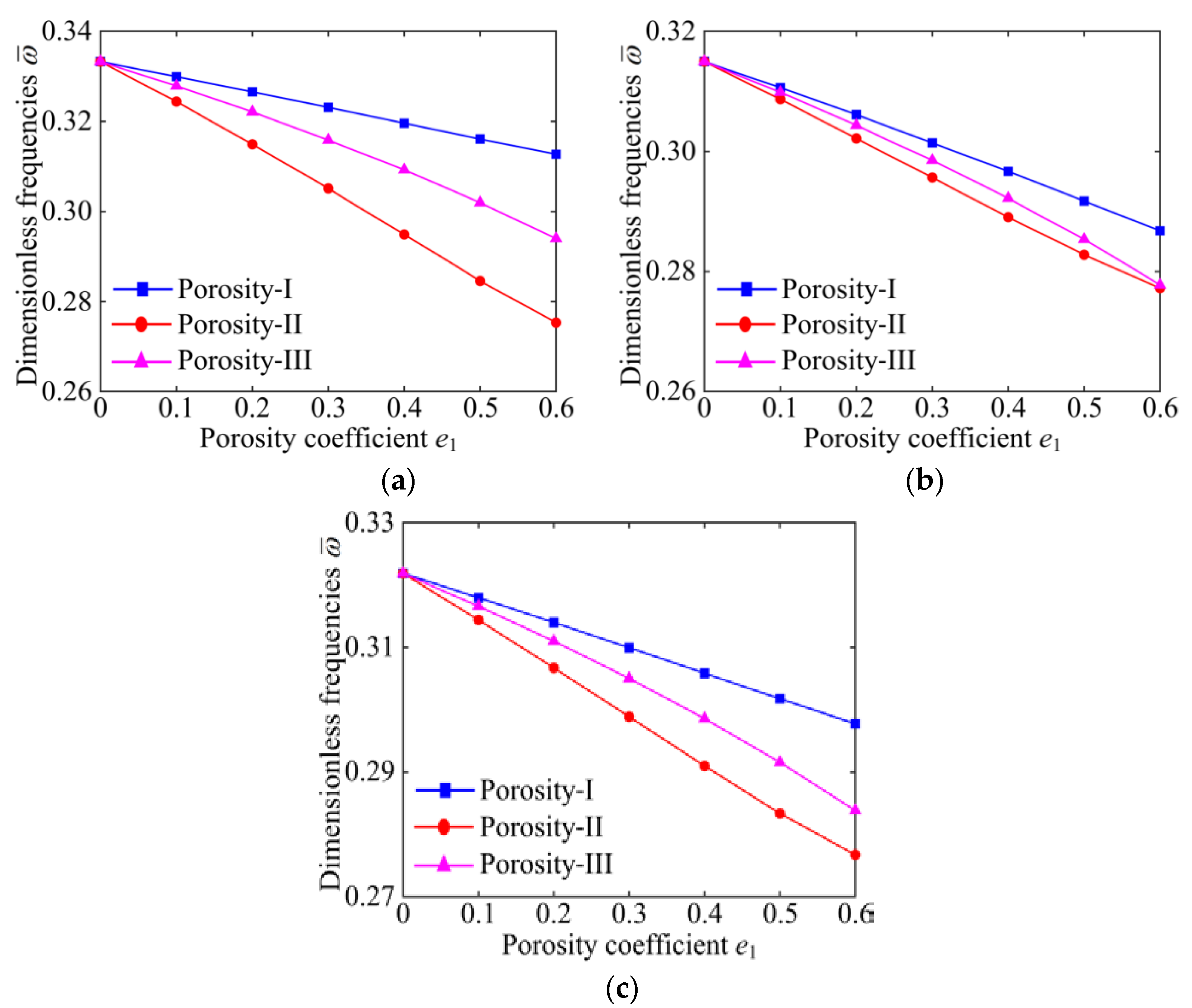
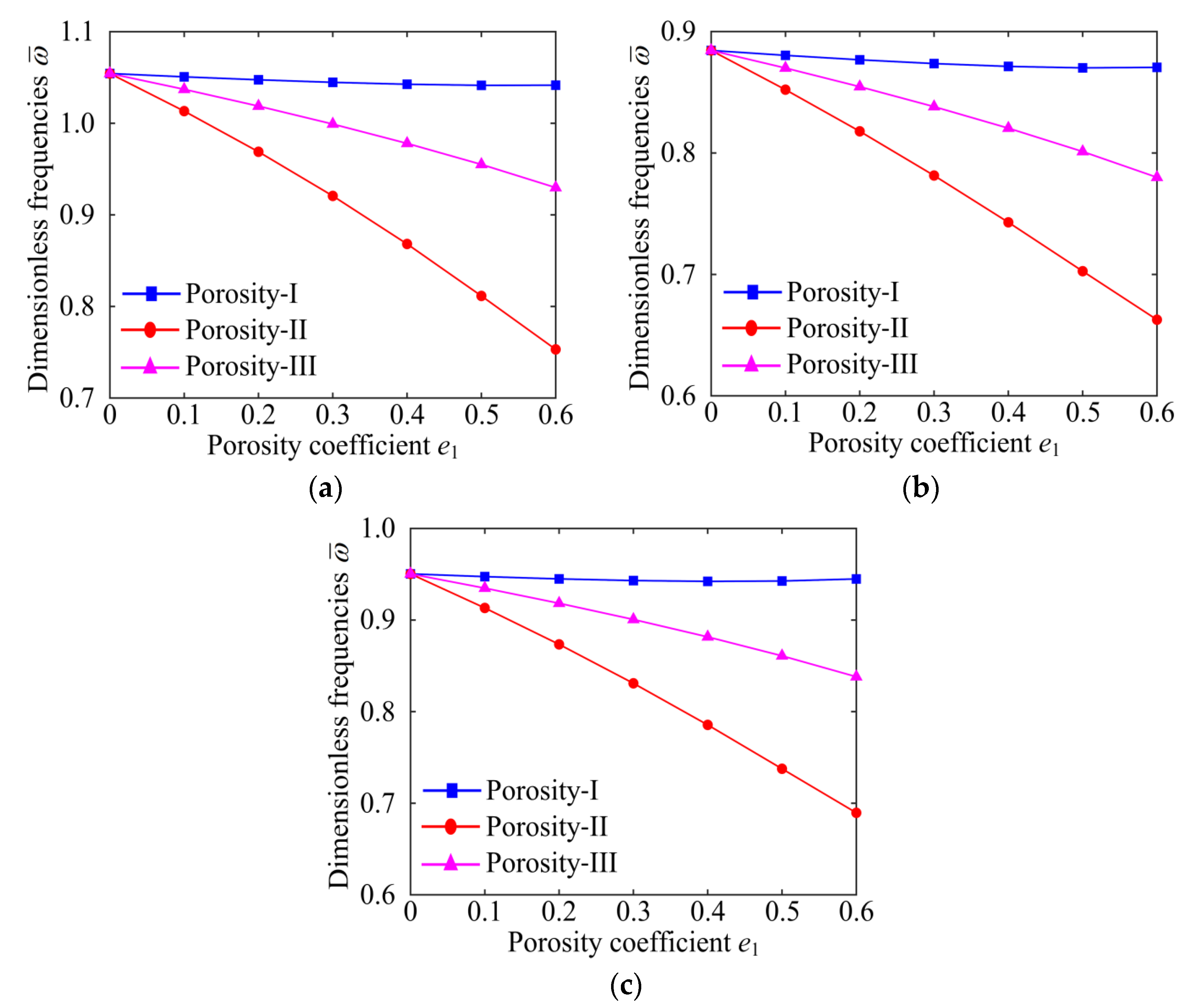
- The porosity coefficient, porosity distribution, GPL distribution pattern, and boundary condition interact with each other and have a coupled influence on the vibration characteristics of the GPLRP, two-cylindrical-panel system.
- (3)
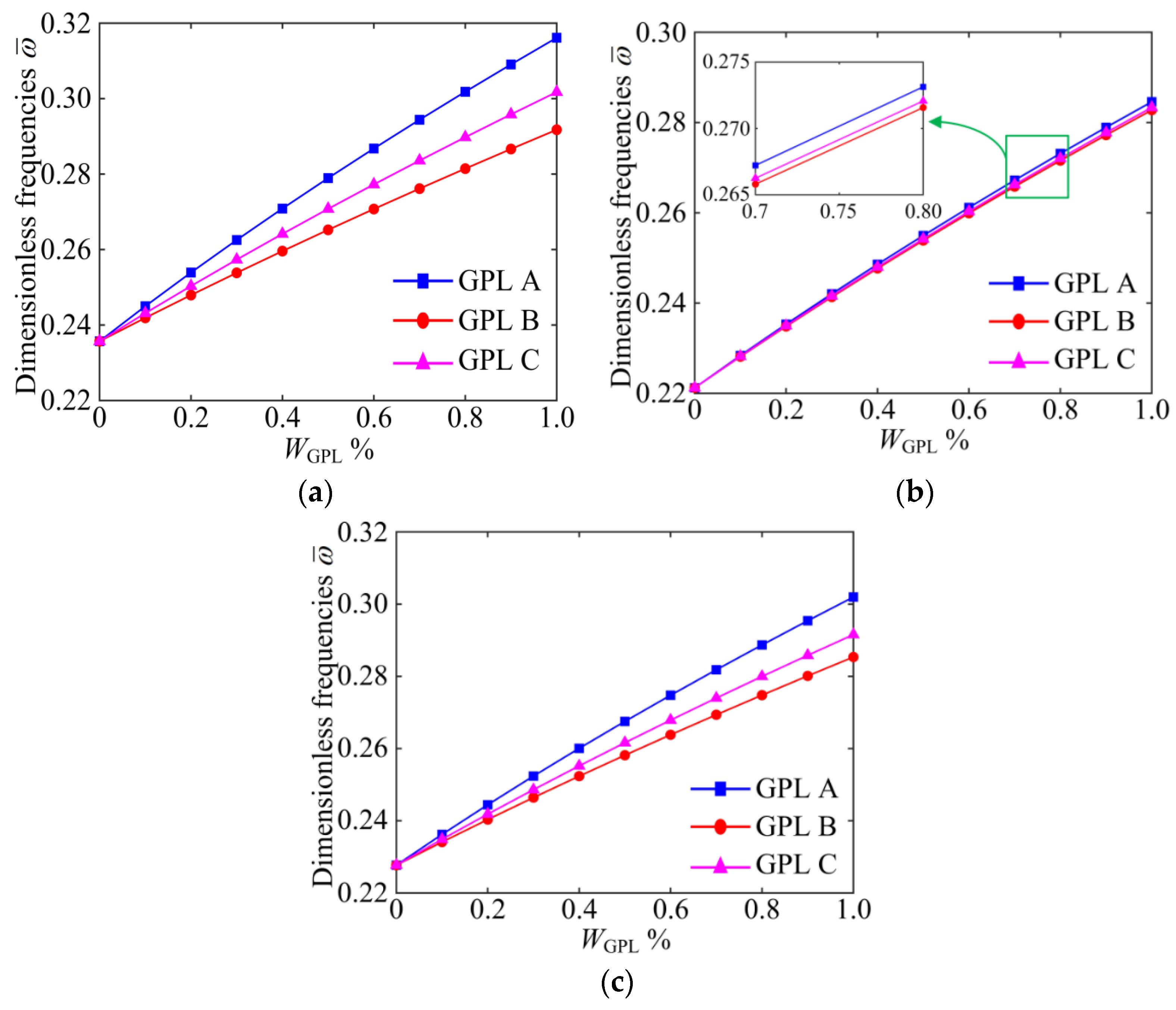
- Increasing the proportion of the GPL filling material can significantly improve the stiffness of the GPLRP, two-cylindrical-panel system, thereby increasing the natural frequency of the system.
Author Contributions
Funding
Conflicts of Interest
References
- Zhai, Y.; Chai, M.; Su, J.; Liang, S. Dynamics properties of composite sandwich open circular cylindrical shells. Compos. Struct. 2018, 189, 148–159. [Google Scholar] [CrossRef]
- Mao, Q.; Pietrzko, S. Experimental study for control of sound transmission through double glazed window using optimally tuned Helmholtz resonators. Appl. Acoust. 2010, 71, 32–38. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Forced transverse vibrations of an elastically connected complex rectangular simply supported double-plate system. J. Sound Vib. 2004, 270, 997–1011. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, D. An exact Fourier series method for vibration analysis of elastically connected laminated composite double-beam system with elastic constraints. Mech. Adv. Mater. Struc. 2021, 28, 2440–2457. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P. Vibrations and Stability of Complex Beam Systems; Springer: New York, NY, USA, 2015. [Google Scholar]
- Mao, Q.; Wattanasakulpong, N. Vibration and stability of a double-beam system interconnected by an elastic foundation under conservative and nonconservative axial forces. Int. J. Mech. Sci. 2015, 93, 1–7. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Free transverse vibrations of elastically connected simply supported double-beam complex system. J. Sound Vib. 2000, 232, 387–403. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Transverse vibrations of elastically connected double-string complex system, Part I: Free vibrations. J. Sound Vib. 2000, 232, 355–366. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Porosity and inhomogeneity effects on the buckling and vibration of double-FGM nanoplates via a quasi-3D refined theory. Compos. Struct. 2019, 220, 289–303. [Google Scholar] [CrossRef]
- Jamalpoor, A.; Hosseini, M. Biaxial buckling analysis of double-orthotropic microplate-systems including in-plane magnetic field based on strain gradient theory. Compos. Part. B-Eng. 2015, 75, 53–64. [Google Scholar] [CrossRef]
- Xing, W.C.; Wang, Y.Q. Vibration characteristics analysis of rigid-flexible spacecraft with double-direction hinged solar arrays. Acta. Astronaut. 2022, 193, 454–468. [Google Scholar] [CrossRef]
- Xing, W.C.; Wang, Y.Q. Vibration characteristics of thin plate system joined by hinges in double directions. Thin-Walled Struct. 2022, 175, 109260. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, Y. Dynamic response of a simply supported viscously damped double-beam system under the moving oscillator. J. Sound Vib. 2016, 384, 194–209. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P. Forced transverse vibration of Rayleigh and Timoshenko double-beam system with effect of compressive axial load. Int. J. Mech. Sci. 2012, 60, 59–71. [Google Scholar] [CrossRef]
- Han, F.; Dan, D.; Cheng, W. Exact dynamic characteristic analysis of a double-beam system interconnected by a viscoelastic layer. Compos. Part B-Eng. 2019, 163, 272–281. [Google Scholar] [CrossRef]
- Brito, W.; Maia, C.; Mendonca, A. Bending analysis of elastically connected Euler–Bernoulli double-beam system using the direct boundary element method. Appl. Math. Model. 2019, 74, 387–408. [Google Scholar] [CrossRef]
- Vu, H.; Ordonez, A.; Karnopp, B. Vibration of a double-beam system. J. Sound Vib. 2000, 229, 807–822. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Ma, G. Effect of compressive axial load on forced transverse vibrations of a double-beam system. Int. J. Mech. Sci. 2008, 50, 299–305. [Google Scholar] [CrossRef]
- Kim, G.; Han, P.; An, K.; Choe, D.; Ri, Y.; Ri, H. Free vibration analysis of functionally graded double-beam system using Haar wavelet discretization method. Eng. Sci. Technol. 2021, 24, 414–427. [Google Scholar] [CrossRef]
- Kim, K.; Han, P.; Jong, K.; Jang, C.; Kim, R. Natural frequency calculation of elastically connected double-beam system with arbitrary boundary condition. AIP. Adv. 2020, 10, 055026. [Google Scholar] [CrossRef]
- Deng, H.; Cheng, W.; Zhao, S. Vibration and buckling analysis of double-functionally graded Timoshenko beam system on Winkler-Pasternak elastic foundation. Compos. Struct. 2017, 160, 152–168. [Google Scholar] [CrossRef]
- Hao, Q.; Zhai, W.; Chen, Z. Free vibration of connected double-beam system with general boundary conditions by a modified Fourier–Ritz method. Arch. Appl. Mech. 2018, 88, 741–754. [Google Scholar] [CrossRef]
- Rahman, M.S.; Lee, Y.-Y. New modified multi-level residue harmonic balance method for solving nonlinearly vibrating double-beam problem. J. Sound Vib. 2017, 406, 295–327. [Google Scholar] [CrossRef]
- Kelly, S.G.; Srinivas, S. Free vibrations of elastically connected stretched beams. J. Sound Vib. 2009, 326, 883–893. [Google Scholar] [CrossRef]
- Han, F.; Dan, D.; Cheng, W. An exact solution for dynamic analysis of a complex double-beam system. Compos. Struct. 2018, 193, 295–305. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Free transverse vibrations of an elastically connected rectangular simply supported double-plate complex system. J. Sound Vib. 2000, 236, 595–608. [Google Scholar] [CrossRef]
- Jeong, K.-H.; Kang, H.-S. Free vibration of multiple rectangular plates coupled with a liquid. Int. J. Mech. Sci. 2013, 74, 161–172. [Google Scholar] [CrossRef]
- Hedrih, K. Double plate system with a discontinuity in the elastic bonding layer. Acta Mech. Sin. 2007, 23, 221–229. [Google Scholar] [CrossRef]
- Hedrih, K.S. Transversal vibrations of double-plate systems. Acta Mech. Sin. 2006, 22, 487–501. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P.; Ristić, M. Vibrations and stability analysis of multiple rectangular plates coupled with elastic layers based on different plate theories. Int. J. Mech. Sci. 2015, 92, 233–244. [Google Scholar] [CrossRef]
- Hedrih, K.R.S.; Simonović, J.D. Non-linear dynamics of the sandwich double circular plate system. Int. J. Nonlin. Mech. 2010, 45, 902–918. [Google Scholar] [CrossRef]
- Simonović, J.D. Multi-frequency analysis of the double circular plate system non-linear dynamics. Nonlinear Dyn. 2012, 67, 2299–2315. [Google Scholar]
- Hedrih, K.R.; Simonović, J.D. Energies of the dynamics in a double circular plate nonlinear system. Int. J. Bifurc. Chaos 2011, 21, 2993–3011. [Google Scholar] [CrossRef]
- Noga, S. Free transverse vibration analysis of an elastically connected annular and circular double-membrane compound system. J. Sound Vib. 2010, 329, 1507–1522. [Google Scholar] [CrossRef]
- Avalle, M.; Belingardi, G.; Montanini, R. Characterization of polymeric structural foams under compressive impact loading by means of energy-absorption diagram. Int. J. Impact. Eng. 2001, 25, 455–472. [Google Scholar] [CrossRef]
- Smith, B.; Szyniszewski, S.; Hajjar, J.; Schafer, B.; Arwade, S. Steel foam for structures: A review of applications, manufacturing and material properties. J. Constr. Steel Res. 2012, 71, 1–10. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Jelovica, J. Nonlinear vibration behavior of functionally graded porous cylindrical panels. Compos. Struct. 2020, 239, 112028. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D. Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 2017, 66, 83–91. [Google Scholar] [CrossRef]
- Sobhy, M. Magneto-electro-thermal bending of FG-graphene reinforced polymer doubly-curved shallow shells with piezoelectromagnetic faces. Compos. Struct. 2018, 203, 844–860. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Nguyen, L.B.; Nguyen, H.B.; Nguyen-Xuan, H. A three-variable high order shear deformation theory for isogeometric free vibration, buckling and instability analysis of FG porous plates reinforced by graphene platelets. Compos. Struct. 2020, 245, 112321. [Google Scholar] [CrossRef]
- Yang, J.; Chen, D.; Kitipornchai, S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 2018, 193, 281–294. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Chai, Q.; Wang, Y.Q. Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Eng. Struct. 2022, 252, 113718. [Google Scholar] [CrossRef]
- Ye, C.; Wang, Y.Q. Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: Internal resonances. Nonlinear Dyn. 2021, 104, 2051–2069. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.Q.; Zhang, Y. Free vibration of functionally graded graphene platelet-reinforced porous beams with spinning movement via differential transformation method. Arch. Appl. Mech. 2021, 91, 4817–4834. [Google Scholar] [CrossRef]
- Teng, M.W.; Wang, Y.Q. Nonlinear forced vibration of simply supported functionally graded porous nanocomposite thin plates reinforced with graphene platelets. Thin-Walled Struct. 2021, 164, 107799. [Google Scholar] [CrossRef]
- Zhou, Z.; Ni, Y.; Tong, Z.; Zhu, S.; Sun, J.; Xu, X. Accurate nonlinear buckling analysis of functionally graded porous graphene platelet reinforced composite cylindrical shells. Int. J. Mech. Sci. 2019, 151, 537–550. [Google Scholar] [CrossRef]
- Twinkle, C.M.; Pitchaimani, J. Free vibration and stability of graphene platelet reinforced porous nano-composite cylindrical panel: Influence of grading, porosity and non-uniform edge loads. Eng. Struct. 2021, 230, 111670. [Google Scholar]
- Soedel, W. Vibrations of Shells and Plates; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zhang, W.; Niu, Y.; Behdinan, K. Vibration characteristics of rotating pretwisted composite tapered blade with graphene coating layers. Aerosp. Sci. Technol. 2020, 98, 105644. [Google Scholar] [CrossRef]


| Porosity Distributions | GPL Distributions | Present | Yang et al. [41] |
|---|---|---|---|
| GPL A | 0.4038 | 0.3958 | |
| Porosity-I | GPL B | 0.3333 | 0.3293 |
| GPL C | 0.3633 | 0.3574 | |
| GPL A | 0.3089 | 0.3072 | |
| Porosity-II | GPL B | 0.2611 | 0.2601 |
| GPL C | 0.2766 | 0.2754 | |
| GPL A | 0.3686 | 0.3627 | |
| Porosity-III | GPL B | 0.3043 | 0.3014 |
| GPL C | 0.3294 | 0.3252 |
| Modes | Present | Oniszczuk [26] |
|---|---|---|
| 1 | 52.8 | 52.8 |
| 2 | 72.0 | 72.0 |
| 3 | 84.5 | 84.5 |
| 4 | 97.7 | 97.7 |
| 5 | 137.3 | 137.3 |
| 6 | 145.8 | 145.8 |
| Mode | (M, N) | |||||||
|---|---|---|---|---|---|---|---|---|
| (7, 7) | (8, 8) | (9, 9) | (10, 10) | (11, 11) | (12, 12) | (13, 13) | ||
| 1 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | |
| 2 | 0.66671 | 0.66671 | 0.66667 | 0.66667 | 0.66667 | 0.66667 | 0.66667 | |
| 3 | 0.69330 | 0.69330 | 0.69330 | 0.69330 | 0.69330 | 0.69330 | 0.69330 | |
| SSSS | 4 | 0.83013 | 0.83013 | 0.83009 | 0.83009 | 0.83009 | 0.83009 | 0.83009 |
| 5 | 0.99756 | 0.99751 | 0.99746 | 0.99746 | 0.99746 | 0.99746 | 0.99746 | |
| 6 | 1.10223 | 1.10134 | 1.10126 | 1.10125 | 1.10125 | 1.10125 | 1.10125 | |
| 1 | 1.04144 | 1.04143 | 1.04143 | 1.04143 | 1.04143 | 1.04143 | 1.04143 | |
| 2 | 1.07692 | 1.07691 | 1.07690 | 1.07690 | 1.07690 | 1.07690 | 1.07690 | |
| CCCC | 3 | 1.14413 | 1.14411 | 1.14411 | 1.14411 | 1.14411 | 1.14411 | 1.14411 |
| 4 | 1.23574 | 1.23571 | 1.23570 | 1.23570 | 1.23570 | 1.23570 | 1.23570 | |
| 5 | 1.28614 | 1.28609 | 1.28607 | 1.28607 | 1.28607 | 1.28607 | 1.28607 | |
| 6 | 1.50574 | 1.50572 | 1.50569 | 1.50569 | 1.50568 | 1.50568 | 1.50568 | |
| Mode | Spring Stiffness K | |||||||
|---|---|---|---|---|---|---|---|---|
| 102 | 104 | 106 | 108 | 1010 | 1012 | 1014 | ||
| SSSS | 1 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | 0.31612 | 0.31612 |
| 2 | 0.31612 | 0.31615 | 0.31920 | 0.54342 | 0.66667 | 0.66667 | 0.66667 | |
| 3 | 0.66667 | 0.66667 | 0.66667 | 0.66667 | 0.69330 | 0.69330 | 0.69330 | |
| 4 | 0.66667 | 0.66668 | 0.66816 | 0.69330 | 0.83009 | 0.83009 | 0.83009 | |
| 5 | 0.69330 | 0.69330 | 0.69330 | 0.80272 | 0.99746 | 0.99746 | 0.99746 | |
| 6 | 0.69330 | 0.69331 | 0.69472 | 0.82358 | 1.10125 | 1.10125 | 1.10125 | |
| CCCC | 1 | 1.04143 | 1.04143 | 1.04143 | 1.04143 | 1.04143 | 1.04143 | 1.04143 |
| 2 | 1.04143 | 1.04144 | 1.04238 | 1.07690 | 1.07690 | 1.07690 | 1.07690 | |
| 3 | 1.07690 | 1.07690 | 1.07690 | 1.13267 | 1.14411 | 1.14411 | 1.14411 | |
| 4 | 1.07690 | 1.07691 | 1.07784 | 1.14411 | 1.23570 | 1.23570 | 1.23570 | |
| 5 | 1.14411 | 1.14411 | 1.14411 | 1.16643 | 1.28607 | 1.28607 | 1.28607 | |
| 6 | 1.14411 | 1.14412 | 1.14498 | 1.22876 | 1.50568 | 1.50568 | 1.50568 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Chi, W.; Luo, J. Free Vibration Analysis of a Graphene-Platelet-Reinforced, Porous, Two-Cylindrical-Panel System. Materials 2022, 15, 6158. https://doi.org/10.3390/ma15176158
Sun X, Chi W, Luo J. Free Vibration Analysis of a Graphene-Platelet-Reinforced, Porous, Two-Cylindrical-Panel System. Materials. 2022; 15(17):6158. https://doi.org/10.3390/ma15176158
Chicago/Turabian StyleSun, Xianguang, Weichao Chi, and Jia Luo. 2022. "Free Vibration Analysis of a Graphene-Platelet-Reinforced, Porous, Two-Cylindrical-Panel System" Materials 15, no. 17: 6158. https://doi.org/10.3390/ma15176158
APA StyleSun, X., Chi, W., & Luo, J. (2022). Free Vibration Analysis of a Graphene-Platelet-Reinforced, Porous, Two-Cylindrical-Panel System. Materials, 15(17), 6158. https://doi.org/10.3390/ma15176158





