Meshless Chebyshev RPIM Solution for Free Vibration of Rotating Cross-Ply Laminated Combined Cylindrical-Conical Shells in Thermal Environment
Abstract
:1. Introduction
2. Theoretical Formulations
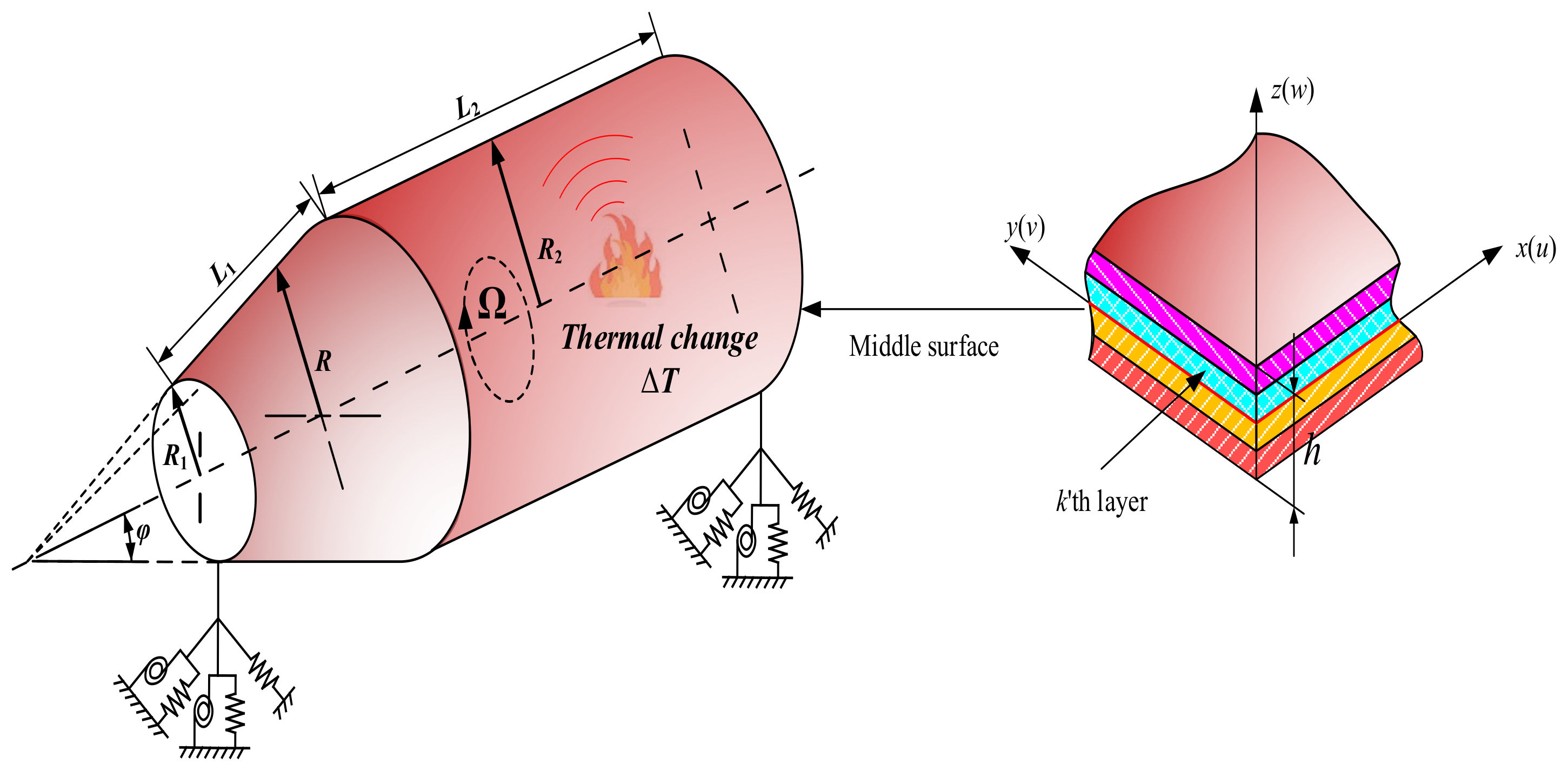
2.1. Description of the Model
2.2. Governing Equations and Boundary Conditions
2.3. Meshfree TRPIM Shape Function
2.4. Discretization of Governing Equations and Boundary Conditions
2.5. Continuous Condition
3. Numerical Results and Discussions
3.1. Verification and Convergence Study
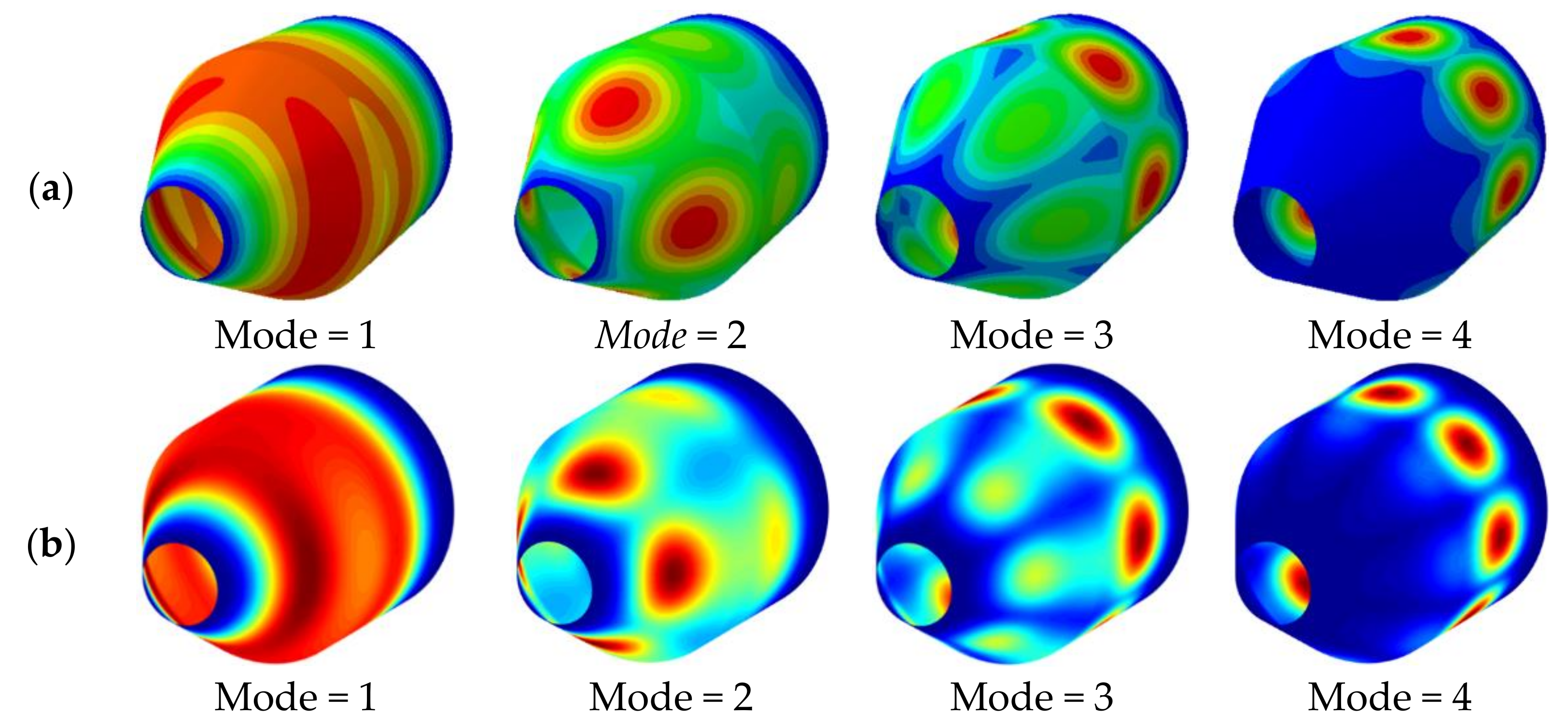
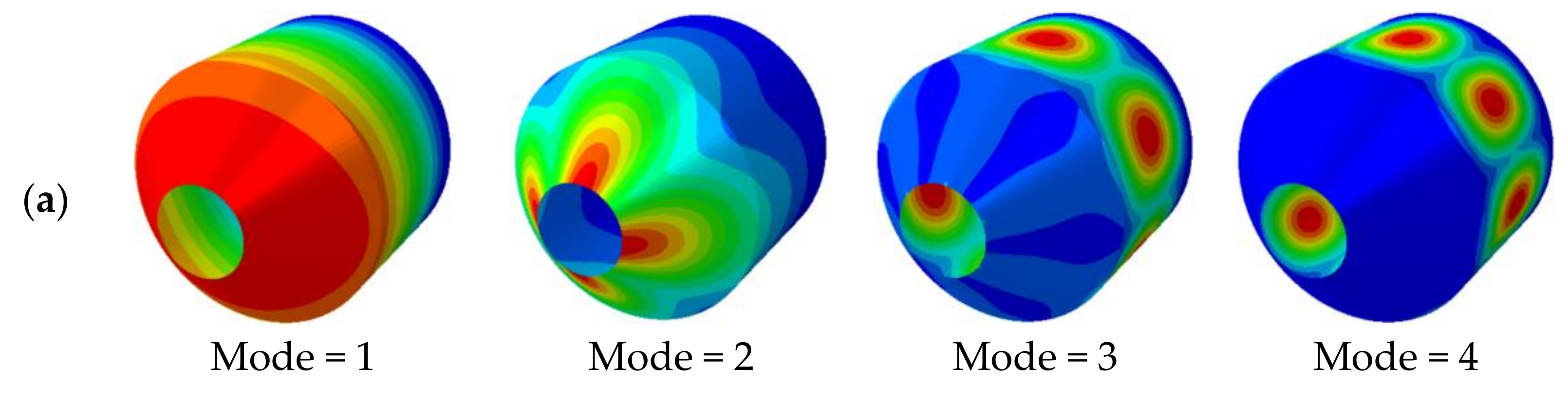
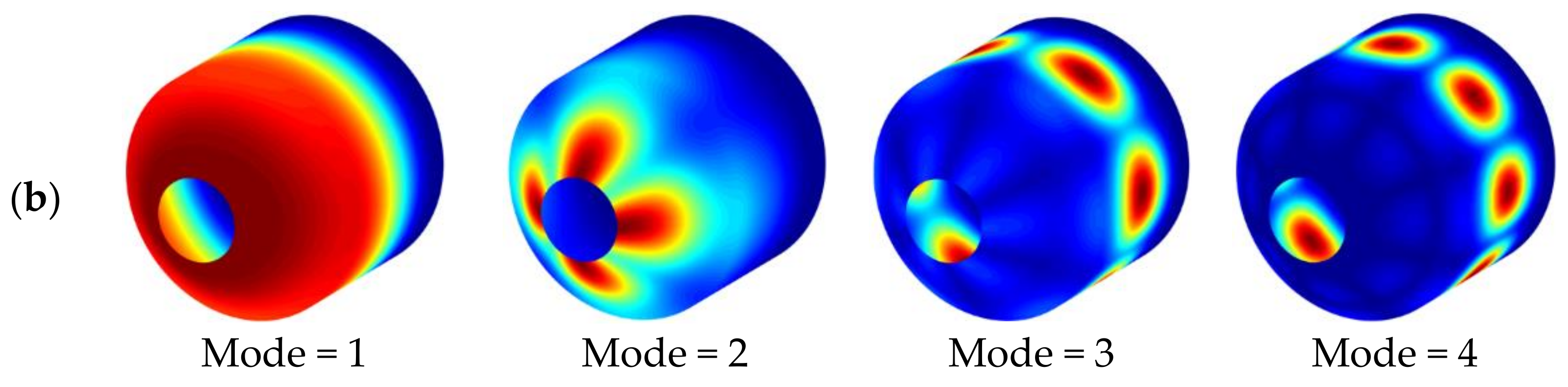
3.2. Numerical Examples
4. Conclusions
- (1)
- The meshless Chebyshev-PRIM technique is effective and has relatively high accuracy in the vibration solution of rotating structures. This method has the advantage of fast convergence, and relatively accurate results can be obtained with a smaller number of nodes.
- (2)
- The increase of the half-apex angle of the conical shell reduces the structural rigidity, so the structural frequency decreases. For the combined structure under the CC boundary, after the cone angle increases to a certain extent, the effect of the rotational speed will decrease, and the frequencies corresponding to different rotational speeds will gradually approach.
- (3)
- If the temperature is too high, thermal stress is accumulated inside the structure, the stiffness of the structure is reduced, and the frequency of the combined structure will also decrease. For the boundary conditions with weakened constraints, such as the CF boundary, thermal buckling also occurs with the increase of the temperature difference.
Author Contributions
Funding
Conflicts of Interest
References
- Haddadpour, H.; Mahmoudkhani, S.; Navazi, H.M. Free vibration analysis of functionally graded cylindrical shells in-cluding thermal effects. Thin-Walled Struct. 2007, 45, 591–599. [Google Scholar] [CrossRef]
- Afshari, H.; Amirabadi, H. Vibration characteristics of rotating truncated conical shells reinforced with agglomerated carbon nanotubes. J. Vib. Control 2021, 28, 1894–1914. [Google Scholar] [CrossRef]
- Jooybar, N.; Malekzadeh, P.; Fiouz, A.; Vaghefi, M. Thermal effect on free vibration of functionally graded truncated conical shell panels. Thin-Walled Struct. 2016, 103, 45–61. [Google Scholar] [CrossRef]
- Shekari, A.; Ghasemi, F.A.; Malekzadehfard, K. Free Damped Vibration of Rotating Truncated Conical Sandwich Shells Using an Improved High-Order Theory. Lat. Am. J. Solids Struct. 2017, 14, 2291–2323. [Google Scholar] [CrossRef]
- Dai, Q.; Cao, Q.; Chen, Y. Frequency analysis of rotating truncated conical shells using the Haar wavelet method. Appl. Math. Model. 2018, 57, 603–613. [Google Scholar] [CrossRef]
- Xiang, X.; Guoyong, J.; Wanyou, L.; Zhigang, L. A numerical solution for vibration analysis of composite laminated conical, cylindrical shell and annular plate structures. Compos. Struct. 2014, 111, 20–30. [Google Scholar] [CrossRef]
- Xue, Y.; Jin, G.; Ma, X.; Chen, H.; Ye, T.; Chen, M.; Zhang, Y. Free vibration analysis of porous plates with porosity distributions in the thickness and in-plane directions using isogeometric approach. Int. J. Mech. Sci. 2019, 152, 346–362. [Google Scholar] [CrossRef]
- Bediz, B. A spectral-Tchebychev solution technique for determining vibrational behavior of thick plates having arbitrary ge-ometry. J. Sound Vib. 2018, 432, 272–289. [Google Scholar] [CrossRef]
- Ye, T.; Jin, G.; Su, Z.; Jia, X. A unified Chebyshev–Ritz formulation for vibration analysis of composite laminated deep open shells with arbi-trary boundary conditions. Arch. Appl. Mech. 2014, 84, 441–471. [Google Scholar] [CrossRef]
- Ma, X.; Jin, G.; Xiong, Y.; Liu, Z. Free and forced vibration analysis of coupled conical–cylindrical shells with arbitrary boundary conditions. Int. J. Mech. Sci. 2014, 88, 122–137. [Google Scholar] [CrossRef]
- Nguyen-Thanh, N.; Rabczuk, T.; Nguyen-Xuan, H.; Bordas, S.P. A smoothed finite element method for shell analysis. Comput. Methods Appl. Mech. Eng. 2008, 198, 165–177. [Google Scholar] [CrossRef]
- Barik, M.; Mukhopadhyay, M. Finite element free flexural vibration analysis of arbitrary plates. Finite Elements Anal. Des. 1998, 29, 137–151. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Viola, E. Four-parameter functionally graded cracked plates of arbitrary shape: A GDQFEM solution for free vibrations. Mech. Adv. Mater. Struct. 2016, 23, 89–107. [Google Scholar] [CrossRef]
- Ye, T.; Jin, G.; Chen, Y.; Shi, S. A unified formulation for vibration analysis of open shells with arbitrary boundary conditions. Int. J. Mech. Sci. 2014, 81, 42–59. [Google Scholar] [CrossRef]
- Caresta, M.; Kessissoglou, N.J. Free vibrational characteristics of isotropic coupled cylindrical–conical shells. J. Sound Vib. 2010, 329, 733–751. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Reddy, J. Winkler–Pasternak foundation effect on the static and dynamic analyses of laminated doubly-curved and degenerate shells and panels. Compos. Part B Eng. 2014, 57, 269–296. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Wang, X.; Du, Y.; Chen, H. Free vibration analysis for composite laminated doubly-curved shells of revolution by a semi analytical method. Compos. Struct. 2018, 201, 86–111. [Google Scholar] [CrossRef]
- Shakouri, M. Free vibration analysis of functionally graded rotating conical shells in thermal environment. Compos. Part B Eng. 2019, 163, 574–584. [Google Scholar] [CrossRef]
- Afshari, H. Effect of graphene nanoplatelet reinforcements on the dynamics of rotating truncated conical shells. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–22. [Google Scholar] [CrossRef]
- Bhangale, R.K.; Ganesan, N.; Padmanabhan, C. Linear thermoelastic buckling and free vibration behavior of functionally graded truncated conical shells. J. Sound Vib. 2006, 292, 341–371. [Google Scholar] [CrossRef]
- Tian, L.; Ye, T.; Jin, G. Vibration analysis of combined conical-cylindrical shells based on the dynamic stiffness method. Thin-Walled Struct. 2021, 159, 107260. [Google Scholar] [CrossRef]
- Qin, Z.; Yang, Z.; Zu, J.; Chu, F. Free vibration analysis of rotating cylindrical shells coupled with moderately thick annular plates. Int. J. Mech. Sci. 2018, 142–143, 127–139. [Google Scholar] [CrossRef]
- Singha, T.D.; Rout, M.; Bandyopadhyay, T.; Karmakar, A. Free vibration of rotating pretwisted FG-GRC sandwich conical shells in thermal environment using HSDT. Compos. Struct. 2020, 257, 113144. [Google Scholar] [CrossRef]
- Talebitooti, M.; Soureshjani, A.H.; Pakravan, I.; Talebitooti, R. Frequency study on panel type of FG-CNTRC joined conical-conical struc-tures. Compos. Struct. 2020, 259, 113241. [Google Scholar] [CrossRef]
- Soureshjani, A.H.; Talebitooti, R.; Talebitooti, M. Thermal effects on the free vibration of joined FG-CNTRC conical-conical shells. Thin-Walled Struct. 2020, 156, 106960. [Google Scholar] [CrossRef]
- Shi, X.; Zuo, P.; Zhong, R.; Guo, C.; Wang, Q. Thermal vibration analysis of functionally graded conical-cylindrical coupled shell based on spectro-geometric method. Thin-Walled Struct. 2022, 175, 109138. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Mohandes, M.; Dimitri, R.; Tornabene, F. Agglomeration Effects on the Vibrations of CNTS/Fiber/Polymer/Metal Hybrid Laminates Cylindrical Shell. Compos. Part B Eng. 2019, 167, 700–716. [Google Scholar] [CrossRef]
- Liu, S.; Ke, Y.; Davar, A.; Jam, J.E.; Lutfor, M.R.; Sarjadi, M.S. The effects of rotation on the frequencies and critical speed of CNTs/fiber/polymer/metal laminates cy-lindrical shell. Arab. J. Chem. 2021, 15, 103575. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Mostafaei, H. Vibration analysis of scale-dependent thin shallow microshells with arbitrary plan-form and boundary conditions. Int. J. Eng. Sci. 2021, 158, 103413. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Mostafaei, H. On the mechanics of microshells of revolution. Int. J. Eng. Sci. 2021, 161, 103450. [Google Scholar] [CrossRef]
- Kwak, S.; Kim, K.; Pyon, S.; Li, Y.; Ri, C. A new meshfree approach for three-dimensional free vibration analysis of thick laminated doubly-shell of revolution. Eng. Anal. Bound. Elements 2021, 134, 199–218. [Google Scholar] [CrossRef]
- Kwak, S.; Kim, K.; An, K.; Jong, G.; Yun, J. A novel meshfree method for three-dimensional natural frequency analysis of thick laminated conical, cylindrical shells and annular plates. Phys. Scr. 2021, 96, 125204. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. An Introduction to Meshfree Methods and Their Programming; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Zarei, A.; Khosravifard, A. Meshfree investigation of the vibrational behavior of pre-stressed laminated composite plates based on a variationally consistent plate model. Eng. Anal. Bound. Elements 2020, 111, 118–133. [Google Scholar] [CrossRef]
- Mellouli, H.; Jrad, H.; Wali, M.; Dammak, F. Free vibration analysis of FG-CNTRC shell structures using the meshfree radial point interpolation method. Comput. Math. Appl. 2020, 79, 3160–3178. [Google Scholar] [CrossRef]
- Zhang, L.; Lei, Z.; Liew, K. Free vibration analysis of functionally graded carbon nanotube-reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method. Compos. Struct. 2015, 120, 189–199. [Google Scholar] [CrossRef]
- Fallah, N.; Delzendeh, M. Free vibration analysis of laminated composite plates using meshless finite volume method. Eng. Anal. Bound. Elem. 2018, 88, 132–144. [Google Scholar] [CrossRef]
- Kwak, S.; Kim, K.; Jang, P.; Ri, Y.; Kim, I. A meshfree local weak-form method for free vibration analysis of an open laminated cylindrical shell with elliptical section. Compos. Struct. 2021, 275, 114484. [Google Scholar] [CrossRef]
- Qatu, M.S. Vibration of Laminated Shells and Plates; Elsevier: Amsterdam, The Netherlands, 2004; Volume 60, pp. 379–404. [Google Scholar]
- Kwak, S.; Kim, K.; Jong, G.; Kim, Y.; Pang, K. Free vibration analysis of laminated elliptic cylindrical panel with varying thickness using a meshfree method. Eur. Phys. J. Plus 2022, 137, 173. [Google Scholar] [CrossRef]
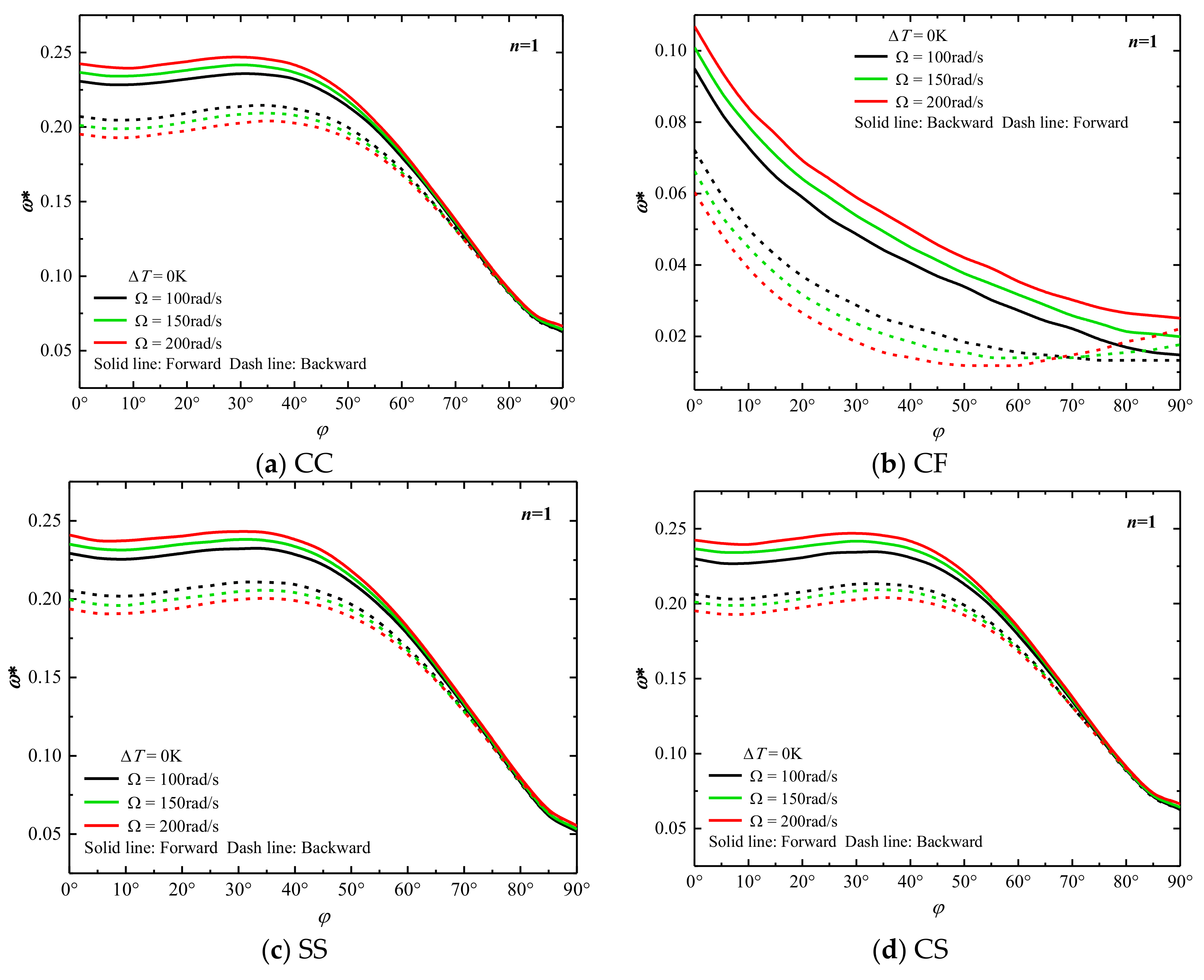
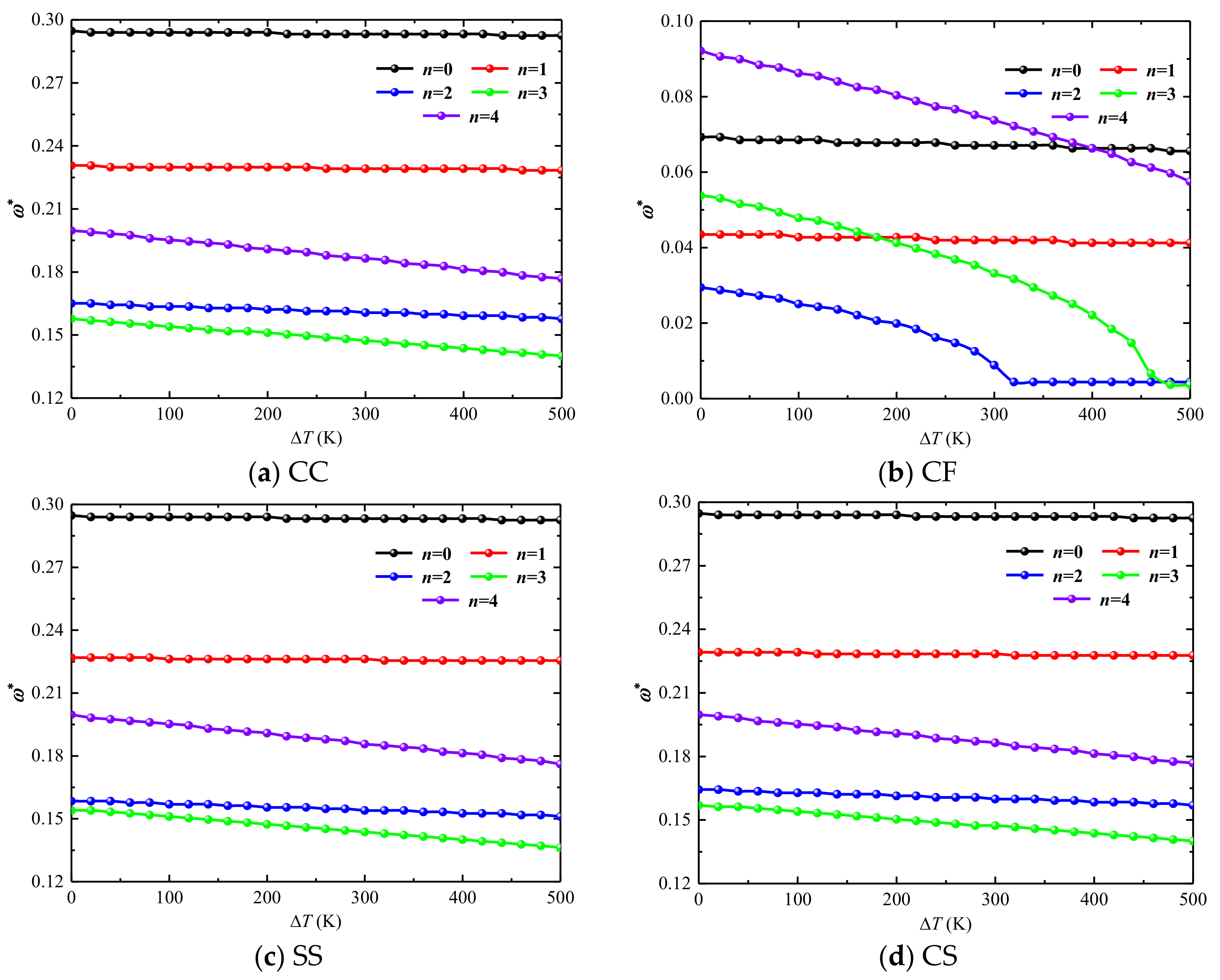
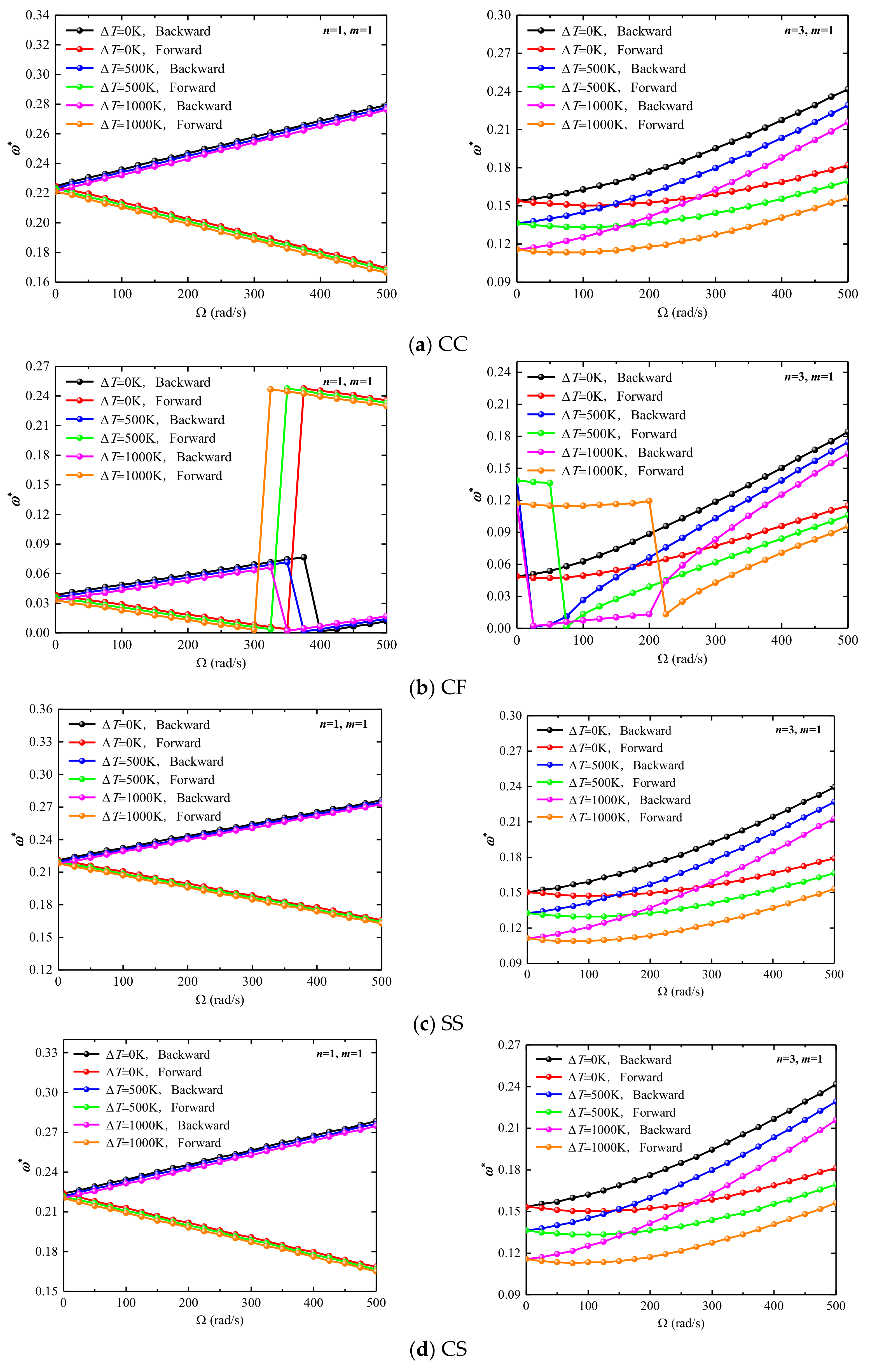
| N | CC | SS | FC | CF | ||||
|---|---|---|---|---|---|---|---|---|
| n = 1 | n = 2 | n = 1 | n = 2 | n = 1 | n = 2 | n = 1 | n = 2 | |
| 5 | 0.2328 | 0.1812 | 0.2232 | 0.1754 | 0.1171 | 0.0803 | 0.0494 | 0.0339 |
| 6 | 0.2284 | 0.1790 | 0.2262 | 0.1761 | 0.1127 | 0.0825 | 0.0464 | 0.0317 |
| 7 | 0.2306 | 0.1805 | 0.2255 | 0.1754 | 0.1142 | 0.0833 | 0.0457 | 0.0317 |
| 8 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0464 | 0.0324 |
| 9 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 10 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 11 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 12 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 13 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 14 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 15 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 16 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 17 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 18 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 19 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 20 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| 21 | 0.2299 | 0.1798 | 0.2262 | 0.1754 | 0.1135 | 0.0840 | 0.0457 | 0.0317 |
| m | n = 0 | n = 1 | n = 2 | |||
|---|---|---|---|---|---|---|
| FEM | Present | FEM | Present | FEM | Present | |
| 1 | 0.50375 | 0.50305 | 0.29287 | 0.29279 | 0.10203 | 0.09996 |
| 2 | 0.60986 | 0.60985 | 0.63581 | 0.63506 | 0.50290 | 0.50217 |
| 3 | 0.93092 | 0.93082 | 0.81123 | 0.81141 | 0.69148 | 0.69116 |
| 4 | 0.95632 | 0.95612 | 0.93088 | 0.93137 | 0.85890 | 0.85888 |
| 5 | 0.97160 | 0.97134 | 0.94850 | 0.95183 | 0.91607 | 0.91544 |
| 6 | 1.01188 | 1.01142 | 0.99145 | 0.99156 | 0.96048 | 0.96007 |
| n = 3 | n = 4 | n = 5 | ||||
| FEM | Present | FEM | Present | FEM | Present | |
| 1 | 0.09377 | 0.08750 | 0.14460 | 0.14441 | 0.20390 | 0.19930 |
| 2 | 0.39220 | 0.39115 | 0.33034 | 0.32996 | 0.29633 | 0.29579 |
| 3 | 0.51518 | 0.51434 | 0.39562 | 0.39537 | 0.37623 | 0.37013 |
| 4 | 0.75359 | 0.75289 | 0.64458 | 0.64594 | 0.58167 | 0.57874 |
| 5 | 0.79698 | 0.79629 | 0.69114 | 0.69248 | 0.61422 | 0.61285 |
| 6 | 0.91939 | 0.91893 | 0.87194 | 0.87098 | 0.81980 | 0.81642 |
| Ω* | n | FEM | Present | ||
|---|---|---|---|---|---|
| w*b | w*f | w*b | w*f | ||
| 0.01 rad/s | 1 | 0.5264 | 0.5264 | 0.5267 | 0.5267 |
| 2 | 0.3769 | 0.3769 | 0.3774 | 0.3774 | |
| 3 | 0.2873 | 0.2873 | 0.2869 | 0.2869 | |
| 4 | 0.236 | 0.236 | 0.2363 | 0.2363 | |
| 5 | 0.2231 | 0.2231 | 0.2246 | 0.2246 | |
| 6 | 0.2474 | 0.2474 | 0.2469 | 0.2469 | |
| 100 rad/s | 1 | 0.5430 | 0.5097 | 0.5432 | 0.5103 |
| 2 | 0.3906 | 0.3648 | 0.3904 | 0.3645 | |
| 3 | 0.3005 | 0.2816 | 0.3010 | 0.2822 | |
| 4 | 0.2527 | 0.2383 | 0.2528 | 0.2387 | |
| 5 | 0.2455 | 0.234 | 0.2469 | 0.2352 | |
| 6 | 0.2747 | 0.2647 | 0.2740 | 0.2645 | |
| 500 rad/s | 1 | 0.6085 | 0.4422 | 0.6090 | 0.4421 |
| 2 | 0.4605 | 0.3308 | 0.4609 | 0.3304 | |
| 3 | 0.4174 | 0.322 | 0.4174 | 0.3222 | |
| 4 | 0.4484 | 0.3756 | 0.4480 | 0.3762 | |
| 5 | 0.5212 | 0.4629 | 0.5220 | 0.4633 | |
| 6 | 0.6157 | 0.5612 | 0.6161 | 0.5608 | |
| φ | Mode | CC | CS | FC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEM | Present | Diff,% | FEM | Present | Diff,% | FEM | Present | Diff,% | ||
| π/6 | 1 | 234.96 | 237.01 | 0.872 | 227.4 | 228.08 | 0.299 | 120.2 | 119.54 | −0.549 |
| 2 | 250.73 | 251.66 | 0.371 | 227.84 | 228.85 | 0.443 | 133.66 | 133.66 | 0 | |
| 3 | 252.19 | 254.21 | 0.801 | 244.34 | 243.77 | −0.233 | 234.47 | 234.16 | −0.132 | |
| 4 | 265.13 | 264.69 | −0.166 | 247.19 | 247.93 | 0.299 | 240.92 | 241.13 | 0.087 | |
| 5 | 272.86 | 274.39 | 0.561 | 265.13 | 264.69 | −0.166 | 270.66 | 270.72 | 0.022 | |
| 6 | 285.89 | 286.71 | 0.287 | 281.3 | 282.09 | 0.281 | 272.89 | 274.28 | 0.509 | |
| π/4 | 1 | 270.23 | 272.39 | 0.799 | 239.64 | 239.73 | 0.038 | 145.93 | 145.81 | −0.082 |
| 2 | 281.53 | 283.4 | 0.664 | 250.99 | 250.54 | −0.179 | 152.71 | 152.7 | −0.007 | |
| 3 | 293.78 | 293.32 | −0.157 | 271.81 | 272.52 | 0.261 | 256.96 | 256.67 | −0.113 | |
| 4 | 294.13 | 296.48 | 0.799 | 293.78 | 293.32 | −0.157 | 268.27 | 270.41 | 0.798 | |
| 5 | 319.31 | 321.55 | 0.702 | 302.2 | 300.76 | −0.477 | 281.31 | 283.08 | 0.629 | |
| 6 | 328.18 | 329.1 | 0.28 | 312.49 | 314.21 | 0.55 | 305.66 | 306.68 | 0.334 | |
| L2/L1 | Ω, rad/s | n | Forward | Backward | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CC | SS | CF | FC | CC | SS | CF | FC | |||
| 0.5 | 50 | 1 | 0.4723 | 0.4561 | 0.1127 | 0.2549 | 0.4826 | 0.4664 | 0.1230 | 0.2667 |
| 2 | 0.3809 | 0.3478 | 0.0847 | 0.1157 | 0.3883 | 0.3559 | 0.0928 | 0.1245 | ||
| 3 | 0.3544 | 0.3153 | 0.1341 | 0.1709 | 0.3595 | 0.3212 | 0.1400 | 0.1776 | ||
| 100 | 1 | 0.4671 | 0.4509 | 0.1083 | 0.2490 | 0.4877 | 0.4715 | 0.1282 | 0.2726 | |
| 2 | 0.3772 | 0.3448 | 0.0818 | 0.1120 | 0.3927 | 0.3595 | 0.0980 | 0.1297 | ||
| 3 | 0.3522 | 0.3139 | 0.1326 | 0.1702 | 0.3640 | 0.3249 | 0.1459 | 0.1820 | ||
| 1 | 50 | 1 | 0.3735 | 0.3618 | 0.0759 | 0.1835 | 0.3846 | 0.3728 | 0.0862 | 0.1945 |
| 2 | 0.3448 | 0.3161 | 0.0361 | 0.0921 | 0.3536 | 0.3249 | 0.0449 | 0.1009 | ||
| 3 | 0.3404 | 0.3028 | 0.0663 | 0.1687 | 0.3470 | 0.3087 | 0.0729 | 0.1754 | ||
| 100 | 1 | 0.3676 | 0.3559 | 0.0707 | 0.1776 | 0.3905 | 0.3780 | 0.0914 | 0.2004 | |
| 2 | 0.3411 | 0.3124 | 0.0332 | 0.0884 | 0.3581 | 0.3293 | 0.0508 | 0.1061 | ||
| 3 | 0.3382 | 0.3006 | 0.0670 | 0.1680 | 0.3507 | 0.3131 | 0.0803 | 0.1805 | ||
| 1.5 | 50 | 1 | 0.2896 | 0.2829 | 0.0553 | 0.1392 | 0.3006 | 0.2947 | 0.0663 | 0.1510 |
| 2 | 0.2505 | 0.2358 | 0.0258 | 0.0781 | 0.2593 | 0.2446 | 0.0346 | 0.0869 | ||
| 3 | 0.2218 | 0.2019 | 0.0597 | 0.1665 | 0.2291 | 0.2092 | 0.0670 | 0.1724 | ||
| 100 | 1 | 0.2837 | 0.2778 | 0.0501 | 0.1334 | 0.3065 | 0.2999 | 0.0715 | 0.1562 | |
| 2 | 0.2461 | 0.2313 | 0.0236 | 0.0744 | 0.2645 | 0.2498 | 0.0420 | 0.0928 | ||
| 3 | 0.2203 | 0.2004 | 0.0612 | 0.1650 | 0.2336 | 0.2137 | 0.0752 | 0.1776 | ||
| 2 | 50 | 1 | 0.2328 | 0.2284 | 0.0420 | 0.1105 | 0.2439 | 0.2402 | 0.0530 | 0.1223 |
| 2 | 0.1864 | 0.1783 | 0.0214 | 0.0700 | 0.1952 | 0.1871 | 0.0302 | 0.0788 | ||
| 3 | 0.1606 | 0.1496 | 0.0575 | 0.1540 | 0.1672 | 0.1569 | 0.0641 | 0.1606 | ||
| 100 | 1 | 0.2269 | 0.2225 | 0.0368 | 0.1046 | 0.2498 | 0.2453 | 0.0589 | 0.1282 | |
| 2 | 0.1820 | 0.1739 | 0.0192 | 0.0670 | 0.2004 | 0.1923 | 0.0376 | 0.0847 | ||
| 3 | 0.1584 | 0.1481 | 0.0589 | 0.1525 | 0.1724 | 0.1621 | 0.0729 | 0.1658 | ||
| φ | Ω, rad/s | n | Forward | Backward | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CC | SS | CF | FC | CC | SS | CF | FC | |||
| π/6 | 50 | 1 | 0.2763 | 0.2645 | 0.0729 | 0.1260 | 0.2881 | 0.2763 | 0.0840 | 0.1378 |
| 2 | 0.2269 | 0.2085 | 0.0766 | 0.1444 | 0.2365 | 0.2173 | 0.0855 | 0.1532 | ||
| 3 | 0.2807 | 0.2652 | 0.2033 | 0.2763 | 0.2881 | 0.2726 | 0.2107 | 0.2829 | ||
| 100 | 1 | 0.2704 | 0.2593 | 0.0670 | 0.1201 | 0.2940 | 0.2822 | 0.0899 | 0.1437 | |
| 2 | 0.2225 | 0.2041 | 0.0729 | 0.1400 | 0.2417 | 0.2225 | 0.0914 | 0.1584 | ||
| 3 | 0.2785 | 0.2630 | 0.2019 | 0.2741 | 0.2925 | 0.2770 | 0.2159 | 0.2873 | ||
| π/4 | 50 | 1 | 0.2859 | 0.2756 | 0.0589 | 0.1297 | 0.2969 | 0.2866 | 0.0700 | 0.1415 |
| 2 | 0.2306 | 0.2115 | 0.0597 | 0.1606 | 0.2402 | 0.2210 | 0.0685 | 0.1695 | ||
| 3 | 0.2549 | 0.2365 | 0.1599 | 0.2520 | 0.2616 | 0.2431 | 0.1665 | 0.2586 | ||
| 100 | 1 | 0.2800 | 0.2697 | 0.0538 | 0.1238 | 0.3028 | 0.2925 | 0.0752 | 0.1474 | |
| 2 | 0.2269 | 0.2078 | 0.0560 | 0.1562 | 0.2453 | 0.2255 | 0.0744 | 0.1746 | ||
| 3 | 0.2527 | 0.2343 | 0.1577 | 0.2498 | 0.2667 | 0.2476 | 0.1717 | 0.2638 | ||
| π/3 | 50 | 1 | 0.2918 | 0.2822 | 0.0494 | 0.1319 | 0.3028 | 0.2940 | 0.0597 | 0.1437 |
| 2 | 0.2343 | 0.2144 | 0.0501 | 0.1857 | 0.2431 | 0.2232 | 0.0597 | 0.1945 | ||
| 3 | 0.2424 | 0.2218 | 0.1356 | 0.2394 | 0.2498 | 0.2291 | 0.1422 | 0.2468 | ||
| 100 | 1 | 0.2859 | 0.2770 | 0.0442 | 0.1260 | 0.3087 | 0.2999 | 0.0648 | 0.1496 | |
| 2 | 0.2299 | 0.2100 | 0.0472 | 0.1812 | 0.2483 | 0.2284 | 0.0656 | 0.1989 | ||
| 3 | 0.2402 | 0.2196 | 0.1341 | 0.2372 | 0.2542 | 0.2336 | 0.1481 | 0.2512 | ||
| π/2 | 50 | 1 | 0.2962 | 0.2873 | 0.0427 | 0.1334 | 0.3080 | 0.2991 | 0.0516 | 0.1451 |
| 2 | 0.2380 | 0.2181 | 0.0457 | 0.2092 | 0.2476 | 0.2269 | 0.0545 | 0.2181 | ||
| 3 | 0.2372 | 0.2144 | 0.1194 | 0.2321 | 0.2439 | 0.2218 | 0.1267 | 0.2387 | ||
| 100 | 1 | 0.2903 | 0.2814 | 0.0383 | 0.1275 | 0.3139 | 0.3043 | 0.0560 | 0.1510 | |
| 2 | 0.2343 | 0.2137 | 0.0427 | 0.2048 | 0.2520 | 0.2321 | 0.0604 | 0.2232 | ||
| 3 | 0.2350 | 0.2129 | 0.1186 | 0.2299 | 0.2483 | 0.2262 | 0.1326 | 0.2439 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Hu, S.; Zhong, R.; Qin, B.; Zhao, X. Meshless Chebyshev RPIM Solution for Free Vibration of Rotating Cross-Ply Laminated Combined Cylindrical-Conical Shells in Thermal Environment. Materials 2022, 15, 6177. https://doi.org/10.3390/ma15176177
Li Z, Hu S, Zhong R, Qin B, Zhao X. Meshless Chebyshev RPIM Solution for Free Vibration of Rotating Cross-Ply Laminated Combined Cylindrical-Conical Shells in Thermal Environment. Materials. 2022; 15(17):6177. https://doi.org/10.3390/ma15176177
Chicago/Turabian StyleLi, Zhen, Shuangwei Hu, Rui Zhong, Bin Qin, and Xing Zhao. 2022. "Meshless Chebyshev RPIM Solution for Free Vibration of Rotating Cross-Ply Laminated Combined Cylindrical-Conical Shells in Thermal Environment" Materials 15, no. 17: 6177. https://doi.org/10.3390/ma15176177
APA StyleLi, Z., Hu, S., Zhong, R., Qin, B., & Zhao, X. (2022). Meshless Chebyshev RPIM Solution for Free Vibration of Rotating Cross-Ply Laminated Combined Cylindrical-Conical Shells in Thermal Environment. Materials, 15(17), 6177. https://doi.org/10.3390/ma15176177






