In Situ Nano-Indentation of a Gold Sub-Micrometric Particle Imaged by Multi-Wavelength Bragg Coherent X-ray Diffraction
Abstract
:1. Introduction
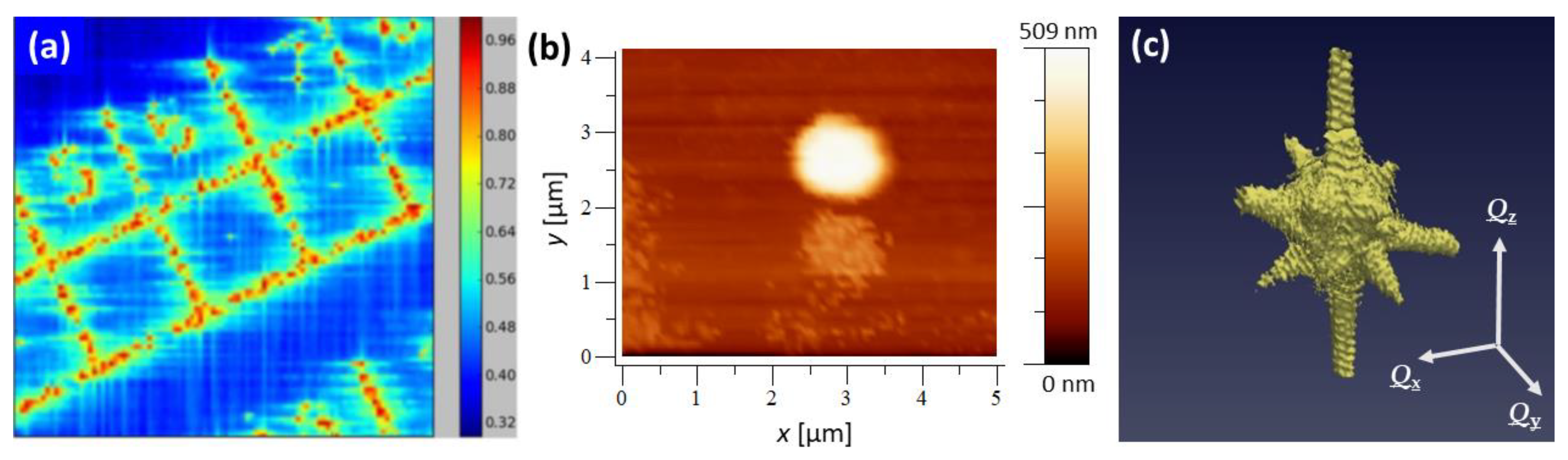
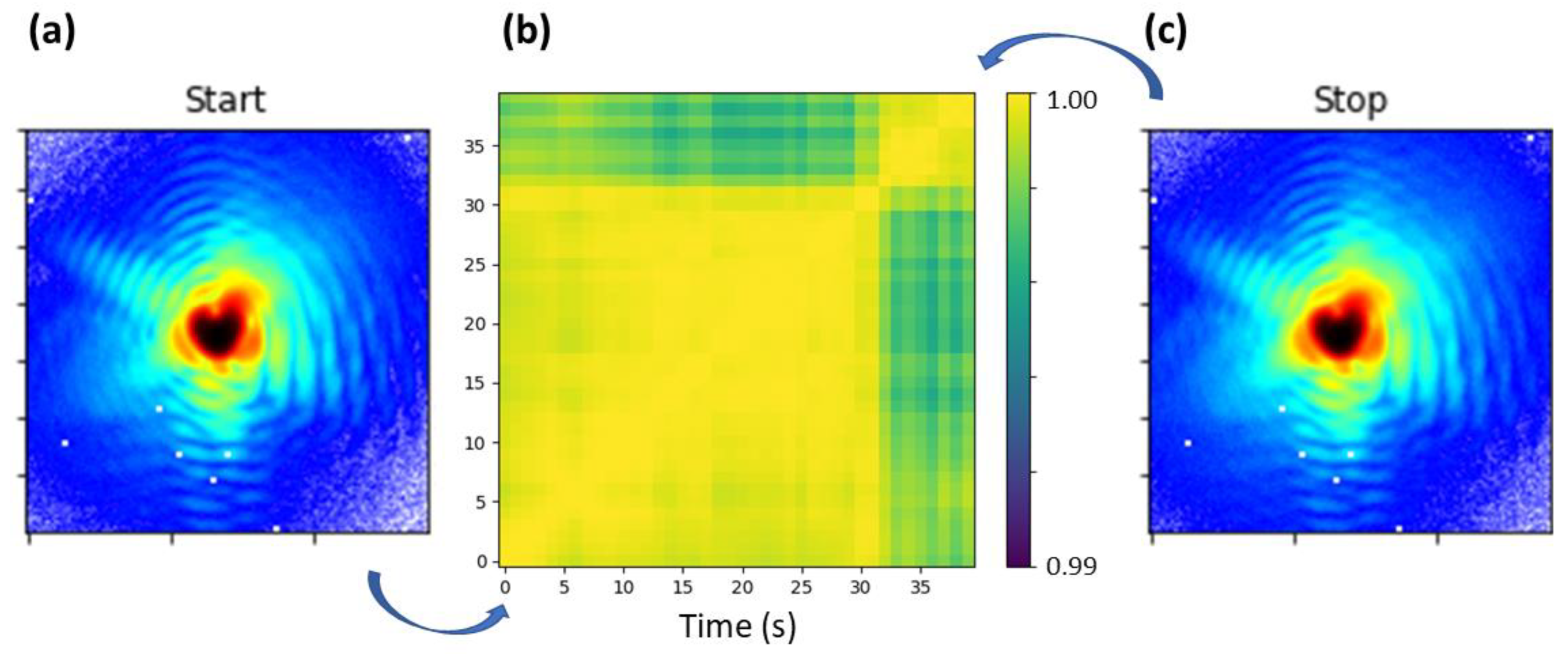
2. Materials and Methods
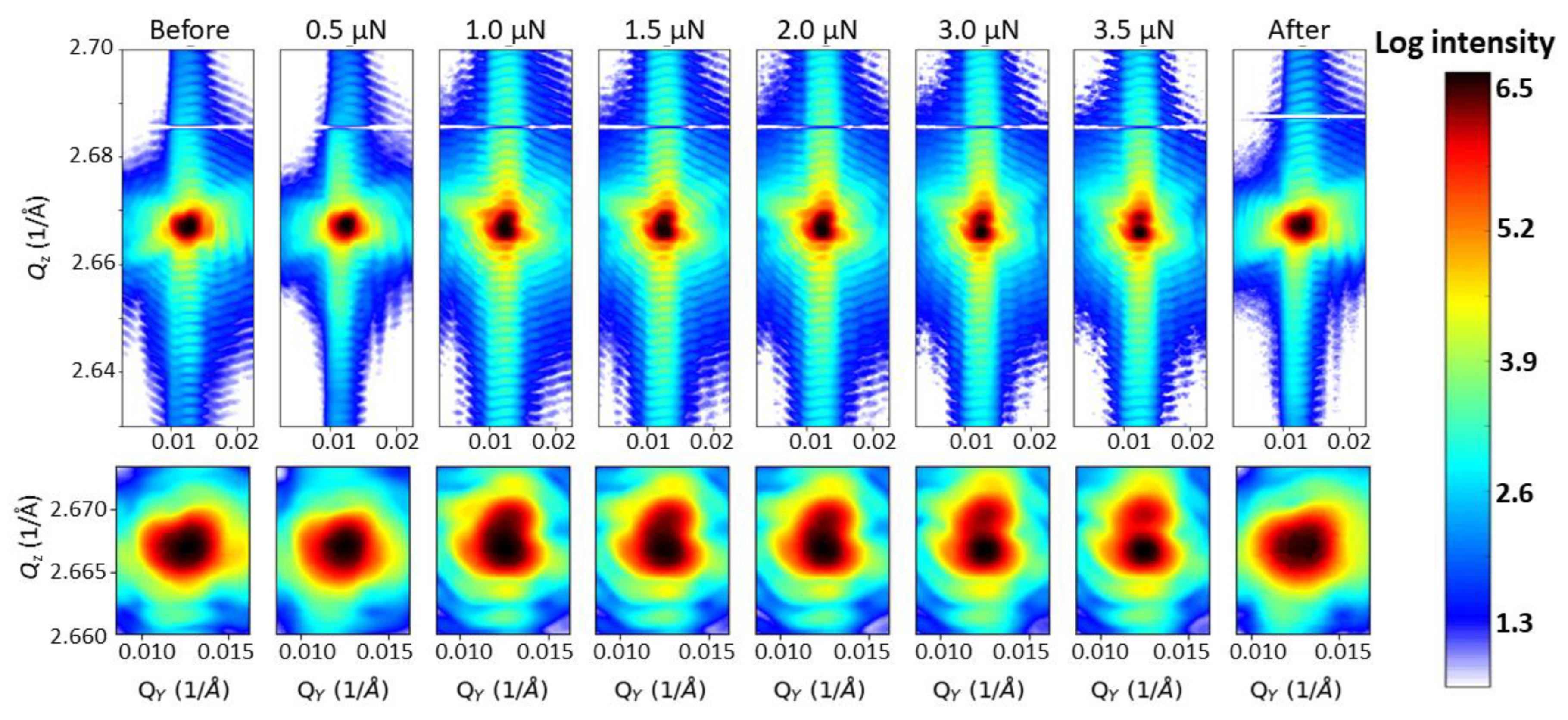
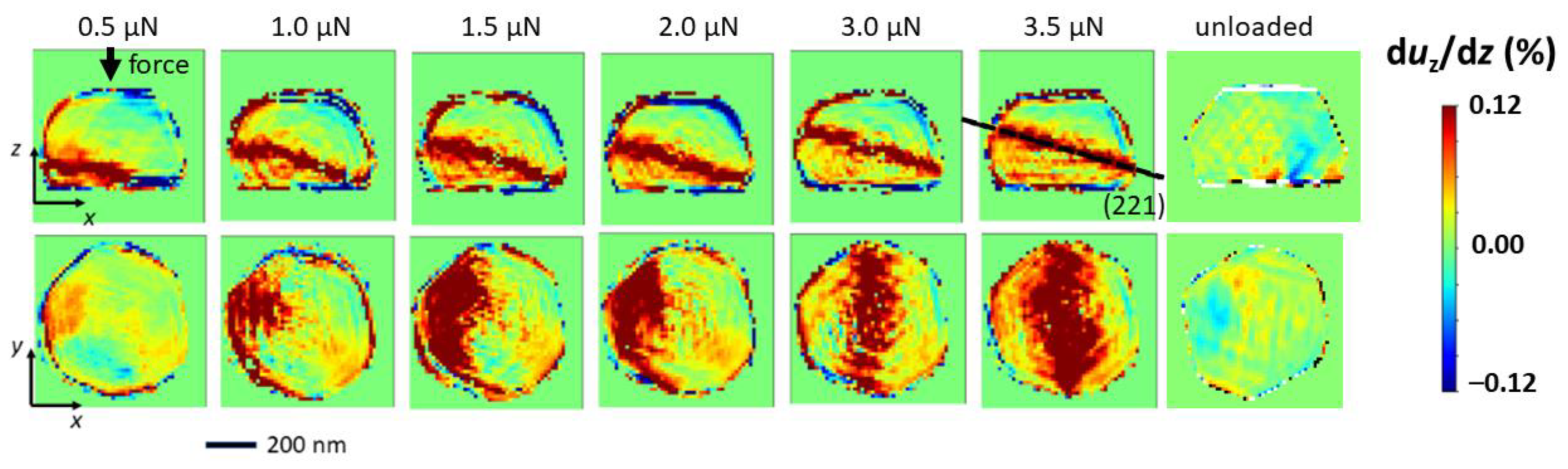
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herring, C.; Galt, J.K. Elastic and plastic properties of very small metal specimens. Phys. Rev. 1952, 85, 1060–1061. [Google Scholar] [CrossRef]
- Brenner, S.S. Tensile strength of whiskers. J. Appl. Phys. 1956, 27, 1484. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample dimensions influence strength and crystal plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Uchic, M.D.; Shade, P.A.; Dimiduk, D.M. Plasticity of micrometer-scale single crystal in compression. Annu. Rev. Mater. Res. 2009, 39, 361–386. [Google Scholar] [CrossRef]
- Kiener, D.; Grosinger, W.; Dehm, G.; Pippan, R. A further step towards an understanding of size-dependent crystal plasticity: In situ tension experiments of miniaturized single-crystal copper samples. Acta Mater. 2008, 56, 580–592. [Google Scholar] [CrossRef]
- Maaß, R.; Van Petegem, S.; Van Swygenhoven, H.; Derlet, P.M.; Volkert, C.A.; Grolimund, D. Time-resolved Laue diffraction of deforming micropillars. Phys. Rev. Lett. 2007, 99, 145505. [Google Scholar] [CrossRef]
- Kirchlechner, C.; Keckes, J.; Micha, J.-S.; Dehm, G. In situ µLaue: Instrumental setup for the deformation of micron sized samples. Adv. Eng. Mat. 2011, 13, 837–844. [Google Scholar] [CrossRef]
- Lee, S.; Im, J.; Yoo, Y.; Bitzek, E.; Kiener, D.; Richter, G.; Kim, B.; Oh, S.H. Reversible cyclic deformation mechanism of gold nanowires by twinning-detwinning transition evidenced from in situ TEM. Nat. Commun. 2014, 5, 3033. [Google Scholar] [CrossRef]
- Sun, J.; He, L.; Lo, Y.-C.; Xu, T.; Bi, H.; Sun, L.; Zhang, Z.; Mao, S.X.; Li, J. Liquid-like pseudoelasticity of sub-10-nm crystalline silver particles. Nat. Mater. 2014, 13, 1007–1012. [Google Scholar] [CrossRef]
- Dehm, G.; Jaya, B.N.; Raghavan, R.; Kirchlechner, C. Overview on micro- and nanomechanical testing: New insights in interface plasticity and fracture at small length scales. Acta Mater. 2018, 142, 248–282. [Google Scholar] [CrossRef]
- Cha, W.; Ulvestad, A.; Allain, M.; Chamard, V.; Harder, R.; Leake, S.J.; Maser, J.; Fuoss, P.H.; Hruszekewycz, S.O. Three-dimensional variable-wavelength X-ray Bragg coherent diffraction imaging. Phys. Rev. Lett. 2016, 117, 225501. [Google Scholar] [CrossRef] [PubMed]
- Lauraux, F.; Cornelius, T.W.; Labat, S.; Richard, M.-I.; Leake, S.; Zhou, T.; Kovalenko, O.; Rabkin, E.; Schülli, T.U.; Thomas, O. Multi-wavelength Bragg coherent X-ray diffraction imaging of Au particles. J. Appl. Crystallogr. 2020, 53, 170–177. [Google Scholar] [CrossRef]
- Ren, Z.; Mastropietro, F.; Langlais, S.; Davydok, A.; Richard, M.-I.; Thomas, O.; Dupraz, M.; Verdier, M.; Beutier, G.; Boesecke, P.; et al. Scanning force microscopy for in situ nanofocused X-ray diffraction studies. J. Synchrotron Radiat. 2014, 21, 1128–1133. [Google Scholar] [CrossRef] [PubMed]
- Dupraz, M.; Beutier, G.; Cornelius, T.W.; Parry, G.; Ren, Z.; Labat, S.; Richard, M.-I.; Chahine, G.A.; Kovalenko, O.; Rabkin, E.; et al. 3D imaging of a dislocation loop at the onset of plasticity in an indented nanocrystal. Nano Lett. 2017, 17, 6696–6701. [Google Scholar] [CrossRef] [PubMed]
- Robinson, I.; Harder, R. Coherent X-Ray Diffraction Imaging of Strain at the Nanoscale. Nat. Mater. 2009, 8, 291. [Google Scholar] [CrossRef]
- Dupraz, M.; Beutier, G.; Rodney, D.; Mordehai, D.; Verdier, M. Signature of dislocations and stacking faults of face-centred cubic nanocrystals in coherent X-ray diffraction patterns: A numerical study. J. Appl. Crystallogr. 2015, 48, 621–644. [Google Scholar] [CrossRef]
- Cornelius, T.W.; Davydok, A.; Jacques, V.L.R.; Grifone, R.; Schülli, T.; Richard, M.-I.; Beutier, G.; Verdier, M.; Metzger, T.H.; Pietsch, U.; et al. In situ 3D reciprocal space mapping during mechanical deformation. J. Synchrotron Radiat. 2012, 19, 688–694. [Google Scholar] [CrossRef]
- Davydok, A.; Cornelius, T.W.; Ren, Z.; Leclere, C.; Chahine, G.; Schülli, T.; Lauraux, F.; Richter, G.; Thomas, O. In Situ Coherent X-ray Diffraction during Three-Point Bending of a Au Nanowire: Visualization and Quantification. Quantum Beam Sci. 2018, 2, 24. [Google Scholar] [CrossRef]
- Kovalenko, O.; Greer, J.R.; Rabkin, E. Solid-state dewetting of thin iron films on sapphire substrates controlled by grain boundary diffusion. Acta Mater. 2013, 61, 3148. [Google Scholar] [CrossRef]
- Leake, S.J.; Chahine, G.A.; Djazouli, H.; Zhou, T.; Richter, C.; Hilhorst, J.; Petit, L.; Richard, M.-I.; Morawe, C.; Barrett, R.; et al. The nanodiffraction beamline ID01/ESRF: A microscope for imaging strain and structure. J. Synchrotron Radiat. 2019, 26, 571–584. [Google Scholar] [CrossRef]
- Chahine, G.A.; Richard, M.-I.; Homs-Regojo, R.A.; Tran-Caliste, T.N.; Carbone, D.; Jacques, V.L.R.; Grifone, R.; Boesecke, P.; Katzer, J.; Costina, I.; et al. Imaging of strain and lattice orientation by quick scanning X-ray microscopy combined with three-dimensional reciprocal space mapping. J. Appl. Crystallogr. 2014, 47, 762. [Google Scholar] [CrossRef]
- Chahine, G.A.; Zoellner, M.H.; Richard, M.-I.; Guha, S.; Reich, C.; Zaumseil, P.; Capellini, G.; Schroeder, T.; Schülli, T.U. Lattice tilt and strain mapped by X-ray scanning nanodiffraction in compositionally graded SiGe/Si microcrystals. Appl. Phys. Lett. 2015, 106, 071902. [Google Scholar] [CrossRef]
- Favre-Nicolin, V.; Girard, G.; Leake, S.; Carnis, J.; Chushkin, Y.; Kieffer, J.; Paleo, P.; Richard, M.-I. PyNX: High-Performance Computing Toolkit for Coherent X-Ray Imaging Based on Operators. J. Appl. Crystallogr. 2020, 53, 5. [Google Scholar] [CrossRef]
- Zimmerman, J.; Bisht, A.; Mishin, Y.; Rabkin, E. Size and shape effect on the strength of platinum nanoparticles. J. Mater. Sci. 2021, 56, 18300–18312. [Google Scholar] [CrossRef]
- Herre, P.; Will, J.; Dierner, M.; Wang, D.; Yokosawa, T.; Zech, T.; Wu, M.; Przybilla, T.; Romeis, S.; Unruh, T.; et al. Rapid fabrication and interface structure of highly faceted epitaxial Ni-Au solid solution nanoparticles on sapphire. Acta Mater. 2021, 220, 117318. [Google Scholar] [CrossRef]
- Jia, N.; Eisenlohr, P.; Roters, F.; Raabe, D.; Zhao, X. Orientation dependence of shear banding in face-centered-cubic single crystals. Acta Mater. 2012, 60, 3415–3434. [Google Scholar] [CrossRef]
- Mordehai, D.; Rabkin, E.; Srolovitz, D.J. Pseudoelastic deformation during nanoscale adhesive contact formation. Phys. Rev. Lett. 2011, 107, 096101. [Google Scholar] [CrossRef]
- Mordehai, D.; Lee, S.-W.; Backes, B.; Srolovitz, D.J.; Nix, W.D.; Rabkin, E. Size effect in compression of single-crystal gold microparticles. Acta Mater. 2011, 59, 5202–5215. [Google Scholar] [CrossRef]
- Sharma, A.; Hickman, J.; Gazit, N.; Rabkin, E.; Mishin, Y. Nickel nanoparticles set a new record of strength. Nat. Commun. 2018, 9, 4102. [Google Scholar] [CrossRef]
- Choi, S.; Chung, M.; Kim, D.; Kim, S.; Yun, K.; Cha, W.; Harder, R.; Kawaguchi, T.; Liu, Y.; Ulvestad, A.; et al. In situ strain evolution on Pt nanoparticles during hydrogen peroxide decomposition. Nano Lett. 2020, 20, 8541–8548. [Google Scholar] [CrossRef]
- Lauraux, F.; Labat, S.; Yehya, S.; Richard, M.-I.; Leake, S.; Zhou, T.; Micha, J.-S.; Robach, O.; Kovalenko, O.; Rabkin, E.; et al. Simultaneous multi-Bragg peak coherent X-ray diffraction imaging. Crystals 2021, 11, 312. [Google Scholar] [CrossRef]
- Leake, S.J.; Favre-Nicolin, V.; Zatterin, E.; Richard, M.-I.; Fernandez, S.; Chahine, G.; Zhou, T.; Boesecke, P.; Djazouli, H.; Schülli, T.U. Coherent nanoscale X-ray probe for crystal interrogation at ID01, ESRF–The European Synchrotron. Mater. Des. 2017, 119, 470–471. [Google Scholar] [CrossRef]
- Mandula, O.; Elzo Aizarna, M.; Eymery, J.; Burghammer, M.; Favre-Nicolin, V. PyNX.Ptycho: A computing library for X-ray coherent diffraction imaging of nanostructures. J. Appl. Cryst. 2016, 49, 1842. [Google Scholar] [CrossRef]
- Ponchut, C.; Rigal, J.M.; Clément, J.; Papillon, E.; Homs, A.; Petitdemange, S. MAXIPIX, a fast readout photon-counting X-ray area detector for synchrotron applications. J. Instr. 2011, 6, C01069. [Google Scholar] [CrossRef]
- Luke, D.R. Relaxed averaged alternating reflections for diffraction imaging. Inverse Probl. 2004, 21, 37–50. [Google Scholar] [CrossRef]
- Fienup, J.R. Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef] [Green Version]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik 1972, 35, 237. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lauraux, F.; Labat, S.; Richard, M.-I.; Leake, S.J.; Zhou, T.; Kovalenko, O.; Rabkin, E.; Schülli, T.U.; Thomas, O.; Cornelius, T.W. In Situ Nano-Indentation of a Gold Sub-Micrometric Particle Imaged by Multi-Wavelength Bragg Coherent X-ray Diffraction. Materials 2022, 15, 6195. https://doi.org/10.3390/ma15186195
Lauraux F, Labat S, Richard M-I, Leake SJ, Zhou T, Kovalenko O, Rabkin E, Schülli TU, Thomas O, Cornelius TW. In Situ Nano-Indentation of a Gold Sub-Micrometric Particle Imaged by Multi-Wavelength Bragg Coherent X-ray Diffraction. Materials. 2022; 15(18):6195. https://doi.org/10.3390/ma15186195
Chicago/Turabian StyleLauraux, Florian, Stéphane Labat, Marie-Ingrid Richard, Steven J. Leake, Tao Zhou, Oleg Kovalenko, Eugen Rabkin, Tobias U. Schülli, Olivier Thomas, and Thomas W. Cornelius. 2022. "In Situ Nano-Indentation of a Gold Sub-Micrometric Particle Imaged by Multi-Wavelength Bragg Coherent X-ray Diffraction" Materials 15, no. 18: 6195. https://doi.org/10.3390/ma15186195
APA StyleLauraux, F., Labat, S., Richard, M.-I., Leake, S. J., Zhou, T., Kovalenko, O., Rabkin, E., Schülli, T. U., Thomas, O., & Cornelius, T. W. (2022). In Situ Nano-Indentation of a Gold Sub-Micrometric Particle Imaged by Multi-Wavelength Bragg Coherent X-ray Diffraction. Materials, 15(18), 6195. https://doi.org/10.3390/ma15186195







