Stress Field Evaluation in Orthotropic Microstructured Composites with Holes as Cosserat Continuum
Abstract
:1. Introduction
2. Cosserat Continuum and Its FEM Implementation
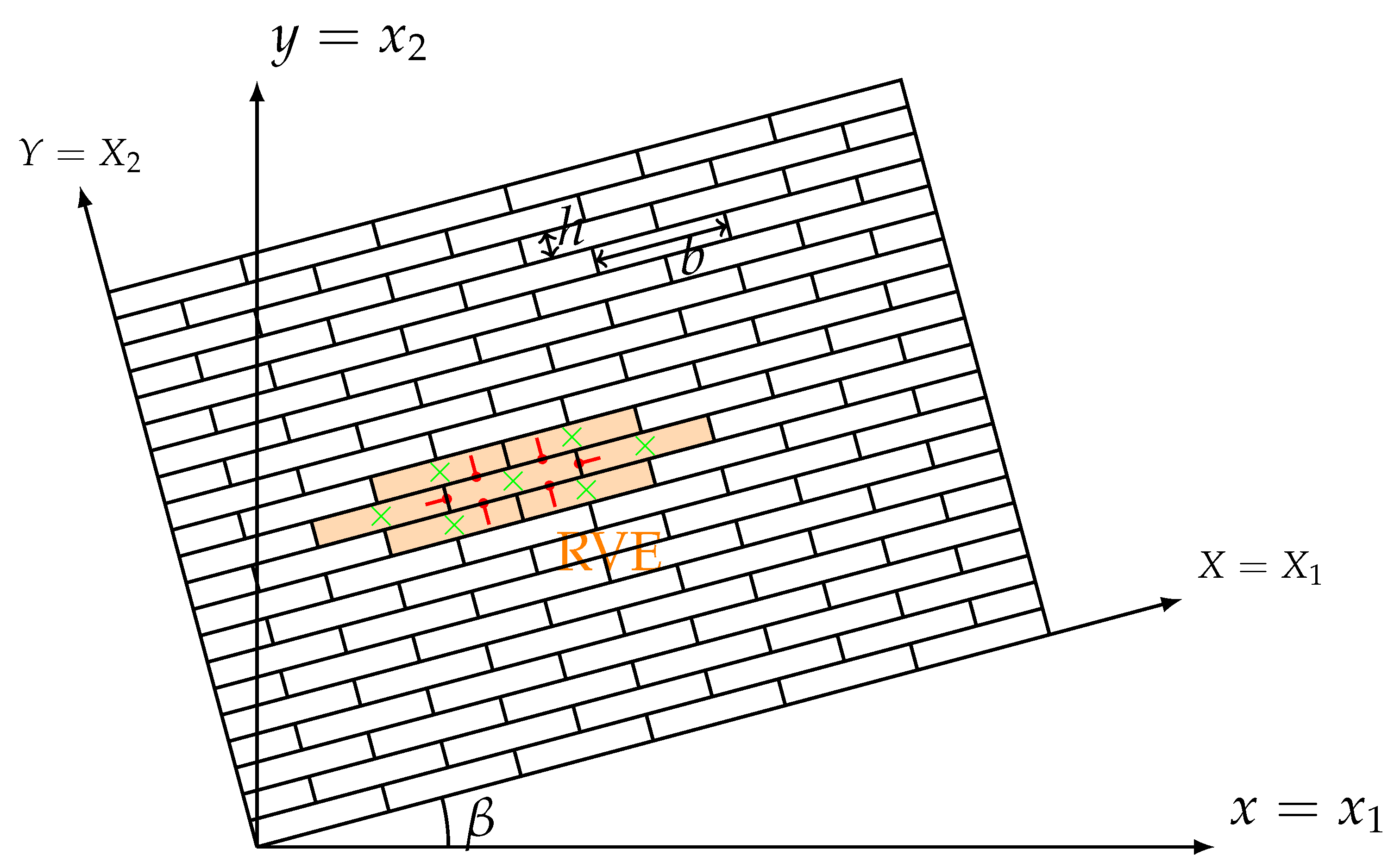
3. Numerical Simulation
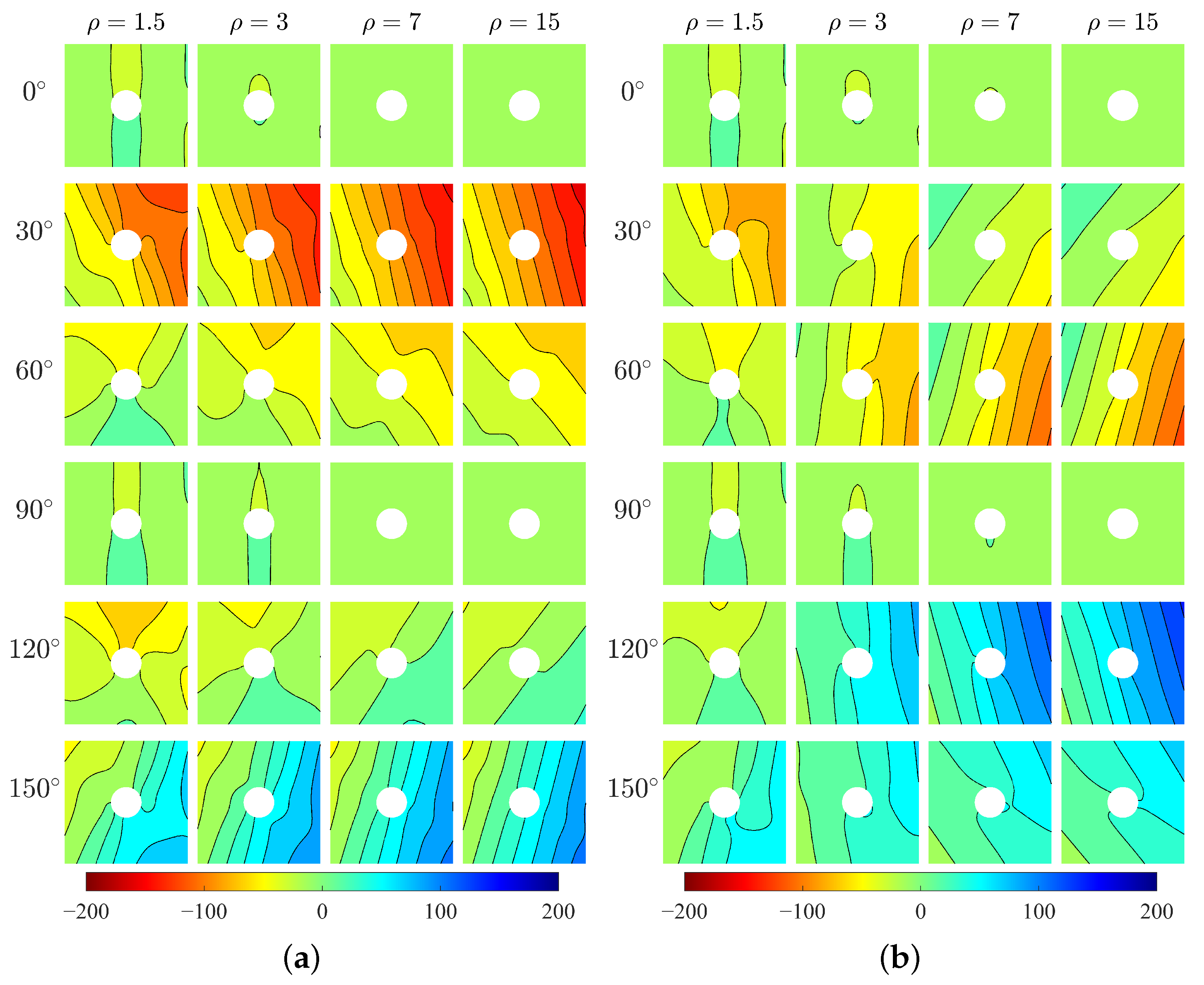
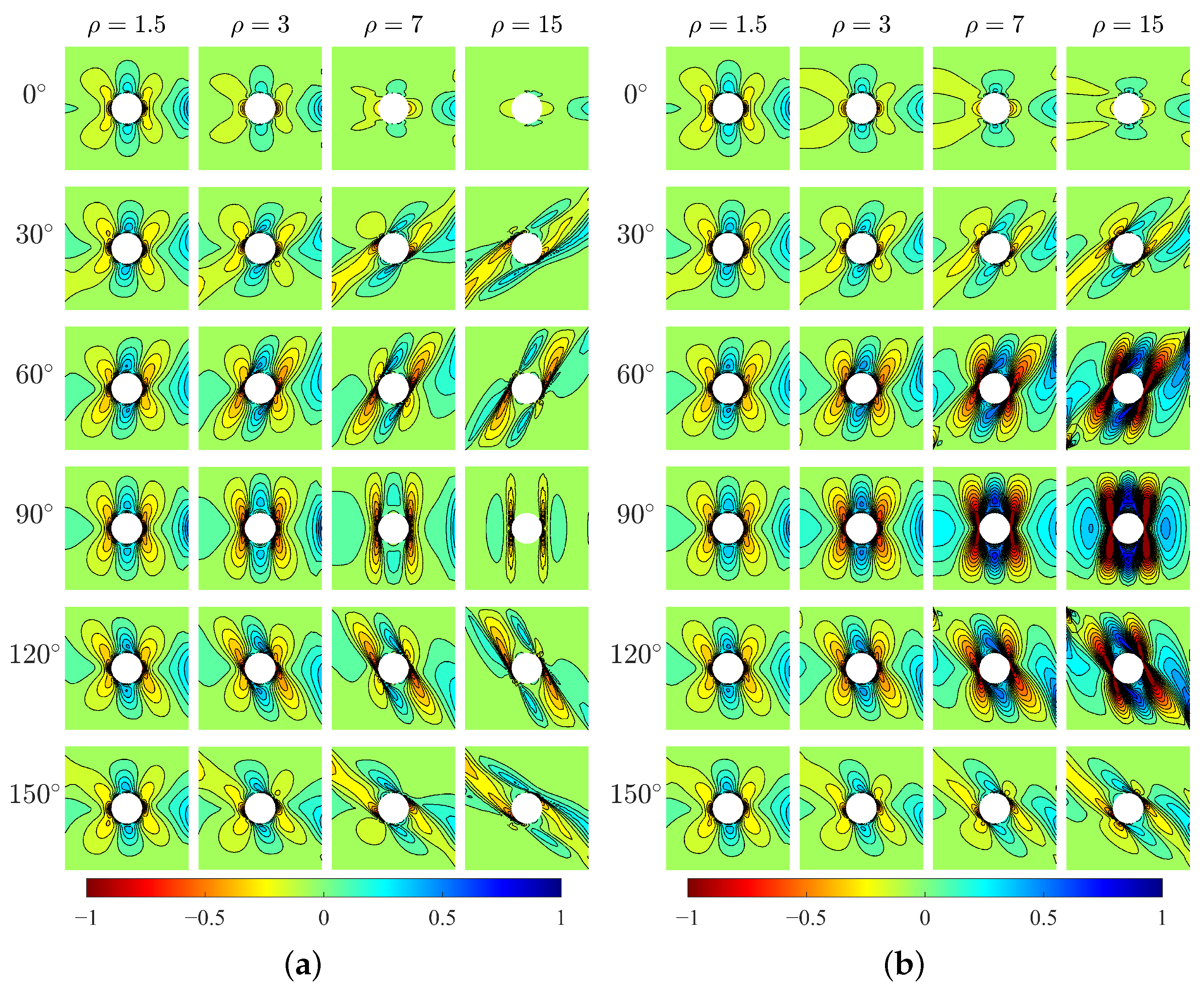
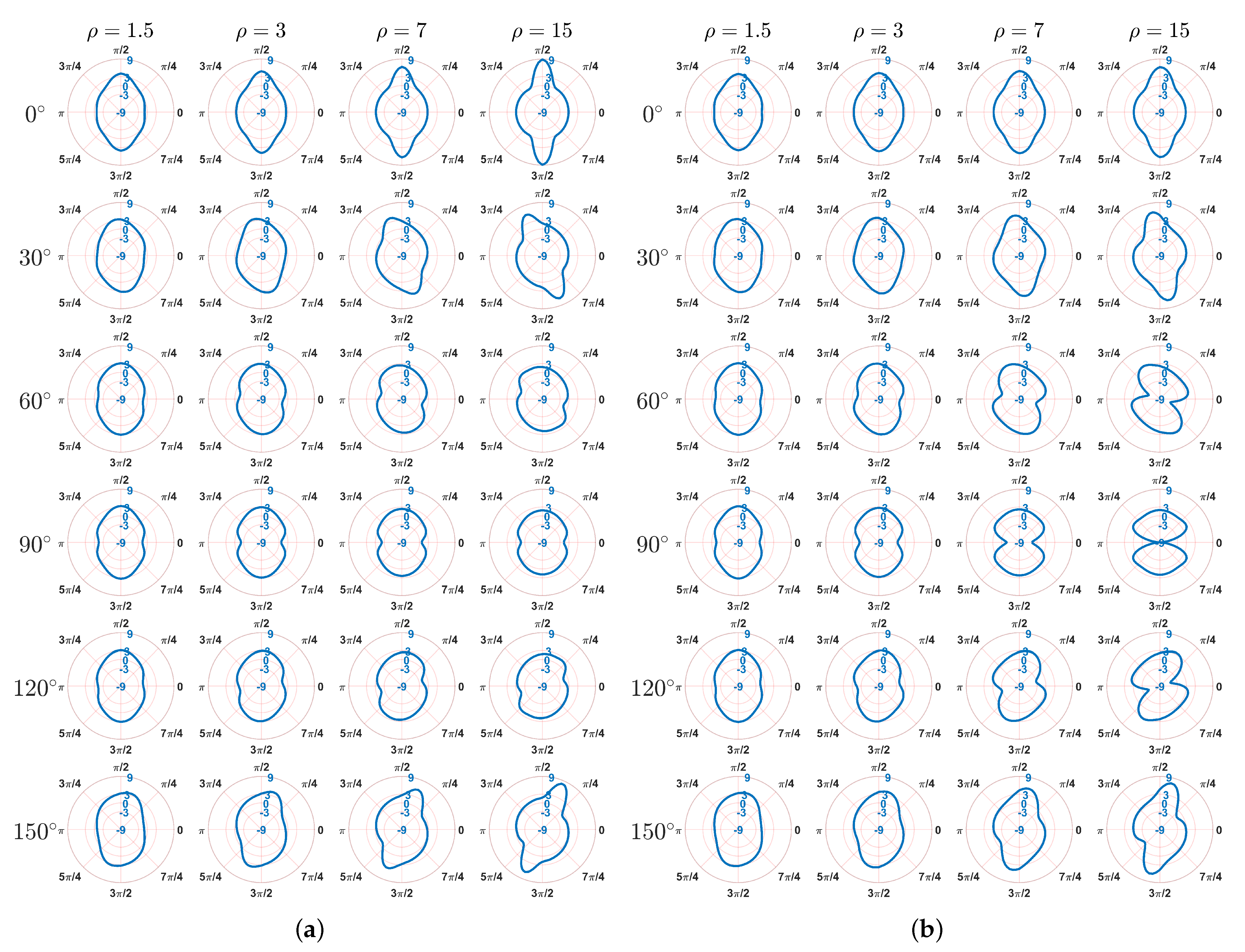
4. Results
5. Discussions
6. Conclusions
- (1)
- The mechanical behavior of microstructured composite changes as the microstructure’s directions , thereby showing a directionality of measurement distribution such as stresses. In general, orthotropic materials show similar behaviors but with different intensities, and the behavior of centrosymmetric is related to various .
- (2)
- The increasing microstructure’s scale can results in more evident effect of and difference between the Cosserat and Cauchy models. Such an effect of is clearer for the centrosymmetric materials than orthotropic materials.
- (3)
- The Cosserat continuum is able to better describe the direction effect of microstructures due to the relative rotation that not only shows the directionality of distribution but also varies with the microstructure direction. The Cauchy continuum does not have such advantages because there is no relative rotation and tangential strains are symmetric.
- (4)
- The extreme value and its location of the hoop stress around the hole depend on . For smaller , the highest and smallest are close to 3 and −1, which is similar with the classical result of the isotropic material. As increases, a highest up to 9 can be observed.
- (5)
- Difference in the hoop stress between the Cosserat and Cauchy model is mainly in the smallest , especially for greater when , and . All the smallest of the Cosserat model are greater than -3, whereas the Cauchy model can have a as low as −9.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moraes, A.; de Figueiredo, R.P.; Vargas, E.d.A., Jr. Mechanics of Cosserat Generalized Continuum and Modelling in Structural Geology. Anuário Instituto Geociências 2020, 43, 366–375. [Google Scholar] [CrossRef]
- Cook, R.F.; Lawn, B.R.; Fairbanks, C.J. Microstructure-strength properties in ceramics: I, effect of crack size on toughness. J. Am. Ceram. Soc. 1985, 68, 604–615. [Google Scholar] [CrossRef]
- Filip, R.; Kubiak, K.; Ziaja, W.; Sieniawski, J. The effect of microstructure on the mechanical properties of two-phase titanium alloys. J. Mater. Process. Technol. 2003, 133, 84–89. [Google Scholar] [CrossRef]
- Hoc, T.; Henry, L.; Verdier, M.; Aubry, D.; Sedel, L.; Meunier, A. Effect of microstructure on the mechanical properties of Haversian cortical bone. Bone 2006, 38, 466–474. [Google Scholar] [CrossRef]
- Liao, Z.; la Monaca, A.; Murray, J.; Speidel, A.; Ushmaev, D.; Clare, A.; Axinte, D.; M’Saoubi, R. Surface integrity in metal machining—Part I: Fundamentals of surface characteristics and formation mechanisms. Int. J. Mach. Tools Manuf. 2021, 162, 103687. [Google Scholar] [CrossRef]
- Nassir, M.; Settari, A.; Wan, R. Joint stiffness and deformation behaviour of discontinuous rock. J. Can. Pet. Technol. 2010, 49, 78–86. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Ding, X.; Xie, S. Scale effect of shear mechanical properties of non-penetrating horizontal rock-like joints. Environ. Earth Sci. 2021, 80, 192. [Google Scholar] [CrossRef]
- Guo, X.; Tan, Z.; Wang, X.; Li, A.; Ma, Z.; Wu, Y. Effect of Bedding Angle and Mineral Composition on Mechanical Properties and Fracture Behavior of Phyllite Under Unloading Confining Pressures. Geotech. Geol. Eng. 2020, 38, 3611–3621. [Google Scholar] [CrossRef]
- Wang, J.; Deng, X.; Cao, W. Numerical Analysis on the Stability of Layered Surrounding Rock Tunnel Under the Conditions of Different Inclination Angle and Thickness. Am. J. Traffic Transp. Eng. 2019, 4, 67–74. [Google Scholar]
- Bauer, S.; Schäfer, M.; Grammenoudis, P.; Tsakmakis, C. Three-dimensional finite elements for large deformation micropolar elasticity. Comput. Methods Appl. Mech. Eng. 2010, 199, 2643–2654. [Google Scholar] [CrossRef]
- Baraldi, D.; Reccia, E.; Cecchi, A. In plane loaded masonry walls: DEM and FEM/DEM models. A critical review. Meccanica 2018, 53, 1613–1628. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Sheng, Y.; Ye, J.; Tan, Y. Discrete element modeling of the microbond test of fiber reinforced composite. Comput. Mater. Sci. 2010, 49, 253–259. [Google Scholar] [CrossRef]
- Reccia, E.; Leonetti, L.; Trovalusci, P.; Cecchi, A. A multiscale/multidomain model for the failure analysis of masonry walls: A validation with a combined FEM/DEM approach. Int. J. Multiscale Comput. Eng. 2018, 16, 325–343. [Google Scholar] [CrossRef]
- Tuna, M.; Kirca, M.; Trovalusci, P. Deformation of atomic models and their equivalent continuum counterparts using Eringen’s two-phase local/nonlocal model. Mech. Res. Commun. 2019, 97, 26–32. [Google Scholar] [CrossRef]
- Trovalusci, P. Molecular Approaches for Multifield Continua: Origins and current developments. In Multiscale Modeling of Complex Materials: Phenomenological, Theoretical and Computational Aspects; Sadowski, T., Trovalusci, P., Eds.; Springer: Vienna, Austria, 2014; pp. 211–278. [Google Scholar]
- Altenbach, H.; Eremeyev, V.A. Generalized Continua—From the Theory to Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2012; Volume 541. [Google Scholar]
- Kunin, I.A. Elastic Media with Microstructure I. One-Dimensional Models; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Tuna, M.; Trovalusci, P. Scale dependent continuum approaches for discontinuous assemblies: ‘Explicit’ and ‘implicit’ non-local models. Mech. Res. Commun. 2020, 103, 103461. [Google Scholar] [CrossRef]
- Eringen, C. Microcontinuum Field Theories; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Pau, A.; Trovalusci, P. Block masonry as equivalent micropolar continua: The role of relative rotations. Acta Mech. 2012, 223, 1455–1471. [Google Scholar] [CrossRef]
- Bigoni, D.; Gourgiotis, P.A. Folding and faulting of an elastic continuum. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160018. [Google Scholar] [CrossRef] [PubMed]
- Adhikary, D.; Dyskin, A. A Cosserat continuum model for layered materials. Comput. Geotech. 1997, 20, 15–45. [Google Scholar] [CrossRef]
- Shirani, M.; Steigmann, D.J. A Cosserat Model of Elastic Solids Reinforced by a Family of Curved and Twisted Fibers. Symmetry 2020, 12, 1133. [Google Scholar] [CrossRef]
- Krishnan, J. A Cosserat Theory for Solid Crystals—With Application to Fiber-Reinforced Plates. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2016. [Google Scholar]
- Chu, X.; Yu, C.; Xu, Y. The dilatancy and numerical simulation of failure behavior of granular materials based on Cosserat model. Interact. Multiscale Mech. 2012, 5, 157–168. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Trovalusci, P.; Luciano, R. Material Symmetries in Homogenized Hexagonal-Shaped Composites as Cosserat Continua. Symmetry 2020, 12, 441. [Google Scholar] [CrossRef] [Green Version]
- Colatosti, M.; Fantuzzi, N.; Trovalusci, P. Time-history analysis of composite materials with rectangular microstructure under shear actions. Materials 2021, 14, 6439. [Google Scholar] [CrossRef]
- Colatosti, M.; Shi, F.; Fantuzzi, N.; Trovalusci, P. Mechanical characterization of composite materials with rectangular microstructure and voids. Arch. Appl. Mech. 2022, 1–16. [Google Scholar] [CrossRef]
- Trovalusci, P.; Masiani, R. Non-linear micropolar and classical continua for anisotropic discontinuous materials. Int. J. Solids Struct. 2003, 40, 1281–1297. [Google Scholar] [CrossRef]
- Trovalusci, P.; Masiani, R. Material symmetries of micropolar continua equivalent to lattices. Int. J. Solids Struct. 1999, 36, 2091–2108. [Google Scholar] [CrossRef]
- Rezaeepazhand, J.; Jafari, M. Stress analysis of perforated composite plates. Compos. Struct. 2005, 71, 463–468, Fifth International Conference on Composite Science and Technology. [Google Scholar] [CrossRef]
- Toubal, L.; Karama, M.; Lorrain, B. Stress concentration in a circular hole in composite plate. Compos. Struct. 2005, 68, 31–36. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative numerical methods based on SFEM and IGA for computing stress concentrations in isotropic plates with discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Leonetti, L.; Trovalusci, P.; Tornabene, F. Some novel numerical applications of Cosserat continua. Int. J. Comput. Methods 2018, 15, 1850054. [Google Scholar] [CrossRef]
- Pandita, S.D.; Nishiyabu, K.; Verpoest, I. Strain concentrations in woven fabric composites with holes. Compos. Struct. 2003, 59, 361–368. [Google Scholar] [CrossRef]
- Savin; Nikolaevich, G. Stress Concentration around Holes. Aeronaut. J. 1961, 65, 772. [Google Scholar] [CrossRef]
- Ramézani, H.; El-Hraiech, A.; Jeong, J.; Benhamou, C.L. Size effect method application for modeling of human cancellous bone using geometrically exact Cosserat elasticity. Comput. Methods Appl. Mech. Eng. 2012, 237, 227–243. [Google Scholar] [CrossRef]
- Eremeyev, V.; Skrzat, A.; Stachowicz, F. On FEM evaluation of stress concentration in micropolar elastic materials. Nanosci. Technol. Int. J. 2016, 7, 297–304. [Google Scholar] [CrossRef]
- Ferreira, A.J.; Fantuzzi, N. MATLAB Codes for Finite Element Analysis: Solids and Structures, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Mühlhaus, H.B. 8-Continuum Models for Layered and Blocky Rock. In Analysis and Design Methods; Fairhurst, C., Ed.; Pergamon: Oxford, UK, 1993; pp. 209–230. [Google Scholar]
- Fantuzzi, N.; Shi, F.; Colatosti, M.; Luciano, R. Multiscale homogenization and analysis of anisotropic assemblies as Cosserat continua. Int. J. Multiscale Comput. Eng. 2022, 20, 87–103. [Google Scholar] [CrossRef]
- Dal Corso, F.; Shahzad, S.; Bigoni, D. Isotoxal star-shaped polygonal voids and rigid inclusions in nonuniform antiplane shear fields. Part II: Singularities, annihilation and invisibility. Int. J. Solids Struct. 2016, 85, 76–88. [Google Scholar] [CrossRef]
- Jafari, M.; Ardalani, E. Stress concentration in finite metallic plates with regular holes. Int. J. Mech. Sci. 2016, 106, 220–230. [Google Scholar] [CrossRef]
- Sharma, D.S. Stress concentration around circular/elliptical/triangular cutouts in infinite composite plate. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011; Volume 3, p. 6. [Google Scholar]
- Xu, Z. Study on the influence of angle of bedding plane on stability of roadway surrounding rock in layered mass. IOP Conf. Ser. Earth Environ. Sci. 2021, 781, 022014. [Google Scholar] [CrossRef]
- Shi, F.; Fantuzzi, N.; Trovalusci, P.; Li, Y.; Wei, Z. The effects of dilatancy in composite assemblies as micropolar continua. Compos. Struct. 2021, 276, 114500. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Trovalusci, P.; Luciano, R. Multiscale analysis of anisotropic materials with hexagonal microstructure as micropolar continua. Int. J. Multiscale Comput. Eng. 2020, 18, 265–284. [Google Scholar] [CrossRef]




| 102.70 | 80.97 | 58.45 | 57.66 | 58.45 | 80.97 | |
| 0 | 10.47 | 10.47 | 0 | 10.47 | 10.47 | |
| 0 | 25.94 | 13.85 | 0 | −13.85 | −25.94 | |
| 0 | 5.66 | −6.44 | 0 | 6.44 | −5.66 | |
| 57.66 | 58.45 | 80.97 | 102.70 | 80.97 | 58.45 | |
| 0 | −6.44 | 5.66 | 0 | −5.66 | 6.44 | |
| 0 | 13.85 | 25.94 | 0 | −25.94 | −13.85 | |
| 28.83 | 51.01 | 74.44 | 75.68 | 74.44 | 51.01 | |
| 0 | 10.47 | 10.47 | 0 | 10.47 | 10.47 | |
| 75.68 | 74.44 | 51.01 | 28.83 | 51.01 | 74.44 | |
| 0.57 | 0.47 | 0.29 | 0.19 | 0.29 | 0.47 | |
| 0 | 0.16 | 0.16 | 0 | −0.16 | −0.16 | |
| 0.19 | 0.29 | 0.47 | 0.57 | 0.47 | 0.29 | |
| 102.70 | 80.97 | 58.45 | 57.66 | 58.45 | 80.97 | |
| 0 | 10.47 | 10.47 | 0 | 10.47 | 10.47 | |
| 0 | 15.80 | 3.71 | 0 | −3.71 | −15.80 | |
| 57.66 | 58.45 | 80.97 | 102.70 | 80.97 | 58.45 | |
| 0 | 3.71 | 15.80 | 0 | −15.80 | −3.71 | |
| 26.13 | 36.60 | 36.60 | 26.13 | 36.60 | 36.60 |
| 237.84 | 183.34 | 93.24 | 57.66 | 93.24 | 183.34 | |
| 0 | 9.46 | 9.46 | 0 | 9.46 | 9.46 | |
| 0 | 85.04 | 74.12 | 0 | −74.12 | −85.04 | |
| 0 | 3.90 | −7.02 | 0 | 7.02 | −3.90 | |
| 57.66 | 93.24 | 183.34 | 237.84 | 183.34 | 93.24 | |
| 0 | −7.02 | 3.90 | 0 | −3.90 | 7.02 | |
| 0 | 74.12 | 85.04 | 0 | −85.04 | −74.12 | |
| 28.83 | 85.14 | 178.83 | 216.22 | 178.83 | 85.14 | |
| 0 | 9.46 | 9.46 | 0 | 9.46 | 9.46 | |
| 216.22 | 178.83 | 85.14 | 28.83 | 85.14 | 178.83 | |
| 3.64 | 2.87 | 1.33 | 0.56 | 1.33 | 2.87 | |
| 0 | 1.33 | 1.33 | 0 | −1.33 | −1.33 | |
| 0.56 | 1.33 | 2.87 | 3.64 | 2.87 | 1.33 | |
| 237.84 | 183.34 | 93.24 | 57.66 | 93.24 | 183.34 | |
| 0 | 9.46 | 9.46 | 0 | 9.46 | 9.46 | |
| 0 | 44.47 | 33.55 | 0 | −33.55 | −44.47 | |
| 57.66 | 93.24 | 183.34 | 237.84 | 183.34 | 93.24 | |
| 0 | 33.55 | 44.47 | 0 | −44.47 | −33.55 | |
| 61.26 | 70.72 | 70.72 | 61.26 | 70.72 | 70.72 |
| 756.76 | 604.96 | 255.41 | 57.66 | 255.41 | 604.96 | |
| 0 | −22.97 | −22.97 | 0 | −22.97 | −22.97 | |
| 0 | 328.47 | 354.99 | 0 | −354.99 | −328.47 | |
| 0 | −52.27 | −25.75 | 0 | 25.75 | 52.27 | |
| 57.66 | 255.41 | 604.96 | 756.76 | 604.96 | 255.41 | |
| 0 | −25.75 | −52.27 | 0 | 52.27 | 25.75 | |
| 0 | 354.99 | 328.47 | 0 | −328.47 | −354.99 | |
| 28.83 | 225.68 | 665.32 | 908.11 | 665.32 | 225.68 | |
| 0 | −22.97 | −22.97 | 0 | −22.97 | −22.97 | |
| 908.11 | 665.32 | 225.68 | 28.83 | 225.68 | 665.32 | |
| 59.06 | 44.97 | 16.81 | 2.72 | 16.81 | 44.97 | |
| 0 | 24.40 | 24.40 | 0 | −24.40 | −24.40 | |
| 2.72 | 16.81 | 44.97 | 59.06 | 44.97 | 16.81 | |
| 756.76 | 604.96 | 255.41 | 57.66 | 255.41 | 604.96 | |
| 0 | −22.97 | −22.97 | 0 | −22.97 | −22.97 | |
| 0 | 138.10 | 164.62 | 0 | −164.62 | −138.10 | |
| 57.66 | 255.41 | 604.96 | 756.76 | 604.96 | 255.41 | |
| 0 | 164.62 | 138.10 | 0 | −138.10 | −164.62 | |
| 234.23 | 211.26 | 211.26 | 234.23 | 211.26 | 211.26 |
| 2486.50 | 2096.86 | 882.44 | 57.66 | 882.44 | 2096.86 | |
| 0 | −217.57 | −217.57 | 0 | −217.57 | −217.57 | |
| 0 | 1189.82 | 1441.04 | 0 | −1441.04 | −1189.82 | |
| 0 | −389.32 | −138.10 | 0 | 138.10 | 389.32 | |
| 57.66 | 882.44 | 2096.86 | 2486.50 | 2096.86 | 882.44 | |
| 0 | −138.10 | −389.32 | 0 | 389.32 | 138.10 | |
| 0 | 1441.04 | 1189.82 | 0 | −1189.82 | −1441.04 | |
| 28.83 | 722.98 | 2546.41 | 3675.70 | 2546.41 | 722.98 | |
| 0 | −217.57 | −217.57 | 0 | −217.57 | −217.57 | |
| 3675.70 | 2546.41 | 722.98 | 28.83 | 722.98 | 2546.41 | |
| 933.59 | 703.25 | 242.57 | 12.23 | 242.57 | 703.25 | |
| 0 | 398.96 | 398.96 | 0 | −398.96 | −398.96 | |
| 12.23 | 242.57 | 703.25 | 933.59 | 703.25 | 242.57 | |
| 2486.50 | 2096.86 | 882.44 | 57.66 | 882.44 | 2096.86 | |
| 0 | −217.57 | −217.57 | 0 | −217.57 | −217.57 | |
| 0 | 400.25 | 651.47 | 0 | −651.47 | −400.25 | |
| 57.66 | 882.44 | 2096.86 | 2486.50 | 2096.86 | 882.44 | |
| 0 | 651.47 | 400.25 | 0 | −400.25 | −651.47 | |
| 926.13 | 708.56 | 708.56 | 926.13 | 708.56 | 708.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, F.; Fantuzzi, N.; Trovalusci, P.; Li, Y.; Wei, Z. Stress Field Evaluation in Orthotropic Microstructured Composites with Holes as Cosserat Continuum. Materials 2022, 15, 6196. https://doi.org/10.3390/ma15186196
Shi F, Fantuzzi N, Trovalusci P, Li Y, Wei Z. Stress Field Evaluation in Orthotropic Microstructured Composites with Holes as Cosserat Continuum. Materials. 2022; 15(18):6196. https://doi.org/10.3390/ma15186196
Chicago/Turabian StyleShi, Farui, Nicholas Fantuzzi, Patrizia Trovalusci, Yong Li, and Zuoan Wei. 2022. "Stress Field Evaluation in Orthotropic Microstructured Composites with Holes as Cosserat Continuum" Materials 15, no. 18: 6196. https://doi.org/10.3390/ma15186196
APA StyleShi, F., Fantuzzi, N., Trovalusci, P., Li, Y., & Wei, Z. (2022). Stress Field Evaluation in Orthotropic Microstructured Composites with Holes as Cosserat Continuum. Materials, 15(18), 6196. https://doi.org/10.3390/ma15186196








