Investigating Morphology and Breakage Evolution Characteristics of Railroad Ballasts over Distinct Supports Subjected to Impact Loading
Abstract
:1. Introduction
2. Materials, Testing Program, and Methods
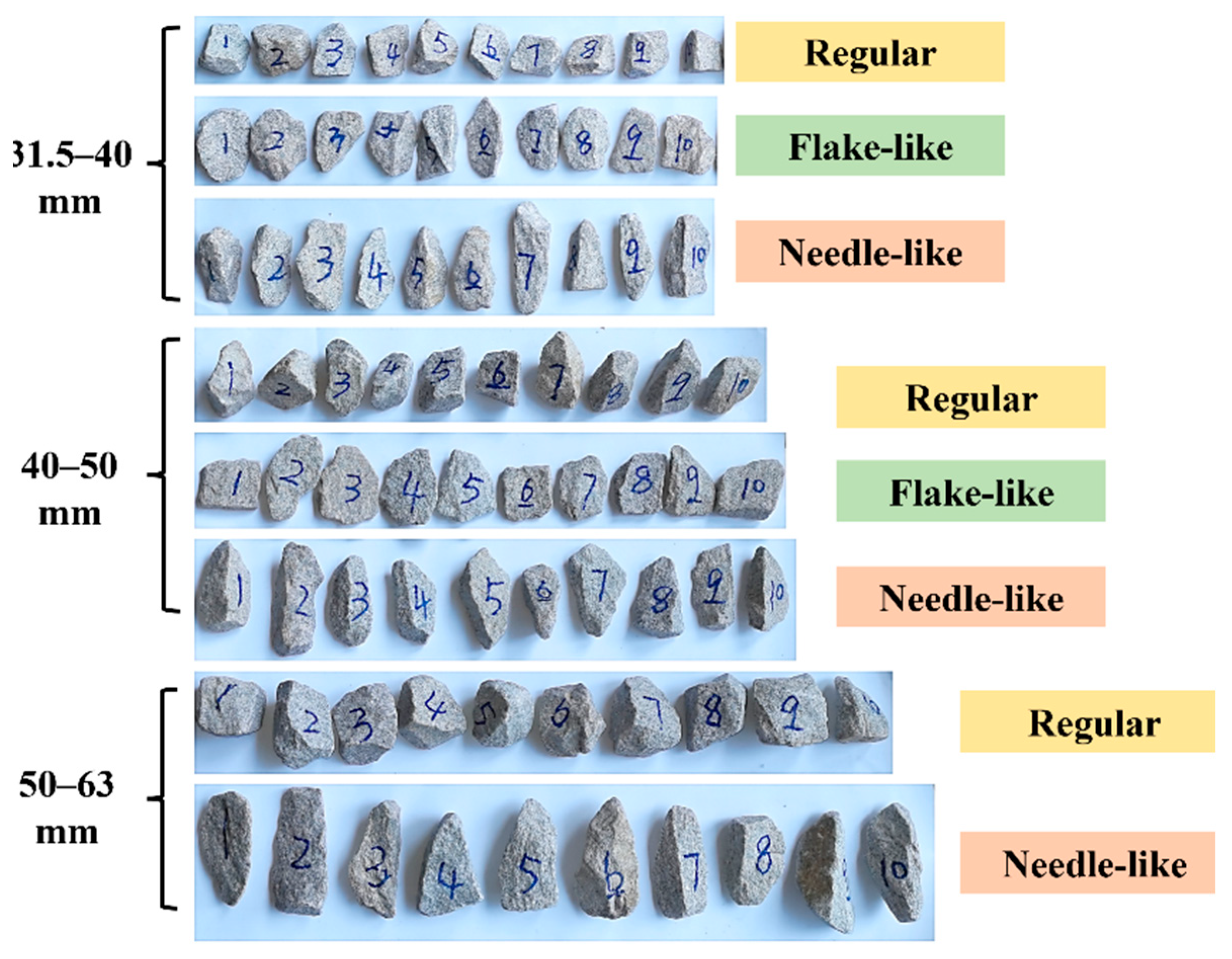
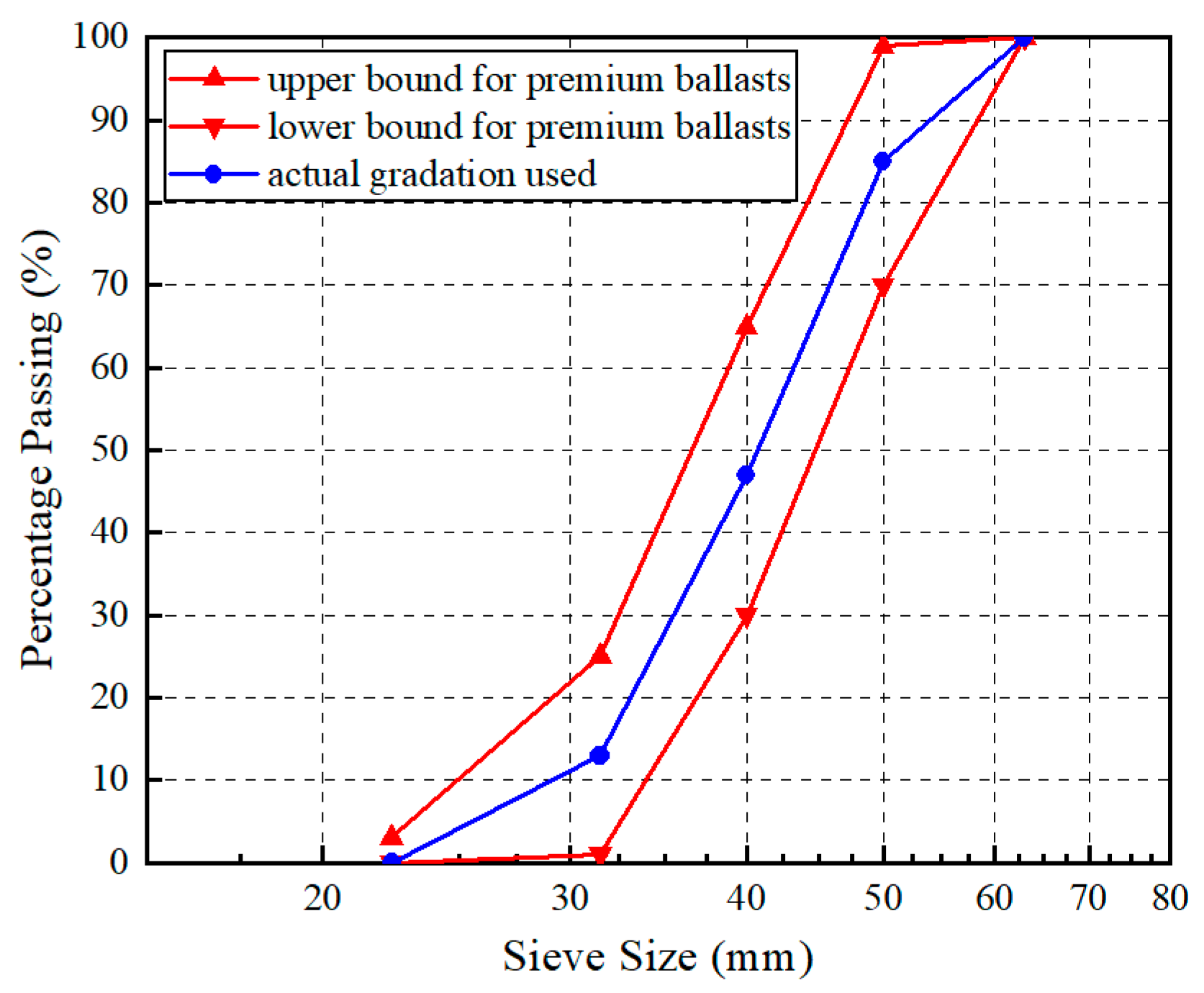
2.1. Materials Tested
2.2. Description of Laboratory Testing Program
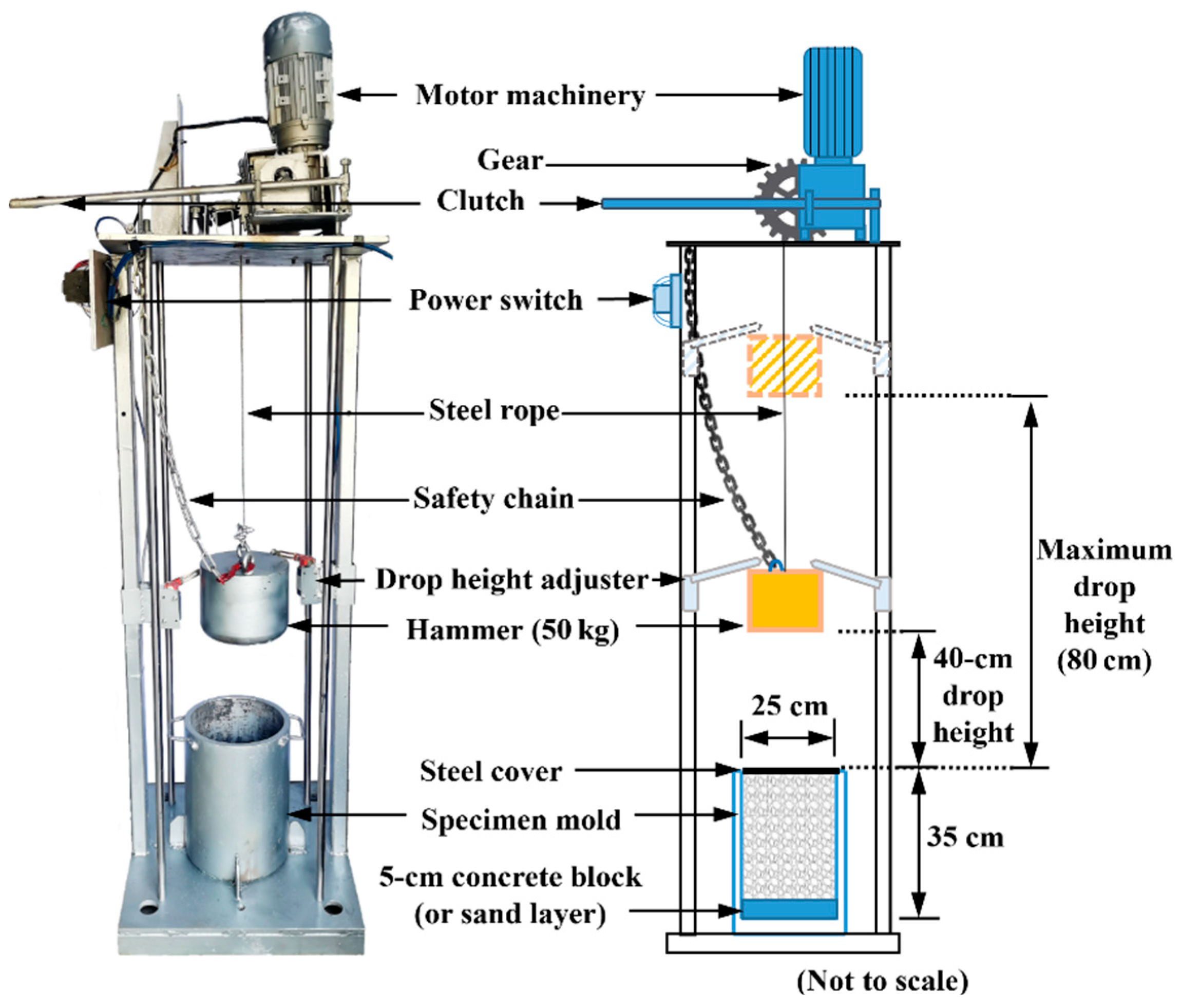
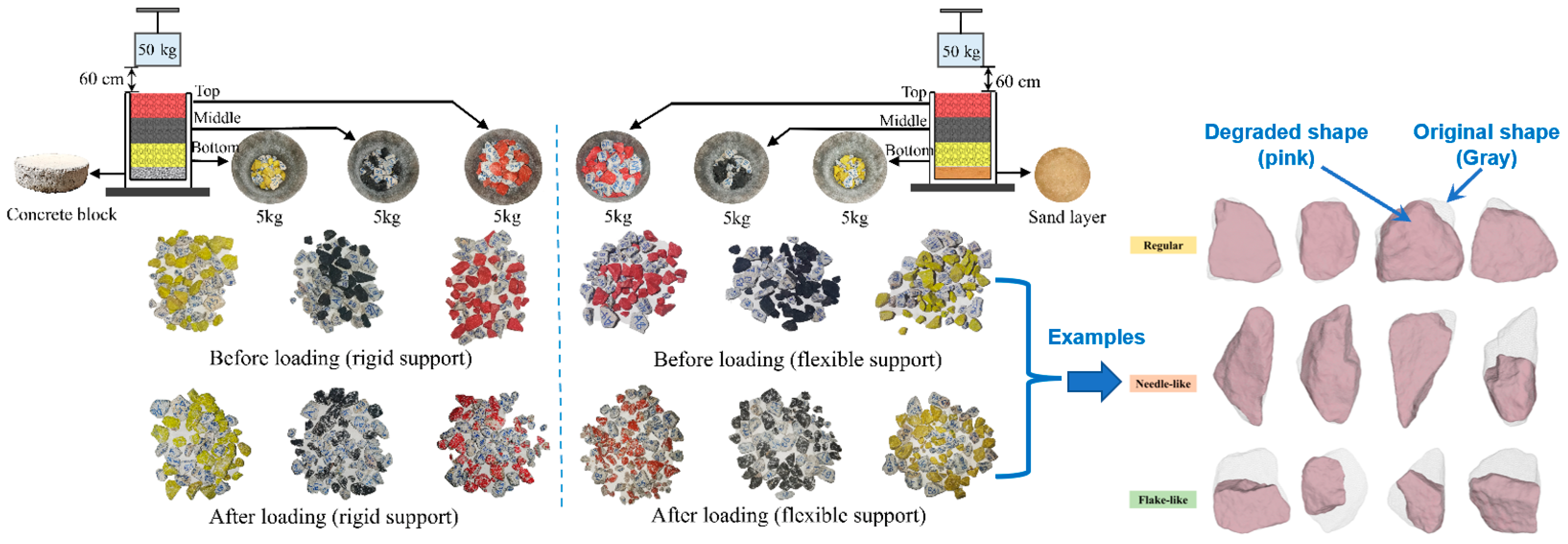
2.2.1. Impact-Loading Apparatus
2.2.2. Impact-Load Tests for Single-Size Ballasts
2.2.3. Impact-Load Tests for Multiple-Size Ballasts
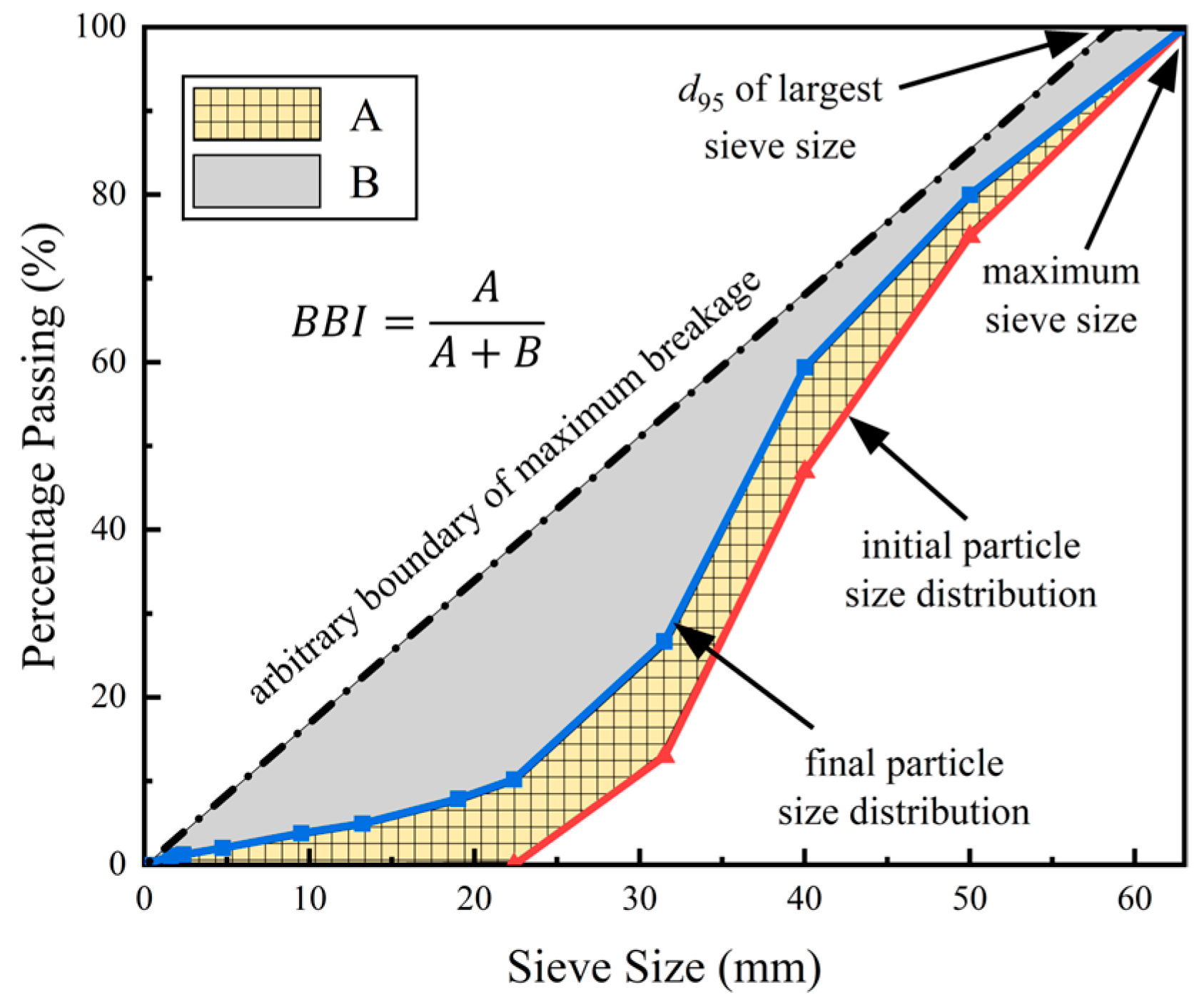
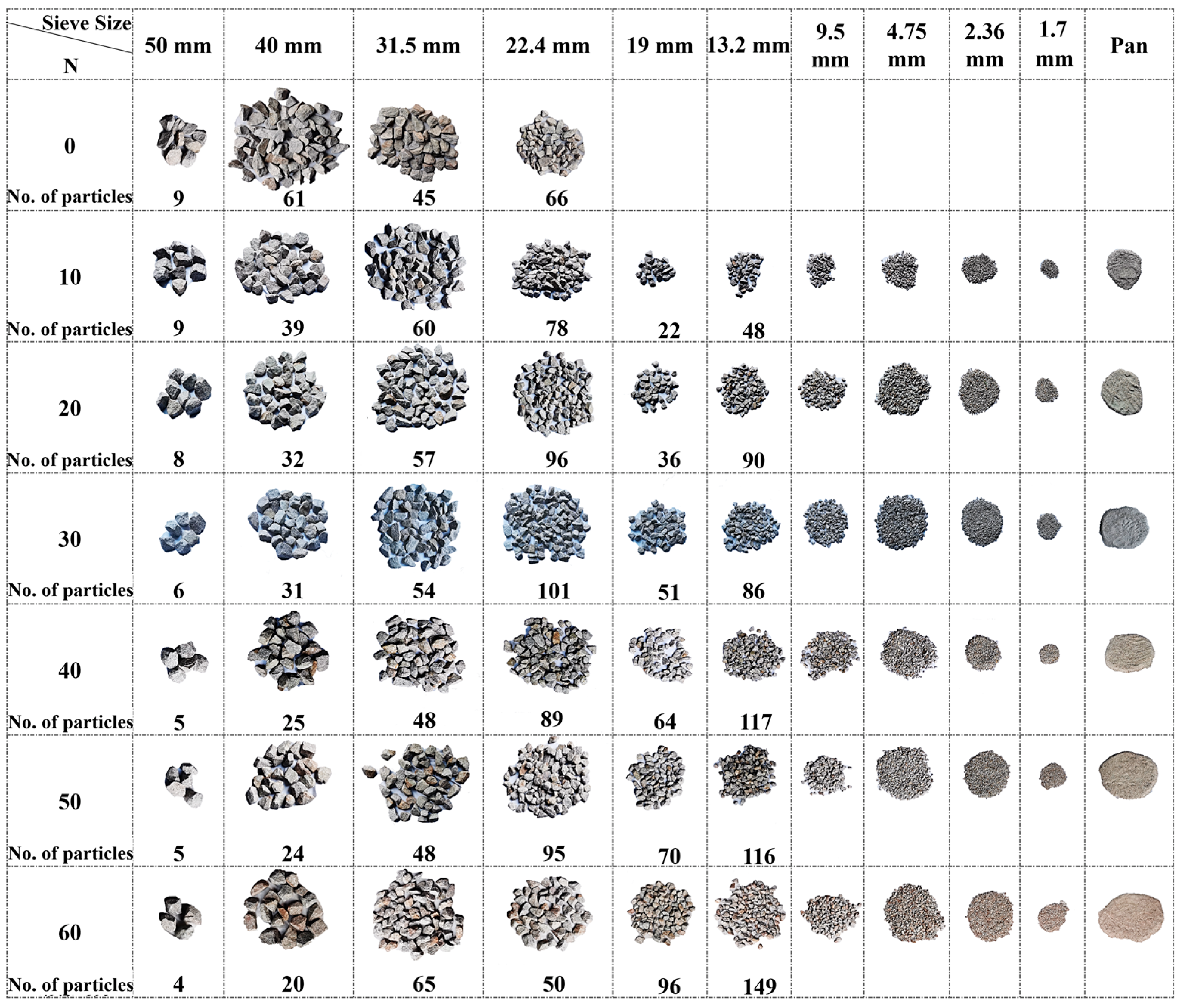
2.3. Particle-Breakge Quantification
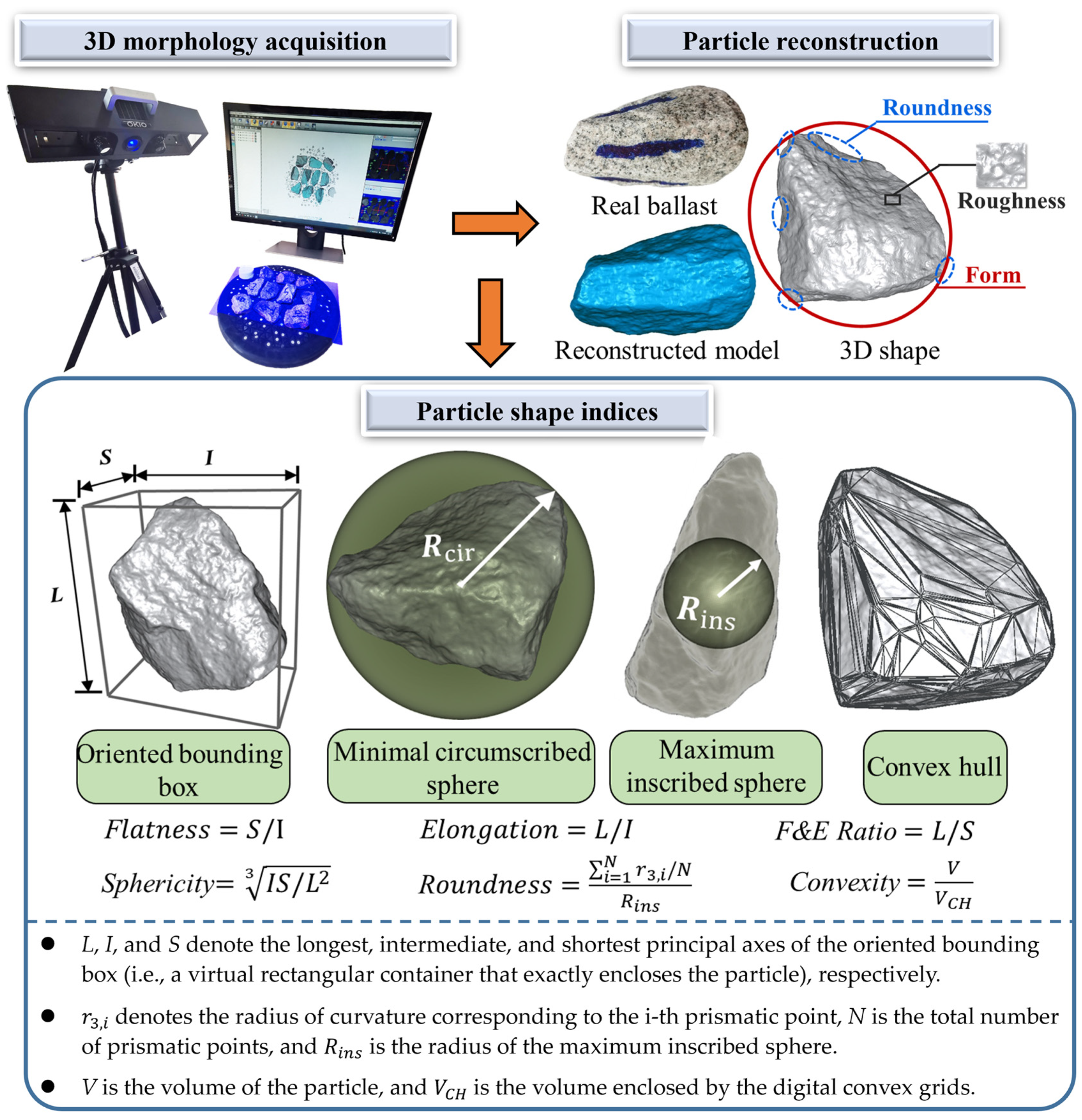
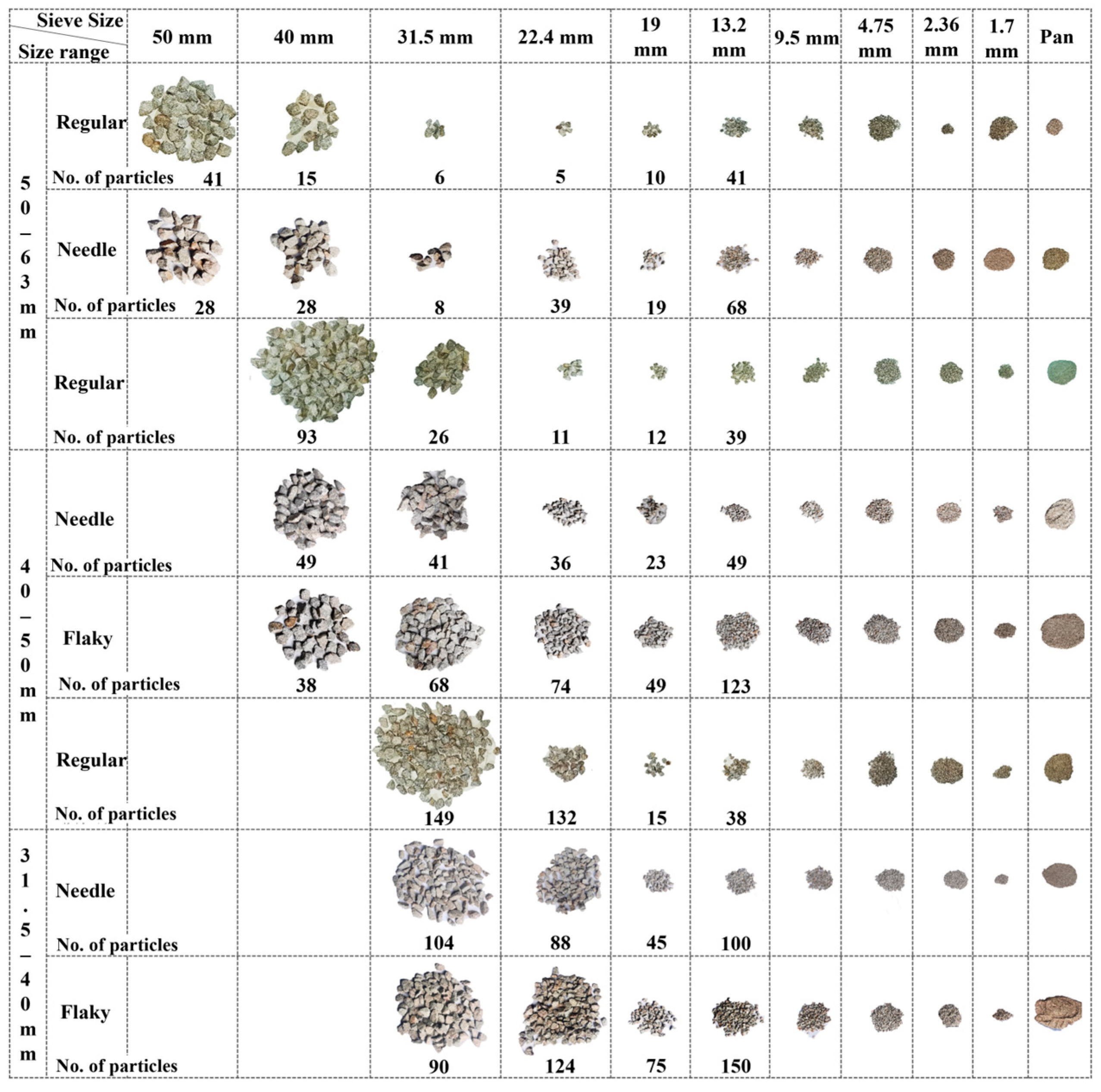
2.4. Particle-Shape Quantification
3. Testing Results and Analysis
3.1. Impact-Load-Test Results of Single-Size Ballasts
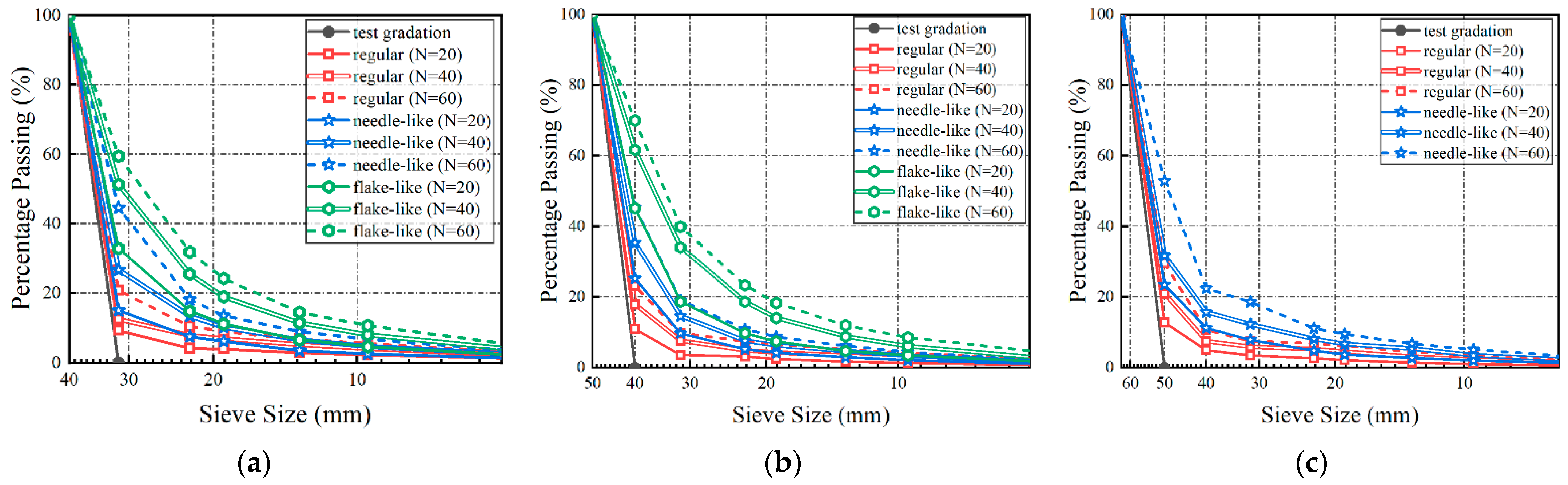
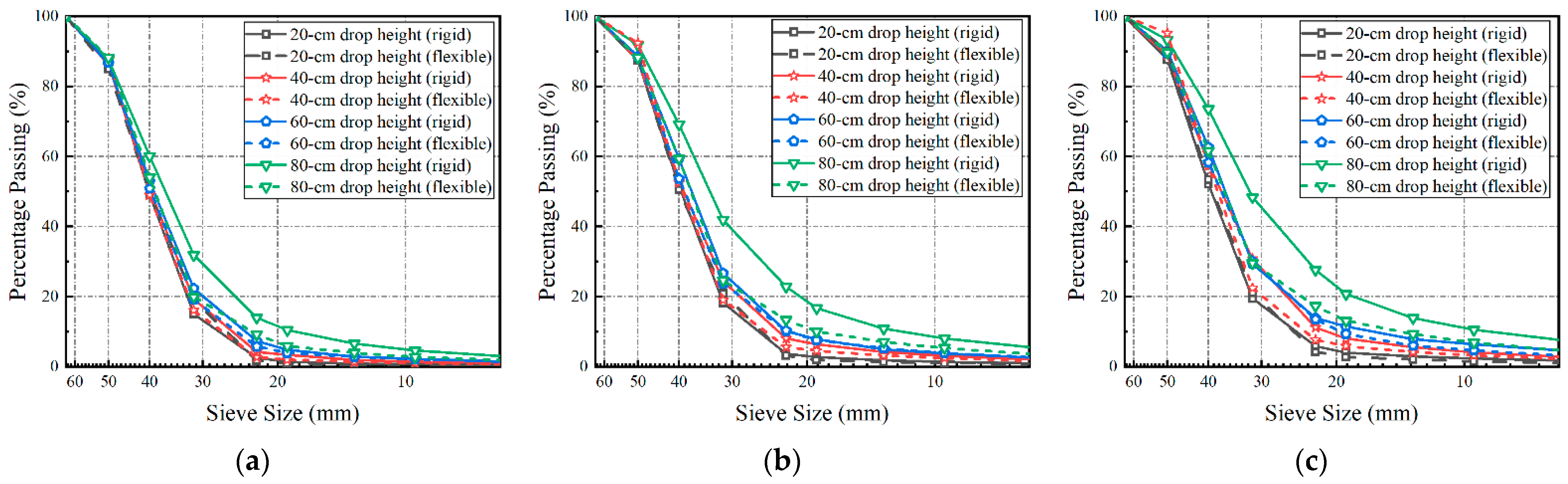
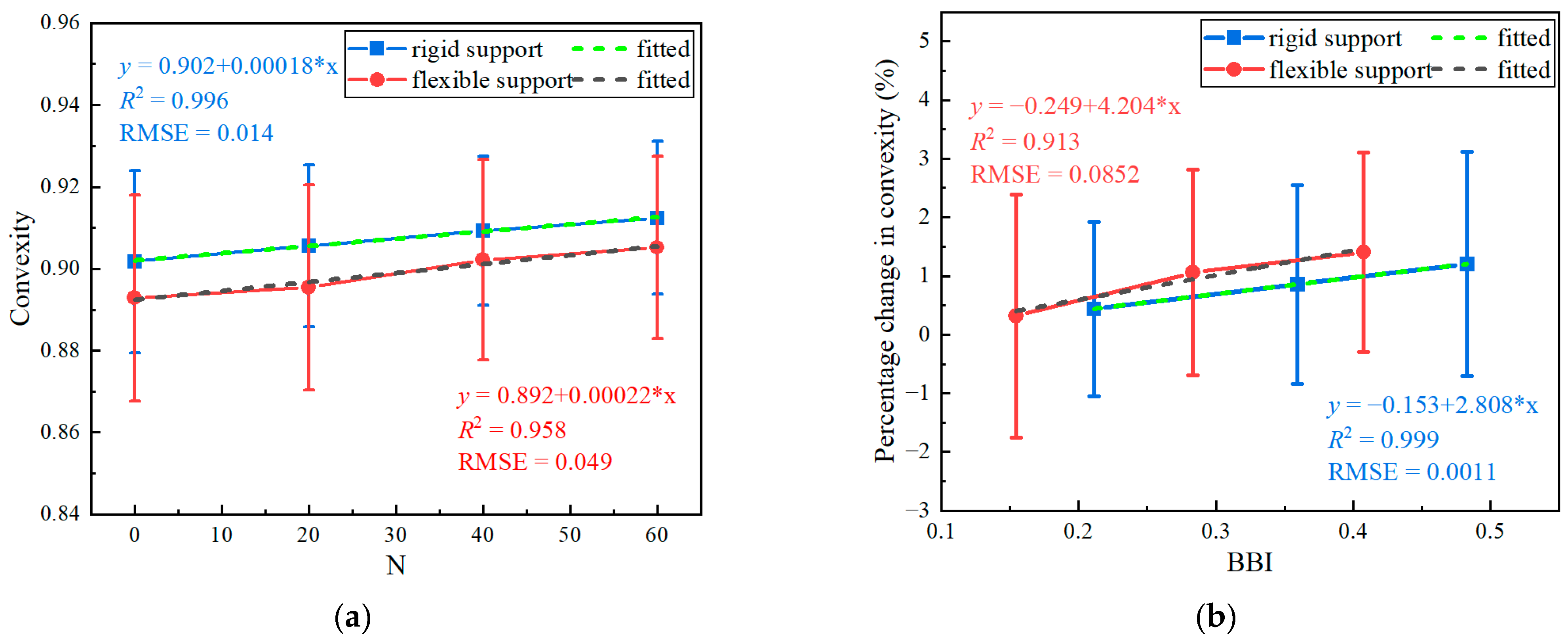
3.2. Impact-Test Results of Multiple-Size Ballasts
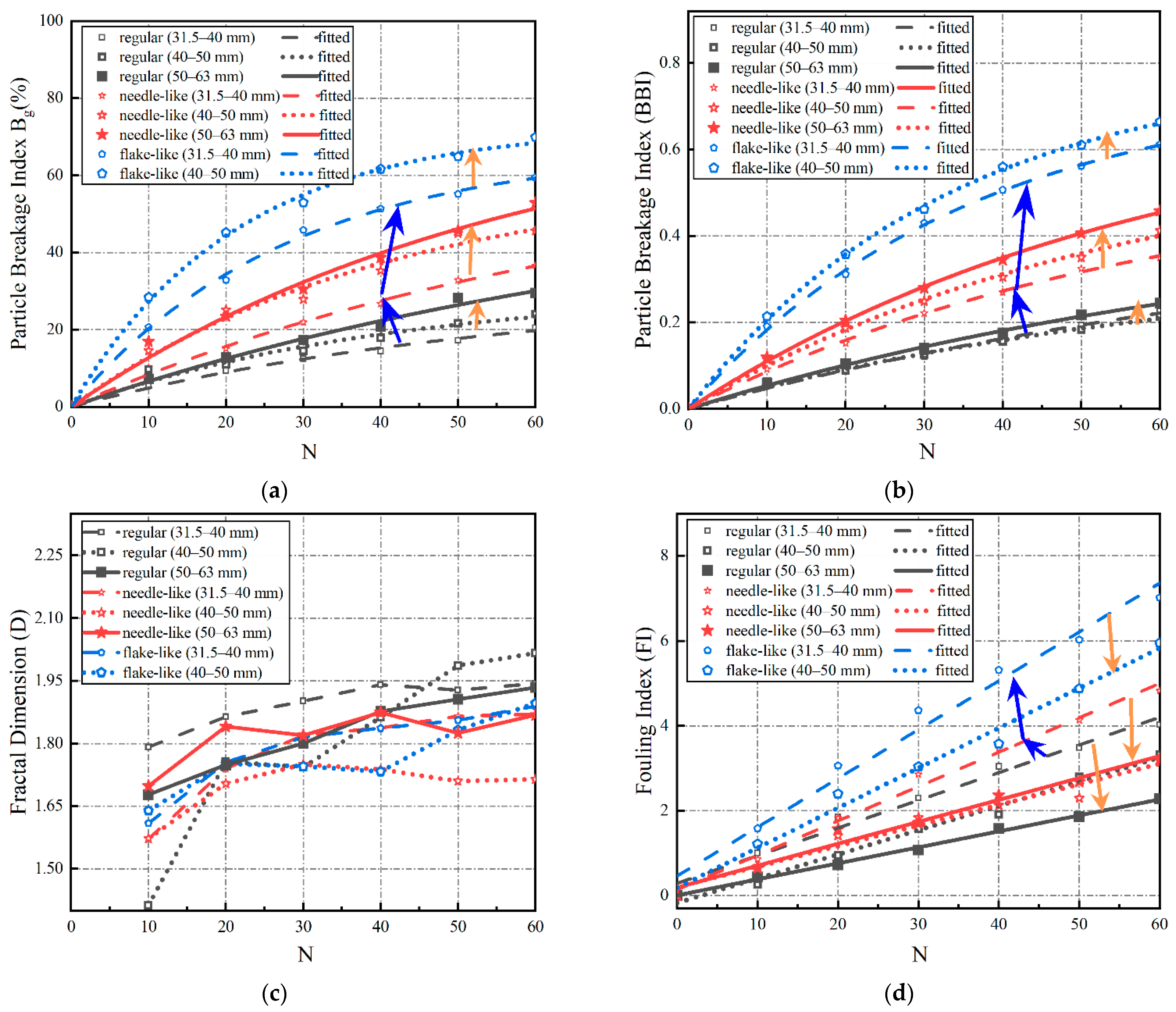
3.3. Degradation Trends and Estimation Models of Particle Shape and Breakage
4. Summary and Conclusions
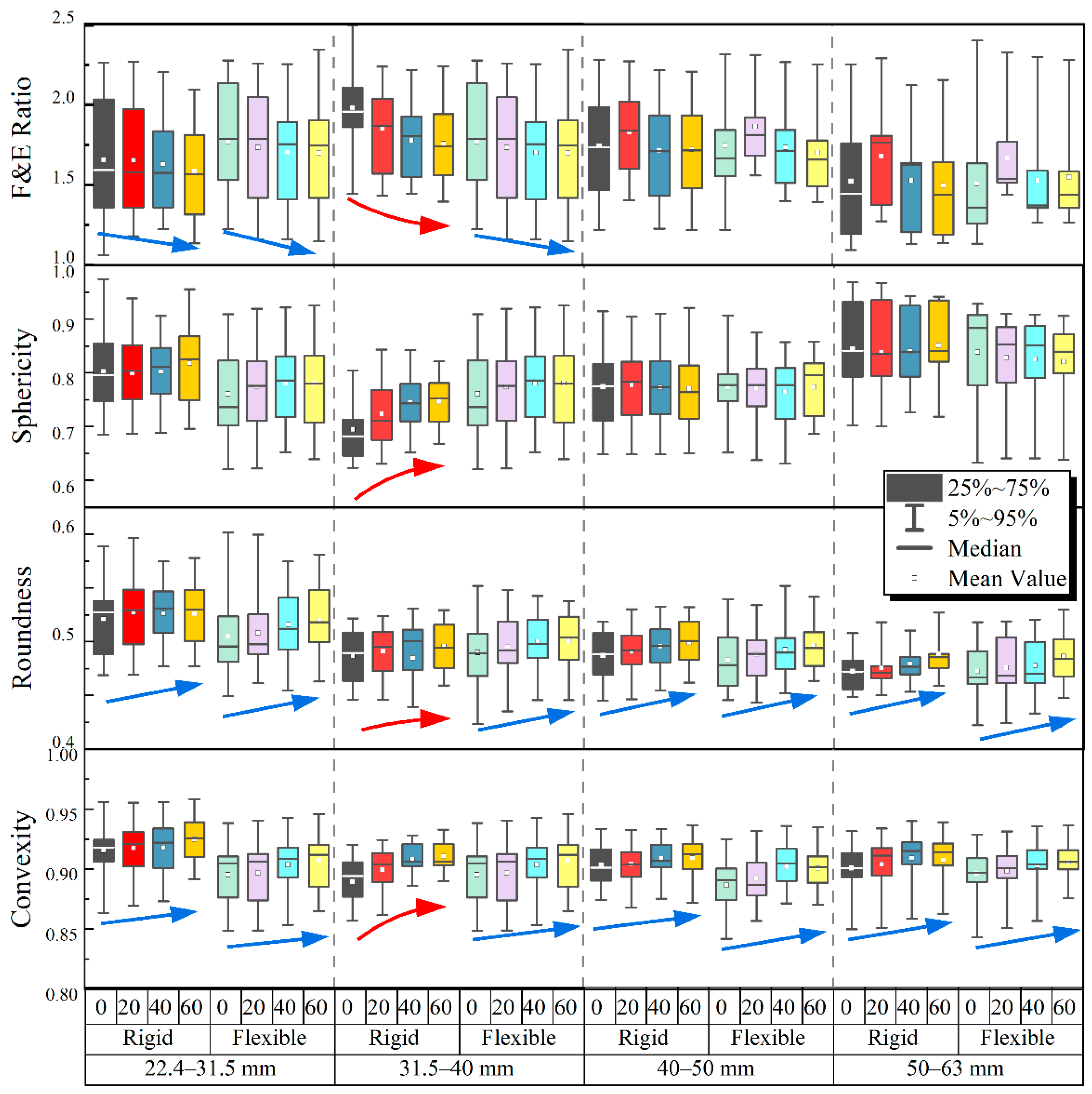
- Both the particle size and shape affect ballast breakage, with a more profound influence exerted by the particle shape. The larger-size particles exhibit more severe breakage and a greater ultimate breakage limit. The breakage of flake-like particles under impact loading is about 1.5–1.66 times higher than that of regular particles, and 1.25–1.5 times higher than that of needle-like particles;
- Under impact loading, small-size ballast particles are more likely to generate fine particles, while large-size ballast particles degrade mainly with sharp corners fractured. The flake-like particles produce more fine particles during the degradation process (e.g., the modified fouling index (FI) of flake-like ballast particles within 31.5–40 mm is about 3.6 times greater than that of regular particles within 50–63 mm);
- Ballast particles over rigid support are more prone to breakage than those over flexible support, with this difference escalated by the increasing impact energy (e.g., the severity of the ballast breakage and fines generation (quantified by the modified FI) increases by 50% and 74% due to the increase in the under-ballast support stiffness by 100 times, and the drop height of 80 cm, respectively). Therefore, the degradation of ballast beds underlain by rigid support (e.g., bridge decks) should be emphasized, and especially for increased axle loads and train speeds;
- The ballast particles gradually tend to become spherical under impact loading, with the angularity and concavity decreasing. The convexity and ballast breakage index (BBI) are promising for describing particle degradation, and their statistical correlation is potentially useful for the transition of ballast-bed-maintenance management from the current plan-based scheduling to condition-based upgrading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lobo-Guerrero, S.; Vallejo, L.E. Discrete element method analysis of railtrack ballast degradation during cyclic loading. Granul. Matter 2006, 8, 195–204. [Google Scholar] [CrossRef]
- Hossain, Z.; Indraratna, B.; Darve, F.; Thakur, P.K. DEM analysis of angular ballast breakage under cyclic loading. Geomech. Geoengin. 2007, 2, 175–181. [Google Scholar] [CrossRef]
- Selig, E.T.; Waters, J.M. Track Geotechnology and Substructure Management; Telford, T., Ed.; American Society of Civil Engineers, Publications Sales Department [Distributor]: New York, NY, USA, 1994. [Google Scholar]
- Marsal, R.J. Large scale testing of rockfill materials. J. Soil Mech. Found. Div. 1967, 93, 27–43. [Google Scholar] [CrossRef]
- Zeghal, M. The impact of grain crushing on road performance. Geotech. Geol. Eng. 2009, 27, 549–558. [Google Scholar] [CrossRef]
- Hardin, B.O. Crushing of soil particles. J. Geotech. Eng. 1985, 111, 1177–1192. [Google Scholar] [CrossRef]
- Lees, G.; Kennedy, C.K. Quality, shape and degradation of aggregates. Q. J. Eng. Geol. 1975, 8, 193–209. [Google Scholar] [CrossRef]
- Sun, Q.D.; Indraratna, B.; Nimbalkar, S. Deformation and degradation mechanisms of railway ballast under high frequency cyclic loading. J. Geotech. Geoenviron. Eng. 2016, 142, 04015056. [Google Scholar] [CrossRef]
- Li, D.; Maal, L. Heavy axle load revenue service bridge approach problems and remedies. In Proceedings of the 2015 Joint Rail Conference, San Jose, CA, USA, 24–26 March 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Nimbalkar, S.; Indraratna, B. Improved Performance of Ballasted Rail Track Using Geosynthetics and Rubber Shockmat. J. Geotech. Geoenviron. Eng. 2016, 142, 04016031. [Google Scholar] [CrossRef]
- Ticona Melo, L.R.; Ribeiro, D.; Calcada, R.; Bittencourt, T.N. Validation of a vertical train-track-bridge dynamic interaction model based on limited experimental data. Struct. Infrastruct. Eng. 2020, 16, 181–201. [Google Scholar] [CrossRef]
- Indraratna, B.; Thakur, P.K.; Vinod, J.S. Experimental and numerical study of railway ballast behavior under cyclic loading. Int. J. Geomech. 2010, 10, 136–144. [Google Scholar] [CrossRef]
- Debecker, B.; Vervoort, A. Two-dimensional discrete element simulations of the fracture behaviour of slate. Int. J. Rock Mech. Min. Sci. 2013, 61, 161–170. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, R.; Chen, J. A new DEM model to simulate the abrasion behavior of irregularly-shaped coarse granular aggregates. Granul. Matter 2021, 23, 61. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Feng, B.; Tutumluer, E.; Hashash, Y.M.; Kaewunruen, S. Evaluation of lateral stability of railway tracks due to ballast degradation. Constr. Build. Mater. 2021, 278, 122342. [Google Scholar] [CrossRef]
- Lim, W.L.; McDowell, G.R.; Collop, A.C. The application of Weibull statistics to the strength of railway ballast. Granul. Matter 2004, 6, 229–237. [Google Scholar] [CrossRef]
- Al-Saoudi, N.K.S.; Hassan, K.H. Evaluation of indirect tensile strength of track ballast using Weibull statistics. Geotech. Geol. Eng. 2012, 30, 1097–1102. [Google Scholar] [CrossRef]
- Koohmishi, M.; Palassi, M. Evaluation of the strength of railway ballast using point load test for various size fractions and particle shapes. Rock Mech. Rock Eng. 2016, 49, 2655–2664. [Google Scholar] [CrossRef]
- Danesh, A.; Palassi, M.; Mirghasemi, A.A. Evaluating the influence of ballast degradation on its shear behaviour. Int. J. Rail Transp. 2018, 6, 145–162. [Google Scholar] [CrossRef]
- Qian, Y.; Boler, H.; Moaveni, M.; Tutumluer, E.; Hashash, Y.M.A.; Ghaboussi, J. Degradation-related changes in ballast gradation and aggregate particle morphology. J. Geotech. Geoenviron. Eng. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- Guo, Y.; Markine, V.; Song, J.; Jing, G. Ballast degradation: Effect of particle size and shape using Los Angeles Abrasion test and image analysis. Constr. Build. Mater. 2018, 169, 414–424. [Google Scholar] [CrossRef]
- Guo, Y.; Markine, V.; Qiang, W.; Zhang, H.; Jing, G. Effects of crumb rubber size and percentage on degradation reduction of railway ballast. Constr. Build. Mater. 2019, 212, 210–224. [Google Scholar] [CrossRef]
- Bian, X.; Shi, K.; Li, W.; Luo, X.; Tutumluer, E.; Chen, Y. Quantification of railway ballast degradation by abrasion testing and computer-aided morphology analysis. J. Mater. Civ. Eng. 2021, 33, 04020411. [Google Scholar] [CrossRef]
- Deiros Quintanilla, I.; Combe, G.; Emeriault, F.; Voivret, C.; Ferellec, J.F. X-ray CT analysis of the evolution of ballast grain morphology along a Micro-Deval test: Key role of the asperity scale. Granul. Matter 2019, 21, 30. [Google Scholar] [CrossRef]
- Indraratna, B.; Lackenby, J.; Christie, D. Effect of confining pressure on the degradation of ballast under cyclic loading. Geotechnique 2005, 55, 325–328. [Google Scholar] [CrossRef]
- Indraratna, B.; Sun, Y.; Nimbalkar, S. Laboratory assessment of the role of particle size distribution on the deformation and degradation of ballast under cyclic loading. J. Geotech. Geoenviron. Eng. 2016, 142, 04016016. [Google Scholar] [CrossRef]
- Nimbalkar, S.; Indraratna, B.; Dash, S.K.; Christie, D. Improved performance of railway ballast under impact loads using shock mats. J. Geotech. Geoenviron. Eng. 2012, 138, 281–294. [Google Scholar] [CrossRef]
- Nimbalkar, S.; Dash, S.K.; Indraratna, B. Performance of ballasted track under impact loading and applications of recycled rubber inclusion. Geotech. Eng. 2018, 49, 13. [Google Scholar]
- Koohmishi, M.; Palassi, M. Effect of particle size distribution and subgrade condition on degradation of railway ballast under impact loads. Granul. Matter 2017, 19, 63. [Google Scholar] [CrossRef]
- Koohmishi, M.; Palassi, M. Degradation of railway ballast under impact loading considering the morphological properties of aggregate. Transp. Geotech. 2020, 25, 100398. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, T.; Ferreira, F.; Rujikiatkamjorn, C.; Shahkolahi, A. Laboratory examination of ballast deformation and degradation under impact loads with synthetic inclusions. Transp. Geotech. 2020, 25, 100406. [Google Scholar] [CrossRef]
- Pan, T.; Tutumluer, E. Evaluation of visual based aggregate shape classifications using the University of Illinois Aggregate Image Analyzer (UIAIA). In Pavement Mechanics and Performance; American Society of Civil Engineers: Shanghai, China, 2006; pp. 203–211. [Google Scholar]
- Wadell, H. Volume, shape, and roundness of rock particles. J. Geol. 1932, 40, 443–451. [Google Scholar] [CrossRef]
- Zheng, J.; He, H.; Alimohammadi, H. Three-dimensional Wadell roundness for particle angularity characterization of granular soils. Acta Geotech. 2021, 16, 133–149. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, Q.; Zheng, H.; Wei, D.; Li, Z.; Gao, L. Three-dimensional particle shape characterizations from half particle geometries. Powder Technol. 2020, 367, 122–132. [Google Scholar] [CrossRef]
- Altuhafi, F.; O’sullivan, C.; Cavarretta, I. Analysis of an image-based method to quantify the size and shape of sand particles. J. Geotech. Geoenviron. Eng. 2013, 139, 1290–1307. [Google Scholar] [CrossRef]
- Maroof, M.A.; Mahboubi, A.; Noorzad, A.; Safi, Y. A new approach to particle shape classification of granular materials. Transp. Geotech. 2020, 22, 100296. [Google Scholar] [CrossRef]
- Moaveni, M.; Qian, Y.; Qamhia, I.I.; Tutumluer, E.; Basye, C.; Li, D. Morphological characterization of railroad ballast degradation trends in the field and laboratory. Transp. Res. Rec. 2016, 2545, 89–99. [Google Scholar] [CrossRef]
- Bian, J.; Xu, P.C.; Zhang, D. Accumulated deformation and broken rules of ballast materials under train load. J. Nanjing Tech. Univ. (Nat. Sci. Ed.) 2019, 41, 261–268. [Google Scholar]
- Insa, R.; Salvador, P.; Inarejos, J.; Medina, L. Analysis of the performance of under-sleeper pads in high-speed line transition zones. Proc. Inst. Civ. Eng. Transp. 2014, 167, 63–77. [Google Scholar] [CrossRef]
- Varandas, J.N.; Hölscher, P.; Silva, M.A.G. Dynamic behaviour of railway tracks on transitions zones. Comput. Struct. 2011, 89, 1468–1479. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Kaewunruen, S. A review of loading conditions for railway track structures due to train and track vertical interaction. Struct. Control Health Monit. 2008, 15, 207–234. [Google Scholar] [CrossRef]
- Qian, Y.; Tutumluer, E.; Hashash, Y.M.; Ghaboussi, J.; Davis, D.D. Ballast settlement ramp to mitigate differential settlement in a bridge transition zone. Transp. Res. Rec. J. Transp. Res. Board 2015, 2476, 45–52. [Google Scholar] [CrossRef]
- Indraratna, B.; Nimbalkar, S.; Christie, D.; Rujikiatkamjorn, C.; Vinod, J. Field assessment of the performance of a ballasted rail track with and without geosynthetics. J. Geotech. Geoenviron. Eng. 2010, 136, 907–917. [Google Scholar] [CrossRef]
- EN 1097-2; Test for Mechanical and Physical Properties of Aggregates—Part 2: Methods for the Determination of Resistance to Fragmentation. British Standards Institution: London, UK, 2010.
- TB/T 2140.2–2018; Railway Ballast—Part 2: Test Method. China Railway Publishing House: Beijing, China, 2018.
- Zingg, T. Beitrag Zur Schotteranalyse. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 1935. [Google Scholar]
- Barrett, P.J. The shape of rock particles, a critical review. Sedimentology 1980, 27, 291–303. [Google Scholar] [CrossRef]
- Tutumluer, E.; Mishra, D.; Hyslip, J.H.; Boler, H.; Hou, W. Mitigation of Differential Movement at Railway Transitions for US High Speed Passenger Rail and Joint Passenger/Freight Corridors. In Proceedings of the IEEE Joint Rail Conference, San Jose, CA, USA, 24–26 March 2015; U.S. Department of Transportation, Federal Railroad Administration: Washington, DC, USA, 2015. [Google Scholar]
- Xiao, Y.; Kong, K.; Aminu, U.F.; Li, Z.; Li, Q.; Zhu, H.; Cai, D. Characterizing and Predicting the Resilient Modulus of Recycled Aggregates from Building Demolition Waste with Breakage-Induced Gradation Variation. Materials 2022, 15, 2670. [Google Scholar] [CrossRef] [PubMed]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle-size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]




| Specimen No. | Size Range (mm) | Shape Category | Drop Height of Hammer (cm) | Under-Ballast Support |
|---|---|---|---|---|
| 1 | 31.5–40 | Regular | 60 | Concrete block |
| 2 | Flake-like | |||
| 3 | Needle-like | |||
| 4 | 40–50 | Regular | 60 | Concrete block |
| 5 | Flake-like | |||
| 6 | Needle-like | |||
| 7 | 50–63 | Regular | 60 | Concrete block |
| 8 | Needle-like |
| Specimen No. | Size Range (mm) | Shape Category ** | Under-Ballast Support | Drop Height (cm) |
|---|---|---|---|---|
| 1 | 22.4–63 | Regular | Concrete block | 20 |
| 2 | 40 | |||
| 3 * | 60 | |||
| 4 | 80 | |||
| 5 | 22.4–63 | Regular | Sand layer | 20 |
| 6 | 40 | |||
| 7 * | 60 | |||
| 8 | 80 |
| Breakage Index | Size-Range (mm) and Shape Coefficients | Regular Shape | Needle-like | Flake-like | |||||
|---|---|---|---|---|---|---|---|---|---|
| 31.5–40 | 40–50 | 50–63 | 31.5–40 | 40–50 | 50–63 | 31.5–40 | 40–50 | ||
| a | 30.59168 | 30.7347 | 58.96191 | 64.65747 | 60.25032 | 79.06351 | 67.05557 | 72.76099 | |
| b | 0.01732 | 0.0237 | 0.001188 | 0.01387 | 0.02406 | 0.01752 | 0.03596 | 0.04695 | |
| 0.99262 | 0.95883 | 0.98892 | 0.99461 | 0.97851 | 0.9847 | 0.9976 | 0.99691 | ||
| BBI | a | 0.47296 | 0.34211 | 0.46998 | 0.56019 | 0.60622 | 0.72009 | 0.75096 | 0.7896 |
| b | 0.01054 | 0.01567 | 0.01216 | 0.01667 | 0.01803 | 0.01662 | 0.02788 | 0.03019 | |
| 0.98952 | 0.99219 | 0.99748 | 0.99847 | 0.99497 | 0.99906 | 0.99921 | 0.99926 | ||
| Modified FI | a | 0.28907 | −0.16959 | 0.00781 | 0.13897 | 0.19846 | 0.19026 | 0.45867 | 0.18457 |
| k | 0.0652 | 0.05712 | 0.03767 | 0.08102 | 0.04852 | 0.05167 | 0.1151 | 0.09415 | |
| 0.97918 | 0.986 | 0.99656 | 0.98976 | 0.95546 | 0.97127 | 0.97721 | 0.98536 | ||
| Breakage Index | Fitted Coefficients | Rigid Support (Concrete Block) | Flexible Support (Sand) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Drop Height | 20 cm | 40 cm | 60 cm | 80 cm | 20 cm | 40 cm | 60 cm | 80 cm | ||
| a | 7.93047 | 28.35468 | 38.44433 | 43.91049 | 8.73478 | 15.23696 | 30.02918 | 36.27785 | ||
| b | 0.02631 | 0.01235 | 0.01246 | 0.02757 | 0.03404 | 0.0207 | 0.01177 | 0.01236 | ||
| 0.73699 | 0.99234 | 0.97842 | 0.99944 | 0.99825 | 0.95393 | 0.99555 | 0.95768 | |||
| BBI | a | 0.50518 | 0.78741 | 0.86425 | 1.24718 | 0.42986 | 0.78046 | 0.82467 | 0.83136 | |
| b | 0.00953 | 0.01015 | 0.014 | 0.02121 | 0.01073 | 0.00941 | 0.01102 | 0.0156 | ||
| 0.98103 | 0.99792 | 0.99881 | 0.99814 | 0.98626 | 0.99848 | 0.99568 | 0.99769 | |||
| D | a | 1.63734 | 1.69482 | 1.75873 | 1.9448 | 1.45094 | 1.65577 | 1.71411 | 1.81566 | |
| b | 0.07974 | 0.10696 | 0.1531 | 0.14758 | 0.14756 | 0.106 | 0.12839 | 0.14887 | ||
| 0.98295 | 0.96913 | 0.96305 | 0.98492 | 0.98888 | 0.98789 | 0.99155 | 0.98618 | |||
| Modified FI | a | −0.13856 | −0.06773 | −0.09337 | 0.17198 | 0.12339 | 0.00823 | 0.2094 | 0.20149 | |
| k | 0.03629 | 0.05657 | 0.08129 | 0.14783 | 0.01972 | 0.04291 | 0.05675 | 0.08479 | ||
| 0.95401 | 0.9572 | 0.93278 | 0.995 | 0.94759 | 0.98817 | 0.95458 | 0.98899 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Jiang, Y.; Tan, P.; Kong, K.; Ali, J.; Mustafina, R.; Zhu, H.; Cai, D. Investigating Morphology and Breakage Evolution Characteristics of Railroad Ballasts over Distinct Supports Subjected to Impact Loading. Materials 2022, 15, 6295. https://doi.org/10.3390/ma15186295
Xiao Y, Jiang Y, Tan P, Kong K, Ali J, Mustafina R, Zhu H, Cai D. Investigating Morphology and Breakage Evolution Characteristics of Railroad Ballasts over Distinct Supports Subjected to Impact Loading. Materials. 2022; 15(18):6295. https://doi.org/10.3390/ma15186295
Chicago/Turabian StyleXiao, Yuanjie, Yu Jiang, Pan Tan, Kunfeng Kong, Joseph Ali, Ralina Mustafina, Hongwei Zhu, and Degou Cai. 2022. "Investigating Morphology and Breakage Evolution Characteristics of Railroad Ballasts over Distinct Supports Subjected to Impact Loading" Materials 15, no. 18: 6295. https://doi.org/10.3390/ma15186295






