Digital Twin Assistant Active Design and Optimization of Steel Mega-Sub Controlled Structural System under Severe Earthquake Waves
Abstract
:1. Introduction
2. Methodologies
2.1. Digital Twin Assistant Active Design and Optimization of MSCSSs
2.2. Finite Element Modeling
2.3. Hilbert–Huang Transform (HHT)
3. Results and Discussions
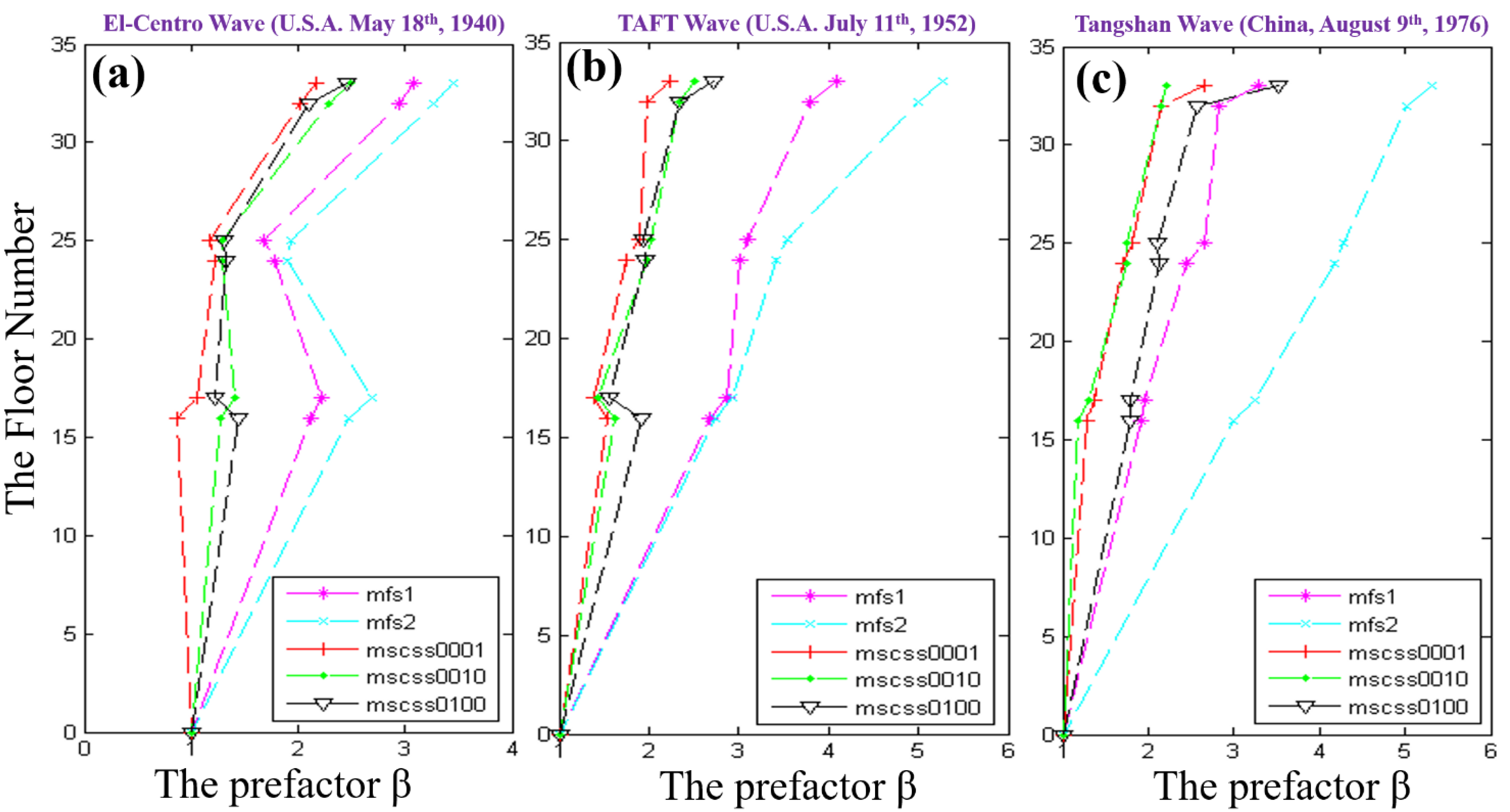
3.1. Optimized Configurations of MSCSS Together with Numerical Analysis
3.2. The Benchmarks of the Ground Motion Waves Together with Their HHTs
3.3. Structure Response Characteristics and Its Optimizations
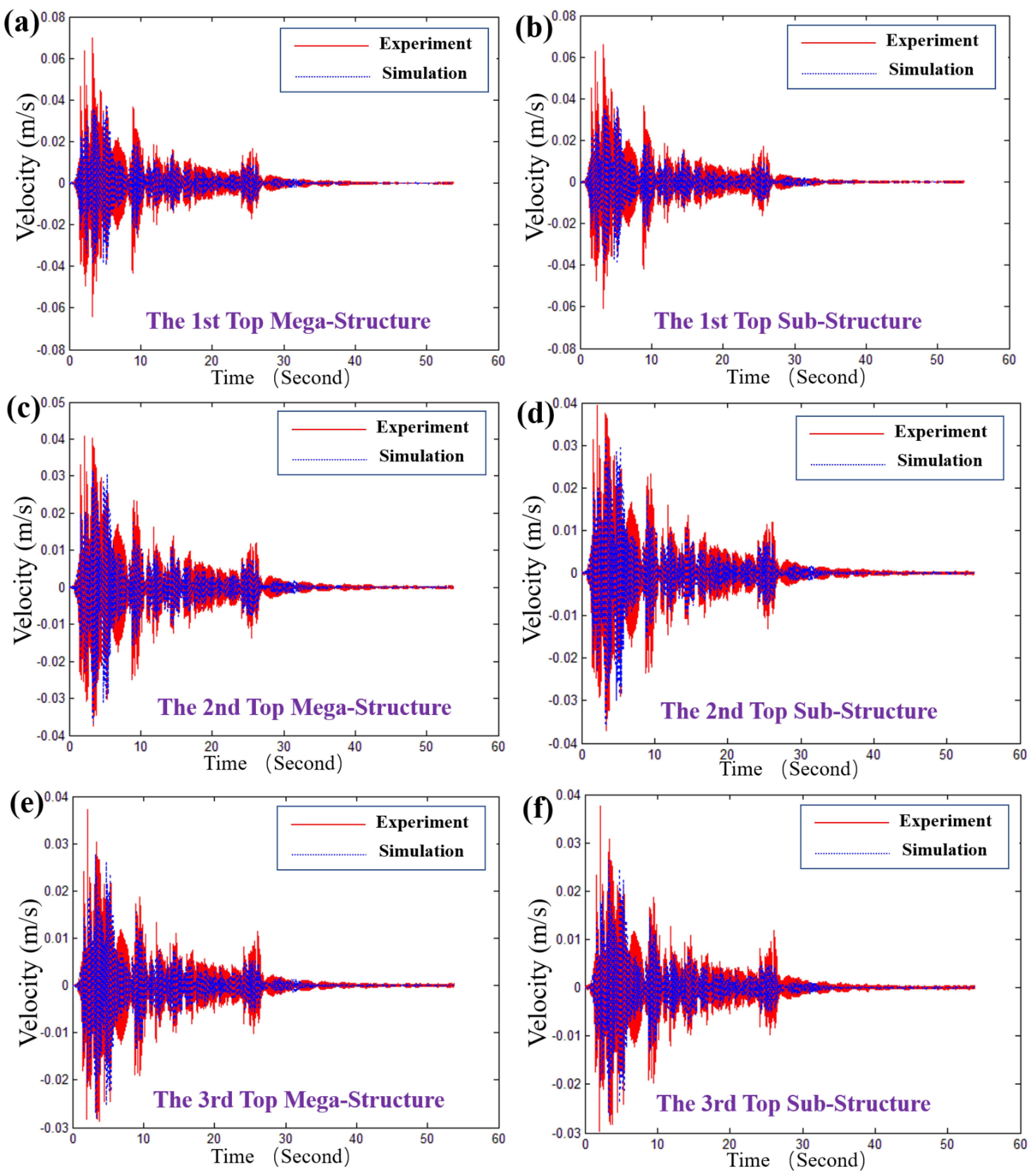
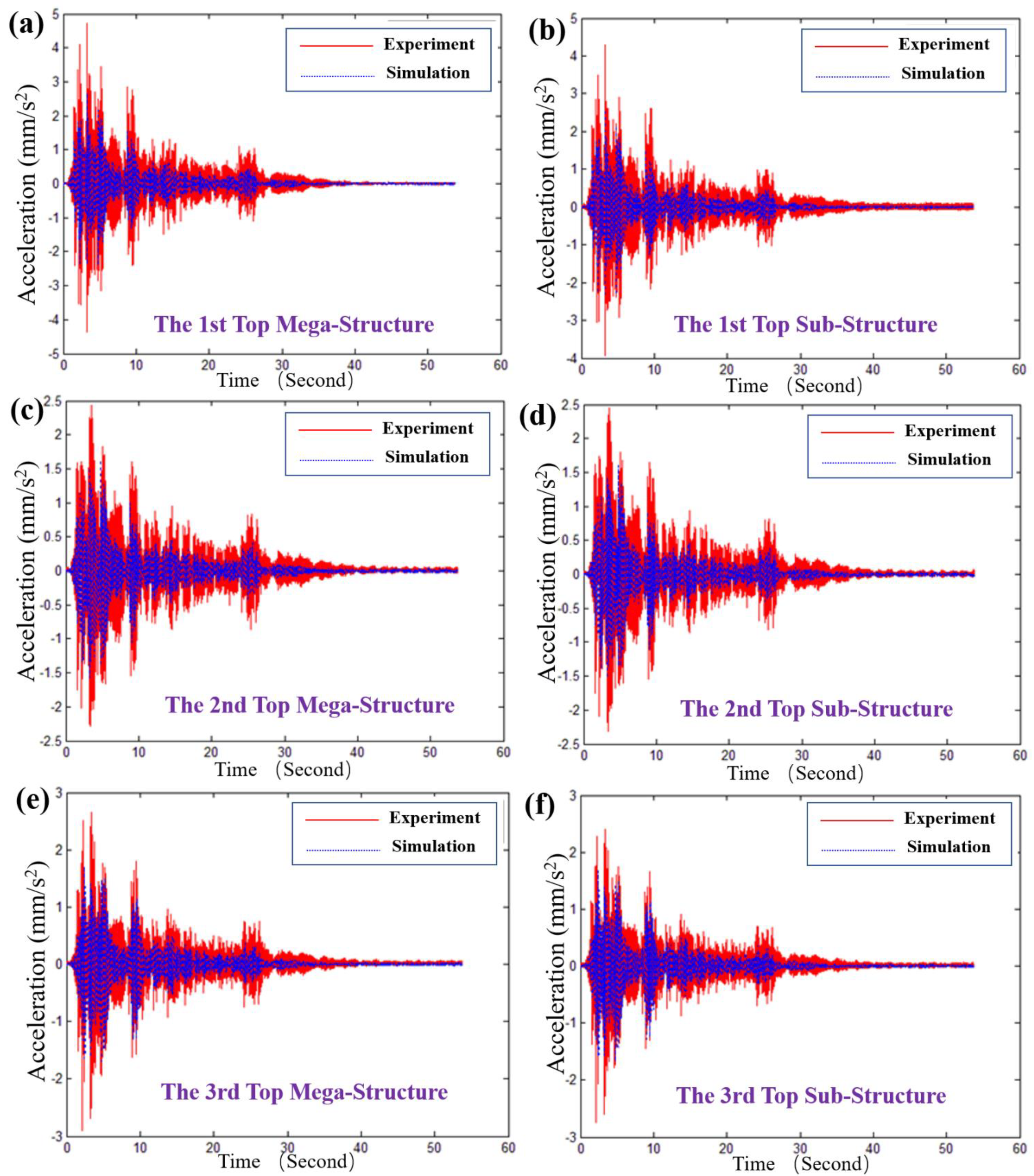
3.4. Experimental Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pollock, T.M.; Allison, J.E.; Backman, D.G.; Boyce, M.C.; Gersh, M.; Holm, E.A.; Lesar, R.; Long, M.; IV, A.C.P.; Schirra, J.J.; et al. Integrated Computational Materials Engineering: A Transformational Discipline for Improved Competitiveness and National Security; The National Academies: Washington, DC, USA, 2008. [Google Scholar]
- Liu, Z.-K.; McDowell, D.L. The Penn State-Georgia Tech CCMD: Ushering in the ICME Era. Int. Mater. Manuf. Innov. 2014, 3, 409–428. [Google Scholar] [CrossRef]
- Wang, W.Y.; Li, J.; Liu, W.; Liu, Z.-K. Integrated computational materials engineering for advanced materials: A brief review. Comput. Mater. Sci. 2019, 158, 42–48. [Google Scholar] [CrossRef]
- Wang, W.Y.; Tang, B.; Lin, D.; Zou, C.; Zhang, Y.; Shang, S.-L.; Guan, Q.; Gao, J.; Fan, L.; Kou, H.; et al. A brief review of data-driven ICME for intelligently discovering advanced structural metal materials: Insight into atomic and electronic building blocks. J. Mater. Res. 2020, 35, 872–889. [Google Scholar] [CrossRef]
- Olson, G.B. Designing a new material world. Science 2000, 288, 993–998. [Google Scholar] [CrossRef]
- Liu, Z.-K. Computational thermodynamics and its applications. Acta Mater. 2020, 200, 745–792. [Google Scholar] [CrossRef]
- Olson, G.B. Computational design of hierarchically structured materials. Science 1997, 277, 1237–1242. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Bjorkman, T.; Blaha, P.; Blugel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in density functional theory calculations of solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef]
- Zou, C.; Li, J.; Wang, W.Y.; Zhang, Y.; Lin, D.; Yuan, R.; Wang, X.; Tang, B.; Wang, J.; Gao, X.; et al. Integrating data mining and machine learning to discover high-strength ductile Titanium alloys. Acta Mater. 2021, 202, 211–221. [Google Scholar] [CrossRef]
- Kusiak, A. Smart manufacturing must embrace big data. Nature 2017, 544, 23–25. [Google Scholar] [CrossRef]
- Nosengo, N. Can artificial intelligence create the next wonder material? Nature 2016, 533, 22–25. [Google Scholar] [CrossRef] [Green Version]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.F.; Falk, C.; Wenny, M.B.; Mollo, A.; Zeller, M.; Friedler, S.A.; Schrier, J.; Norquist, A.J. Machine-learning-assisted materials discovery using failed experiments. Nature 2016, 533, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Ziletti, A.; Kumar, D.; Scheffler, M.; Ghiringhelli, L.M. Insightful classification of crystal structures using deep learning. Nat. Commun. 2018, 9, 2775. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.Y.; Shang, S.L.; Wang, Y.; Han, F.; Darling, K.A.; Wu, Y.; Xie, X.; Senkov, O.N.; Li, J.; Hui, X.D.; et al. Atomic and electronic basis for the serrations of refractory high-entropy alloys. npj Comput. Mater. 2017, 3, 23. [Google Scholar] [CrossRef]
- Wang, W.-Y.; Yin, J.; Chai, Z.; Chen, X.; Zhao, W.; Lu, J.; Sun, F.; Jia, Q.; Gao, X.; Tang, B.; et al. Big data-assisted digital twins for the smart design and manufacturing of advanced materials: From atoms to products. J. Mater. Inform. 2022, 2, 1. [Google Scholar] [CrossRef]
- Zhou, B.-C.; Wang, W.Y.; Liu, Z.-K.; Arroyave, R. Chapter 8—Electrons to Phases of Magnesium. In Integrated Computational Materials Engineering (ICME) for Metals: Concepts and Case Studies; Horstemeyer, M.F., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 237–282. [Google Scholar]
- Huang, L.-F.; Grabowski, B.; Zhang, J.; Lai, M.-J.; Tasan, C.C.; Sandlobes, S.; Raabe, D.; Neugebauer, J. From electronic structure to phase diagrams: A bottom-up approach to understand the stability of titanium-transition metal alloys. Acta Mater. 2016, 113, 311–319. [Google Scholar] [CrossRef]
- Krajewski, P.E.; Hector, L.G., Jr.; Qi, Y.; Mishra, R.K.; Sachdev, A.K.; Bower, A.F.; Curtin, W.A. Atoms to autos: A multi-scale approach to modeling aluminum deformation. JOM 2011, 63, 24–32. [Google Scholar] [CrossRef]
- Olson, G.B.; Kuehmann, C.J. Materials genomics: From CALPHAD to flight. Scr. Mater. 2014, 70, 25–30. [Google Scholar] [CrossRef]
- Fang, P.; Yang, J.; Zheng, L.; Zhong, R.Y.; Jiang, Y. Data analytics-enable production visibility for Cyber-Physical Production Systems. J. Manuf. Syst. 2020, 57, 242–253. [Google Scholar] [CrossRef]
- Botcha, B.; Iquebal, A.S.; Bukkapatnam, S.T.S. Smart manufacturing multiplex. Manuf. Lett. 2020, 25, 102–106. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q. Make more digital twins. Nature 2019, 573, 490–491. [Google Scholar] [CrossRef] [Green Version]
- Boschert, S.; Rosen, R. Chapter 5. Digital Twin—The Simulation Aspect. In Mechatronic Futures: Challenges and Solutions for Mechatronic Systems and Their Designers; Hehenberger, P., Bradley, D., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 59–74. [Google Scholar] [CrossRef]
- Pettey, C. Prepare for the Impact of Digital Twins. Available online: https://www.gartner.com/smarterwithgartner/prepare-for-the-impact-of-digital-twins (accessed on 18 September 2017).
- Yi, Y.; Yan, Y.; Liu, X.; Ni, Z.; Feng, J.; Liu, J. Digital twin-based smart assembly process design and application framework for complex products and its case study. J. Manuf. Syst. 2021, 58, 94–107. [Google Scholar] [CrossRef]
- You, Z.; Wu, C. A framework for data-driven informatization of the construction company. Adv. Eng. Inform. 2019, 39, 269–277. [Google Scholar] [CrossRef]
- Bilal, M.; Oyedele, L.O.; Qadir, J.; Munir, K.; Ajayi, S.O.; Akinade, O.O.; Owolabi, H.A.; Alaka, H.A.; Pasha, M. Big Data in the construction industry: A review of present status, opportunities, and future trends. Adv. Eng. Inform. 2016, 30, 500–521. [Google Scholar] [CrossRef]
- GhaffarianHoseini, A.; Zhang, T.R.; Nwadigo, O.; GhaffarianHoseini, A.; Naismith, N.; Tookey, J.; Raahemifar, K. Application of nD BIM Integrated Knowledge-based Building Management System (BIM-IKBMS) for inspecting post-construction energy efficiency. Renew. Sustain. Energy Rev. 2017, 72, 935–949. [Google Scholar] [CrossRef]
- Yang, A.; Han, M.Z.; Zeng, Q.C.; Sun, Y.H. Adopting Building Information Modeling (BIM) for the development of smart buildings: A review of enabling applications and challenges. Adv. Civ. Eng. 2021, 2021, 8811476. [Google Scholar] [CrossRef]
- Feng, M.Q.; Chai, W. Design of a mega-sub-controlled building system under stochastic wind loads. Probab. Eng. Mech. 1997, 12, 149–162. [Google Scholar] [CrossRef]
- Abdulhadi, M.; Zhang, X.; Fan, B.; Moman, M. Substructure design optimization and nonlinear responses control analysis of the mega-sub controlled structural system (MSCSS) under earthquake action. Earthq. Eng. Eng. Vib. 2021, 20, 687–704. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, X.J.; Cherry, S.; Lian, Y.D.; Zhang, J.L.; Jiang, J.S. A new proposed passive mega-sub controlled structure and response control. J. Earthq. Eng. 2009, 13, 252–274. [Google Scholar] [CrossRef]
- Cai, T.; Zhang, X. On optimizing control parameters for suppressing vibration of MSCSS under earthquake excitation. Chin. J. Comput. Mech. 2014, 31, 565–570. [Google Scholar]
- Abdulhadi, M.; Zhao, X.; Fan, B.Q.; Moman, M. Design, optimization and nonlinear response control analysis of the mega sub-controlled structural system (MSCSS) under earthquake action. J. Earthq. Tsunami 2020, 14, 2050013. [Google Scholar] [CrossRef]
- Cai, T.; Zhang, X.; Lian, Y.; Li, B. Research on model design and shaking table experiment of mega-sub controlled structures system. Ind. Constr. 2016, 46, 139–143. [Google Scholar]
- Wu, H.; Xie, M.; Ma, K.; Wang, Y. Research on the optimum layout scheme of additional dampers inserted in MSCSS under non-stationary seismic excitation. Ind. Constr. 2018, 48, 93–98. [Google Scholar]
- Qi, Q.; Tao, F. Digital twin and big data towards smart manufacturing and industry 4.0: 360 degree comparison. IEEE Access 2018, 6, 3585–3593. [Google Scholar] [CrossRef]
- Wang, X.W.; Zhang, X.; Shahzad, M.M.; Shi, X.Y. Research on the disaster prevention mechanism of mega-sub controlled structural system by vulnerability analysis. Structures 2021, 33, 4481–4491. [Google Scholar] [CrossRef]
- Wang, X.W.; Zhang, X.A.; Shahzad, M.M.; Wang, T.L. Research on dynamic response characteristics and control effect of mega-sub controlled structural system under long-period ground motions. Structures 2021, 29, 225–234. [Google Scholar] [CrossRef]
- Haukaas, T.; Scott, M.H. Shape sensitivities in the reliability analysis of nonlinear frame structures. Comput. Struct. 2006, 84, 964–977. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H.; Xin, Y. Data driven structural dynamic response reconstruction using segment based generative adversarial networks. Eng. Struct. 2021, 234, 111970. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Shahzad, M.M. A novel structural damage identification scheme based on deep learning framework. Structures 2021, 29, 1537–1549. [Google Scholar] [CrossRef]


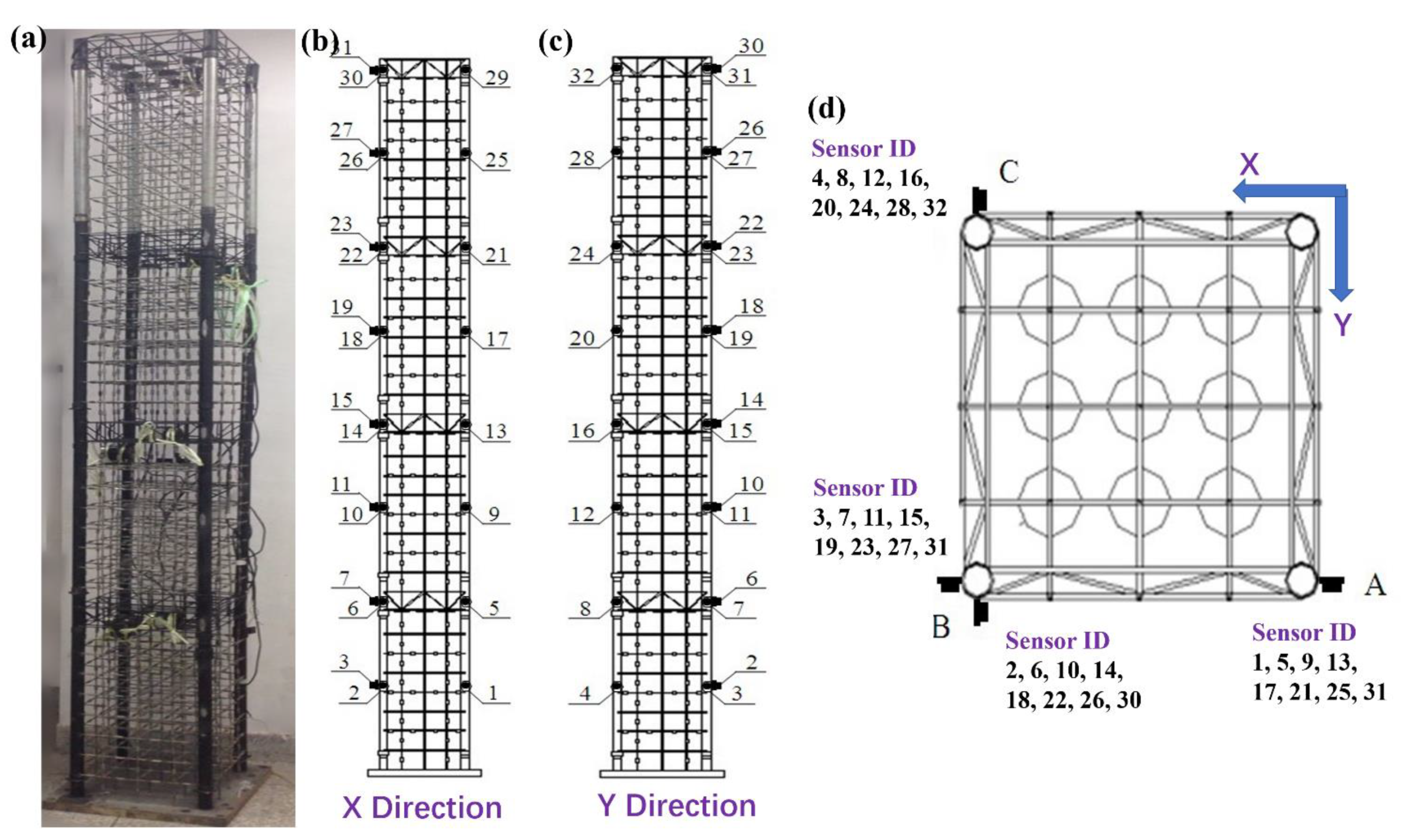
| Quantities | Symbol | Similarity | Ratio (Real Structure/Virtual Model) | |
|---|---|---|---|---|
| Materials Properties | Stress | 1.0 | ||
| Strain | 1.0 | |||
| Elastic Modulus | 1.0 | |||
| Poisson Ratio | 1.0 | |||
| Density | 100 | |||
| Geometrical Features | Length | 0.01 | ||
| Area | 0.0001 | |||
| Linear Displacement | 0.01 | |||
| Angular Displacement | 1.0 | |||
| Dynamic Properties | Mass | 0.0001 | ||
| Stiffness | 0.01 | |||
| Intrinsic Cycle | 0.1 | |||
| Frequency | 10 | |||
| Damping | 0.001 | |||
| Velocity | 0.1 | |||
| Acceleration | 1.0 | |||
| Gravity | 1.0 |
| Damping Coefficient (kN s/mm) | 0.22 | 0.33 | 0.55 | 1.1 | 5.5 | 11 |
| Stiffness(kN/mm) | 1.492 | 2.24 | 3.73 | 7.47 | 37.3 | 74.7 |
| Configuration | 1st-Order Mode | 2nd-Order Mode | 3rd-Order Mode | 4th-Order Mode | 5th-Order Mode | 6th-Order Mode |
|---|---|---|---|---|---|---|
| MFS1 | 6.9454 | 6.9454 | 17.4612 | 21.5471 | 21.5471 | 36.6435 |
| MFS2 | 6.4599 | 6.4599 | 17.4600 | 20.3890 | 20.3890 | 34.4588 |
| MSCSS0001 | 5.6767 | 5.6767 | 17.4703 | 18.2615 | 18.2615 | 22.6706 |
| MSCSS0010 | 6.4510 | 6.4510 | 18.3690 | 21.3575 | 21.3578 | 29.3068 |
| MSCSS0100 | 6.4616 | 6.4616 | 13.4373 | 21.4225 | 21.4225 | 31.2013 |
| Configuration | 1st Megastructure Top Floor | 1st Substructure Top Floor | 2nd Megastructure Top Floor | 2nd Substructure Top Floor | 3rd Megastructure Top Floor | 3rd Substructure Top Floor |
|---|---|---|---|---|---|---|
| MFS1 | 0.0701 | 0.0687 | 0.0566 | 0.0550 | 0.0448 | 0.0424 |
| MSCSS0001 | 0.0358 | 0.0359 | 0.0308 | 0.0306 | 0.0270 | 0.0257 |
| MSCSS0010 | 0.0378 | 0.0369 | 0.0317 | 0.0315 | 0.0278 | 0.0264 |
| MSCSS0100 | 0.0598 | 0.0582 | 0.0485 | 0.0523 | 0.0384 | 0.0370 |
| Configuration | 1st Megastructure Top Floor | 1st Substructure Top Floor | 2nd Megastructure Top Floor | 2nd Substructure Top Floor | 3rd Megastructure Top Floor | 3rd Substructure Top Floor |
|---|---|---|---|---|---|---|
| MFS1 | 0.3135 | 0.3069 | 0.2479 | 0.2381 | 0.1612 | 0.1494 |
| MSCSS0001 | 0.2169 | 0.2174 | 0.1877 | 0.1821 | 0.1329 | 0.1246 |
| MSCSS0010 | 0.2248 | 0.2204 | 0.1921 | 0.1862 | 0.1341 | 0.1256 |
| MSCSS0100 | 0.1582 | 0.1539 | 0.1288 | 0.1361 | 0.0963 | 0.0903 |
| Configuration | 1st Megastructure Top Floor | 1st Substructure Top Floor | 2nd Megastructure Top Floor | 2nd Substructure Top Floor | 3rd Megastructure Top Floor | 3rd Substructure Top Floor |
|---|---|---|---|---|---|---|
| MFS1 | 0.0356 | 0.0349 | 0.0291 | 0.0280 | 0.0186 | 0.0174 |
| MSCSS0001 | 0.0287 | 0.0287 | 0.0244 | 0.0236 | 0.0166 | 0.0155 |
| MSCSS0010 | 0.0296 | 0.0291 | 0.0248 | 0.0240 | 0.0169 | 0.0157 |
| MSCSS0100 | 0.0348 | 0.0343 | 0.0298 | 0.0302 | 0.0201 | 0.0188 |
| Configuration | 1st Megastructure Top Floor | 1st Substructure Top Floor | 2nd Megastructure Top Floor | 2nd Substructure Top Floor | 3rd Megastructure Top Floor | 3rd Substructure Top Floor |
|---|---|---|---|---|---|---|
| MFS1 | 4.77958 | 4.56826 | 3.26028 | 3.25423 | 3.0092 | 2.92027 |
| MSCSS0001 | 2.54298 | 2.55961 | 1.61258 | 1.58138 | 1.66917 | 1.64302 |
| MSCSS0010 | 2.66669 | 2.58399 | 1.62786 | 1.5999 | 1.70185 | 1.67041 |
| MSCSS0100 | 3.60737 | 3.35749 | 1.92975 | 2.22256 | 2.41596 | 2.41865 |
| Configuration | 1st Megastructure Top Floor | 1st Substructure Top Floor | 2nd Megastructure Top Floor | 2nd Substructure Top Floor | 3rd Megastructure Top Floor | 3rd Substructure Top Floor |
|---|---|---|---|---|---|---|
| MFS1 | 13.28673 | 12.98759 | 10.5392 | 10.23442 | 12.5419 | 12.23583 |
| MSCSS0001 | 11.54402 | 11.57088 | 8.31653 | 7.80441 | 11.27876 | 11.02887 |
| MSCSS0010 | 11.91685 | 11.62903 | 8.63159 | 8.15865 | 11.95438 | 11.67911 |
| MSCSS0100 | 9.28152 | 9.02504 | 6.52034 | 6.75927 | 6.43695 | 6.55522 |
| Configuration | 1st Megastructure Top Floor | 1st Substructure Top Floor | 2nd Megastructure Top Floor | 2nd Substructure Top Floor | 3rd Megastructure Top Floor | 3rd Substructure Top Floor |
|---|---|---|---|---|---|---|
| MFS1 | 1.53296 | 1.49571 | 1.43937 | 1.40308 | 1.00678 | 0.93036 |
| MSCSS0001 | 1.33797 | 1.34093 | 1.0238 | 0.96878 | 0.85073 | 0.81348 |
| MSCSS0010 | 1.41850 | 1.38444 | 1.00713 | 0.96938 | 0.89715 | 0.85761 |
| MSCSS0100 | 1.31576 | 1.29558 | 1.09562 | 1.16114 | 0.72263 | 0.67056 |
| Frequency | MFS1 | MSCSS0001 | ||||
|---|---|---|---|---|---|---|
| SAP2000 | Experiment | Error Bar | SAP2000 | Experiment | Error Bar | |
| 1st-order model | 6.945409 | 6.783 | 2.34% | 5.676658 | 5.130 | 9.63% |
| 2nd-order model | 6.945409 | 6.883 | 0.90% | 5.676658 | 5.313 | 6.41% |
| 3rd-order model | 17.46115 | 13.448 | 22.98% | 17.4703 | 9.587 | 45.12% |
| 4th-order model | 21.54708 | 21.687 | −0.65% | 18.2615 | 13.716 | 24.89% |
| 5th-order model | 21.54708 | 21.810 | −1.22% | 18.2615 | 14.166 | 22.43% |
| 6th-order model | 36.64346 | 41.056 | −12.04% | 22.6706 | 21.811 | 3.79% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Zhang, X.-A.; Sun, F.; Wang, W.Y. Digital Twin Assistant Active Design and Optimization of Steel Mega-Sub Controlled Structural System under Severe Earthquake Waves. Materials 2022, 15, 6382. https://doi.org/10.3390/ma15186382
Wei Z, Zhang X-A, Sun F, Wang WY. Digital Twin Assistant Active Design and Optimization of Steel Mega-Sub Controlled Structural System under Severe Earthquake Waves. Materials. 2022; 15(18):6382. https://doi.org/10.3390/ma15186382
Chicago/Turabian StyleWei, Zheng, Xun-An Zhang, Feng Sun, and William Yi Wang. 2022. "Digital Twin Assistant Active Design and Optimization of Steel Mega-Sub Controlled Structural System under Severe Earthquake Waves" Materials 15, no. 18: 6382. https://doi.org/10.3390/ma15186382
APA StyleWei, Z., Zhang, X.-A., Sun, F., & Wang, W. Y. (2022). Digital Twin Assistant Active Design and Optimization of Steel Mega-Sub Controlled Structural System under Severe Earthquake Waves. Materials, 15(18), 6382. https://doi.org/10.3390/ma15186382







