Hydrogen-Induced Dislocation Nucleation and Plastic Deformation of
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. GB Energy and GB Structure
3.2. Hydrogen Segregation at GBs
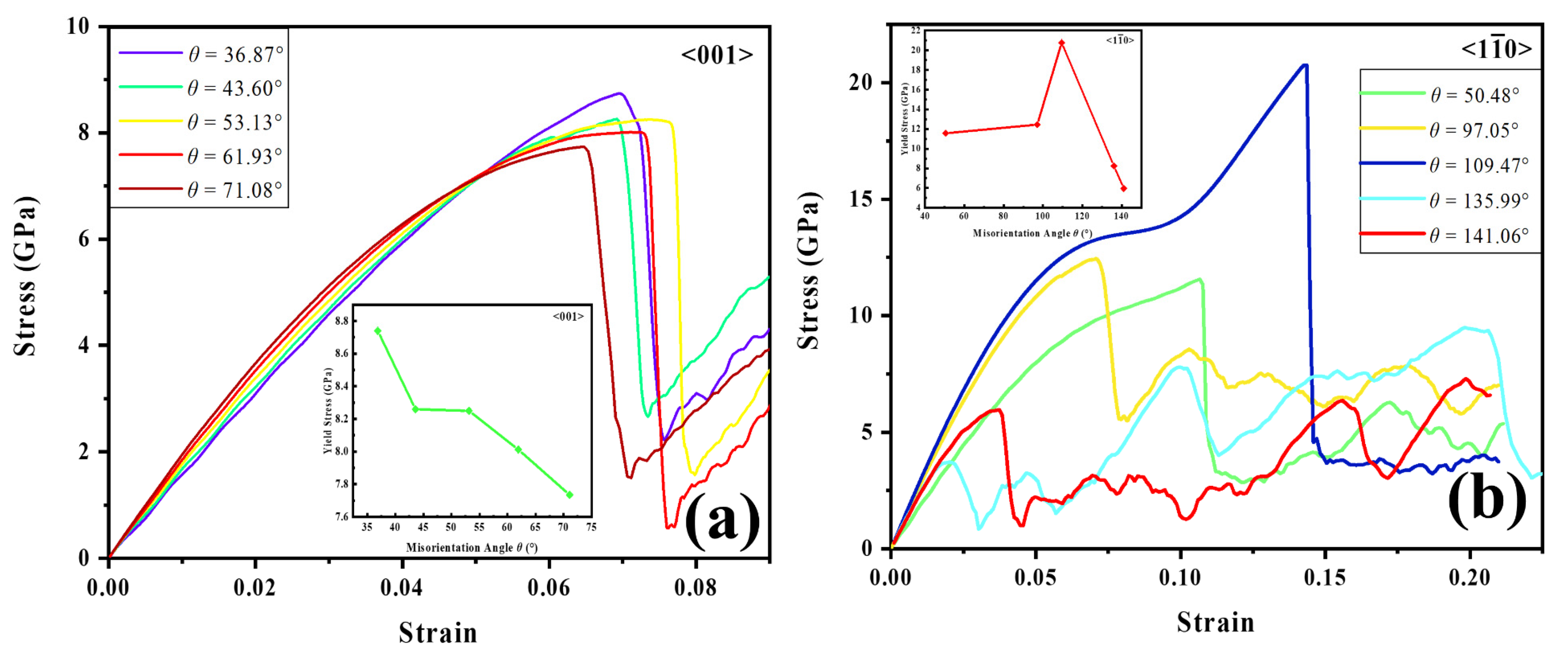
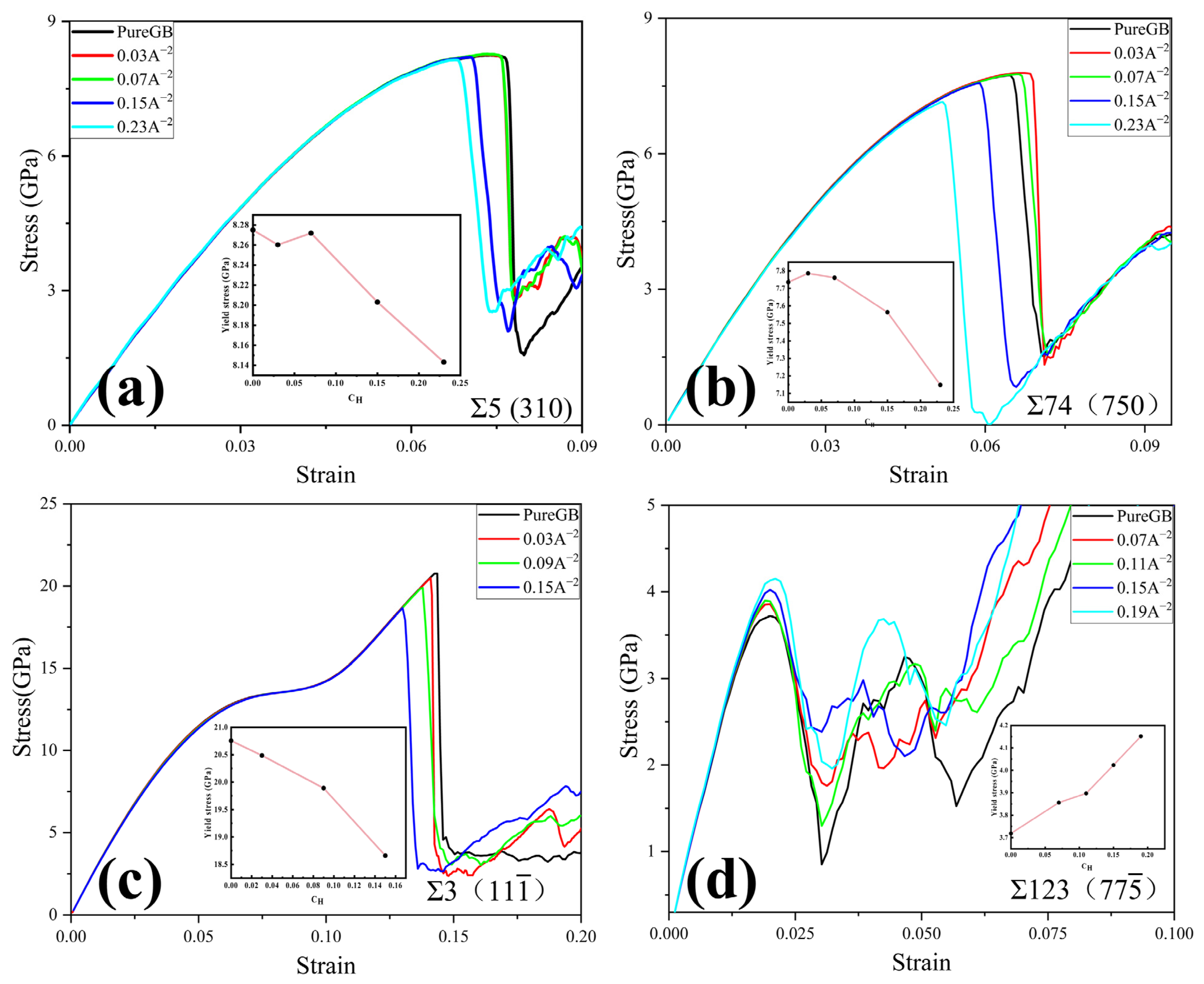
3.3. Effects of Hydrogen on the Dislocation Nulceaiton and Plastic Deformation of GBs
3.3.1. Dislocation Nucleation Strength Influenced by Hydrogen in GB Model
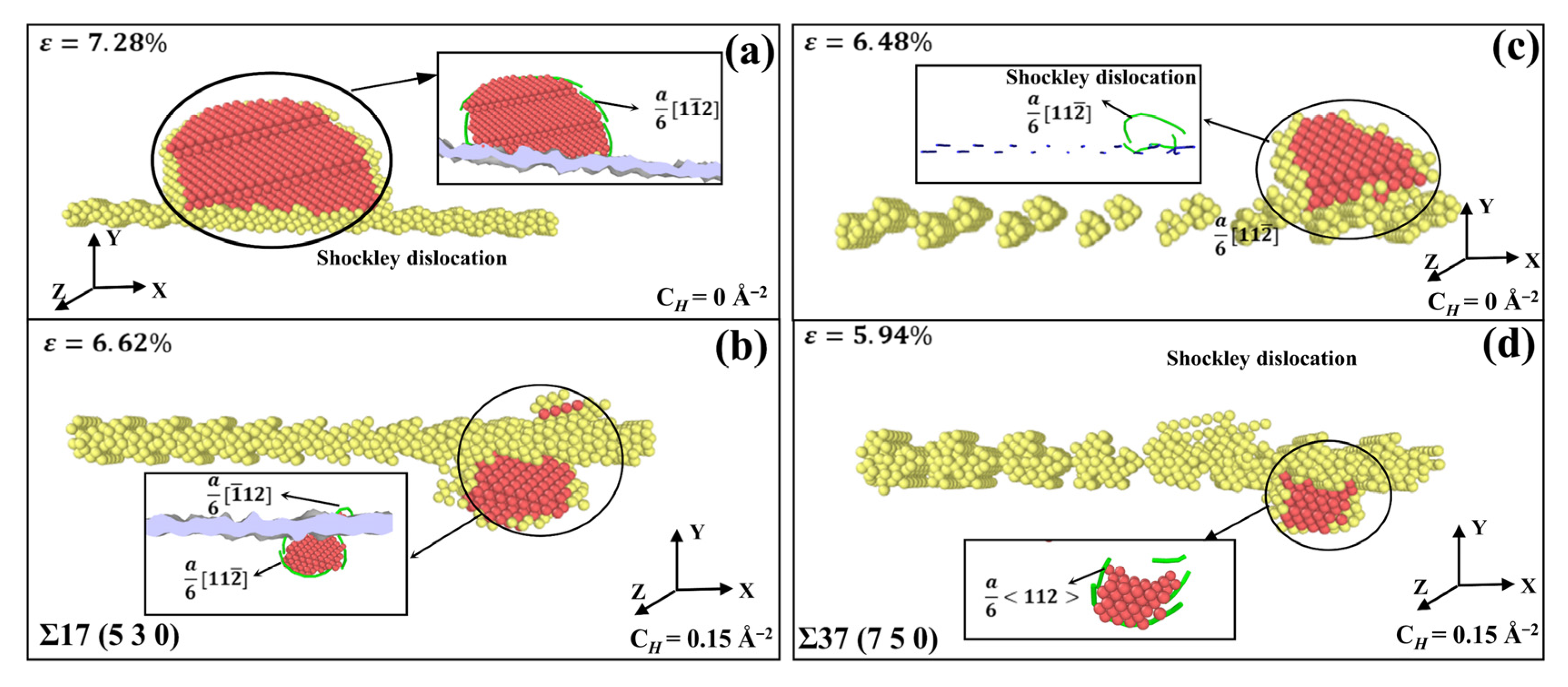
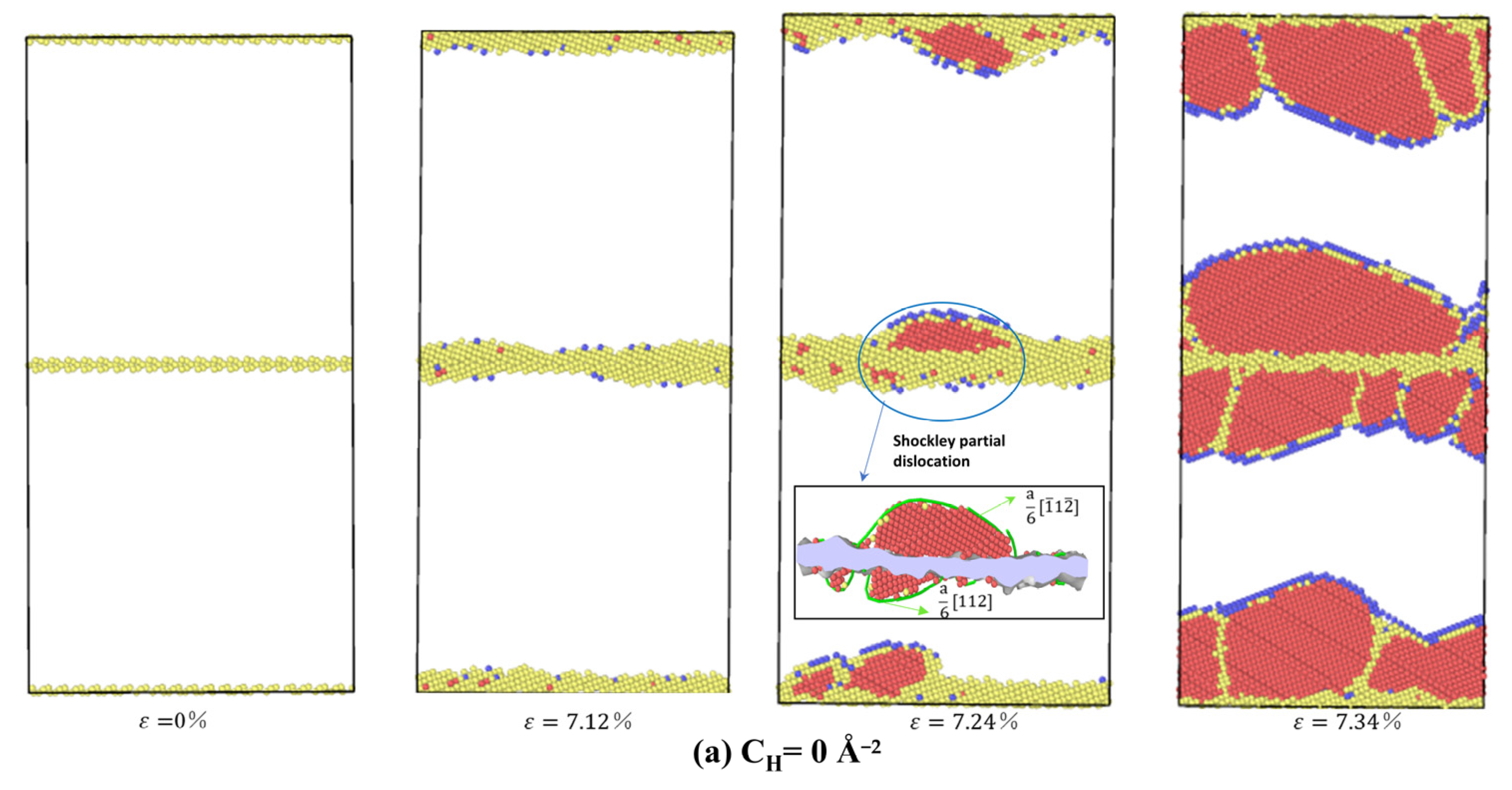
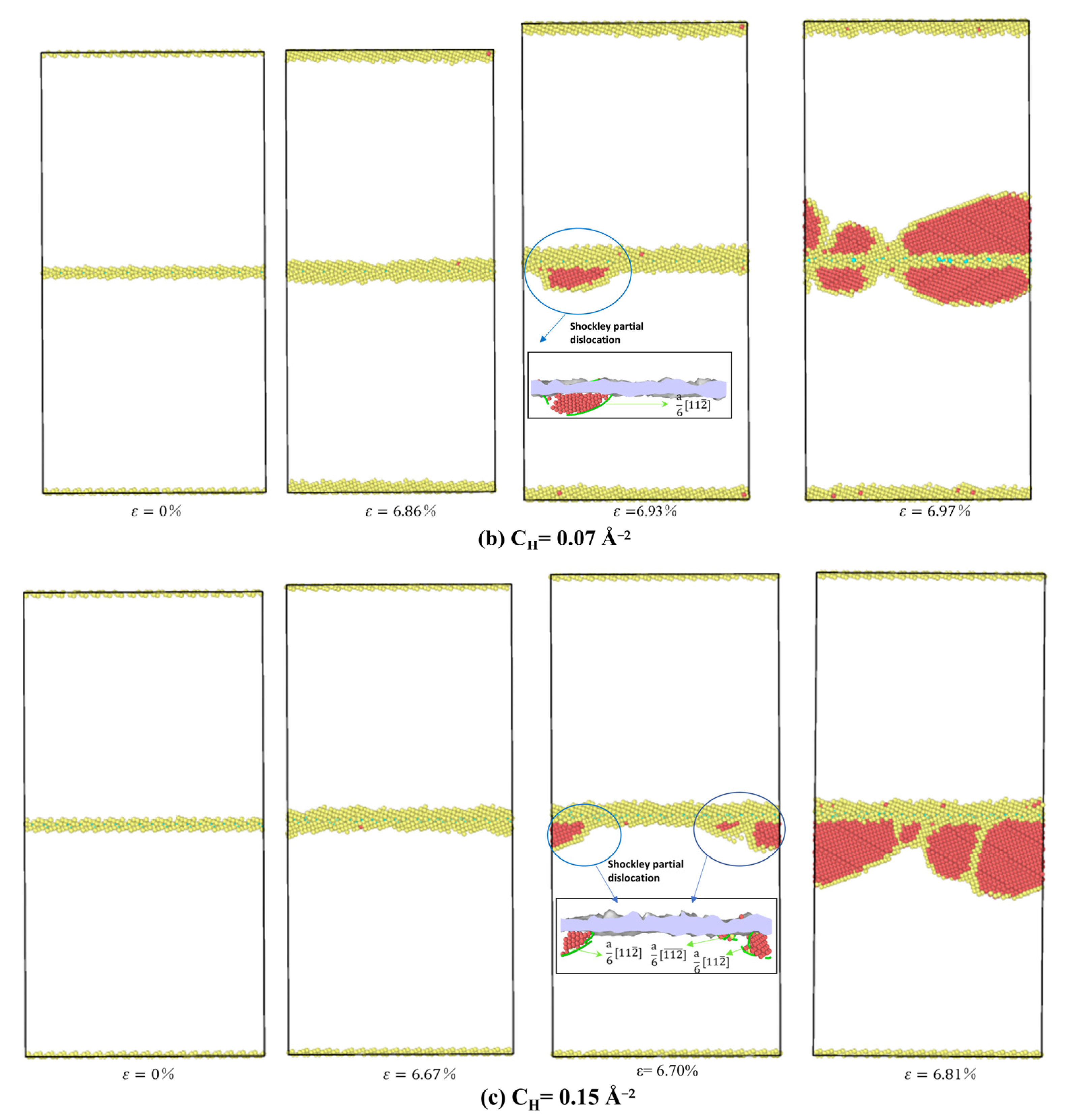
3.3.2. The Influence of Hydrogen Segregation on Dislocation Nucleation of STGB
3.3.3. The Influence of Hydrogen Segregation on Dislocation Nucleation of STGB
4. Summary
- (1)
- The ability of the GB to trap H atoms is very sensitive to the GB structure and GB energy. The GBs with higher GB energy own a larger free volume, thus trapping more H atoms. There are essentially no H atoms segregating at the Σ3 () STGB, while for other STGBs, H atoms are distributed within a region ±5 Å from the boundary planes.
- (2)
- For STGB, the plastic deformation mechanism is dominated by HDN. H segregation disorders the GB structure and promotes the HDN event, leading to a reduced yield stress with increasing H concentration.
- (3)
- For STGB, the yield stress is increased or decreased as the H concentration increases, depending on the GB structure. The reduced stress is associated with the H atoms disordering the boundary structure, while the increased stress is attributed to the fact that the presence of H inhibits the structural transformation and dislocation nucleation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| GB | grain boundary |
| STGBs | symmetrical tilt grain boundaries |
| HDN | heterogeneous dislocation nucleation |
| HE | hydrogen embrittlement |
| IHE | internal hydrogen embrittlement |
| EHE | environmental hydrogen embrittlement |
| HEDE | hydrogen-enhanced decohesion |
| HELP | hydrogen enhanced localized plasticity |
| MD | molecular dynamics |
| EAM | embedded-atom method |
| LAMMPS | large-scale atomic/molecular massively parallel simulator |
| NPT | isothermal–isobaric ensemble |
| CNA | common neighbor analysis |
| CSP | centro-symmetry parameter |
| DXA | dislocation extraction algorithm |
| OVITO | open visualization tool |
References
- Khanna, M. COVID-19: A cloud with a silver Lining for renewable energy? Appl. Econ. Perspect. Policy 2021, 43, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Robertson, I.M.; Sofronis, P.; Nagao, A.; Martin, M.L.; Wang, S.; Gross, D.W.; Nygren, K.E. Hydrogen embrittlement understood. Metall. Mater. Trans. A 2015, 46, 2323–2341. [Google Scholar] [CrossRef]
- Lynch, S. Hydrogen embrittlement phenomena and mechanisms. Corros. Rev. 2012, 30, 105–123. [Google Scholar] [CrossRef]
- Troiano, A.R. The role of hydrogen and other interstitials in the mechanical behavior of metals. Metallogr. Microstruct. Anal. 2016, 5, 557–569. [Google Scholar] [CrossRef]
- Oriani, R. A mechanistic theory of hydrogen embrittlement of steels. Ber. Bunsenges. Phys. Chem. 1972, 76, 848–857. [Google Scholar]
- Lynch, S. Progress towards understanding mechanisms of hydrogen embrittlement and stress corrosion cracking. In Proceedings of the CORROSION 2007, Nashville, TN, USA, 11–15 March 2007; pp. 074931–0749355. [Google Scholar]
- He, S.; Ecker, W.; Pippan, R.; Razumovskiy, V.I. Hydrogen-enhanced decohesion mechanism of the special Σ5 (0 1 2)[1 0 0] grain boundary in Ni with Mo and C solutes. Comput. Mater. Sci. 2019, 167, 100–110. [Google Scholar] [CrossRef]
- Knott, J.F. Fracture toughness and hydrogen-assisted crack. Hydrog. Eff. Mater. 2013, 387, 385–408. [Google Scholar]
- Li, X.; Ma, X.; Zhang, J.; Akiyama, E.; Wang, Y.; Song, X. Review of hydrogen embrittlement in metals: Hydrogen diffusion, hydrogen characterization, hydrogen mechanism and prevention. Acta Metall. Sin. (Engl. Lett.) 2020, 33, 759–773. [Google Scholar] [CrossRef]
- Wasim, M.; Djukic, M.B.; Ngo, T.D. Influence of hydrogen-enhanced plasticity and decohesion mechanisms of hydrogen embrittlement on the fracture resistance of steel. Eng. Fail. Anal. 2021, 123, 105312. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Pei, L.; Zhang, C.; Tieu, K. Influence of solute hydrogen on the interaction of screw dislocations with vicinal twin boundaries in nickel. Scripta Mater. 2019, 173, 115–119. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, Y.; Yang, C.; Hu, H. Fracture strain model for hydrogen embrittlement based on hydrogen enhanced localized plasticity mechanism. Int. J. Hydrogen Energy 2020, 45, 25541–25554. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, C.S.; Kim, M.H.; Lee, J.M. Numerical analysis of hydrogen transport using a hydrogen-enhanced localized plasticity mechanism. Proc. World Acad. Sci. Eng. Technol. 2012, 58, 398–401. [Google Scholar]
- Nagao, A.; Dadfarnia, M.; Somerday, B.P.; Sofronis, P.; Ritchie, R.O. Hydrogen-enhanced-plasticity mediated decohesion for hydrogen-induced intergranular and “quasi-cleavage” fracture of lath martensitic steels. J. Mech. Phys. Solids 2018, 112, 403–430. [Google Scholar] [CrossRef]
- Bechtle, S.; Kumar, M.; Somerday, B.P.; Launey, M.E.; Ritchie, R.O. Grain-boundary engineering markedly reduces susceptibility to intergranular hydrogen embrittlement in metallic materials. Acta Mater. 2009, 57, 4148–4157. [Google Scholar] [CrossRef]
- Martin, M.L.; Dadfarnia, M.; Nagao, A.; Wang, S.; Sofronis, P. Enumeration of the hydrogen-enhanced localized plasticity mechanism for hydrogen embrittlement in structural materials. Acta Mater. 2019, 165, 734–750. [Google Scholar] [CrossRef]
- Oudriss, A.; Creus, J.; Bouhattate, J.; Conforto, E.; Berziou, C.; Savall, C.; Feaugas, X. Grain size and grain-boundary effects on diffusion and trapping of hydrogen in pure nickel. Acta Mater. 2012, 60, 6814–6828. [Google Scholar] [CrossRef]
- He, Y.; Su, Y.; Yu, H.; Chen, C. First-principles study of hydrogen trapping and diffusion at grain boundaries in γ-Fe. Int. J. Hydrogen Energy 2021, 46, 7589–7600. [Google Scholar] [CrossRef]
- Muránsky, O.; Karatchevtseva, I.; Danon, A.E.; Holmes, R.; Huai, P.; Zhang, Z. Impact of dislocations and dislocation substructures on molten salt corrosion of alloys under plasticity-imparting conditions. Corros. Sci. 2020, 176, 108915. [Google Scholar] [CrossRef]
- Ogawa, Y.; Takakuwa, O.; Okazaki, S.; Funakoshi, Y.; Matsuoka, S.; Matsunaga, H. Hydrogen-assisted fatigue crack-propagation in a Ni-based superalloy 718, revealed via crack-path crystallography and deformation microstructures. Corros. Sci. 2020, 174, 108814. [Google Scholar] [CrossRef]
- Ogawa, Y.; Takakuwa, O.; Okazaki, S.; Okita, K.; Funakoshi, Y.; Matsunaga, H.; Matsuoka, S. Pronounced transition of crack initiation and propagation modes in the hydrogen-related failure of a Ni-based superalloy 718 under internal and external hydrogen conditions. Corros. Sci. 2019, 161, 108186. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W. A nanoscale mechanism of hydrogen embrittlement in metals. Acta Mater. 2011, 59, 1557–1569. [Google Scholar] [CrossRef]
- Jothi, S.; Croft, T.; Brown, S. Influence of grain boundary misorientation on hydrogen embrittlement in bi-crystal nickel. Int. J. Hydrogen Energy 2014, 39, 20671–20688. [Google Scholar] [CrossRef]
- Bertsch, K.; Wang, S.; Nagao, A.; Robertson, I. Hydrogen-induced compatibility constraints across grain boundaries drive intergranular failure of Ni. Mater. Sci. Eng. A 2019, 760, 58–67. [Google Scholar] [CrossRef]
- Chen, Y.S.; Lu, H.; Liang, J.; Rosenthal, A.; Liu, H.; Sneddon, G.; Cairney, J.M. Observation of hydrogen trapping at dislocations, grain boundaries, and precipitates. Science 2020, 367, 171–175. [Google Scholar] [CrossRef] [PubMed]
- Griesche, A.; Dabah, E.; Kannengiesser, T.; Kardjilov, N.; Hilger, A.; Manke, I. Three-dimensional imaging of hydrogen blister in iron with neutron tomography. Acta Mater. 2014, 78, 14–22. [Google Scholar] [CrossRef]
- Tehranchi, A.; Curtin, W. Atomistic study of hydrogen embrittlement of grain boundaries in nickel: I. Fracture. J. Mech. Phys. Solids 2017, 101, 150–165. [Google Scholar] [CrossRef]
- Yu, H.; Olsen, J.S.; Olden, V.; Alvaro, A.; He, J.; Zhang, Z. Cohesive zone simulation of grain size and misorientation effects on hydrogen embrittlement in nickel. Eng. Fail. Anal. 2017, 81, 79–93. [Google Scholar] [CrossRef]
- Huang, S.; Chen, D.; Song, J.; McDowell, D.L.; Zhu, T. Hydrogen embrittlement of grain boundaries in nickel: An atomistic study. NPJ Comput. Mater. 2017, 3, 1–8. [Google Scholar] [CrossRef]
- Alvaro, A.; Jensen, I.T.; Kheradmand, N.; Løvvik, O.; Olden, V. Hydrogen embrittlement in nickel, visited by first principles modeling, cohesive zone simulation and nanomechanical testing. Int. J. Hydrogen Energy 2015, 40, 16892–16900. [Google Scholar] [CrossRef]
- Geng, W.; Freeman, A.J.; Wu, R.; Geller, C.; Raynolds, J. Embrittling and strengthening effects of hydrogen, boron, and phosphorus on a Σ 5 nickel grain boundary. Phys. Rev. B 1999, 60, 7149. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Shiga, M.; Kaburaki, H. First-principles study on segregation energy and embrittling potency of hydrogen in niσ5 (012) tilt grain boundary. J. Phys. Soc. Jpn. 2004, 73, 441–449. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Pei, L.; Zhang, C.; Wang, R.; Tieu, K. Atomistic simulations of hydrogen effects on tensile deformation behaviour of [0 0 1] twist grain boundaries in nickel. Comput. Mater. Sci. 2019, 159, 12–23. [Google Scholar] [CrossRef]
- Liang, S.; Huang, M.; Zhao, L.; Zhu, Y.; Li, Z. Effect of multiple hydrogen embrittlement mechanisms on crack propagation behavior of FCC metals: Competition vs. synergy. Int. J. Plast. 2021, 143, 103023. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Pei, L.; Zhang, C.; Wang, R. Atomistic investigation of hydrogen induced decohesion of Ni grain boundaries. Mech. Mater. 2020, 150, 103586. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Angelo, J.E.; Moody, N.R.; Baskes, M.I. Trapping of hydrogen to lattice defects in nickel. Modell. Simul. Mater. Sci. Eng. 1995, 3, 289. [Google Scholar] [CrossRef]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos: Interdiscip. J. Nonlinear Sci. 2009, 19, 041111. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Pei, L.; Zhang, C.; Wang, R.; Tieu, K. Influence of hydrogen environment on dislocation nucleation and fracture response of <1 1 0> grain boundaries in nickel. Comput. Mater. Sci. 2019, 165, 40–50. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Physics 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Schiøtz, J.; Di Tolla, F.D.; Jacobsen, K.W. Softening of nanocrystalline metals at very small grain sizes. Nature 1998, 391, 561–563. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.; Hamilton, J. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Dislocation detection algorithm for atomistic simulations. Model. Simul. Mater. Sci. Eng. 2010, 18, 025016. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Mori, T.; Miura, H.; Tokita, T.; Haji, J.; Kato, M. Determination of the energies of [001] twist boundaries in Cu with the shape of boundary SiO2 particles. Philos. Mag. Lett. 1988, 58, 11–15. [Google Scholar] [CrossRef]
- Spearot, D.E.; Sangid, M.D. Insights on slip transmission at grain boundaries from atomistic simulations. Curr. Opin. Solid State Mater. Sci. 2014, 18, 188–195. [Google Scholar] [CrossRef]
- Wolf, D.; Phillpot, S. Role of the densest lattice planes in the stability of crystalline interfaces: A computer simulation study. Mater. Sci. Eng. A 1989, 107, 3–14. [Google Scholar] [CrossRef]
- Harris, T.; Latanision, M. Grain boundary diffusion of hydrogen in nickel. Metall. Trans. A 1991, 22, 351–355. [Google Scholar] [CrossRef]
- Ding, Y.; Yu, H.; Zhao, K.; Lin, M.; Xiao, S.; Ortiz, M.; Zhang, Z. Hydrogen-induced transgranular to intergranular fracture transition in bi-crystalline nickel. Scr. Mater. 2021, 204, 114122. [Google Scholar] [CrossRef]
- Yan, F.; Mouton, I.; Stephenson, L.T.; Breen, A.J.; Chang, Y.; Ponge, D.; Gault, B. Atomic-scale investigation of hydrogen distribution in a TiMo alloy. Scr. Mater. 2019, 162, 321–325. [Google Scholar] [CrossRef]
- Hahn, E.N.; Meyers, M.A. Grain-size dependent mechanical behavior of nanocrystalline metals. Mater. Sci. Eng. A 2015, 646, 101–134. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Tucker, G.J.; McDowell, D.L. Structure and free volume of <1 1 0> symmetric tilt grain boundaries with the E structural unit. Acta Mater. 2007, 55, 3959–3969. [Google Scholar] [CrossRef]
- Robertson, I.M.; Birnbaum, H.K.; Sofronis, P. Hydrogen effects on plasticity. Dislocations Solids 2009, 15, 249–293. [Google Scholar]
- Robertson, I.M. The effect of hydrogen on dislocation dynamics. Eng. Fract. Mech. 2001, 68, 671–692. [Google Scholar] [CrossRef]
- Martin, M.L.; Somerday, B.P.; Ritchie, R.O.; Sofronis, P.; Robertson, I.M. Hydrogen-induced intergranular failure in nickel revisited. Acta Mater. 2012, 60, 2739–2745. [Google Scholar] [CrossRef]
- Wang, S.; Martin, M.L.; Sofronis, P.; Ohnuki, S.; Hashimoto, N.; Robertson, I.M. Hydrogen-induced intergranular failure of iron. Acta Mater. 2014, 69, 275–282. [Google Scholar] [CrossRef]
- Ferreira, P.J.; Robertson, I.M.; Birnbaum, H.K. Hydrogen effects on the character of dislocations in high-purity aluminum. Acta Mater. 1999, 47, 2991–2998. [Google Scholar] [CrossRef]
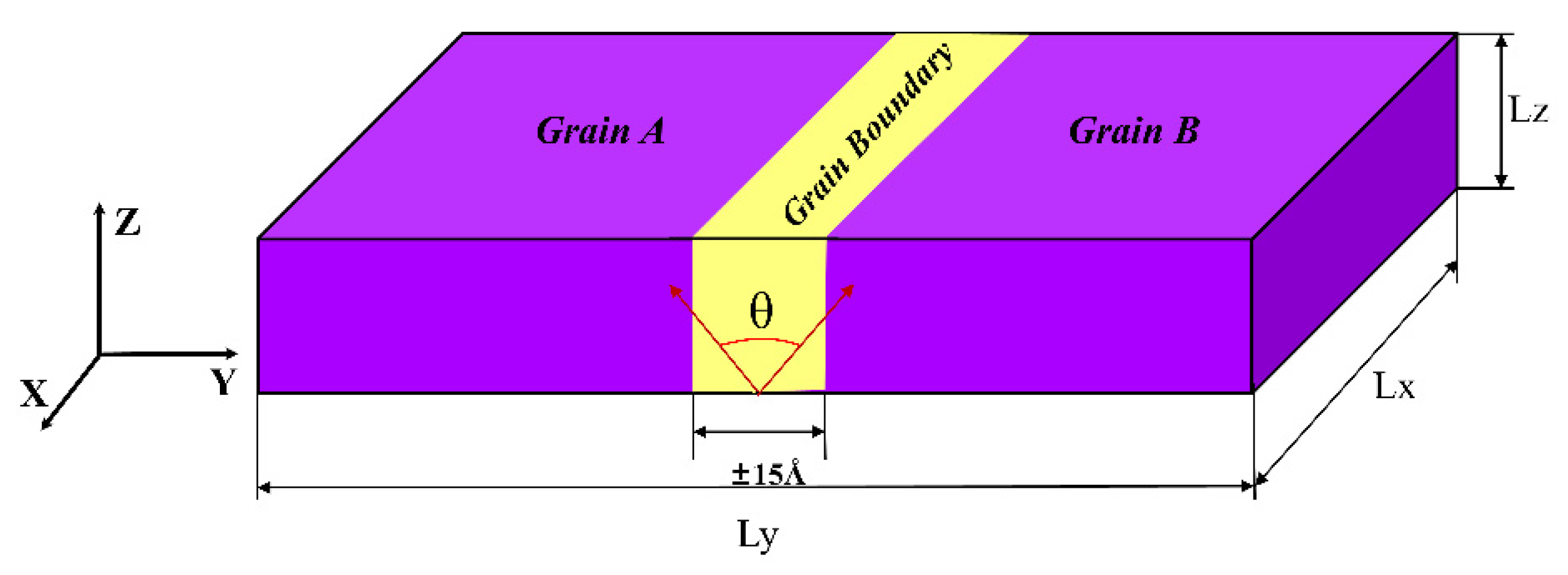
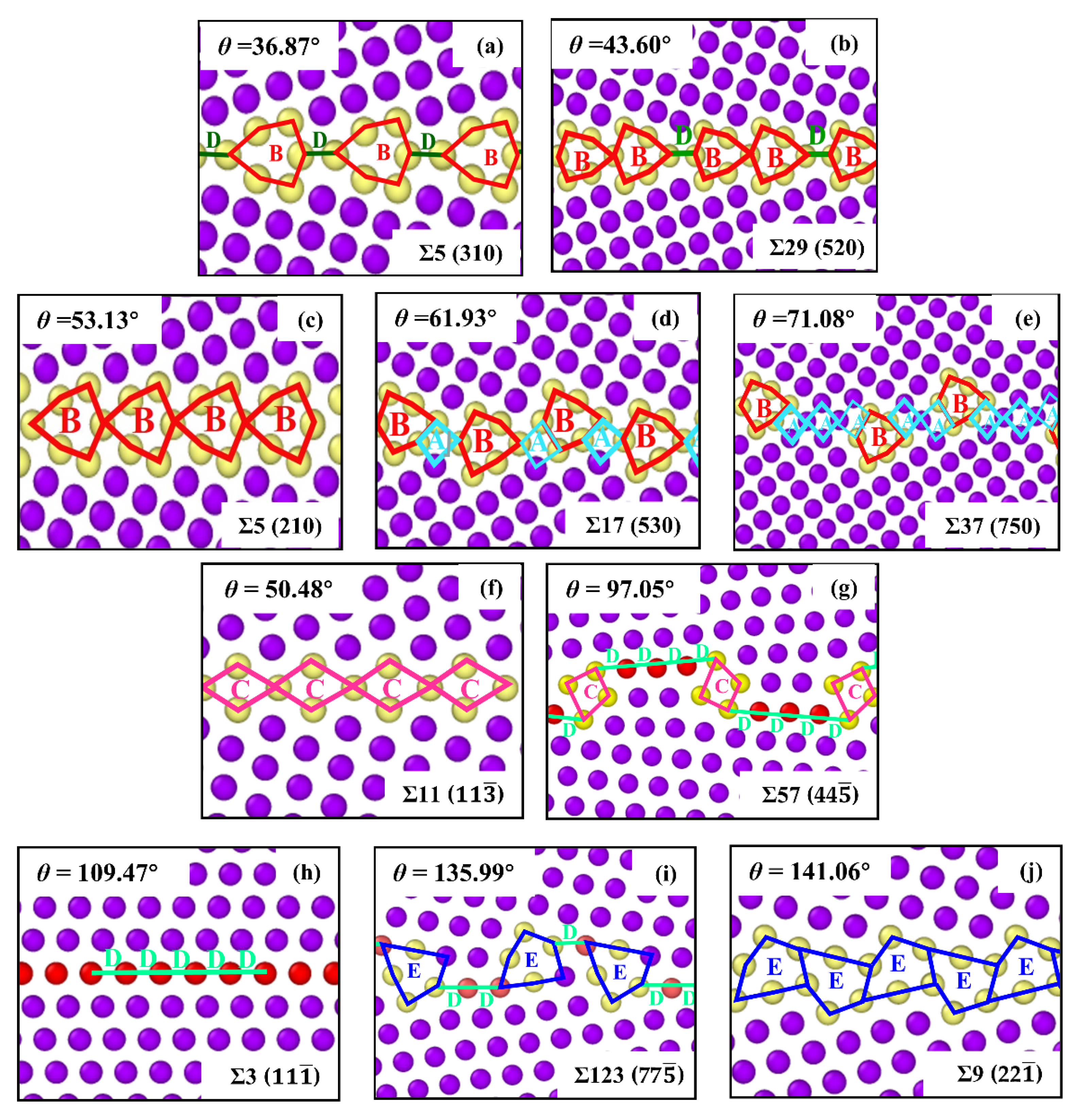

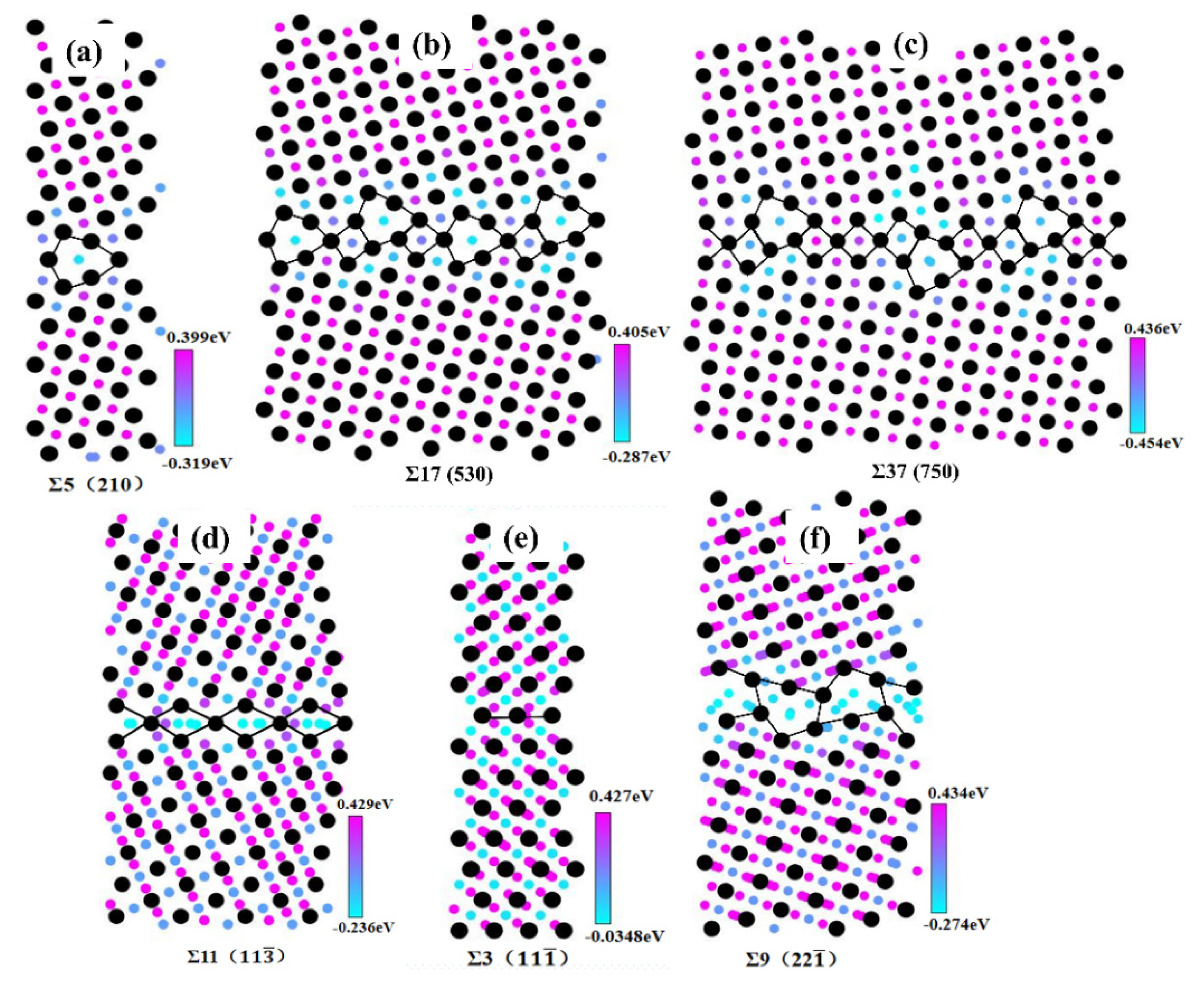



| GB Type | Angle | Model Size | GB Structure | GB Energy |
|---|---|---|---|---|
| θ (°) | ||||
| Σ5 () | 36.87° | 11.13 × 22.26 × 3.52 | |DBDB| | 1126.25 |
| Σ29 () | 43.60° | 15.16 × 22.75 × 3.52 | |BBD| | 1240.23 |
| Σ5 () | 53.13° | 15.74 × 22.04 × 3.52 | |BBB| | 1183.13 |
| Σ17 () | 61.93° | 16.42 × 24.63 × 3.52 | |BABA| | 1110.48 |
| Σ37 () | 71.08° | 15.14 × 24.24 × 3.52 | |BAAABAA| | 999.80 |
| Σ11 () | 50.48° | 13.21 × 23.35 × 4.98 | |CC| | 375.83 |
| Σ57 (4 4) | 97.05° | 18.79 × 26.58 × 4.98 | |CD| | 731.83 |
| Σ3 () | 109.47° | 16.38 × 23.17 × 4.98 | |DDDD| | 50.38 |
| Σ123 (7) | 135.99° | 11.04 × 23.42 × 4.98 | |EDDED| | 860.61 |
| Σ9 (2 2) | 141.06° | 11.95 × 23.23 × 4.98 | |EE| | 1097.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wu, Z.; Teng, L.; Deng, G.; Wang, R.; Lu, C.; Li, W.; Huang, X.; Liu, Y.
Hydrogen-Induced Dislocation Nucleation and Plastic Deformation of
Li J, Wu Z, Teng L, Deng G, Wang R, Lu C, Li W, Huang X, Liu Y.
Hydrogen-Induced Dislocation Nucleation and Plastic Deformation of
Li, Jiaqing, Ziyue Wu, Lin Teng, Guanyu Deng, Rui Wang, Cheng Lu, Weidong Li, Xin Huang, and Yu Liu.
2022. "Hydrogen-Induced Dislocation Nucleation and Plastic Deformation of
Li, J., Wu, Z., Teng, L., Deng, G., Wang, R., Lu, C., Li, W., Huang, X., & Liu, Y.
(2022). Hydrogen-Induced Dislocation Nucleation and Plastic Deformation of










