Mechanical Properties Study of Miniature Steel Specimens Based on the Small Punch Test and Simulation Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Uniaxial Tensile Test
2.3. Small Punch Test
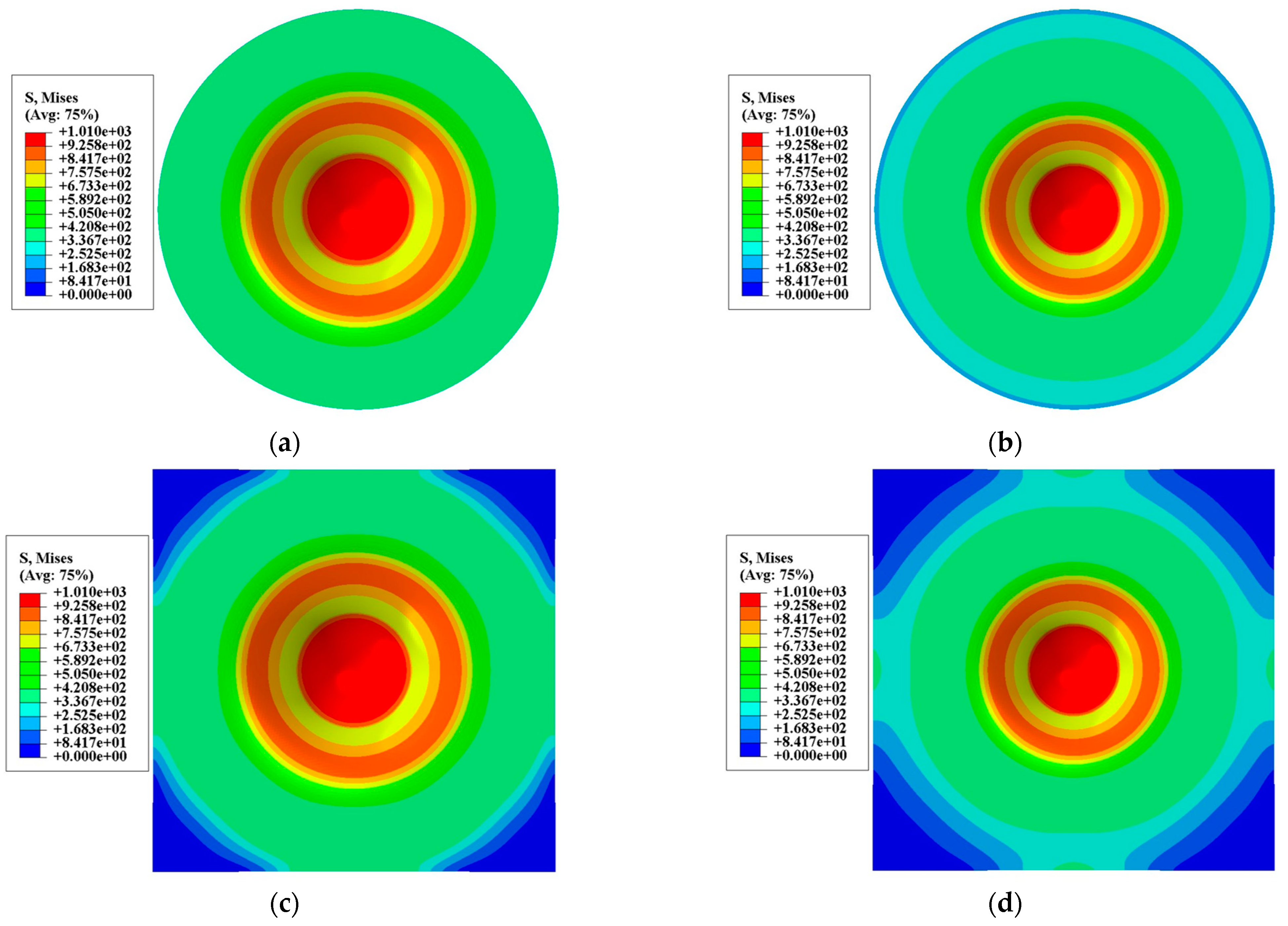
2.4. FE Model and Numerical Simulation
3. Results
3.1. SPT Experiment Results
3.2. SPT Simulation Results
3.3. Calibration of Loading System Compliance
4. Discussion
4.1. Correlation between SPT Curve and Tensile Properties before and after Compliance Calibration
4.1.1. Correlation with Ultimate Tensile Strength (σUTS)
4.1.2. Correlation with Yield Stress (σYS)
4.2. Effect of Different Specimen Sizes on SPT Curve
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Manahan, M.P.; Argon, A.S.; Harling, O.K. The development of a miniaturized disk bend test for the determination of postirradiation mechanical properties. J. Nucl. Mater. 1981, 104, 1545–1550. [Google Scholar] [CrossRef]
- Nowik, K.; Oksiuta, Z. Experimental and numerical small punch tests of the 14Cr ODS ferritic steel. Acta Mechanica et Automatica 2022, 16, 225–232. [Google Scholar] [CrossRef]
- Bruchhausen, M.; Holmström, S.; Simonovski, I.; Austin, T.; Lapetite, J.M.; Ripplinger, S.; de Haan, F. Recent developments in small punch testing: Tensile properties and DBTT. Theor. Appl. Fract. Mech. 2016, 86, 2–10. [Google Scholar] [CrossRef]
- Cheng, Z.Y.; Sun, J.R.; Tai, P.F.; Zhang, L.Q.; Wei, Y.T.; Chang, H.L.; Thuku, R.; Gichuhi, K.M. Comparative Study between Small Punch Tests and Finite Element Analysis of Miniature Steel Specimens. J. Mater. Eng. Perform. 2021, 30, 9094–9107. [Google Scholar] [CrossRef]
- Cao, Y.; Zu, Y.; Zhen, Y.; Li, F.; Wu, G. Determination of the true stress-strain relations of high-grade pipeline steels based on small punch test correlation method. Int. J. Pres. Ves. Pip. 2022, 199, 104739. [Google Scholar] [CrossRef]
- Contreras, M.A.; Rodriguez, C.; Belzunce, F.J.; Betegon, C. Use of the small punch test to determine the ductile-to-brittle transition temperature of structural steels. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 727–737. [Google Scholar] [CrossRef]
- Ha, J.S.; Fleury, E. Small punch tests to estimate the mechanical properties of steels for steam power plant: II. Fracture toughness. Int. J. Pres. Ves. Pip. 1998, 75, 707–713. [Google Scholar] [CrossRef]
- Lancaster, R.J.; Jeffs, S.P.; Illsley, H.W.; Argyrakis, C.; Hurst, R.C.; Baxter, G.J. Development of a novel methodology to study fatigue properties using the small punch test. Mater. Sci. Eng. A 2019, 748, 21–29. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Xu, L.Y.; Han, Y.D.; Jing, H.Y. Fatigue performance of Hastelloy X at elevated temperature via small punch fatigue test. Theor. Appl. Fract. Mech. 2021, 116, 103118. [Google Scholar] [CrossRef]
- Lewis, D.T.S.; Lancaster, R.J.; Jeffs, S.P.; Illsley, H.W.; Davies, S.J.; Baxter, G.J. Characterising the fatigue performance of additive materials using the small punch test. Mater. Sci. Eng. A 2019, 754, 719–727. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.W. Relationship between strain and central deflection in small punch creep specimens. Int. J. Pres. Ves. Pip. 2003, 80, 397–404. [Google Scholar] [CrossRef]
- Rouse, J.P.; Cortellino, F.; Sun, W.; Hyde, T.H.; Shingledecker, J. Small punch creep testing: Review on modelling and data interpretation. Mater. Sci. Technol. 2013, 29, 1328–1345. [Google Scholar] [CrossRef]
- Dymáček, P. Recent developments in small punch testing: Applications at elevated temperatures. Theor. Appl. Fract. Mech. 2016, 86, 25–33. [Google Scholar] [CrossRef]
- Yoon, K.B.; Nguyen, T.T. Estimation of high-temperature fracture parameters for small punch specimen with a surface crack. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1224–1236. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yoon, K.B. Fully plastic J-integral and C* equations for small punch test specimen with a surface crack. Int. J. Pres. Ves. Pip. 2020, 188, 104214. [Google Scholar] [CrossRef]
- Li, Y.Z.; Dymacek, P.; Hurst, R.; Stevens, P. A novel methodology for determining creep crack initiation and growth properties using FEM with notched small punch specimens. Theor. Appl. Fract. Mech. 2021, 116, 103112. [Google Scholar] [CrossRef]
- Chittibabu, V.; Rao, K.S.; Rao, P.G. Factors affecting the mechnical properties of compact bone and miniature specimen test techniques: A review. Adv. Sci. Technol. Res. J. 2016, 10, 169–183. [Google Scholar] [CrossRef]
- Gulcimen, B.; Hahner, P. Determination of creep properties of a P91 weldment by small punch testing and a new evaluation approach. Mater. Sci. Eng. A 2013, 588, 125–131. [Google Scholar] [CrossRef]
- Wen, W.; Jackson, G.A.; Li, H.; Sun, W. An experimental and numerical study of a CoNiCrAlY coating using miniature specimen testing techniques. Int. J. Mech. Sci. 2019, 157, 348–356. [Google Scholar] [CrossRef]
- Soltysiak, S.; Selent, M.; Roth, S.; Abendroth, M.; Hoffmann, M.; Biermann, H.; Kuna, M. High-temperature small punch test for mechanical characterization of a nickel-base super alloy. Mater. Sci. Eng. A 2014, 613, 259–263. [Google Scholar] [CrossRef]
- EN 10371; Metallic Materials–Small Punch Test Method. European Committee for Standardization: Brussel, Belgium, 2021.
- CWA 15627; Small Punch Test method for Metallic Materials. European Committee for Standardization: Brussel, Belgium, 2007.
- GB/T 29459.1; Small Punch Test Methods of Metallic Materials for In-Service Pressure Equipments—Part 1: General Requirements. Chinese Standard: Beijing, China, 2012.
- GB/T 29459.2; Small Punch Test Methods of Metallic Materials for In-Service Pressure Equipments—Part 2: Method of Test for Tensile Properties at Room Temperature. Chinese Standard: Beijing, China, 2012.
- ASTM E3205; Standard Test Method for Small Punch Testing of Metallic Materials. ANSI: New York, NY, USA, 2022.
- Kalidindi, S.R.; Abusafieh, A.; El-Danaf, E. Accurate characterization of machine compliance for simple compression testing. Exp. Mech. 1997, 37, 210–215. [Google Scholar] [CrossRef]
- Sánchez-Ávila, D.; Orozco-Caballero, A.; Martinez, E.; Portoles, L.; Barea, R.; Carreno, F. High-accuracy compliance correction for nonlinear mechanical testing: Improving Small Punch Test characterization. Nucl. Mater. Energy 2021, 26, 100914. [Google Scholar] [CrossRef]
- Janca, A.; Siegl, J.; Hausild, P. Small punch test evaluation methods for material characterisation. J. Nucl. Mater. 2016, 481, 201–213. [Google Scholar] [CrossRef]
- Altstadt, E.; Houska, M.; Simonovski, I.; Bruchhausen, M.; Holmström, S.; Lacalle, R. On the estimation of ultimate tensile stress from small punch testing. Int. J. Mech. Sci. 2018, 136, 85–93. [Google Scholar] [CrossRef]
- Altstadt, E.; Ge, H.E.; Kuksenko, V.; Serrano, M.; Houska, M.; Lasan, M.; Bruchhausen, M.; Lapetite, J.M.; Dai, Y. Critical evaluation of the small punch test as a screening procedure for mechanical properties. J. Nucl. Mater. 2016, 472, 186–195. [Google Scholar] [CrossRef]
- Lucas, G.E.; Okada, A.; Kiritani, M. Parametric analysis of the disc bend test. J. Nucl. Mater. 1986, 141, 532–535. [Google Scholar] [CrossRef]
- Campitelli, E.N.; Spatig, P.; Bonade, R.; Hoffelner, W.; Victoria, M. Assessment of the constitutive properties from small ball punch test: Experiment and modeling. J. Nucl. Mater. 2004, 335, 366–378. [Google Scholar] [CrossRef]
- Xu, T.; Guan, K.S.; Wang, Z.W. Study on standardization of small punch test (1)—general requirements. Press. Vessel. Technol. 2010, 27, 37–46. (In Chinese) [Google Scholar]
- Zhou, Z.X.; Ling, X. Ductile Damage Analysis for Small Punch Specimens of Type 304 Stainless Steel Based on GTN Model. J. Test. Eval. 2009, 37, 538–544. [Google Scholar]
- Andrés, D.; Dymacek, P. Study of the upper die clamping conditions in the small punch test. Theor. Appl. Fract. Mech. 2016, 86, 117–123. [Google Scholar] [CrossRef]
- Peng, J.; Vijayanand, V.D.; Knowles, D.; Truman, C.; Mostafavi, M. The sensitivity ranking of ductile material mechanical properties, geometrical factors, friction coefficients and damage parameters for small punch test. Int. J. Pres. Ves. Pip. 2021, 193, 104468. [Google Scholar] [CrossRef]
- Moreno, M.F. Effects of thickness specimen on the evaluation of relationship between tensile properties and small punch testing parameters in metallic materials. Mater. Des. 2018, 157, 512–522. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, H.; Wang, Y.Q.; Richardson, M.; Liu, X.D.; Knowles, D.; Mostafavi, M. Correlation study on tensile properties of Cu, CuCrZr and W by small punch test and uniaxial tensile test. Fusion Eng. Des. 2022, 177, 113061. [Google Scholar] [CrossRef]
- Moreno, M.F.; Bertolino, G.; Yawny, A. The significance of specimen displacement definition on the mechanical properties derived from Small Punch Test. Mater. Des. 2016, 95, 623–631. [Google Scholar] [CrossRef]
- Hähner, P.; Soyarslan, C.; Cakan, B.G.; Bargmann, S. Determining tensile yield stresses from Small Punch tests: A numerical-based scheme. Mater. Des. 2019, 182, 107974. [Google Scholar] [CrossRef]
- Guo, J.Q.; Tang, C.Z.Z.; Lai, H.S. Microstructure and Mechanical Properties of Co32Cr28Ni32.94Al4.06Ti3 High-Entropy Alloy. Materials 2022, 15, 1444. [Google Scholar] [CrossRef]
- ABAQUS Users Manual, Version 6.10-1; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2010.
- Chica, J.C.; Diez, P.M.B.; Calzada, M.P. Development of an improved prediction method for the yield strength of steel alloys in the Small Punch Test. Mater. Des. 2018, 148, 153–166. [Google Scholar] [CrossRef]
- Barsanescu, P.D.; Comanici, A.M. von Mises hypothesis revised. Acta. Mech. 2017, 228, 433–446. [Google Scholar] [CrossRef]
- Von Mises, R. Mechanik der festen Körper im plastisch deformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1913, 1913, 582–592. [Google Scholar]
- Chica, J.C.; Diez, P.M.B.; Calzada, M.P. Improved correlation for elastic modulus prediction of metallic materials in the Small Punch Test. Int. J. Mech. Sci. 2017, 134, 112–122. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Al Hattamleh, O.; Almuflih, A.S. Optimization of the Structural Performance of Buried Reinforced Concrete Pipelines in Cohesionless Soils. Materials 2022, 15, 4051. [Google Scholar] [CrossRef]
- Almasabha, G.; Alshboul, O.; Shehadeh, A.; Almuflih, A.S. Machine Learning Algorithm for Shear Strength Prediction of Short Links for Steel Buildings. Buildings 2022, 12, 775. [Google Scholar]
- Lucon, E.; Benzing, J.; Hrabe, N. Development and Validation of Small Punch Testing at NIST; US Department of Commerce National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020.
- Garcia, T.E.; Rodriguez, C.; Belzunce, F.J.; Suarez, C. Estimation of the mechanical properties of metallic materials by means of the small punch test. J. Alloys Compd. 2014, 582, 708–717. [Google Scholar] [CrossRef]
- Mao, X.Y.; Takahashi, H. Development of a Further-Miniaturized Specimen of 3 Mm Diameter for Tem Disk (Phi-3 Mm) Small Punch Tests. J. Nucl. Mater. 1987, 150, 42–52. [Google Scholar] [CrossRef]
- Rodriguez, C.; Cabezas, J.G.; Cardenas, E.; Belzunce, F.J.; Betegon, C. Mechanical Properties Characterization of Heat-Affected Zone Using the Small Punch Test. Weld. J. 2009, 88, 188–192. [Google Scholar]
- Lancaster, R.J.; Jeffs, S.P.; Haigh, B.J.; Barnard, N.C. Derivation of material properties using small punch and shear punch test methods. Mater. Des. 2022, 215, 110473. [Google Scholar] [CrossRef]















| Steel | Chemical Composition (wt%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Cr | Mo | Ni | Nb | |
| 316L | 0.015 | 0.70 | 0.54 | 0.02 | 0.007 | 16.53 | 2 | 11.55 | — |
| 347L | 0.04 | 0.75 | 1.97 | 0.02 | 0.01 | 18.5 | — | 11.0 | 0.95 |
| Composition | Co | Cr | Ni | Al | Ti |
|---|---|---|---|---|---|
| Atomic ratio (%) | 32 | 28 | 32.94 | 4.06 | 3 |
| Weight ratio (%) | 34.11 | 26.34 | 34.97 | 1.98 | 2.60 |
| Materials | Yield Stress (σYS)/MPa | Ultimate Tensile Strength (σUTS)/MPa | Uniform Elongation (ε)/% |
|---|---|---|---|
| 316L | 350 | 635 | 58.1 |
| 347L | 320 | 540 | 9.5 |
| Co32Cr28Ni32.94Al4.06Ti3 | 530 | 985 | 37.2 |
| Set No. | Specimen Type | Specimen Diameter d (mm) | Punch Radius r (mm) | Receiving Hole Radius D (mm) | Specimen Thickness h0 (mm) | Edge Type |
|---|---|---|---|---|---|---|
| 2D | round | 10 mm | 1.25 mm | 4 mm | 0.5 mm | Full clamped |
| 3D | round | 10 mm/8 mm | 1.25 mm | 4 mm | 0.5 mm | Full clamped |
| 3D | square | 10 mm/8 mm | 1.25 mm | 4 mm | 0.5 mm | Full clamped |
| Compliance | Steel | um (mm) | Fm/h02 (MPa) | Fm/(h0·um) (Mpa) |
|---|---|---|---|---|
| Before | 316L | 1.70 | 8720 | 2565 |
| 347L | 2.14 | 8000 | 1869 | |
| Co32Cr28Ni32.94Al4.06Ti3 | 2.40 | 12,212 | 2544 | |
| After | 316L | 2.10 | 8748 | 2573 |
| 347L | 1.83 | 8088 | 2573 | |
| Co32Cr28Ni32.94Al4.06Ti3 | 2.19 | 12,268 | 2800 |
| Compliance | Steel | Fy_Mao/h02 (MPa) | Fy_CEN/h02 (MPa) | Fy_t/10/h02 (MPa) | Fy_t/100/h02 (MPa) |
|---|---|---|---|---|---|
| Before | 316L | 768 | 684 | 868 | 548 |
| 347L | 956 | 928 | 1173 | 845 | |
| Co32Cr28Ni32.94Al4.06Ti3 | 1410 | 1372 | 1710 | 1321 | |
| After | 316L | 760 | 668 | 788 | 560 |
| 347L | 895 | 797 | 1141 | 756 | |
| Co32Cr28Ni32.94Al4.06Ti3 | 1323 | 1253 | 1652 | 1202 |
| β1 | β2 | Materials | Method | Reference |
|---|---|---|---|---|
| 0.36 | - | SUS316, PCA, HT-60, A533B, HT-9 | Fy_Mao | Mao and Takahashi [51] |
| 0.39 | - | 316L and F82H | Fy_CEN | Campitelli et al. [32] |
| 0.38 | - | HAZ of 30CrMo5-2 | Fy_CEN | Rodriguez et al. [52] |
| 0.364 | - | Different steels and Al alloy | Fy_t/10 | Garcia et al. [50] |
| 0.442 | - | Different steels and Al alloy | Fy_CEN | Garcia et al. [50] |
| 0.476 | - | Different steels and Al alloy | Fy_Mao | Garcia et al. [50] |
| 0.349 | 133.48 | Ti-6Al-4V, Stainless Steel, Cu, Al, In718 | Fy_Mao | Lancaster et al. [53] |
| Material | Specimen Diameter (mm) | Specimen Shape | ||
|---|---|---|---|---|
| 316L | 8 | 10 | Round specimen | Square specimen |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Guo, Z.; Liu, K. Mechanical Properties Study of Miniature Steel Specimens Based on the Small Punch Test and Simulation Methods. Materials 2022, 15, 6542. https://doi.org/10.3390/ma15196542
Zhang J, Guo Z, Liu K. Mechanical Properties Study of Miniature Steel Specimens Based on the Small Punch Test and Simulation Methods. Materials. 2022; 15(19):6542. https://doi.org/10.3390/ma15196542
Chicago/Turabian StyleZhang, Jingwei, Zijian Guo, and Kanglin Liu. 2022. "Mechanical Properties Study of Miniature Steel Specimens Based on the Small Punch Test and Simulation Methods" Materials 15, no. 19: 6542. https://doi.org/10.3390/ma15196542
APA StyleZhang, J., Guo, Z., & Liu, K. (2022). Mechanical Properties Study of Miniature Steel Specimens Based on the Small Punch Test and Simulation Methods. Materials, 15(19), 6542. https://doi.org/10.3390/ma15196542






