Heat Transfer Analysis of 3D Printed Wax Injection Mold Used in Investment Casting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Background
2.1.1. Fourier Law
2.1.2. The Navier–Stokes Equation
2.1.3. Nonisothermal Flow
2.2. Experimental Values of Material Properties
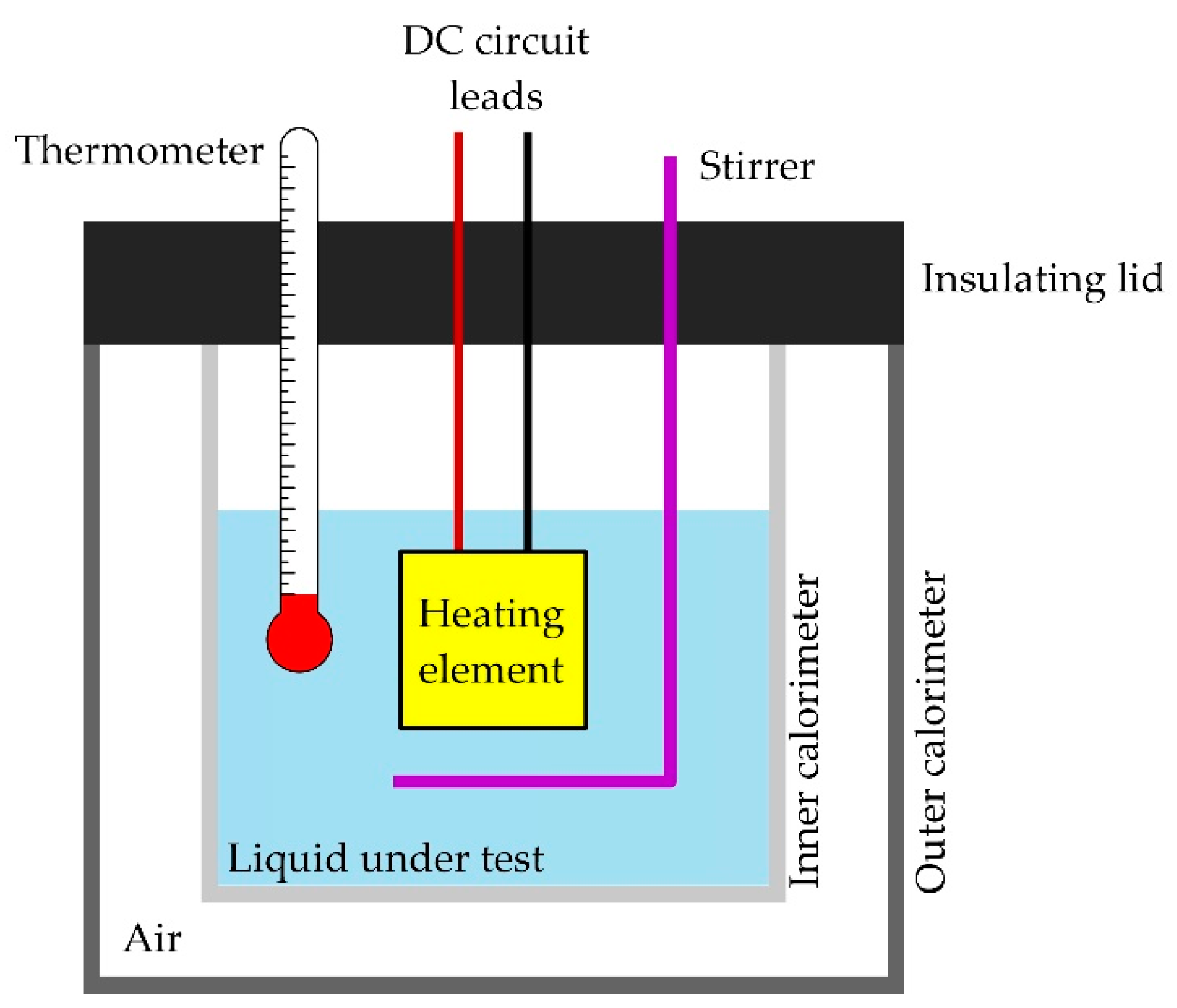
2.2.1. Determination of Thermal Conductivity
2.2.2. Determination of Specific Heat
2.3. Computational Model
2.3.1. The Finite Element Method (FEM)
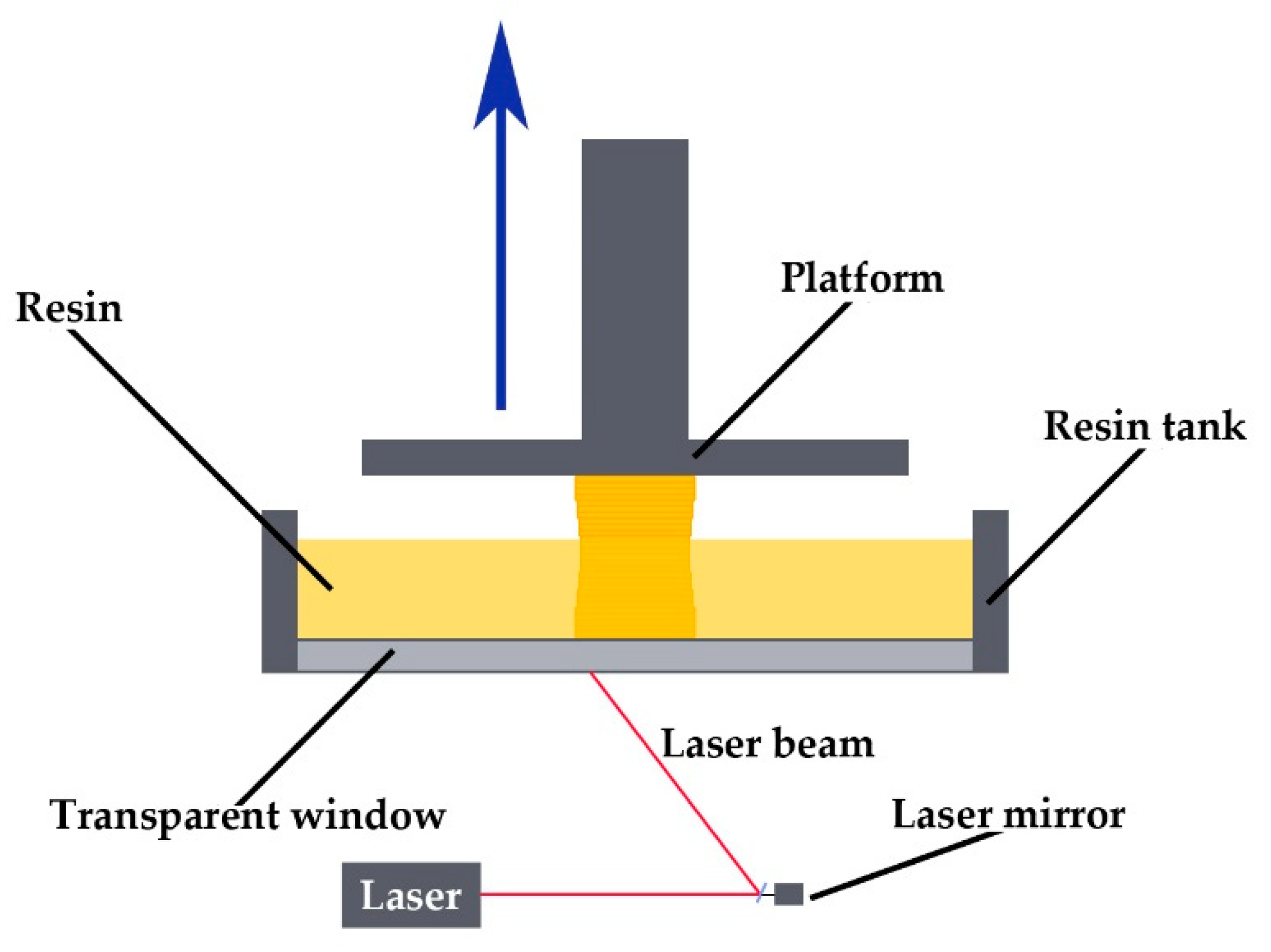
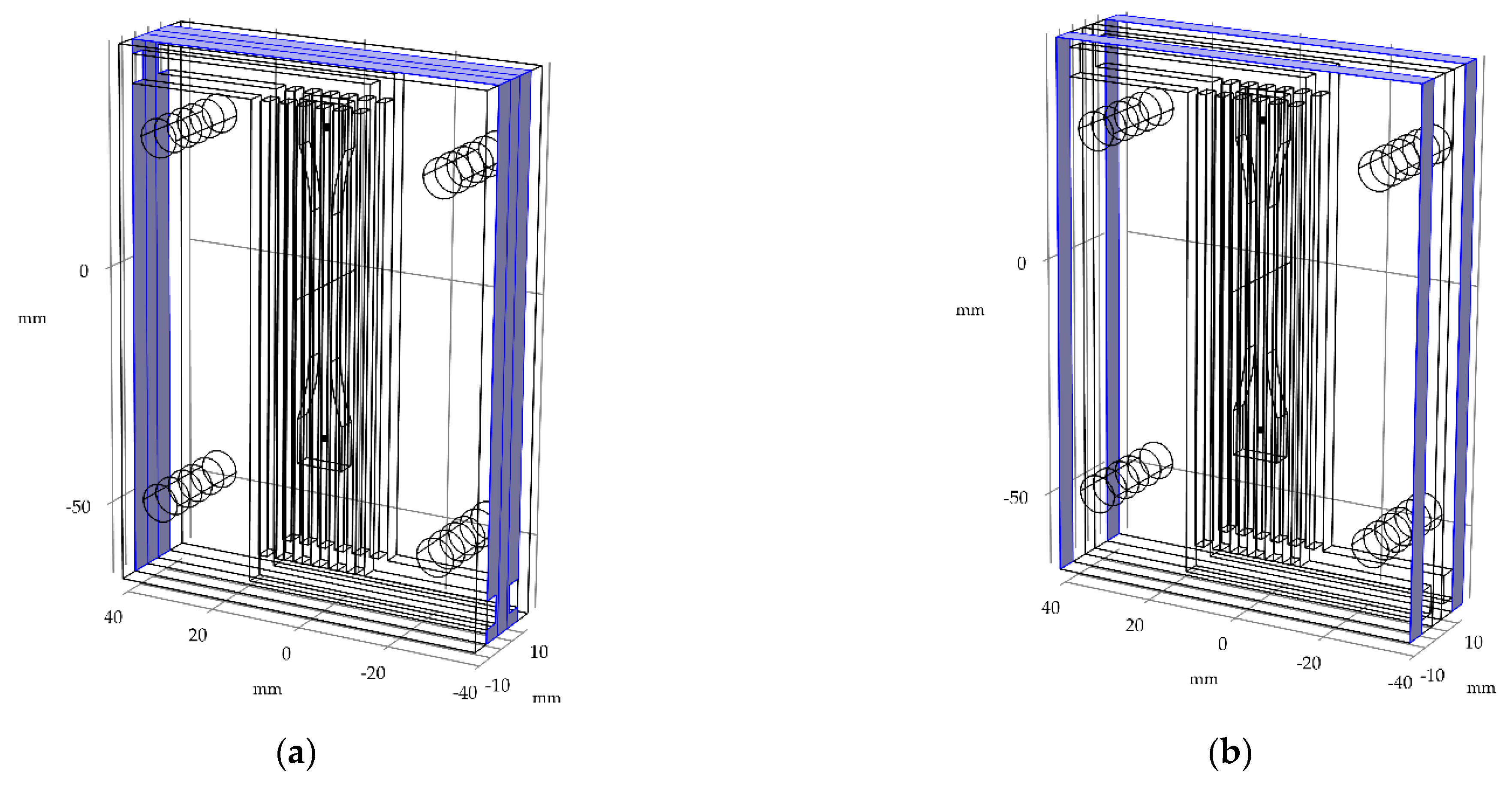
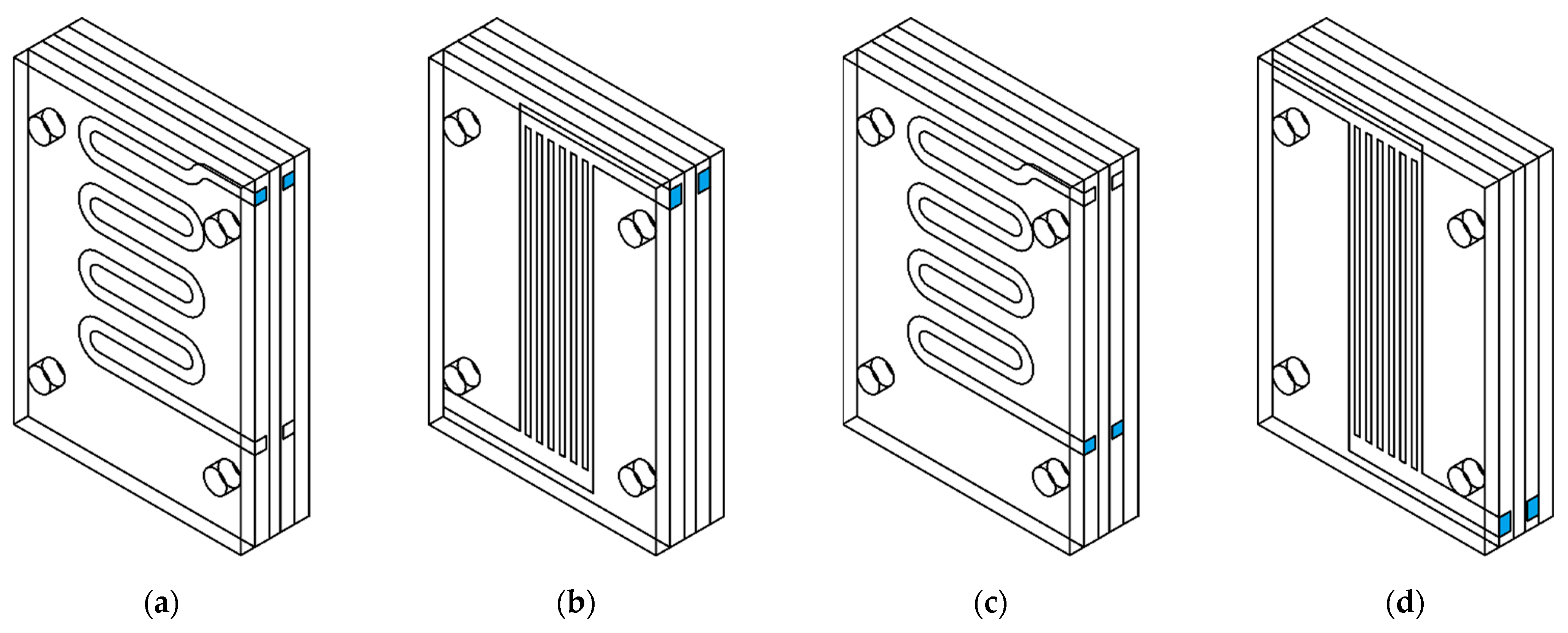
2.3.2. Model and Wax Injection Mold
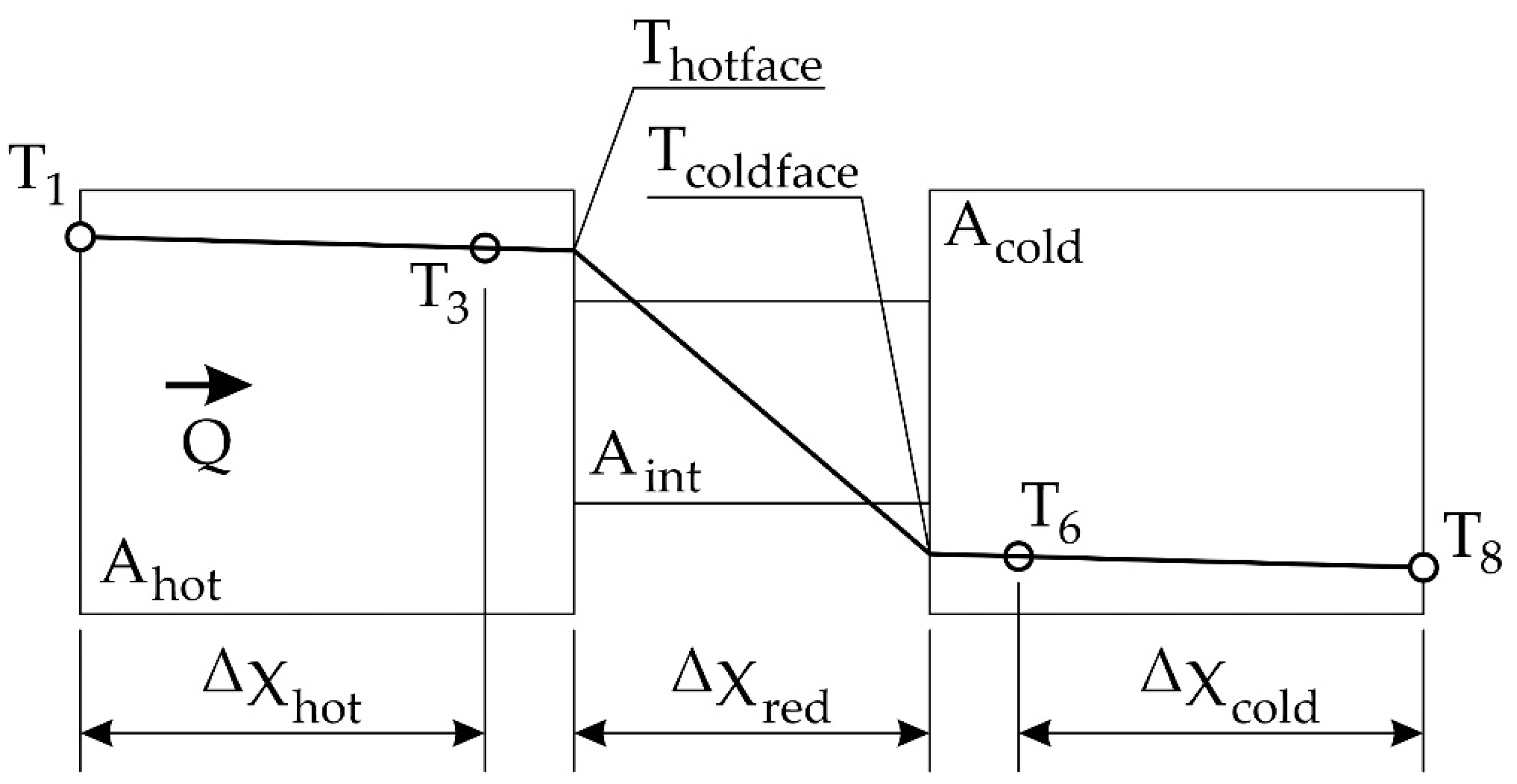
2.3.3. Boundary Conditions
Heat Transfer Boundary Conditions
Fluid Flow Boundary Conditions
2.3.4. Meshing
2.3.5. Simulation and Material Settings
3. Results and Discussion
3.1. The Measured Thermal Parameters of Materials
3.1.1. Thermal Conductivity
3.1.2. The Specific Heat
3.2. Wax Injection Molds without Cooling Channels
3.3. Wax Injection Molds with Different Variation of Cooling Channel
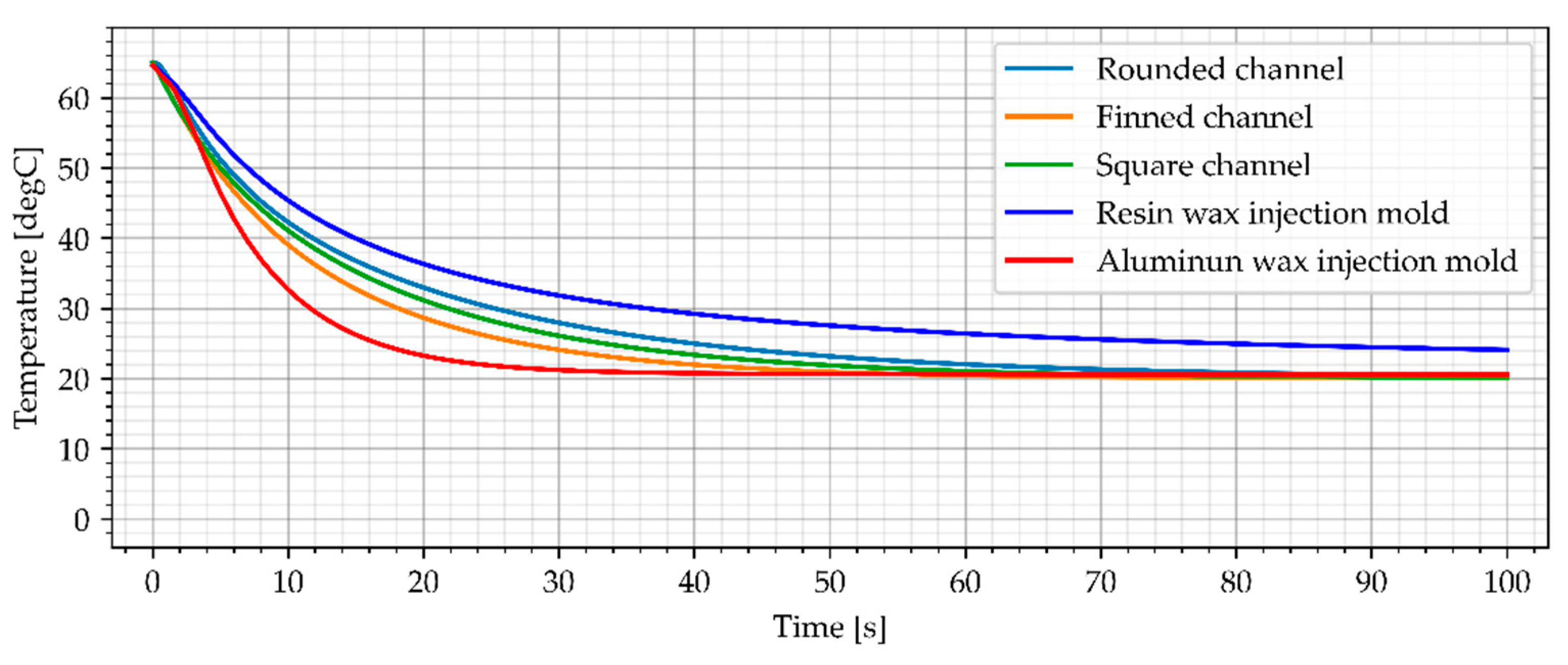
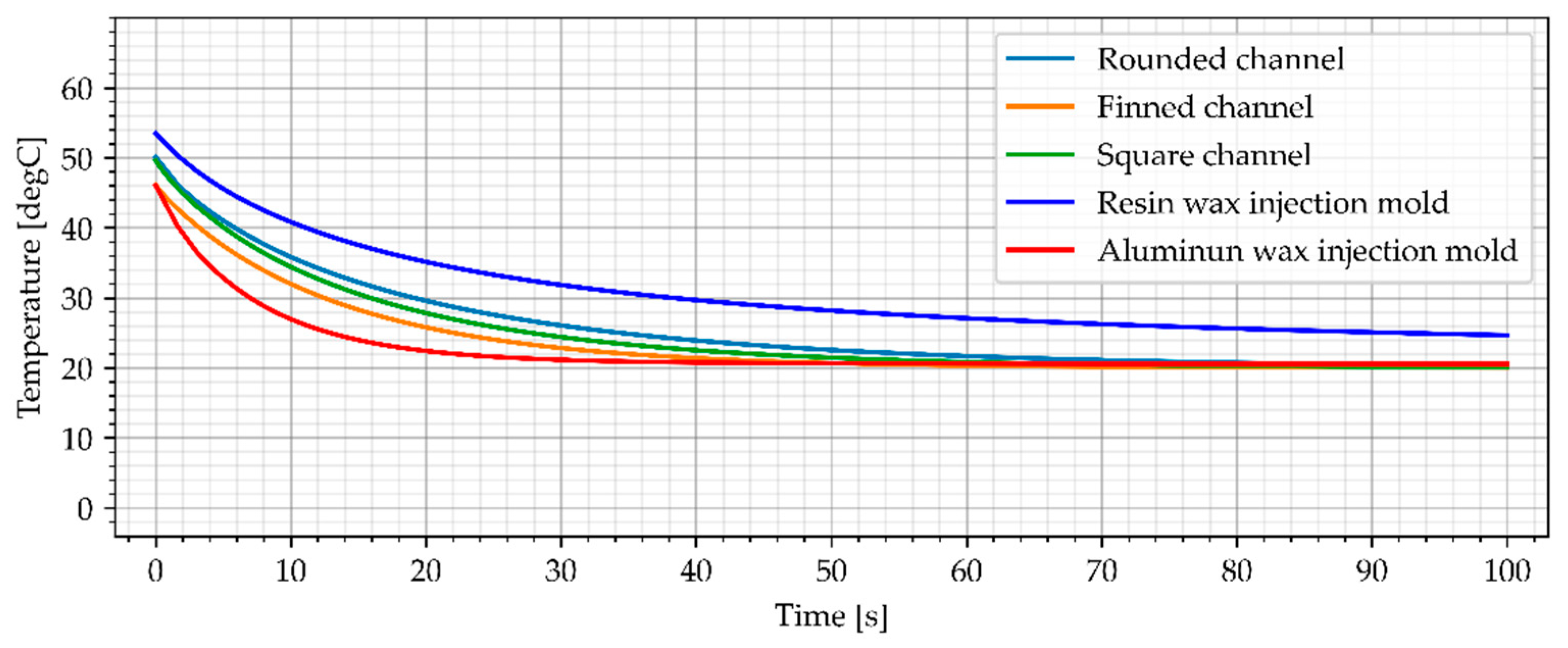
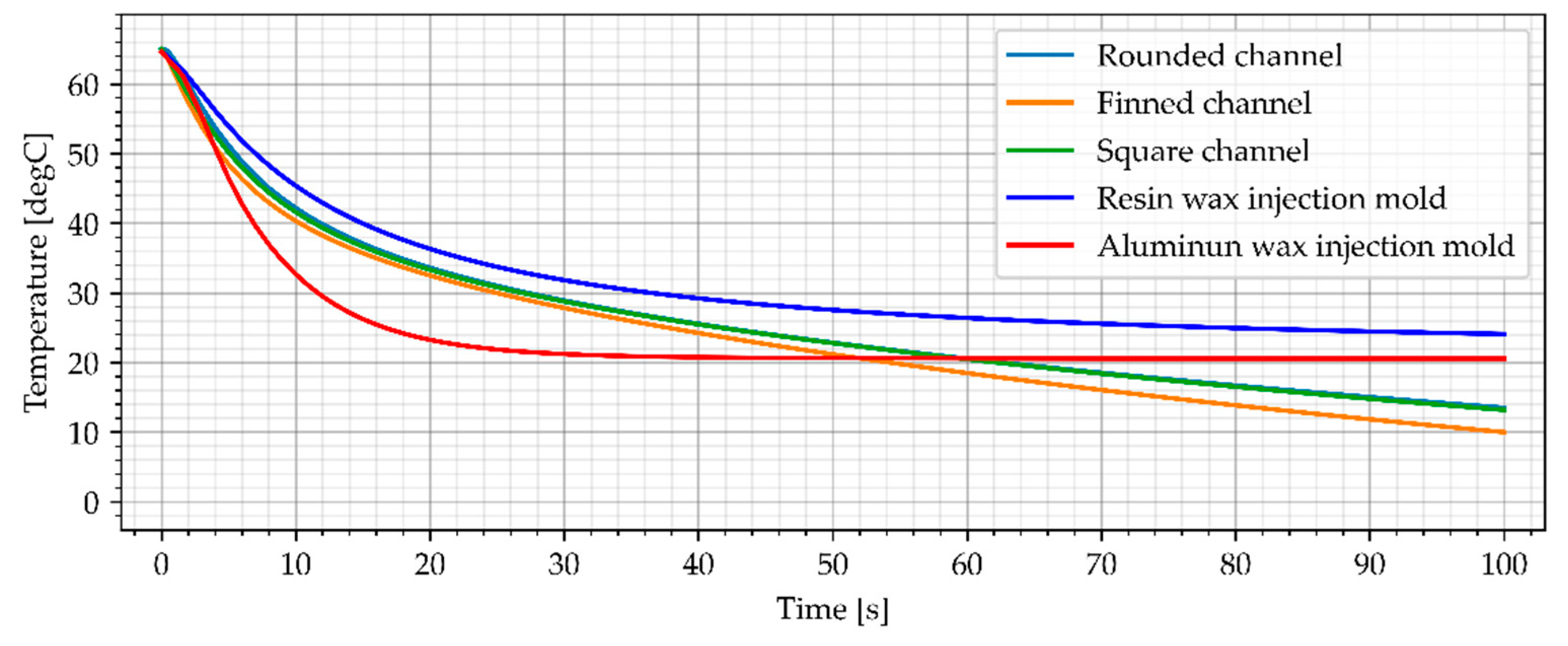
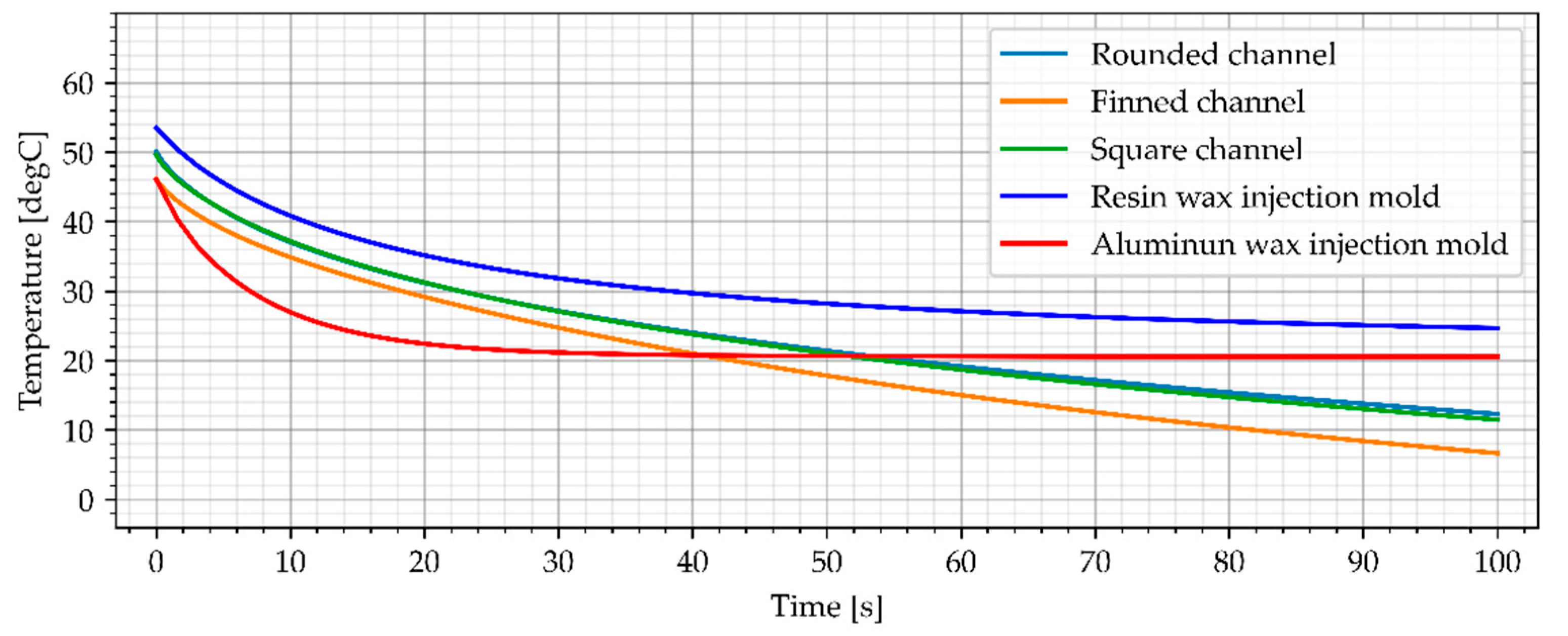
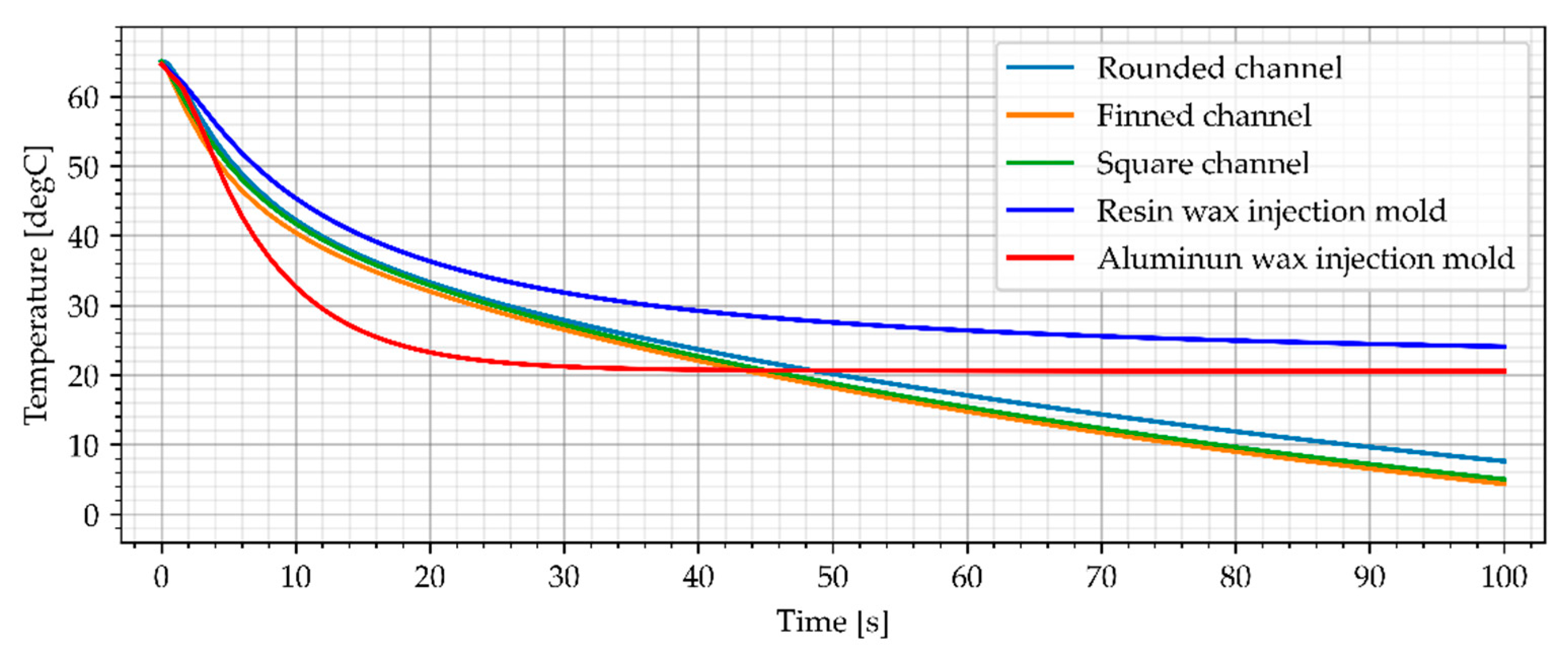
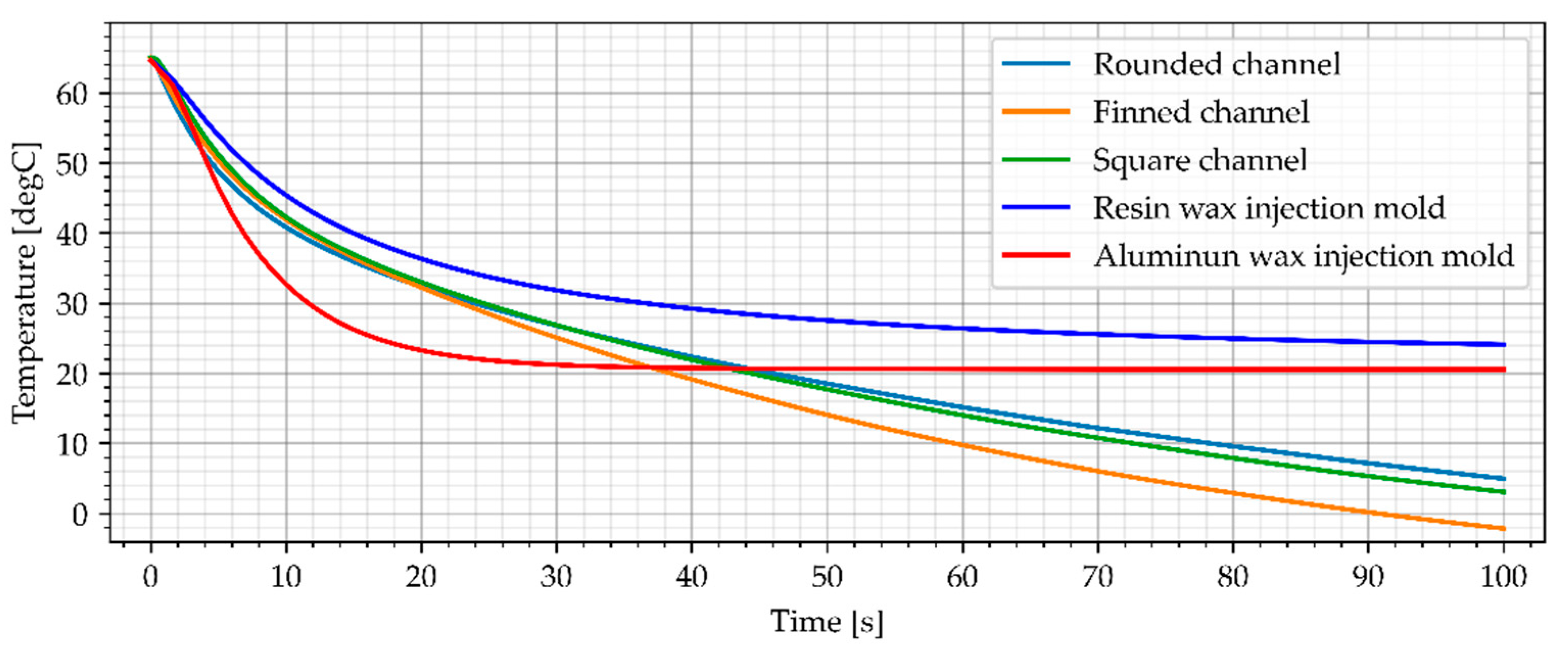
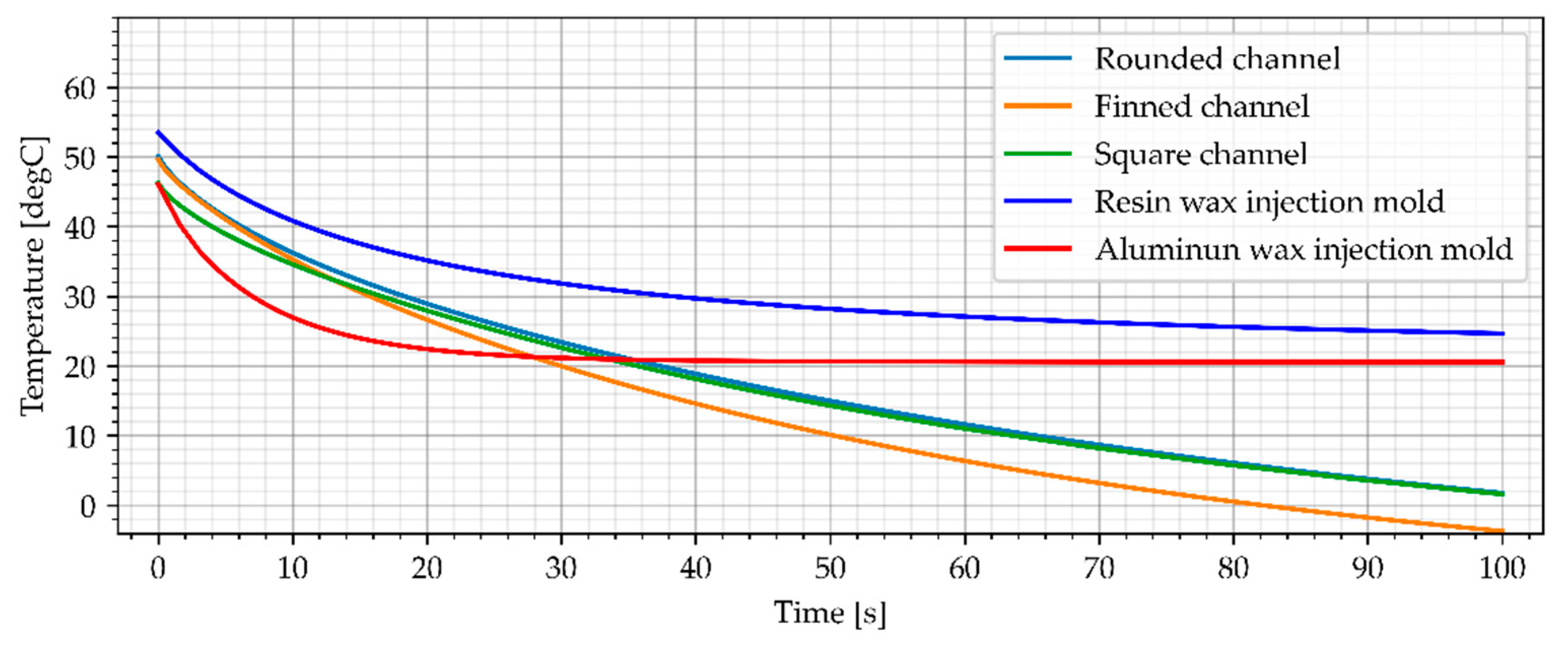
3.3.1. Water Cooling
3.3.2. Air Cooling, Flow Rate of 0.0003 kg/s
3.3.3. Air Cooling, Flow Rate of 0.0006 kg/s
3.3.4. Air Cooling, Flow Rate of 0.001 kg/s
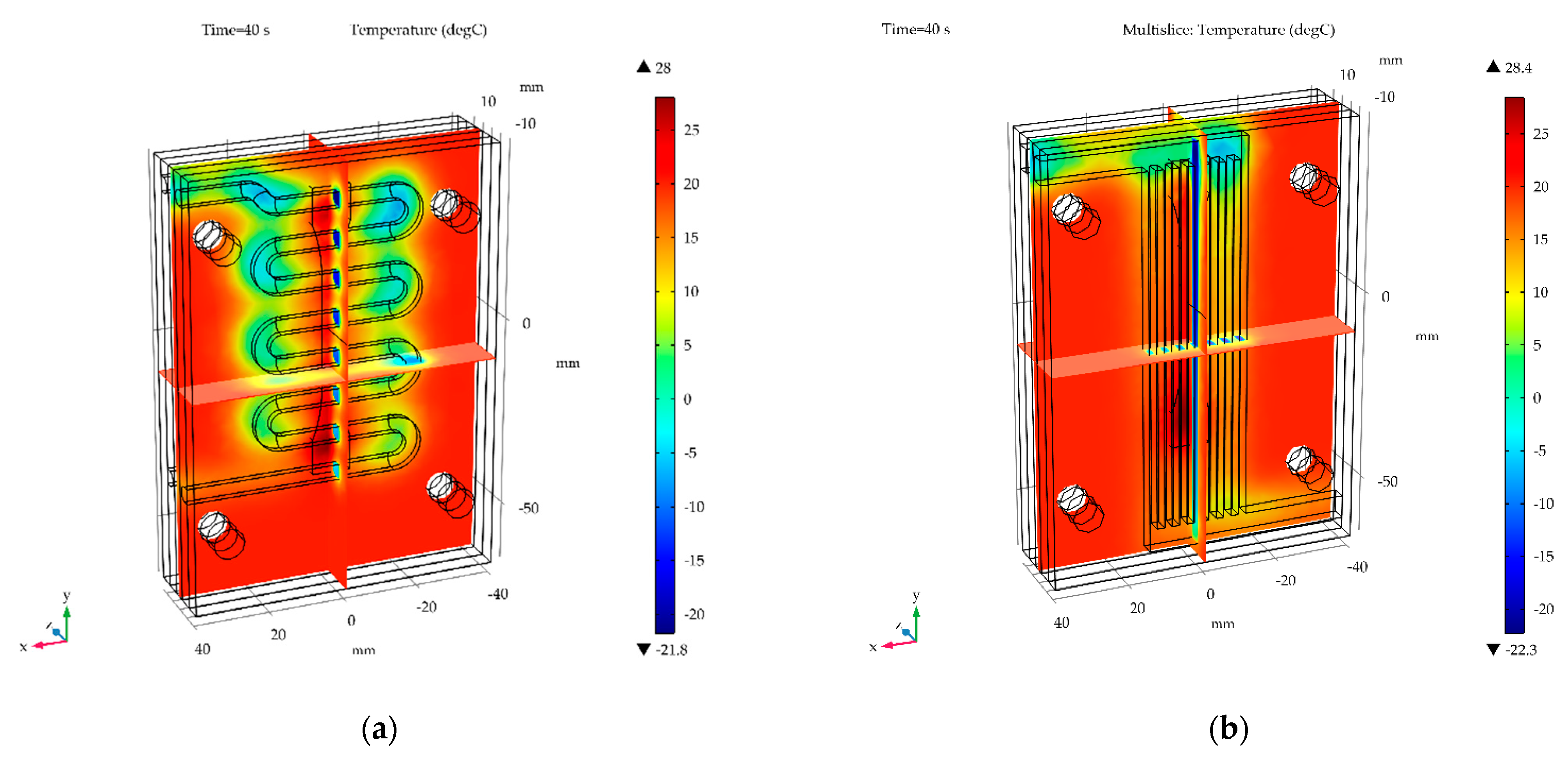
3.4. Temperature Distribution in Wax Injection Mold
3.5. Results Summary
4. Conclusions
- Water at room temperature has the best ability to receive heat in the first stage of cooling process (about 25 s).
- After reaching the temperature from point 1, cold air cooling with highest flow rate of 0.001 kg/s is the most effective process.
- After about 30–35 s, air cooling becomes more effective than heat dissipation through aluminum material.
- The finite element method (FEM) analysis used in this study can be successfully used to carry out thermal analyses, thanks to which it is much easier to plan the production process (e.g., calculation of production capacity). However, it should be emphasized that errors in result estimation can occur. Hence, experimental validation of obtained results in crucial.
- The 3D printed wax injection molds, under certain conditions, can be successfully used in the production process. However, in order to accelerate production, it is worth using cooling channels, which can significantly speed up the production process. This approach appears to present an ideal substitute for traditional wax injection molds for low-volume production which, moreover, does not require additional, new materials in the production flow.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ignaszak, Z.; Popielarski, P.; Hajkowski, J.; Prunier, J.B. Problem of acceptability of internal porosity in semi-finished cast product as new trend—Tolerance of damage present in modern design office. Defect Diffus. Forum 2012, 326–328, 612–619. [Google Scholar] [CrossRef]
- Ignaszak, Z.; Hajkowski, J.; Popielarski, P. Mechanical properties gradient existing in real castings taken into account during design of cast components. Defect Diffus. Forum 2013, 334–335, 314–321. [Google Scholar] [CrossRef]
- Matta, A.; Raju, D.; Suman, K. The Integration of CAD/CAM and Rapid Prototyping in Product Development: A Review. Mater. Today Proc. 2015, 2, 3438–3445. [Google Scholar] [CrossRef]
- Hutton, D.V. Fundamentals of Finite Element Analysis, 1st ed.; The McGraw-Hill: New York, NY, USA, 2004; pp. 1–17, 222–256. [Google Scholar]
- Chybowski, L.; Grzadziel, Z.; Gawdzinska, K. Simulation and experimental studies of a multi-tubular floating sea wave damper. Energies 2018, 11, 1012. [Google Scholar] [CrossRef]
- Hajkowski, J.; Popielarski, P.; Ignaszak, Z. Cellular automaton finite element method applied for microstructure prediction of aluminium casting treated by laser beam. Arch. Foundry Eng. 2019, 19, 111–118. [Google Scholar]
- Wang, S.; Millogo, J.D. Rapid prototype mold for wax patterns with the help of phase change materials. Int. J. Adv. Manuf. Technol. 2011, 62, 35–41. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S. Rapid Manufacturing The Technologies and Applications of Rapid Prototyping and Rapid Tooling, 1st ed.; Springer: London, UK, 2001; pp. 16–20. [Google Scholar]
- Sika, R.; Ignaszak, Z. Data Acquisition procedures for A&DM systems dedicated for foundry industry. In Proceedings of the 2nd International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, DSMIE-2019, Lutsk, Ukraine, 11–14 June 2019. [Google Scholar]
- Osman Zahid, M.; Case, K.; Watts, D. End mill tools integration in CNC machining for rapid manufacturing processes: Simulation studies. Prod. Manuf. Res. 2015, 3, 274–288. [Google Scholar] [CrossRef]
- Górski, F.; Zawadzki, P.; Wichniarek, R.; Kuczko, W.; Żukowska, M.; Wesołowska, I.; Wierzbicka, N. Automated Design of Customized 3D-Printed Wrist Orthoses on the Basis of 3D Scanning. Comput. Exp. Simul. Eng. 2019, 75, 1133–1143. [Google Scholar]
- Campbell, J. Complete Casting Handbook, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2015; pp. 871–878. [Google Scholar]
- Macku, M.; Horacek, M. Applying RP-FDM Technology to Produce Prototype Castings Using the Investment Casting Method. Arch. Foundry Eng. 2012, 12, 75–82. [Google Scholar] [CrossRef]
- Naplocha, K.; Dmitruk, A.; Mayer, P.; Kaczmar, J.W. Design of honeycomb structures produced by investment casting. Arch. Foundry Eng. 2019, 19, 76–80. [Google Scholar]
- Czarnecka-Komorowska, D.; Grzeskowiak, K.; Popielarski, P.; Barczewski, M.; Gawdzinska, K.; Poplawski, M. Polyethylene wax modified by organoclay bentonite used in the lost-wax casting process: Processing-structure-property relationships. Materials 2020, 13, 2255. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies, 3rd ed.; Springer: Cham, Switzerland, 2021; pp. 1–12. [Google Scholar]
- Kuo, C.-C.; Chen, W.-H.; Liu, Y.-L.; Liao, W.-J.; Huang, B.-Y.; Tsai, R.-L. Development of a low-cost wax injection mold with high cooling efficiency. Int. J. Adv. Manuf. Technol. 2017, 93, 2081–2088. [Google Scholar] [CrossRef]
- Berger, G.R.; Gruber, D.P.; Friesenbichler, W.; Teichert, C.; Burgsteiner, M. Replication of stochastic and geometric micro structures—aspects of visual appearance. Int. Polym. Processing 2011, 26, 313–322. [Google Scholar] [CrossRef]
- PolyJet Materials. Available online: https://www.objective3d.com.au/wp-content/uploads/2016/10/AB_PJ_InjectionMolding_1115.pdf (accessed on 7 September 2022).
- Surace, R.; Basile, V.; Bellantone, V.; Modica, F.; Fassi, I. Micro Injection Molding of Thin Cavities Using Stereolithography for Mold Fabrication. Polymers 2021, 13, 1848. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Singh, R.; Ahuja, I. Investigations for Mechanical Properties of Hybrid Investment Casting: A Case Study. Mater. Sci. Forum 2014, 808, 89–95. [Google Scholar] [CrossRef]
- Using Castable Wax Resin. Available online: https://support.formlabs.com/s/article/Using-Castable-Wax-Resin?language=en_US (accessed on 5 August 2022).
- Dudek, P.; Rapacz-Kmita, A. Rapid Prototyping: Technologies, Materials and Advances. Arch. Met. Mater. 2016, 61, 891–896. [Google Scholar] [CrossRef]
- Chhabra, M.; Singh, R. Rapid casting solutions: A review. Rapid Prototyp. J. 2011, 17, 328–350. [Google Scholar] [CrossRef]
- Kroma, A.; Adamczak, O.; Sika, R.; Górski, F.; Kuczko, W.; Grześkowiak, K. Modern Reverse Engineering Methods Used to Modification of Jewelry. Adv. Sci. Technol. Res. J. 2020, 14, 298–306. [Google Scholar] [CrossRef]
- DLP Materials. Available online: https://cpspolymers.com/dlp (accessed on 5 August 2022).
- Kroma, A.; Mendak, M.; Jakubowicz, M.; Gapiński, B.; Popielarski, P. Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting. Materials 2021, 14, 6758. [Google Scholar] [CrossRef]
- Ignaszak, Z.; Popielarski, P.; Strek, T. Estimation of Coupled Thermo-Physical and Thermo-Mechanical Properties of Porous Thermolabile Ceramic Material using Hot Distortion Plus® test. Defect Diffus. Forum 2011, 312–315, 764–769. [Google Scholar] [CrossRef]
- Jopek, H.; Stręk, T. Thermoauxetic Behavior of Composite Structures. Materials 2018, 11, 294. [Google Scholar] [CrossRef] [PubMed]
- Nienartowicz, M.; Strek, T. Topology Optimization of the Effective Thermal Properties of Two-Phase Composites. In Recent Advances in Computational Mechanics; Taylor & Francis Group: London, UK, 2014; pp. 223–236. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; p. 4. [Google Scholar]
- Fourier, J. The Analytical Theory of Heat; Cambridge University Press: Cambridge, UK, 2009; p. 1. [Google Scholar]
- Brenner, G. CFD in Process Engineering. In 100 Volumes of Notes on Numerical Fluid Mechanics; Hirschel, E.H., Krause, E., Eds.; Springer: Berlin, Germany, 2011; pp. 351–360. ISBN 978-3-540-70804-9. [Google Scholar]
- Mehdi, P.; Raja, S.; Zhang, C. Investigating thermal comfort and occupants position impacts on building sustainability using CFD and BIM. In Proceedings of the 9th International Conference of the Architectural Science Association, Melbourne, VIC, Australia, 2–4 December 2015. [Google Scholar]
- Friedlander, S. Stability of Flows. In Encyclopedia of Mathematical Physics; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–7. [Google Scholar]
- Chang, W.; Kikuchi, N. Analysis of non-isothermal mold filling process in resin transfer molding (RTM) and structural reaction injection molding. Comput. Mech. 1995, 16, 22–35. [Google Scholar] [CrossRef]
- Barakos, G.; Mitsoulis, E. Non-isothermal viscoelastic simulations of extrusion through dies and prediction of the bending phenomenon. J. Non-Newton. Fluid Mech. 1996, 62, 55–79. [Google Scholar] [CrossRef]
- Réti, T.; Gergely, M.; Tardy, P. Mathematical treatment of non-isothermal transformations. Mater. Sci. Technol. 1987, 3, 365–371. [Google Scholar] [CrossRef]
- Nalbndi, H.; Seiiedlou, S.; Alizadeh, B. Application of non-isothermal simulation in optimization of food drying process. J. Food Sci. Technol. 2020, 58, 2325–2336. [Google Scholar] [CrossRef]
- Khan, M.; Afaq, S.K.; Khan, N.U.; Ahmad, S. Cycle time reduction in injection molding process by selection of robust cooling channel design. ISRN Mech. Eng. 2014, 2014, 968484. [Google Scholar] [CrossRef]
- Palacios, A.; Cong, L.; Navarro, M.E.; Ding, Y.; Barreneche, C. Thermal conductivity measurement techniques for characterizing thermal energy storage materials—A review. Renew. Sustain. Energy Rev. 2019, 108, 32–52. [Google Scholar] [CrossRef]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement techniques for thermal conductivity and interfacial thermal conductance of bulk and thin film materials. J. Electron. Packag. 2016, 138, 040802. [Google Scholar] [CrossRef]
- Zábranský, M.; Růžička, V.; Domalski, E.S. Heat capacity of liquids: Critical Review and recommended values. supplement I. J. Phys. Chem. Ref. Data 2001, 30, 1199–1689. [Google Scholar] [CrossRef]
- Lakshmikumar, S.T.; Gopal, E.S.R. Heat-Capacity Measurements—Progress in Experimental-Techniques. J. Indian Inst. Sci. Sect. A-Eng. Technol. 1981, 63, 277–329. [Google Scholar]
- Rosen, P.F.; Woodfield, B.F. Standard methods for heat capacity measurements on a quantum design physical property measurement system. J. Chem. Thermodyn. 2020, 141, 105974. [Google Scholar] [CrossRef]
- Ginnings, D.C.; Furukawa, G.T. Heat capacity standards for the range 14 to 1200° K. J. Am. Chem. Soc. 1953, 75, 522–527. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 115–164. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method for Fluid Dynamics, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 31–80, 127–153. [Google Scholar]
- ISO 527-2:2012; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. International Organization for Standardization based in Switzerland: Geneva, Switzerland, 2012.
- Massé, H.; Arquis, É.; Delaunay, D.; Quilliet, S.; Le Bot, P.H. Heat transfer with mechanically driven thermal contact resistance at the polymer–mold interface in injection molding of polymers. Int. J. Heat Mass Transf. 2004, 47, 2015–2027. [Google Scholar] [CrossRef]
- Lucyshyn, T.; Des Enffans d’Avernas, L.-V.; Holzer, C. Influence of the Mold Material on the Injection Molding Cycle Time and Warpage Depending on the Polymer Processed. Polymers 2021, 13, 3196. [Google Scholar] [CrossRef] [PubMed]
- Çengel, Y.; Ghajar, A. Heat and Mass Transfer: Fundamentals and Applications, 5th ed.; The McGraw-Hill: New York, NY, USA, 2015; p. 393. [Google Scholar]
- Vortec Standard Cold Air Guns. Available online: https://www.vortec.com/standard-cold-air-guns/overview (accessed on 7 September 2022).
- Jiang, N. A second-order ensemble method based on a blended backward differentiation formula time stepping scheme for time-dependent navier-stokes equations. Numer. Methods Part. Differ. Equ. 2016, 33, 34–61. [Google Scholar] [CrossRef]
- Takizawa, K.; Tezduyar, T.E.; Otoguro, Y. Stabilization and discontinuity-capturing parameters for space–time flow computations with finite element and isogeometric discretizations. Comput. Mech. 2018, 62, 1169–1186. [Google Scholar] [CrossRef]
- Calorimeter. Instrument. Available online: https://www.britannica.com/technology/calorimeter (accessed on 7 September 2022).
- Calorimeter KL-12Mn/KL-12Mn2 “Guidelines for Calorimetric Testing”. Available online: https://sitech.apsl.edu.pl/instytut-nauk-scislych-i-technicznych/dydaktyka/laboratoria/pracownia-fizykochemicznej-inzynierii-materialoznawstwa-soa/wytyczne-do-badan-kalorymetrycznych.pdf (accessed on 7 September 2022).



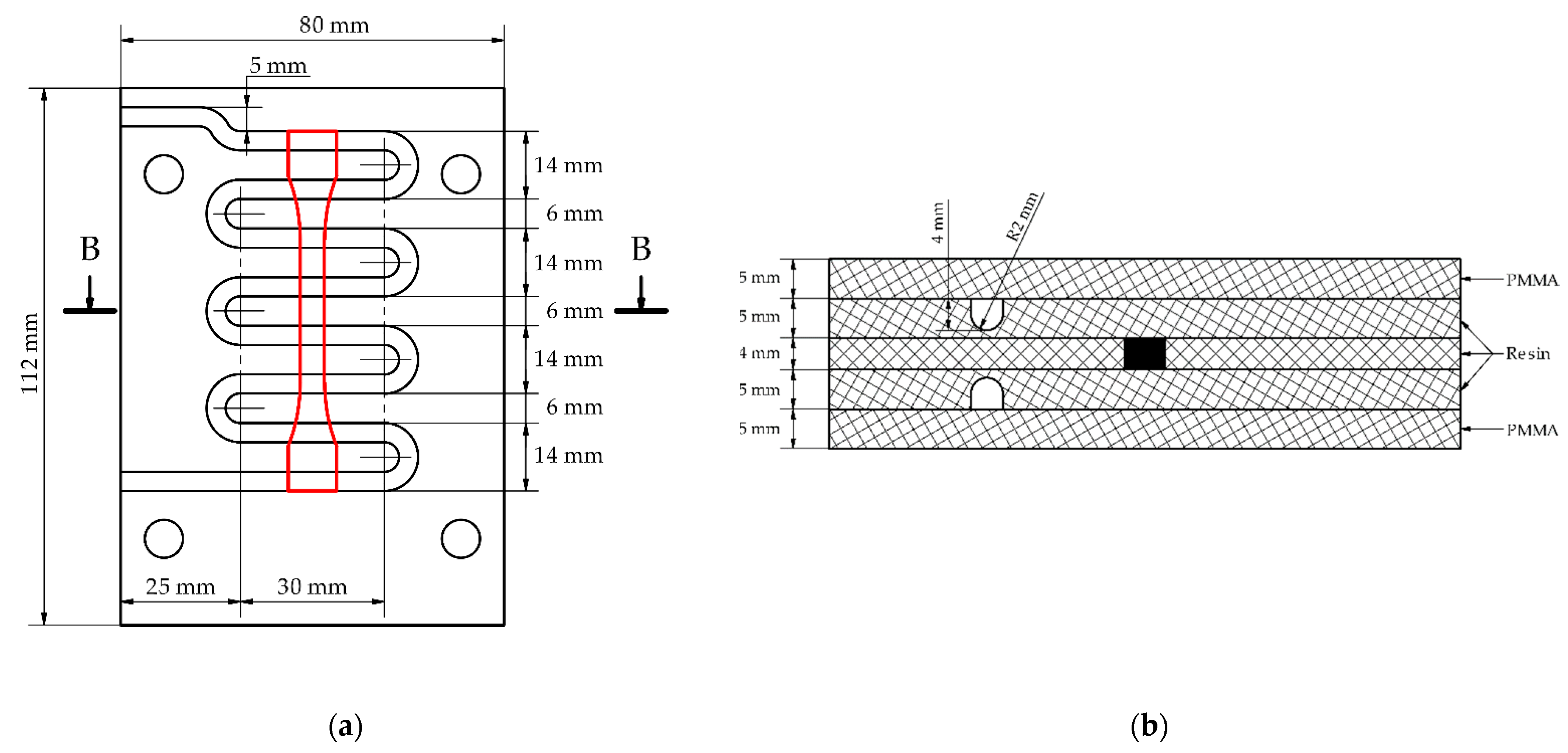
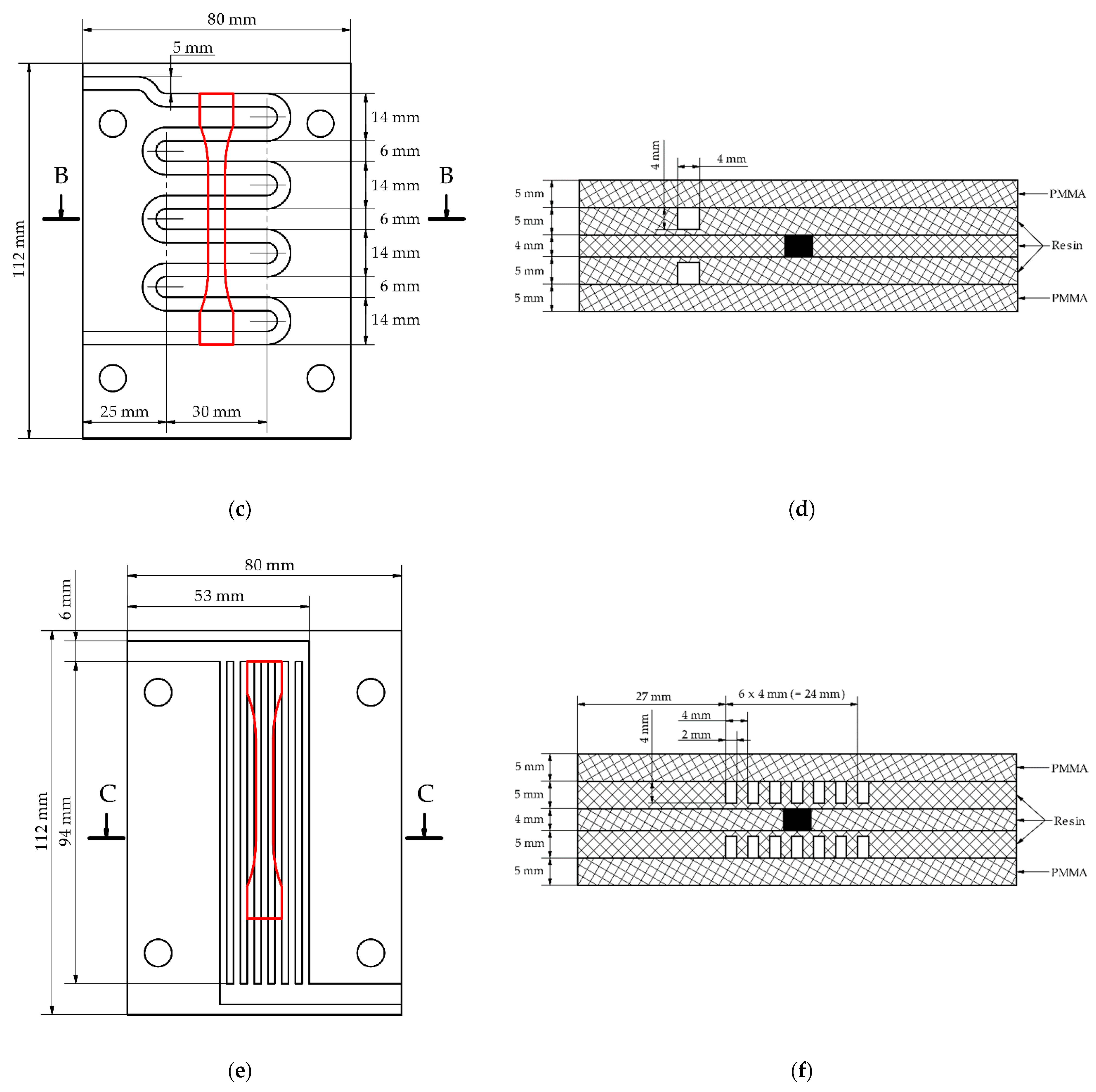






| Name | No. | Value [mm] |
|---|---|---|
| Total length | l3 | ≥75 |
| The length of the part delimited by parallel lines | l1 | 30.0 ± 0.5 |
| Radius | r | ≥30 |
| The distance between wide parallel parts | l2 | 58 ± 2 |
| Width at the ends | b2 | 10 ± 0.5 |
| Width of the narrow part | b1 | 5.0 ± 0.5 |
| Thickness | h | ≥2 |
| Length of the measuring section | l0 | 10 ± 0.2 |
| Initial distance between the handles | l | l2 (−0, +2) |
| Setting Name | Finned Version | Square Channel | Rounded Channel | No Channels |
|---|---|---|---|---|
| max. element size (laminar flow) [mm] | 3.00 | 2.94 | 2.94 | NA |
| min. element size (laminar flow)[mm] | 0.60 | 0.88 | 0.88 | NA |
| max. growth rate (laminar flow) [mm] | 1.15 | 1.15 | 1.15 | NA |
| max. element size (solid)[mm] | 4.00 | 6.16 | 6.16 | 3.92 |
| min. element size (solid) [mm] | 0.40 | 0.45 | 0.45 | 0.17 |
| max. growth rate (solid) [mm] | 1.35 | 1.40 | 1.40 | 1.35 |
| max. element size (boundaries) [mm] | 1.00 | 2.94 | 2.94 | NA |
| min. element size (boundaries) [mm] | 0.08 | 0.88 | 0.88 | NA |
| max. growth rate (boundaries) [mm] | 1.10 | 1.15 | 1.15 | NA |
| min. skewness of elements | 0.41 | 0.28 | 0.22 | 0.34 |
| min. volume versus length | 0.43 | 0.38 | 0.37 | 0.38 |
| Number of elements | 113,916 | 134,418 | 184,703 | 64,812 |
| Property | Temperature | Value | Unit |
|---|---|---|---|
| Thermal conductivity of wax | 40 °C | 0.35 | W/(m K) |
| 50 °C | 0.37 | ||
| 60 °C | 0.39 | ||
| Thermal conductivity of resin | 40 °C | 0.50 | W/(m K) |
| 50 °C | 0.53 | ||
| 60 °C | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burlaga, B.; Kroma, A.; Poszwa, P.; Kłosowiak, R.; Popielarski, P.; Stręk, T. Heat Transfer Analysis of 3D Printed Wax Injection Mold Used in Investment Casting. Materials 2022, 15, 6545. https://doi.org/10.3390/ma15196545
Burlaga B, Kroma A, Poszwa P, Kłosowiak R, Popielarski P, Stręk T. Heat Transfer Analysis of 3D Printed Wax Injection Mold Used in Investment Casting. Materials. 2022; 15(19):6545. https://doi.org/10.3390/ma15196545
Chicago/Turabian StyleBurlaga, Bartłomiej, Arkadiusz Kroma, Przemysław Poszwa, Robert Kłosowiak, Paweł Popielarski, and Tomasz Stręk. 2022. "Heat Transfer Analysis of 3D Printed Wax Injection Mold Used in Investment Casting" Materials 15, no. 19: 6545. https://doi.org/10.3390/ma15196545
APA StyleBurlaga, B., Kroma, A., Poszwa, P., Kłosowiak, R., Popielarski, P., & Stręk, T. (2022). Heat Transfer Analysis of 3D Printed Wax Injection Mold Used in Investment Casting. Materials, 15(19), 6545. https://doi.org/10.3390/ma15196545










