Optical Properties and Light-Induced Charge Transfer in Selected Aromatic C60 Fullerene Derivatives and in Their Bulk Heterojunctions with Poly(3-Hexylthiophene)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Methods
3. Results
3.1. Optical Absorption Spectroscopy
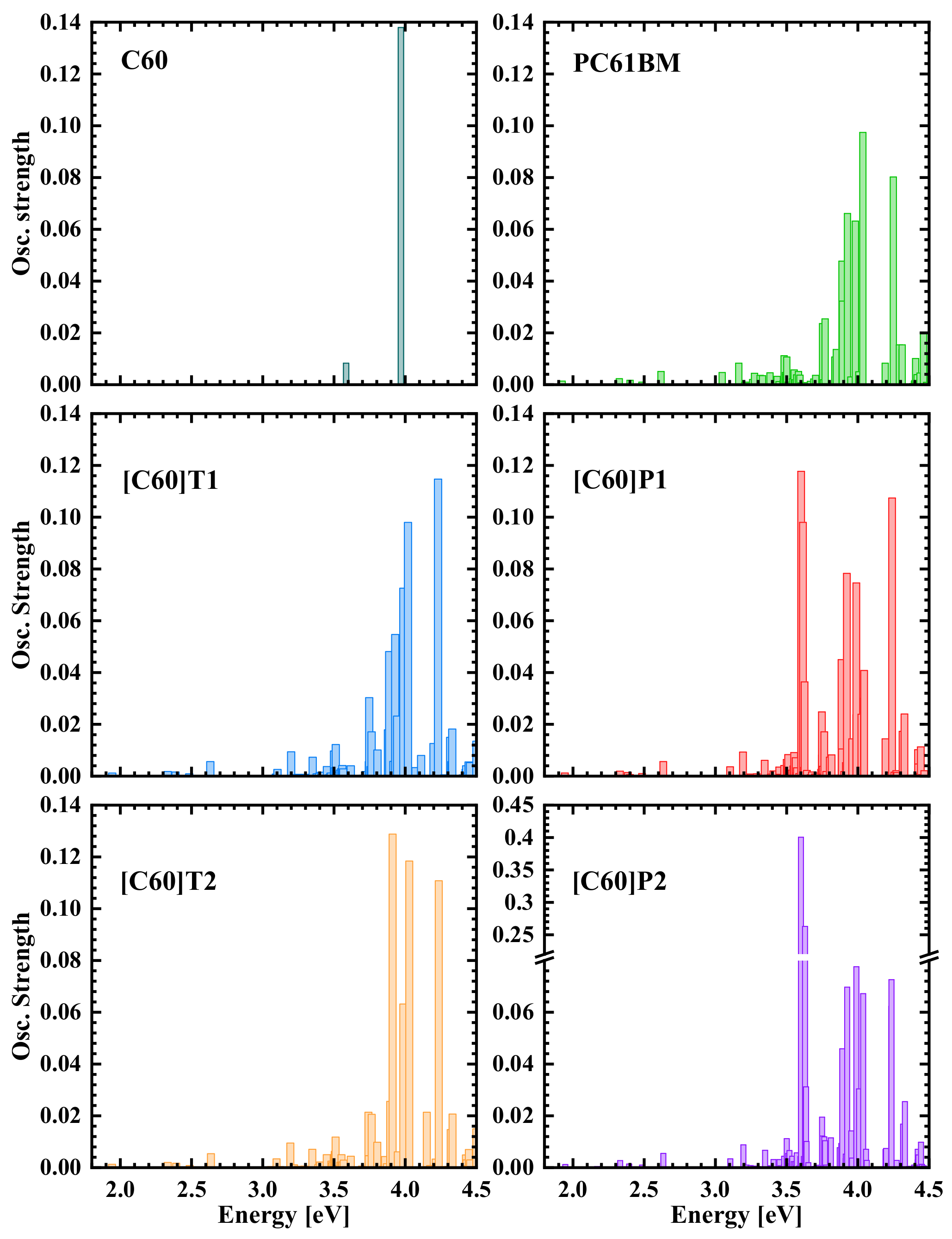
3.2. Density Functional Theory Calculations of Optical Transitions
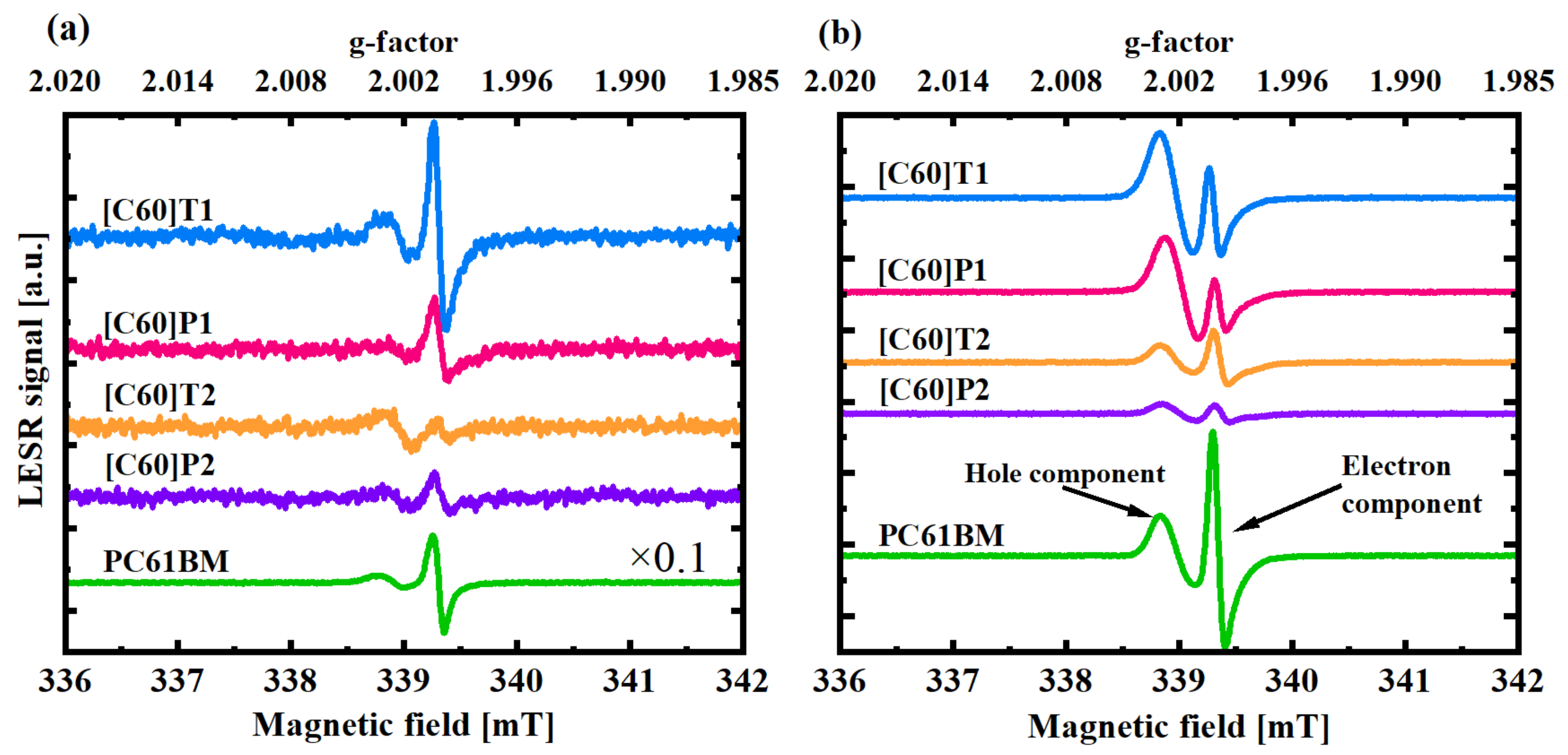
3.3. Electron Spin Resonance
3.3.1. Signal Analysis
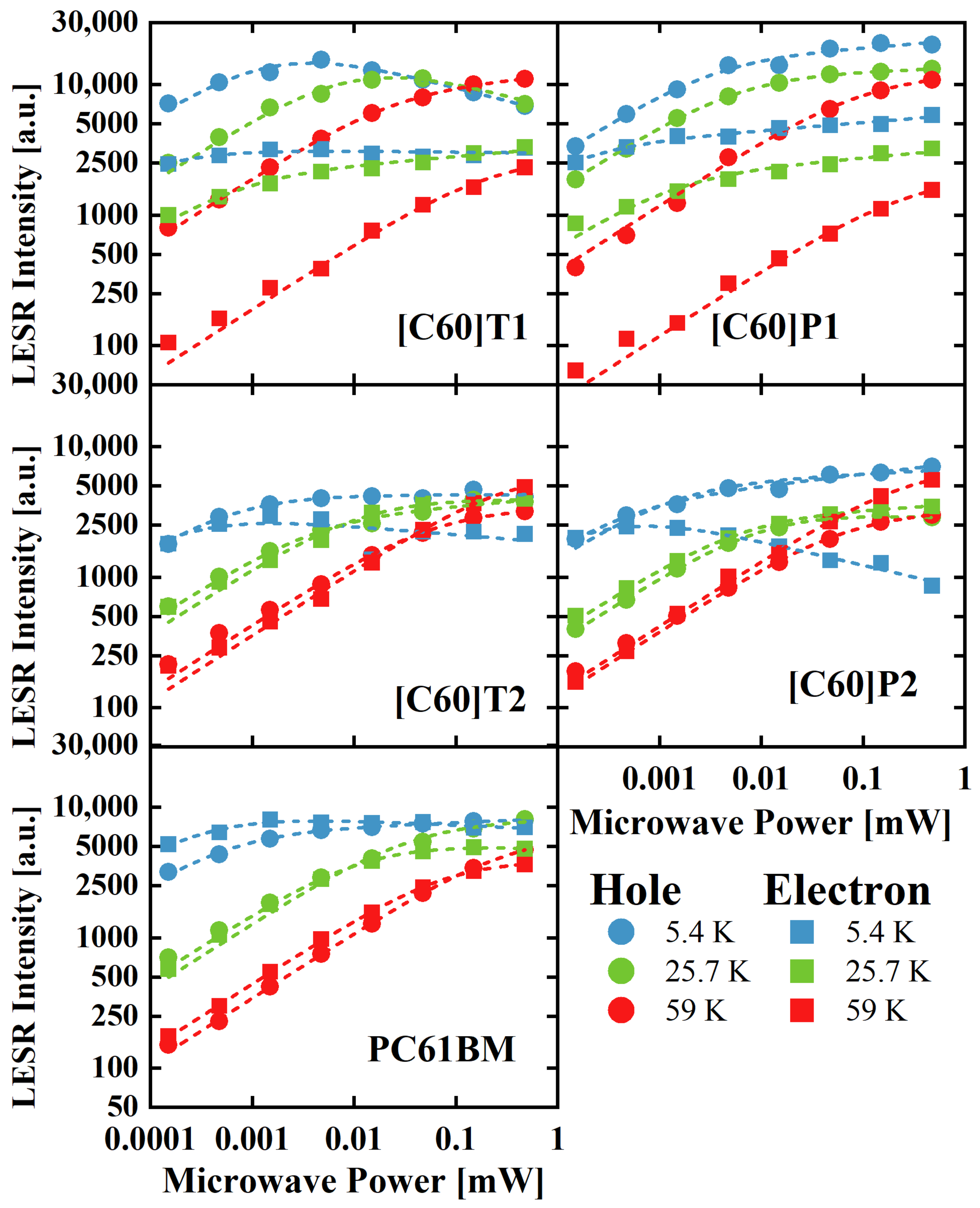
3.3.2. LESR Signal Saturation
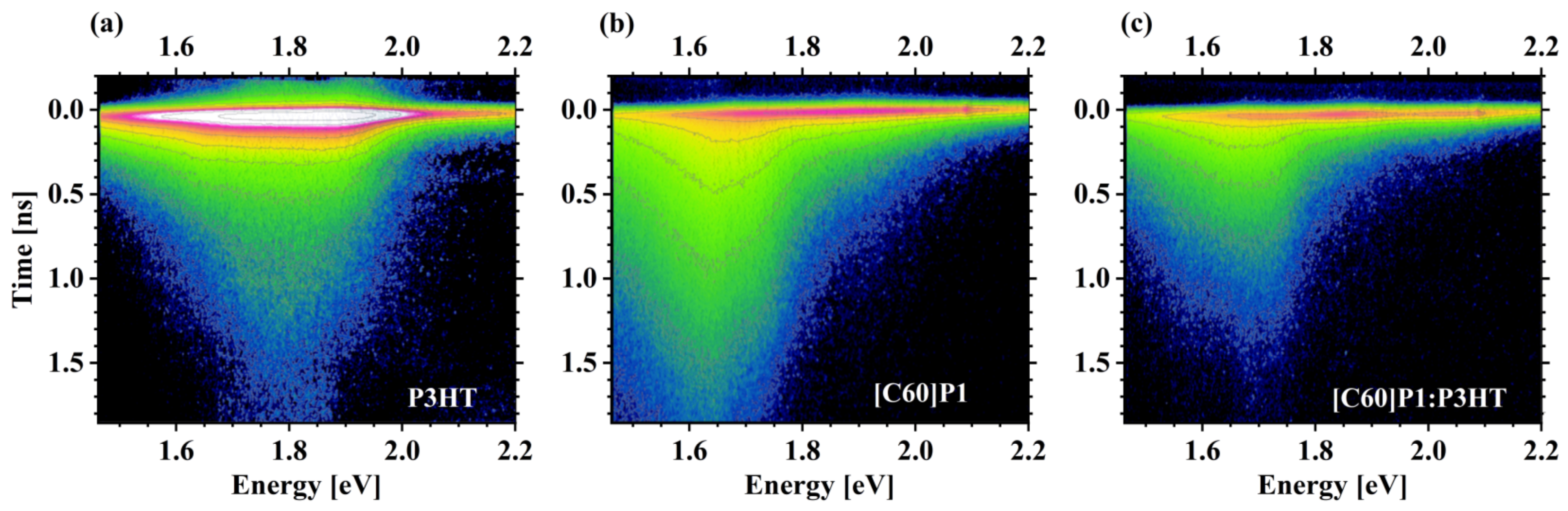
3.4. Photoluminescence
3.5. Preliminary Solar Cells Construction with the Newly Synthesized Fullerenes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lalwani, G.; Sitharaman, B. Multifunctional Fullerene- and Metallofullerene-Based Nanobiomaterials. Nano Life 2013, 3, 1342003. [Google Scholar] [CrossRef] [Green Version]
- Friedl, J.; Lebedeva, M.A.; Porfyrakis, K.; Stimming, U.; Chamberlain, T.W. All-Fullerene-Based Cells for Nonaqueous Redox Flow Batteries. J. Am. Chem. Soc. 2018, 140, 401–405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bischak, C.G.; Flagg, L.Q.; Yan, K.; Li, C.Z.; Ginger, D.S. Fullerene Active Layers for n-Type Organic Electrochemical Transistors. ACS Appl. Mater. Interfaces 2019, 11, 28138–28144. [Google Scholar] [CrossRef]
- Brabec, C.J.; Sariciftci, N.S.; Hummelen, J.C. Plastic solar cells. Adv. Funct. Mater. 2001, 11, 15–26. [Google Scholar] [CrossRef]
- Deibel, C.; Dyakonov, V. Polymer-fullerene bulk heterojunction solar cells. Rep. Prog. Phys. 2010, 73, 096401. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Firdaus, Y.; Isikgor, F.H.; Nugraha, M.I.; Yengel, E.; Harrison, G.T.; Hallani, R.; El-Labban, A.; Faber, H.; Ma, C.; et al. Self-assembled monolayer enables hole transport layer-free organic solar cells with 18% efficiency and improved operational stability. ACS Energy Lett. 2020, 5, 2935–2944. [Google Scholar] [CrossRef]
- Li, S.; Zhan, L.; Jin, Y.; Zhou, G.; Lau, T.; Qin, R.; Shi, M.; Li, C.; Zhu, H.; Lu, X.; et al. Asymmetric Electron Acceptors for High-Efficiency and Low-Energy-Loss Organic Photovoltaics. Adv. Mater. 2020, 32, e2001160. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Lin, H.; Li, M.; Ma, B.; Zhang, R.; Du, X.; Zheng, C.; Yang, G.; Tao, S. Ternary organic solar cells with enhanced charge transfer and stability combining the advantages of polymer acceptors and fullerene acceptors. Org. Electron. 2022, 104, 106471. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, 865–871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Time-dependent density-functional theory for multicomponent systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Ciechanowicz, S.A.G.; Korona, K.P.; Wolos, A.; Drabinska, A.; Iwan, A.; Tazbir, I.; Wojtkiewicz, J.; Kaminska, M. Toward Better Efficiency of Air-Stable Polyazomethine-Based Organic Solar Cells Using Time-Resolved Photoluminescence and Light-Induced Electron Spin Resonance as Verification Methods. J. Phys. Chem. C 2016, 120, 11415–11425. [Google Scholar] [CrossRef]
- Niklas, J.; Mardis, K.; Banks, B.P.; Grooms, G.M.; Sperlich, A.; Dyakonov, V.; Beaupré, S.; Leclerc, M.; Xu, T.; Yu, L.; et al. Highly-efficient charge separation and polaron delocalization in polymer-fullerene bulk-heterojunctions: A comparative multi-frequency EPR and DFT study. Phys. Chem. Chem. Phys. 2013, 15, 9562–9574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konkin, A.; Sensfuss, S.; Roth, H.-K.; Nazmutdinova, G.; Schroedner, M.; Al-Ibrahim, M.; Egbe, D. LESR study on PPV-PPE/PCBM composites for organic photovoltaics. Synth. Met. 2005, 148, 199–204. [Google Scholar] [CrossRef]
- Zoriniants, G.; Dyakonov, V.; Scharber, M.; Brabec, C.; Janssen, R.; Hummelen, J.; Sariciftci, N. Light-induced ESR studies in conjugated polymer-fullerene composites. Synth. Met. 1999, 102, 1241–1242. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, S.-I.; Tanaka, H.; Kuroda, S.-I.; Toda, A.; Nagano, S.; Seki, T.; Kimoto, A.; Abe, J. Electron spin resonance observation of field-induced charge carriers in ultrathin-film transistors of regioregular poly(3-hexylthiophene) with controlled in-plane chain orientation. Appl. Phys. Lett. 2010, 96, 3–6. [Google Scholar] [CrossRef]
- Poluektov, O.G.; Filippone, S.; Martín, N.; Sperlich, A.; Deibel, C.; Dyakonov, V. Spin signatures of photogenerated radical anions in polymer-[70]fullerene bulk heterojunctions: High frequency pulsed EPR spectroscopy. J. Phys. Chem. B 2010, 114, 14426–14429. [Google Scholar] [CrossRef] [Green Version]
- Bingel, C. Cyclopropanierung von Fullerenen. Eur. J. Inorg. Chem. 1993, 126, 1957–1959. [Google Scholar] [CrossRef]
- Nierengarten, J.; Gramlich, V.; Cardullo, F.; Diederich, F. Regio- and Diastereoselective Bisfunctionalization of C60 and Enantioselective Synthesis of a C60 Derivative with a Chiral Addition Pattern. Angew. Chem. Int. Ed. 1996, 35, 2101–2103. [Google Scholar] [CrossRef]
- Herranz, M.Á.; Cox, C.T.; Echegoyen, L. Retrocyclopropanation reactions of fullerenes: Complete product analyses. J. Org. Chem. 2003, 68, 5009–5012. [Google Scholar] [CrossRef]
- Piotrowski, P.; Mech, W.; Zarębska, K.; Krajewski, M.; Korona, K.; Kamińska, M.; Skompska, M.; Kaim, A. Mono- and Di-Pyrene [60]Fullerene and [70]Fullerene Derivatives as Potential Components for Photovoltaic Devices. Molecules 2021, 26, 1561. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Ren, S.L.; Wang, Y.; Rao, A.M.; McRae, E.; Holden, J.M.; Hager, T.; Wang, K.; Lee, W.; Ni, H.F.; Selegue, J.; et al. Ellipsometric determination of the optical constants of C60 (Buckminsterfullerene) films. Appl. Phys. Lett. 1991, 59, 2678–2680. [Google Scholar] [CrossRef]
- Barry, N.P.E.; Therrien, B. Pyrene: The Guest of Honor. In Organic Nanoreactors; Sadjadi, S., Ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2016; pp. 422–461. [Google Scholar]
- Holland, D.M.P.; Trofimov, A.B.; Seddon, E.A.; Gromov, E.V.; Korona, T.; de Oliveira, N.; Archer, L.E.; Joyeux, D.; Nahon, L. Excited electronic states of thiophene: High resolution photoabsorption Fourier transform spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2014, 16, 21629–21644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Chen, H.; Chen, Y.; Wei, Z.; Pu, Z. DFT Study on Methanofullerene Derivative [6,6]-Phenyl-C61 Butyric Acid Methyl Ester. Acta Phys.-Chim. Sin. 2008, 24, 1353–1358. [Google Scholar] [CrossRef]
- Mohajeri, A.; Omidvar, A. Fullerene-based materials for solar cell applications: Design of novel acceptors for efficient polymer solar cells-A DFT study. Phys. Chem. Chem. Phys. 2015, 17, 22367–22376. [Google Scholar] [CrossRef]
- Roy, J.K.; Kar, S.; Leszczynski, J. Optoelectronic properties of C60 and C70 fullerene derivatives: Designing and evaluating novel candidates for efficient P3HT polymer solar cells. Materials 2019, 12, 2282. [Google Scholar] [CrossRef] [Green Version]
- Peverati, R.; Truhlar, D.G. Quest for a universal density functional: The accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 372, 1–52. [Google Scholar] [CrossRef]
- Sperlich, A.; Kraus, H.; Deibel, C.; Blok, H.; Schmidt, J.; Dyakonov, V. Reversible and irreversible interactions of poly(3-hexylthiophene) with oxygen studied by spin-sensitive methods. J. Phys. Chem. B 2011, 115, 13513–13518. [Google Scholar] [CrossRef] [Green Version]
- Carati, C.; Gasparini, N.; Righi, S.; Tinti, F.; Fattori, V.; Savoini, A.; Cominetti, A.; Po, R.; Bonoldi, L.; Camaioni, N. Pyrene-Fullerene Interaction and Its Effect on the Behavior of Photovoltaic Blends. J. Phys. Chem. C 2016, 120, 6909–6919. [Google Scholar] [CrossRef]
- Krinichnyi, V.I.; Yudanova, E.I.; Denisov, N.N. Light-induced EPR study of charge transfer in poly(3-hexylthiophene)/ fullerene bulk heterojunction. J. Chem. Phys. 2009, 131, 044515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krinichnyi, V.I.; Yudanova, E.I. Light-induced EPR study of charge transfer in P3HT/bis-PCBM bulk heterojunctions. AIP Adv. 2011, 1, 022131. [Google Scholar] [CrossRef] [Green Version]
- Brabec, C.J.; Zerza, G.; Cerullo, G.; De Silvestri, S.; Luzzati, S.; Hummelen, J.C.; Sariciftci, S. Tracing photoinduced electron transfer process in conjugated polymer/fullerene bulk heterojunctions in real time. Chem. Phys. Lett. 2001, 340, 232–236. [Google Scholar] [CrossRef] [Green Version]
- Wudl, F.; Sariciftci, N.; Smilowitz, L.; Heeger, A. Photoinduced Electron Transfer from a Conducting Polymer to Buckminsterfullerene. Science 1992, 258, 1474–1476. [Google Scholar] [CrossRef]
- Stankowski, J.; Piekara-Sady, L.; Kempiński, W. EPR of a fullerene-molecule-derived paramagnetic center as a mesoscopic conducting object. Appl. Magn. Reson. 2000, 19, 539–546. [Google Scholar] [CrossRef]
- Möbius, K. Untersuchung von einfachen pi-Elektronensystem en mit Hilfe von Elektronenspin-Resonanz und Polarographie. Z. Nat. 1965, 20a, 1093–1102. [Google Scholar] [CrossRef]
- Wertz, J.E.; Bolton, J.R. Electron Spin Resonance—Elementary Theory and Practical Applications, 1st ed.; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Lembicz, F.; Podgórska, D.; Ukielski, R.; Piatek, M. Saturation ESR spectroscopy of PA12 polyamide. Eur. Polym. J. 2004, 40, 1217–1221. [Google Scholar] [CrossRef]
- Altenbach, C.; Greenhalgh, D.A.; Khorana, H.G.; Hubbell, W.L. A collision gradient method to determine the immersion depth of nitroxides in lipid bilayers: Application to spin-labeled mutants of bacteriorhodopsin. Proc. Natl. Acad. Sci. USA 1994, 91, 1667–1671. [Google Scholar] [CrossRef] [Green Version]
- Beletskaya, E.A.; Lukina, E.A.; Uvarov, M.N.; Popov, A.A.; Kulik, L.V. Geminate recombination in organic photovoltaic blend PCDTBT/PC71BM studied by out-of-phase electron spin echo spectroscopy. J. Chem. Phys. 2020, 152, 044706. [Google Scholar] [CrossRef]
- Lukina, E.A.; Popov, A.A.; Uvarov, M.N.; Suturina, E.A.; Reijerse, E.J.; Kulik, L.V. Light-induced charge separation in a P3HT/PC70BM composite as studied by out-of-phase electron spin echo spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 28585–28593. [Google Scholar] [CrossRef]
- Presselt, M.; Herrmann, F.; Hoppe, H.; Shokhovets, S.; Runge, E.; Gobsch, G. Influence of phonon scattering on exciton and charge diffusion in polymer-fullerene solar cells. Adv. Energy Mater. 2012, 2, 999–1003. [Google Scholar] [CrossRef]
- Laquai, F.; Andrienko, D.; Mauer, R.; Blom, P.W.M. Charge Carrier Transport and Photogeneration in P3HT: PCBM Photovoltaic Blends. Macromol. Rapid Commun. 2015, 36, 1001–1025. [Google Scholar] [CrossRef] [Green Version]
- Campoy-Quiles, M.; Ferenczi, T.A.M.; Agostinelli, T.; Etchegoin, P.G.; Kim, Y.; Anthopoulos, T.D.; Stavrinou, P.N.; Bradley, D.D.C.; Nelson, J. Morphology evolution via self-organization and lateral and vertical diffusion in polymer:fullerene solar cell blends. Nat. Mater. 2008, 7, 158–164. [Google Scholar] [CrossRef] [PubMed]
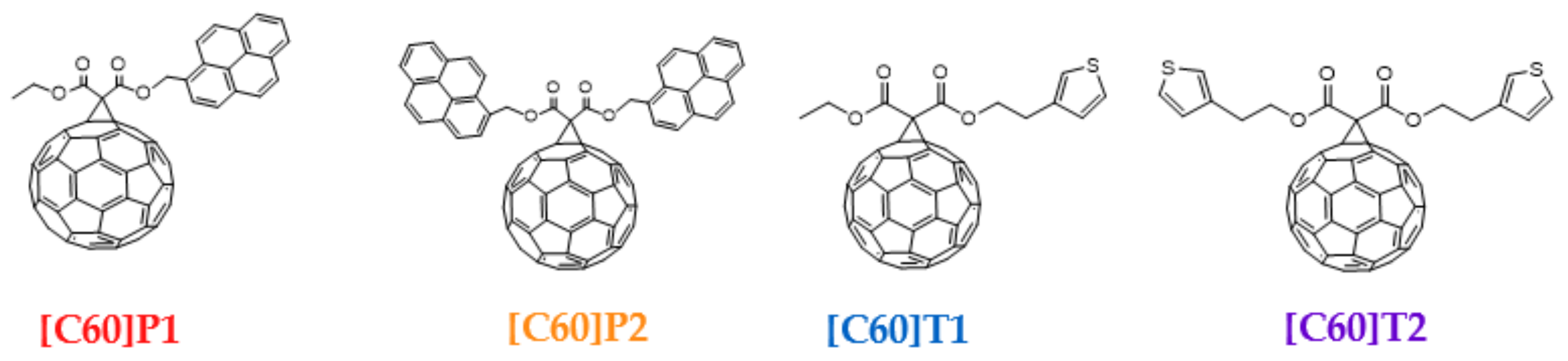



| Material | PC61BM | [C60]T1 | [C60]P1 | |
|---|---|---|---|---|
| Spatial distribution of HOMO/HOMO-1 and LUMO isosurfaces |  |  | 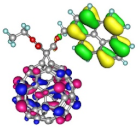 | 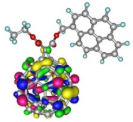 HOMO-1 |
| LUMO [eV] | −3.09 | −3.12 | −3.10 | |
| HOMO [eV] | −5.66 | −5.70 | −5.50 | −5.68 |
| Frontier Molecular Orbital gaps [eV] | 2.57 | 2.58 | 2.40 | 2.58 |
| Material | [C60]T2 | [C60]P2 | ||
| Spatial distribution of HOMO/HOMO-1/HOMO-2 and LUMO isosurfaces | 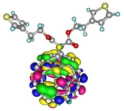 |  | 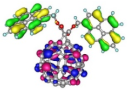 HOMO-1 | 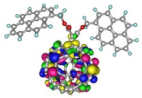 HOMO-2 |
| LUMO [eV] | −3.15 | −3.06 | ||
| HOMO [eV] | −5.73 | −5.48 | −5.50 | −5.65 |
| Frontier Molecular Orbital gaps [eV] | 2.58 | 2.38 | 2.44 | 2.59 |
| gx | gy | gz | giso | |
|---|---|---|---|---|
| PC61BM− | 2.0001 | 2.0001 | 1.9992 | 1.9998 |
| P3HT+ | 2.0026 | 2.0023 | 2.0012 | 2.0020 |
| [C60]T1− | 2.0005 | 2.0005 | 1.9998 | 2.0003 |
| P3HT+ | 2.0032 | 2.0022 | 2.0012 | 2.0022 |
| [C60]P1− | 2.0003 | 2.0001 | 1.9998 | 2.0000 |
| P3HT+ | 2.0031 | 2.0022 | 2.0011 | 2.0021 |
| [C60]T2− | 1.9999 | 1.9999 | 1.9999 | 1.9999 |
| P3HT+ | 2.0034 | 2.0022 | 2.0011 | 2.0022 |
| [C60]P2− | 2.0002 | 1.9999 | 1.9999 | 2.0000 |
| P3HT+ | 2.0034 | 2.0022 | 2.0011 | 2.0022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krajewski, M.; Piotrowski, P.; Mech, W.; Korona, K.P.; Wojtkiewicz, J.; Pilch, M.; Kaim, A.; Drabińska, A.; Kamińska, M. Optical Properties and Light-Induced Charge Transfer in Selected Aromatic C60 Fullerene Derivatives and in Their Bulk Heterojunctions with Poly(3-Hexylthiophene). Materials 2022, 15, 6908. https://doi.org/10.3390/ma15196908
Krajewski M, Piotrowski P, Mech W, Korona KP, Wojtkiewicz J, Pilch M, Kaim A, Drabińska A, Kamińska M. Optical Properties and Light-Induced Charge Transfer in Selected Aromatic C60 Fullerene Derivatives and in Their Bulk Heterojunctions with Poly(3-Hexylthiophene). Materials. 2022; 15(19):6908. https://doi.org/10.3390/ma15196908
Chicago/Turabian StyleKrajewski, Maciej, Piotr Piotrowski, Wojciech Mech, Krzysztof P. Korona, Jacek Wojtkiewicz, Marek Pilch, Andrzej Kaim, Aneta Drabińska, and Maria Kamińska. 2022. "Optical Properties and Light-Induced Charge Transfer in Selected Aromatic C60 Fullerene Derivatives and in Their Bulk Heterojunctions with Poly(3-Hexylthiophene)" Materials 15, no. 19: 6908. https://doi.org/10.3390/ma15196908
APA StyleKrajewski, M., Piotrowski, P., Mech, W., Korona, K. P., Wojtkiewicz, J., Pilch, M., Kaim, A., Drabińska, A., & Kamińska, M. (2022). Optical Properties and Light-Induced Charge Transfer in Selected Aromatic C60 Fullerene Derivatives and in Their Bulk Heterojunctions with Poly(3-Hexylthiophene). Materials, 15(19), 6908. https://doi.org/10.3390/ma15196908