Eccentric Compressive Behavior of Round-Ended Rectangular Concrete-Filled Steel Tubes with Different Central Angles
Abstract
:1. Introduction
2. Research Methods
2.1. Experimental Program
2.1.1. Specimens Preparation
2.1.2. Test Method
2.2. Finite Element Method (FEM)
3. Results and Discussion
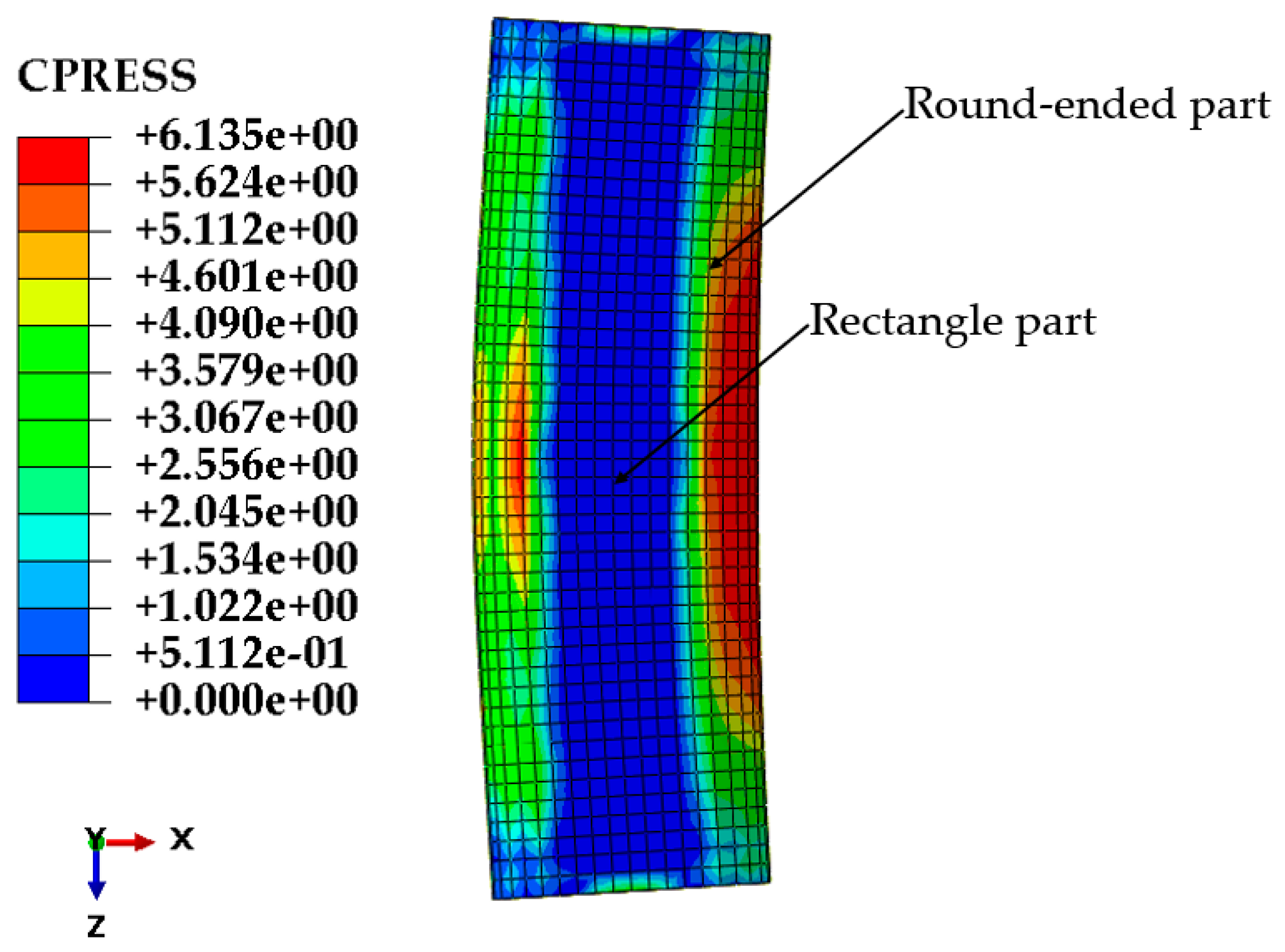
3.1. Failure Model
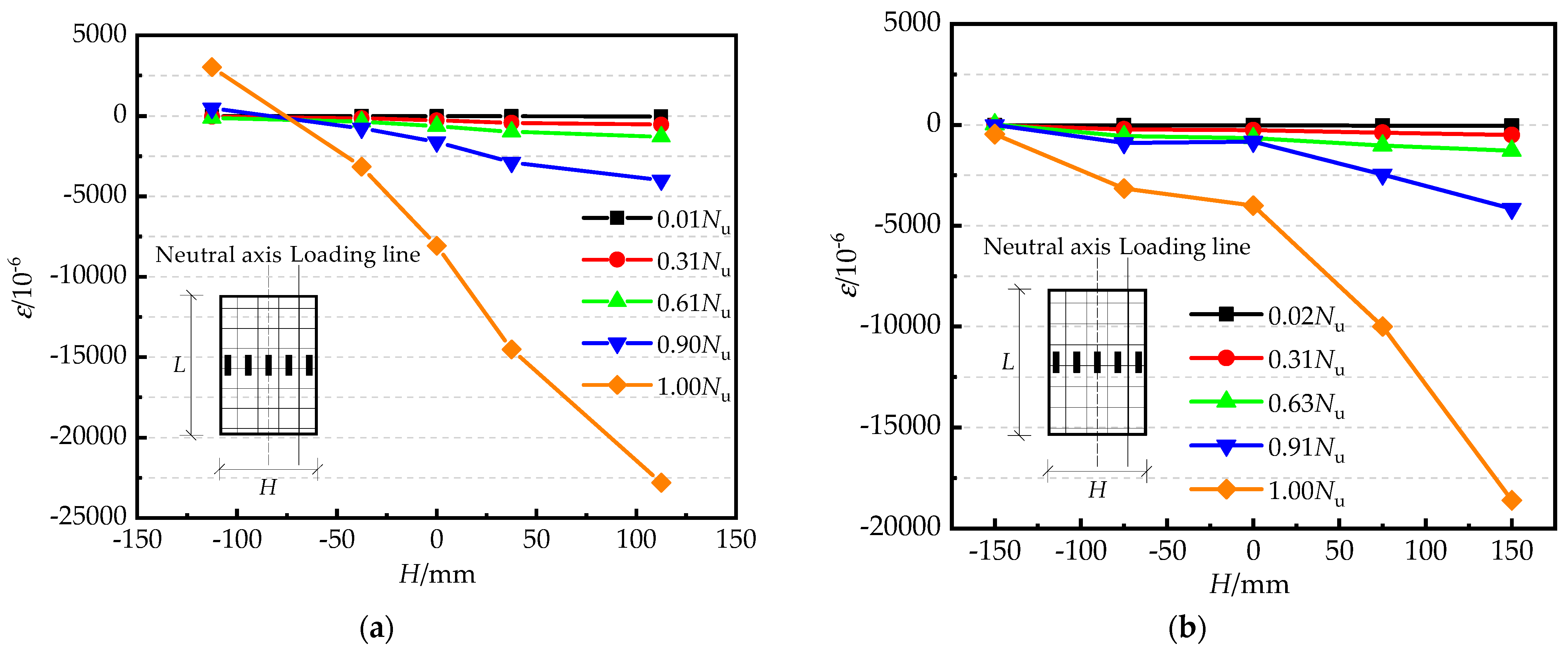
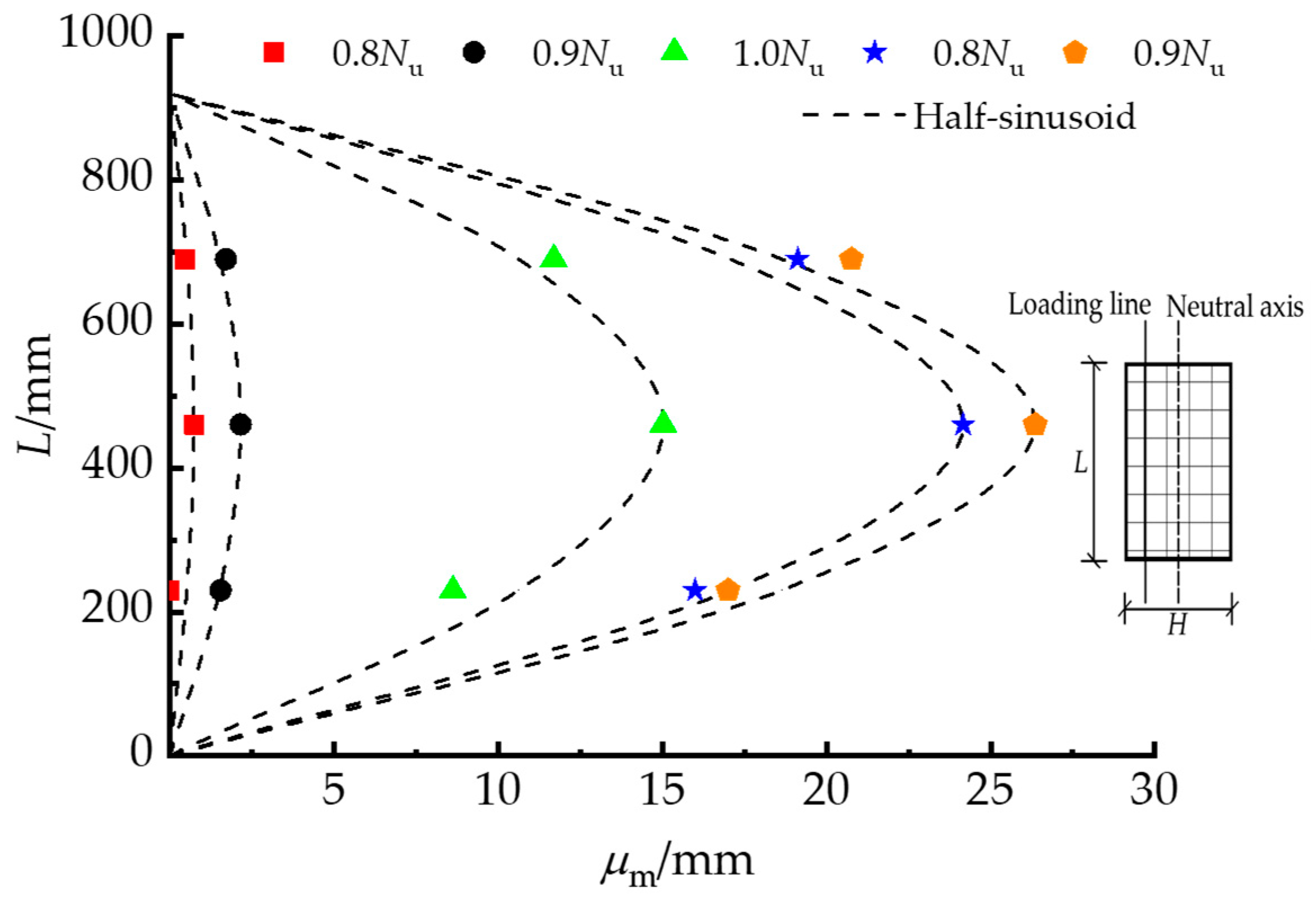
3.2. Axial Load and Mid-Length Lateral Deformation Relationship
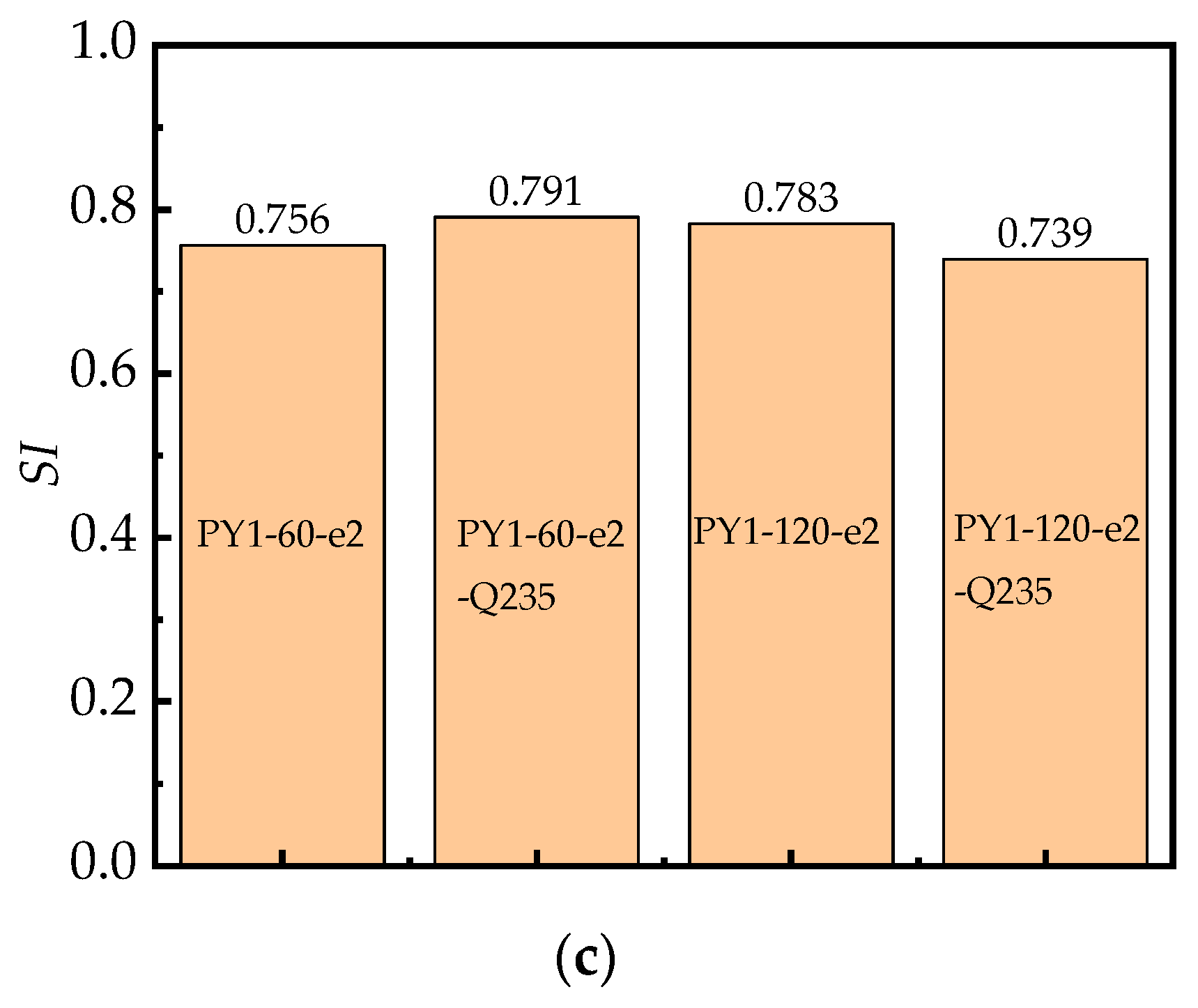
3.3. Parameter Analysis on Material Utilization
3.4. Confinement Effect
3.5. Calculation and Verified of Eccentric Compression Bearing Capacity
4. Conclusions
- (1)
- The typical failure mode of RRCFST stub columns is buckling of the steel tube in the compression zone; this local buckling is accompanied by concrete shear damage when the θ is minor. Increased θ, reduced κ and enhanced fy contribute to improving the local buckling resistance of RRCFSTs, while optimizing the design parameter combinations between them needs further study;
- (2)
- Specimens in FEM and experiment reveal similar deformation and bearing capacity, which represents another possible method to study the eccentric performance of RRCFSTs in addition to experiments: numerical simulations;
- (3)
- Typical ductility quantification methods are ineffective for RRCFSTs under static load due to the favorable post-yield deformation ability, and additional tests are necessary to evaluate their performance and response during dynamic activity;
- (4)
- Material efficiency can be improved with an increased θ and a reduced κ. SI, i.e., material utilization, rises by 0.2% to 3% for every 60° increase in θ, which is particularly noticeable with a large eccentricity. And it reduces by 2.7% to 8.3% for a 0.5 increase in aspect ratio, but there is an unknown tendency as the steel strength changes. SI is always less than 1.0 when axial force and bending moment work together;
- (5)
- Study of the confined effect verified the assumptions discussed in the failure modes. A smaller κ and larger θ contribute to enhancing the confinement effect at the round-ended part, resulting in less local buckling occurring at columns. However, local buckling still occurred in the rectangular part due to the weaker interaction relationship between the steel tube and concrete;
- (6)
- Current codes cannot be used to calculate the eccentric ultimate bearing capacity of RRCFST stub columns with different center angles. A simplified calculating approach has been demonstrated and validated in this study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, Q.H.; Gardner, L.; Han, L.H.; Song, T.Y. Fire performance of steel reinforced concrete-filled stainless steel tubular (CFSST) columns with square cross-sections. Thin-Walled Struct. 2019, 143, 106197. [Google Scholar] [CrossRef]
- Xin, L.; Li, X.; Zhang, Z.; Zhao, L. Seismic behavior of long-span concrete-filled steel tubular arch bridge subjected to near-fault fling-step motions. Eng. Struct. 2019, 180, 148–159. [Google Scholar] [CrossRef]
- Shao, C.; Qi, Q.; Wang, M.; Xiao, Z.; Wei, W.; Hu, C.; Xiao, L. Experimental study on the seismic performance of round-ended hollow piers. Eng. Struct. 2019, 195, 309–323. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, S.; Li, P.; Liu, C. Sectional Optimization of Round-ended Rectangular Concrete-filled Steel Tubular Columns Under Eccentric Compression. J. Archit. Civ. Eng. 2021, 38, 1–12. [Google Scholar] [CrossRef]
- Murali, G.; Abid, S.R.; Amran, Y.H.M.; Abdelgader, H.S.; Fediuk, R.; Susrutha, A.; Poonguzhali, K. Impact performance of novel multi-layered prepacked aggregate fibrous composites under compression and bending. Structures 2020, 28, 1502–1515. [Google Scholar] [CrossRef]
- Han, L. Concrete Filled Steel Tubular Structure: Theory and Practice; Science Press: Beijing, China, 2016. [Google Scholar]
- Jia, H.J.; Dai, H. Numeric analysis on seismic performance of RC round-ended piers with HRBF500 steel bars. Appl. Mech. Mater. 2012, 226–228, 1577–1580. [Google Scholar] [CrossRef]
- Cha, S.L.; Lee, J.S.; Park, C.K.; Kim, J.K.; Kwon, S.H. Experimental investigation on behavior of rectangular concrete-filled tubular columns considering diaphragms. Materials 2020, 13, 4412. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, J.; Wang, W.; Wang, Z. Performance and design of eccentrically-loaded concrete- fi lled round-ended elliptical hollow section stub columns. J. Constr. Steel Res. 2018, 150, 99–114. [Google Scholar] [CrossRef]
- Alatshan, F.; Osman, S.A.; Mashiri, F.; Hamid, R. Explicit simulation of circular CFST stub columns with external steel confinement under axial compression. Materials 2020, 13, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Wu, Y.; Yu, X.; Gao, Y. Behavior of concrete-filled round-ended steel tubular (CFRST) column under eccentric compression. J. Build. Struct. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Ma, X.; Shen, Q.; Sheng, M. Study on equivalent constitutive relation and axial compressive behavior of round-ended elliptical concrete-filled steel tube columns. J. He Fei Univ. Technol. Nat. Sci. 2019, 42, 74–80, 87. [Google Scholar]
- Ren, Z.; Wang, D. Behavior of Round-ended Concrete filled Steel Tube Stub Column with Different Central Angles Under Axial Load. J. Archit. Civ. Eng. 2020, 37, 77–87. [Google Scholar] [CrossRef]
- Xie, J.X.; Lu, Z.A. Numerical simulation and test study on non-uniform area of round-ended CFST tubular tower. ICIC 2010 -3rd Int. Conf. Inf. Comput. 2010, 4, 19–22. [Google Scholar] [CrossRef]
- Gu, L.; Ding, F.; Fu, L.; Li, G. Mechanical Behavior of Concrete-filled Round-ended Steel Tubular Stub Columns Under Axial Load. China J. Highw. Transp. 2014, 27, 57–63. [Google Scholar] [CrossRef]
- Xie, E.; Wang, Z.; Lin, S.; Zhou, J. Mechanism analysis on concrete-filled round-end steel tubular stub columns under axial load. J. Fuzhou Univ. Nat. Sci. Ed. 2015, 43, 517–522. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Patel, V.I. Round-ended rectangular concrete-filled steel tubular short columns: FE investigation under axial compression. J. Constr. Steel Res. 2018, 140, 222–236. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, L.; Xu, L. An efficient approach for numerical simulation of concrete-filled round-ended steel tubes. J. Constr. Steel Res. 2020, 170, 106086. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Q. Numerical analysis and design of thin-walled RECFST stub columns under axial compression. Thin Walled Struct. 2018, 129, 166–182. [Google Scholar] [CrossRef]
- Golewski, G.L. Evaluation of fracture processes under shear with the use of DIC technique in fly ash concrete and accurate measurement of crack path lengths with the use of a new crack tip tracking method. Measurement 2021, 181, 109632. [Google Scholar] [CrossRef]
- Li, G.C.; Chen, B.W.; Yang, Z.J.; Liu, Y.P.; Feng, Y.H. Experimental and numerical behavior of eccentrically loaded square concrete-filled steel tubular long columns made of high-strength steel and concrete. Thin-Walled Struct. 2021, 159, 107289. [Google Scholar] [CrossRef]
- JGJ55; Specification for Mix Proportion Design of Ordinary Concrete. Architecture & Building Press: Beijing, China, 2011.
- GB50010-2010; Code for Design of Concrete Structures. Architecture& Building Press: Beijing, China, 2010.
- Zhang, F.; Ma, J.; Nan, Y. Parameters Selection and Verification Calculation of Concrete Plastic Damage Model. China Concr. Cem. Prod. 2021, 1, 7–11. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A Plastic-Damage Model. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Z.; Xue, J.; Chen, Y.; Liu, Z. A review of experimental results of steel reinforced recycled aggregate concrete members and structures in China (2010–2016). Procedia Eng. 2017, 210, 109–119. [Google Scholar] [CrossRef]
- Faxing, D.; Lei, F.; Zhiwu, Y.; Gang, L. Mechanical performances of concrete-filled steel tubular stub columns with round ends under axial loading. Thin-Walled Struct. 2015, 97, 22–34. [Google Scholar] [CrossRef]
- McCann, F.; Gardner, L.; Qiu, W. Experimental study of slender concrete-filled elliptical hollow section beam-columns. J. Constr. Steel Res. 2015, 113, 185–194. [Google Scholar] [CrossRef]
- Eurocode 4; Design of Composite Steel and Concrete Structure. British Standards Institution: London, UK, 1994.
- Ren, Z.; Wang, G.; Li, P. Study on Bearing Capacity of Concrete-filled Round-ended Steel Tubular Stub with Variable Center Angle Under Axial Compression. J. Wuhan Univ. Technol. 2020, 42, 29–36. [Google Scholar] [CrossRef]
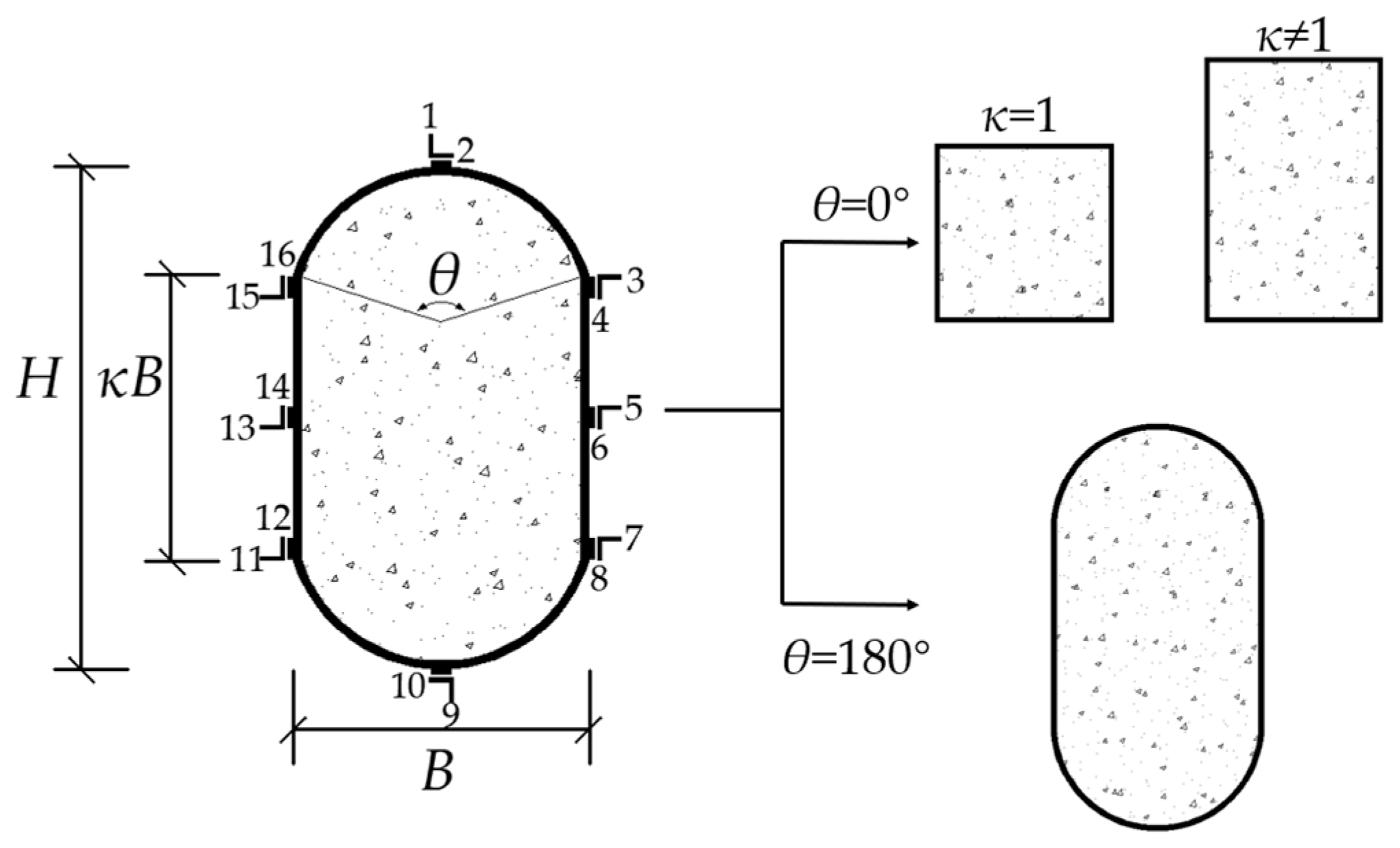
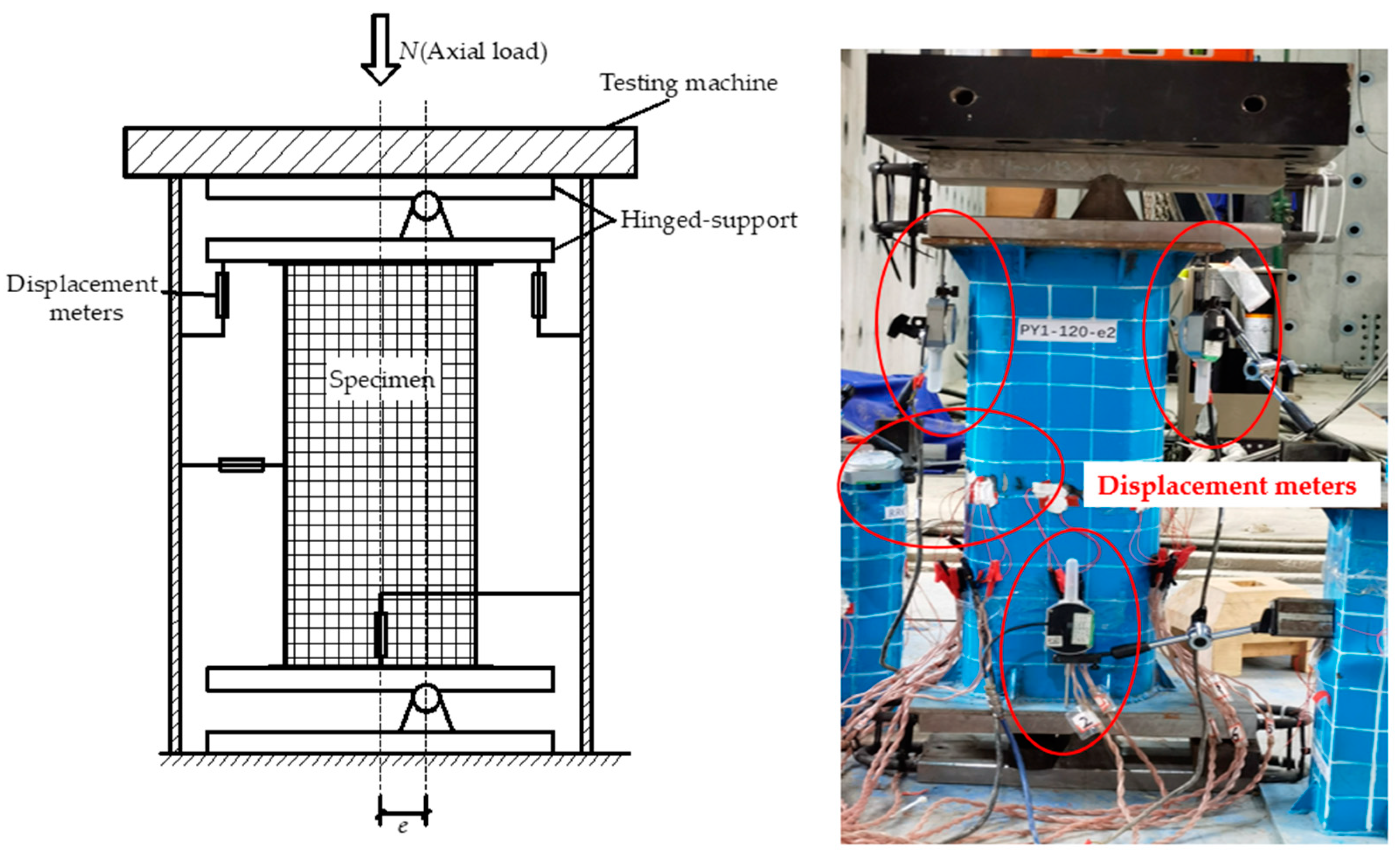
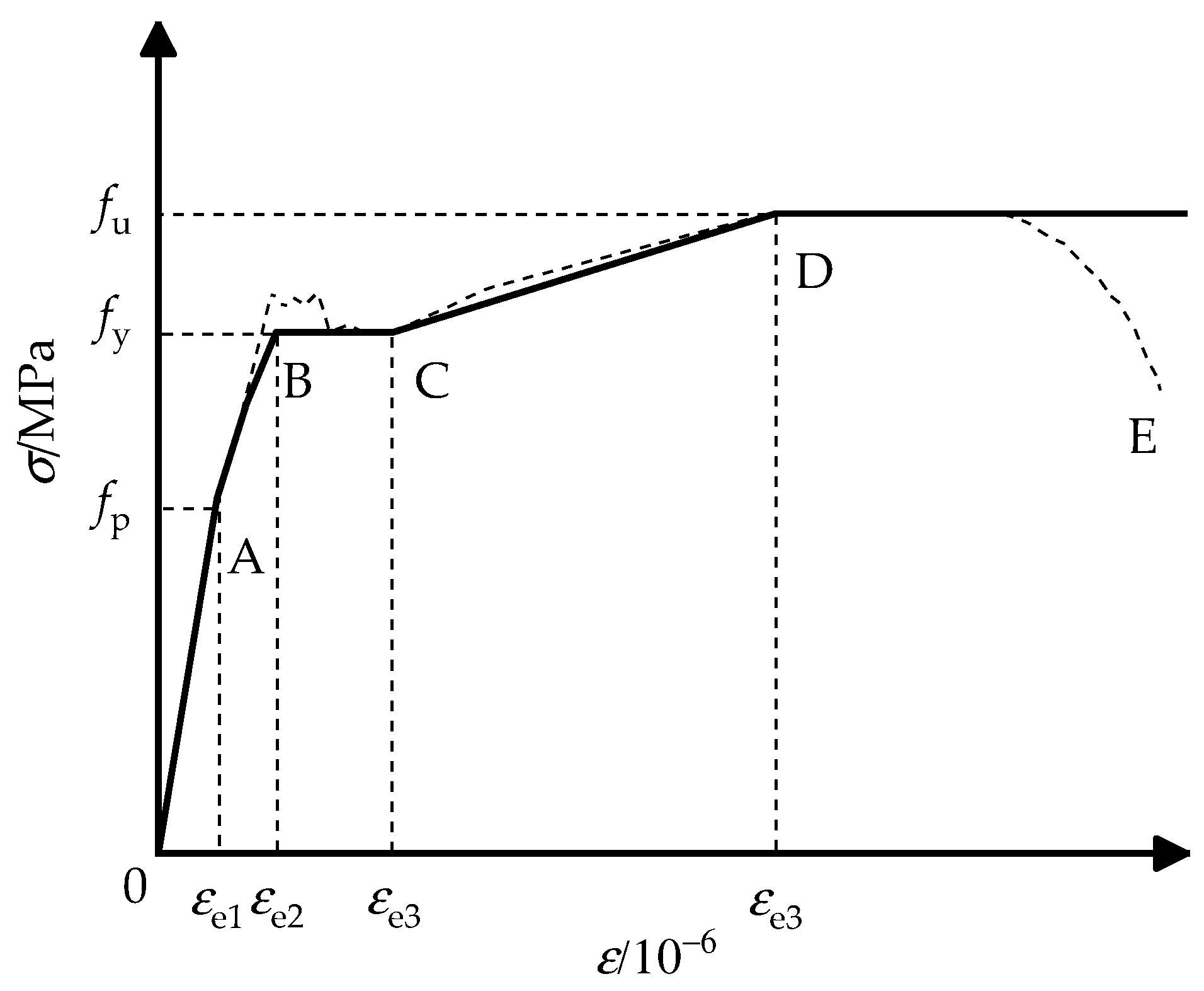
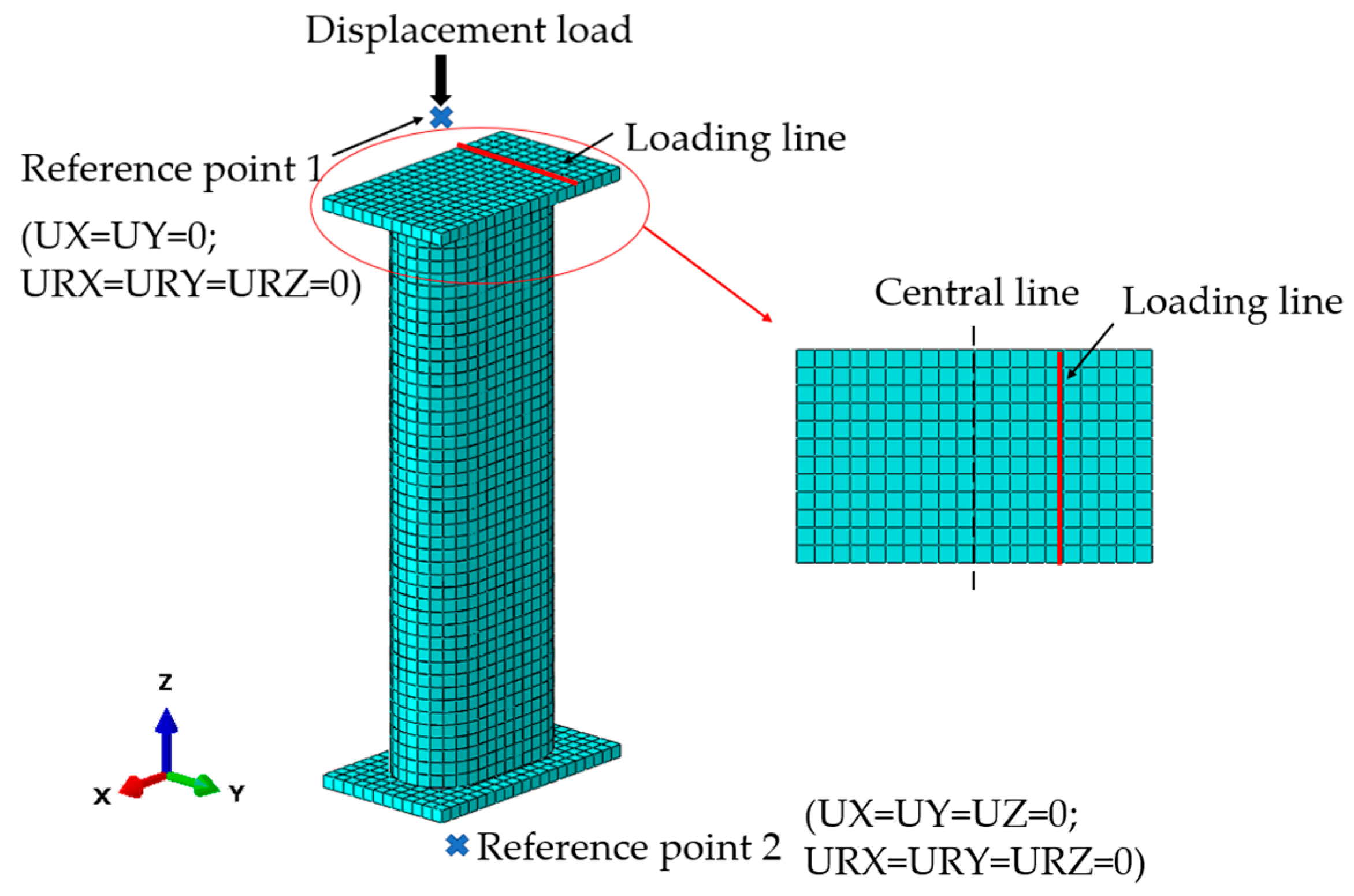






| Identifier | H × B × L/mm3 | (κ, θ) | i/mm | e/2i | e/mm |
|---|---|---|---|---|---|
| PY1-0-e1 | 153 × 148 × 450 | (1, 0) | 43.35 | 0.15 | 13.01 |
| PY1-60-e1 | 189 × 153 × 550 | (1, 60) | 51.48 | 0.15 | 15.44 |
| PYRE1-60-e1 | 187 × 151 × 550 | (1, 60) | 51.48 | 0.15 | 15.44 |
| PY1-120-e1 | 232 × 152 × 650 | (1, 120) | 62.19 | 0.15 | 18.66 |
| PYRE1-120-e1 | 235 × 150 × 650 | (1, 120) | 62.19 | 0.15 | 18.66 |
| PY0.5-180-e1-Q235 | 225 × 150 × 675 | (1, 180) | 57.96 | 0.15 | 17.39 |
| PY1-180-e1-Q235 | 300 × 150 × 920 | (1, 180) | 79.02 | 0.15 | 25 |
| PY1.5-180-e1-Q235 | 375 × 150 × 1160 | (1.5, 180) | 100.31 | 0.15 | 30.09 |
| PY1-60-e2 | 188 × 152 × 550 | (1, 60) | 51.48 | 0.3 | 30.89 |
| PY1-60-e2-Q235 | 188 × 152 × 550 | (1, 60) | 51.48 | 0.3 | 30.89 |
| PY1-120-e2 | 237 × 150 × 650 | (1, 120) | 62.19 | 0.3 | 37.31 |
| PY1-120-e2-Q235 | 235 × 150 × 650 | (1, 120) | 62.19 | 0.3 | 37.31 |
| PY0.5-60-e2 | 110 × 153 × 445 | (0.5, 60) | 30.1 | 0.3 | 18.06 |
| PY0.5-120-e2 | 156 × 155 × 500 | (0.5, 120) | 41 | 0.3 | 24.60 |
| PY0.5-180-e2 | 224 × 152 × 650 | (0.5, 180) | 58 | 0.3 | 34.80 |
| Identifier | fy/MPa | fu/MPa | Es/GPa | γ |
|---|---|---|---|---|
| Q235 | 279 | 418.5 | 225 | 0.27 |
| Q345 | 361 | 541.5 | 240 | 0.27 |
| Identifier | Nuf | Nue | Ratio (Nuf/Nue) |
|---|---|---|---|
| PY1-0-e1 | 1140 | 1187 | 0.960 |
| PY1-60-e1 | 1301 | 1287 | 1.011 |
| PYRE1-60-e1 | 1301 | 1306 | 0.996 |
| PY1-120-e1 | 1510 | 1450 | 1.041 |
| PYRE1-120-e1 | 1510 | 1489 | 1.014 |
| PY0.5-180-e1-Q235 | 1406 | 1478 | 0.951 |
| PY1-180-e1-Q235 | 1758 | 1638 | 1.073 |
| PY1.5-180-e1-Q235 | 1825 | 1732 | 1.054 |
| PY1-60-e2 | 1086 | 1136 | 0.956 |
| PY1-60-e2-Q235 | 957 | 981 | 0.976 |
| PY1-120-e2 | 1275 | 1248 | 1.022 |
| PY1-120-e2-Q235 | 1116 | 1020 | 1.094 |
| PY0.5-60-e2 | 715 | 717 | 0.997 |
| PY0.5-120-e2 | 952 | 954 | 0.998 |
| PY0.5-180-e2 | 1278 | 1205 | 1.061 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Li, Q.; Wang, G.; Wei, W.; Abbas, M.A.A.M. Eccentric Compressive Behavior of Round-Ended Rectangular Concrete-Filled Steel Tubes with Different Central Angles. Materials 2022, 15, 456. https://doi.org/10.3390/ma15020456
Ren Z, Li Q, Wang G, Wei W, Abbas MAAM. Eccentric Compressive Behavior of Round-Ended Rectangular Concrete-Filled Steel Tubes with Different Central Angles. Materials. 2022; 15(2):456. https://doi.org/10.3390/ma15020456
Chicago/Turabian StyleRen, Zhigang, Qi Li, Gaoyu Wang, Wei Wei, and Mohammed A. A. M. Abbas. 2022. "Eccentric Compressive Behavior of Round-Ended Rectangular Concrete-Filled Steel Tubes with Different Central Angles" Materials 15, no. 2: 456. https://doi.org/10.3390/ma15020456
APA StyleRen, Z., Li, Q., Wang, G., Wei, W., & Abbas, M. A. A. M. (2022). Eccentric Compressive Behavior of Round-Ended Rectangular Concrete-Filled Steel Tubes with Different Central Angles. Materials, 15(2), 456. https://doi.org/10.3390/ma15020456







