Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics
Abstract
:1. Introduction
2. Mathematical Modeling
3. Physical Configuration and Numerical Scheme
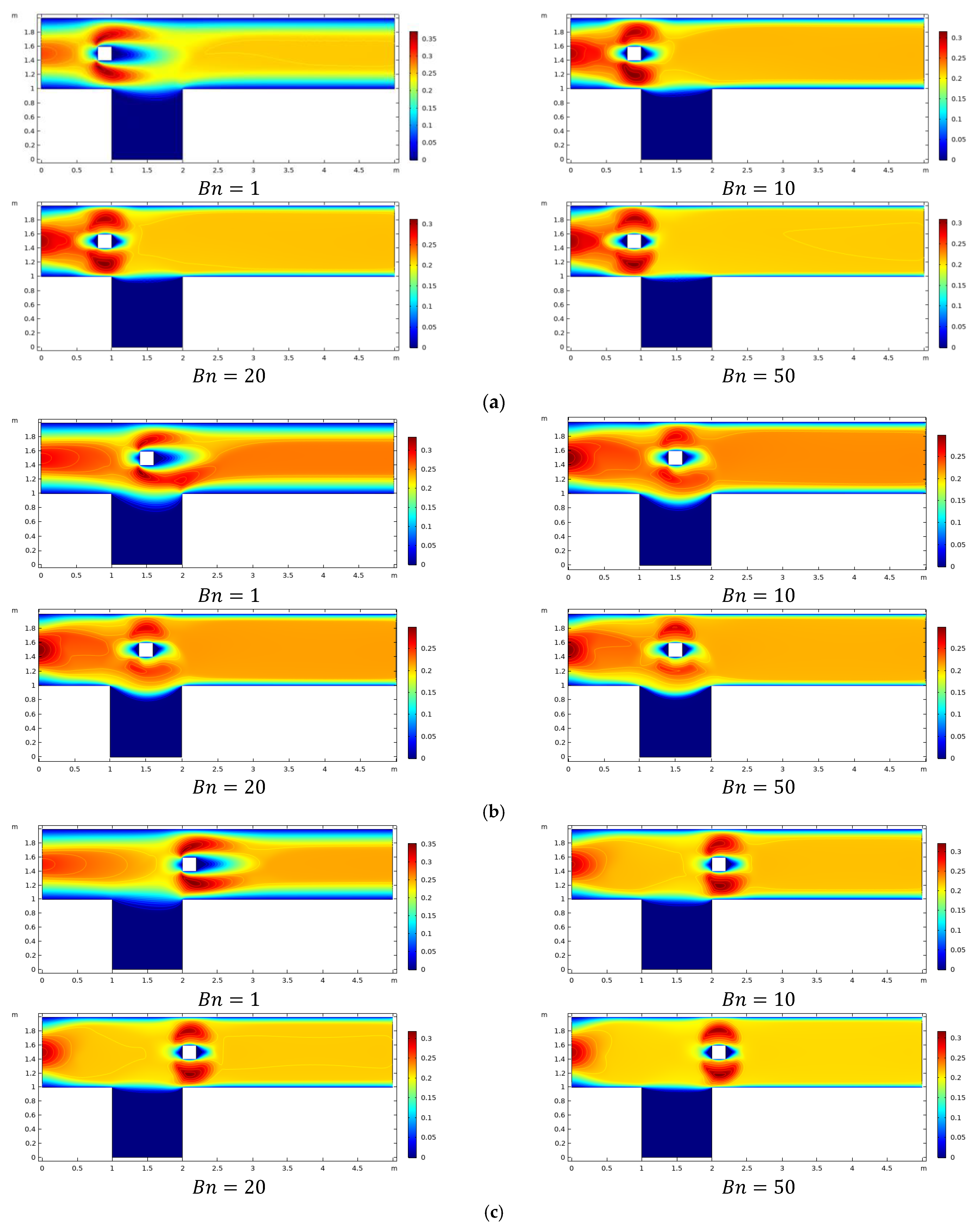
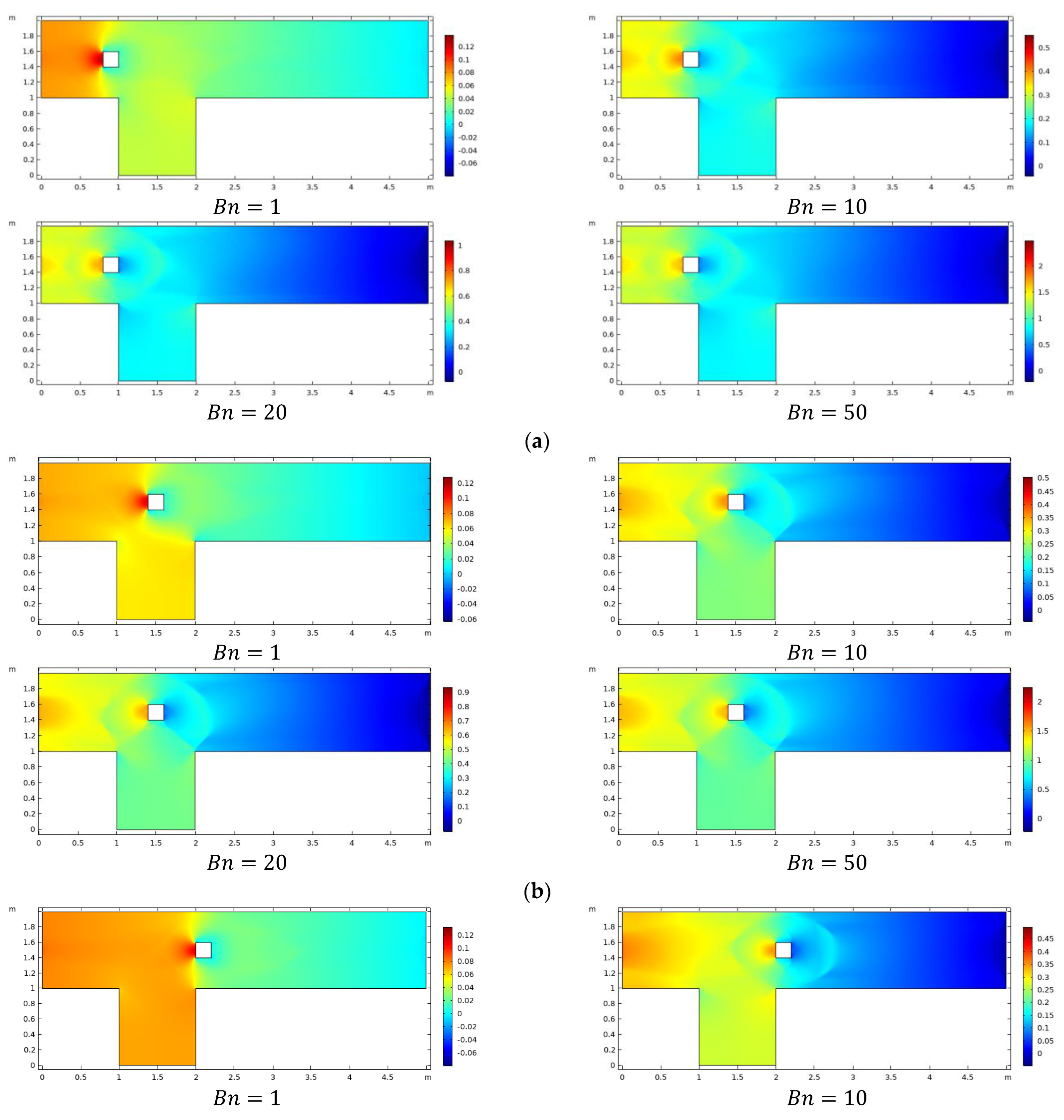
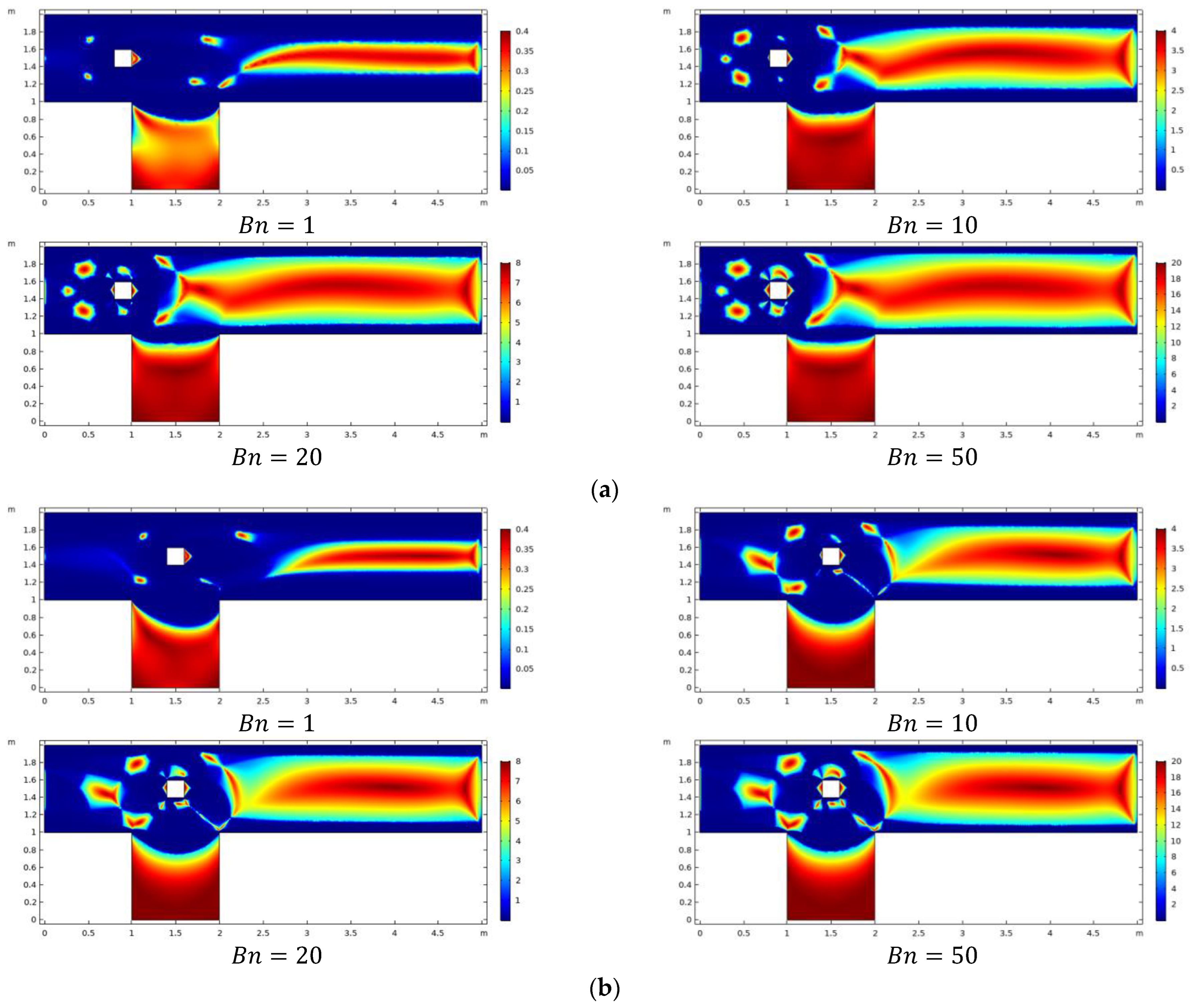
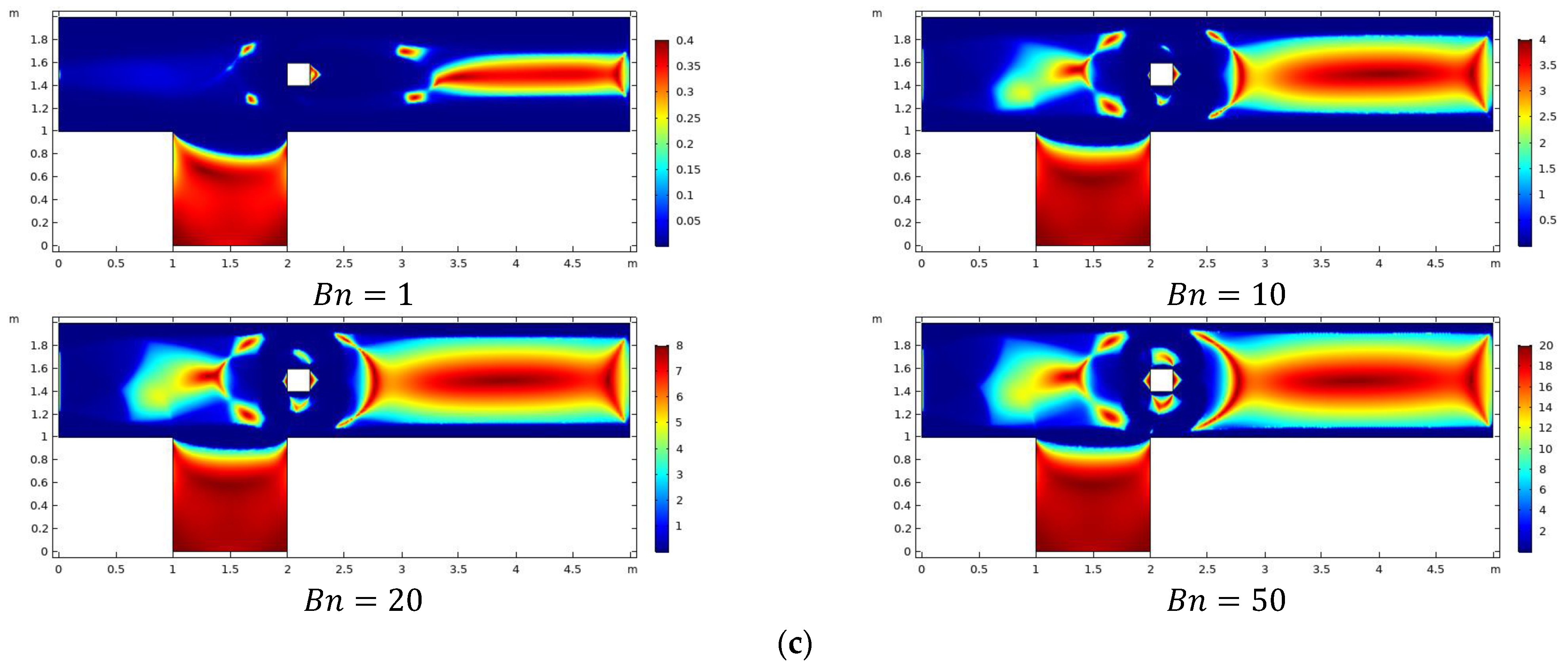
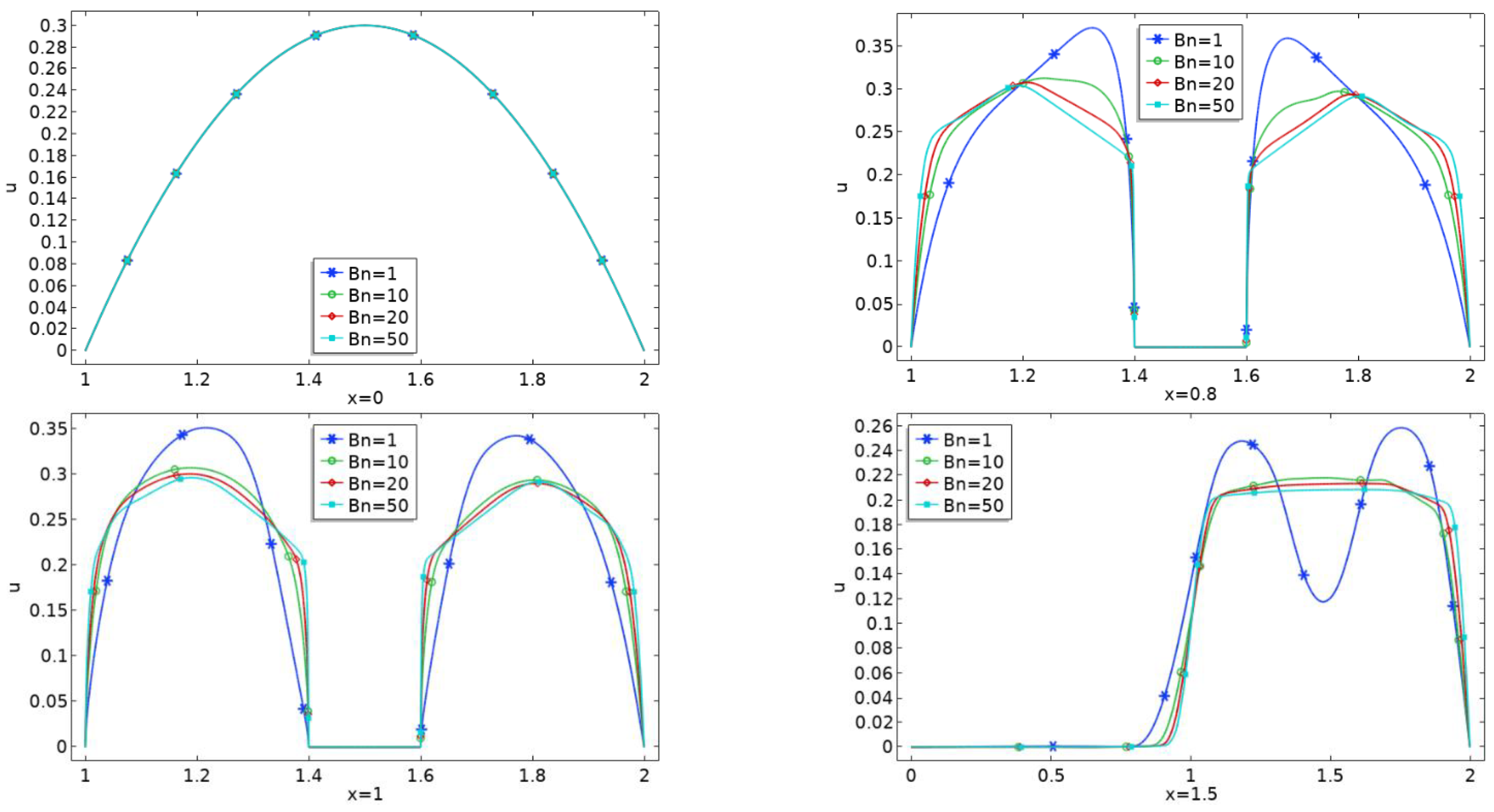
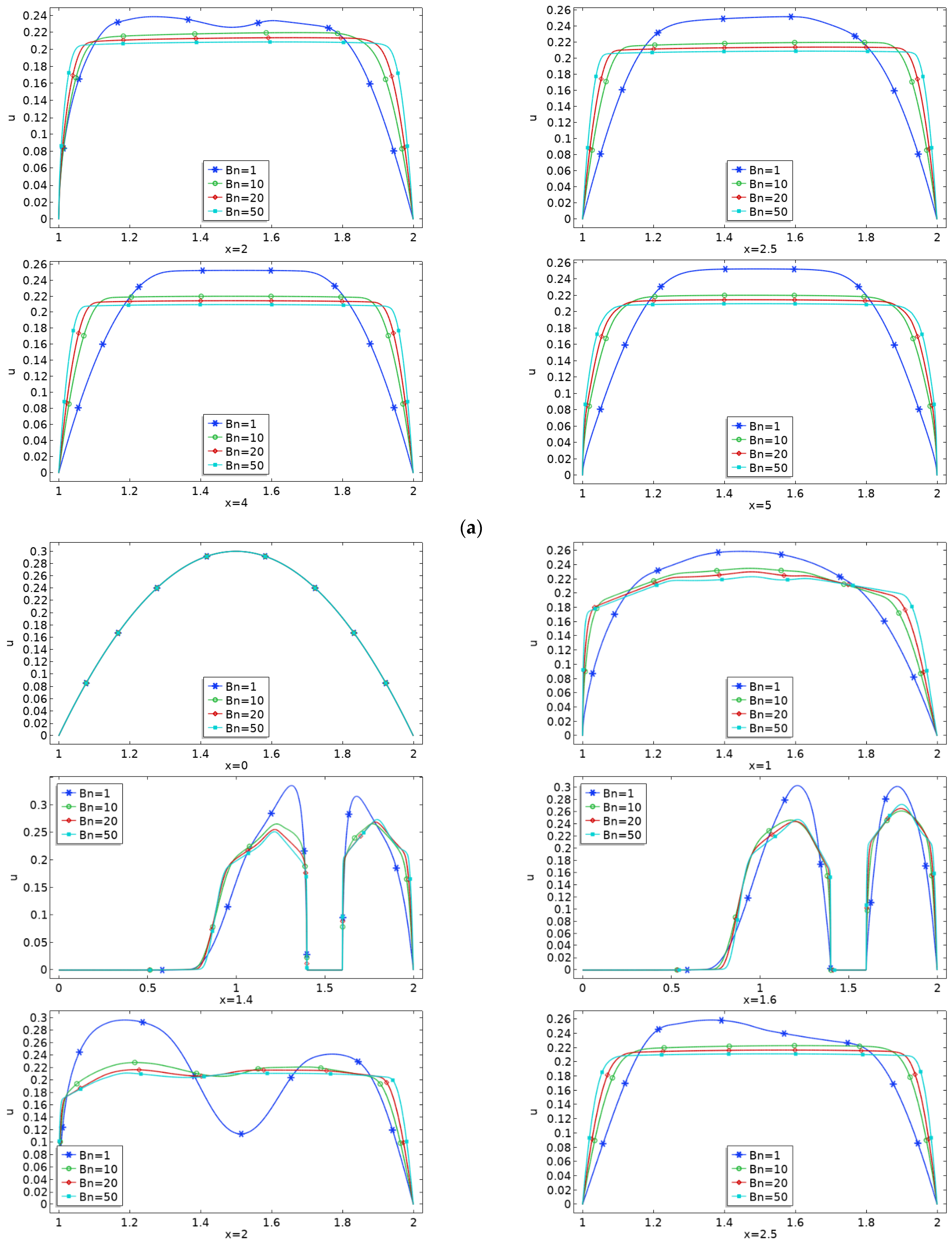
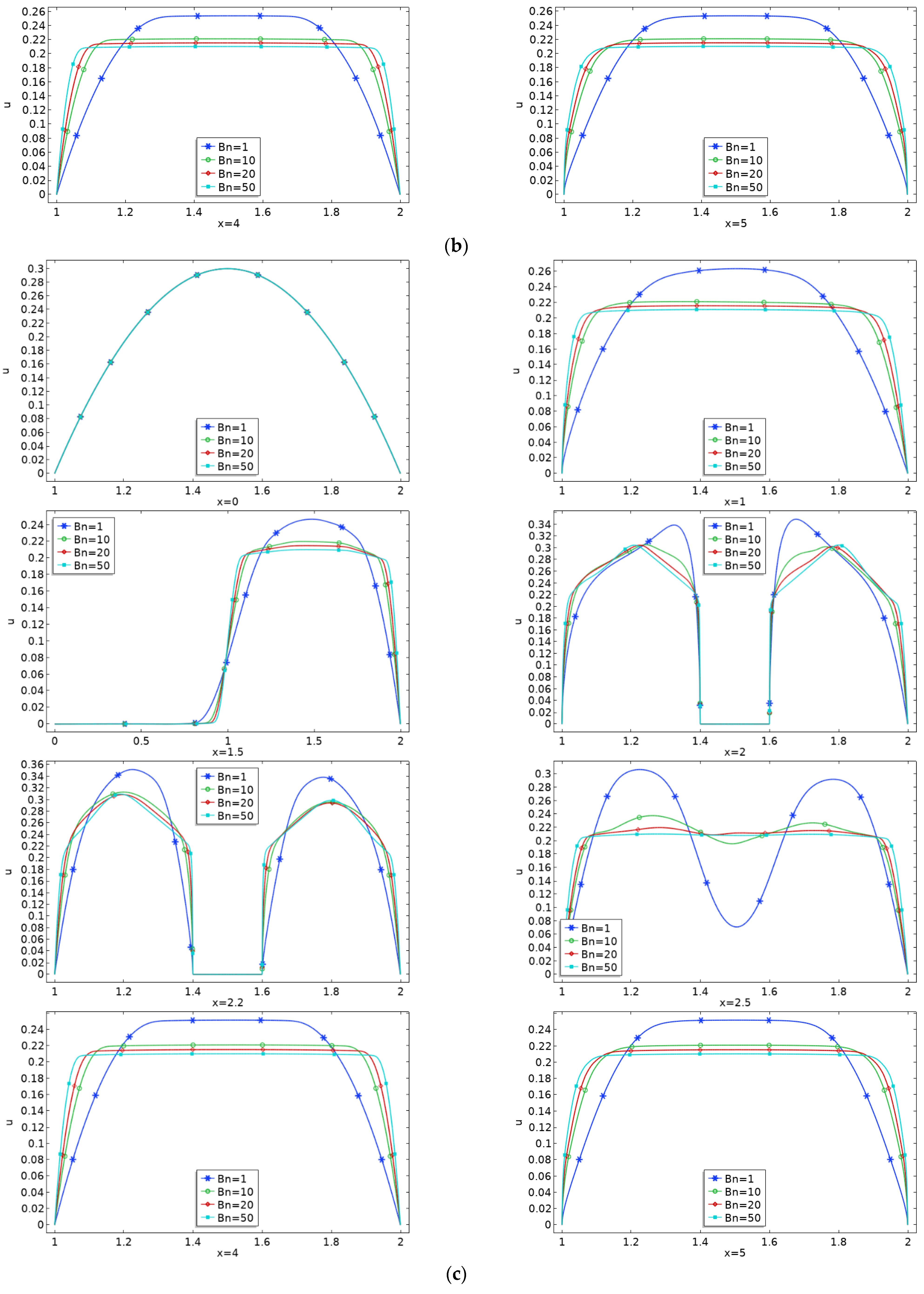
4. Results and Discussions
5. Conclusions
- As the Bn increases, pressure drops become more vigorous for all obstacle positions.
- The pressure drop is influenced by the placement of the obstacle, which increases at C1, lowers at C2, and finally boosts at C3.
- Lift coefficient changes sign-on C2 when Bn exceeds the value Bn = 10 while on other grids, sign change does not occur.
- Negative lift coefficients are obtained when upward forces dominate, while positive values are obtained when downward forces dominate.
- Pressure has stagnant values at the front of the obstacle where fluid is interacting with it.
- Plug zone enhances in the channel downstream of the obstacle with augmentation in Bn limiting the shear zone in the vicinity of the obstacle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Yield Stress | |
| Plastic Viscosity | |
| Stress Tensor | |
| Rate of Strain Tensor | |
| Dimensional Velocity Vector | |
| Dimensionless Velocity Vector | |
| Velocity at inlet | |
| Average Velocity | |
| Shear Rate | |
| Dimensional pressure | |
| Dimensionless pressure | |
| Dimensional Stress growth parameter | |
| M | Dimensionless Stress growth parameter |
| Reynold number | |
| Bingham number | |
| # EL | Number of Elements |
| # DOF | Number of degrees of freedom |
| Drag Coefficient | |
| Lift Coefficient |
References
- Shwedov, F.N. La Rigidite de liquids. Rapp. Congr. Intern. Phys. Paris 1900, 1, 478–483. [Google Scholar]
- Bingham, E.C. Fluidity and Plasticity; McGraw-Hill: New York, NY, USA, 1922; Volume 2. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Colloid Polym. Sci. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Casson, N. A Flow Equation for Pigment-Oil Suspensions of the Printing Ink type. Rheol. Disperse Syst. 1959, 3, 84–104. [Google Scholar]
- Bird, R.B.; Dai, G.; Yarusso, B.J. The Rheology and Flow of Viscoplastic Materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Fluid Mechanics. In Dynamics of Polymeric Liquids, 2nd ed.; John Wiley and Sons Inc.: New York, NY, USA, 1987; Volume 1, p. 784. [Google Scholar]
- Bercovier, M.; Engelman, M. A finite-element method for incompressible non-Newtonian flows. J. Comput. Phys. 1980, 36, 313–326. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Flows of Materials with Yield. J. Rheol. 1987, 31, 385–404. [Google Scholar] [CrossRef]
- Barnes, H.A. The yield stress—A review—Everything flows? J. Nonnewton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Syrakos, A.; Georgiou, G.C.; Alexandrou, A.N. Solution of the square lid-driven cavity flow of a Bingham plastic using the finite volume method. J. Non-Newton. Fluid Mech. 2013, 195, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Mitsoulis, E.; Zisis, T. Flow of Bingham plastics in a lid-driven square cavity. J. Non-Newton. Fluid Mech. 2001, 101, 173–180. [Google Scholar] [CrossRef]
- Dean, E.J.; Glowinski, R.; Guidoboni, G. On the numerical simulation of Bingham visco-plastic flow: Old and new results. J. Non-Newton. Fluid Mech. 2007, 142, 36–62. [Google Scholar] [CrossRef]
- Kefayati, G.; Huilgol, R. Lattice Boltzmann method for the simulation of the steady flow of a Bingham fluid in a pipe of square cross-section. Eur. J. Mech.-B/Fluids 2017, 65, 412–422. [Google Scholar] [CrossRef]
- Kefayati, G. FDLBM simulation of magnetic field effect on non-Newtonian blood flow in a cavity driven by the motion of two facing lids. Powder Technol. 2014, 253, 325–337. [Google Scholar] [CrossRef]
- Mahmood, R.; Kousar, N.; Yaqub, M.; Jabeen, K. Numerical Simulations of the Square Lid Driven Cavity Flow of Bingham Fluids Using Nonconforming Finite Elements Coupled with a Direct Solver. Adv. Math. Phys. 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Obando, B.; Takahashi, T. Existence of weak solutions for a Bingham fluid-rigid body system. Ann. De L’institut Henri Poincaré C Anal. Non Linéaire 2018, 36, 1281–1309. [Google Scholar] [CrossRef] [Green Version]
- Nouar, C.; Frigaard, I. Nonlinear stability of Poiseuille flow of a Bingham fluid: Theoretical results and comparison with phenomenological criteria. J. Non-Newton. Fluid Mech. 2001, 100, 127–149. [Google Scholar] [CrossRef]
- Borrelli, A.; Patria, M.C.; Piras, E. Spatial decay estimates in the problem of entry flow for a Bingham fluid filling a pipe. Math. Comput. Model. 2004, 40, 23–42. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Zhu, K.-Q. Couette–Poiseuille flow of Bingham fluids between two porous parallel plates with slip conditions. J. Non-Newton. Fluid Mech. 2008, 153, 1–11. [Google Scholar] [CrossRef]
- Barletta, A.; Magyari, E. Buoyant Couette–Bingham flow between vertical parallel plates. Int. J. Therm. Sci. 2008, 47, 811–819. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P. The Effect of Internal and External Heating on the Free Convective Flow of a Bingham Fluid in a Vertical Porous Channel. Fluids 2019, 4, 95. [Google Scholar] [CrossRef] [Green Version]
- Patel, N.; Ingham, D. Analytic solutions for the mixed convection flow of non-newtonian fluids in parallel plate ducts. Int. Commun. Heat Mass Transf. 1994, 21, 75–84. [Google Scholar] [CrossRef]
- Schäfer, M.; Turek, S.; Durst, F.; Krause, E.; Rannacher, R. Benchmark Computations of Laminar Flow Around a Cylinder. Notes Numer. Fluid Mech. (NNFM) 1996, 48, 547–566. [Google Scholar]
- Williamson, C.H.K. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Hussain, S.; Schieweck, F.; Turek, S. An Efficient and Stable Finite Element Solver of Higher Order in Space and Time for Non-Stationary Incompressible Flow. Int. J. Numer. Meth. Fluids 2013, 73, 927–952. [Google Scholar] [CrossRef]
- Kanaris, N.; Grigoriadis, D.; Kassinos, S. Three dimensional flow around a circular cylinder confined in a plane channel. Phys. Fluids 2011, 23, 064106. [Google Scholar] [CrossRef] [Green Version]
- Rajani, B.; Kandasamy, A.; Majumdar, S. Numerical simulation of laminar flow past a circular cylinder. Appl. Math. Model. 2009, 33, 1228–1247. [Google Scholar] [CrossRef]
- Adachi, K.; Yoshioka, N. On creeping flow of a visco-plastic fluid past a circular cylinder. Chem. Eng. Sci. 1973, 28, 215–226. [Google Scholar] [CrossRef]
- Tokpavi, D.L.; Magnin, A.; Jay, P. Very slow flow of Bingham viscoplastic fluid around a circular cylinder. J. Non-Newton. Fluid Mech. 2008, 154, 65–76. [Google Scholar] [CrossRef]
- Tokpavi, D.L.; Jay, P.; Magnin, A.; Jossic, L. Experimental study of the very slow flow of a yield stress fluid around a circular cylinder. J. Non-Newton. Fluid Mech. 2009, 164, 35–44. [Google Scholar] [CrossRef]
- Nirmalkar, N.; Chhabra, R.; Poole, R. Laminar forced convection heat transfer from a heated square cylinder in a Bingham plastic fluid. Int. J. Heat Mass Transf. 2013, 56, 625–639. [Google Scholar] [CrossRef]
- Mossaz, S.; Jay, P.; Magnin, A. Non-recirculating and recirculating inertial flows of a viscoplastic fluid around a cylinder. J. Non-Newton. Fluid Mech. 2012, 177–178, 64–75. [Google Scholar] [CrossRef]
- Syrakos, A.; Georgiou, G.C.; Alexandrou, A.N. Thixotropic flow past a cylinder. J. Non-Newton. Fluid Mech. 2015, 220, 44–56. [Google Scholar] [CrossRef] [Green Version]
- Syrakos, A.; Georgiou, G.C.; Alexandrou, A.N. Cessation of the lid-driven cavity flow of Newtonian and Bingham fluids. Rheol. Acta 2016, 55, 51–66. [Google Scholar] [CrossRef]
- Abbasi, W.S.; Islam, S.U.; Faiz, L.; Rahman, H. Numerical investigation of transitions in flow states and variation in aerodynamic forces for flow around square cylinders arranged inline. Chin. J. Aeronaut. 2018, 31, 2111–2123. [Google Scholar] [CrossRef]
- Mahmood, R.; Bilal, S.; Majeed, A.H.; Khan, I.; Sherif, E.S.M. A Comparative Analysis of Flow Features of Newtonian and Power Law Material: A New Configuration. J. Mater. Res. Technol. 2020, 9, 1978–1987. [Google Scholar] [CrossRef]
- Khan, I.; Memon, A.A.; Memon, M.A.; Bhatti, K.; Shaikh, G.M.; Baleanu, D.; Alhussain, Z.A. Finite Element Least Square Technique for Newtonian Fluid Flow through a Semicircular Cylinder of Recirculating Region via COMSOL Multiphysics. J. Math. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Soto, H.P.; Martins-Costa, M.L.; Fonseca, C.; Frey, S. A numerical investigation of inertia flows of Bingham-Papanastasiou fluids by an extra stress-pressure-velocity galerkin least-squares method. J. Braz. Soc. Mech. Sci. Eng. 2010, 32, 450–460. [Google Scholar] [CrossRef] [Green Version]
- Majeed, A.H.; Jarad, F.; Mahmood, R.; Saddique, I. Topological Characteristics of Obstacles and Nonlinear Rheological Fluid Flow in Presence of Insulated Fins: A Fluid Force Reduction Study. Math. Probl. Eng. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Ferronato, M. Preconditioning for Sparse Linear Systems at the Dawn of the 21st Century: History, Current Developments, and Future Perspectives. ISRN Appl. Math. 2012, 2012, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Mehmood, A.; Mahmood, R.; Majeed, A.H.; Awan, F.J. Flow of the Bingham-Papanastasiou Regularized Material in a Channel in the Presence of Obstacles: Correlation between Hydrodynamic Forces and Spacing of Obstacles. Model. Simul. Eng. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Majeed, A.H.; Mahmood, R.; Abbasi, W.S.; Usman, K. Numerical Computation of MHD Thermal Flow of Cross Model over an Elliptic Cylinder: Reduction of Forces via Thickness Ratio. Math. Probl. Eng. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Mahmood, R.; Bilal, S.; Majeed, A.H.; Khan, I.; Nisar, K.S. CFD analysis for characterization of non-linear power law material in a channel driven cavity with a square cylinder by measuring variation in drag and lift forces. J. Mater. Res. Technol. 2020, 9, 3838–3846. [Google Scholar] [CrossRef]

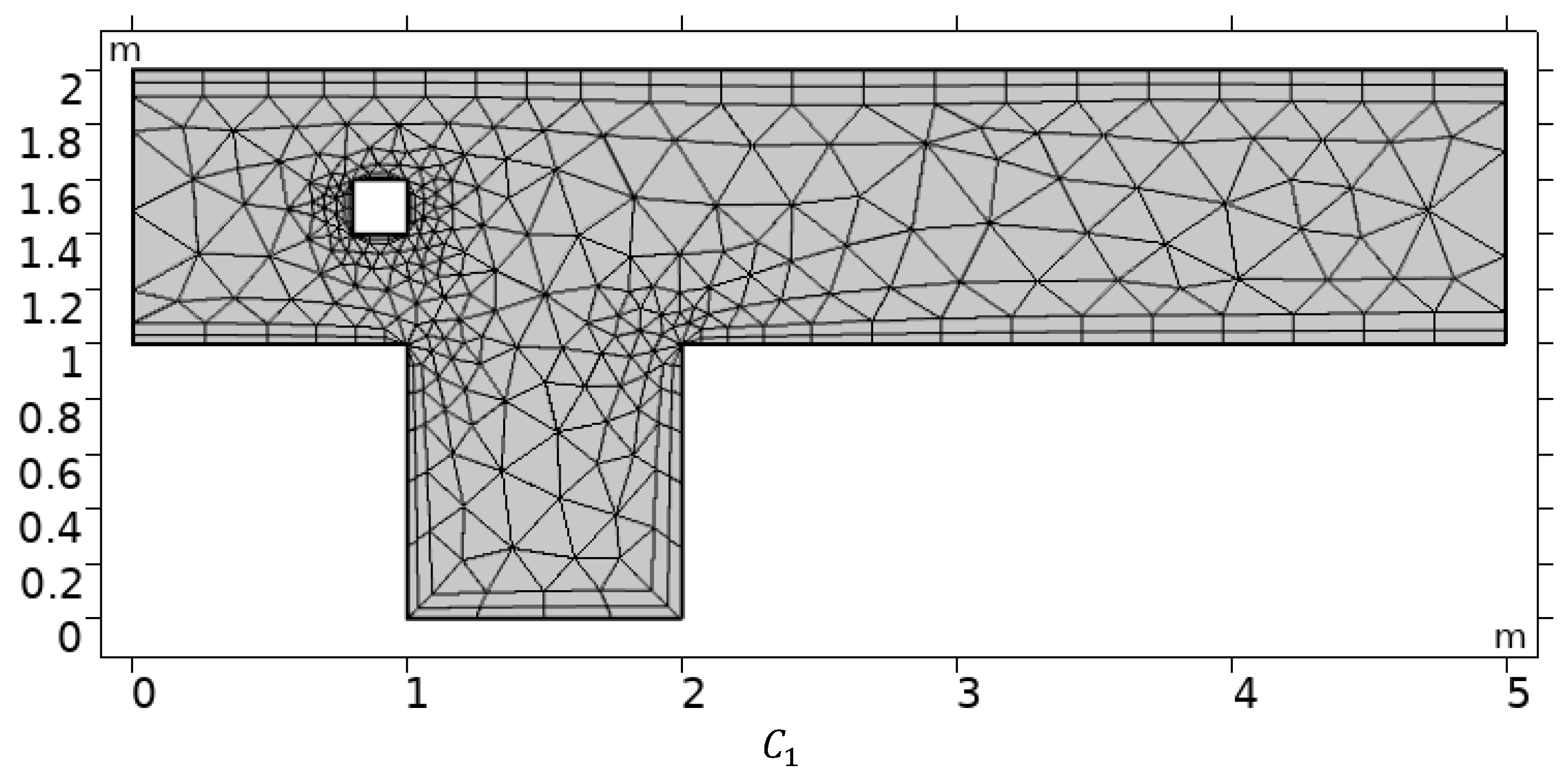


| Refinement Level | # EL | # DOF |
|---|---|---|
| 769 | 4032 | |
| 1167 | 6130 | |
| 1786 | 9245 | |
| 2962 | 15,171 | |
| 3590 | 21,648 | |
| 6707 | 33,213 | |
| 16,139 | 78,925 | |
| 39,724 | 191,180 | |
| 52,844 | 250,024 |
| Bn | C1 | C2 | C3 |
|---|---|---|---|
| δp = p2 − p1 | δp = p2 − p1 | δp = p2 − p1 | |
| 1 | 0.105098 | 0.089917 | 0.102492 |
| 5 | 0.178537 | 0.161953 | 0.182264 |
| 10 | 0.277829 | 0.260403 | 0.285607 |
| 15 | 0.379743 | 0.362457 | 0.391536 |
| 20 | 0.485614 | 0.471741 | 0.498451 |
| 25 | 0.590631 | 0.580957 | 0.608244 |
| 30 | 0.698603 | 0.690398 | 0.718537 |
| 35 | 0.809055 | 0.799874 | 0.828990 |
| 40 | 0.920618 | 0.909552 | 0.940283 |
| 45 | 1.032414 | 1.019508 | 1.052340 |
| 50 | 1.144143 | 1.129823 | 1.164679 |
| Bn | C1 | C2 | C3 | |||
|---|---|---|---|---|---|---|
| CD | CL | CD | CL | CD | CL | |
| 1 | 6.511467 | −0.24909 | 5.718770 | −0.373510 | 6.615889 | 0.28946 |
| 5 | 12.31288 | −0.61309 | 11.31525 | −0.630990 | 12.61671 | 0.35282 |
| 10 | 19.78717 | −0.90407 | 18.61922 | −0.219770 | 20.29534 | 0.72005 |
| 15 | 27.24873 | −1.16007 | 26.00279 | 0.395369 | 27.93196 | 1.21576 |
| 20 | 34.7233 | −1.41867 | 33.41197 | 0.909717 | 35.54671 | 1.75848 |
| 25 | 42.18845 | −1.71279 | 40.81667 | 1.348083 | 43.13843 | 2.30321 |
| 30 | 49.65995 | −2.05944 | 48.21088 | 1.743551 | 50.71272 | 2.83111 |
| 35 | 57.127 | −2.43912 | 55.59006 | 2.106661 | 58.27419 | 3.33006 |
| 40 | 64.58501 | −2.82462 | 62.96177 | 2.438490 | 65.82729 | 3.80311 |
| 45 | 72.04071 | −3.20601 | 70.31964 | 2.741542 | 73.36969 | 4.25363 |
| 50 | 79.48114 | −3.58121 | 77.67343 | 3.022520 | 80.90281 | 4.68517 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, R.; Hussain Majeed, A.; Ain, Q.u.; Awrejcewicz, J.; Siddique, I.; Shahzad, H. Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics. Materials 2022, 15, 529. https://doi.org/10.3390/ma15020529
Mahmood R, Hussain Majeed A, Ain Qu, Awrejcewicz J, Siddique I, Shahzad H. Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics. Materials. 2022; 15(2):529. https://doi.org/10.3390/ma15020529
Chicago/Turabian StyleMahmood, Rashid, Afraz Hussain Majeed, Qurrat ul Ain, Jan Awrejcewicz, Imran Siddique, and Hasan Shahzad. 2022. "Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics" Materials 15, no. 2: 529. https://doi.org/10.3390/ma15020529
APA StyleMahmood, R., Hussain Majeed, A., Ain, Q. u., Awrejcewicz, J., Siddique, I., & Shahzad, H. (2022). Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics. Materials, 15(2), 529. https://doi.org/10.3390/ma15020529







