Simulation of the Peritectic Phase Transition in Fe-C Alloys
Abstract
:1. Introduction
2. Governing Equations of the Multi-Phase CA Model and Computation Procedure
2.1. Governing Equations
2.2. Computation Procedure
3. Results and Discussion
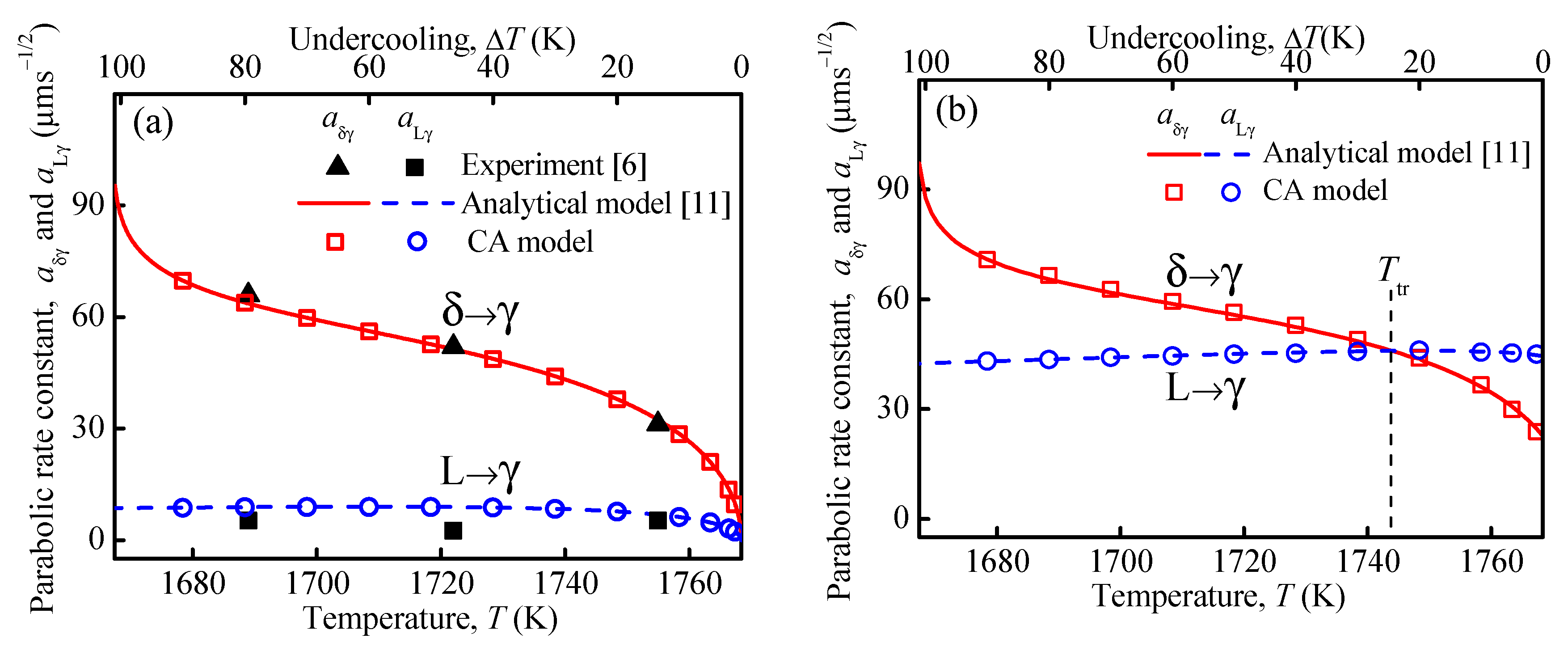
3.1. Growth Kinetics and Microstructural Evolution during Peritectic Transformation


3.2. Microstructural Evolution during Peritectic Reaction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kerr, H.; Cisse, J.; Bolling, G. On equilibrium and non-equilibrium peritectic transformations. Acta Metall. 1974, 22, 677–686. [Google Scholar] [CrossRef]
- Das, A.; Manna, I.; Pabi, S. A numerical model of peritectic transformation. Acta Metall. 1999, 47, 1379–1388. [Google Scholar] [CrossRef]
- Griesser, S.; Bernhard, C.; Dippenaar, R. Effect of nucleation undercooling on the kinetics and mechanism of the peritectic phase transition in steel. Acta Mater. 2014, 81, 111–120. [Google Scholar] [CrossRef]
- Matsuura, K.; Itoh, Y.; Narita, T. A solid-liquid diffusion couple study of a peritectic reaction in iron-carbon system. ISIJ Int. 1993, 33, 583–587. [Google Scholar] [CrossRef] [Green Version]
- Matsuura, K.; Kudoh, M.; Itoh, Y.; Maruyama, H. Effects of cooling rate on growth behavior of austenite phase during peritectic reaction in iron-barbon binary alloy. ISIJ Int. 1995, 35, 1483–1488. [Google Scholar] [CrossRef] [Green Version]
- Matsuura, K.; Maruyama, H.; Itoh, Y.; Kudoh, M.; Ishii, K. Rate of peritectic reaction in iron-carbon system measured by solid/liquid diffusion couple method. ISIJ Int. 1995, 35, 183–187. [Google Scholar] [CrossRef] [Green Version]
- Shibata, H.; Arai, Y.; Suzuki, M.; Emi, T. Kinetics of peritectic reaction and transformation in Fe-C alloys. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2000, 31, 981–991. [Google Scholar] [CrossRef]
- Phelan, D.; Reid, M.; Dippenaar, R. Kinetics of the peritectic phase transformation: In-situ measurements and phase field modeling. Metall. Mater. Trans. A 2006, 37, 985–994. [Google Scholar] [CrossRef]
- Griesser, S.; Bernhard, C.; Dippenaar, R. Mechanism of the peritectic phase transition in Fe–C and Fe–Ni alloys under conditions close to chemical and thermal equilibrium. ISIJ Int. 2014, 54, 466–473. [Google Scholar] [CrossRef] [Green Version]
- Fredriksson, H.; Nylén, T. Mechanism of peritectic reactions and transformations. Met. Sci. 1982, 16, 283–294. [Google Scholar] [CrossRef]
- Pan, S.; Zhu, M. Peritectic transformation with non-linear solute distribution in all three phases: Analytical solution, phase-field modeling and experiment comparison. Acta Mater. 2018, 146, 63–75. [Google Scholar] [CrossRef]
- Bosze, W.P.; Trivedi, R. On the kinetic expression for the growth of precipitate plates. Metall. Trans. 1974, 5, 511–512. [Google Scholar] [CrossRef]
- Ueshima, Y.; Mizoguchi, S.; Matsumiya, T.; Kajioka, H. Analysis of solute distribution in dendrites of carbon steel with δ/γ transformation during solidification. Metall. Trans. B 1986, 17, 845–859. [Google Scholar] [CrossRef]
- Tiaden, J.; Nestler, B.; Diepers, H.; Steinbach, I. The multiphase-field model with an integrated concept for modelling solute diffusion. Phys. D Nonlinear Phenom. 1998, 115, 73–86. [Google Scholar] [CrossRef]
- Ohno, M.; Matsuura, K. Diffusion-controlled peritectic reaction process in carbon steel analyzed by quantitative phase-field simulation. Acta Mater. 2010, 58, 6134–6141. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Stratmann, M.; Du, Y.; Sundman, B.; Steinbach, I. Incorporating the CALPHAD sublattice approach of ordering into the phase-field model with finite interface dissipation. Acta Mater. 2015, 88, 156–169. [Google Scholar] [CrossRef]
- Luo, S.; Liu, G.; Wang, P.; Wang, X.; Wang, W.; Zhu, M. In situ observation and phase-field modeling of peritectic solidification of low-carbon steel. Metall. Mater. Trans. A 2020, 51, 767–777. [Google Scholar] [CrossRef]
- Zhang, Q.; Fang, H.; Xue, H.; Tang, Q.; Pan, S.; Rettenmayr, M.; Zhu, M. Modeling of melting and resolidification of equiaxed microstructures in a temperature gradient. Scr. Mater. 2018, 151, 28–32. [Google Scholar] [CrossRef]
- Zhang, Q.; Shen, X.; Wang, Z.; Zhang, S.; Zhu, M. Microstructure evolution during dendrite coarsening in an isothermal environment: 3-D cellular automaton modeling and experiments. J. Mater. Sci. 2021, 56, 10393–10405. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for cellular automata for the simulation of dendritic solidification-A review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Ren, N.; Panwisawas, C.; Li, J.; Xia, M.; Dong, H.; Li, J. Solute enrichment induced dendritic fragmentation in directional solidification of nickel-based superalloys. Acta Mater. 2021, 215, 117043. [Google Scholar] [CrossRef]
- Dong, H.; Lee, P. Simulation of the columnar-to-equiaxed transition in directionally solidified Al-Cu alloys. Acta Mater. 2005, 53, 659–668. [Google Scholar] [CrossRef]
- Yuan, L.; Lee, P. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation. Model. Simul. Mater. Sci. Eng. 2010, 18. [Google Scholar] [CrossRef]
- Pineau, A.; Guillemot, G.; Tourret, D.; Karma, A.; Gandin, C.A. Growth competition between columnar dendritic grains–Cellular automaton versus phase field modeling. Acta Mater. 2018, 155, 286–301. [Google Scholar] [CrossRef]
- Hu, M.; Wang, T.; Fang, H.; Zhu, M. Modeling of gas porosity and microstructure formation during dendritic and eutectic solidification of ternary Al-Si-Mg alloys. J. Mater. Sci. Technol. 2021, 76, 76–85. [Google Scholar] [CrossRef]
- Fang, H.; Tang, Q.; Zhang, Q.; Gu, T.; Zhu, M. Modeling of microstructure and microsegregation formation during solidification of Al-Si-Mg alloys. Int. J. Heat Mass Transf. 2019, 133, 371–381. [Google Scholar] [CrossRef]
- Su, B.; Han, Z.; Liu, B. Cellular automaton simulation of peritectic solidification of a C-Mn steel. China Foundry 2012, 9, 221–225. [Google Scholar]
- Yamazaki, M.; Satoh, J.; Ohsasa, K.; Matsuura, K. Numerical model of solidification structure formation in Fe-C alloy with peritectic transformation. ISIJ Int. 2008, 48, 362–367. [Google Scholar] [CrossRef] [Green Version]
- Ogawa, J.; Natsume, Y. Cellular automaton modelling to predict multi-phase solidification microstructures for Fe-C peritectic alloys. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012059. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, H.; Tang, Q.; Zhang, Q.; Pan, S.; Zhu, M. Cellular automaton modeling of peritectic transformation. Eur. Phys. J. E 2020, 43, 17. [Google Scholar] [CrossRef]
- Zhu, M.; Stefanescu, D. Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys. Acta Mater. 2007, 55, 1741–1755. [Google Scholar] [CrossRef]
- Shin, Y.H.; Hong, C.P. Modeling of dendritic growth with convection using a modified cellular automation model with a diffuse interface. ISIJ Int. 2002, 42, 359–367. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Tang, Q.; Zhang, Q.; Fan, Y.; Pan, S.; Rettenmayr, M.; Zhu, M. Simulation of the Peritectic Phase Transition in Fe-C Alloys. Materials 2022, 15, 537. https://doi.org/10.3390/ma15020537
Fang H, Tang Q, Zhang Q, Fan Y, Pan S, Rettenmayr M, Zhu M. Simulation of the Peritectic Phase Transition in Fe-C Alloys. Materials. 2022; 15(2):537. https://doi.org/10.3390/ma15020537
Chicago/Turabian StyleFang, Hui, Qianyu Tang, Qingyu Zhang, Yiming Fan, Shiyan Pan, Markus Rettenmayr, and Mingfang Zhu. 2022. "Simulation of the Peritectic Phase Transition in Fe-C Alloys" Materials 15, no. 2: 537. https://doi.org/10.3390/ma15020537





