First Principles Investigation of Binary Chromium Carbides Cr7C3, Cr3C2 and Cr23C6: Electronic Structures, Mechanical Properties and Thermodynamic Properties under Pressure
Abstract
:1. Introduction
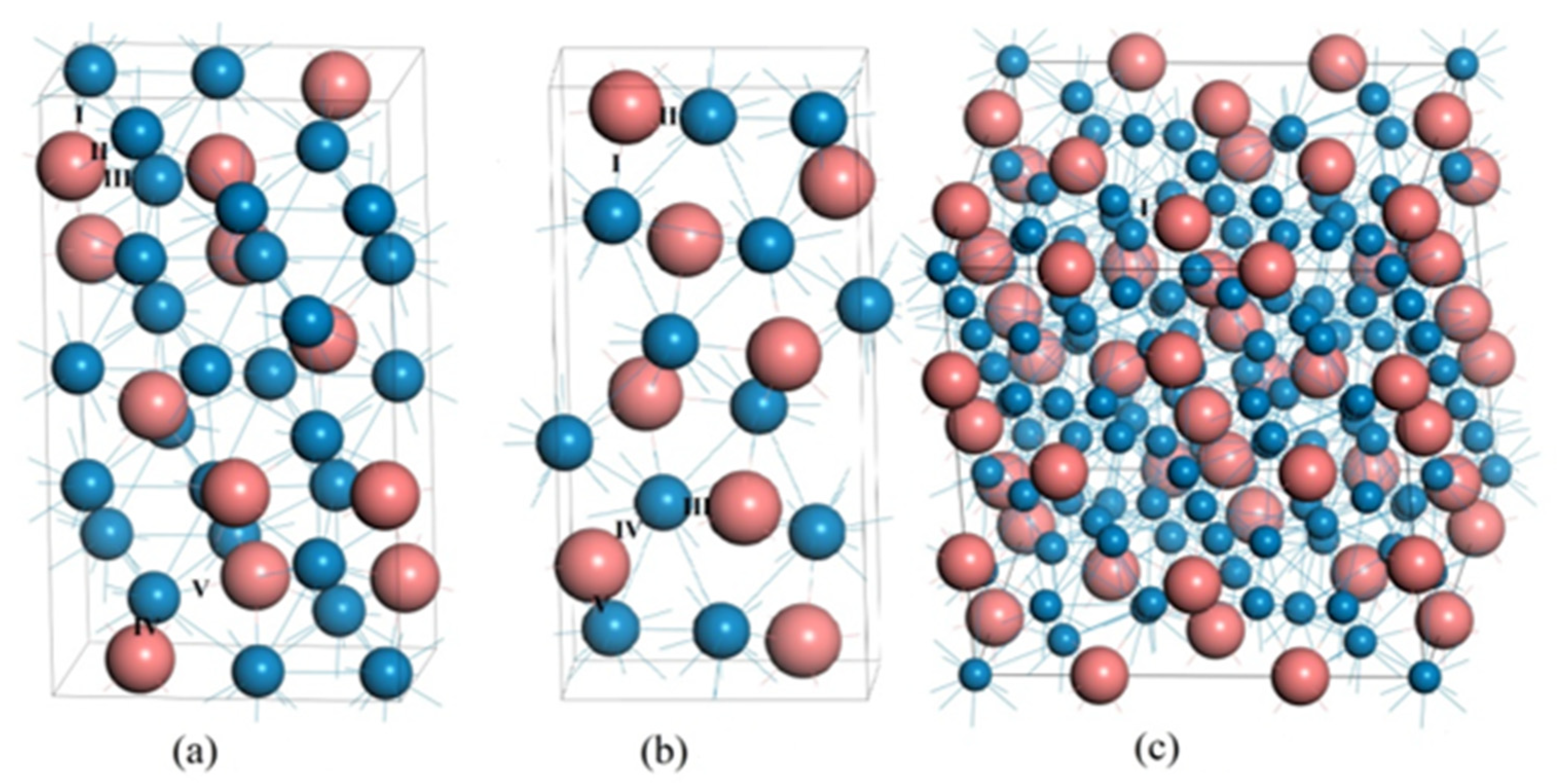
2. Calculation Methods and Models
3. Results
3.1. Lattice Parameters
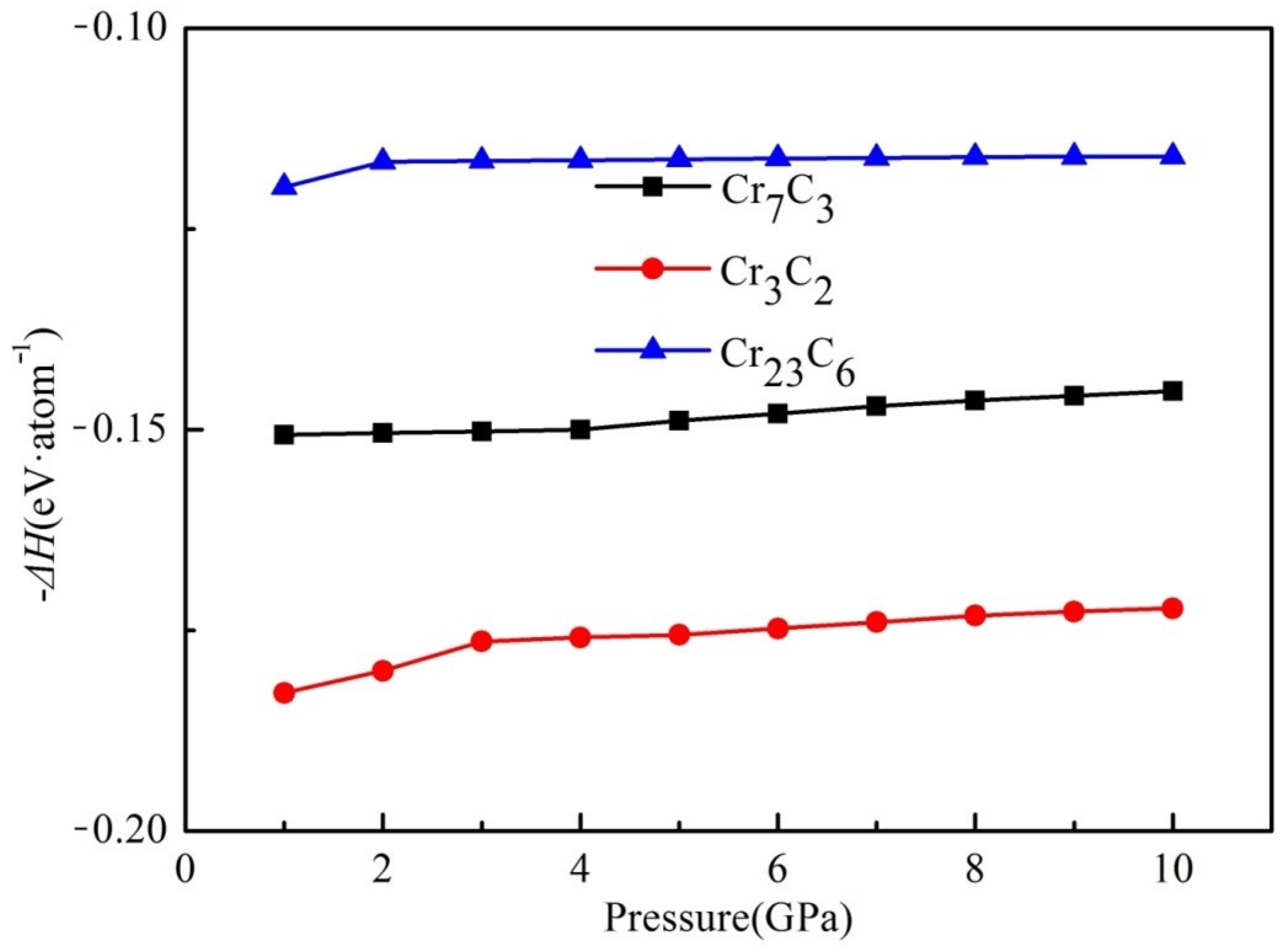
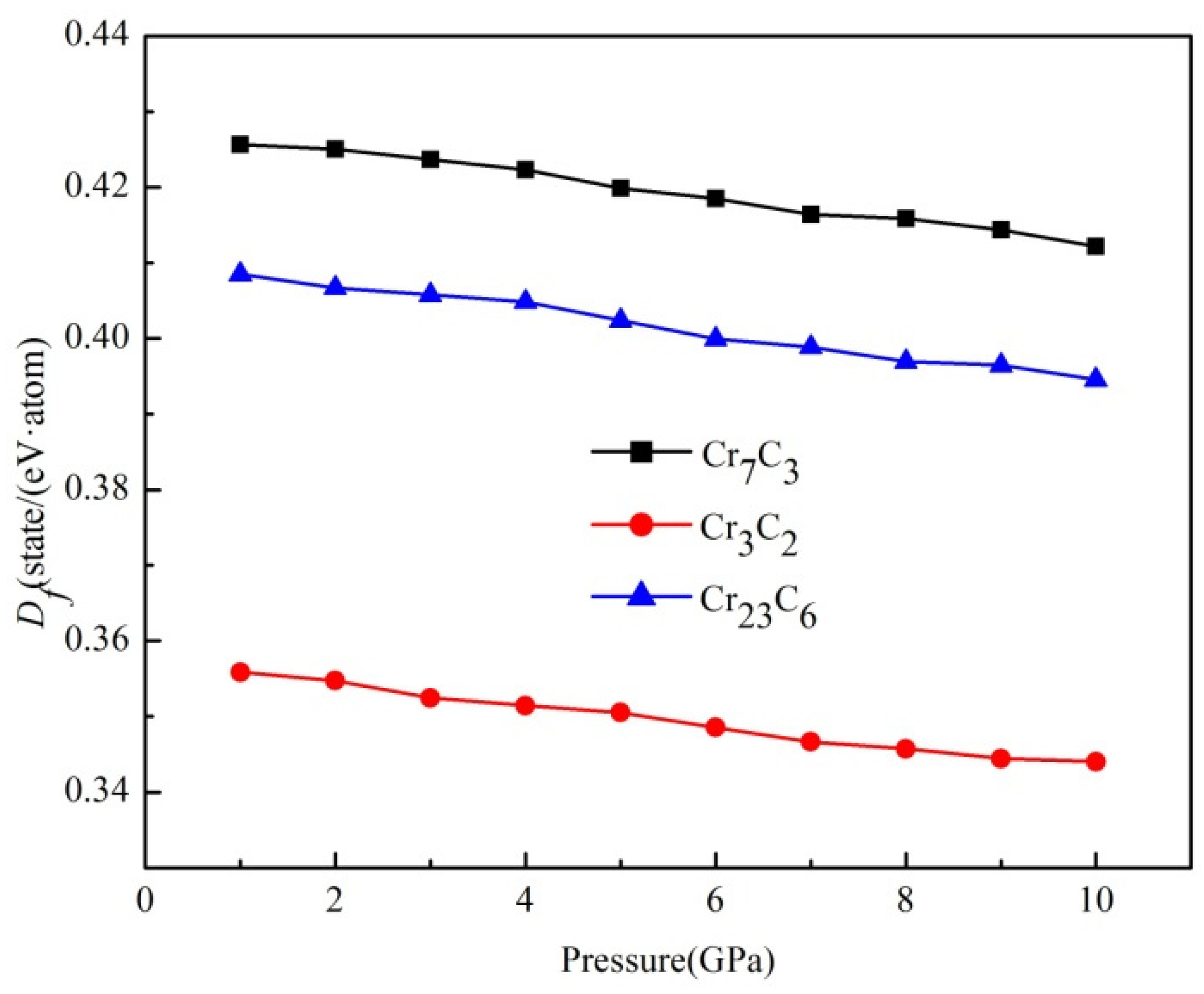
3.2. Formation Enthalpy
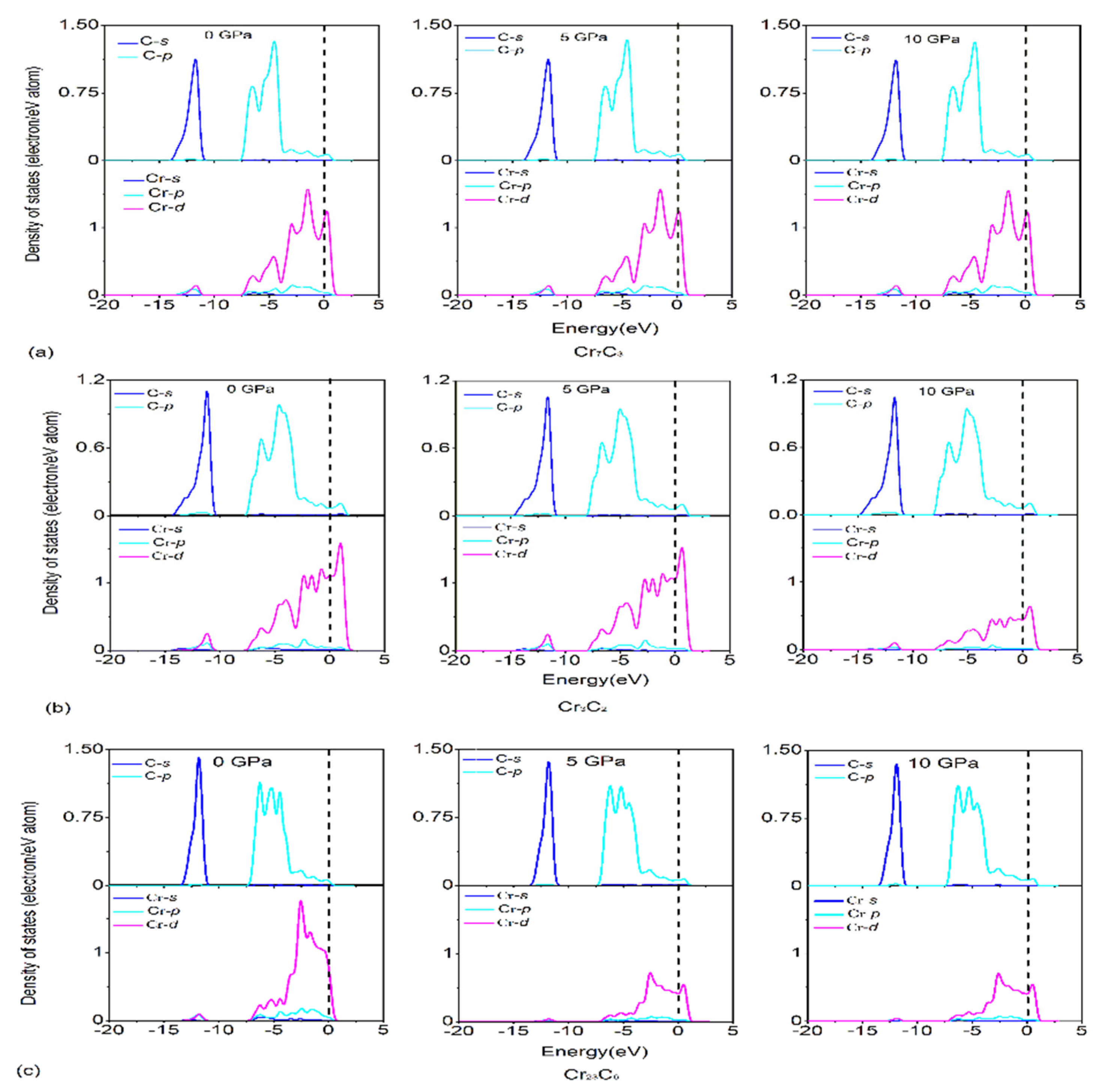
3.3. Electronic Structures
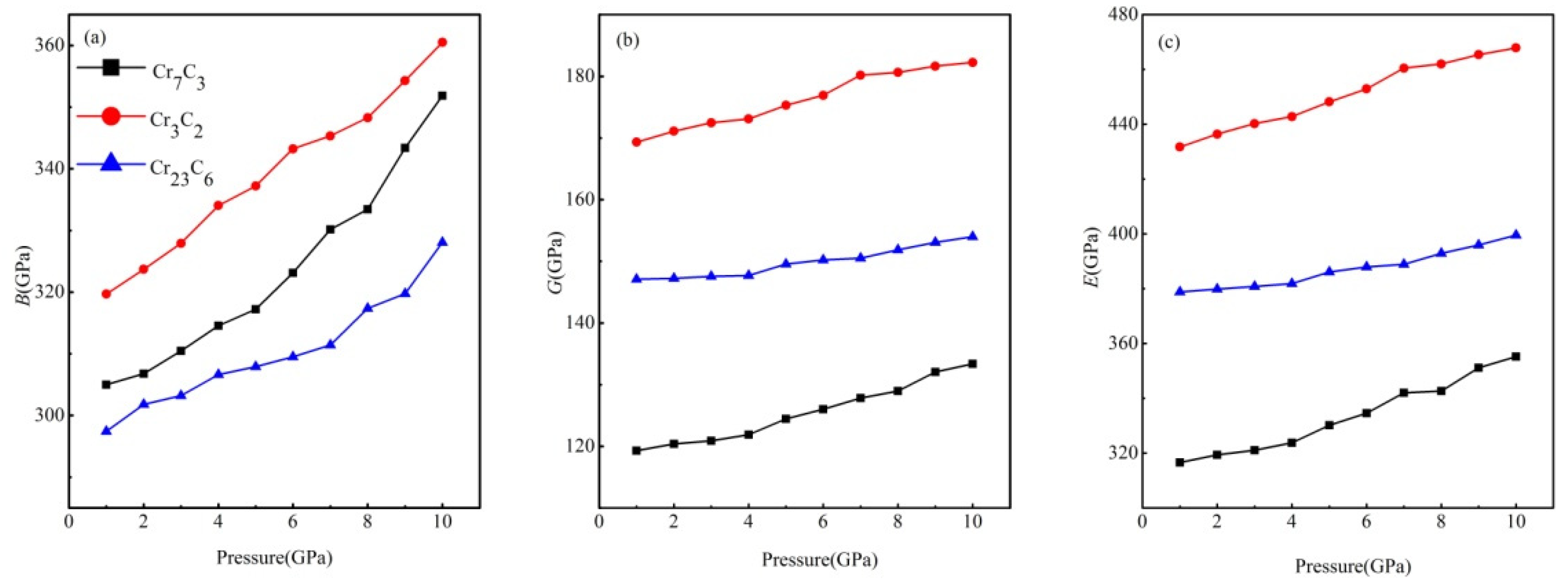
3.4. Mechanical Characterizations
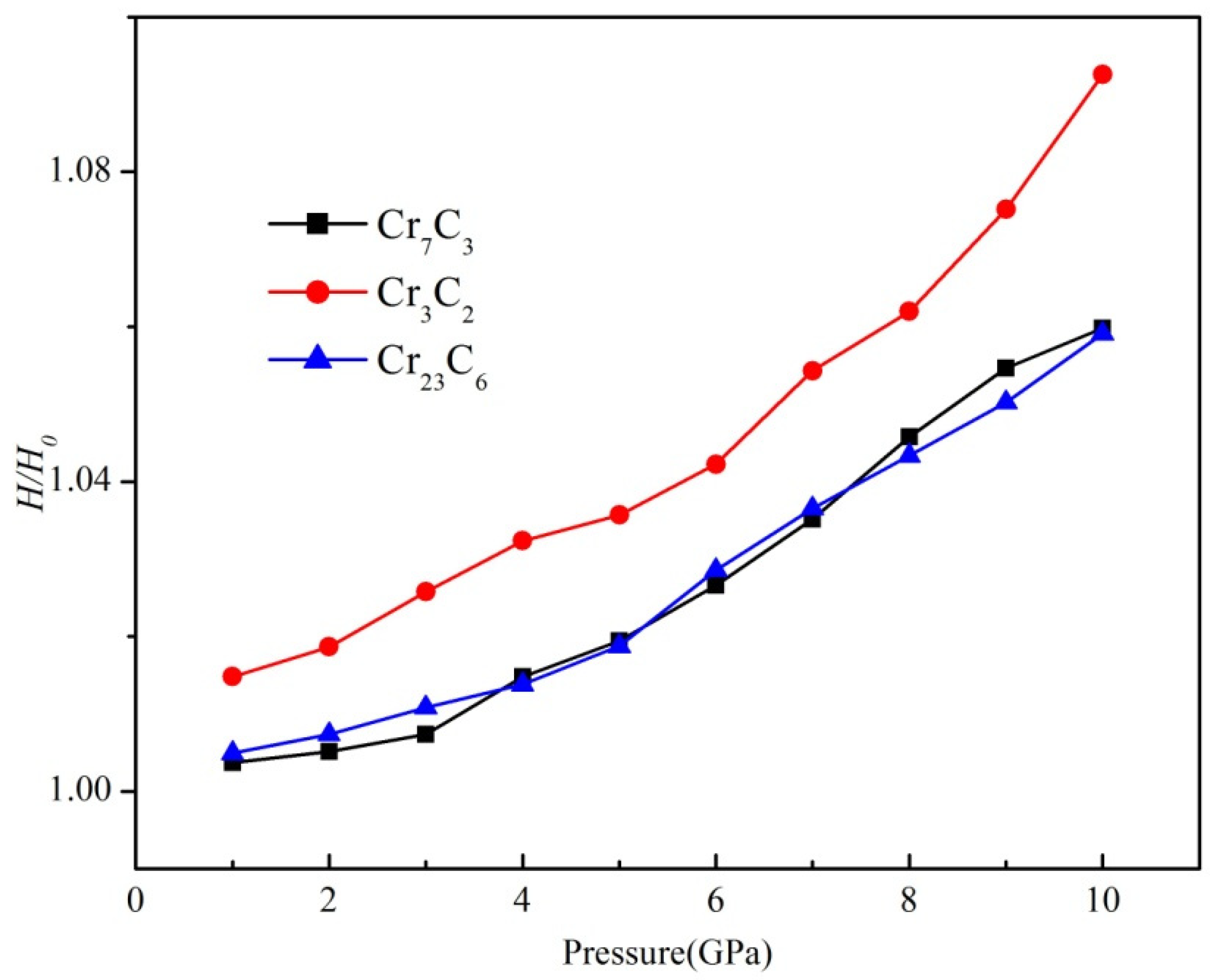
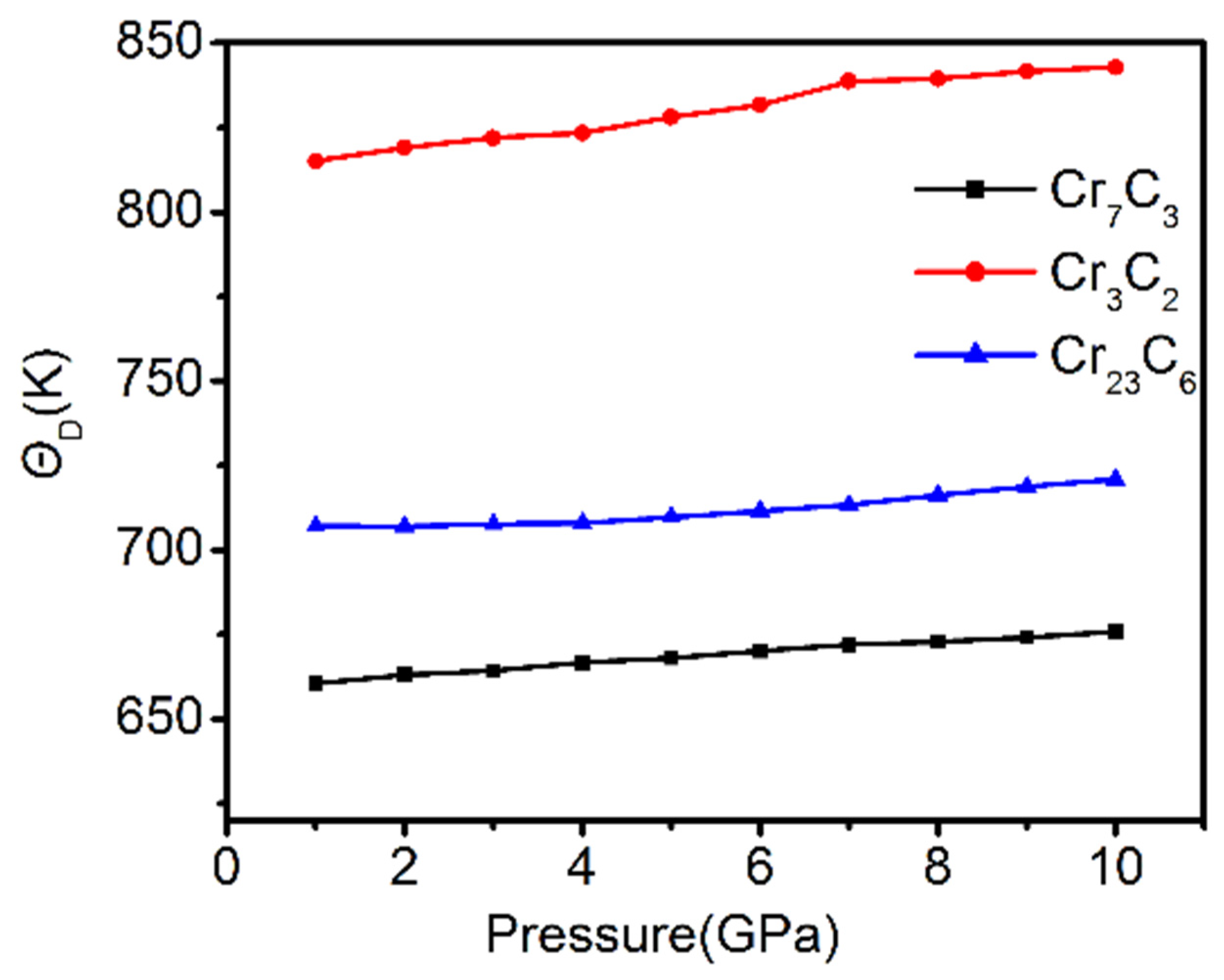
3.5. Thermodynamic Stability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Loubiére, S.; Laurent, C.; Bonino, J.P.; Rousset, A. Elaboration, microstructure and reactivity of Cr3C2 powders of different morphology. Mater. Res. Bull. 1995, 30, 1535–1546. [Google Scholar] [CrossRef] [Green Version]
- Kok, Y.N.; Hovsepian, P.E. Resistance of nanoscale multilayer C/Cr coatings against environmental attack. Surf. Coat. Technol. 2006, 201, 3596–3605. [Google Scholar] [CrossRef]
- Cheng, F.; Wang, Y.; Yang, T. Microstructure and wear properties of Fe-VC-Cr7C3 composite coating on surface of cast steel. Mater. Charact. 2008, 59, 488–492. [Google Scholar] [CrossRef]
- Xie, J.; Chen, N.X.; Shen, J.; Teng, L.; Seetharaman, S. Atomistic study on the structure and thermodynamic properties of CrC, MnC, FeC. Acta Mater. 2005, 53, 2727–2732. [Google Scholar] [CrossRef]
- Cintho, O.M.; Favilla, E.A.P.; Capocchi, J.D.T. Mechanical-thermal synthesis of chromium carbides. J. Alloys Compd. 2007, 439, 189–195. [Google Scholar] [CrossRef]
- Sadangi, R.K.; McCandlish, L.E.; Kear, B.H.; Seegopaul, P. Synthesis and characterization of sub-micron vanadium and chromium carbide grain growth inhibitors. In Proceedings of the 1998 International Conference on Powder Metallurgy & Particulate Materials Sponsored by the Metal Powder Industries Federation and APMI International, Las Vegas, NV, USA, 31 May–4 June 1998. [Google Scholar]
- Music, A.; Kreissig, U.; Mertens, R.; Schneider, J.M. Electronic structure and mechanical properties of Cr7C3. Phys. Lett. A 2004, 326, 473–476. [Google Scholar] [CrossRef]
- Kleykamp, H. Thermodynamic studies on chromium carbides by the electromotive force (emf) method. Alloys Compd. 2001, 321, 138–145. [Google Scholar] [CrossRef]
- Jiang, C. First-principles study of structural, elastic, and electronic properties of chromium carbides. Appl. Phys. Lett. 2008, 92, 041909. [Google Scholar] [CrossRef]
- Čekada, M.; Panjan, P.; Maček, M.; ŠmíD, P. Comparison of structural and chemical properties of Cr-based hard coatings. Surf. Coat. Technol. 2002, 152, 31–35. [Google Scholar] [CrossRef]
- Coltters, R.G.; Belton, G.R. High temperature thermodynamic properties of the chromium carbides Cr7C3 and Cr3C2 determined using a galvanic cell technique. Metall. Trans. B 1984, 15, 517–521. [Google Scholar] [CrossRef]
- Hirota, K.; Mitani, K.; Yoshinaka, M.; Yamaguchi, O. Simultaneous synthesis and consolidation of chromium carbides (Cr3C2, Cr7C 3 and Cr23C6) by pulsed electric-current pressure sintering. Mater. Sci. Eng. A 2005, 399, 154–160. [Google Scholar] [CrossRef]
- Esteve, J.; Romero, J.; Gómez, M.; Lousa, A. Cathodic chromium carbide coatings for molding die applications. Surf. Coat. Technol. 2004, 188, 506–510. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, H.; Yin, F.; Fan, Y.; Zhang, Y. Interfacial microstructure and properties of diamond/Cu-xCr composites for electronic packaging applications. Rare Met. 2011, 30, 94–98. [Google Scholar] [CrossRef]
- Hussainova, I.; Jasiuk, I.; Sardela, M.; Antonov, M. Micromechanical properties and erosive wear performance of chromium carbide based cermets. Wear 2009, 267, 152–159. [Google Scholar] [CrossRef]
- Tian, B.; Lind, C.; Paris, O. Influence of Cr23C6 carbides on dynamic recrystallization in hot deformed Nimonic 80a alloys. Met. Sci. Eng. A 2003, 359, 44–51. [Google Scholar] [CrossRef]
- Schroder, D.V.; Pribran, J.K. An Introduction to Thermal Physics; Addison Wesley Longman: New York, NY, USA, 1999; Volume 2008, p. 311. [Google Scholar]
- Min, T.; Gao, Y.M.; Li, Y.F.; Yang, Y.; Li, R.T.; Xie, X.J. First-Principles Calculation Study on the Electronic Structures, Hardness and Debye Temperatures of Chromium Carbides. Rare Met. Mater. Eng. 2012, 41, 0271. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Fanan, S.B.; Mota, R.; Baierle, R.J.; Paiva, G.; Silva, A.J.R.D.; Fazzio, A. Stability investigation and thermal behavior of a hypothetical silicon nanotube. J. Mol. Struct. Theochem. 2001, 539, 101–106. [Google Scholar]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Jiang, D.; Zhong, S.; Xiao, W.; Liu, D.; Wu, M.; Liu, S. Structural, mechanical, electronic, and thermodynamic properties of pure tungsten metal under different pressures: A first-principles study. Int. J. Quantum Chem. 2020, 120, e26231. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 059904. [Google Scholar] [CrossRef]
- Šimůnek, A.; Vackář, J. Hardness of covalent and ionic crystals: First-principle calculations. Phys. Rev. Lett. 2006, 96, 085501. [Google Scholar] [CrossRef] [Green Version]
- Glaser, J.; Schmitt, R.; Meyer, H.J. Neue Strukturverfeinerung und Eigenschaften von Cr3C2/Structure Refinement and Properties of Cr3C2. Z. Nat. B 2003, 58, 929–933. [Google Scholar] [CrossRef]
- Gao, F.M. Hardness of nanocrystalline diamonds. Phys. Rev. B 2006, 73, 132104. [Google Scholar] [CrossRef]
- Rouault, A.; Herpin, P.; Fruchart, R. Études christallographique des carbures Cr7C3 et Mn7C3. Ann. Chim. 1970, 5, 461–470. [Google Scholar]
- Yakel, H.L. Atom distributions in tau-carbide phases: Fe and Cr distributions in (Cr23−xFex)C6 with x = 0, 0·74, 1·70, 4·13 and 7·36. Acta Crystallogr. B 2010, 43, 230–238. [Google Scholar] [CrossRef]
- de Wijs, G.A.; de Boer, P.K.; de Groot, R.A. Anomalous behavior of the semiconducting gap in WO3 from first-principles calculations. Phys. Rev. B 1999, 59, 2684–2693. [Google Scholar] [CrossRef] [Green Version]
- Price, D.L.; Cooper, B.R. Total energies and bonding for crystallographic structures in titanium-carbon and tungsten-carbon systems. Phys. Rev. B 1989, 39, 4945–4957. [Google Scholar] [CrossRef]
- Xiao, B.; Xing, J.D.; Feng, J.; Zhou, C.T.; Li, Y.F.; Su, W.; Xie, Y.H. A comparative study of Cr7C3, Fe3C and Fe2B in cast iron both from ab initio calculations and experiments. J. Phys. D Appl. Phys. 2009, 42, 115415. [Google Scholar] [CrossRef]
- Henriksson, K.O.E.; Sandberg, N.; Wallenius, J. Carbides in stainless steels: Results from ab initio investigations. Appl. Phys. Lett. 2008, 93, 191912. [Google Scholar] [CrossRef]
- Deligoz, E.; Ciftci, Y.O.; Jochyml, P.T.; Colakoglu, K. The first principles study on PtC compound. Mater. Chem. Phys. 2008, 111, 29–33. [Google Scholar] [CrossRef]
- Swain, M. Structure and Properties of Ceramics; VCH: New York, NY, USA, 1994. [Google Scholar]
- Wang, Y.L. Performance and Application of Functional Ceramics; The Science Publishing Company: Beijing, China, 2003. [Google Scholar]
- Zhou, Y. Science of Ceramics Material; Harbin Institute of Technology Press: Harbin, China, 1995. [Google Scholar]
- Nam, D.; Lee, S. Effect of tempering on Microstructure, hardness, wear resistance, and fracture toughness of Cr3C2/steel surface composites fabricated by high-energy electron-beam irradiation. Metall. Mater. Trans. A 2008, 39, 2615–2625. [Google Scholar] [CrossRef] [Green Version]
- Li, K.Y.; Yang, P.; Xue, D.F. Anisotropic hardness prediction of crystalline hard materials from the electronegativity. Acta Mater. 2012, 60, 35–42. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, L.; Li, B.; Wu, P.; Song, Q. Structural, elastic and electronic properties of intermetallics in the Pt–Sn system: A density functional investigation. Comput. Mater. Sci. 2009, 46, 921–931. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954; Volume 10. [Google Scholar]
- Nikolussi, M.; Shang, S.L.; Gressmann, T.; Leineweber, A.; Mittemeijer, E.J.; Wang, Y.; Liu, Z.K. Extreme elastic anisotropy of cementite, Fe3C: First-principles calculations and experimental evidence. Scr. Mater. 2008, 59, 814–817. [Google Scholar] [CrossRef]
- Jang, J.H.; Kim, I.G.; Bhadeshia, H.K.D.H. Substitutional solution of silicon in cementite: A first-principles study. Comput. Mater. Sci. 2009, 44, 1319–1326. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.; Yu, C.; Chen, J.M. First-principles calculations of mechanical properties of TiC and TiN. J. Alloys Compd. 2009, 485, 542–547. [Google Scholar] [CrossRef]
- Gilman, J.J.; Roberts, B.W. Elastic Constants of TiC and TiB2. J. Appl. Phys. 1961, 32, 1405. [Google Scholar] [CrossRef]
- Liu, Z.L.; Chen, X.R.; Wang, Y.L. First-principles calculations of elastic properties of LiBC. Physical B 2006, 381, 139–143. [Google Scholar] [CrossRef]
- Siwark, P.; Garbiec, D.; Rogalewicz, M. The effect of Cr3C2 and Ta C additives on microstructures, hardness and fracture toughness of WC-6Co tool material fabricated by spark plasma sintering. Mater. Res. 2017, 20, 780–785. [Google Scholar] [CrossRef] [Green Version]
- Sin’ko, G.V.; Smirnow, N.A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure. J. Phys. Condens. Matter 2002, 14, 6989. [Google Scholar]
- Anderson, O.L. A Simplified Method for Calculating the Debye Temperature from Elastic Constants. J. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]


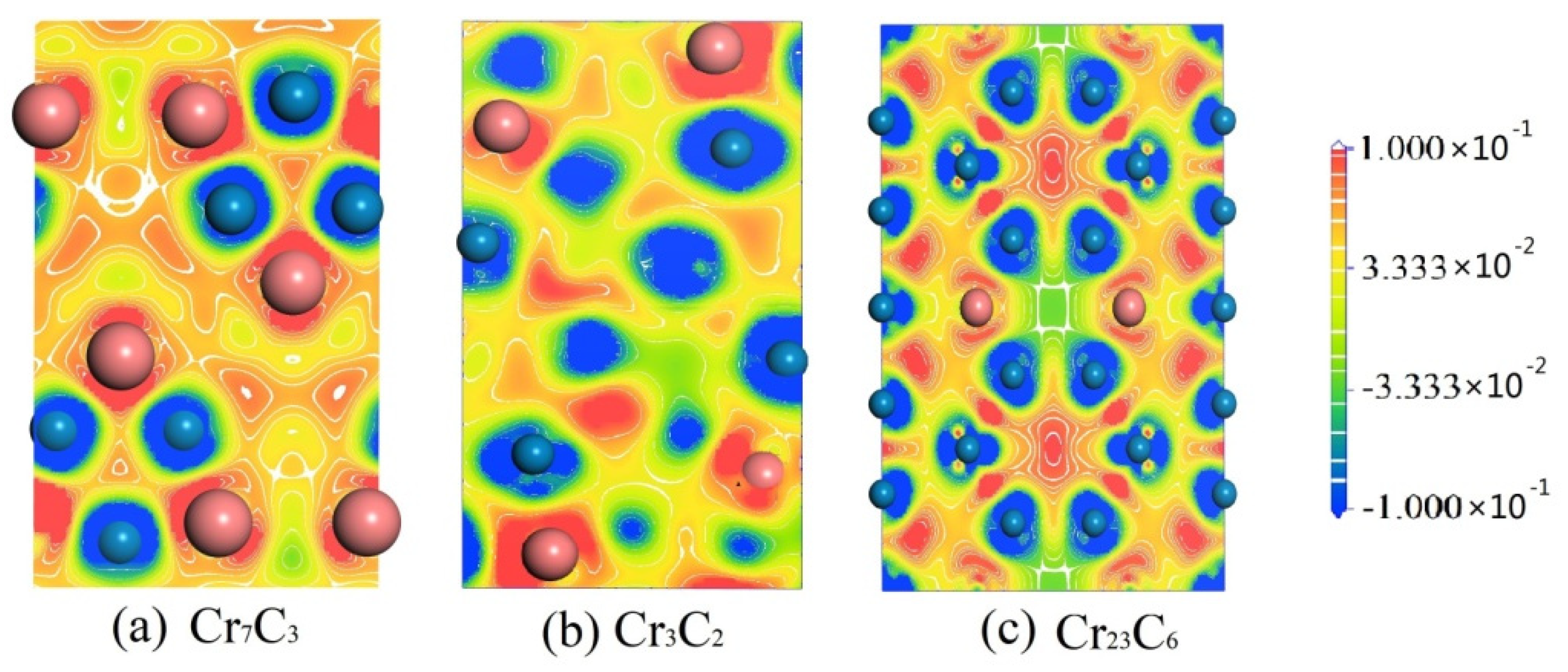
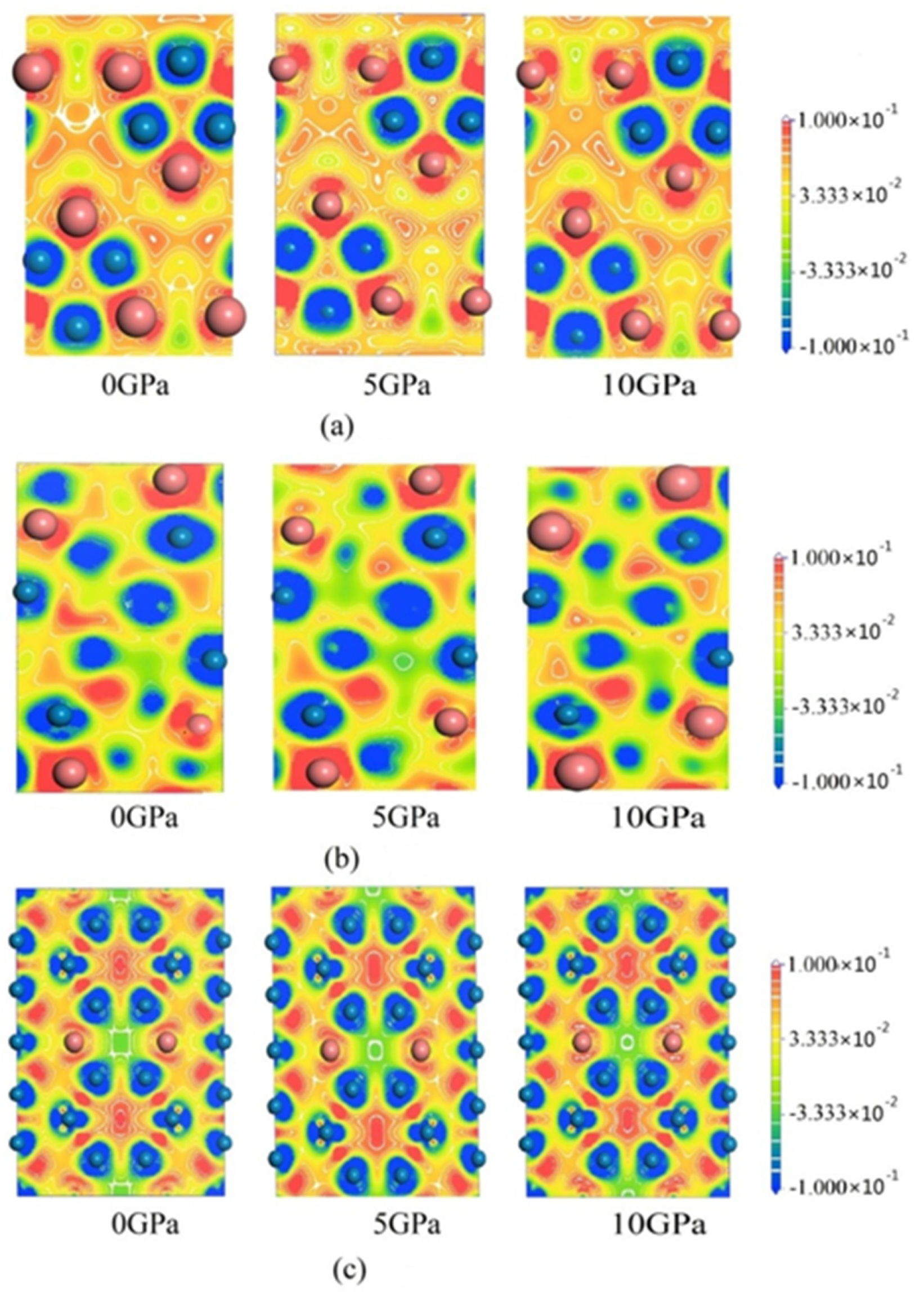

| Compounds | Lattice Parameters (Å) | −2ΔH/ (eV·Atom)−1 | Df/ State (eV·Atom)−1 | ||
|---|---|---|---|---|---|
| a | b | c | |||
| Cr7C3 | 4.45 (4.51 a, 4.53 c) | 6.84 (6.90 a, 7.01 c) | 11.97 (12.08 a, 12.14 c) | 0.183 (0.112 a, 0.149 b) | 0.42 (0.43 a) |
| Cr3C2 | 5.48 (5.49 a, 5.54 d) | 2.79 (2.79 a, 2.83 d) | 11.47 (11.47 a, 11.49 d) | 0.157 (0.15 b, 0.114 a) | 0.36 (0.36 a) |
| Cr23C6 | 10.55 (10.55 a, 10.66 e) | 10.55 (10.55 a, 10.66 e) | 10.55 (10.55 a, 10.66 e) | 0.122 (0.123 b, 0.087 a) | 0.41 (0.42 a) |
| Phase | C11/GPa | C12/GPa | C13/GPa | C22/GPa | C23/GPa | C33/GPa | C44/GPa | C55/GPa | C66/GPa |
|---|---|---|---|---|---|---|---|---|---|
| Cr7C3 | 459.9 | 262.7 | 251.0 | 512.6 | 280.2 | 525.1 | 186.2 | 142.9 | 114.2 |
| (410.1, c 409) a | (252, a 241.1) c | (227, a 203.7) c | (441, c 376) a | (333, a 257.3) c | (459.5, c 409) a | (168, c 145) a | (124.3, c 123) a | (108.3, c 82) a | |
| Cr3C2 | 463.0 | 212.5 | 228.2 | 543.6 | 227.5 | 495.3 | 235.8 | 116.1 | 240.0 |
| (484, a 447.1) c | (229, a 217.5) c | (243.3, c 243) a | (554, a 545.3) c | (244, a 217.9) c | (491, a 471.2) c | (237.7, c 230) a | (116.6, c 111) a | (241.3, c 235) a | |
| Cr23C6 | 486.3 | 201.0 | 149.6 | ||||||
| (487, f 481, a 473.8) c | (209, a 200, f 186.6) c | (149, f 146.7, c 138) a | |||||||
| Phase | C11/C33 | C12/ C13 | C44/C66 | B/GPa | G/GPa | B/G | E/GPa | v | |
| Cr7C3 | 0.88 | 1.05 | 1.63 | 341.7 | 133.1 | 2.57 | 353.4 | 0.33 | |
| (312, a 311.7, e 309, b 300.6) c | (143.9, d 118.0, c 82) a | (2.55) a | (374, e 371, b 313.0, c 226) a | (0.38, a 0.33) c | |||||
| Cr3C2 | 0.94 | 0.93 | 0.98 | 314.7 | 166.1 | 1.89 | 423.7 | 0.28 | |
| (329, a 312.9) c | (162.1, c 162) a | (1.93) a | (416, a 414.7) c | (0.29, a 0.28) c | |||||
| Cr23C6 | 1.00 | 1.00 | 1.00 | 296.1 | 146.8 | 2.02 | 377.9 | 0.29 | |
| (300, a 282.3) c | (145.4, c 137) a | (1.94) a | (372.3, c 357) a | (0.30, a 0.28) c |
| Phase | Species | s | p | d | Total | Charge(e) |
|---|---|---|---|---|---|---|
| Cr7C3 | C | 1.38 | 3.16 | 4.53 | −0.53 | |
| C | 1.38 | 3.17 | 4.55 | −0.55 | ||
| Cr | 2.08 | 6.66 | 5.01 | 13.74 | 0.26 | |
| Cr Cr | 2.09 2.07 | 6.69 6.76 | 5.00 5.00 | 13.78 13.82 | 0.22 0.18 | |
| Cr3C2 | C | 1.40 | 3.09 | 4.49 | −0.49 | |
| C | 1.40 | 3.11 | 4.51 | −0.51 | ||
| Cr Cr Cr | 2.13 2.14 2.15 | 6.61 6.54 6.50 | 4.96 4.99 4.98 | 13.70 13.67 13.63 | 0.30 0.33 0.37 | |
| Cr23C6 | C Cr Cr | 1.38 2.17 2.10 | 3.21 6.73 6.76 | 5.00 5.00 | 13.90 13.86 | −0.59 0.10 0.14 |
| Phase | Bond | HGao/GPa | |||
|---|---|---|---|---|---|
| Cr7C3 | C-Cr | 364.74 | 0.192 | 17.27 | 13.5 (18.3 a) |
| C-Cr C-Cr C-Cr C-Cr C-Cr | 17.19 15.55 14.81 14.50 13.67 | ||||
| Cr3C2 | C-Cr C-Cr C-Cr C-Cr C-Cr C-Cr | 175.47 | 0.160 | 29.03 27.25 22.35 19.81 8.46 8.17 | 18.2 (20.9 a) |
| Cr23C6 | C-Cr | 1178.28 | 0.163 | 11.24 | 10.1 (13.2 a) |
| C-Cr | 9.07 |
| Phase | Chemical Bond | Hvani/GPa | fw | Hv/ GPa | ||||
|---|---|---|---|---|---|---|---|---|
| [100] | [010] | [001] | [110] | [111] | ||||
| Cr7C3 | Cr-C | 24.93 | 24.16 | 21.05 | 26.53 | 25.79 | 0.019 | 26.17 |
| Cr3C2 | Cr-C | 22.78 | 21.47 | 21.57 | 22.23 | 24.16 | 0.019 | 23.30 |
| Cr23C6 | Cr-C | 16.42 | 15.18 | 21.91 | 17.86 | 21.15 | 0.041 | 19.09 |
| Phase | ||||
|---|---|---|---|---|
| 10,894.29(8051.65 a) | 5516.13(4087.19 a) | 6183.41(4580.90 a) | 731(785 a, 646 b) | |
| 11,447.63(8812.80 a) | 6371.63(4878.25 a) | 7095.38(5343.72 a) | 850(785 a, 785 b) | |
| 10,692.17(8152.31 a) | 5841.449(4504.88 a) | 6514.34(5019.43 a) | 744(691 a, 671 b) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Ji, X.; Zhao, L.; Zhai, W.; Xu, L.; Dong, H.; Liu, Y.; Peng, J. First Principles Investigation of Binary Chromium Carbides Cr7C3, Cr3C2 and Cr23C6: Electronic Structures, Mechanical Properties and Thermodynamic Properties under Pressure. Materials 2022, 15, 558. https://doi.org/10.3390/ma15020558
Sun L, Ji X, Zhao L, Zhai W, Xu L, Dong H, Liu Y, Peng J. First Principles Investigation of Binary Chromium Carbides Cr7C3, Cr3C2 and Cr23C6: Electronic Structures, Mechanical Properties and Thermodynamic Properties under Pressure. Materials. 2022; 15(2):558. https://doi.org/10.3390/ma15020558
Chicago/Turabian StyleSun, Liang, Xiongshuai Ji, Liang Zhao, Wenyan Zhai, Liujie Xu, Hui Dong, Yanmin Liu, and Jianhong Peng. 2022. "First Principles Investigation of Binary Chromium Carbides Cr7C3, Cr3C2 and Cr23C6: Electronic Structures, Mechanical Properties and Thermodynamic Properties under Pressure" Materials 15, no. 2: 558. https://doi.org/10.3390/ma15020558
APA StyleSun, L., Ji, X., Zhao, L., Zhai, W., Xu, L., Dong, H., Liu, Y., & Peng, J. (2022). First Principles Investigation of Binary Chromium Carbides Cr7C3, Cr3C2 and Cr23C6: Electronic Structures, Mechanical Properties and Thermodynamic Properties under Pressure. Materials, 15(2), 558. https://doi.org/10.3390/ma15020558







