Hybrid Prepreg Tapes for Composite Manufacturing: A Case Study
Abstract
1. Introduction
2. Experimental
2.1. Materials Used
2.2. Preparation of Tapes
2.3. Characterization and Test Methods
3. Spreading Process
- A.
- Assumption of the constant area during spreading in combination with Kemp racetrack cross-section of tape leads to the relation [28]:
- B.
- Assumption of constant perimeter during spreading in combination with Kemp racetrack cross-section of tape leads to the relation [29]:
4. Results and Discussion
4.1. Hybrid Tape Geometry
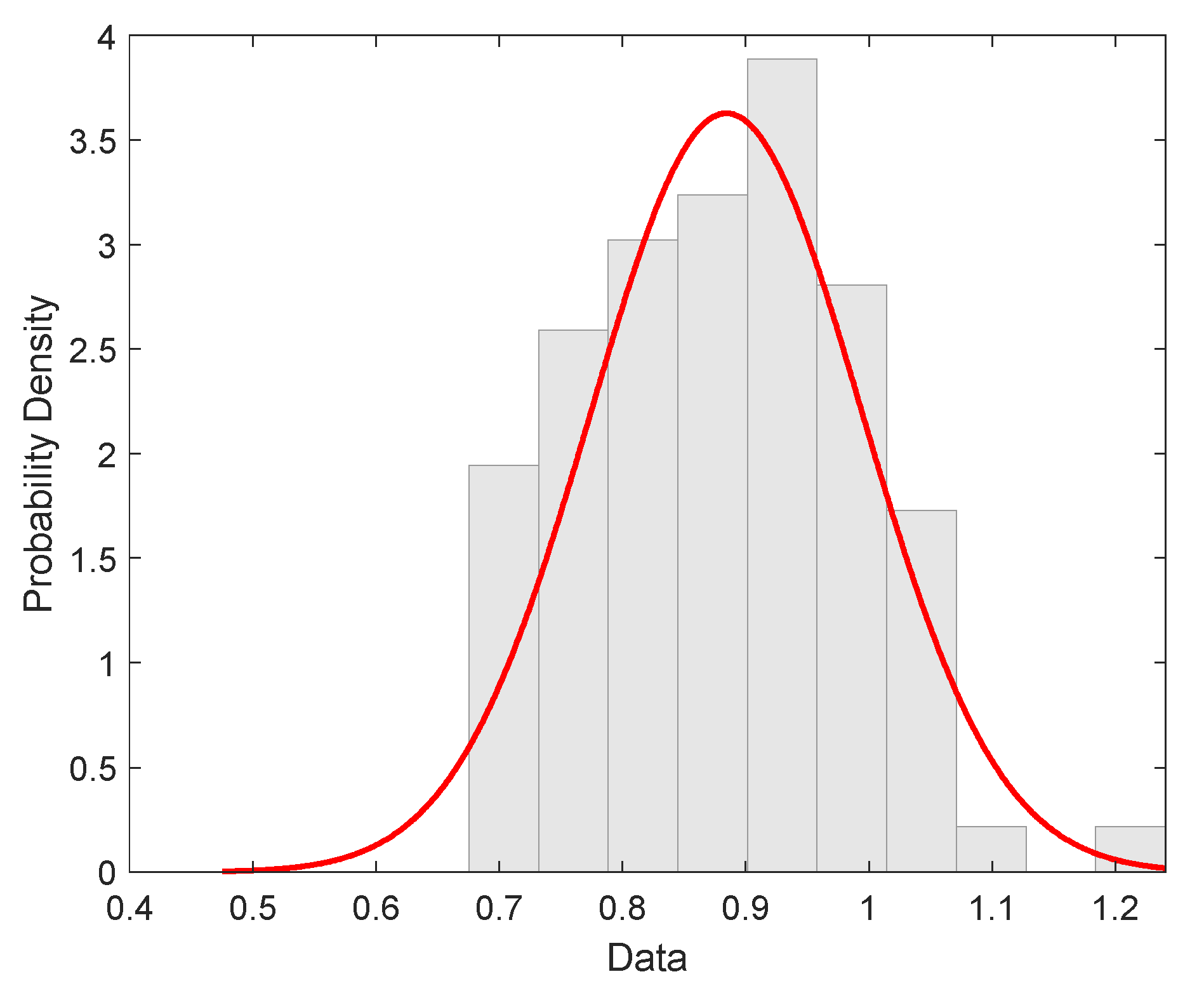
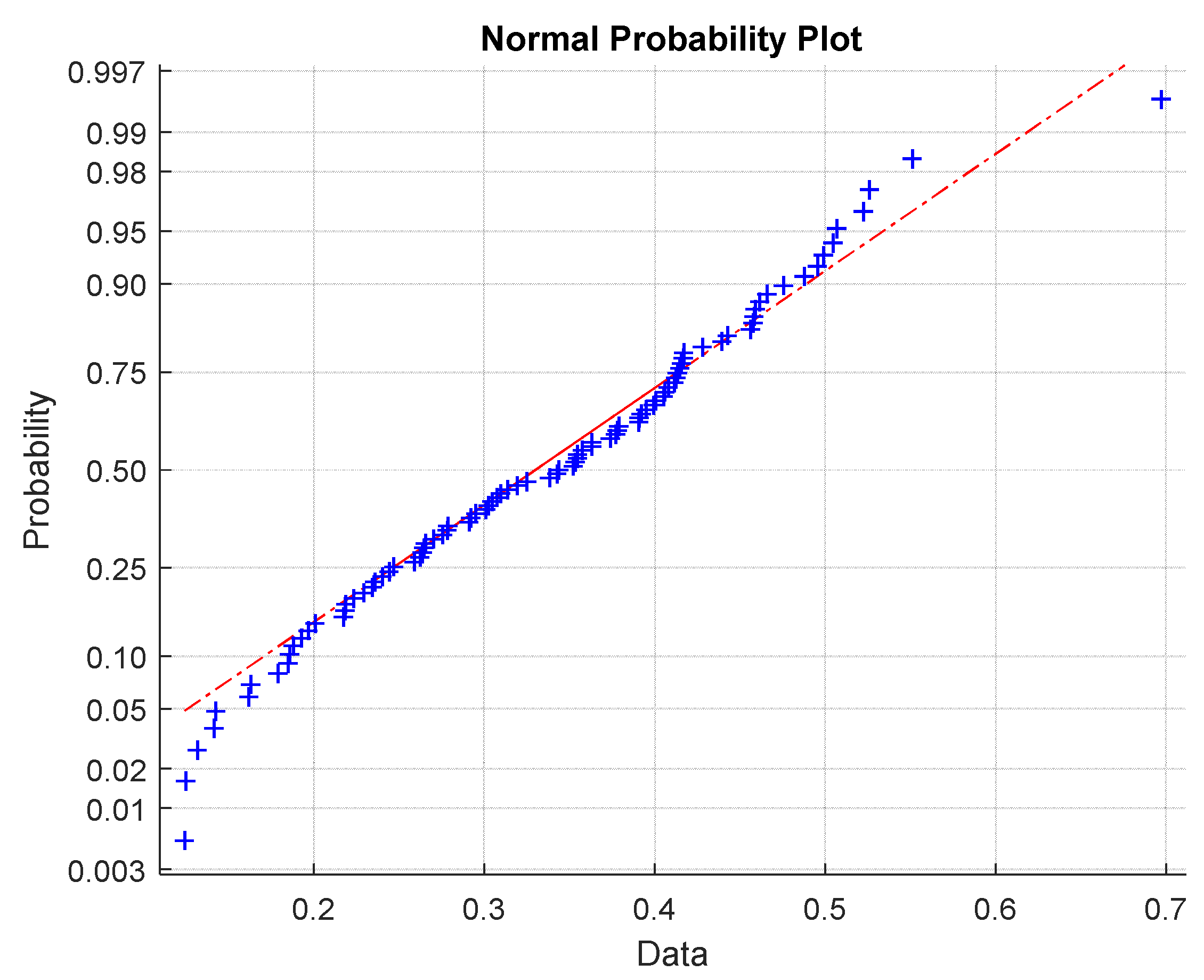
4.2. Fiber Strength Distribution
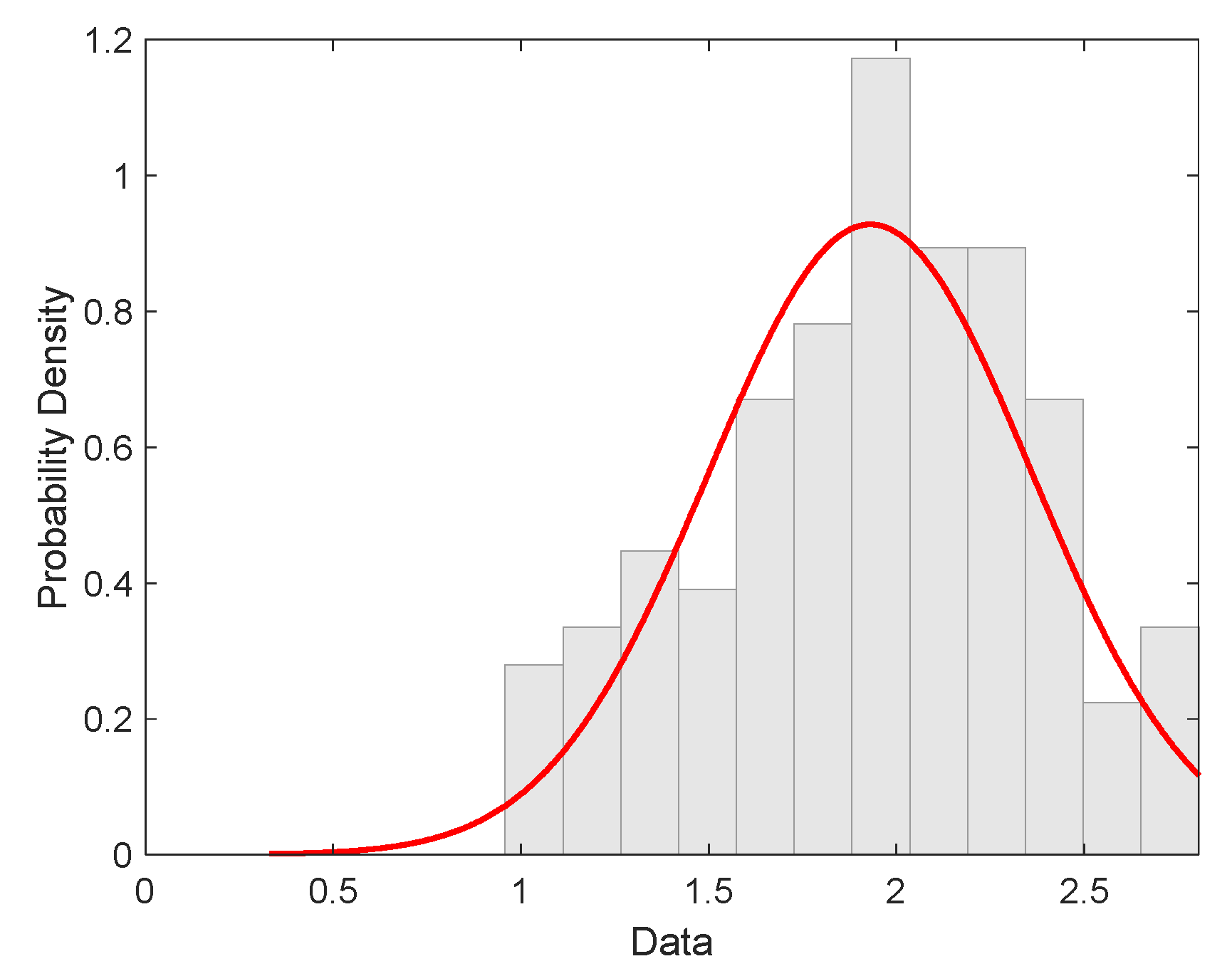
4.3. Roving Strength Distribution
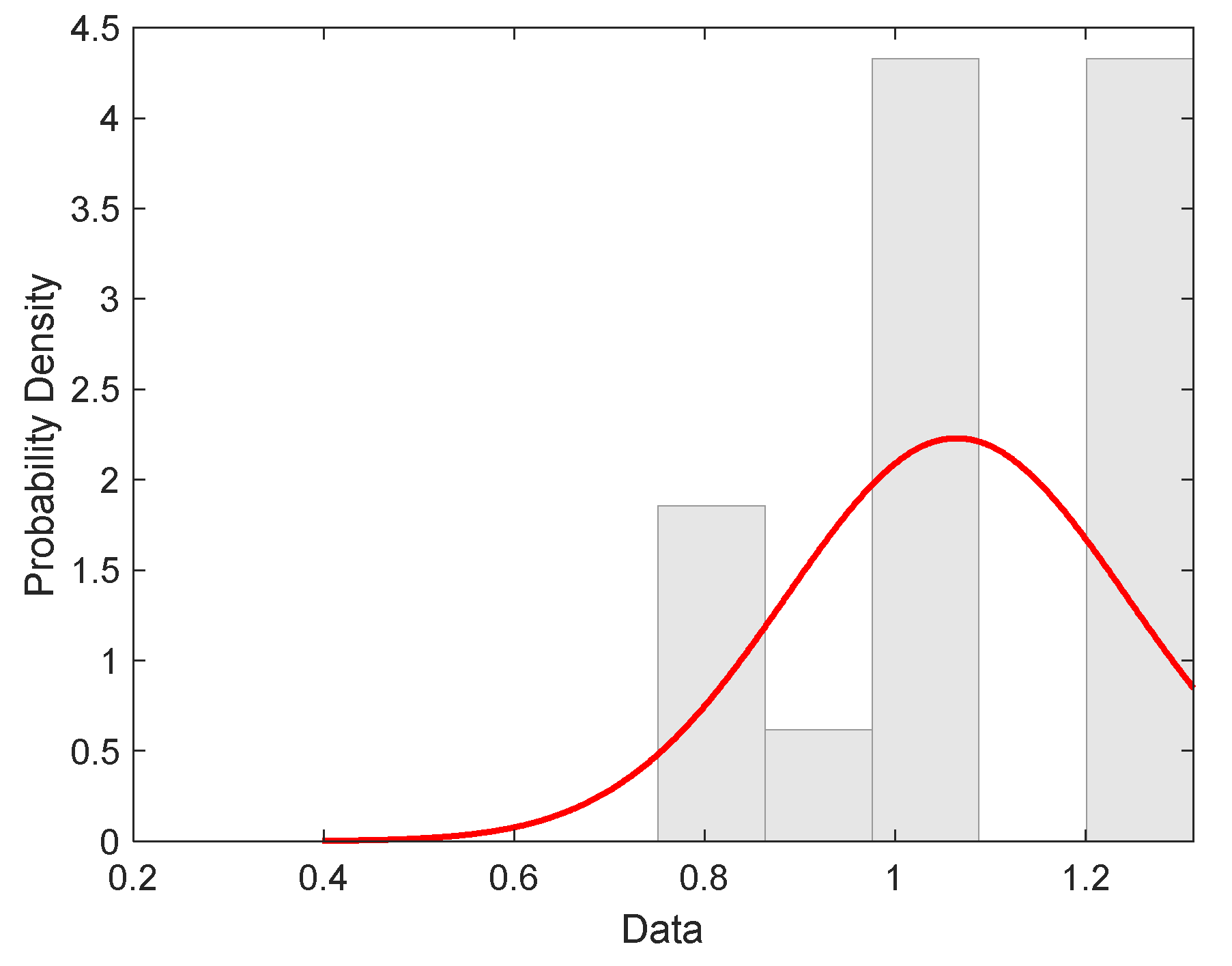
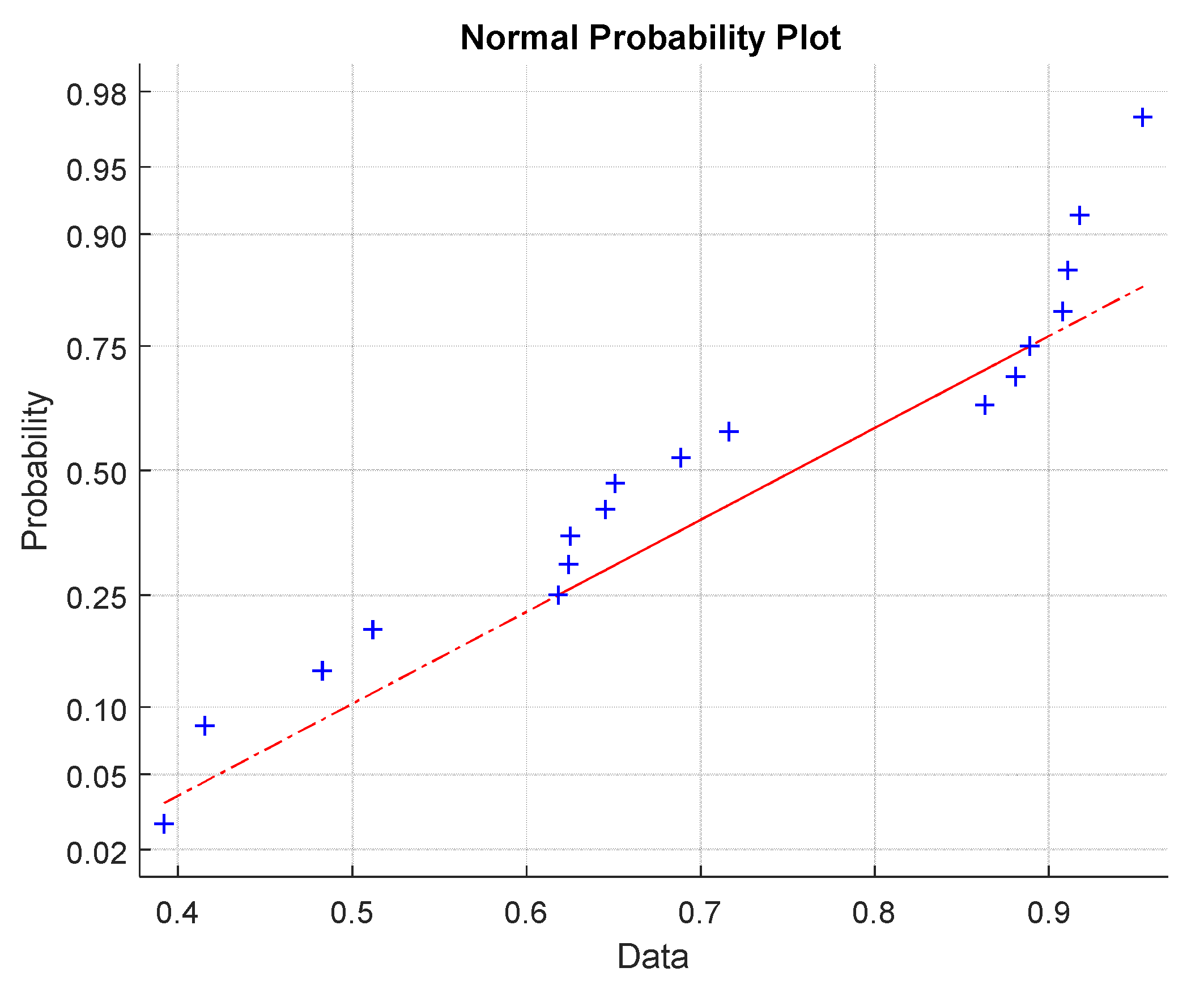
4.4. Hybrid Tapes Strength Distribution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ngo, T.D. (Ed.) Introduction to Composite Materials. In Composite and Nanocomposite Materials—From Knowledge to Industrial Applications; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Sathishkumar, T.P.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Nunes, J.P.; Van Hattum, F.W.J.; Bernardo, C.A.; Silva, J.F.; Marques, A.T. Advances in Thermoplastic Matrix Towpregs Processing. J. Thermoplast. Compos. Mater. 2004, 17, 523–544. [Google Scholar] [CrossRef]
- Global Advanced Polymer Composites Market is Expected to Reach USD 16.83 Billion by 2025: Fior Markets, GlobeNewswire News Room, 20 February 2020. Available online: http://www.globenewswire.com/news-release/2020/02/20/1988157/0/en/Global-Advanced-Polymer-Composites-Market-is-Expected-to-Reach-USD-16-83-Billion-by-2025-Fior-Markets.html (accessed on 11 February 2021).
- A Review of the Global Composites Market and Turkish Composites Market. Available online: https://www.reinforcer.com/en/category/detail/A-Review-of-the-Global-Composites-Market-and-Turkish-Composites-Market/61/350/0 (accessed on 11 February 2021).
- Thomason, J.; Jenkins, P.; Yang, L. Glass Fibre Strength—A Review with Relation to Composite Recycling. Fibers 2016, 4, 18. [Google Scholar] [CrossRef]
- Bauer, R.S.; Stewart, S.L.; Stenzenberger, H.D. Composite Materials, Thermoset Polymer-Matrix; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Thomason, J.; Yang, L.; Meier, R. The properties of glass fibres after conditioning at composite recycling temperatures. Compos. Part A Appl. Sci. Manuf. 2014, 61, 201–208. [Google Scholar] [CrossRef]
- Hu, N. (Ed.) Composites and their properties. In BoD–Books on Demand; IntechOpen: Rijeka, Croatia, 2012. [Google Scholar]
- Mesquita, F.; Bucknell, S.; Leray, Y.; Lomov, S.V.; Swolfs, Y. Single carbon and glass fibre properties characterised using large data sets obtained through automated single fibre tensile testing. Compos. Part A Appl. Sci. Manuf. 2021, 145, 106389. [Google Scholar] [CrossRef]
- Mei, M.; He, Y.; Yang, X.; Wei, K.; Qu, Z.; Fang, D. Shear deformation characteristics and defect evolution of the biaxial ±45° and 0/90° glass non-crimp fabrics. Compos. Sci. Technol. 2020, 193, 108137, ISSN 0266-3538. [Google Scholar] [CrossRef]
- Artemenko, S.E. Polymer Composite Materials Made from Carbon, Basalt, and Glass Fibres. Structure and Properties. Fibre Chem. 2003, 35, 226–229. [Google Scholar] [CrossRef]
- Venkataraman, M.; Militký, J.; Mishra, R.; Kremenakova, D.; Petru, M. Tensile Properties of Glass Roving and Hybrid Tapes. IOP Conf. Ser. Mater. Sci. Eng. 2019, 553, 012055. [Google Scholar] [CrossRef]
- Kovacevic, S.; Brnada, S.; Dobnik-Dubrovski, P. Analysis of the Mechanical Properties of Woven Fabrics from Glass and Basalt Yarns. Fibres Text. East. Eur. 2015, 23, 83–91. [Google Scholar] [CrossRef][Green Version]
- Summerscales, J.; Short, D. Carbon fibre and glass fibre hybrid reinforced plastics. Composites 1978, 9, 157–166. [Google Scholar] [CrossRef]
- Biron, M. Chapter 6—Thermoplastic Composites. In Thermoplastics and Thermoplastic Composites, 3rd ed.; Biron, M., Ed.; William Andrew Publishing: Norwich, NY, USA, 2018; pp. 821–882. [Google Scholar] [CrossRef]
- Swolfs, Y.; Verpoest, I.; Gorbatikh, L. Recent advances in fibre-hybrid composites: Materials selection, opportunities and applications. Int. Mater. Rev. 2019, 64, 181–215. [Google Scholar] [CrossRef]
- Binetruy, C. Composites Manufacturing Overview of Current Advances and Challenges for the Future. In Proceedings of the the ECCM 16—16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Maddaloni, G.; Parcesepe, E.; Franco, A.; Bonati, A.; Occhiuzzi, A.; Pecce, M.R. Experimental characterization of tensile strength of steel and fibre rovings also under environmental conditioning. Compos. Part B Eng. 2021, 217, 108895. [Google Scholar] [CrossRef]
- Venkataraman, M.; Militky, J.; Pulicek, R.; Novotna, J. Sophisticated Glass Tapes for Fabrication of Composites. J. Fiber Bioeng. Inform. 2019, 12, 35–42. [Google Scholar] [CrossRef]
- El-Dessouky, H.M.; Lawrence, C.; Mcgrail, T.; Broughton, B. Ultra-Light Weight Thermoplastic Composites: Tow-Spreading Technology. In Proceedings of the ECCM15—15th European Conference on Composite Materials, Venice, Italy, 24–28 June 2012. [Google Scholar]
- Molyneux, M.; Murray, P.; Murray, B.P. Prepreg, tape and fabric technology for advanced composites. Composites 1983, 14, 87–91. [Google Scholar] [CrossRef]
- Haincová, E.; Hájková, P.; Kohout, J. Prepregs for Temperature Resistant Composites. Materials 2019, 12, 4012. [Google Scholar] [CrossRef] [PubMed]
- Rinne, H. The Weibull Distribution. A Handbook; Chapman & Hall: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wilson, S. Lateral spreading of fibre tows. J. Eng. Math. 1997, 32, 19–26. [Google Scholar] [CrossRef]
- Irfan, M.S.; Machavaram, V.R.; Mahendran, R.S.; Shotton-Gale, N.; Wait, C.F.; Paget, M.A.; Hudson, M.; Fernando, G.F. Lateral spreading of a fiber bundle via mechanical means. J. Compos. Mater. 2011, 46, 311–330. [Google Scholar] [CrossRef]
- Militký, J.; Venkataraman, M.; Baheti, V.; Novotná, J.; Pulicek, R.; Samková, A.; Karolína, V.; Pavel, S.; Dana, K.; Rajesh, M.; et al. Characterization and Strength Distribution of Fibrous Glass Tapes. In Recent Trends in Fibrous Material Science; Technical University of Liberec: Liberec, Czech Republic, 2019; pp. 9–52. [Google Scholar]
- Neckar, B. Yarn. Creation, Structure and Properties; SNTL: Prague, Czech Republic, 1990. (In Czech) [Google Scholar]
- Meloun, M.; Militky, J. Book-035 Statistical Data Analysis, A Practical Guide with 1250 Exercises and Answer Key on CD; Woodhead Publishing: New Delhi, India, 2011. [Google Scholar]
- Naresh, K.; Shankar, K.; Velmurugan, R. Reliability analysis of tensile strengths using Weibull distribution in glass/epoxy and carbon/epoxy composites. Compos. Part B Eng. 2018, 133, 129–144. [Google Scholar] [CrossRef]
- Monteiro, S.N.; Margem, F.M.; Braga, F.D.O.; da Luz, F.S.; Simonassi, N.T. Weibull analysis of the tensile strength dependence with fiber diameter of giant bamboo. J. Mater. Res. Technol. 2017, 6, 317–322. [Google Scholar] [CrossRef]
- Pan, N. A Detailed Examination of the Translation Efficiency of Fiber Strength into Composite Strength. J. Reinf. Plast. Compos. 1995, 14, 2–28. [Google Scholar] [CrossRef]









| Properties | Unit | Value |
|---|---|---|
| Fineness | Tex | 1200 |
| Filament diameter | µm | 16 |
| Tensile strength | N | 450 |
| Material | Standard | Resin | Manufacturer | Acronym |
|---|---|---|---|---|
| Roving | ASTM D 1505 | - | Slovakia | SL |
| Hybrid tape | ASTM C 338 | CHS-EPOXY 200 V 55 | Czech Republic–TUL and Večerník | SLT |
| Material | Width ‘a’ [mm] | Thickness ‘b’ [mm] | DT [mm] | α | β | αc |
|---|---|---|---|---|---|---|
| SLT µ = 0.9 | 5.122 | 0.158 | 0.81 | 6.34 | 0.196 | 4.05 |
| SLT µ = 0.7 | 5.122 | 0.158 | 0.92 | 5.57 | 0.172 | 4.603 |
| Material | Mean Value [GPa] | Standard Deviation [GPa] | Coefficient of Variation [%] |
|---|---|---|---|
| Fibers from SL | 1.93 | 0.43 | 22.37 |
| Material | Mean Value [GPa] | Standard Deviation [GPa] | Threshold A [GPa] | Weibull Form C [-] | Weibull Scale B [GPa] |
|---|---|---|---|---|---|
| SL | 0.88 | 0.11 | 0.57 | 3.10 | 0.35 |
| Material | Mean Value [GPa] | Standard Deviation [GPa] | Threshold A [GPa] | Weibull Form C [-] | Weibull Scale B [GPa] |
|---|---|---|---|---|---|
| SLT | 1.06 | 0.18 | 0.36 | 4.49 | 0.77 |
| Material | Tape [GPa] | Fiber [GPa] | Matrix [GPa] | |
|---|---|---|---|---|
| SLT | 1.064 | 0.568 | 0.496 | 0.178 |
| Material | Mean Pred. [GPa] | Standard Deviation Pred. [GPa] |
|---|---|---|
| SLT | 1.1835 | 0.0117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkataraman, M.; Militký, J.; Samková, A.; Karthik, D.; Křemenáková, D.; Petru, M. Hybrid Prepreg Tapes for Composite Manufacturing: A Case Study. Materials 2022, 15, 619. https://doi.org/10.3390/ma15020619
Venkataraman M, Militký J, Samková A, Karthik D, Křemenáková D, Petru M. Hybrid Prepreg Tapes for Composite Manufacturing: A Case Study. Materials. 2022; 15(2):619. https://doi.org/10.3390/ma15020619
Chicago/Turabian StyleVenkataraman, Mohanapriya, Jiří Militký, Alžbeta Samková, Daniel Karthik, Dana Křemenáková, and Michal Petru. 2022. "Hybrid Prepreg Tapes for Composite Manufacturing: A Case Study" Materials 15, no. 2: 619. https://doi.org/10.3390/ma15020619
APA StyleVenkataraman, M., Militký, J., Samková, A., Karthik, D., Křemenáková, D., & Petru, M. (2022). Hybrid Prepreg Tapes for Composite Manufacturing: A Case Study. Materials, 15(2), 619. https://doi.org/10.3390/ma15020619









