Programmable Density of Laser Additive Manufactured Parts by Considering an Inverse Problem
Abstract
1. Introduction
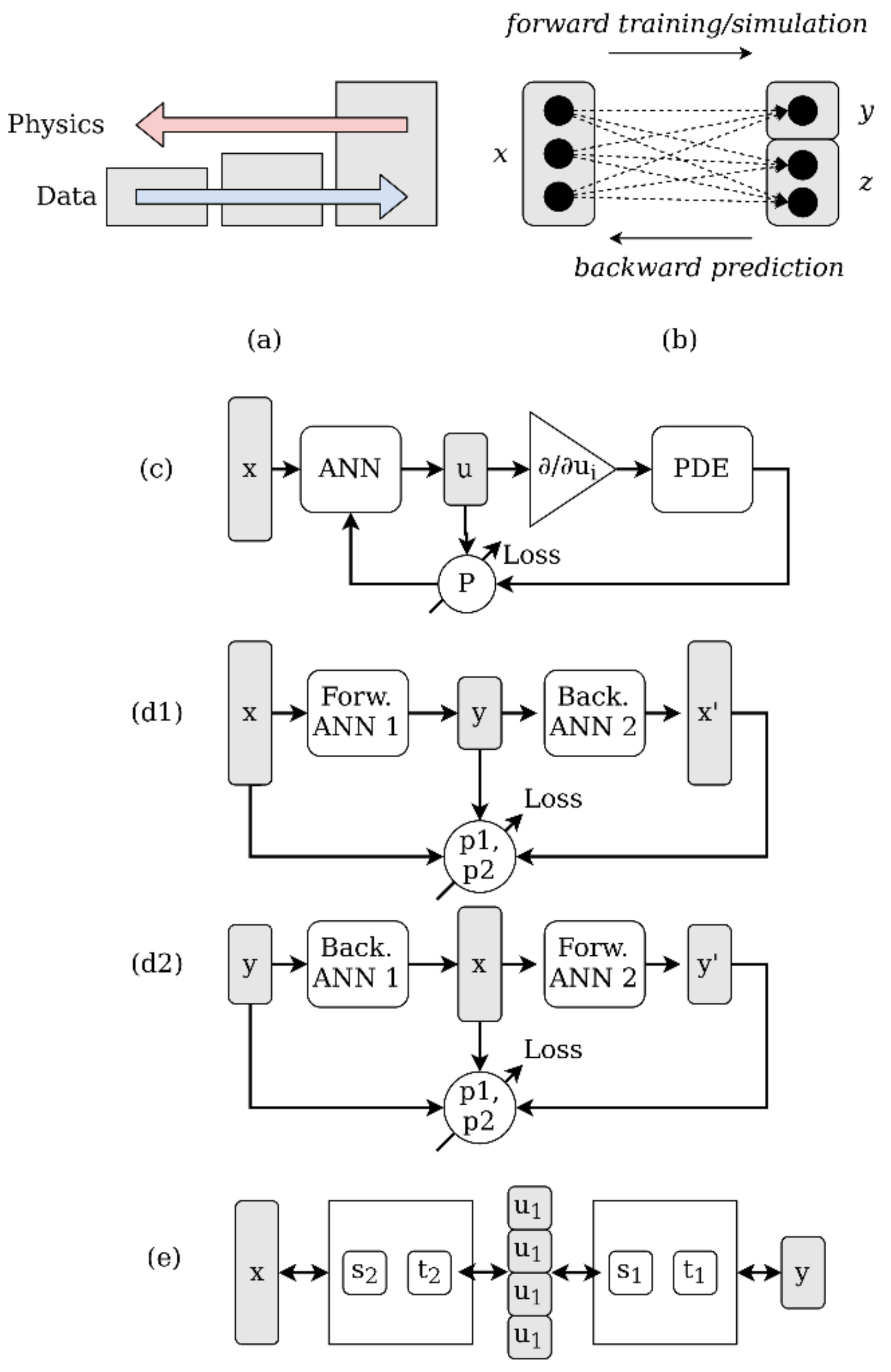
2. Inverse Problems with Data-Driven Methods
3. Materials and Methods
3.1. LPBF and Metallography
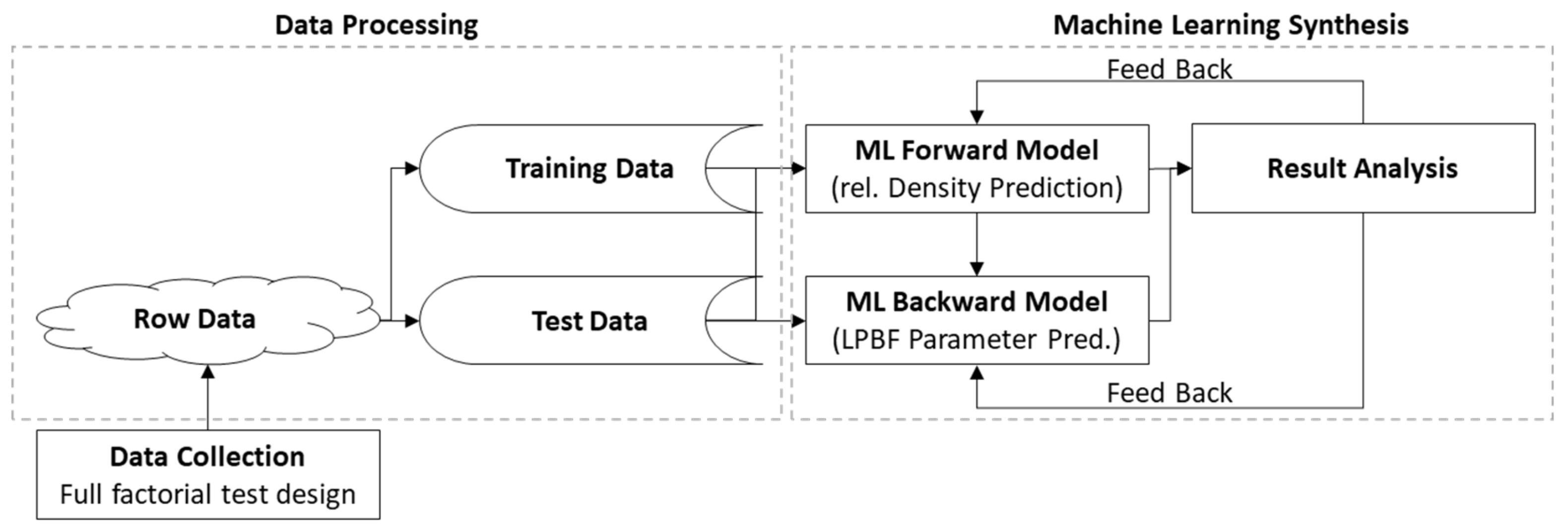
3.2. Data Analysis and Preparation
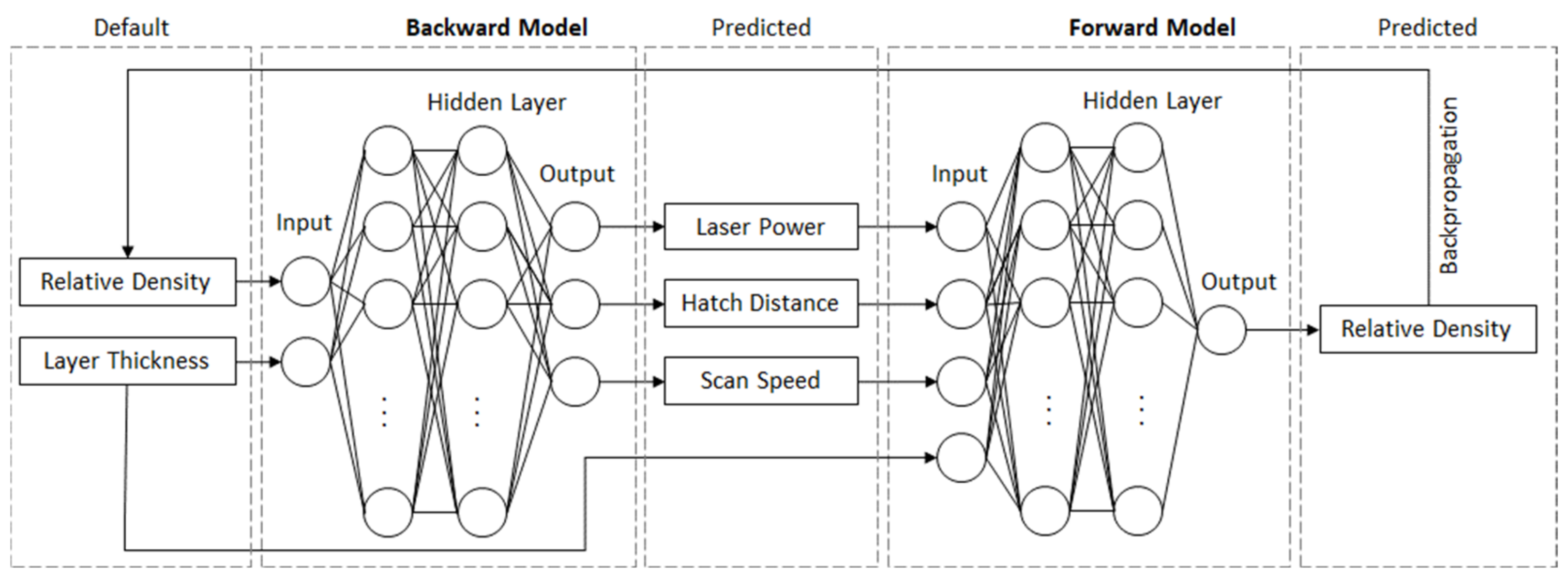
3.3. Modeling
4. Results and Discussion
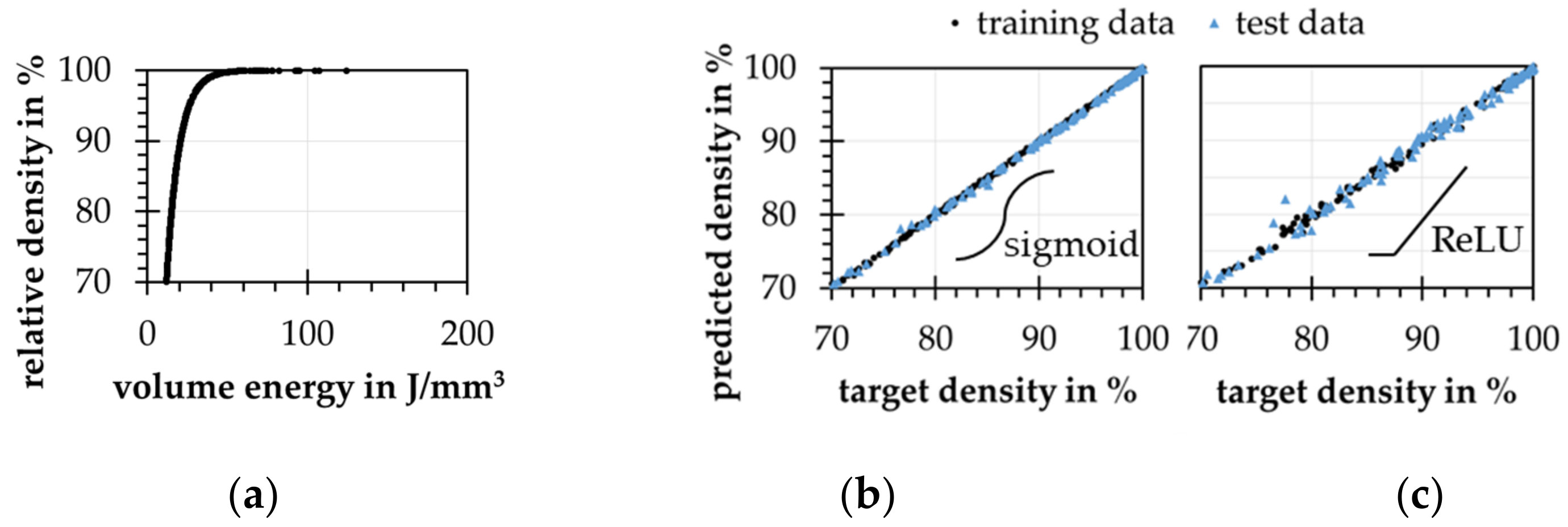
4.1. Examination of the LPBF Process
4.2. Data Analysis
4.3. Forward Modeling Problem-Density Prediction
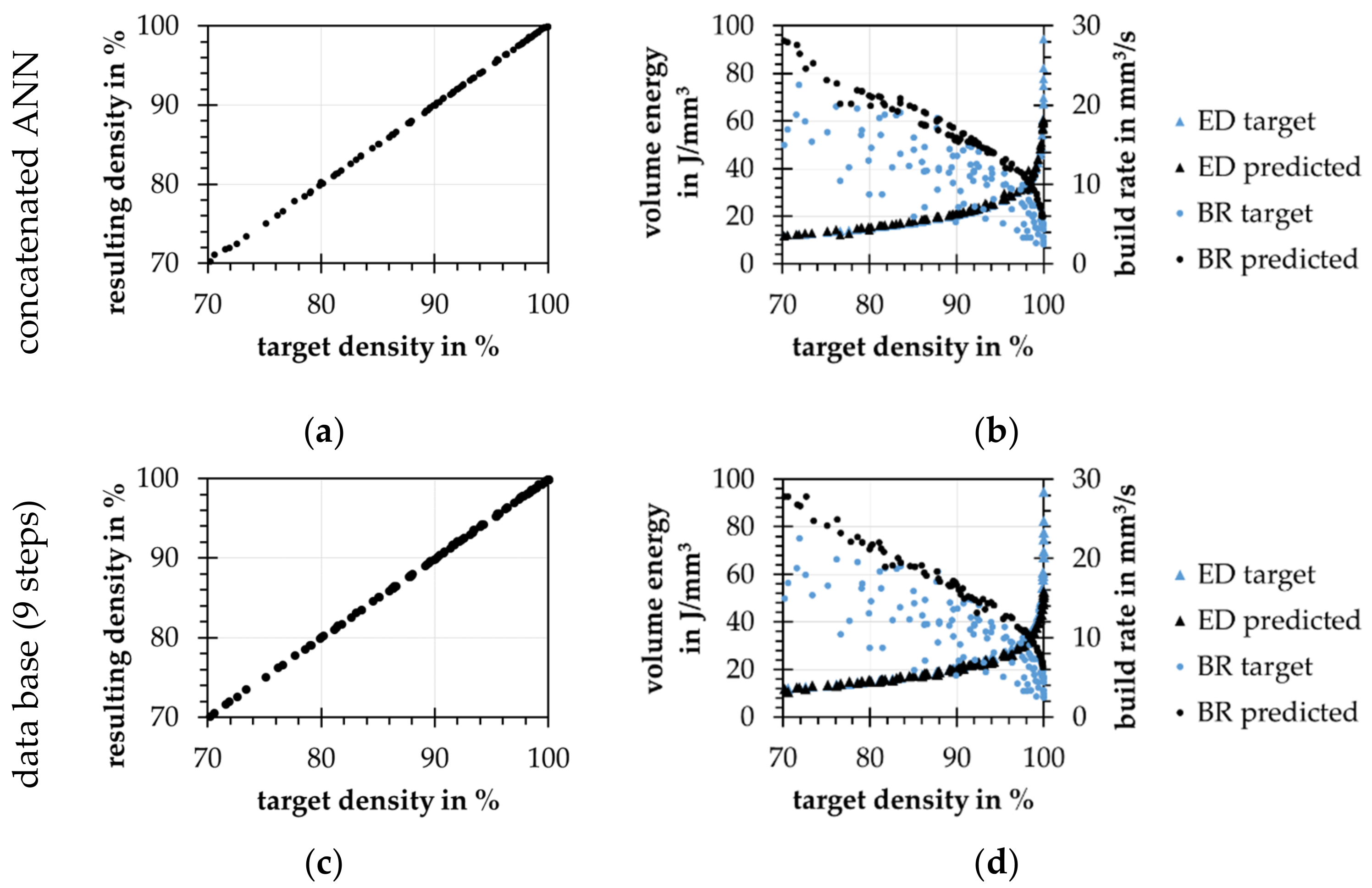
4.4. Backward Modeling Problem-Process Parameter Prediction
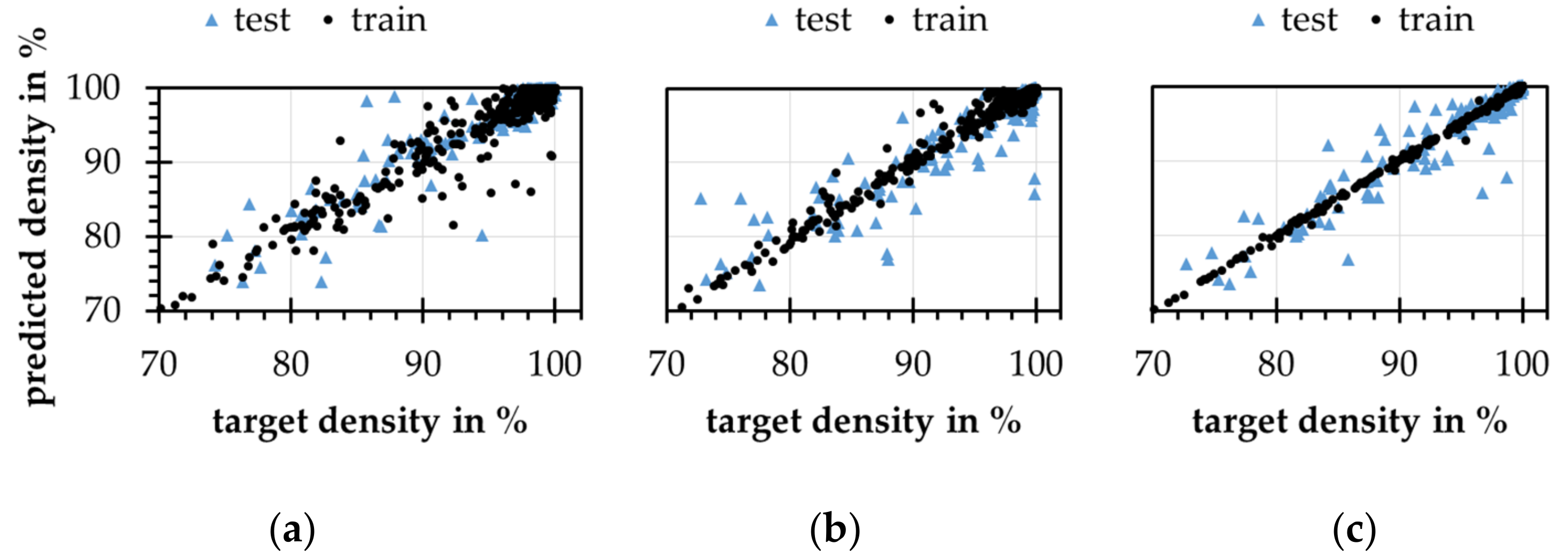
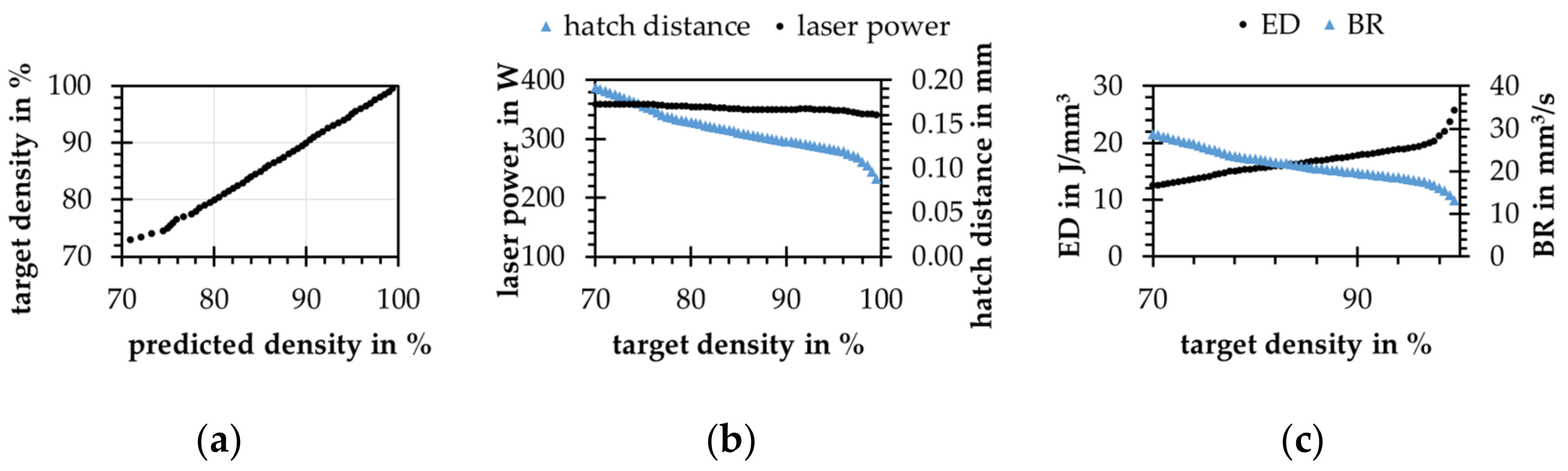
4.5. Real Data Application
4.6. Summary of the Results
- Boundaries of the process window reached with the statistical test series and different kinds of pores and mechanisms could be mapped.
- Problems with statistical test series for machine learning are detected and evaluated for the article’s target of linking the relative density and the LPBF process parameters.
- Theoretical solvability of the inverse problem evaluated by synthetic data for both model approaches (concatenated ANN and database).
- Database approach shows strong jumps for chosen process parameters, while the concatenated ANNs choosing process parameters smooth and strategic
- By adding hints, the concatenated ANN model is guided by learning to increase the build rates of predicted process parameters.
- Concatenated ANNs could learn real data problems, but pure quality and fuzziness of the real data worsen the results of the models.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network | MSQ | Mean squared loss hint |
| BR | Build rate | MVAE | Modified variational autoencoder |
| Layer thickness | Batch size | ||
| EBM | Electron beam melting | NSGA-II | Non-dominated sorting genetic algorithm |
| ED | Energy density | PDE | Partial differential equation |
| Transfer function | PINN | Physics-informed neural network | |
| GAN | Generative adversarial network | Laser power | |
| HIP | Hot isostatic pressing | Relative density | |
| Hatch distance | ReLU | Rectified linear unit | |
| INN | Invertible neural network | ROI | Region of interest |
| LMD | Laser metal deposition | Standard deviation related to the relative density | |
| LPBF | Laser powder bed fusion, also powder base fusion with laser beam (PBF-LB) and selective laser melting (SLM) | Scan speed | |
| MLin | Mean linear loss hint | Internal model parameters | |
| MMD | Maximum mean discrepancy | Input/feature variable |
References
- Vora, J.; Parmar, H.; Chaudhari, R.; Khanna, S.; Doshi, M.; Patel, V.V. Experimental investigations on mechanical properties of multi-layered structure fabricated by GMAW-based WAAM of SS316L. J. Mater. Res. Technol. 2022, 20, 2748–2757. [Google Scholar] [CrossRef]
- Wycisk, E. Ermüdungseigenschaften der Laseradditiv Gefertigten Titanlegierung TiAl6V4; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Thomas, D.S.; Gilbert, S.W. Costs and Cost Effectiveness of Additive Manufacturing; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2014. [Google Scholar]
- Ma, M.; Wang, Z.; Gao, M.; Zeng, X. Layer thickness dependence of performance in high-power selective laser melting of 1Cr18Ni9Ti stainless steel. J. Mater. Process. Technol. 2015, 215, 142–150. [Google Scholar] [CrossRef]
- Bertoli, U.S.; Wolfer, A.J.; Matthews, M.J.; Delplanque, J.P.R.; Schoenung, J.M. On the limitations of volumetric energy density as a design parameter for selective laser melting. Mater. Des. 2017, 113, 331–340. [Google Scholar] [CrossRef]
- Liu, W.; Chen, C.; Shuai, S.; Zhao, R.; Liu, L.; Wang, X.; Hu, T.; Xuan, W.; Li, C.; Yu, J.; et al. Study of pore defect and mechanical properties in selective laser melted Ti6Al4V alloy based on X-ray computed tomography. Mater. Sci. Eng. A 2020, 797, 139981. [Google Scholar] [CrossRef]
- Gebhardt, A. Generative Fertigungsverfahren: Rapid Prototyping-Rapid Tooling-Rapid Manufacturing, 3rd ed.; Hanser: München, Germany, 2007; ISBN 978-3-446-22666-1. [Google Scholar]
- Herzog, D.; Bartsch, K.; Bossen, B. Productivity optimization of laser powder bed fusion by hot isostatic pressing. Addit. Manuf. 2020, 36, 101494. [Google Scholar] [CrossRef]
- Vasileska, E.; Demir, A.G.; Colosimo, B.M.; Previtali, B. A novel paradigm for feedback control in LPBF: Layer-wise correction for overhang structures. Adv. Manuf. 2022, 10, 326–344. [Google Scholar] [CrossRef]
- Liverani, E.; Fortunato, A. Additive manufacturing of AISI 420 stainless steel: Process validation, defect analysis and mechanical characterization in different process and post-process conditions. Int. J. Adv. Manuf. Technol. 2021, 117, 809–821. [Google Scholar] [CrossRef]
- Park, H.S.; Nguyen, D.S.; Le-Hong, T.; Van Tran, X. Machine learning-based optimization of process parameters in selective laser melting for biomedical applications. J. Intell. Manuf. 2022, 33, 1843–1858. [Google Scholar] [CrossRef]
- Bai, S.; Perevoshchikova, N.; Sha, Y.; Wu, X. The effects of selective laser melting process parameters on relative density of the AlSi10Mg parts and suitable procedures of the archimedes method. Appl. Sci. 2019, 9, 583. [Google Scholar] [CrossRef]
- Shamsdini, S.; Shakerin, S.; Hadadzadeh, A.; Amirkhiz, B.S.; Mohammadi, M. A trade-off between powder layer thickness and mechanical properties in additively manufactured maraging steels. Mater. Sci. Eng. A 2020, 776, 139041. [Google Scholar] [CrossRef]
- Welsch, A.; Eitle, V.; Buxmann, P. Maschinelles Lernen. HMD Prax. Wirtsch. 2018, 55, 366–382. [Google Scholar] [CrossRef]
- Minbashian, A.; Bright, J.E.; Bird, K.D. A comparison of artificial neural networks and multiple regression in the context of research on personality and work performance. Organ. Res. Methods 2010, 13, 540–561. [Google Scholar] [CrossRef]
- Lee, J.W.; Park, W.B.; Do Lee, B.; Kim, S.; Goo, N.H.; Sohn, K.S. Dirty engineering data-driven inverse prediction machine learning model. Sci. Rep. 2020, 10, 20443. [Google Scholar] [CrossRef]
- Yu, X.; Chu, Y.; Jiang, F.; Guo, Y.; Gong, D. SVMs classification based two-side cross domain collaborative filtering by inferring intrinsic user and item features. Knowl.-Based Syst. 2018, 141, 80–91. [Google Scholar] [CrossRef]
- Yu, X.; Yang, J.; Xie, Z. Training SVMs on a bound vectors set based on Fisher projection. Front. Comput. Sci. 2014, 8, 793–806. [Google Scholar] [CrossRef]
- Ardizzone, L.; Kruse, J.; Wirkert, S.; Rahner, D.; Pellegrini, E.W.; Klessen, R.S.; Maier-Hein, L.; Rother, C.; Köthe, U. Analyzing inverse problems with invertible neural networks. arXiv 2019, arXiv:1808.04730. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. Regularization, Bayesian inference, and machine learning methods for inverse problems. Entropy 2021, 23, 1673. [Google Scholar] [CrossRef] [PubMed]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Chen, Y. Inverse Design of Materials by Machine Learning. Materials 2022, 15, 1811. [Google Scholar] [CrossRef]
- Kadeethum, T.; Jørgensen, T.M.; Nick, H.M. Physics-Informed Neural Networks for Solving Inverse Problems of Nonlinear Biot's Equations: Batch Training. In Proceedings of the 54th U.S. Rock Mechanics/Geomechanics Symposium, Golden, Colorado, USA, 28 June–1 July 2020. physical event cancelled. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Alpaydin, E. Maschinelles Lernen, 2nd ed.; De Gruyter Oldenbourg: Berlin, Germany; Boston, MA, USA, 2019. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real nvp. arXiv 2016, arXiv:1605.08803. [Google Scholar] [CrossRef]
- Kanne-Schludde, T. Erzeugung Synthetischer Trainingsdaten Für Die Deep Learning Basierte Bestimmung von GPS-Koordinaten Aus Fotos Am Beispiel Der Notre Dame. 2020. Available online: https://users.informatik.haw-hamburg.de/~ubicomp/projekte/master2020-proj/kanne_hp.pdf (accessed on 7 October 2022).
- Batista, G.E.; Monard, M.C. An analysis of four missing data treatment methods for supervised learning. Appl. Artif. Intell. 2003, 17, 519–533. [Google Scholar] [CrossRef]
- Kelleher, J.D.; Mac Namee, B.; D’arcy, A. Fundamentals of Machine Learning for Predictive Data Analytics: Algorithms, Worked Examples, and Case Studies; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Brownlee, J. Data Preparation for Machine Learning: Data Cleaning, Feature Selection, and Data Transforms in Python; Machine Learning Mastery: San Juan, Puerto Rico, 2020. [Google Scholar]
- Facebook, PyTorch: Machine Learning Framework: Facebook. 2021. Available online: https://pytorch.org/ (accessed on 7 October 2022).
- Liu, Z.; Zhou, J. Introduction to Graph Neural Networks. In Synthesis Lectures on Artificial Intelligence and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2020; Volume 14, pp. 1–127. [Google Scholar] [CrossRef]
- Ning, J.; Wang, W.; Zamorano, B.; Liang, S.Y. Analytical modeling of lack-of-fusion porosity in metal additive manufacturing. Appl. Phys. A 2019, 125, 797. [Google Scholar] [CrossRef]
- Wang, T.; Dai, S.; Liao, H.; Zhu, H. Pores and the formation mechanisms of SLMed AlSi10Mg. Rapid Prototyp. J. 2020, 26, 1657–1664. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA; London, UK, 2012. [Google Scholar]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, Z.; Yan, J. Machine learning for metal additive manufacturing: Predicting temperature and melt pool fluid dynamics using physics-informed neural networks. Comput. Mech. 2021, 67, 619–635. [Google Scholar] [CrossRef]


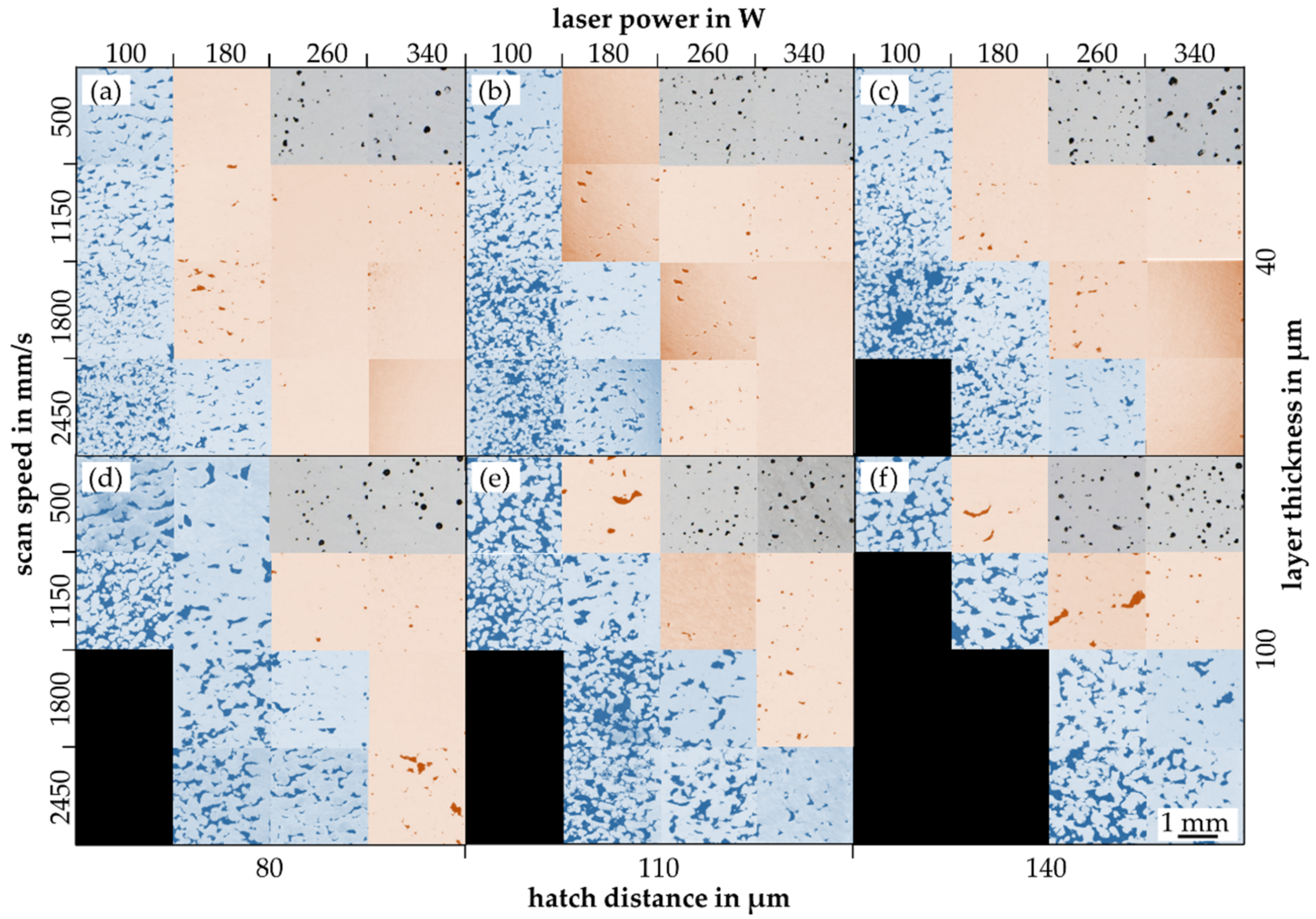




| Factor | Step I | Step II | Step III | Step IV |
|---|---|---|---|---|
| DS in µm | 40 | 50 | 80 | 100 |
| PL in W | 100 | 180 | 260 | 340 |
| vS in mm/s | 500 | 1150 | 1800 | 2450 |
| hS in mm | 0.05 | 0.08 | 0.11 | 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altmann, M.L.; Bosse, S.; Werner, C.; Fechte-Heinen, R.; Toenjes, A. Programmable Density of Laser Additive Manufactured Parts by Considering an Inverse Problem. Materials 2022, 15, 7090. https://doi.org/10.3390/ma15207090
Altmann ML, Bosse S, Werner C, Fechte-Heinen R, Toenjes A. Programmable Density of Laser Additive Manufactured Parts by Considering an Inverse Problem. Materials. 2022; 15(20):7090. https://doi.org/10.3390/ma15207090
Chicago/Turabian StyleAltmann, Mika León, Stefan Bosse, Christian Werner, Rainer Fechte-Heinen, and Anastasiya Toenjes. 2022. "Programmable Density of Laser Additive Manufactured Parts by Considering an Inverse Problem" Materials 15, no. 20: 7090. https://doi.org/10.3390/ma15207090
APA StyleAltmann, M. L., Bosse, S., Werner, C., Fechte-Heinen, R., & Toenjes, A. (2022). Programmable Density of Laser Additive Manufactured Parts by Considering an Inverse Problem. Materials, 15(20), 7090. https://doi.org/10.3390/ma15207090








