The Influence of Closed-Cell W-Shaped Liner Parameters on the Penetration Performance of Integral Annular Shaped Charge
Abstract
:1. Introduction
2. Simulation Calculation
2.1. Simulation Model
2.2. Material Parameters
3. Scheme Design of Orthogonal Optimization Simulation and Result Analysis
3.1. Orthogonal Optimization Scheme Design
3.2. Simulation Results and Analysis
- (1)
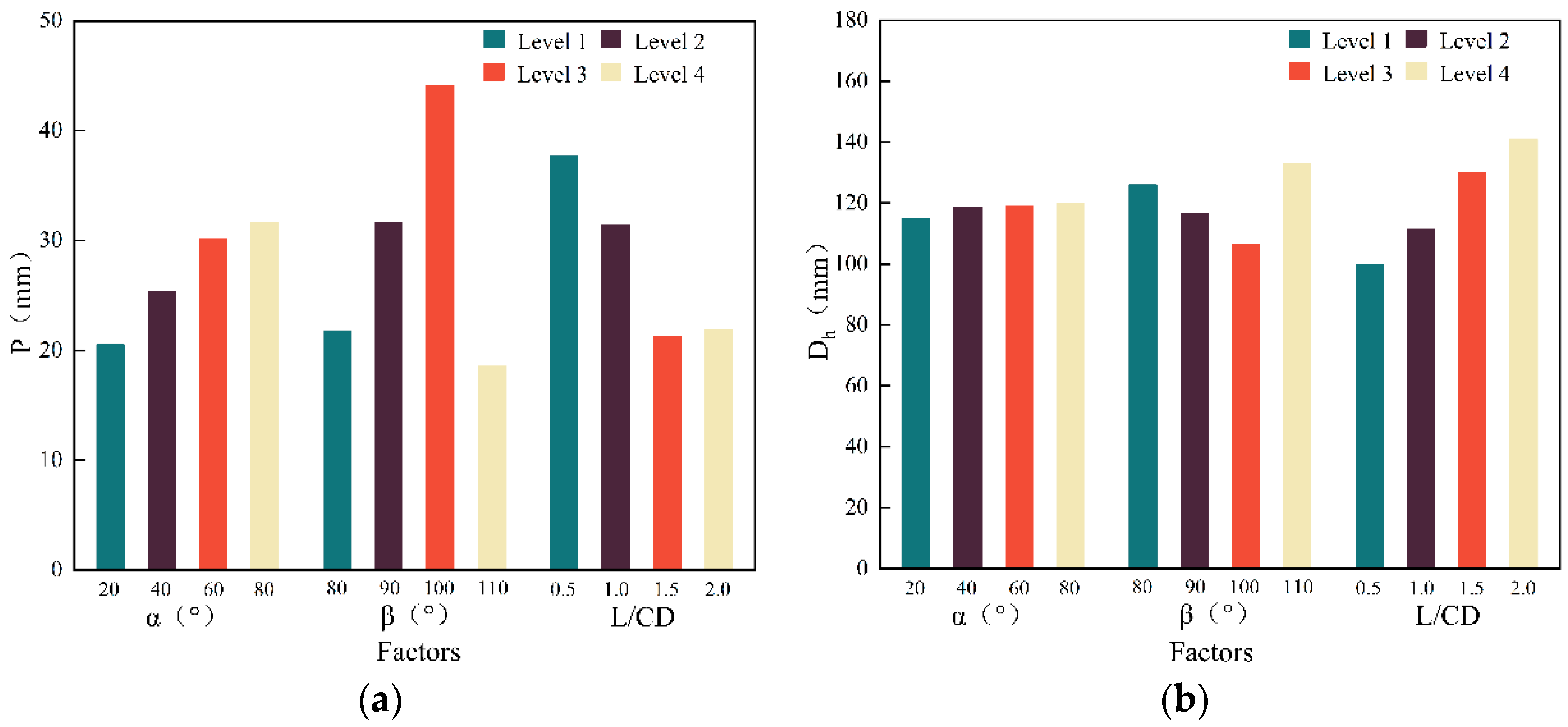
- The factors affecting penetration depth can be ranked in descending order of their influence: the inverted cone angle α, the cone angle of liner β, and the charge length-diameter ratio L/CD.
- (2)
- The factors affecting opening diameters can be ranked in descending order of their influence: the cone angle of the liner β, the inverted cone angle α, and the charge length-diameter ratio L/CD.
- (1)
- The inverted cone angle is the main factor that influences the penetration depth. As the inverted cone angle increases, the penetration depth grows first and then goes down, reaching its maximum value when the inverted cone angle α = 60°. Therefore, an inverted cone angle α = 60° is selected in the new annular shaped charge structure;
- (2)
- The cone angle of the liner is a major contributor to the opening diameter. A larger cone angle of the liner would result in a bigger opening diameter at a lower penetration depth. When it reaches about 100°, there is no big difference in the penetration depth. It would be a more ideal situation if the opening diameter was as large as possible. Therefore, the cone angle of the liner is taken as 90° in the new structure;
- (3)
- The charge length-diameter ratio has less influence on the penetration depth and opening diameter than the previous two factors. Increasing the length-diameter ratio can speed up the jet and deepen the penetration depth. The increasing penetration depth would be slowed down in which few benefits would be found when the ratio is above 1.5 and the opening diameter is less affected by the charge length-diameter ratio compared with the other two. With all-rounded consideration, the length-diameter ratio of 1.5 is taken in the new structure;
- (4)
- Given all of that, the optimum scheme parameters of the overall annular shaped charge structure of the new closed-cell W-shaped liner are inverted cone angle α = 60°, the cone angle of the liner β = 90°, and the charge length-diameter ratio L/CD = 1.5.
4. Optimization Scheme Simulation and Result Analysis
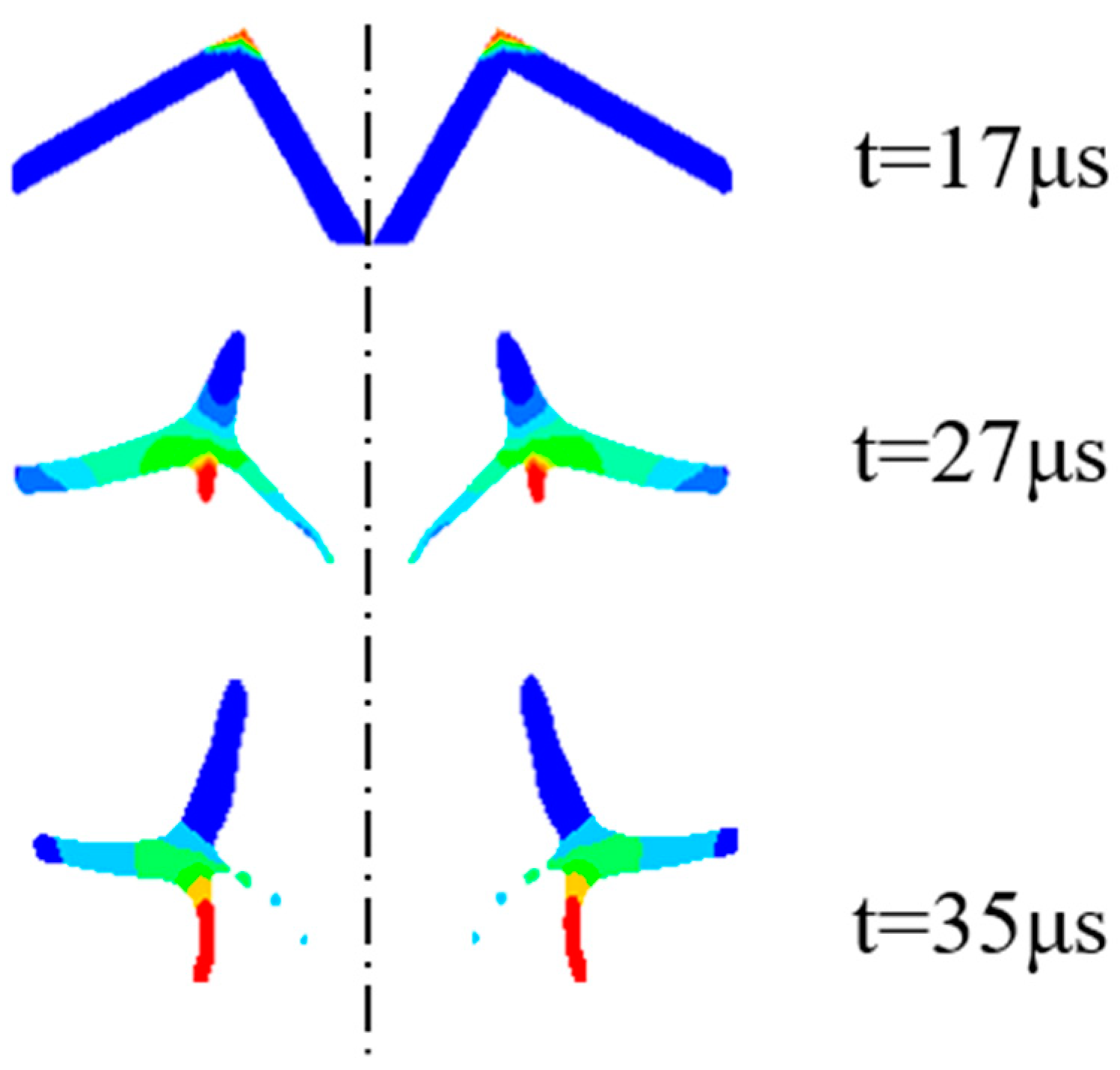
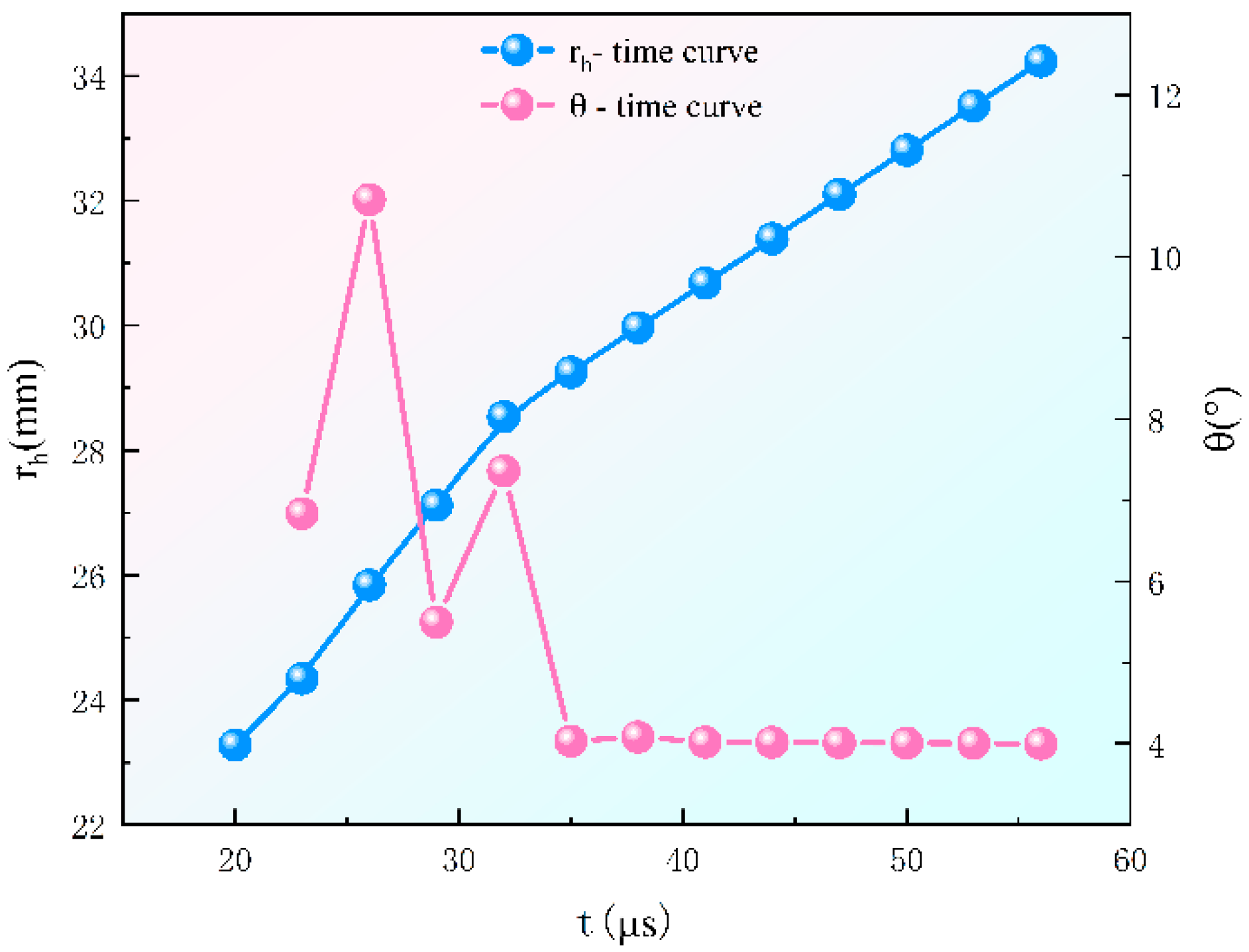
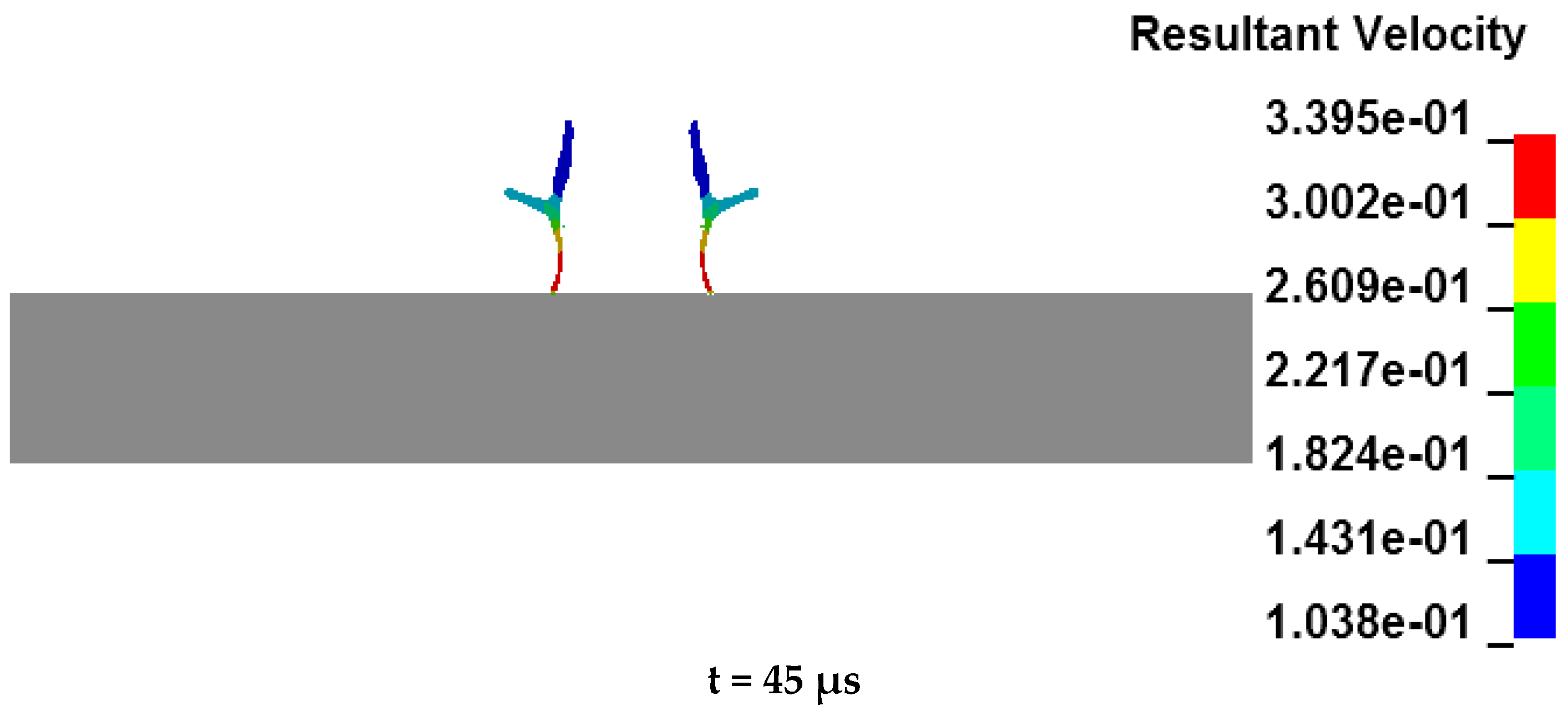
4.1. Analysis of the Formation Process of the Annular Jet
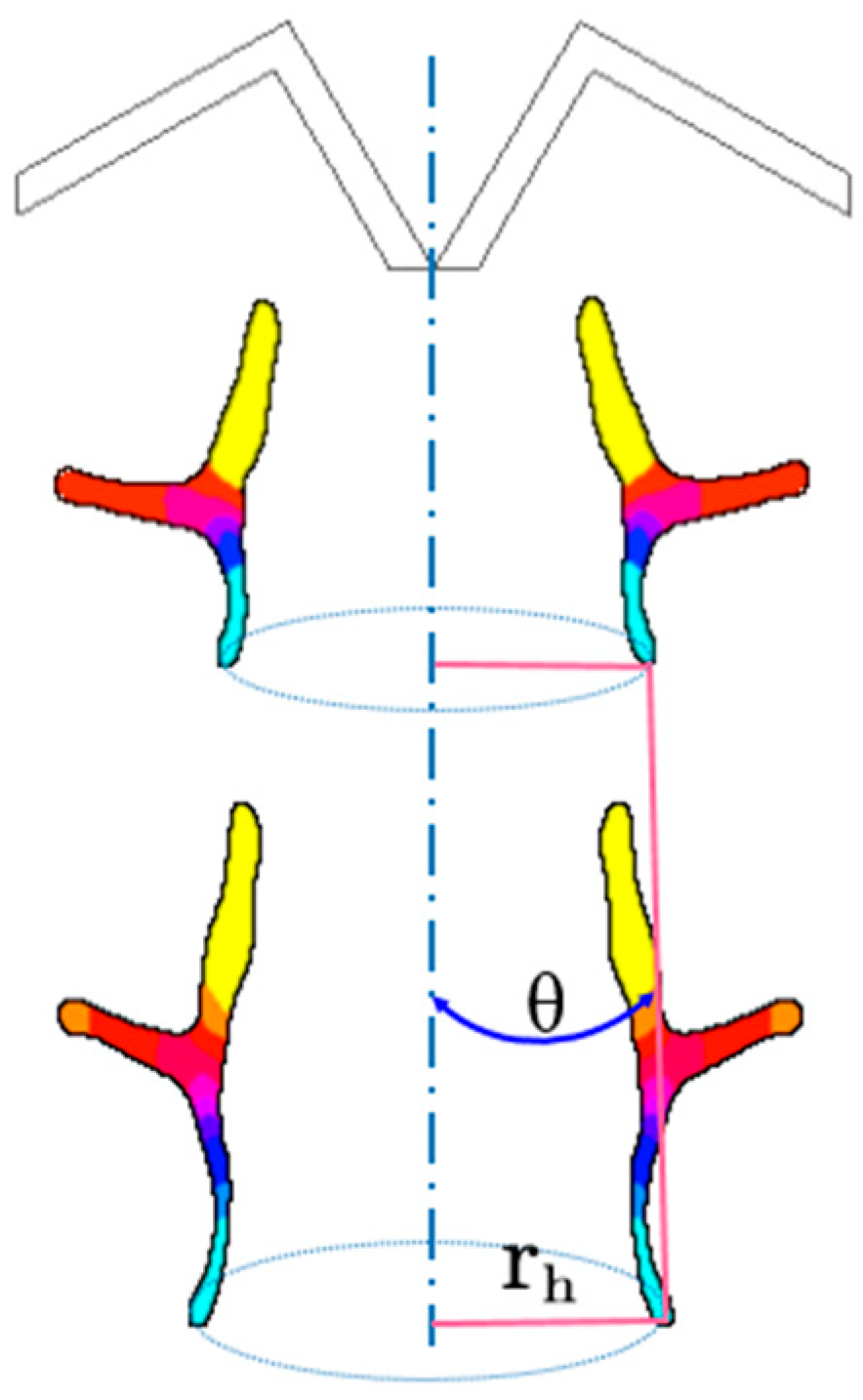
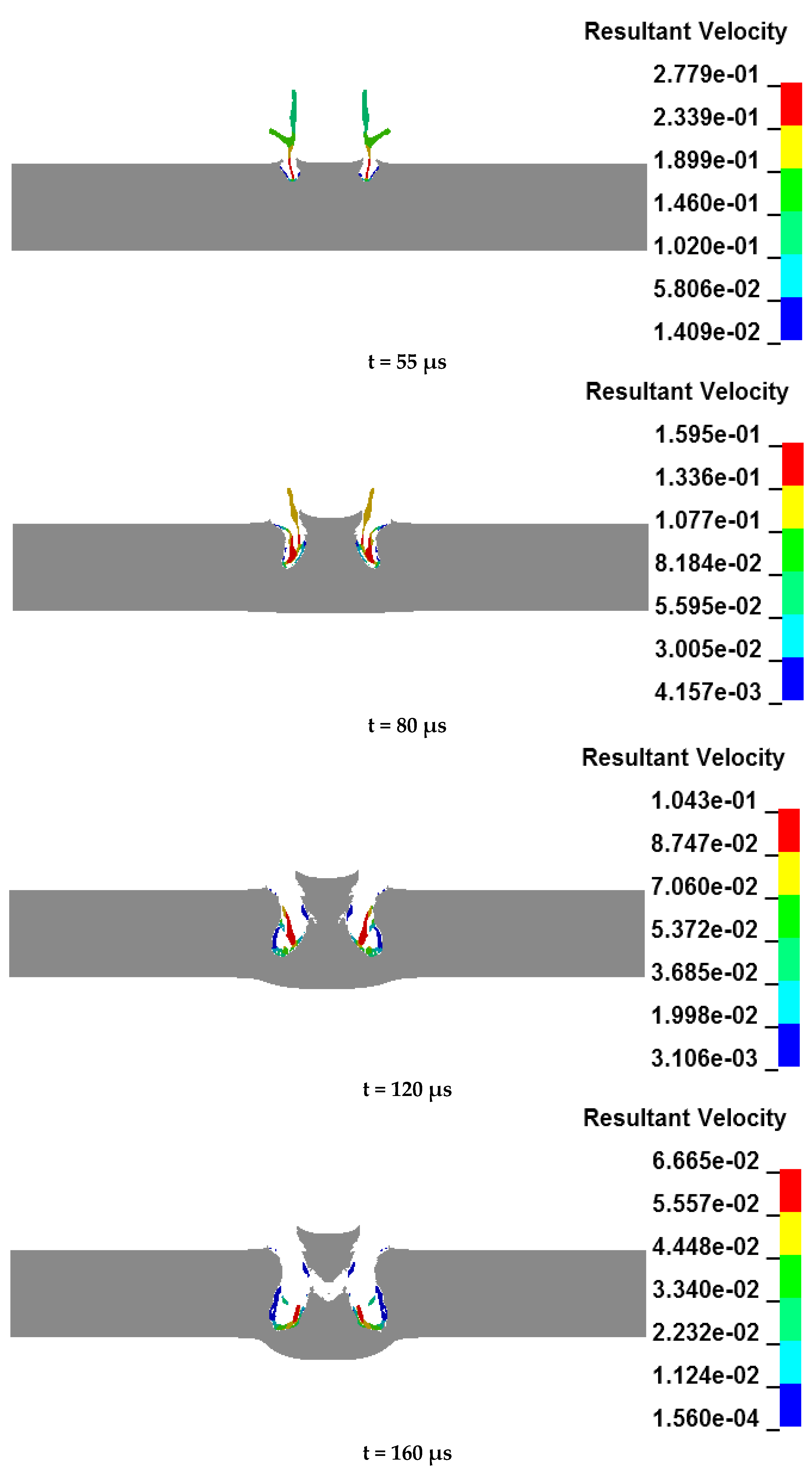
4.2. Analysis of the Penetration Process
4.3. Experiment Verification
- (1)
- Arrange the site according to the schematic diagram of the test layout;
- (2)
- Test the detonating line to ensure that the line is unblocked;
- (3)
- Place the test bomb and connect the detonating line;
- (4)
- Detonates the test bomb and measure the hole diameter with a rigid ruler.
5. Conclusions
- (1)
- The simulation analysis shows that the influence of various factors on the penetration depth is sequenced as: inverted cone angle > cone angle of the liner > charge length-diameter ratio, and that on the penetration depth can be ordered as: cone angle of the liner > inverted cone angle > charge length-diameter ratio. The inverted cone angle and the cone angle of the liner are the main influencing factors of penetration depth and opening aperture, respectively. The penetration depth first increases and then drops as the inverted cone angle becomes larger. The opening diameter becomes larger as the cone angle of the liner rises;
- (2)
- The optimum overall annular shaped charge structure with both excellent penetration depth and an opening aperture is obtained through orthogonal optimization design, in which the inverted cone angle is 60°, the cone angle of the cover is 90°, and the length to diameter ratio of the charge is 1.5;
- (3)
- The static armor-piercing test results of the optimized annular shaped charge structure show that the opening diameter can reach 95.0 mm (equivalent to 0.83 CD) while the annular jet penetrates the armored steel target with a thickness of 60.0 mm (equivalent to 0.53 CD). The numerical simulation is in agreement with the experimental data. The research results are of great significance in guiding the design of the front-stage annular shaped charge structure of the multi-effect destructive warhead.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leidel, D.J. A Design Study of an Annular-Jet Charge for Explosive Cutting; Drexel University: Philadelphia, PA, USA, 1978. [Google Scholar]
- Ckick, M.C. Development of a cookie-cutter explosively formed projectile. In Proceedings of the 17th International Symposium on Ballistics, Midrand, South Africa, 23–27 March 1998. [Google Scholar]
- Meister, J.; Häller, F. Experimental and Numerical Studies of Annular Projectile Charges. 2001, pp. 7–11. Available online: https://www.semanticscholar.org/paper/EXPERIMENTAL-AND-NUMERICAL-STUDIES-OF-ANNULAR-Meister-H%C3%A4ller/8b404e1a75130b10ad929bda66d73ec79939200a (accessed on 11 October 2022).
- König, P.J.; Mostert, F.J. The Design and Performance of Annular EFP’S. In Proceedings of the 19th International Symposium of Ballistics, Interlaken, Switzerland, 7–11 May 2001. [Google Scholar]
- Richard, F.; Thompson, L.M.; Ng, W. Toroidal warhead development. In Proceedings of the 25th International Symposium on Ballistics (ISB), Beijing, China, 17–21 May 2010. [Google Scholar]
- Li, Y.L.; Huang, Y.H.; Zhang, Y.S.; Gao, T.H.; Zhang, P.J.; Fu, Y.Y. Numerical simulation of double explosively formed ring warhead. In Proceedings of the 25th International Symposium on Ballistics (ISB), Beijing, China, 17–21 May 2010. [Google Scholar]
- Wang, C.; Huang, F.; Ning, J. Jet formation and penetration mechanism of W typed shaped charge. Acta Mech. Sin. Xuebao 2009, 25, 107–120. [Google Scholar] [CrossRef]
- Fu, L.; Wang, W.L.; Jiang, Y.Z.; Huang, X.F.; Lv, J. Uniform design on the forward annular shaped charge of torpedo tandem warhead. Appl. Mech. Mater. 2014, 556–562, 1523–1526. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, J.T. Optimum Design on Annular Cutter of Tandem Warhead. Optim. Des. Annu. Cut Tandem Warhead 2010, 30, 93–96. [Google Scholar]
- Zhang, Z.; Wang, C.; Xu, W.; Hu, H. Penetration of annular and general jets into underwater plates. Comput. Part Mech. 2021, 8, 289–296. [Google Scholar] [CrossRef]
- Xu, W.; Wang, C.; Yuan, J. Impact performance of an annular shaped charge designed by convolutional neural networks. Thin-Walled Struct. 2021, 160, 107241. [Google Scholar] [CrossRef]
- Xu, W.; Wang, C.; Yuan, J.; Zhang, Z.; Deng, T. Assessment of Penetration Performance and Optimum Design of a Bore-Center Annular Shaped Charge. Propellants Explos. Pyrotech. 2019, 44, 1628–1639. [Google Scholar] [CrossRef]
- Xu, W.; Wang, C.; Chen, D. Formation of a bore-center annular shaped charge and its penetration into steel targets. Int. J. Impact Eng. 2019, 127, 122–134. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, Z.; Yin, J.; Yi, J. Formation and Penetration Capability of an Annular-Shaped Charge. Math. Probl. Eng. 2021, 2021, 6660189. [Google Scholar] [CrossRef]
- Si, Y.R.; Zhang, Q.; Zhang, X.; Tian, Z. On the Perforation Characteristics of Concrete Wall Induced by Annular Jet and Central EFP Combined Warhead. Binggong Xuebao/Acta Armamentarii 2021, 42, 1569–1579. (In Chinese) [Google Scholar]
- Li, W.; Wang, X.; Li, W. The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator. Int. J. Impact Eng. 2010, 37, 414–424. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A Computational Constitutive Model and Data for Metals Subjected to Large Strain, High Strain Rates and High Pressures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; Volume 21, pp. 541–548. [Google Scholar]
- Huang, Z. Theory and Practice of Shaped Charge; Beijing Institute of Technology Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
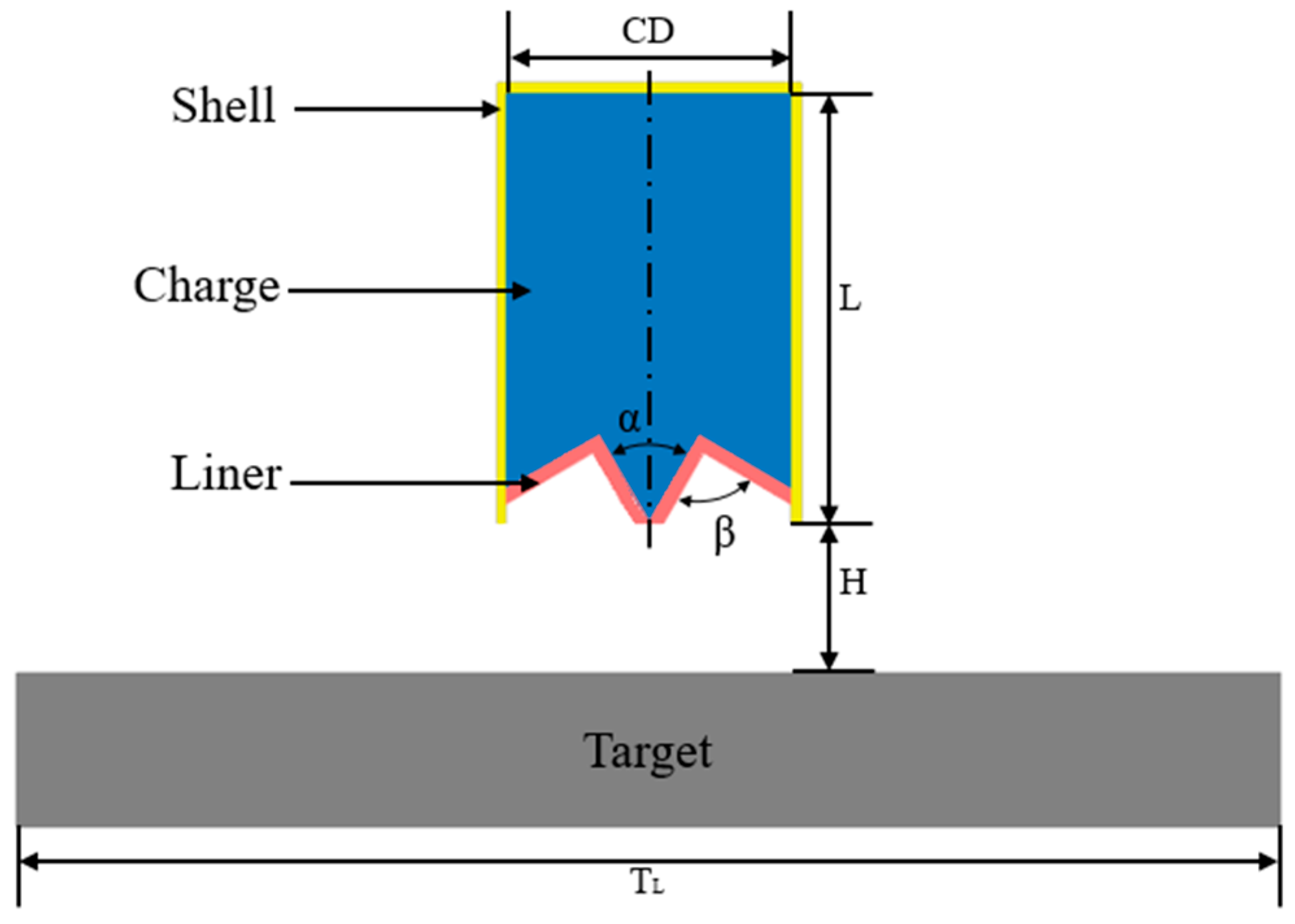





| ρ/(g·cm−3) | A/GPa | B/GPa | R1 | R2 | ω | E/(J·mm−3) |
|---|---|---|---|---|---|---|
| 1.713 | 524.2 | 7.768 | 4.2 | 1.1 | 0.34 | 8.499 |
| Material | ρ/(g·cm−3) | A | B | C | n | m |
|---|---|---|---|---|---|---|
| Red copper | 8.96 | 0.09 | 0.29 | 0.02 | 0.31 | 1.09 |
| steel | 7.896 | 350.0 | 275.0 | 0.022 | 0.36 | 1.0 |
| Armored steel | 7.83 | 1450 | 382.5 | 0.018 | 0.245 | 1.06 |
| Level | Factor | ||
|---|---|---|---|
| L/CD | α (°) | β (°) | |
| 1 | 0.5 | 20 | 80 |
| 2 | 1.0 | 40 | 90 |
| 3 | 1.5 | 60 | 100 |
| 4 | 2.0 | 80 | 110 |
| No. | L/CD | α (°) | β (°) | P (mm) | Dh (mm) |
|---|---|---|---|---|---|
| 1 | 0.5 | 20 | 80 | 31.5 | 99.4 |
| 2 | 0.5 | 40 | 90 | 22.0 | 99.4 |
| 3 | 0.5 | 60 | 100 | 18.5 | 110.6 |
| 4 | 0.5 | 80 | 110 | 12.9 | 149.2 |
| 5 | 1.0 | 20 | 90 | 20.5 | 120.0 |
| 6 | 1.0 | 40 | 80 | 25.5 | 91.6 |
| 7 | 1.0 | 60 | 110 | 34.2 | 126.4 |
| 8 | 1.0 | 80 | 100 | 21.0 | 137 |
| 9 | 1.5 | 20 | 100 | 19.6 | 133.8 |
| 10 | 1.5 | 40 | 110 | 20.7 | 136.6 |
| 11 | 1.5 | 60 | 80 | 62.0 | 91.6 |
| 12 | 1.5 | 80 | 90 | 20.7 | 115.4 |
| 13 | 2.0 | 20 | 110 | 17.8 | 140.8 |
| 14 | 2.0 | 40 | 100 | 25.8 | 128.4 |
| 15 | 2.0 | 60 | 90 | 62.1 | 96.6 |
| 16 | 2.0 | 80 | 80 | 21.0 | 115.6 |
| P (mm) | Dh (mm) | |||||
|---|---|---|---|---|---|---|
| L/CD | α (°) | β (°) | L/CD | α (°) | β (°) | |
| K1 | 81.9 | 86.7 | 150.7 | 458.6 | 504 | 398.2 |
| K2 | 101.2 | 126.5 | 125.6 | 475 | 466 | 445.4 |
| K3 | 120.4 | 176.5 | 84.9 | 476.4 | 425.2 | 519.8 |
| K4 | 126.4 | 74.3 | 85.2 | 481.4 | 531.2 | 563 |
| K1/4 | 20.5 | 21.7 | 37.7 | 114.7 | 126 | 99.6 |
| K2/4 | 25.3 | 31.6 | 31.4 | 118.8 | 116.5 | 111.4 |
| K3/4 | 30.1 | 44.1 | 21.6 | 119.1 | 106.3 | 130.0 |
| K4/4 | 31.6 | 18.6 | 21.3 | 120.0 | 132.8 | 140.8 |
| S | 11.1 | 25.5 | 16.6 | 5.3 | 26.5 | 41.2 |
| Result | Opening Diameter | Existing Diameter | Penetration Depth |
|---|---|---|---|
| Numerical simulation | 94.3 mm | 81.6 mm | 60.0 mm |
| Experiment | 95.0 mm | 86.3 mm | 60.0 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Fu, J.; Liang, F.; Yin, L.; Ren, K.; Yuan, H.; Li, H.; Zhao, T.; Chen, Z. The Influence of Closed-Cell W-Shaped Liner Parameters on the Penetration Performance of Integral Annular Shaped Charge. Materials 2022, 15, 7155. https://doi.org/10.3390/ma15207155
Yang Z, Fu J, Liang F, Yin L, Ren K, Yuan H, Li H, Zhao T, Chen Z. The Influence of Closed-Cell W-Shaped Liner Parameters on the Penetration Performance of Integral Annular Shaped Charge. Materials. 2022; 15(20):7155. https://doi.org/10.3390/ma15207155
Chicago/Turabian StyleYang, Zhilin, Jianping Fu, Fudi Liang, Likui Yin, Kai Ren, Hao Yuan, Hongxin Li, Taiyong Zhao, and Zhigang Chen. 2022. "The Influence of Closed-Cell W-Shaped Liner Parameters on the Penetration Performance of Integral Annular Shaped Charge" Materials 15, no. 20: 7155. https://doi.org/10.3390/ma15207155
APA StyleYang, Z., Fu, J., Liang, F., Yin, L., Ren, K., Yuan, H., Li, H., Zhao, T., & Chen, Z. (2022). The Influence of Closed-Cell W-Shaped Liner Parameters on the Penetration Performance of Integral Annular Shaped Charge. Materials, 15(20), 7155. https://doi.org/10.3390/ma15207155





