Dosimetric Impact on the Flattening Filter and Addition of Gold Nanoparticles in Radiotherapy: A Monte Carlo Study on Depth Dose Using the 6 and 10 MV FFF Photon Beams
Abstract
1. Introduction
2. Materials and Methods
2.1. Monte Carlo Simulation
2.2. Calculation of the Increase of Dose Enhancement Due to FF Removal
3. Results
4. Discussion
4.1. Dependences of Dose Enhancement on the Depth and NP Concentration
4.2. Dependence of Dose Enhancement on the Photon Beam Energy
4.3. Dependence of Dose Enhancement on the Presence of FF
4.4. Dependence of the Increase of Dose Enhancement on the Absence of FF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lomax, M.E.; Folkes, L.K.; O’neill, P. Biological consequences of radiation-induced DNA damage: Relevance to radiotherapy. Clin. Oncol. 2013, 25, 578–585. [Google Scholar] [CrossRef] [PubMed]
- Mladenov, E.; Magin, S.; Soni, A.; Iliakis, G. DNA double-strand break repair as determinant of cellular radiosensitivity to killing and target in radiation therapy. Front. Oncol. 2013, 3, 113. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Zhang, Y.; Liu, C.; Zhang, M.; Han, S. Application of radiosensitizers in cancer radiotherapy. Int. J. Nanomed. 2021, 16, 1083. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yang, J.; Fu, S.; Wu, J. Gold nanoparticles as radiosensitizers in cancer radiotherapy. Int. J. Nanomed. 2020, 15, 9407. [Google Scholar] [CrossRef]
- Jones, B.L.; Krishnan, S.; Cho, S.H. Estimation of microscopic dose enhancement factor around gold nanoparticles by Monte Carlo calculations. Med. Phys. 2010, 37, 3809–3816. [Google Scholar] [CrossRef]
- Zheng, X.J.; Chow, J.C. Radiation dose enhancement in skin therapy with nanoparticle addition: A Monte Carlo study on kilovoltage photon and megavoltage electron beams. World J. Radiol. 2017, 9, 63. [Google Scholar] [CrossRef]
- Martelli, S.; Chow, J.C. Dose enhancement for the flattening-filter-free and flattening-filter photon beams in nanoparticle-enhanced radiotherapy: A Monte Carlo phantom study. Nanomaterials 2020, 10, 637. [Google Scholar] [CrossRef]
- Bortfeld, T. IMRT: A review and preview. Phys. Med. Biol. 2006, 51, R363. [Google Scholar] [CrossRef]
- Chow, J.C.L.; Grigorov, G.N.; Yazdani, N. SWIMRT: A graphical user interface using the sliding window algorithm to construct a fluence map machine file. J. Appl. Clin. Med. Phys. 2006, 7, 69–85. [Google Scholar] [CrossRef]
- Chow, J.C.; Owrangi, A.M. A surface energy spectral study on the bone heterogeneity and beam obliquity using the flattened and unflattened photon beams. Rep. Pract. Oncol. Radiother. 2016, 21, 63–70. [Google Scholar] [CrossRef]
- Zwahlen, D.R.; Lang, S.; Hrbacek, J.; Glanzmann, C.; Kloeck, S.; Najafi, Y.; Streller, T.; Studer, G.; Zaugg, K.; Luetolf, U.M. The use of photon beams of a flattening filter-free linear accelerator for hypofractionated volumetric modulated arc therapy in localized prostate cancer. Int. J. Radiat. Oncol. Biol. Phys. 2012, 83, 1655–1660. [Google Scholar] [CrossRef]
- Vassiliev, O.N.; Titt, U.; Pönisch, F.; Kry, S.F.; Mohan, R.; Gillin, M.T. Dosimetric properties of photon beams from a flattening filter free clinical accelerator. Phys. Med. Biol. 2006, 51, 1907. [Google Scholar] [CrossRef]
- Chow, J.C.; Owrangi, A.M. Mucosal dosimetry on unflattened photon beams: A Monte Carlo phantom study. Biomed. Phys. Eng. Express 2018, 5, 015007. [Google Scholar] [CrossRef]
- Wang, Y.; Khan, M.K.; Ting, J.Y.; Easterling, S.B. Surface dose investigation of the flattening filter-free photon beams. Int. J. Radiat. Oncol. Biol. Phys. 2012, 83, e281–e285. [Google Scholar] [CrossRef]
- Chow, J.C.L. Photon and electron interactions with gold nanoparticles: A Monte Carlo study on gold nanoparticle-enhanced radiotherapy. Nanobiomater. Med. Imaging 2016, 8, 45–70. [Google Scholar] [CrossRef]
- Chow, J.C.L. Dose enhancement effect in radiotherapy: Adding gold nanoparticles to tumor in cancer treatment. In Nanostructures for Cancer Therapy; Elsevier: Amsterdam, The Netherlands, 2017; pp. 383–403. [Google Scholar]
- Leung, M.K.; Chow, J.C.; Chithrani, B.D.; Lee, M.J.; Oms, B.; Jaffray, D.A. Irradiation of gold nanoparticles by x-rays: Monte Carlo simulation of dose enhancements and the spatial properties of the secondary electrons production. Med. Phys. 2011, 38, 624–631. [Google Scholar] [CrossRef]
- Chow, J.C. Depth dose enhancement on flattening-filter-free photon beam: A Monte Carlo Study in nanoparticle-enhanced radiotherapy. Appl. Sci. 2020, 10, 7052. [Google Scholar] [CrossRef]
- Sharma, M.; Chow, J.C. Skin dose enhancement from the application of skin-care creams using FF and FFF photon beams in radiotherapy: A Monte Carlo phantom evaluation. AIMS Bioeng. 2020, 7, 82–90. [Google Scholar] [CrossRef]
- Dzierma, Y.; Licht, N.; Nuesken, F.; Ruebe, C. Beam properties and stability of a flattening-filter free 7 MV beam—An overview. Med. Phys. 2012, 39, 2595–2602. [Google Scholar] [CrossRef]
- Georg, D.; Knöös, T.; McClean, B. Current status and future perspective of flattening filter free photon beams. Med. Phys. 2011, 38, 1280–1293. [Google Scholar] [CrossRef]
- Rogers, D.W. Fifty years of Monte Carlo simulations for medical physics. Phys. Med. Biol. 2006, 51, R287. [Google Scholar] [CrossRef]
- Chow, J.C. A performance evaluation on Monte Carlo simulation for radiation dosimetry using cell processor. J. Comput. Methods Sci. Eng. 2011, 11, 1–12. [Google Scholar] [CrossRef]
- Chow, J.C. Monte Carlo Nanodosimetry in Gold Nanoparticle-Enhanced Radiotherapy; Nova Science Publishers: New York, NY, USA, 2018. [Google Scholar]
- Jabeen, M.; Chow, J.C. Gold Nanoparticle DNA Damage by Photon Beam in a Magnetic Field: A Monte Carlo Study. Nanomaterials 2021, 11, 1751. [Google Scholar] [CrossRef]
- He, C.; Chow, J.C. Gold nanoparticle DNA damage in radiotherapy: A Monte Carlo study. AIMS Bioeng. 2016, 3, 352–361. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.J.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Rogers, D.W.; Kawrakow, I.; Seuntjens, J.P.; Walters, B.R.; Mainegra-Hing, E. NRC user codes for EGSnrc. In NRCC Report PIRS-702 (Rev. B); NRC Canada: Ottawa, ON, Canada, 2003. [Google Scholar]
- Constantin, M.; Perl, J.; LoSasso, T.; Salop, A.; Whittum, D.; Narula, A.; Svatos, M.; Keall, P.J. Modeling the TrueBeam linac using a CAD to Geant4 geometry implementation: Dose and IAEA-compliant phase space calculations. Med. Phys. 2011, 38, 4018–4024. [Google Scholar] [CrossRef]
- Chow, J.C.; Owrangi, A.M. Dosimetric dependences of bone heterogeneity and beam angle on the unflattened and flattened photon beams: A Monte Carlo comparison. Radiat. Phys. Chem. 2014, 101, 46–52. [Google Scholar] [CrossRef]
- Hainfeld, J.F.; Slatkin, D.N.; Smilowitz, H.M. The use of gold nanoparticles to enhance radiotherapy in mice. Phys. Med. Biol. 2004, 49, N309. [Google Scholar] [CrossRef]
- Sheeraz, Z.; Chow, J.C. Evaluation of dose enhancement with gold nanoparticles in kilovoltage radiotherapy using the new EGS geometry library in Monte Carlo simulation. AIMS Biophys. 2021, 8, 337–345. [Google Scholar] [CrossRef]
- Chow, J.C. Recent progress in Monte Carlo simulation on gold nanoparticle radiosensitization. AIMS Biophys. 2018, 5, 231–244. [Google Scholar] [CrossRef]
- Vlastou, E.; Pantelis, E.; Efstathopoulos, E.P.; Karaiskos, P.; Kouloulias, V.; Platoni, K. Quantification of Nanoscale Dose Enhancement in Gold Nanoparticle-Aided External Photon Beam Radiotherapy. Cancers 2022, 14, 2167. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.; Kim, J.M.; Kim, J. Influence of concentration, nanoparticle size, beam energy, and material on dose enhancement in radiation therapy. J. Radiat. Res. 2017, 58, 405–411. [Google Scholar] [CrossRef] [PubMed]
- Mahdavi, M.; KhademAbolfazli, M.; Mahdavi, S.R.; Ataei, G. Effect of gold nanoparticle on percentage depth dose enhancement on megavoltage energy in MAGICA polymer gel dosimeter. J. Biomed. Phys. Eng. 2013, 3, 37. [Google Scholar] [PubMed]
- Foster, R.D.; Speiser, M.P.; Solberg, T.D. Commissioning and verification of the collapsed cone convolution superposition algorithm for SBRT delivery using flattening filter-free beams. J. Appl. Clin. Med. Phys. 2014, 15, 39–49. [Google Scholar] [CrossRef]
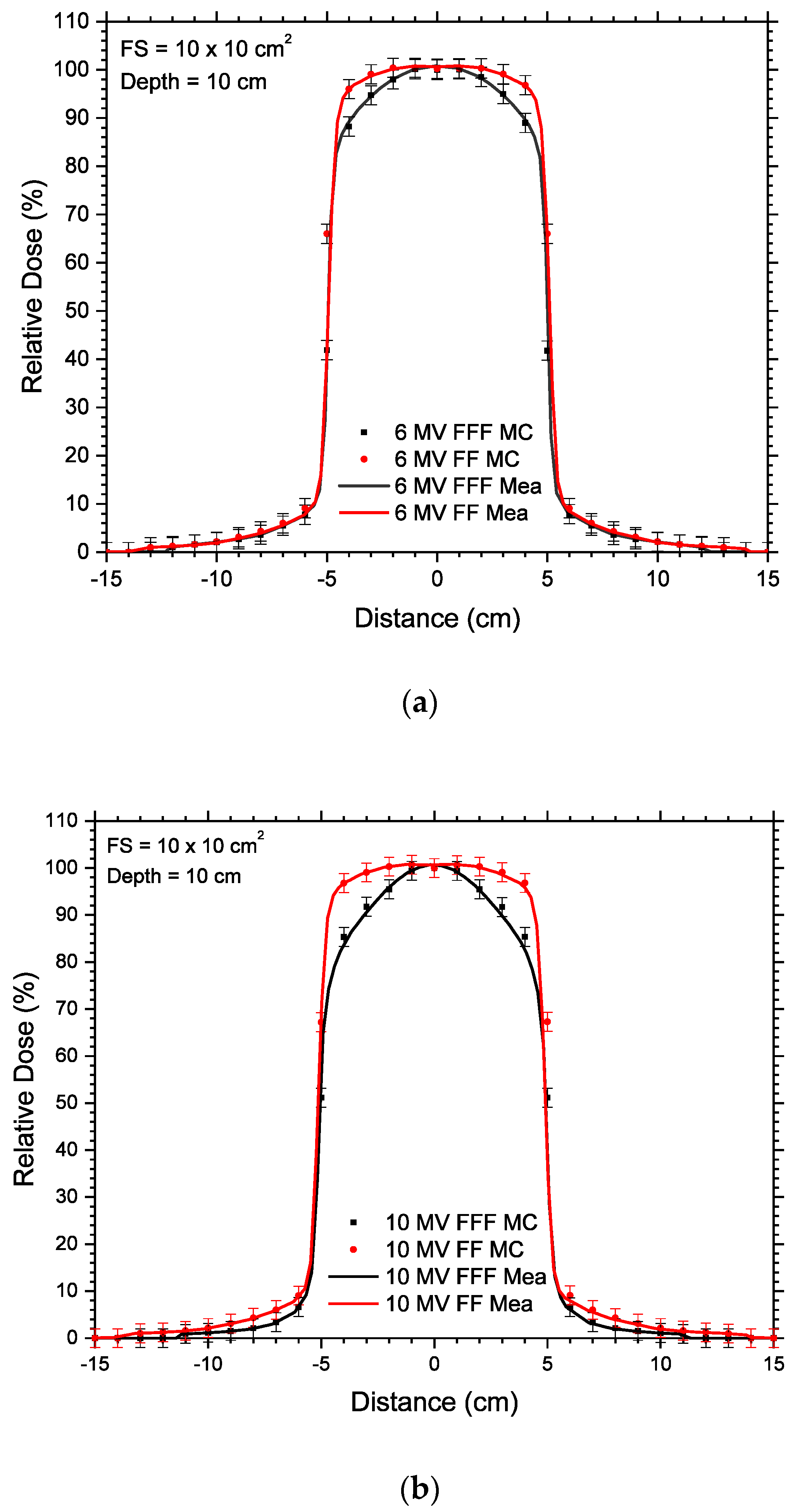
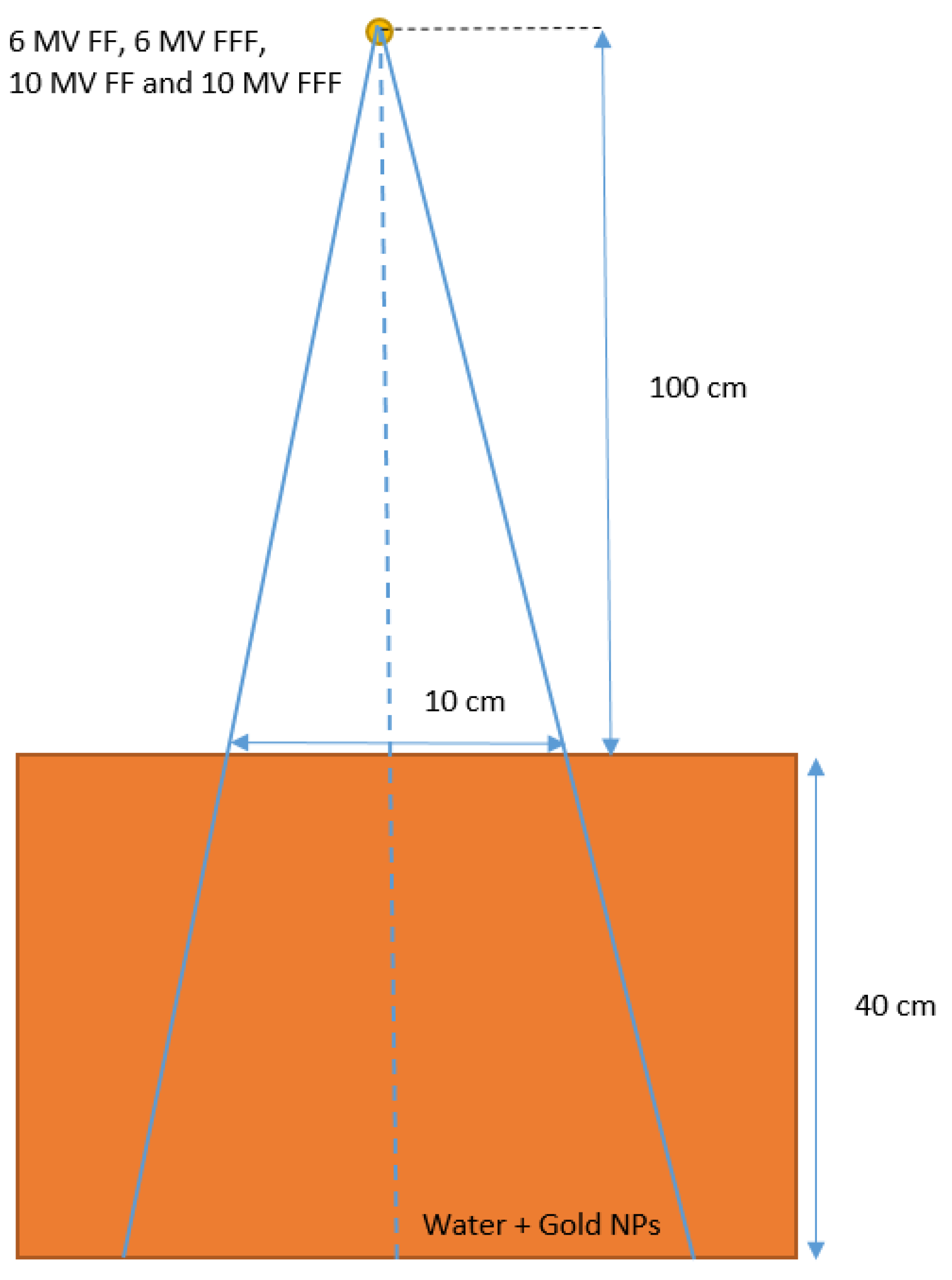

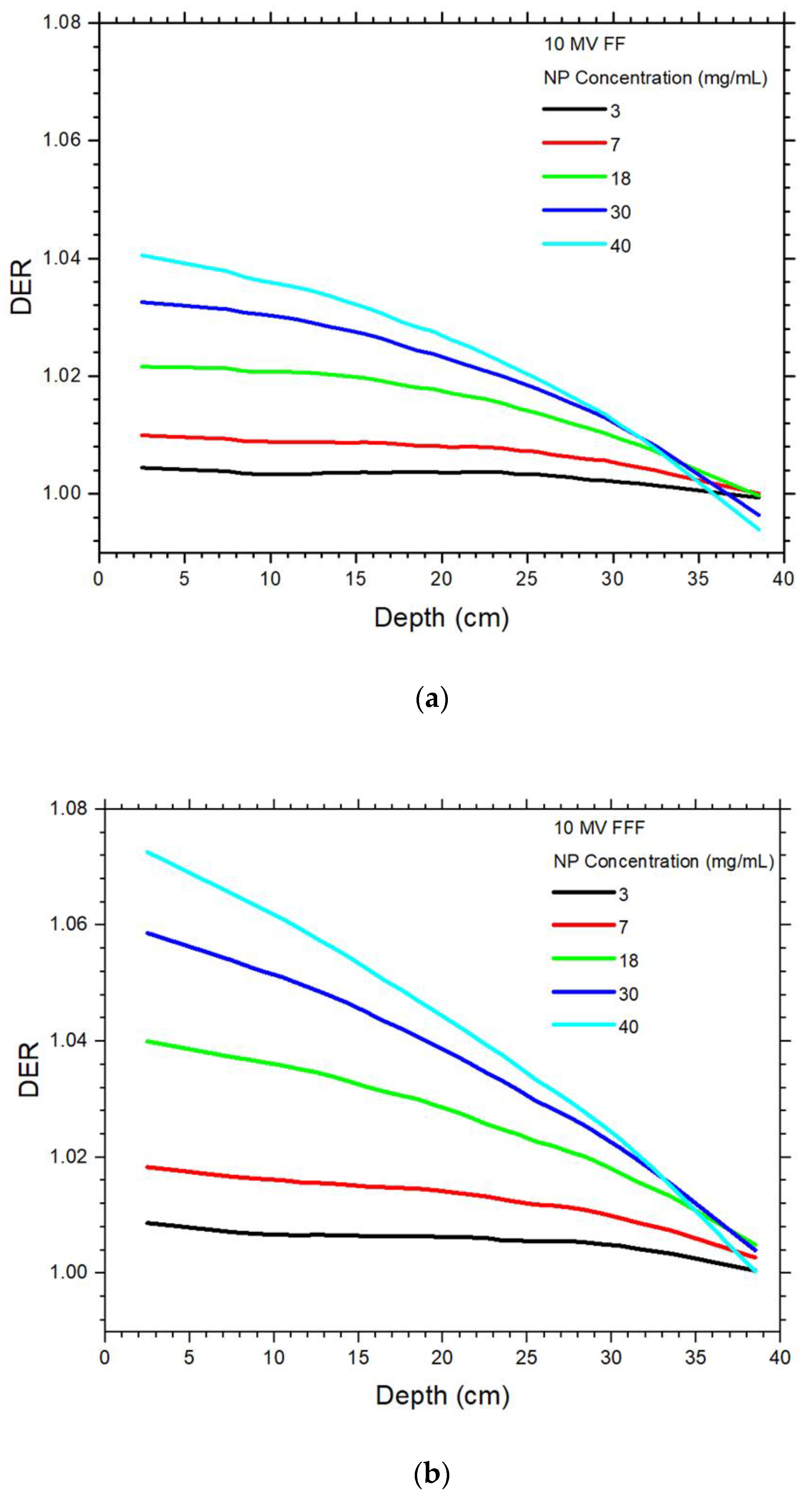
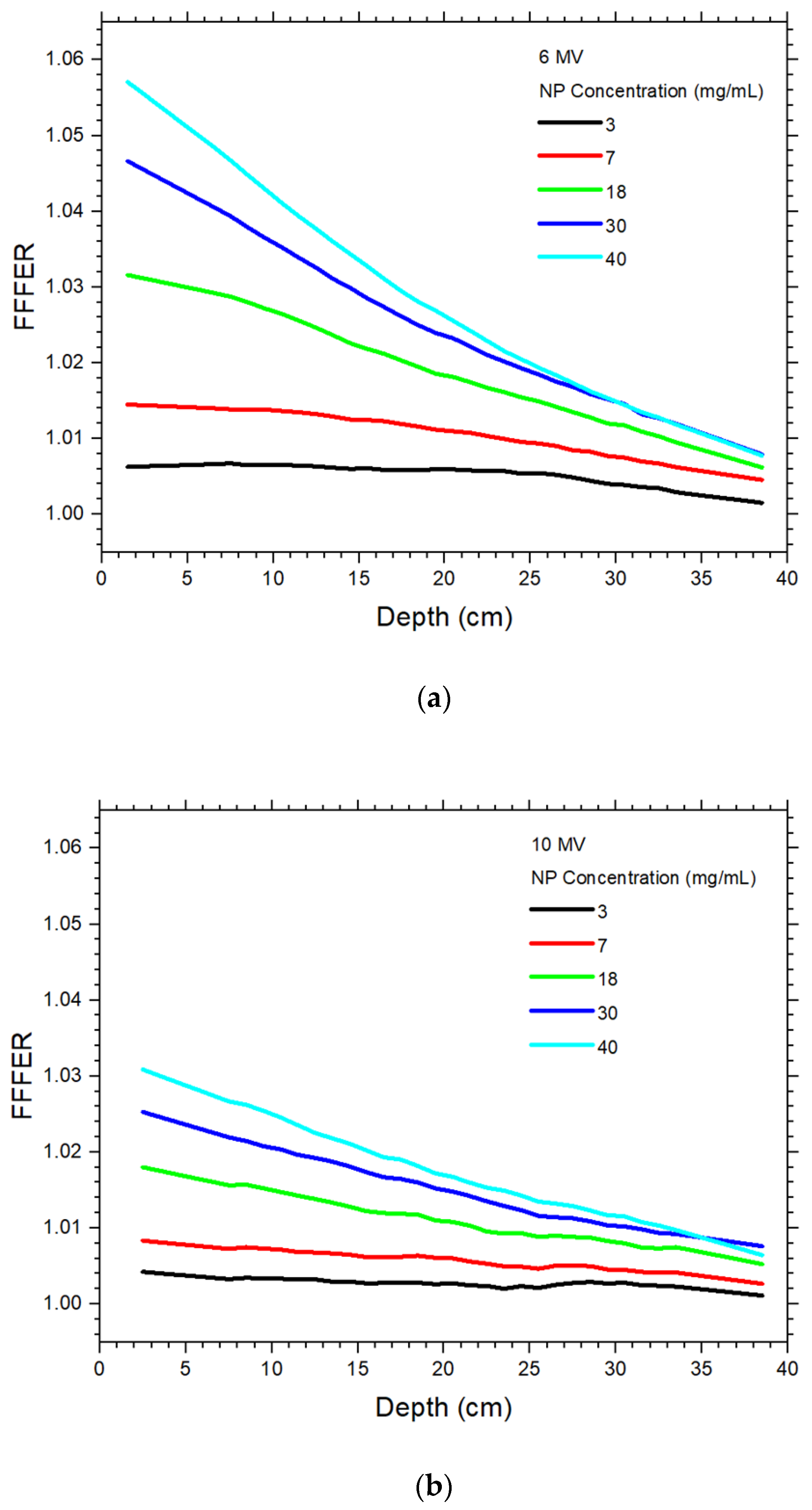
| 6 MV FF | 6 MV FFF | |||||||||
| Concentration (mg/mL) | 3 | 7 | 18 | 30 | 40 | 3 | 7 | 18 | 30 | 40 |
| 2 cm | 1.0087 | 1.0185 | 1.0412 | 1.0611 | 1.0752 | 1.0150 | 1.0331 | 1.0736 | 1.1093 | 1.1347 |
| 5 cm | 1.0080 | 1.0186 | 1.0413 | 1.0606 | 1.0737 | 1.0146 | 1.0329 | 1.0723 | 1.1049 | 1.1277 |
| 10 cm | 1.0074 | 1.0187 | 1.0411 | 1.0588 | 1.0702 | 1.0140 | 1.0326 | 1.0687 | 1.0961 | 1.1142 |
| 15 cm | 1.0074 | 1.0177 | 1.0387 | 1.0533 | 1.0624 | 1.0135 | 1.0304 | 1.0614 | 1.0833 | 1.0972 |
| 20 cm | 1.0070 | 1.0163 | 1.0347 | 1.0461 | 1.0532 | 1.0130 | 1.0274 | 1.0534 | 1.0704 | 1.0801 |
| 25 cm | 1.0062 | 1.0143 | 1.0294 | 1.0382 | 1.0434 | 1.0117 | 1.0238 | 1.0447 | 1.0574 | 1.0635 |
| 30 cm | 1.0050 | 1.0115 | 1.0228 | 1.0285 | 1.0318 | 1.0089 | 1.0190 | 1.0348 | 1.0435 | 1.0466 |
| 35 cm | 1.0037 | 1.0079 | 1.0144 | 1.0166 | 1.0162 | 1.0061 | 1.0135 | 1.0227 | 1.0272 | 1.0266 |
| 10 MV FF | 10 MV FFF | |||||||||
| Concentration (mg/mL) | 3 | 7 | 18 | 30 | 40 | 3 | 7 | 18 | 30 | 40 |
| 2 cm | 1.0044 | 1.0099 | 1.0215 | 1.0325 | 1.0405 | 1.0086 | 1.0183 | 1.0399 | 1.0586 | 1.0726 |
| 5 cm | 1.0040 | 1.0095 | 1.0214 | 1.0318 | 1.0388 | 1.0077 | 1.0173 | 1.0383 | 1.0558 | 1.0683 |
| 10 cm | 1.0032 | 1.0088 | 1.0207 | 1.0300 | 1.0356 | 1.0066 | 1.0160 | 1.0358 | 1.0510 | 1.0611 |
| 15 cm | 1.0036 | 1.0087 | 1.0196 | 1.0271 | 1.0316 | 1.0063 | 1.0149 | 1.0321 | 1.0449 | 1.0525 |
| 20 cm | 1.0035 | 1.0079 | 1.0171 | 1.0227 | 1.0262 | 1.0062 | 1.0139 | 1.0281 | 1.0379 | 1.0433 |
| 25 cm | 1.0033 | 1.0071 | 1.0137 | 1.0179 | 1.0196 | 1.0054 | 1.0118 | 1.0227 | 1.0297 | 1.0333 |
| 30 cm | 1.0050 | 1.0115 | 1.0228 | 1.0285 | 1.0318 | 1.0047 | 1.0095 | 1.0172 | 1.0216 | 1.0231 |
| 35 cm | 1.0037 | 1.0079 | 1.0144 | 1.0166 | 1.0162 | 1.0022 | 1.0055 | 1.0099 | 1.0108 | 1.0092 |
| 6 MV | 10 MV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Concentration (mg/mL) | 3 | 7 | 18 | 30 | 40 | 3 | 7 | 18 | 30 | 40 |
| 2 cm | 1.0063 | 1.0143 | 1.0311 | 1.0454 | 1.0553 | 1.0042 | 1.0083 | 1.0179 | 1.0252 | 1.0308 |
| 5 cm | 1.0065 | 1.0140 | 1.0297 | 1.0417 | 1.0502 | 1.0036 | 1.0076 | 1.0165 | 1.0232 | 1.0283 |
| 10 cm | 1.0065 | 1.0136 | 1.0264 | 1.0352 | 1.0410 | 1.0033 | 1.0071 | 1.0147 | 1.0203 | 1.0245 |
| 15 cm | 1.0060 | 1.0124 | 1.0218 | 1.0284 | 1.0327 | 1.0027 | 1.0061 | 1.0122 | 1.0173 | 1.0202 |
| 20 cm | 1.0059 | 1.0109 | 1.0181 | 1.0232 | 1.0255 | 1.0027 | 1.0060 | 1.0108 | 1.0148 | 1.0167 |
| 25 cm | 1.0054 | 1.0093 | 1.0148 | 1.0184 | 1.0193 | 1.0021 | 1.0046 | 1.0088 | 1.0116 | 1.0134 |
| 30 cm | 1.0038 | 1.0074 | 1.0117 | 1.0145 | 1.0144 | 1.0028 | 1.0044 | 1.0079 | 1.0101 | 1.0115 |
| 35 cm | 1.0023 | 1.0055 | 1.0081 | 1.0103 | 1.0102 | 1.0018 | 1.0035 | 1.0065 | 1.0085 | 1.0084 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spina, A.; Chow, J.C.L. Dosimetric Impact on the Flattening Filter and Addition of Gold Nanoparticles in Radiotherapy: A Monte Carlo Study on Depth Dose Using the 6 and 10 MV FFF Photon Beams. Materials 2022, 15, 7194. https://doi.org/10.3390/ma15207194
Spina A, Chow JCL. Dosimetric Impact on the Flattening Filter and Addition of Gold Nanoparticles in Radiotherapy: A Monte Carlo Study on Depth Dose Using the 6 and 10 MV FFF Photon Beams. Materials. 2022; 15(20):7194. https://doi.org/10.3390/ma15207194
Chicago/Turabian StyleSpina, Armando, and James C. L. Chow. 2022. "Dosimetric Impact on the Flattening Filter and Addition of Gold Nanoparticles in Radiotherapy: A Monte Carlo Study on Depth Dose Using the 6 and 10 MV FFF Photon Beams" Materials 15, no. 20: 7194. https://doi.org/10.3390/ma15207194
APA StyleSpina, A., & Chow, J. C. L. (2022). Dosimetric Impact on the Flattening Filter and Addition of Gold Nanoparticles in Radiotherapy: A Monte Carlo Study on Depth Dose Using the 6 and 10 MV FFF Photon Beams. Materials, 15(20), 7194. https://doi.org/10.3390/ma15207194







