Effects of Operating Conditions and Pit Area Ratio on the Coefficient of Friction of Textured Assemblies in Lubricated Reciprocating Sliding
Abstract
1. Introduction
2. Materials and Methods
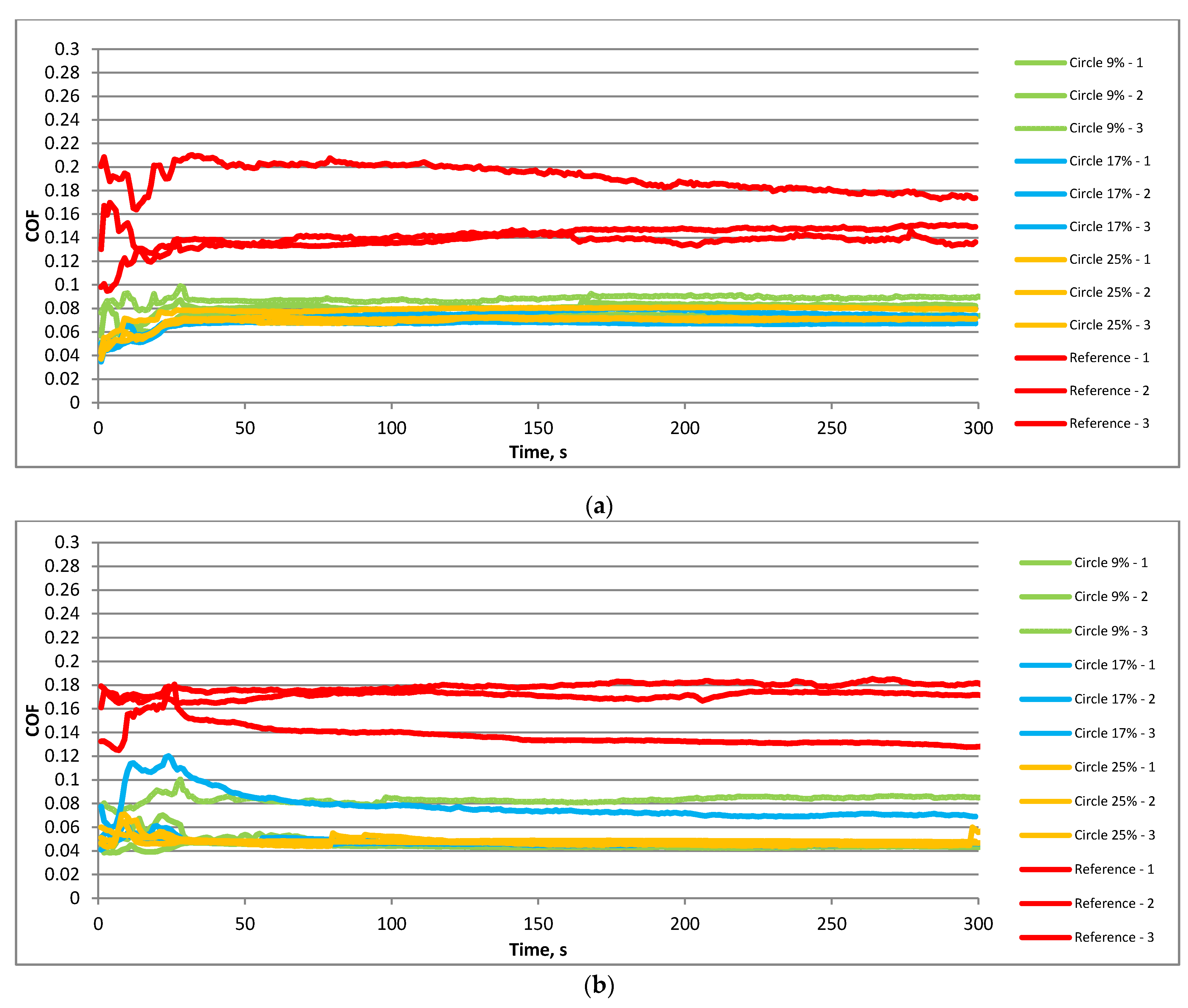
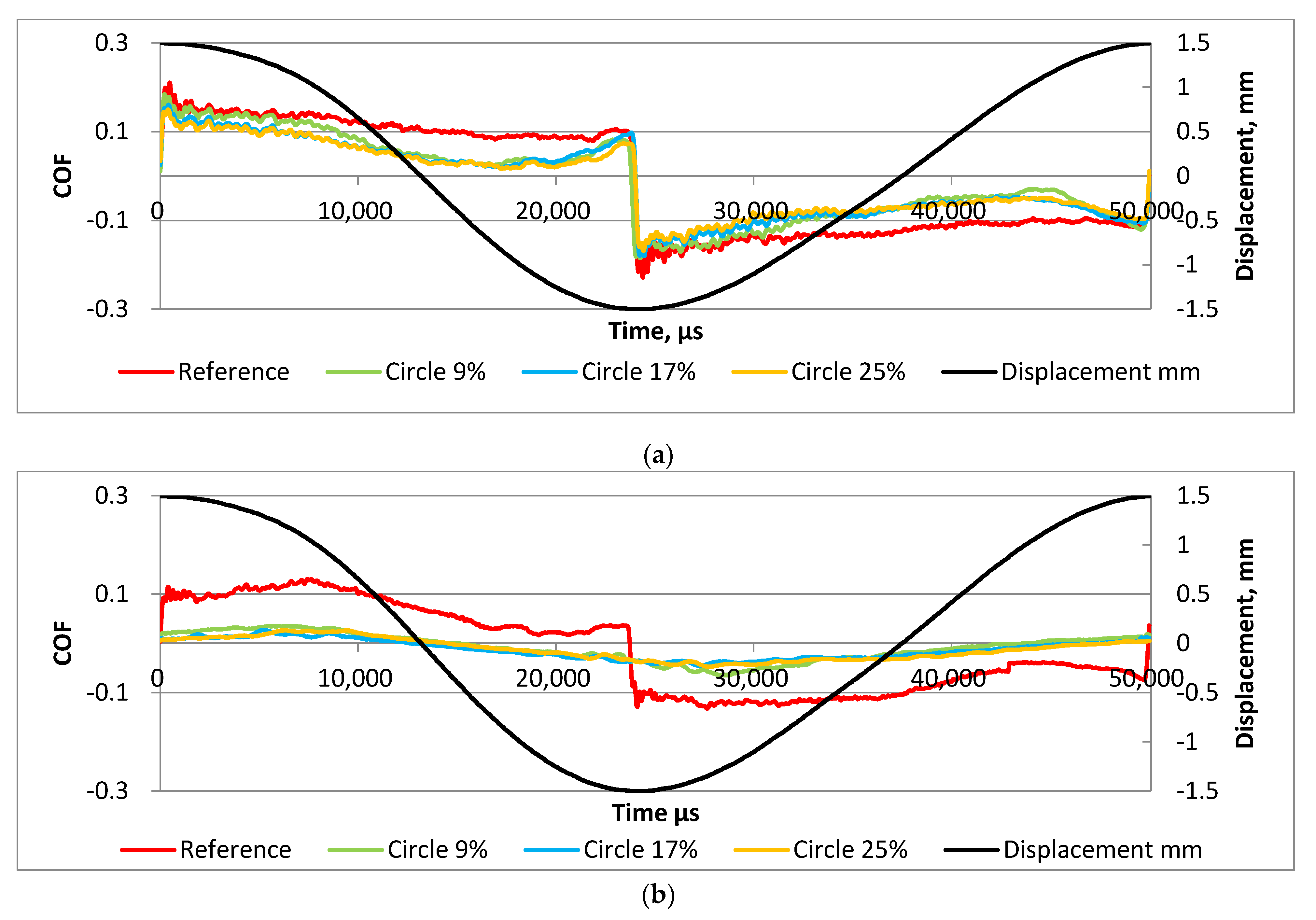
3. Results and Discussion
4. Conclusions
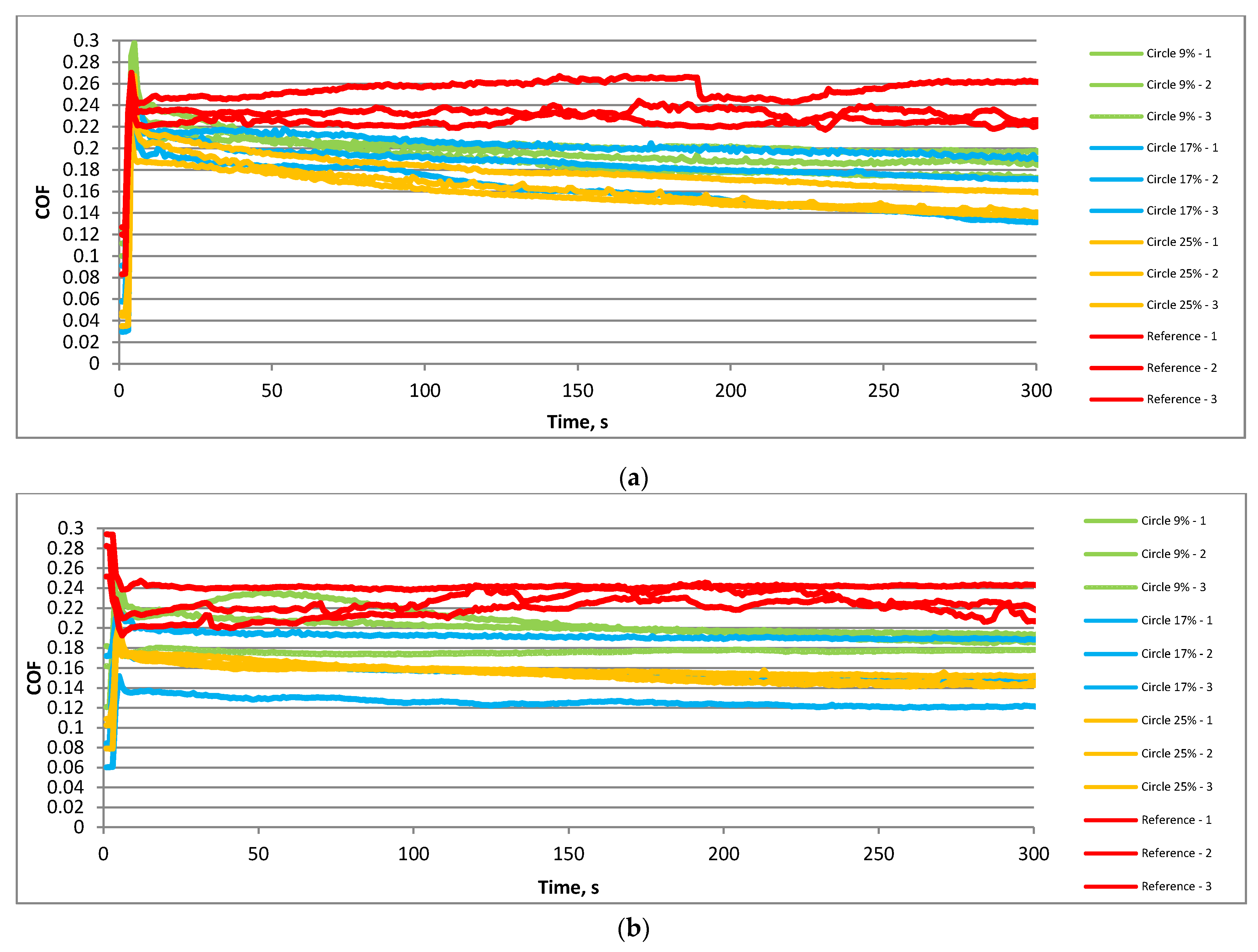
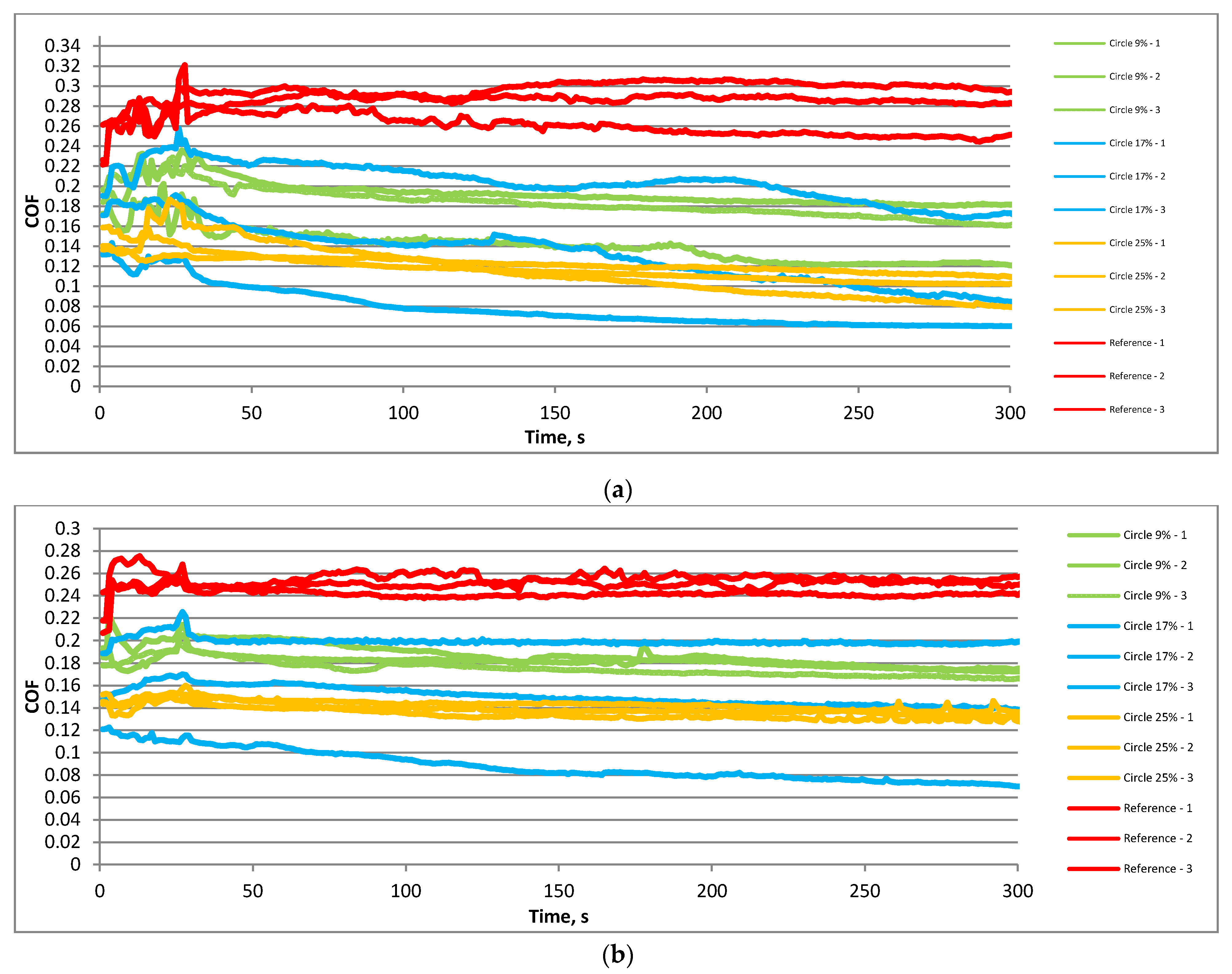
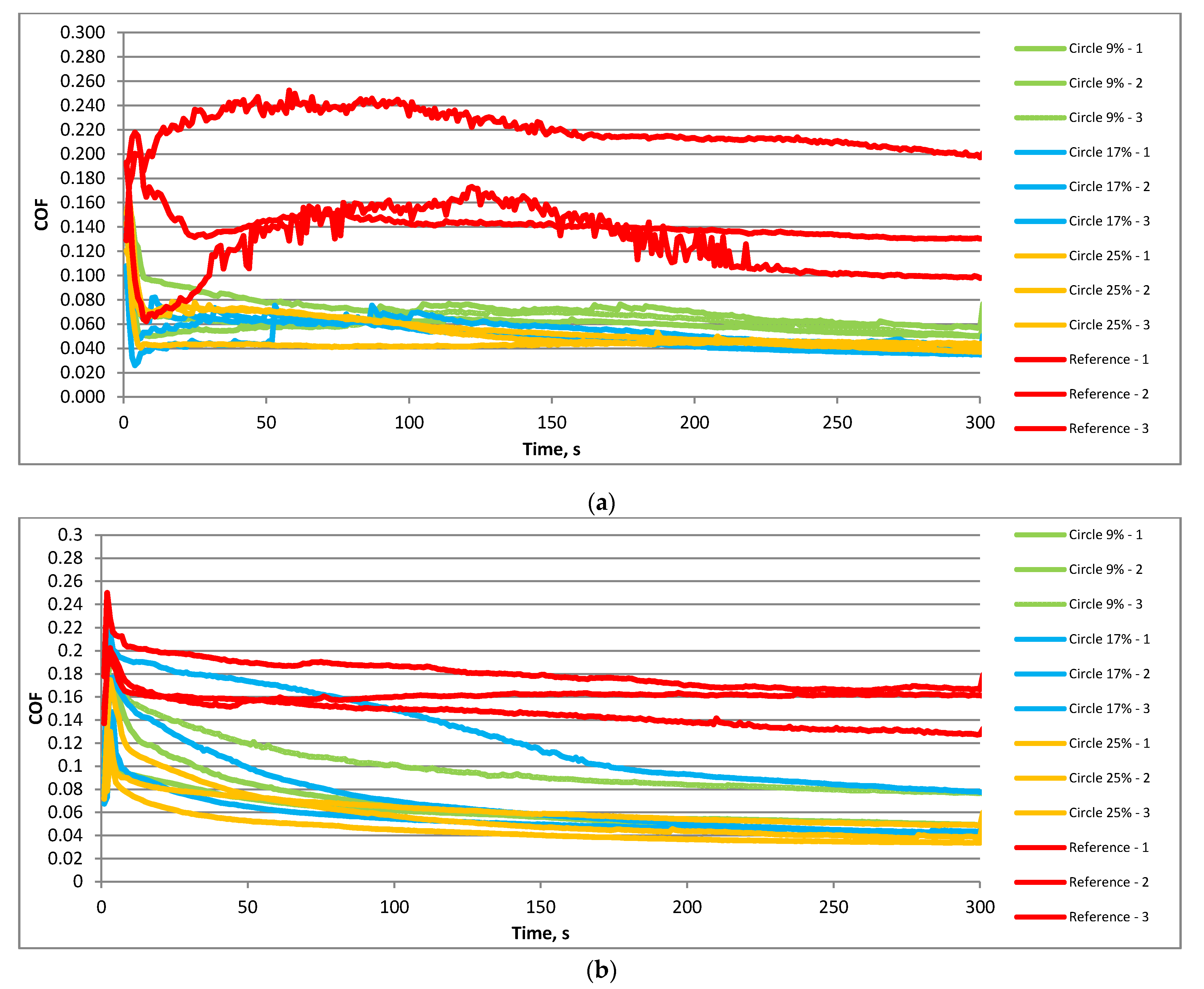
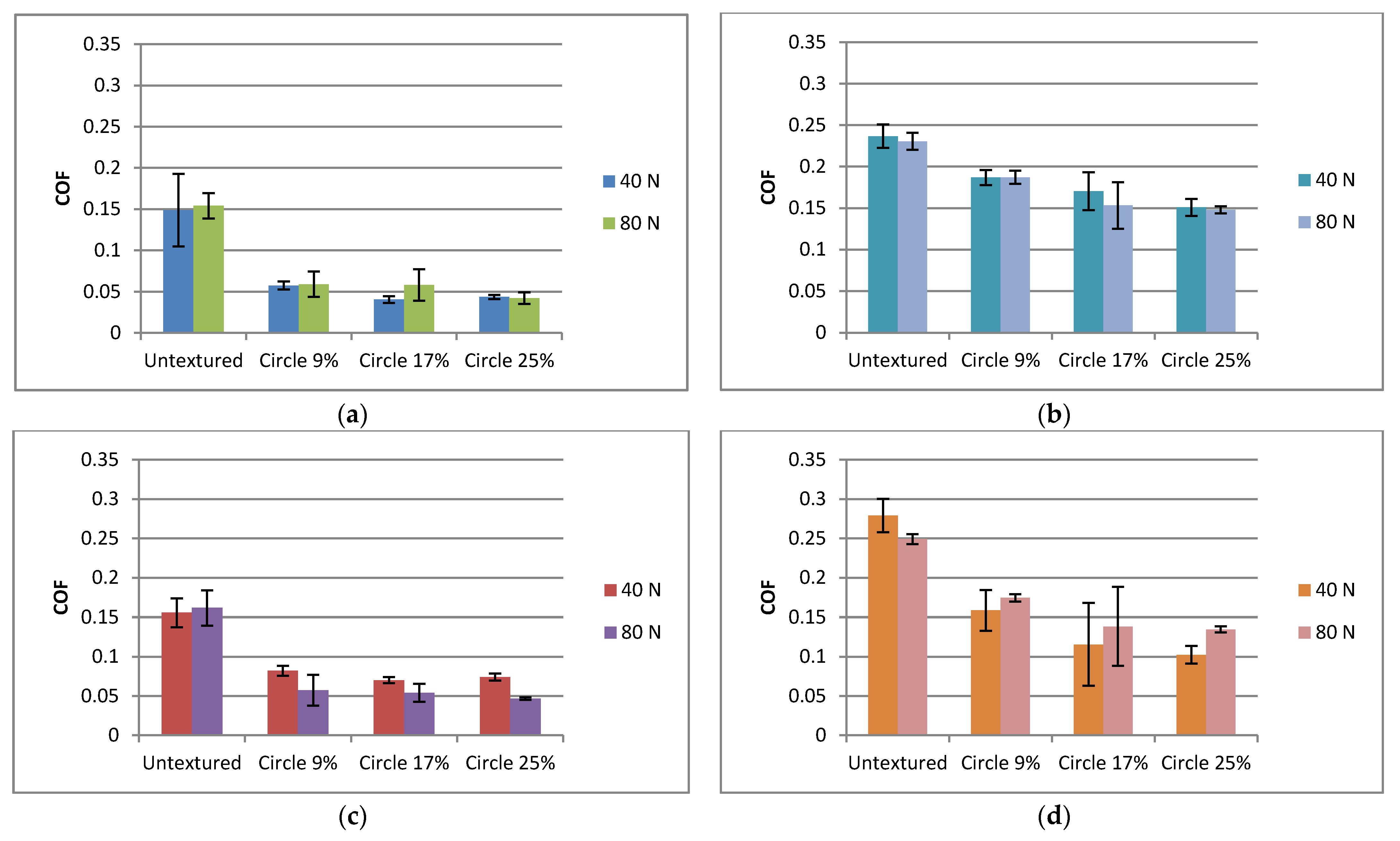
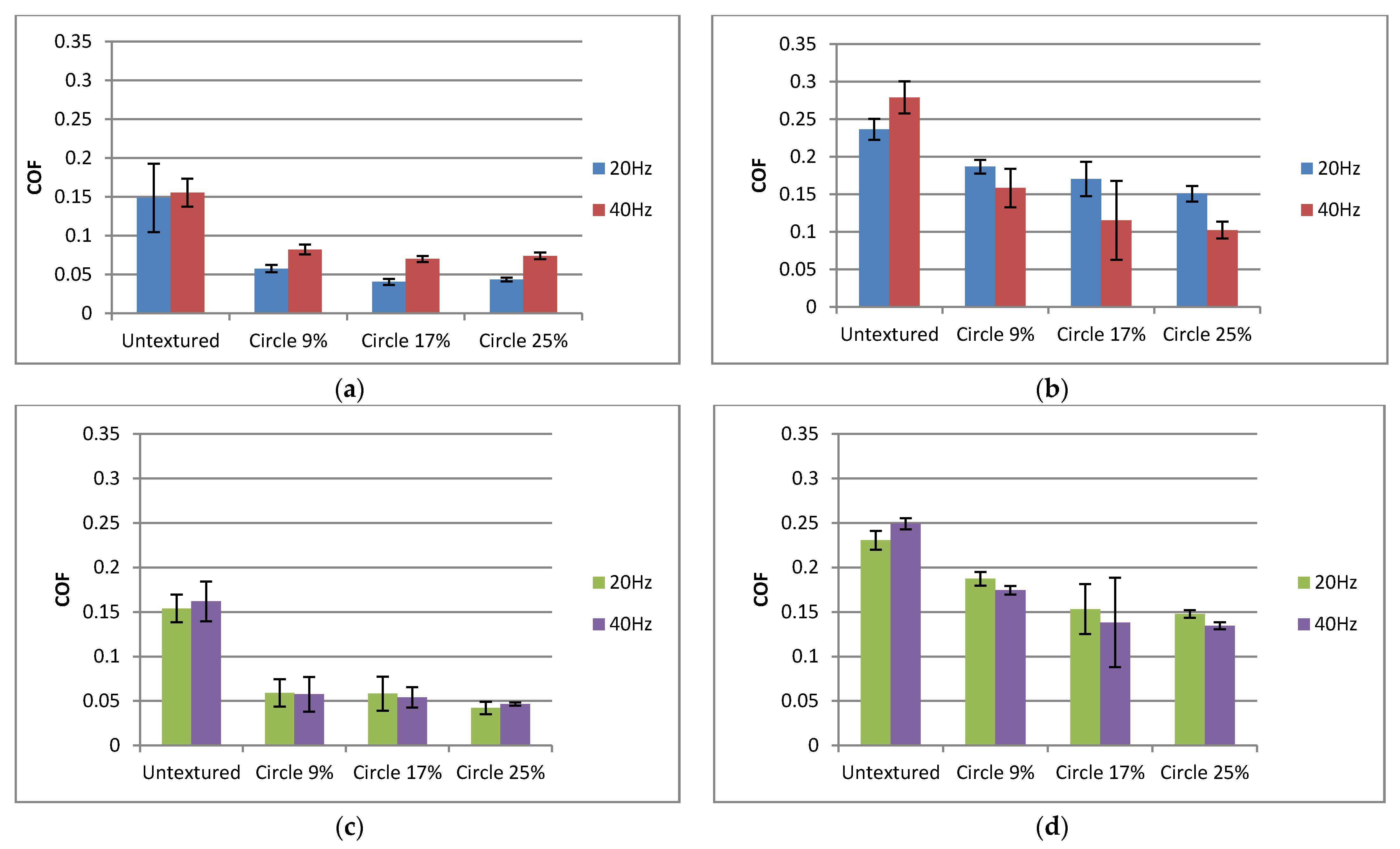
- In all tested conditions, surface texturing led to friction reductions of sliding pairs in lubricated reciprocating motions. In most cases, the friction coefficient of textured assemblies decreased with time, contrary to behaviors of untextured sliding pairs.
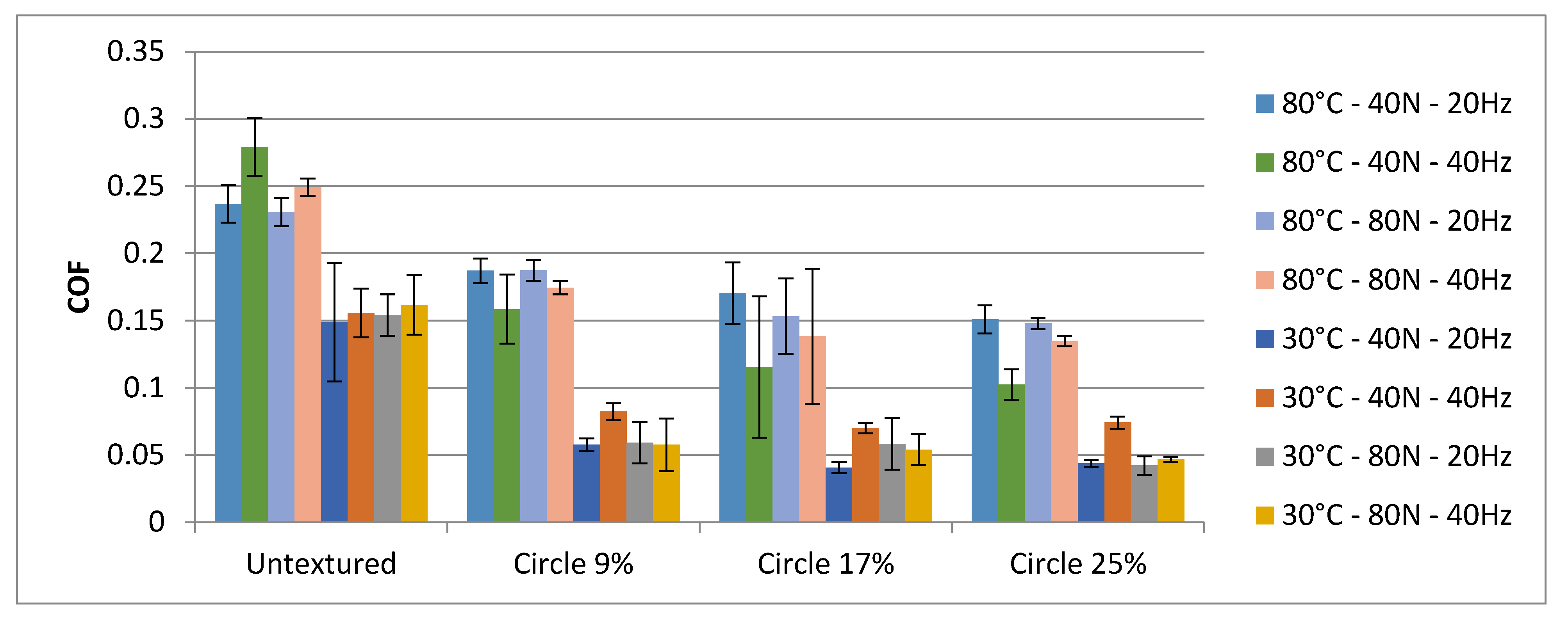
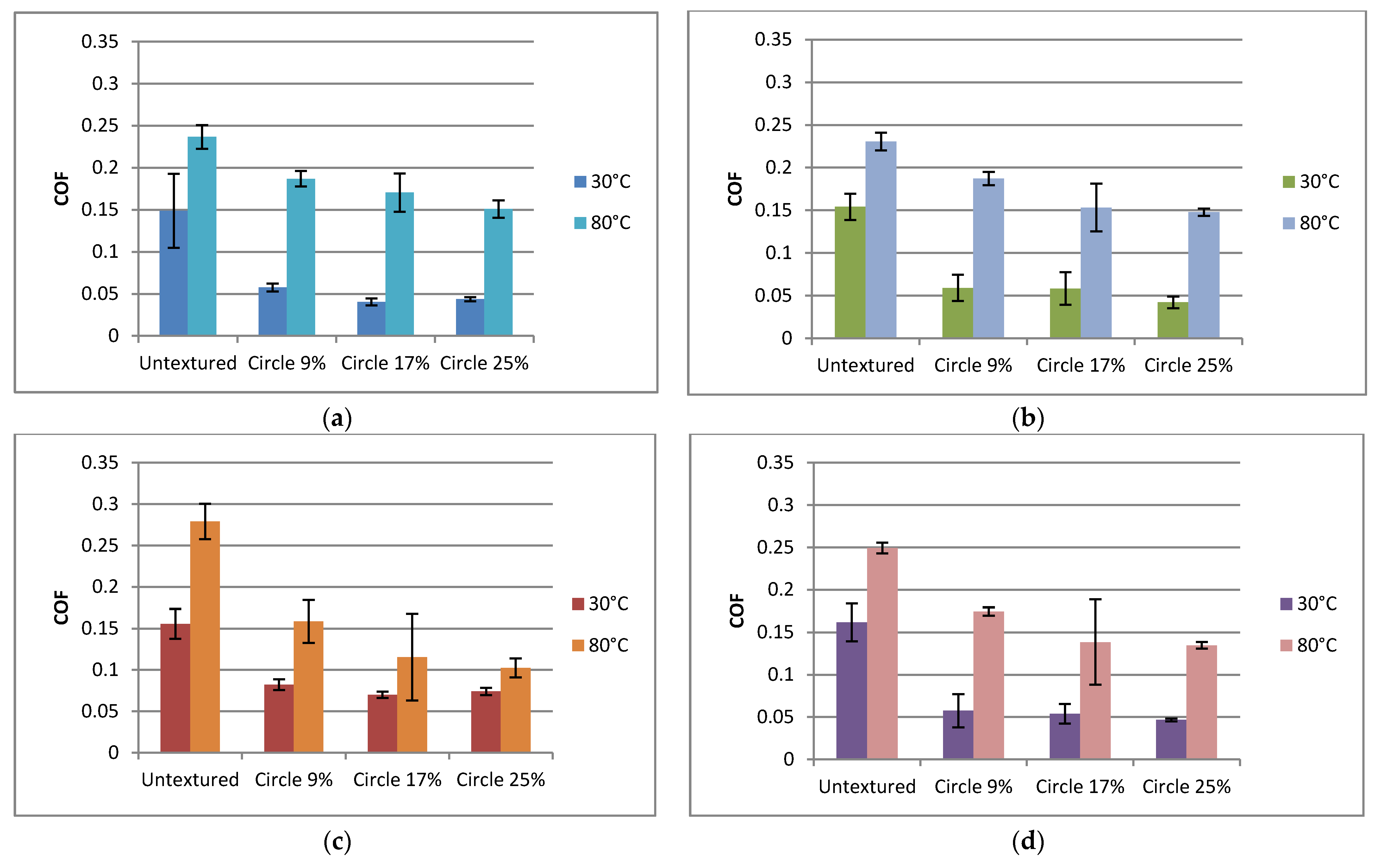
- Friction decreases were higher at lower temperatures (up to 4.5 times) compared to higher temperatures (up to 2.5 times).
- The impact of the pit area ratio was visible at higher temperatures. The highest dimple density of 25% led to a smaller coefficient of friction than the smallest pit area ratio of 9%. The sliding pair with a middle density of 17% was characterized by large variation of the friction force. This behavior was obtained independently of normal load and frequency. At lower temperatures, the impact of the pit area ratio of a disc sample was visible only for smaller normal loads and frequencies of oscillation—the smallest density of dimples led to the largest friction.
- At lower temperatures, the coefficients of friction were smaller compared to tests at higher temperatures.
- For a higher frequency of oscillations at lower temperatures, an increase in normal load from 40 to 80 N led to a smaller coefficient of friction when textured surfaces were tested, contrary to work at higher temperatures. The opposite behavior was obtained for untextured samples. When the oscillation frequency was lower, the effect of the normal load on the coefficient of friction was marginal.
- At lower temperatures and normal loads, a higher frequency of oscillation led to higher coefficients of friction of textured sliding pairs, contrary to tests at higher temperatures. When the normal load was higher, the higher oscillation frequency corresponded to a lower coefficient of the friction of textured assemblies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choi, C.; Ma, Y.; Li, X.; Ma, X.; Hipwell, M.C. Finger Pad Topography beyond Fingerprints: Understanding the Heterogeneity Effect of Finger Topography for Human–Machine Interface Modeling. ACS Appl. Mater. Interfaces 2021, 13, 3303–3310. [Google Scholar] [CrossRef]
- Li, X.; Ma, Y.; Choi, C.; Ma, X.; Chatterjee, S.; Lan, S.; Hipwell, M.C. Nanotexture Shape and Surface Energy Impact on Electroadhesive Human–Machine Interface Performance. Adv. Mater. 2021, 33, 2008337. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Huang, W.; Wang, X. Dimple patterns design for different circumstances. Lubr. Sci. 2011, 25, 67–78. [Google Scholar] [CrossRef]
- Nsilani Kouediatouka, A.; Ma, Q.; Liu, Q.; Mawignon, F.J.; Rafique, F.; Dong, G. Design Methodology and Application of Surface Texture: A Review. Coatings 2022, 12, 1015. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R. Functional importance of honed cylinder liner surface texture: A review. Tribol. Int. 2022, 167, 107409. [Google Scholar] [CrossRef]
- Etsion, I. State of the Art in Laser Surface Texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Marian, M.; Almqvist, A.; Rosenkranz, A.; Fillon, M. Numerical micro-texture optimization for lubricated contacts—A critical discussion. Friction 2022. [Google Scholar] [CrossRef]
- Hwang, D.; Kim, D.; Lee, S. Influence of wear particle interaction in the sliding interface on friction of metals. Wear 1999, 225–229, 427–439. [Google Scholar] [CrossRef]
- Gachot, C.; Rosenkranz, A.; Hsu, S.M.; Costa, H.L. A critical assessment of surface texturing for friction and wear improvement. Wear 2017, 372–373, 21–41. [Google Scholar] [CrossRef]
- Lu, P.; Wood, R.J.K. Tribological performance of surface texturing in mechanical applications—A review. Surf. Topogr. Metrol. Prop. 2020, 8, 043001. [Google Scholar] [CrossRef]
- Hsu, S.M.; Jing, Y.; Zhao, F. Self-adaptive surface texture design for friction reduction across the lubrication regimes. Surf. Topogr. Metrol. Prop. 2016, 4, 014004. [Google Scholar] [CrossRef]
- Wang, X.; Adachi, K.; Otsuka, K.; Kato, K. Optimization of the surface texture for silicon carbide sliding in water. Appl. Surf. Sci. 2006, 253, 1282–1286. [Google Scholar] [CrossRef]
- Segu, D.Z.; Choi, S.G.; Choi, J.H.; Kim, S.S. The effect of multi-scale laser textured surface on lubrication regime. Appl. Surf. Sci. 2013, 270, 58–63. [Google Scholar] [CrossRef]
- Segu, D.Z.; Hwang, P. Friction control by multi-shape textured surface under pin-on-disc test. Tribol. Int. 2015, 91, 111–117. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Rosenkranz, A.; Szurdak, A.; Grüber, M.; Gachot, C.; Hirt, G.; Mücklich, F. Multi-scale surface patterning—An approach to control friction and lubricant migration in lubricated systems. Ind. Lubr. Tribol. 2019, 71, 1007–1016. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Rosenkranz, A.; Szurdak, A.; König, F.; Jacobs, G.; Hirt, G.; Mücklich, F. From lab to application—Improved frictional performance of journal bearings induced by single- and multi-scale surface patterns. Tribol. Int. 2018, 127, 500–508. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-Scale Surface Texturing in Tribology—Current Knowledge and Future Perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Huang, Y.-H.; Tsai, P.-C.; Hwang, G.-L. Tribological Properties of Carbon Nanocapsule Particles as Lubricant Additive. J. Tribol. 2014, 136, 041801. [Google Scholar] [CrossRef] [PubMed]
- Rosenkranz, A.; Grützmacher, P.G.; Gachot, C.; Costa, H.L. Surface Texturing in Machine Elements—A Critical Discussion for Rolling and Sliding Contacts. Adv. Eng. Mater. 2019, 21, 1900194. [Google Scholar] [CrossRef]
- Vlădescu, S.C.; Medina, S.; Olver, A.V.; Pegg, I.G.; Reddyhoff, T. Lubricant film thickness and friction force measurements in a laser surface textured reciprocating line contact simulating the piston ring–liner pairing. Tribol. Int. 2016, 98, 317–329. [Google Scholar] [CrossRef]
- Profito, F.J.; Vlădescu, S.-C.; Reddyhoff, T.; Dini, D. Transient experimental and modelling studies of laser-textured micro-grooved surfaces with a focus on piston-ring cylinder liner contacts. Tribol. Int. 2017, 113, 125–136. [Google Scholar] [CrossRef]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Effects of cylinder liner surface topography on friction and wear of liner-ring system at low temperature. Tribol. Int. 2018, 121, 148–160. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Nylund, N.-O.; Mäkelä, K.; Erdemir, A. Global energy consumption due to friction in trucks and buses. Tribol. Int. 2014, 78, 94–114. [Google Scholar] [CrossRef]
- Etsion, I.; Sher, E. Improving fuel efficiency with laser surface textured piston rings. Tribol. Int. 2009, 42, 542–547. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Grabon, W.; Koszela, W.; Pawlus, P.; Ochwat, S. Improving tribological behaviour of piston ring–cylinder liner frictional pair by liner surface texturing. Tribol. Int. 2013, 61, 102–108. [Google Scholar] [CrossRef]
- Koszela, W.; Pawlus, P.; Reizer, R.; Liskiewicz, T. The combined effect of surface texturing and DLC coating on the functional properties of internal combustion engines. Tribol. Int. 2018, 127, 470–477. [Google Scholar] [CrossRef]
- Vlădescu, S.-C.; Ciniero, A.; Tufail, K.; Gangopadhyay, A.; Reddyhoff, T. Optimization of Pocket Geometry for Friction Reduction in Piston–Liner Contacts, Tribol. Trans. 2018, 61, 522–531. [Google Scholar]
- Vlădescu, S.-C.; Ciniero, A.; Tufail, K.; Gangopadhyay, A.; Reddyhoff, T. Looking into a laser textured piston ring-liner contact. Tribol. Int. 2017, 115, 140–153. [Google Scholar] [CrossRef]
- Vlădescu, S.-C.; Olver, A.V.; Pegg, I.G.; Reddyhoff, T. Combined friction and wear reduction in a reciprocating contact through laser surface texturing. Wear 2016, 358–359, 51–61. [Google Scholar] [CrossRef]
- Vlădescu, S.-C.; Medina, S.; Olver, A.V.; Pegg, I.G.; Reddyhoff, T. The Transient Friction Response of a Laser-Textured, Reciprocating Contact to the Entrainment of Individual Pockets. Tribol. Lett. 2016, 62, 19. [Google Scholar] [CrossRef]
- Costa, H.L.; Hutchings, I.M. Hydrodynamic lubrication of textured steel surfaces under reciprocating sliding conditions. Tribol. Int. 2007, 40, 1227–1238. [Google Scholar] [CrossRef]
- Shen, C.; Khonsari, M.M. Numerical optimization of texture shape for parallel surfaces under unidirectional and bidirectional sliding. Tribol. Int. 2015, 82, 1–11. [Google Scholar] [CrossRef]
- Morris, N.; Leighton, M.; De la Cruz, M.; Rahmani, R.; Rahnejat, H.; Howell-Smith, S. Combined numerical and experimental investigation of the micro-hydrodynamics of chevron-based textured patterns influencing conjunctional friction of sliding contacts. Proc. IMechE Part J J. Eng. Tribol. 2015, 229, 316–335. [Google Scholar] [CrossRef]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Howell-Smith, S. A Numerical Model to Study the Role of Surface Textures at Top Dead CenterReversal in the Piston Ring to Cylinder Liner Contact. J. Tribol. 2016, 138, 021703. [Google Scholar] [CrossRef]
- Lu, P.; Wood, R.J.K.; Gee, M.G.; Wang, L.; Pfleging, W. The Friction Reducing Effect of Square-Shaped Surface Textures Under Lubricated Line-Contacts—An Experimental Study. Lubricants 2016, 4, 26. [Google Scholar] [CrossRef]
- Lu, P.; Wood, R.J.K.; Gee, M.G.; Wang, L.; Pfleging, W. A Novel Surface Texture Shape for Directional Friction Control. Tribol. Lett. 2018, 66, 51. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, W.; Dzierwa, A.; Reizer, R.; Pawlus, P. Effects of oil pocket shape and density on friction in reciprocating sliding. Eksploat. I Niezawodn. 2022, 24, 338–345. [Google Scholar] [CrossRef]
- Galda, L.; Dzierwa, A.; Sep, J.; Pawlus, P. The effect of oil pockets shape and distribution on seizure resistance in lubricated sliding. Tribol. Lett. 2010, 37, 301–311. [Google Scholar] [CrossRef]
- Koszela, W.; Dzierwa, A.; Galda, L.; Pawlus, P. Experimental investigation of oil pockets effect on abrasive wear resistance. Tribol. Int. 2012, 46, 145–153. [Google Scholar] [CrossRef]
- Nakano, M.; Korenaga, A.; Miyake, K.; Murakami, T.; Ando, Y.; Usami, H.; Sasaki, S. Applying micro-texture to cast iron surfaces to reduce the friction coefficient under lubricated conditions. Tribol. Lett. 2007, 28, 131–137. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Zhou, F.; Zhu, D. Preliminary investigation of the effect of dimple size on friction in line contacts. Tribol. Int. 2009, 42, 1118–1123. [Google Scholar] [CrossRef]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Evolutions of cylinder liner surface texture and tribological performance of piston ring-liner assembly. Tribol. Int. 2018, 127, 545–556. [Google Scholar] [CrossRef]


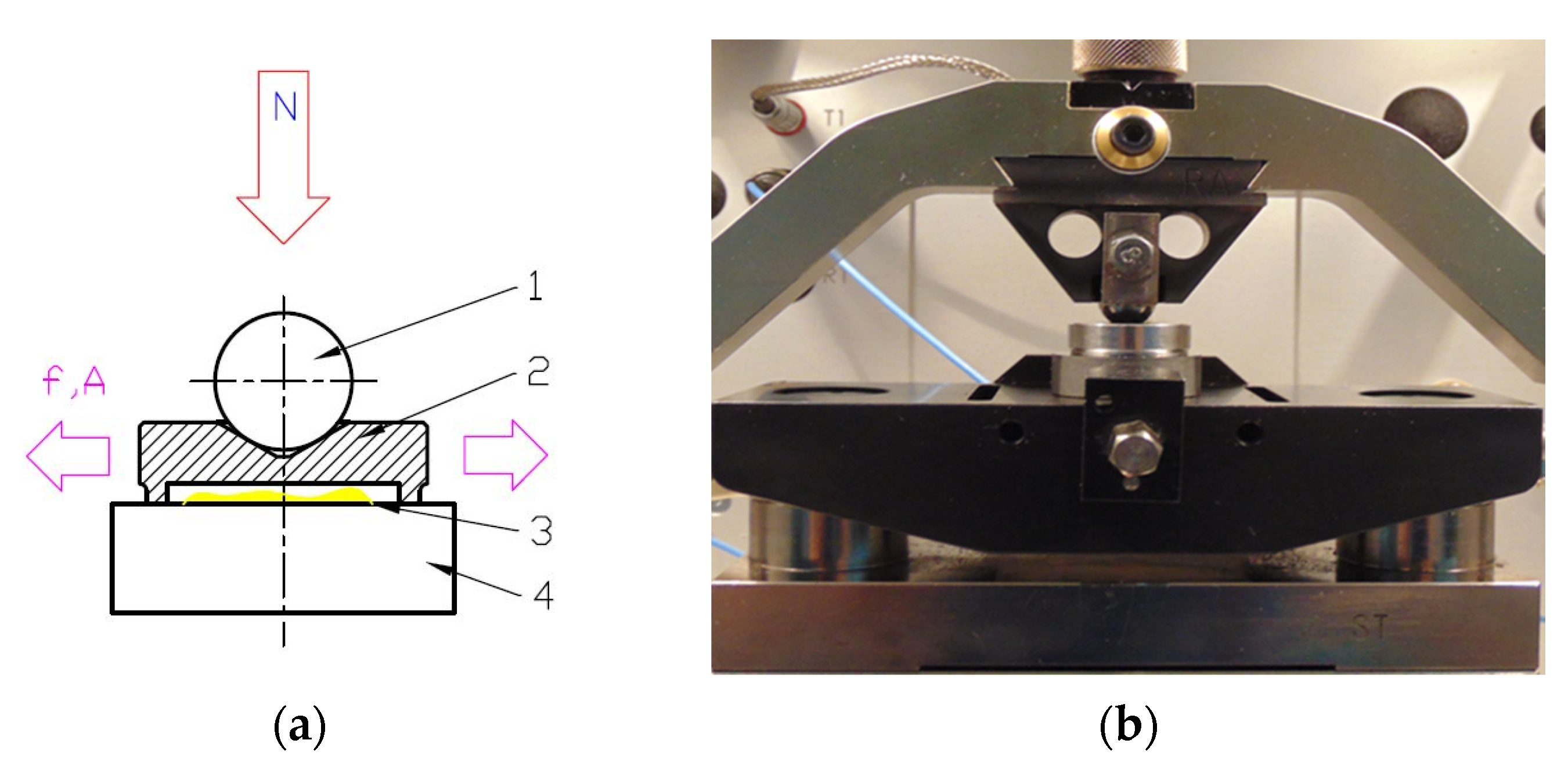

| Parameter | Value |
|---|---|
| Laser power | 20 W (100%) |
| Focal length | 254 mm |
| Focal diameter | 64 µm |
| Pulse duration | 1.5 ns |
| Pulse repetition rate | 820 kHz |
| Marking speed | 200 mm/s |
| Marking path pattern | Cross-line bidirectional |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wos, S.; Koszela, W.; Dzierwa, A.; Pawlus, P. Effects of Operating Conditions and Pit Area Ratio on the Coefficient of Friction of Textured Assemblies in Lubricated Reciprocating Sliding. Materials 2022, 15, 7199. https://doi.org/10.3390/ma15207199
Wos S, Koszela W, Dzierwa A, Pawlus P. Effects of Operating Conditions and Pit Area Ratio on the Coefficient of Friction of Textured Assemblies in Lubricated Reciprocating Sliding. Materials. 2022; 15(20):7199. https://doi.org/10.3390/ma15207199
Chicago/Turabian StyleWos, Slawomir, Waldemar Koszela, Andrzej Dzierwa, and Pawel Pawlus. 2022. "Effects of Operating Conditions and Pit Area Ratio on the Coefficient of Friction of Textured Assemblies in Lubricated Reciprocating Sliding" Materials 15, no. 20: 7199. https://doi.org/10.3390/ma15207199
APA StyleWos, S., Koszela, W., Dzierwa, A., & Pawlus, P. (2022). Effects of Operating Conditions and Pit Area Ratio on the Coefficient of Friction of Textured Assemblies in Lubricated Reciprocating Sliding. Materials, 15(20), 7199. https://doi.org/10.3390/ma15207199









