Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection
Abstract
1. Introduction
2. Materials and Methods
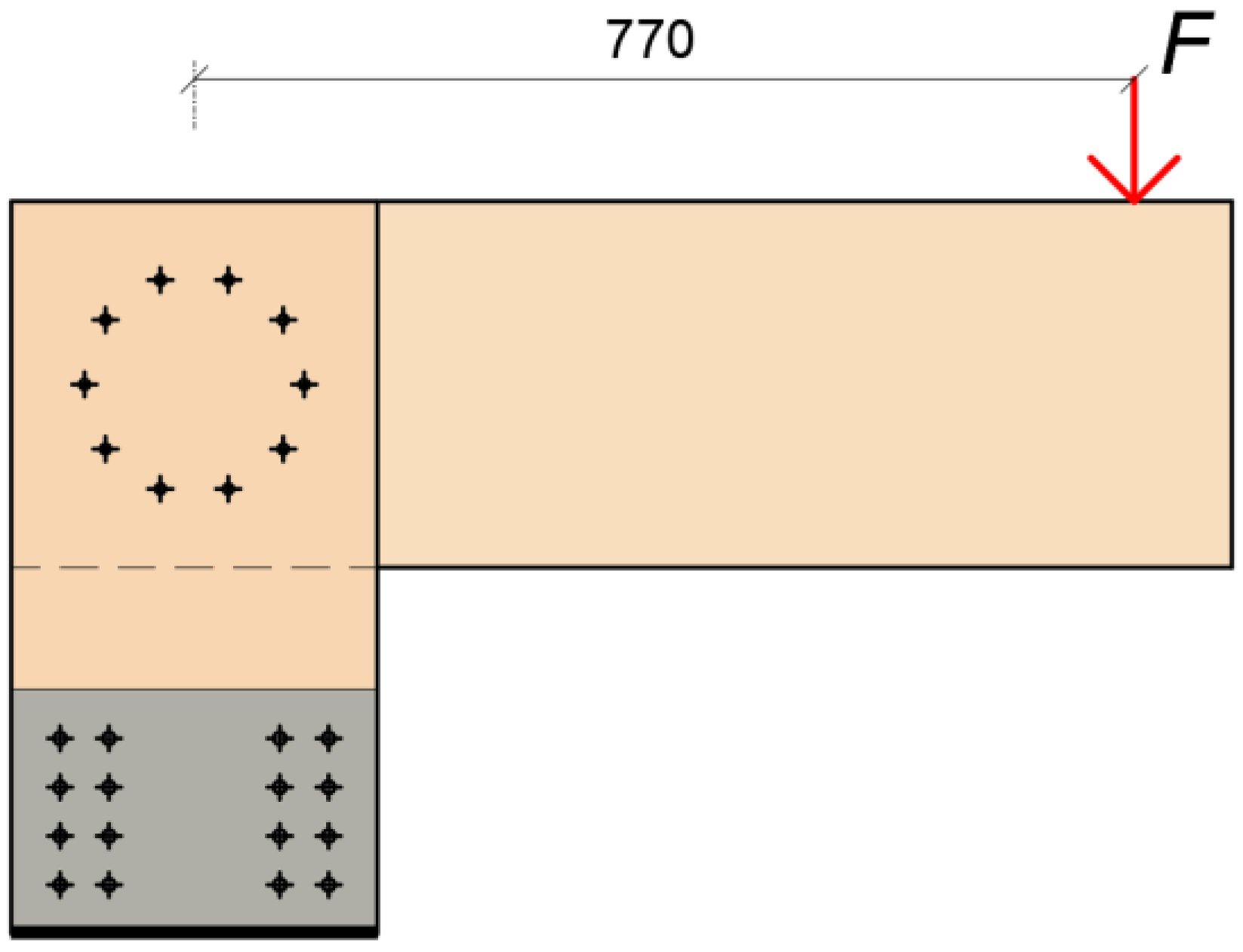
2.1. Description of Construction and Geometry
2.2. Description of the Testing Machine
2.3. Description of the Testing
- Estimation of the maximum force Fest for the tested connection based on experience, calculation, or pretests;
- Loading of the specimen to 40% of the estimated maximum force, 0.4·Fest, then holding for 30 s;
- Unloading to 10% of the estimated maximum force, 0.1·Fest, then holding for 30 s;
- Reloading until the specimen fails.
2.4. Experimental Testing
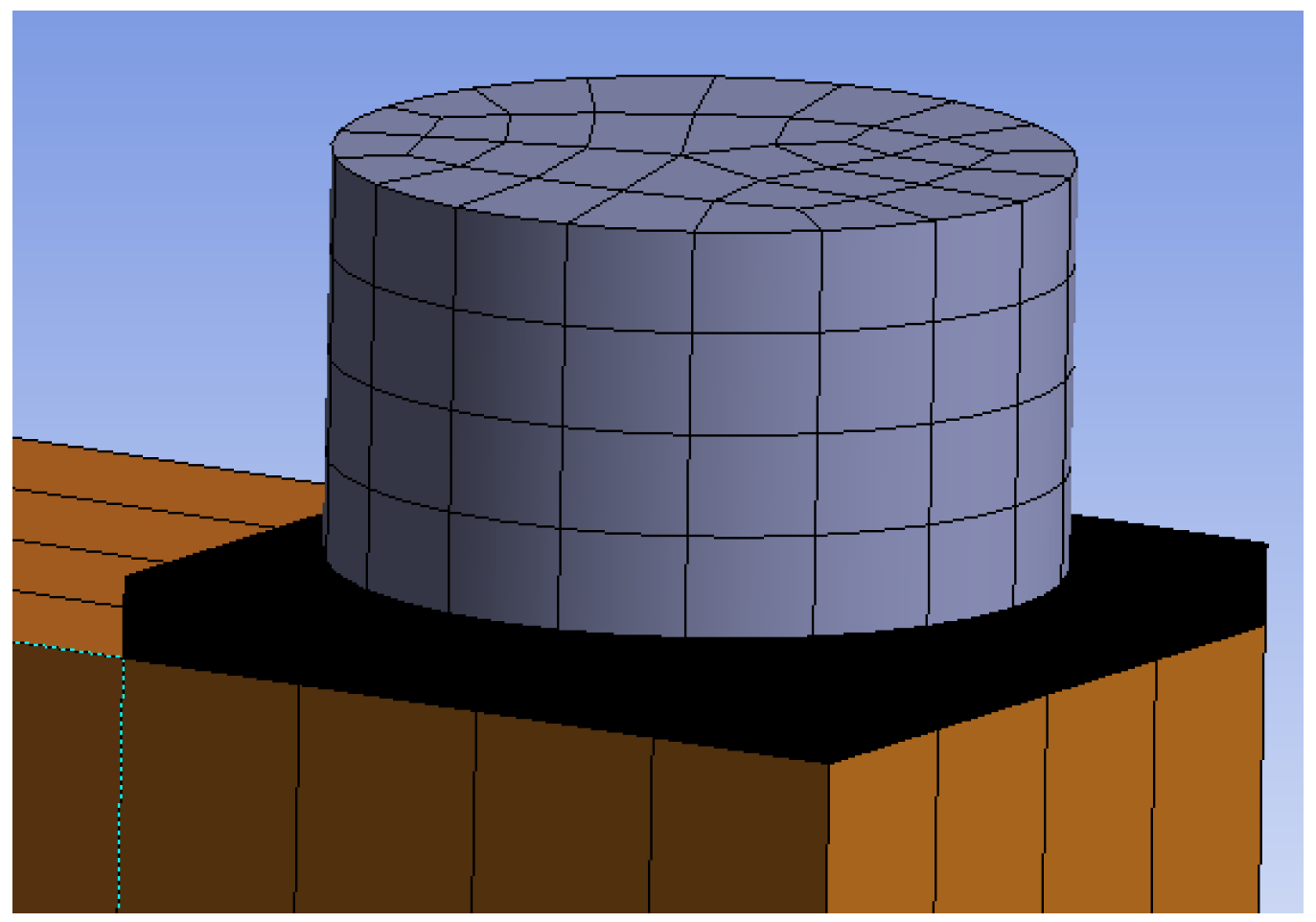
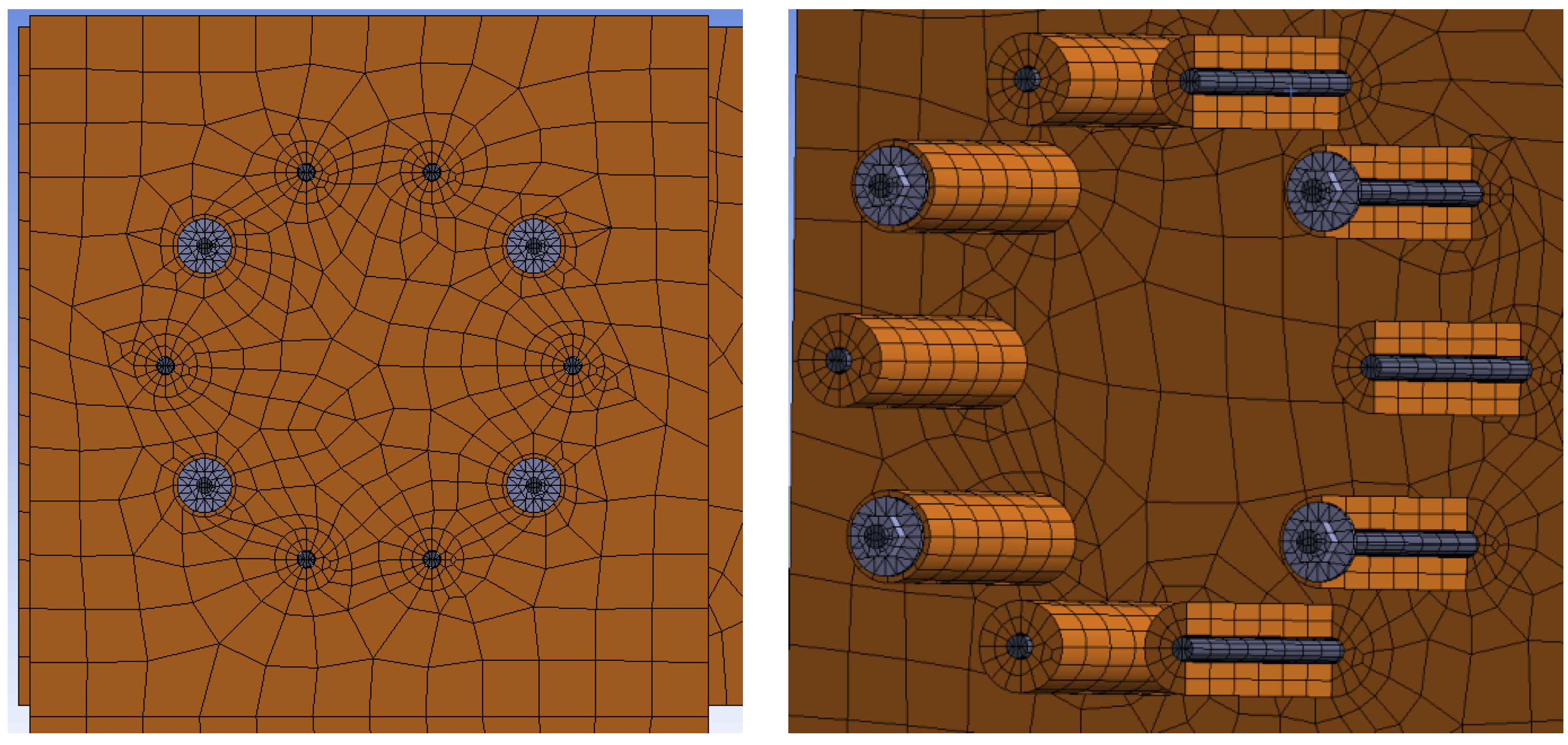
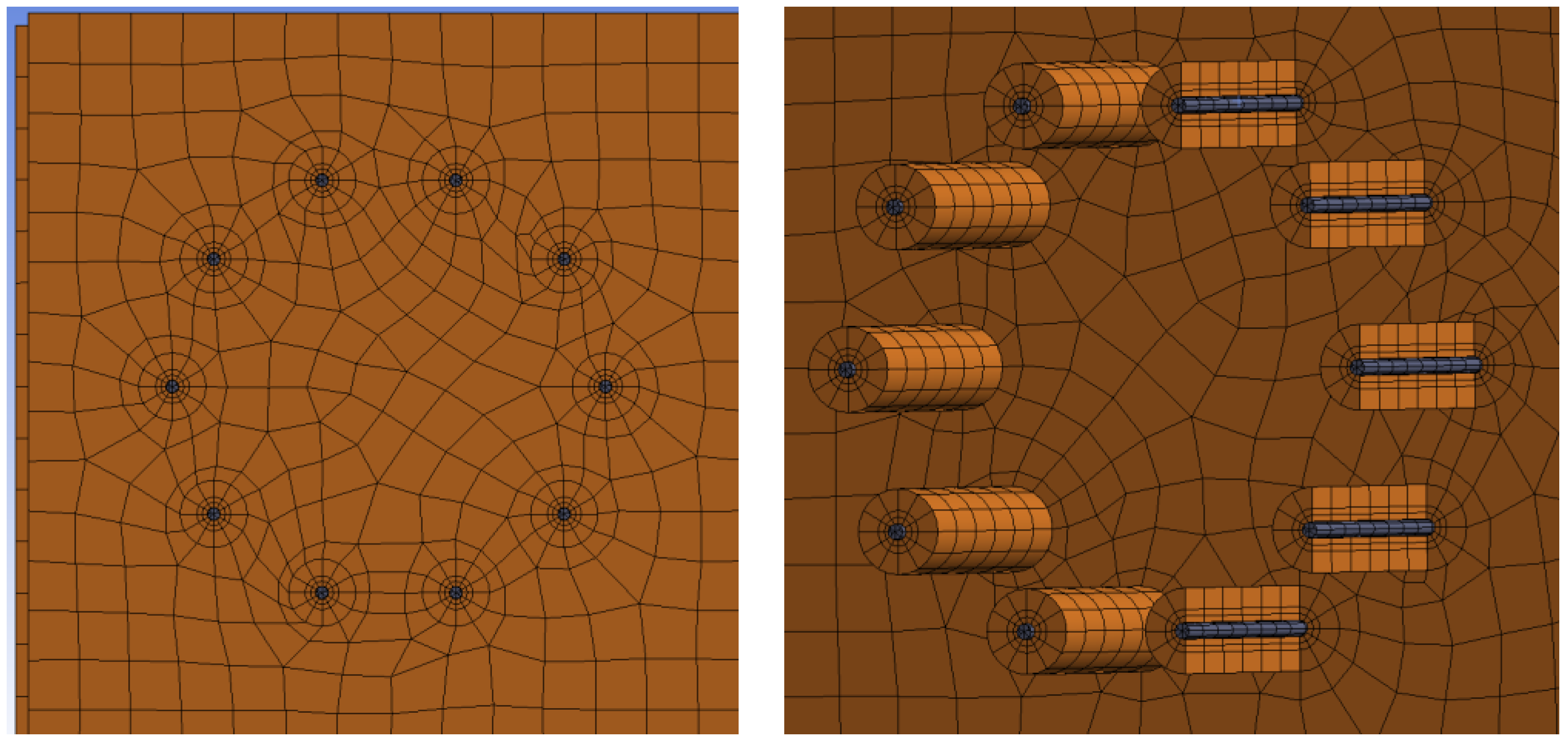
2.5. Numerical Modeling
3. Results
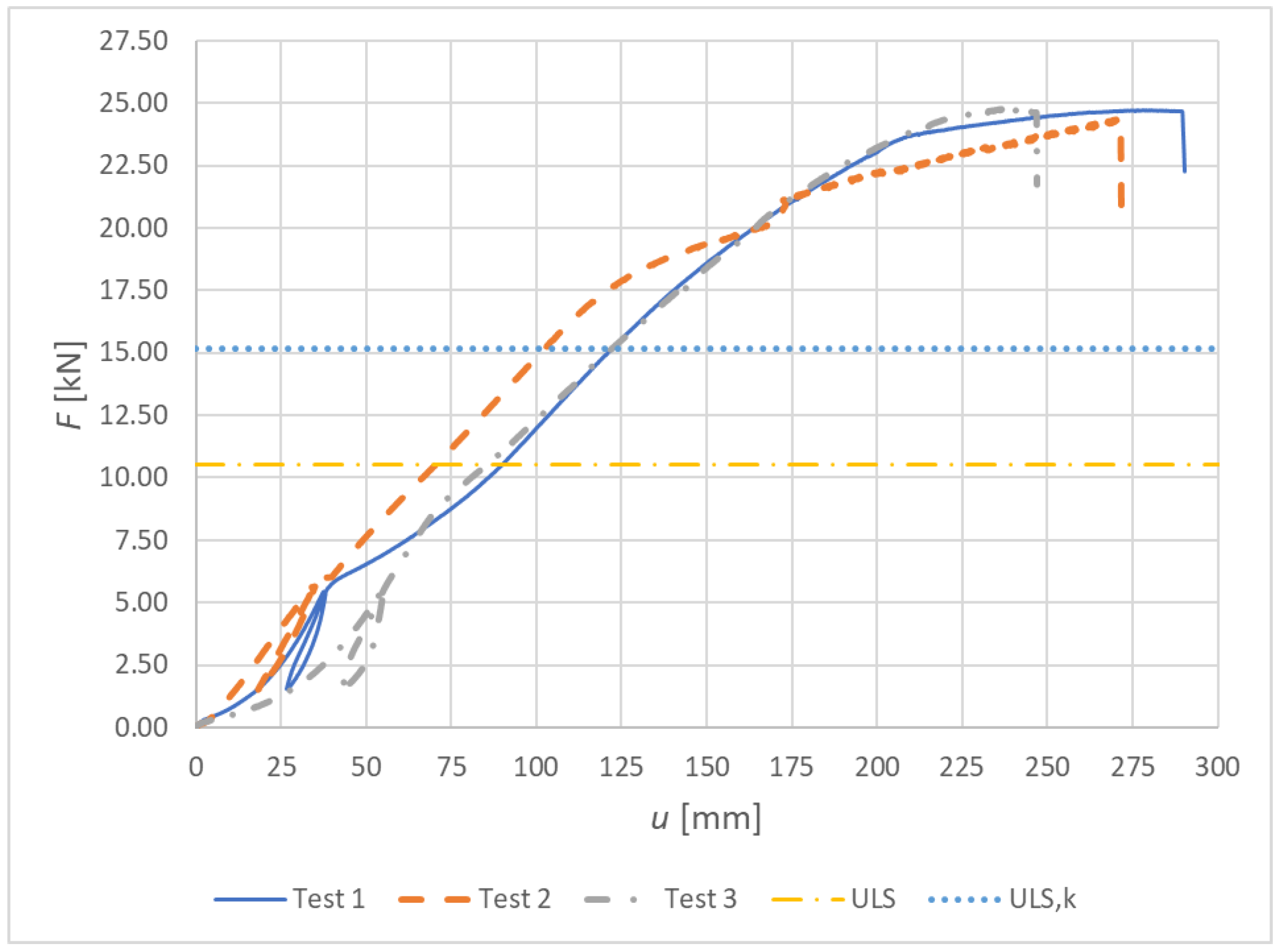
3.1. Results of Experimental Testing
3.1.1. Experiment A, Bolts and Dowels
3.1.2. Experiment B, Fully Threaded Screws
3.2. Tabular Results of the Experimental Testing
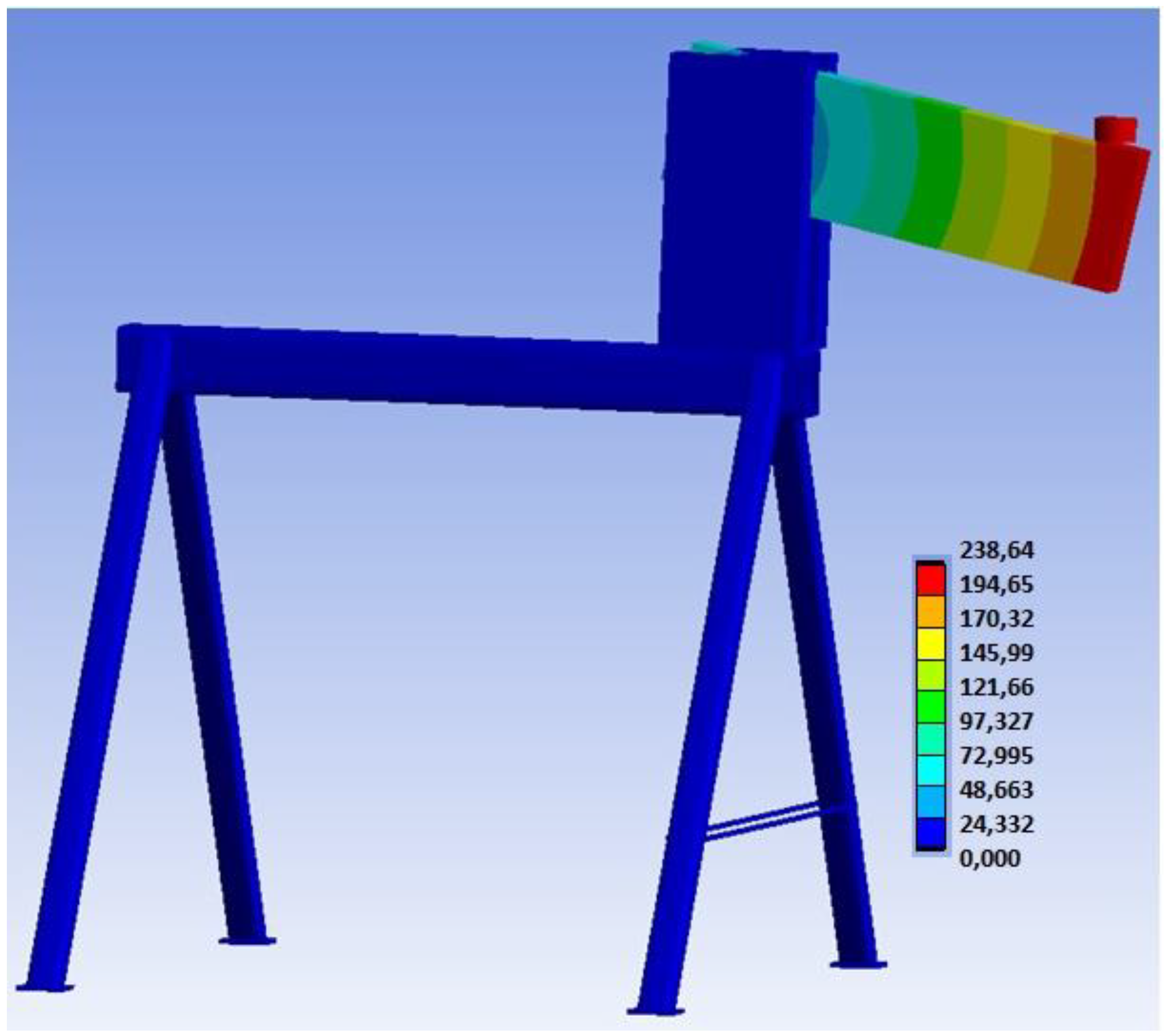
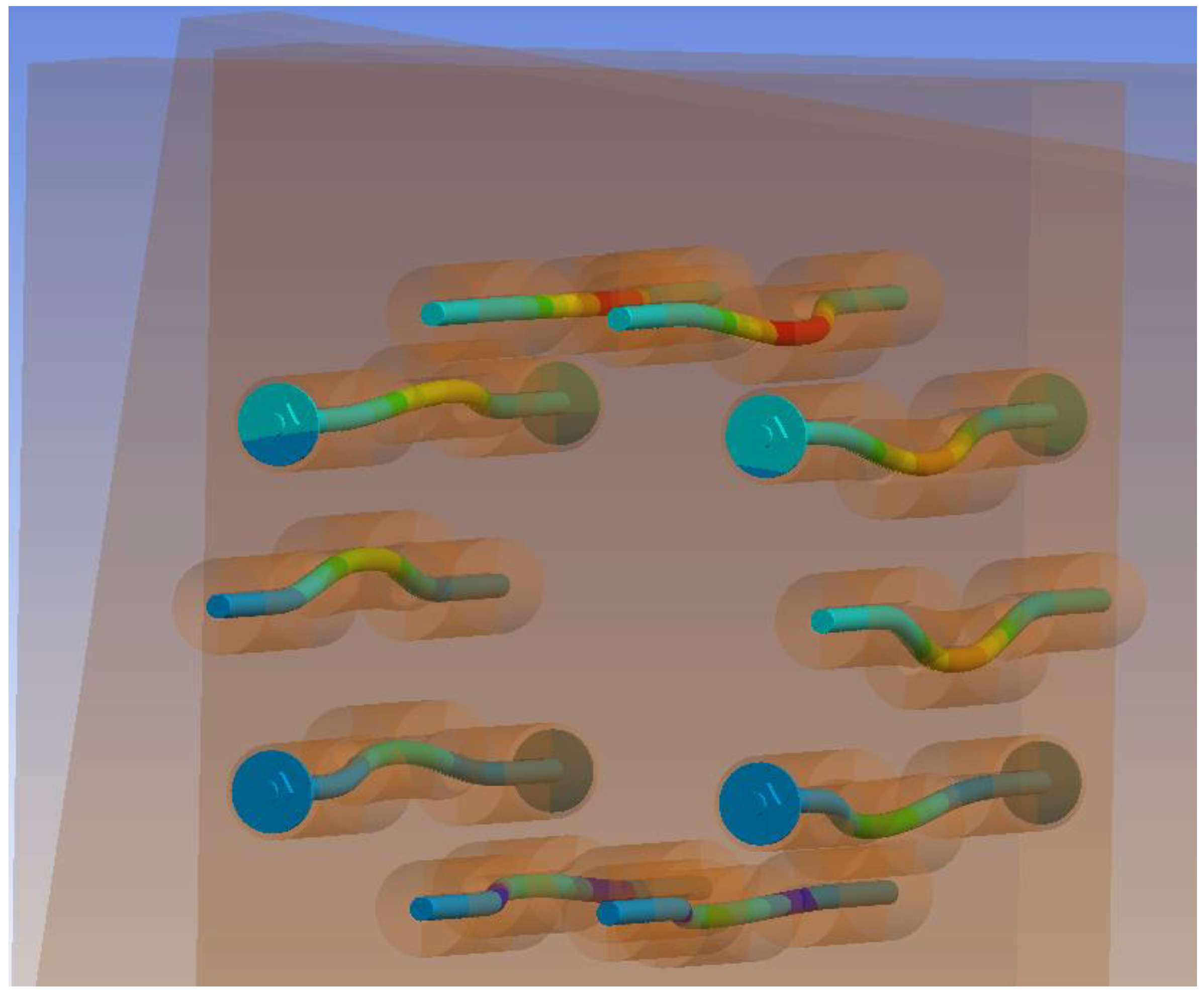
3.3. Results of Numerical Modeling
3.3.1. Experiment A, Bolts and Dowels
3.3.2. Experiment B, Fully Threaded Screws
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wilson, T.R.C. Tests made to determine lateral resistance of wire nails. Eng. Rec. 1917, 75, 303–304. [Google Scholar]
- Johansen, K.W. Forsög med Träforbindelser. Danmarks Tekniske Höjskole Medd. No. 10; Laboratoriet for bygningsteknik: Copenhagen, Denmark, 1941. (In Danish) [Google Scholar]
- Johansen, K.W. Theory of Timber Connections; International association for bridge and structural engineering: Zurich, Switzerland, 1949; pp. 249–262. [Google Scholar]
- Larsen, H.J.K.W. Johansen’s nail tests. Bygn. Medd. 1977, 48, 9–30. [Google Scholar]
- Möller, T. En ny metod för beräkning av spikförband. In Report No. 117; Chalmers University of Technology: Chalmersplatsen, Sweden, 1951. [Google Scholar]
- Kuenzi, E.W. Theoretical design of nailed or bolted connection under lateral load. In Report No: D1951; States Department of Agriculture, Forest Service, Forest Laboratory Products: Madison, WI, USA, 1955. [Google Scholar]
- Winkler, E. Die lehre von elastizitatunffestigheit. Dominicus Prague Czechoslov. 1867. [Google Scholar]
- Foshi, R.O. Modeling the hysteretic response of mechanical connections for wood structures. In Proceedings of the 6th World Conference of Timber Engineering, Whistler, CA, Canada, 31 July–3 August 2000. [Google Scholar]
- Meyer, A. Die Tragfähigkeit von Nagelverbindungen bei statischer Belastung. HOLZ Als Roh-Und Werkst. 1957, 15, 96–109. [Google Scholar] [CrossRef]
- Doyle, D.V. Performance of connections with eight bolts in laminated Douglas-fir; U.S. Forest Service Research Paper FPL 10; U.S. Forest Service: Missoula, MT, USA, 1964. [Google Scholar]
- Mack, J.J. The strength and stiffness of nailed connections under short-duration loading. In Division of Forest Products; Commonwealth Scientific and Industrial Research Organization: South Melbourne, Australia, 1966. [Google Scholar]
- Larsen, H.J.; Reestrup, V. Tests on screws in wood. Bygningsstatiske Medd. 1969, 1, 3–36. [Google Scholar]
- Norén, B. Formler för hallfasthet hos mekaniska träförband. In Formulas Indicating the Strength of Mechanical Wood Connections; Medd. Series B, No. 226; Svenska Träforskningsinstitutet: Stockholm, Sweden, 1974. (In Swedish) [Google Scholar]
- Larsen, H.J. The yield load of bolted and nailed connections. In Proceedings of the International Union of Forestry Research Organizations Working Group on Structural Utilization, Pretoria, South Africa, 22 September–12 October 1973. [Google Scholar]
- Larsen, H.J. Design of bolted connections. In International Council for Building Research Studies and Documentation, Working Commission W 18—Timber Structures; Karlsruhe Institute of Technology: Bordeaux, France, 1979. [Google Scholar]
- CIB. Structural timber design code. In International Council for Building Research Studies and Documentation, Working Group W18—Timber Structures, 6th ed.; CIB-W18: St. Andrews, NB, Canada, 1983. [Google Scholar]
- Smith, I.A.; Whale, L.R.J. Mechanical timber connections. In TRADA Research Report 18/86; TRADA: High Wycombe, UK, 1986. [Google Scholar]
- Ehlbeck, J.; Werner, H. Tragfähigkeit von Laubholzverbindungen mit stabförmigen Verbindungsmitteln. Versuchsanst. für Stahl, Holz und Steine, Abt. Ingenieurholzbau; Universität Karlsruhe: Karlsruhe, Germany, 1992. [Google Scholar]
- Blass, H.J.; Bienhaus, A.; Krämer, V. Effective bending capacity of dowel-type fasteners. Proc. PRO 2000, 22, 71–80. [Google Scholar]
- EN 1995-1-1; Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. Czech Standards Institute: Praha, Czech Republic, 2006.
- Timber Structures According To Eurocode 5; STEP 1: Design and construction materials; Translated by Bohumil Kozelouh; KODR: Zlin, Czech Republic, 1998; ISBN 80-238-2620-4. (In Czech)
- Solarino, F.; Giresini, L.; Chang, W.-S.; Huang, H. Experimental Tests on a Dowel-Type Timber Connection and Validation of Numerical Models. Buildings 2017, 7, 116. [Google Scholar] [CrossRef]
- Vavrusova, K.; Mikolasek, D.; Lokaj, A.; Klajmonova, K.; Sucharda, O. Determination of carrying capacity of steel-timber connections with steel rods glued-in parallel to grain. Wood Res. 2016, 61, 733–740. [Google Scholar]
- Chybiński, M.; Polus, Ł. Mechanical Behaviour of Aluminium-Timber Composite Connections with Screws and Toothed Plates. Materials 2022, 15, 68. [Google Scholar] [CrossRef]
- Chybiński, M.; Polus, Ł. Experimental Study of Aluminium-Timber Composite Bolted Connections Strengthened with Toothed Plates. Materials 2022, 15, 5271. [Google Scholar] [CrossRef]
- Cai, Y.; Young, B. Effects of end distance on thin sheet steel bolted connections. Eng. Struct. 2019, 196, 109331. [Google Scholar] [CrossRef]
- Požgaj, A.; Kürjatko, S. Wood properties of spruce from forests affected by pollution in Czechoslovakia. IAWA J. 1986, 7, 405–410. [Google Scholar] [CrossRef]
- Mirski, R.; Dziurka, D.; Chuda-Kowalska, M.; Wieruszewski, M.; Kawalerczyk, J.; Trociński, A. The Usefulness of Pine Timber (Pinus sylvestris L.) for the Production of Structural Elements. Part I: Evaluation of the Quality of the Pine Timber in the Bending Test. Materials 2019, 13, 3957. [Google Scholar] [CrossRef] [PubMed]
- Mirski, R.; Dziurka, D.; Chuda-Kowalska, M.; Kawalerczyk, J.; Kuliński, M.; Łabęda, K. The Usefulness of Pine Timber (Pinus sylvestris L.) for the Production of Structural Elements. Part II: Strength Properties of Glued Laminated Timber. Materials 2020, 13, 4029. [Google Scholar] [CrossRef] [PubMed]
- Nowak, T.; Karolak, A.; Sobótka, M.; Wyjadłowski, M. Assessment of the Condition of Wharf Timber Sheet Wall Material by Means of Selected Non-Destructive Methods. Materials 2019, 12, 1532. [Google Scholar] [CrossRef] [PubMed]
- Nowak, T.; Patalas, F.; Karolak, A. Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects. Materials 2021, 14, 1941. [Google Scholar] [CrossRef]
- Bragov, A.; Igumnov, L.; dell’Isola, F.; Konstantinov, A.; Lomunov, A.; Iuzhina, T. Dynamic Testing of Lime-Tree (Tilia Eu-ropoea) and Pine (Pinaceae) for Wood Model Identification. Materials 2020, 13, 5261. [Google Scholar] [CrossRef] [PubMed]
- Olaoye, K.; Aguda, L.; Ogunleye, B. Prediction of Mechanical Properties of Hardwood Species Using the Longitudinal Vib-ration Acoustic Method. For. Prod. J. 2021, 71, 391. [Google Scholar] [CrossRef]
- Martínez, R.D.; Balmori, J.-A.; Llana, D.F.; Bobadilla, I. Wood Density and Moisture Content Estimation by Drilling Chips Extraction Technique. Materials 2020, 13, 1699. [Google Scholar] [CrossRef] [PubMed]
- Dobes, P.; Lokaj, A.; Mikolasek, D. Load-Carrying Capacity of Double-Shear Bolted Connections with Slotted-In Steel Plates in Squared and Round Timber Based on the Experimental Testing, European Yield Model, and Linear Elastic Fracture Mechanics. Materials 2022, 15, 2720. [Google Scholar] [CrossRef]
- Braun, M.; Pełczyński, J.; Al Sabouni-Zawadzka, A.; Kromoser, B. Calibration and Validation of a Linear-Elastic Numerical Model for Timber Step Connections Based on the Results of Experimental Investigations. Materials 2022, 15, 1639. [Google Scholar] [CrossRef]
- Burawska-Kupniewska, I.; Beer, P. Near-Surface Mounted Reinforcement of Sawn Timber Beams-FEM Approach. Materials 2021, 14, 2780. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.R.; Li, Z.Y.; Feng, S.Y.; Zhu, H.; Kang, S.B. Effects of bolted connections on behaviour of timber frames under combined vertical and lateral loads. Constr. Build. Mater. 2021, 293, 123542. [Google Scholar] [CrossRef]
- Wang, M.; Song, X.; Gu, X.; Tang, J. Bolted glulam beam-column connections under different combinations of shear and bending. Eng. Struct. 2019, 181, 281–292. [Google Scholar] [CrossRef]
- Wang, X.T.; Zhu, E.C.; Niu, S.; Wang, H.J. Analysis and test of stiffness of bolted connections in timber structures. Constr. Build. Mater. 2021, 303, 124495. [Google Scholar] [CrossRef]
- Johanides, M.; Kubincova, L.; Mikolasek, D.; Lokaj, A.; Sucharda, O.; Mynarcik, P. Analysis of Rotational Stiffness of the Timber Frame Connection. Sustainability 2021, 13, 156. [Google Scholar] [CrossRef]
- Johanides, M.; Mikolasek, D.; Lokaj, A.; Mynarcik, P.; Marcalikova, Z.; Sucharda, O. Rotational Stiffness and Carrying Capacity of Timber Frame Corners with Dowel Type Connections. Materials 2021, 14, 7429. [Google Scholar] [CrossRef]
- Johanides, M.; Lokaj, A.; Mikolasek, D.; Mynarcik, P.; Dobes, P.; Sucharda, O. Timber Semirigid Frame Connection with Improved Deformation Capacity and Ductility. Buildings 2022, 12, 583. [Google Scholar] [CrossRef]
- Johanides, M.; Lokaj, A.; Dobes, P.; Mikolasek, D. Numerical and Experimental Analysis of the Rotational Stiffness of a Timber Semi-Rigid Dowel-Type Connection. Materials 2022, 15, 5622. [Google Scholar] [CrossRef] [PubMed]
- LaborTech. Available online: https://www.labortech.cz (accessed on 25 November 2021).
- EN 26891; Timber Structures. Joints Made with Mechanical Fasteners. General Principles for the Determination of Strength and Deformation Characteristics. Czech Office for Standards. Metrology and Testing: Praha, Czech Republic, 1994.
- ANSYS. Available online: https://www.ansys.com/ (accessed on 25 November 2021).
- Brožovský, J.; Alois, M. Metoda konečných Prvkůve Stavební Mechanice. 2012. Available online: https://docplayer.cz/414068-Metoda-konecnych-prvku-ve-stavebni-mechanice.html (accessed on 15 May 2022).
- Mikolášek, D. Numerické Modelování Vybraných Spojů Dřevěných Konstrukcí. Disertační Práce; Vysoká škola báňská–Technická univerzita Ostrava: Ostrava, Czech Republic, 2012. [Google Scholar]
- Gunderson, R.A.; Goodman, J.R.; Bodig, J. Plate Tests for Determination of Elastic Parameters of Wood. Wood Sci. 1973, 5, 241–248. [Google Scholar]
- The Engineering Tool Box. Available online: https://www.engineeringtoolbox.com/friction-coefficients-d_778.html (accessed on 15 May 2022).


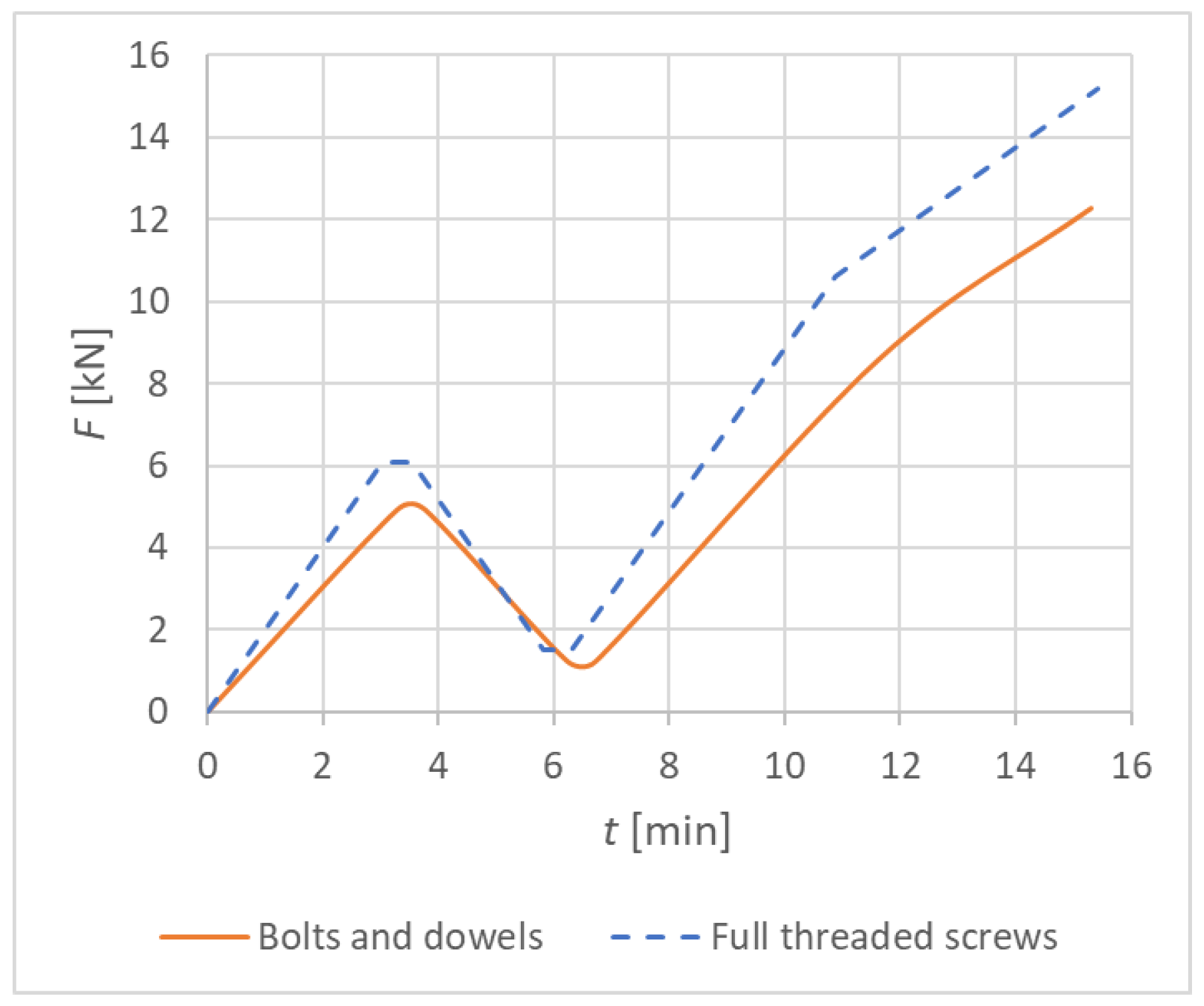











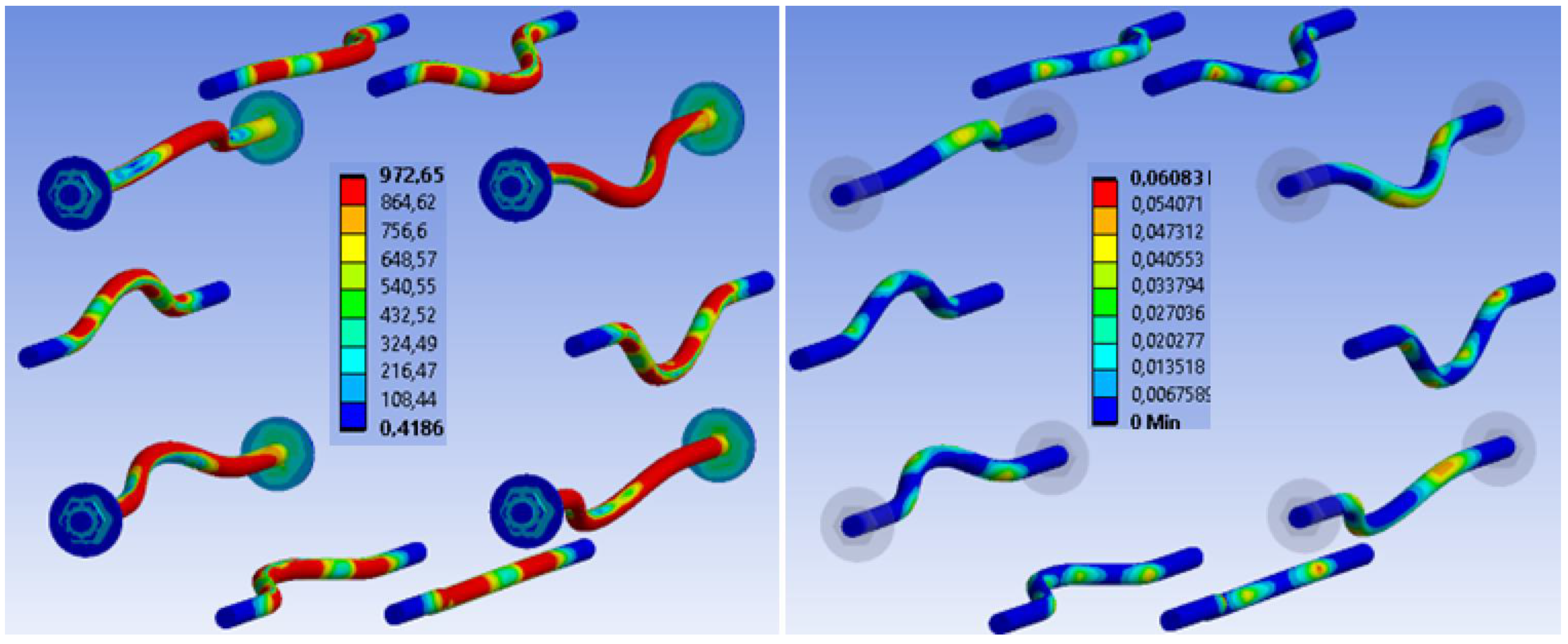


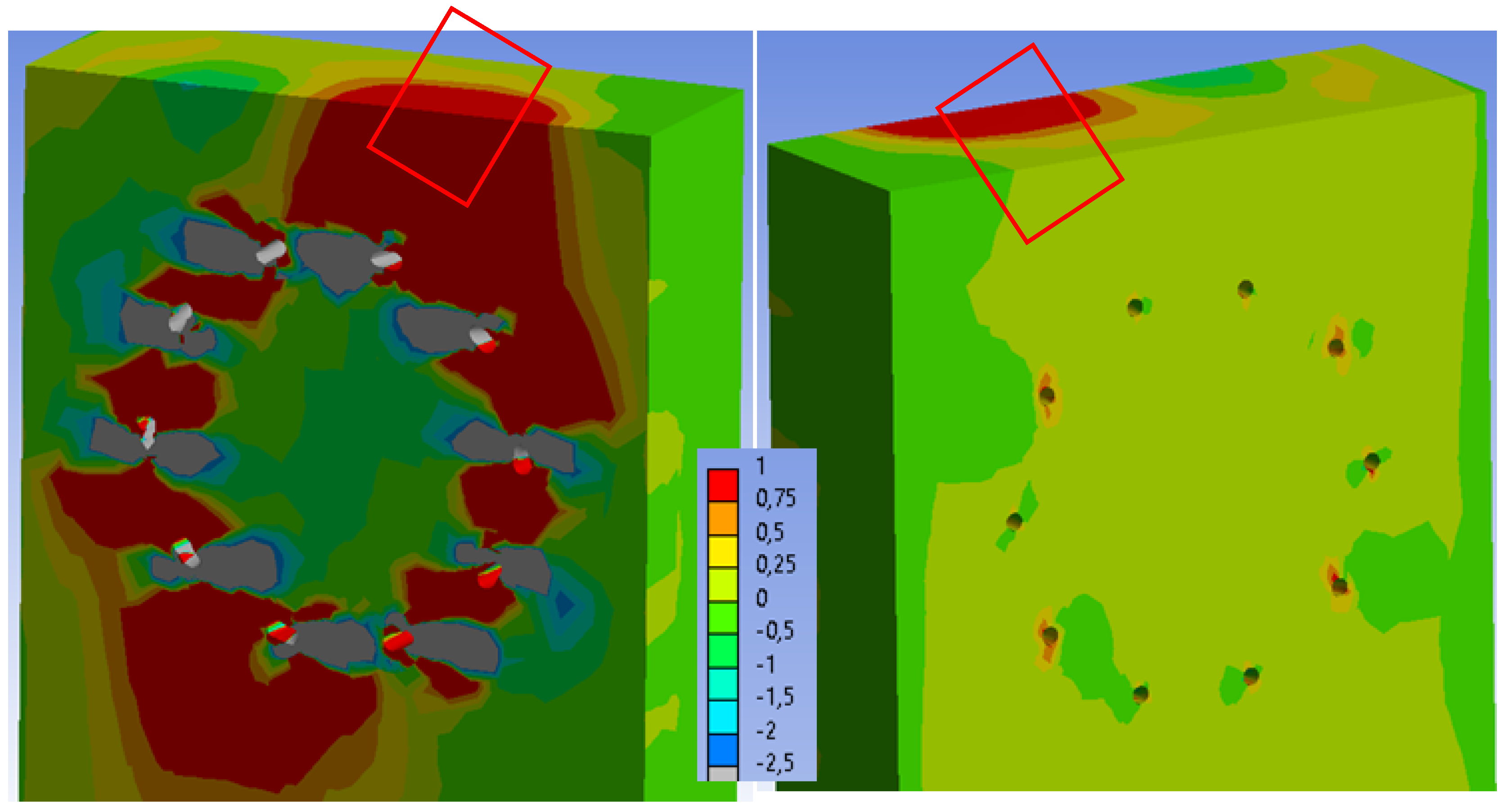
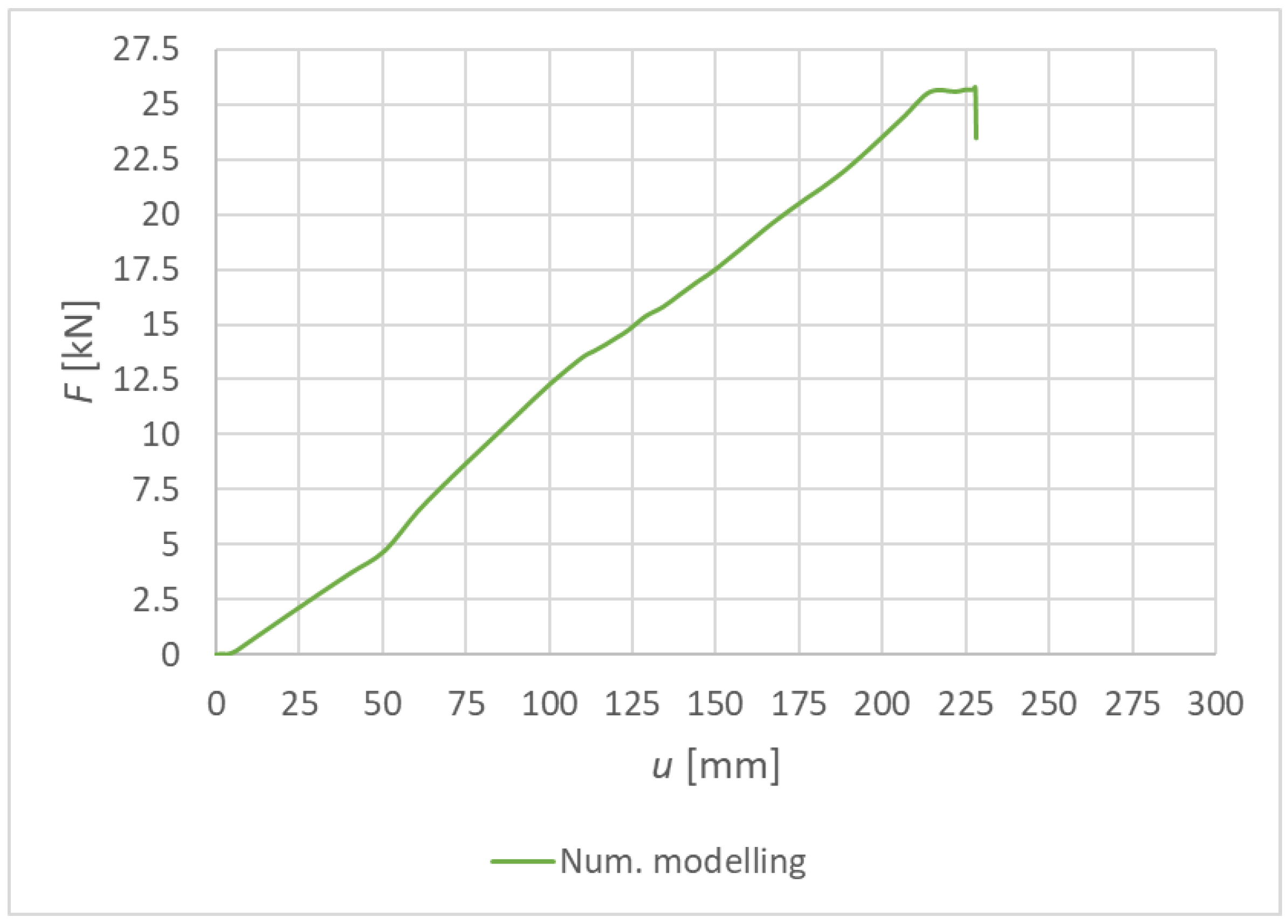
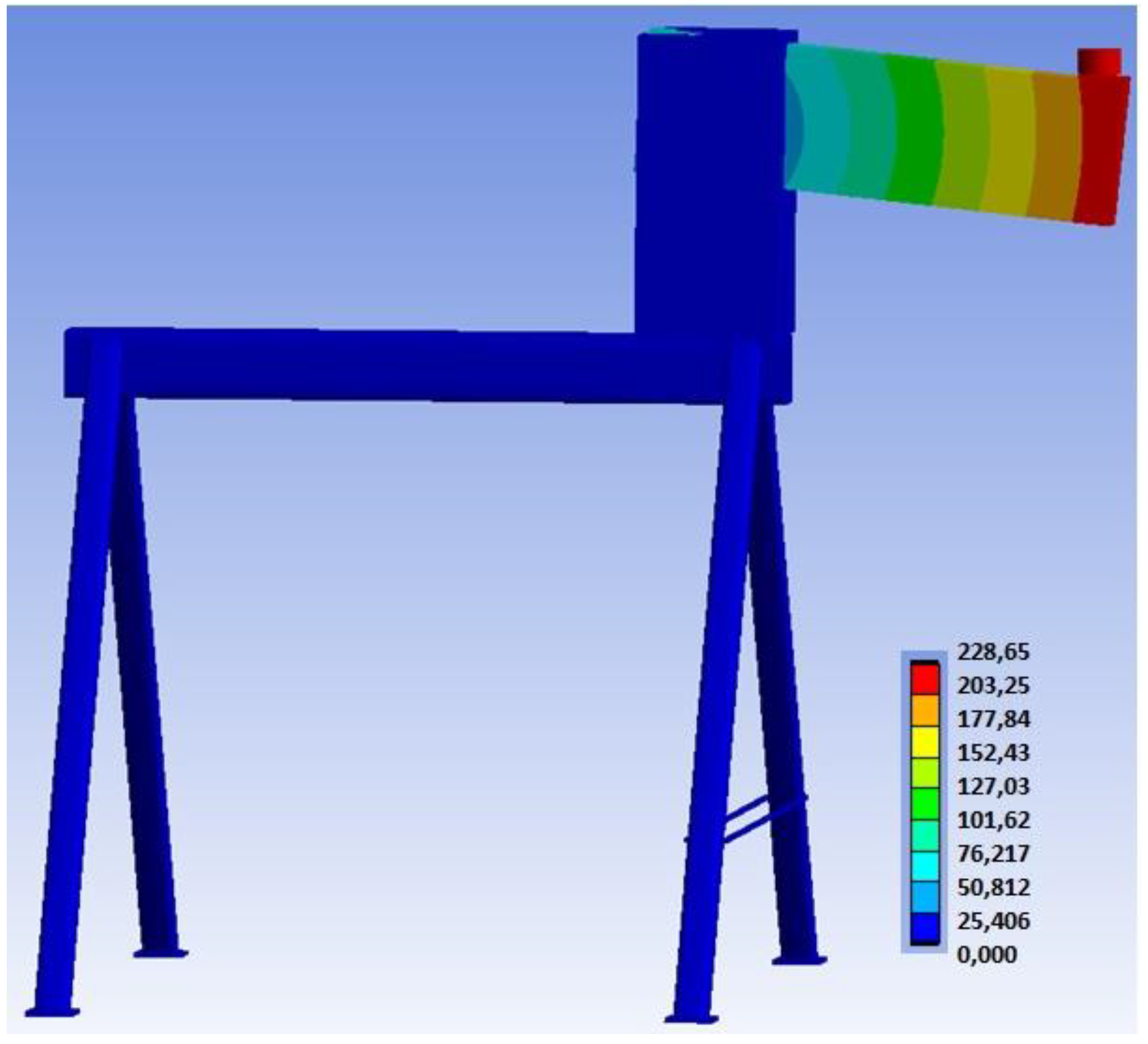
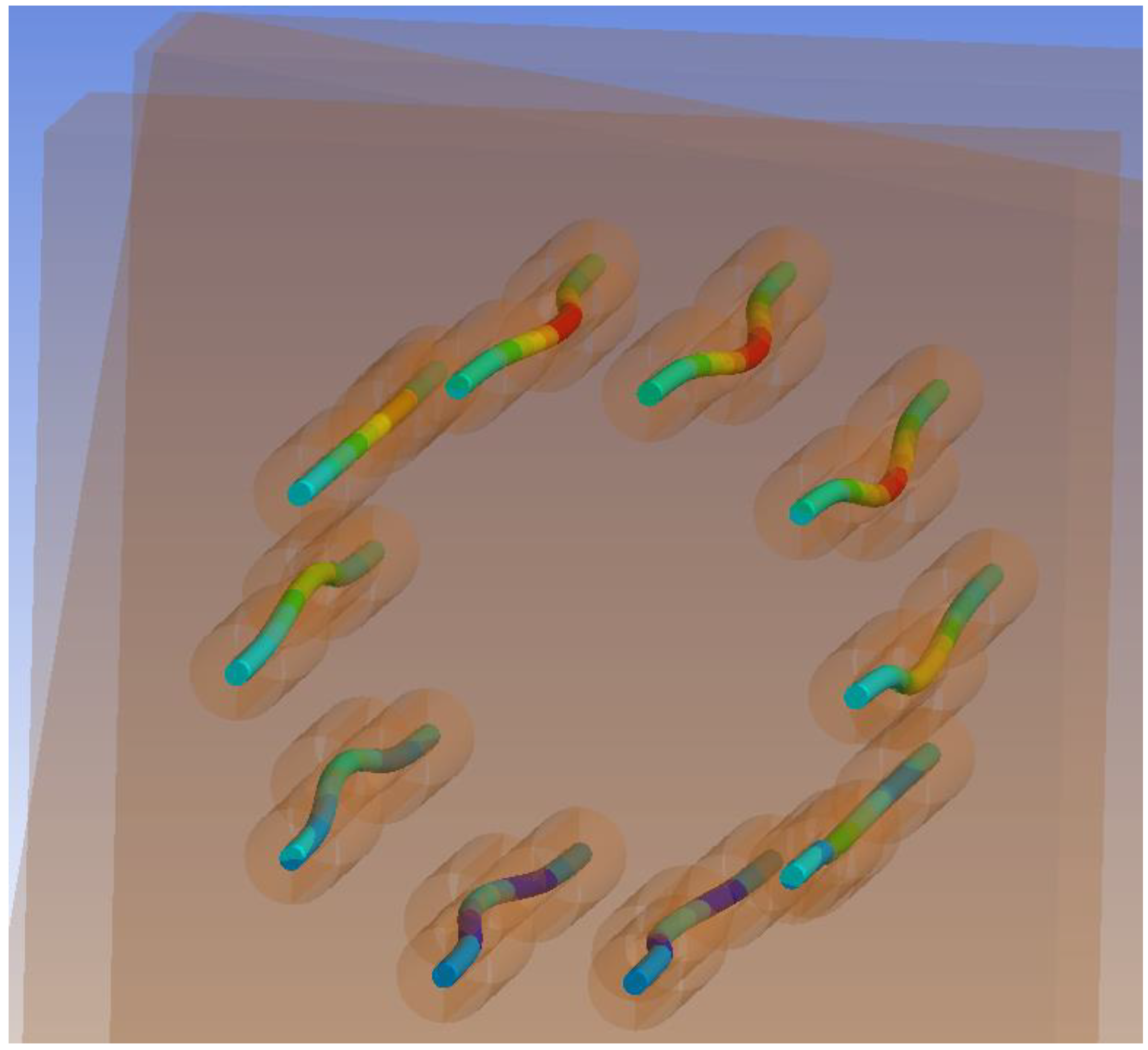

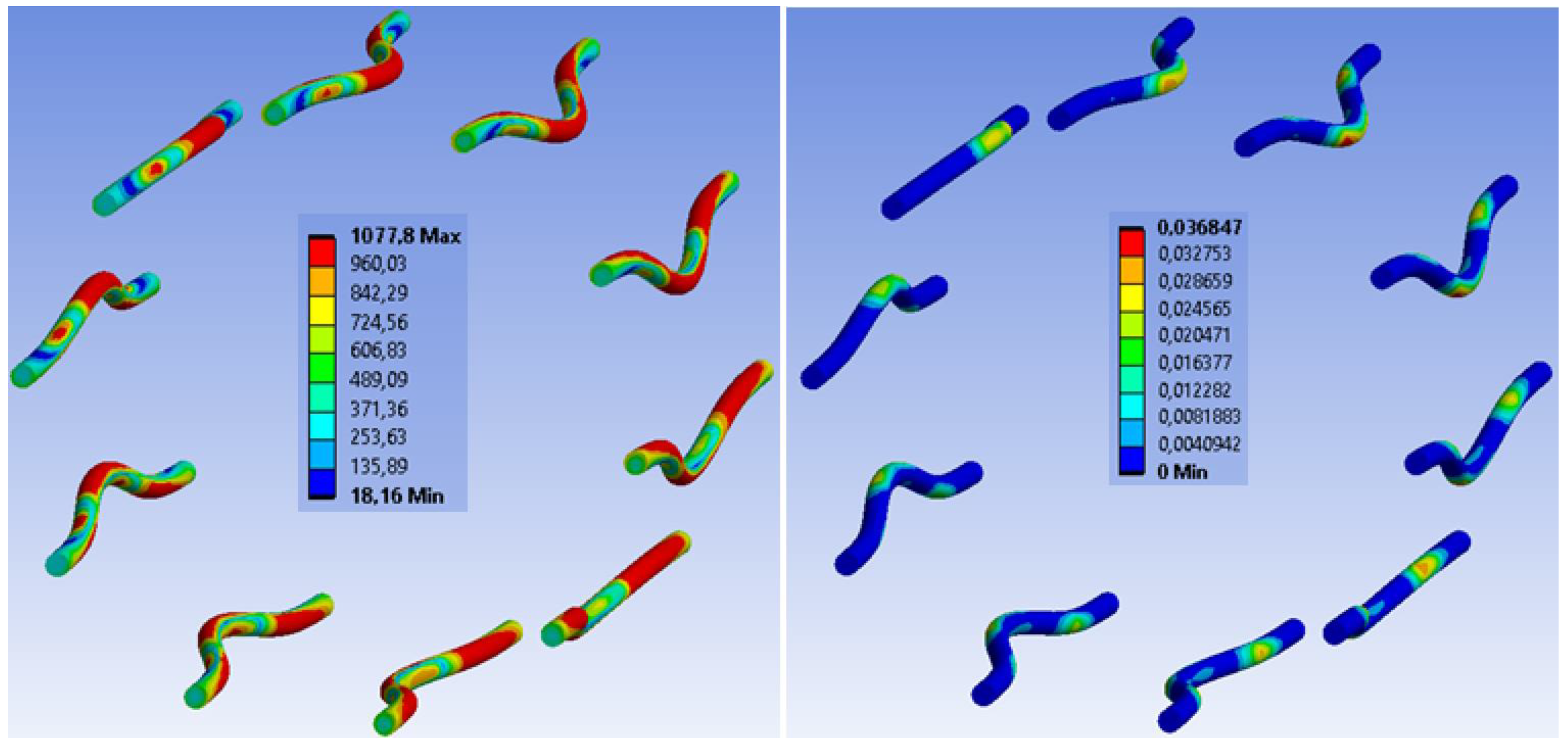

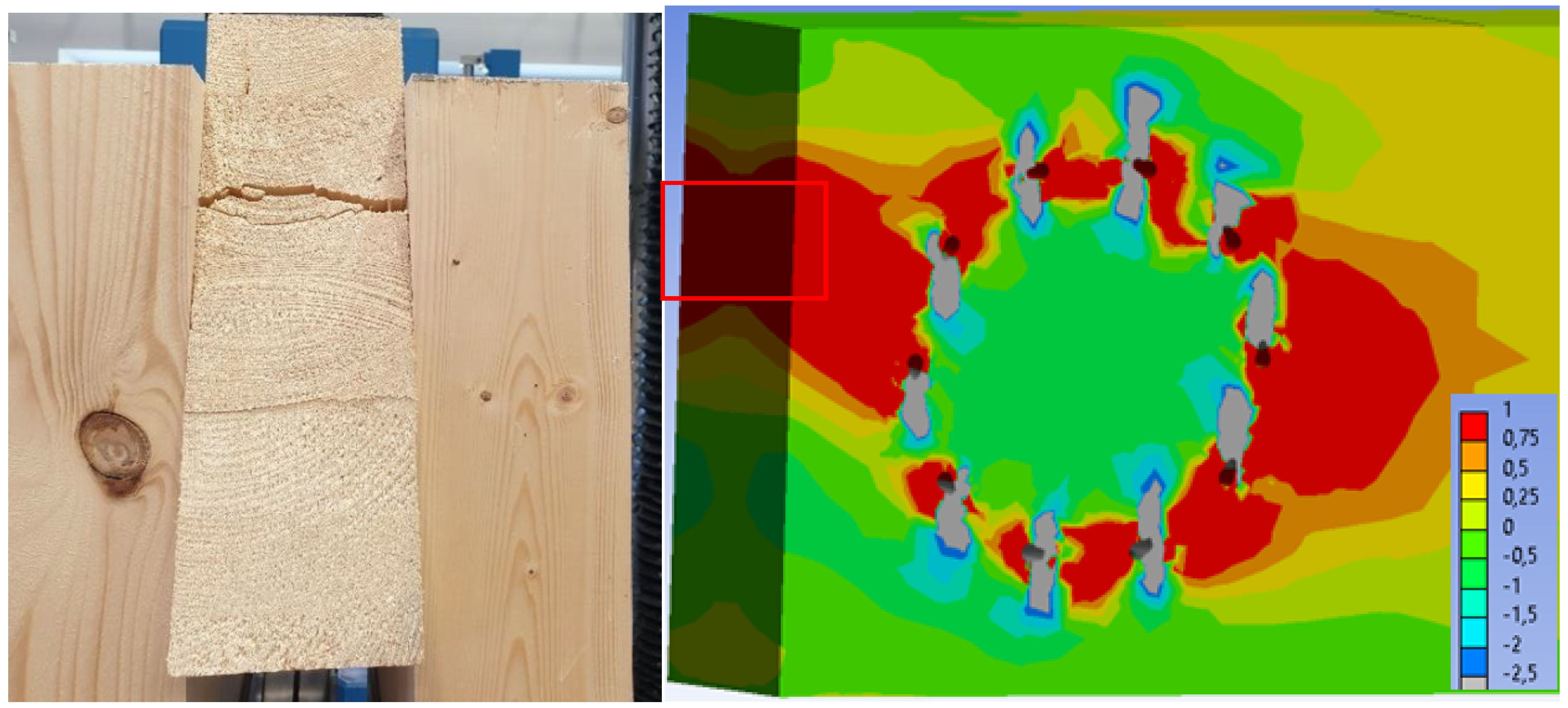
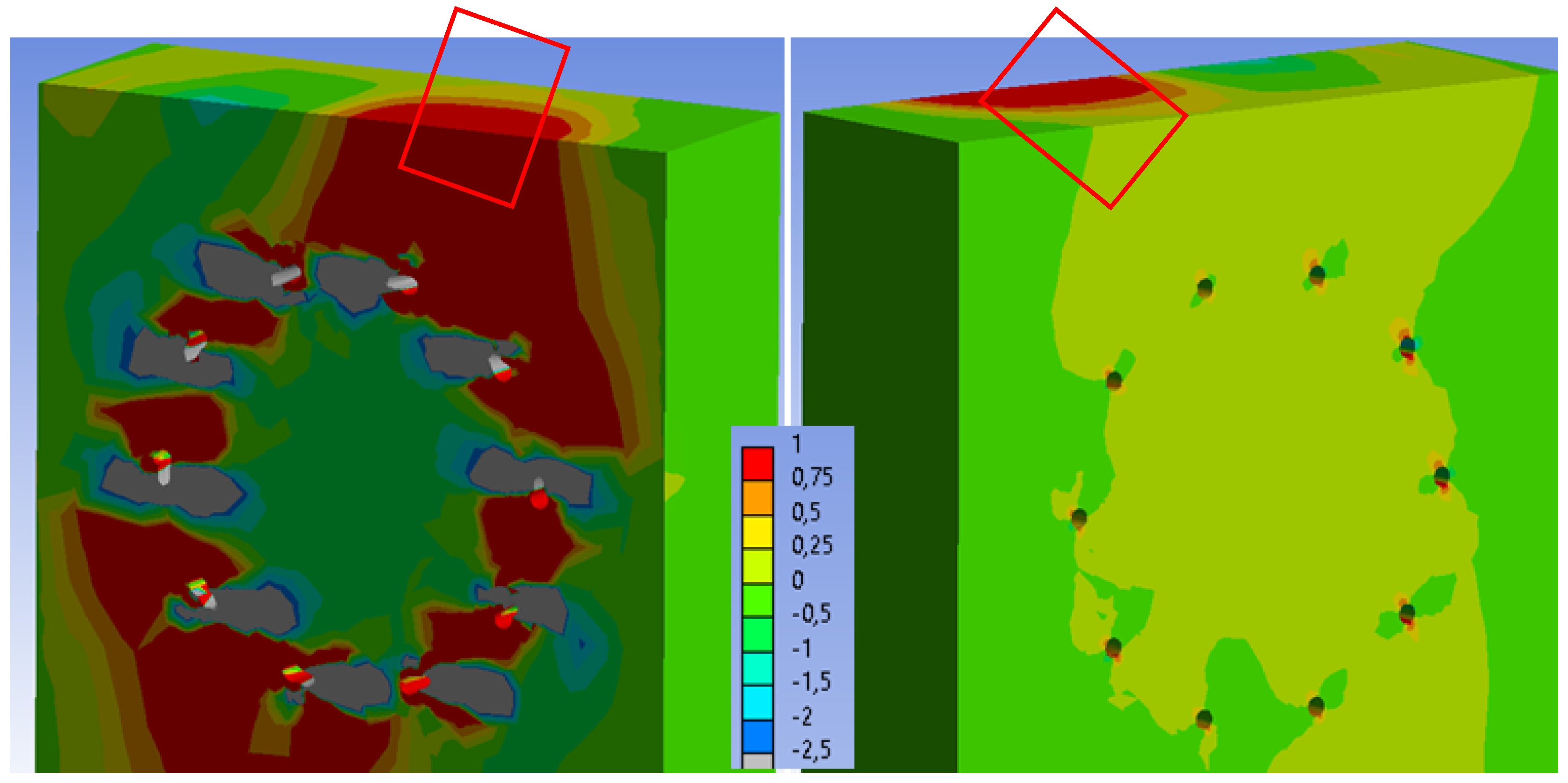

| Loading Step | Bolts and Dowels | Fully Threaded Screws | ||
|---|---|---|---|---|
| From (kN) | To (kN) | From (kN) | To (kN) | |
| Step 1 | 0 | 4.90 | 0 | 6.08 |
| Step 2 | Hold | Hold | ||
| Step 3 | 4.90 | 1.23 | 6.08 | 1.52 |
| Step 4 | Hold | Hold | ||
| Step 5 | 1.23 | 8.58 | 1.52 | 10.63 |
| Step 6 | 8.58 | 12.26 | 10.63 | 15.19 |
| Timber Properties | Value | Unit |
|---|---|---|
| Young’s modulus in X | 9200 | MPa |
| Young’s modulus in Y | 740 | MPa |
| Young’s modulus in Z | 400 | MPa |
| Poisson’s ratio in XY | 0.47 | - |
| Poisson’s ratio in YZ | 0.25 | - |
| Poisson’s ratio in XZ | 0.37 | - |
| Shear modulus in XY | 650 | MPa |
| Shear modulus in YZ | 38 | MPa |
| Shear modulus in XZ | 700 | MPa |
| Steel Properties | Value | Unit |
|---|---|---|
| Young’s modulus | 190,000 | MPa |
| Poisson’s ratio | 0.30 | - |
| Hill Yield Criterion | Value | Unit |
|---|---|---|
| Yield strength in X | 32 | MPa |
| Yield strength in Y | 1 | MPa |
| Yield strength in Z | 1 | MPa |
| Yield strength in XY | 6 | MPa |
| Yield strength in YZ | 3 | MPa |
| Yield strength in XZ | 6 | MPa |
| Bolts and Dowels | ||
| Value | Unit | |
| Yield strength | 670 | MPa |
| Ultimate strength | 970 | MPa |
| Hardening modulus | 1000 | MPa |
| Fully Threaded Screws | ||
| Value | Unit | |
| Yield strength | 690 | MPa |
| Ultimate strength | 1075 | MPa |
| Hardening modulus | 1000 | MPa |
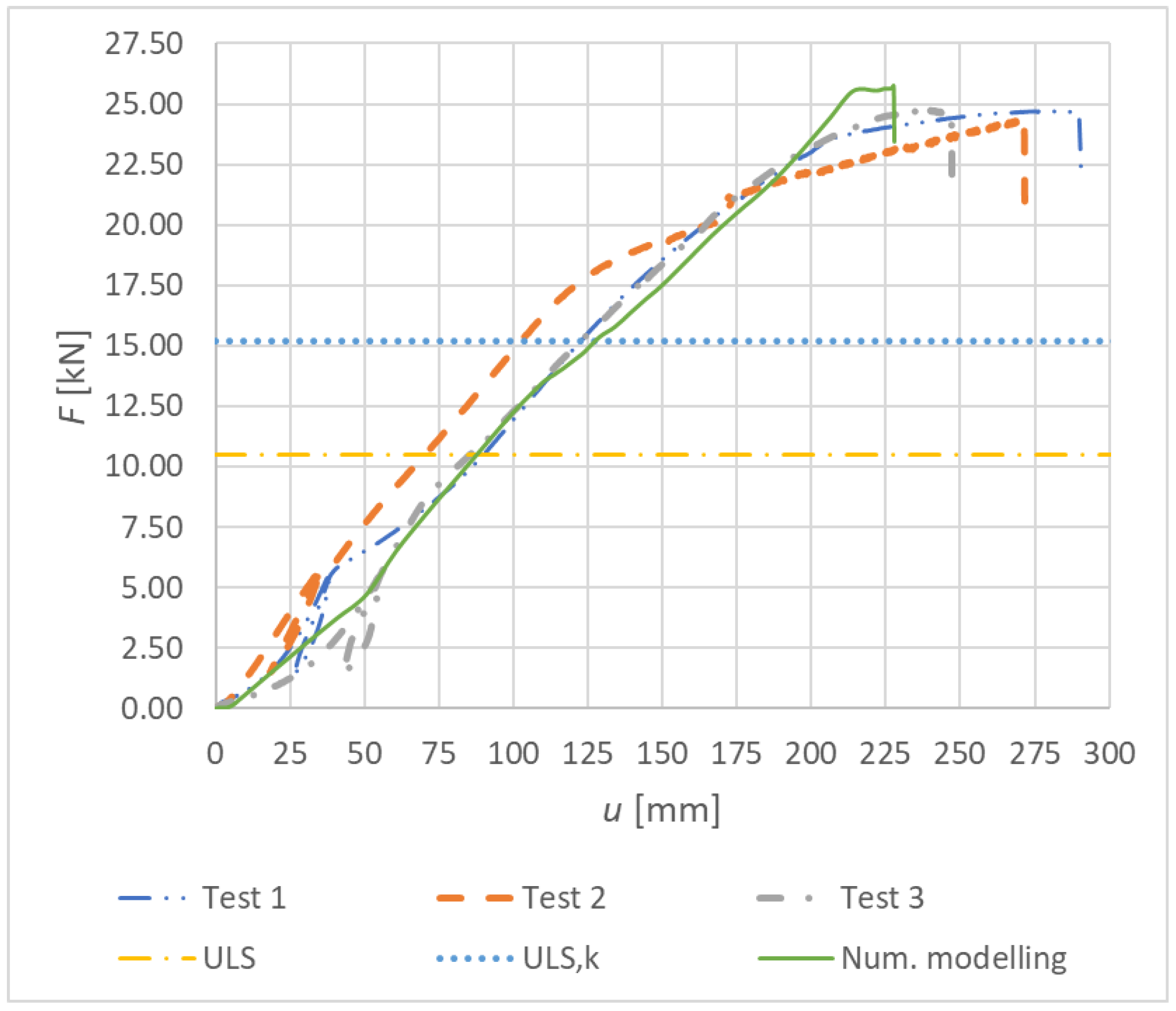
| Specimen | Fmax,test (kN) | Fmax,d (kN) | Fmax,k (kN) | d (-) | k (-) | u (mm) | M (kNm) |
|---|---|---|---|---|---|---|---|
| 1 | 22.29 | 8.51 | 12.26 | 2.62 | 1.82 | 290.60 | 17.16 |
| 2 | 21.78 | 2.56 | 1.78 | 295.67 | 16.77 | ||
| 3 | 22.02 | 2.59 | 1.80 | 283.56 | 16.96 |
| Specimen | Fmax,test (kN) | Fmax,d (kN) | Fmax,k (kN) | d (-) | k (-) | u (mm) | M (kNm) |
|---|---|---|---|---|---|---|---|
| 1 | 24.72 | 10.52 | 15.19 | 2.35 | 1.63 | 290.50 | 19.03 |
| 2 | 24.37 | 2.32 | 1.60 | 271.85 | 18.76 | ||
| 3 | 24.65 | 2.34 | 1.62 | 247.10 | 18.98 |
| Fnum (kN) | u (mm) | M (kNm) |
|---|---|---|
| 22.60 | 238.64 | 17.40 |
| Fnum (kN) | u (mm) | M (kNm) |
|---|---|---|
| 25.75 | 228.65 | 19.83 |
| Method | Specimen | u (mm) | F (kN) | M (kNm) | Difference F (%) | Difference u (%) |
|---|---|---|---|---|---|---|
| Numerical model | - | 238.4 | 22.60 | 17.40 | - | - |
| Experimental test | 1 | 290.60 | 22.29 | 17.16 | 1.40 | 17.96 |
| 2 | 295.67 | 21.78 | 16.77 | 3.76 | 19.37 | |
| 3 | 283.56 | 22.02 | 16.96 | 2.59 | 15.93 |
| Method | Specimen | u (mm) | F (kN) | M (kNm) | Difference F (%) | Difference u (%) |
|---|---|---|---|---|---|---|
| Numerical model | - | 227.80 | 25.75 | 19.83 | - | - |
| Experimental test | 1 | 290.50 | 24.72 | 19.03 | 4.20 | 21.58 |
| 2 | 271.85 | 24.37 | 18.76 | 5.70 | 16.20 | |
| 3 | 247.10 | 24.65 | 18.98 | 4.48 | 7.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johanides, M.; Lokaj, A.; Dobes, P.; Mikolasek, D. Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection. Materials 2022, 15, 7222. https://doi.org/10.3390/ma15207222
Johanides M, Lokaj A, Dobes P, Mikolasek D. Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection. Materials. 2022; 15(20):7222. https://doi.org/10.3390/ma15207222
Chicago/Turabian StyleJohanides, Marek, Antonin Lokaj, Pavel Dobes, and David Mikolasek. 2022. "Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection" Materials 15, no. 20: 7222. https://doi.org/10.3390/ma15207222
APA StyleJohanides, M., Lokaj, A., Dobes, P., & Mikolasek, D. (2022). Numerical and Experimental Analysis of the Load-Carrying Capacity of a Timber Semi-Rigid Dowel-Type Connection. Materials, 15(20), 7222. https://doi.org/10.3390/ma15207222








