Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of Tortuosity in Hexagonal Close-Packed and Face-Centered Cubic Lattices)
Abstract
:1. Introduction
2. Samples and Measuring Device Used to Measure the Sound Absorption Coefficient
2.1. Transmission Loss Measurement
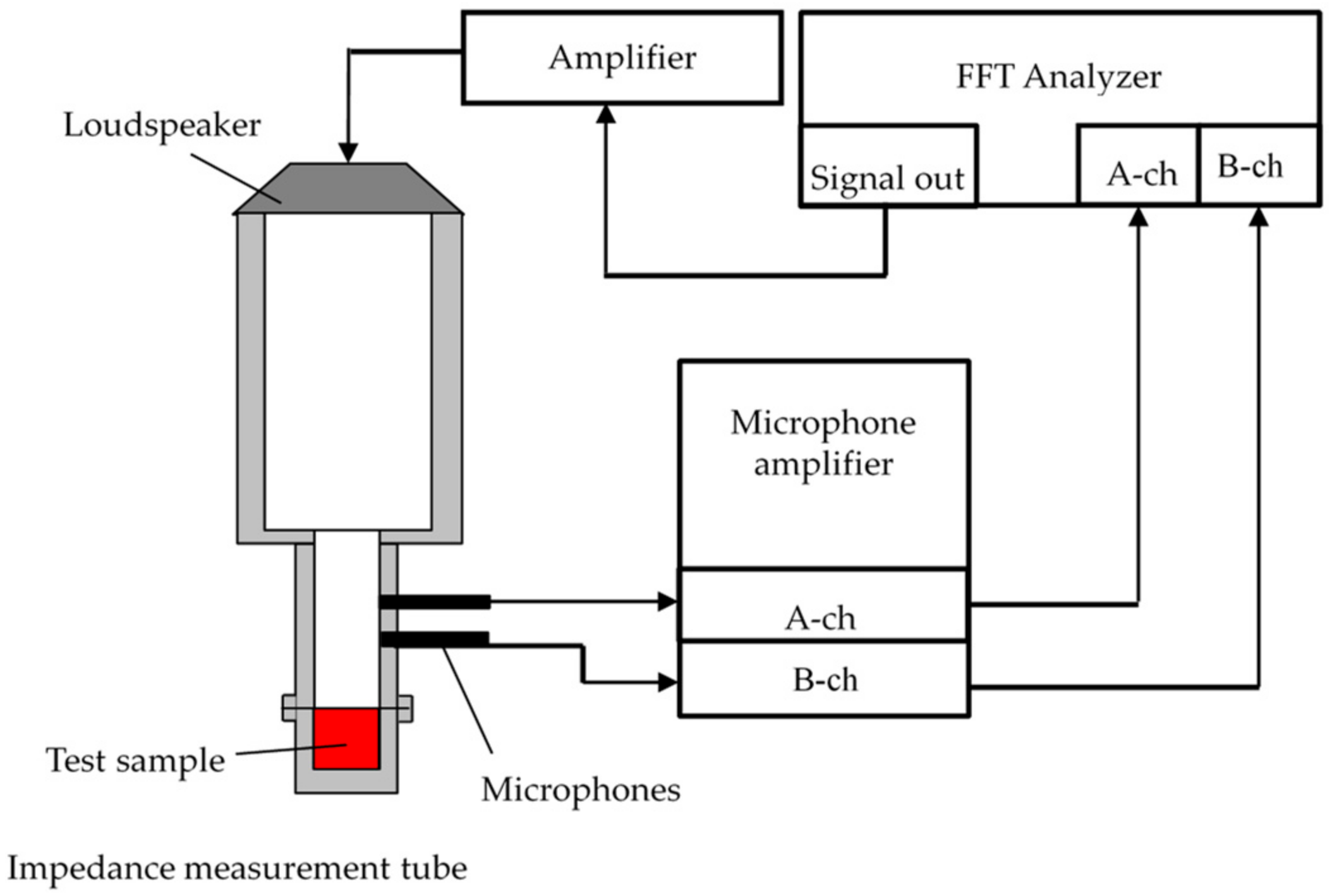
2.2. Measurement Equipment for Sound Absorption Coefficient
3. Measurement Method and Results of Tortuosity
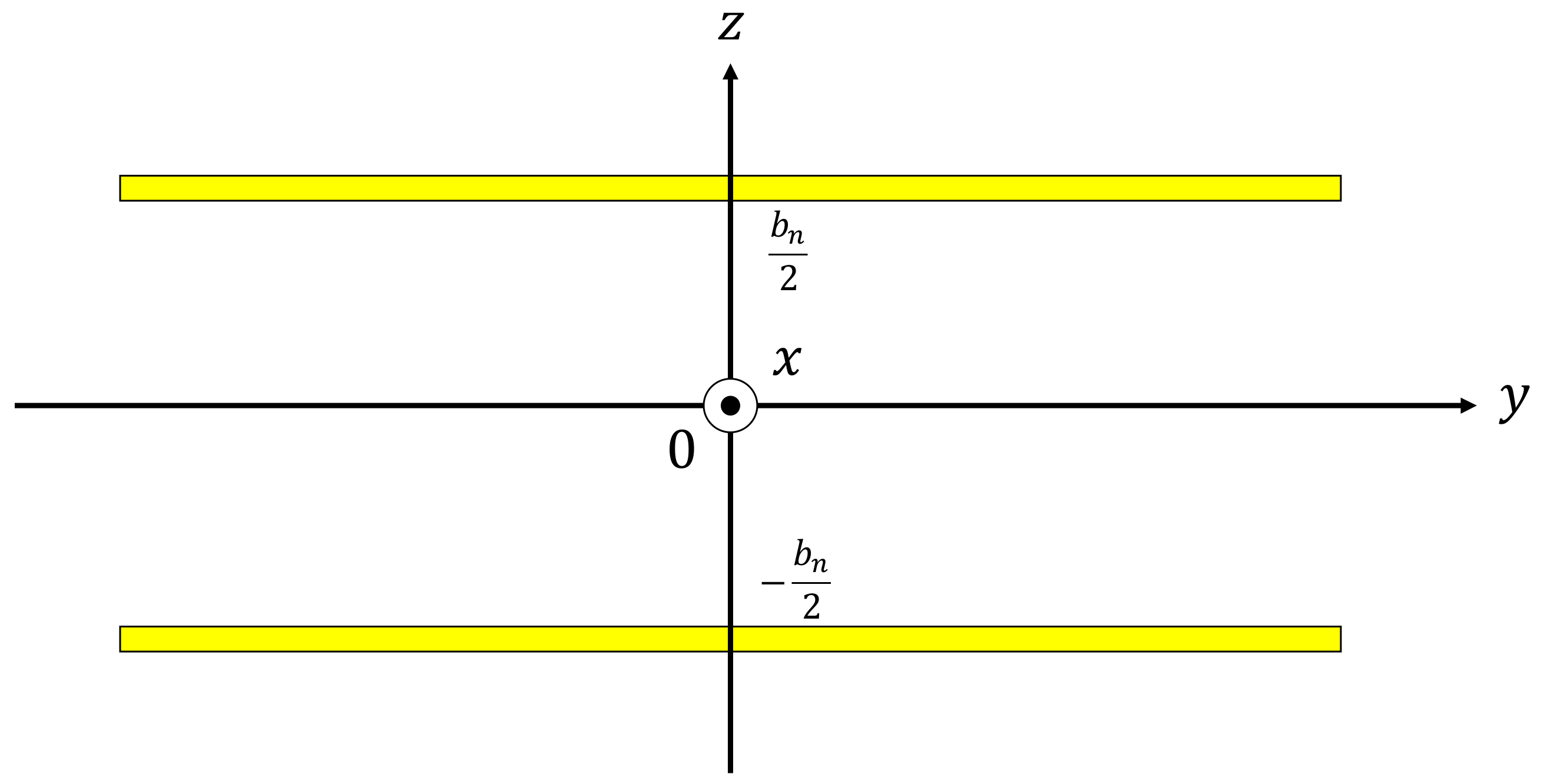
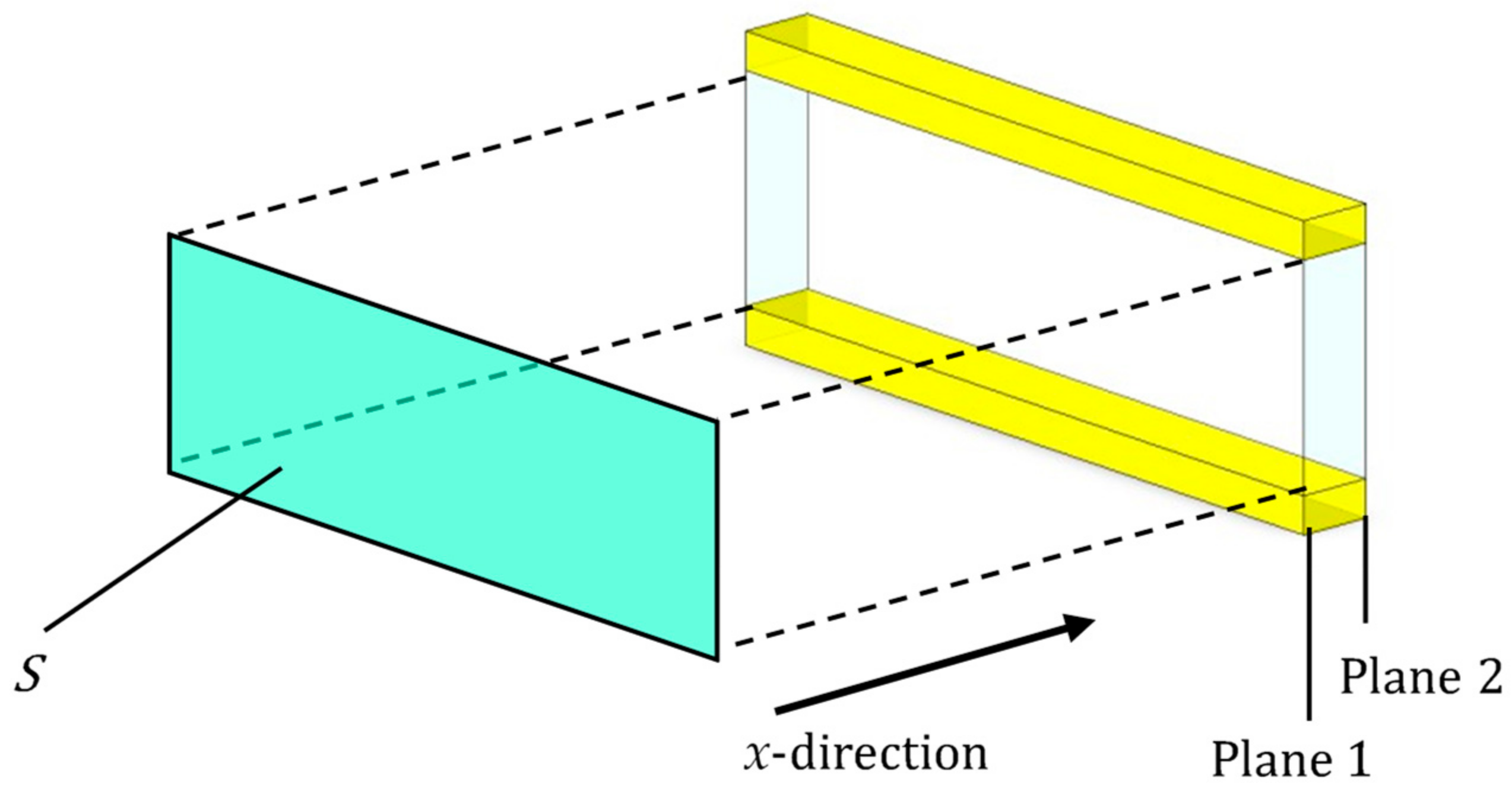
3.1. Overview of Tortuosity
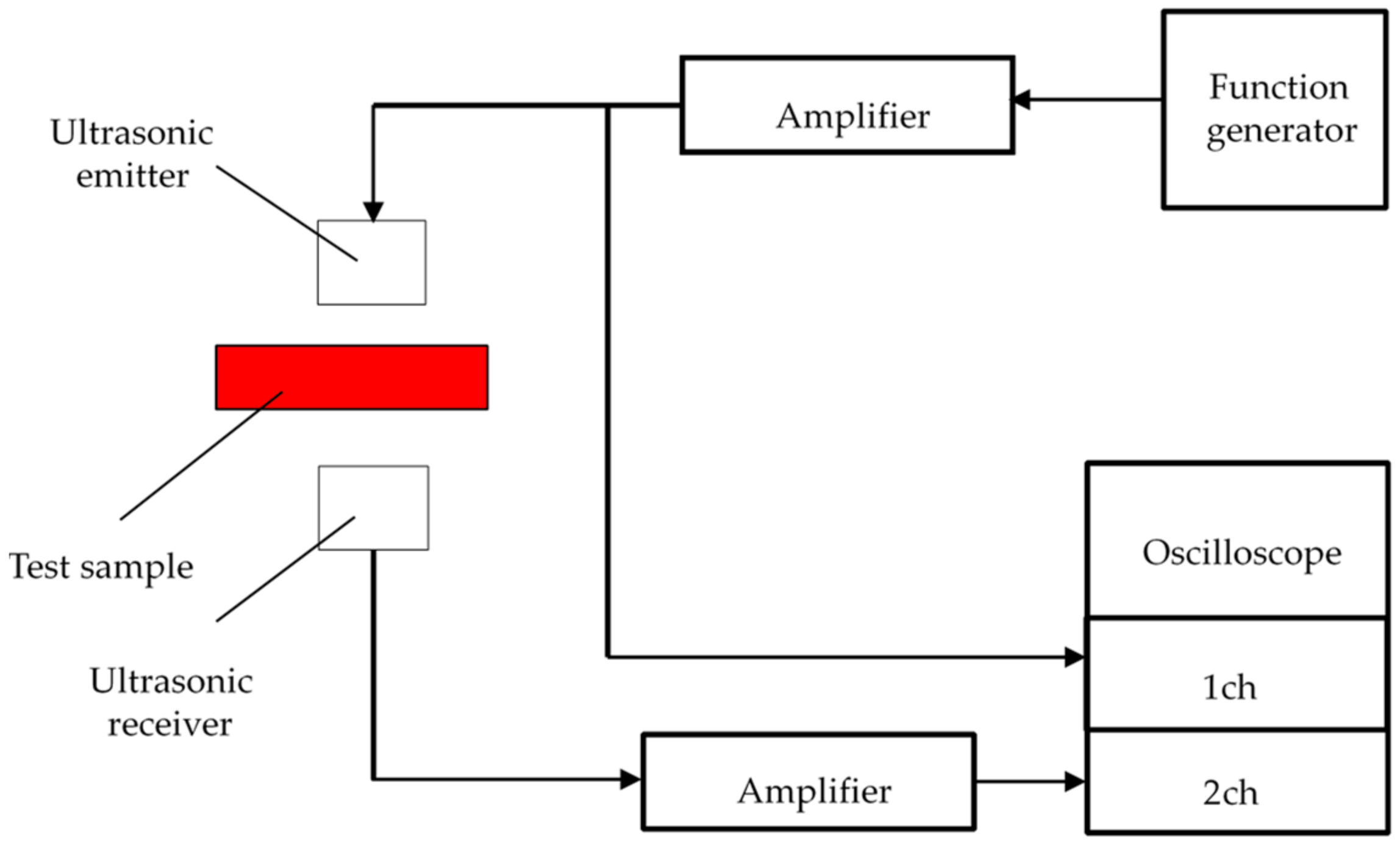
3.2. Tortuosity Measurement
4. Theoretical Analysis
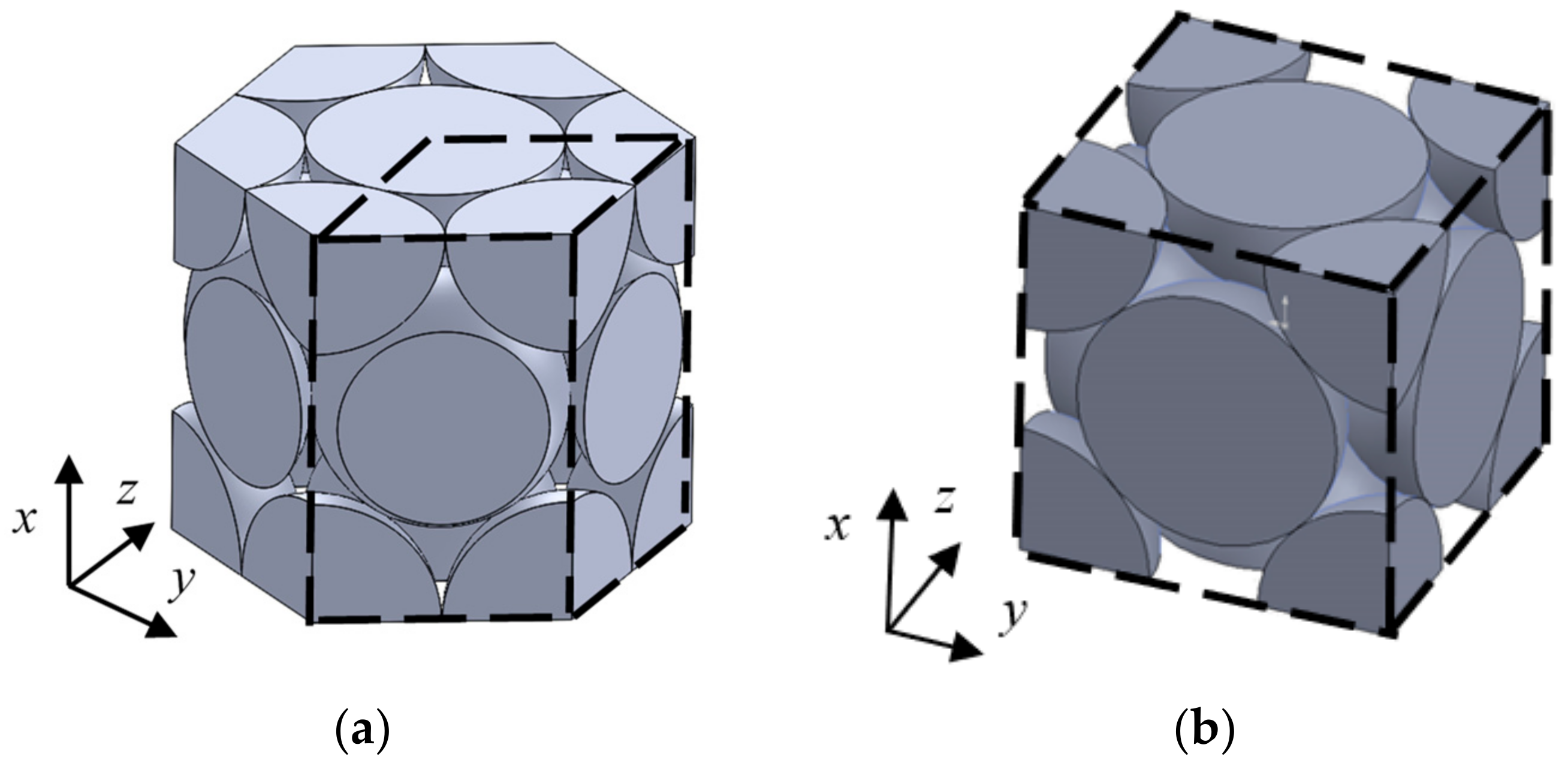
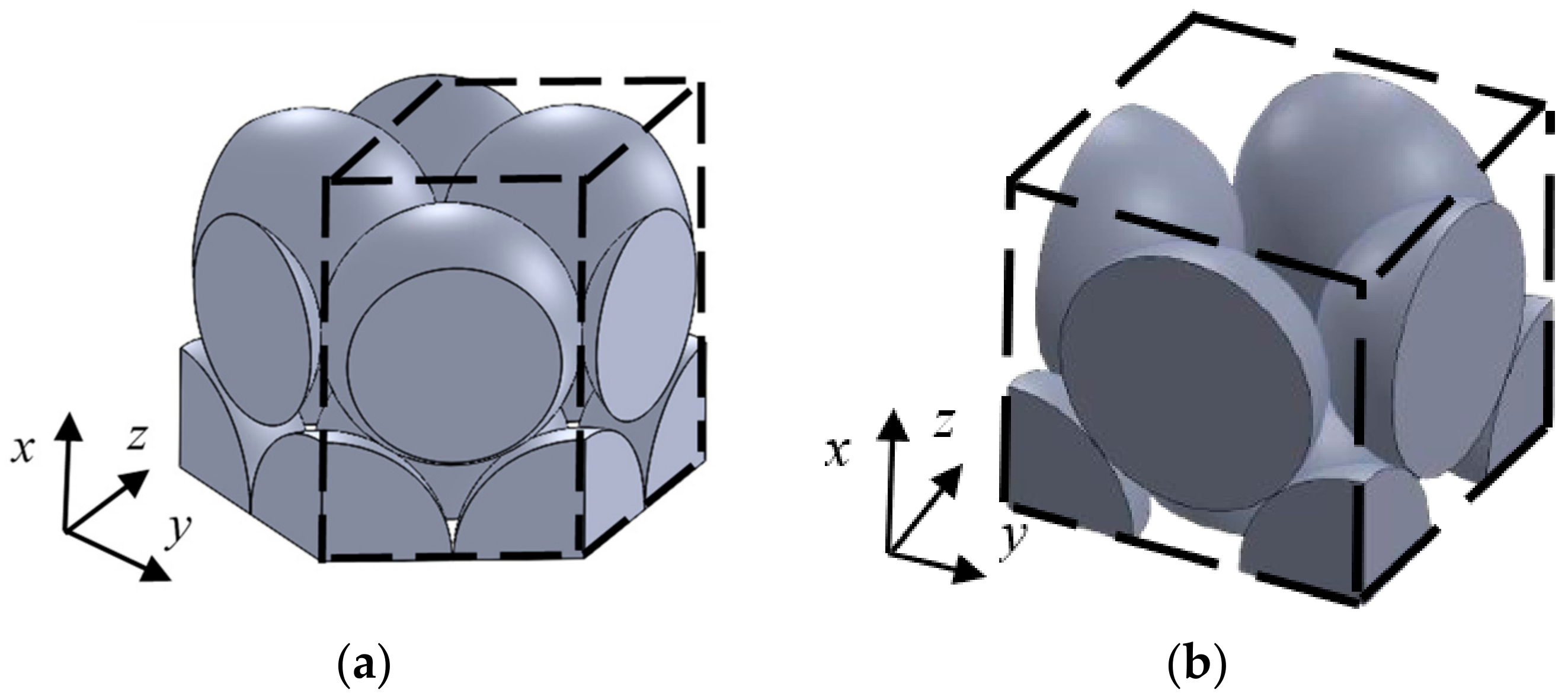
4.1. Analysis Units and Element Division
4.2. Derivation of the Surface Area of a Sphere in a Divided Element
4.3. Derivation of the Volume of the Clearance in a Divided Element
4.4. Propagation Constant and Characteristic Impedance Considering Tortuosity
4.5. Transfer Matrix
4.6. Normal Incident Sound Absorption Coefficient
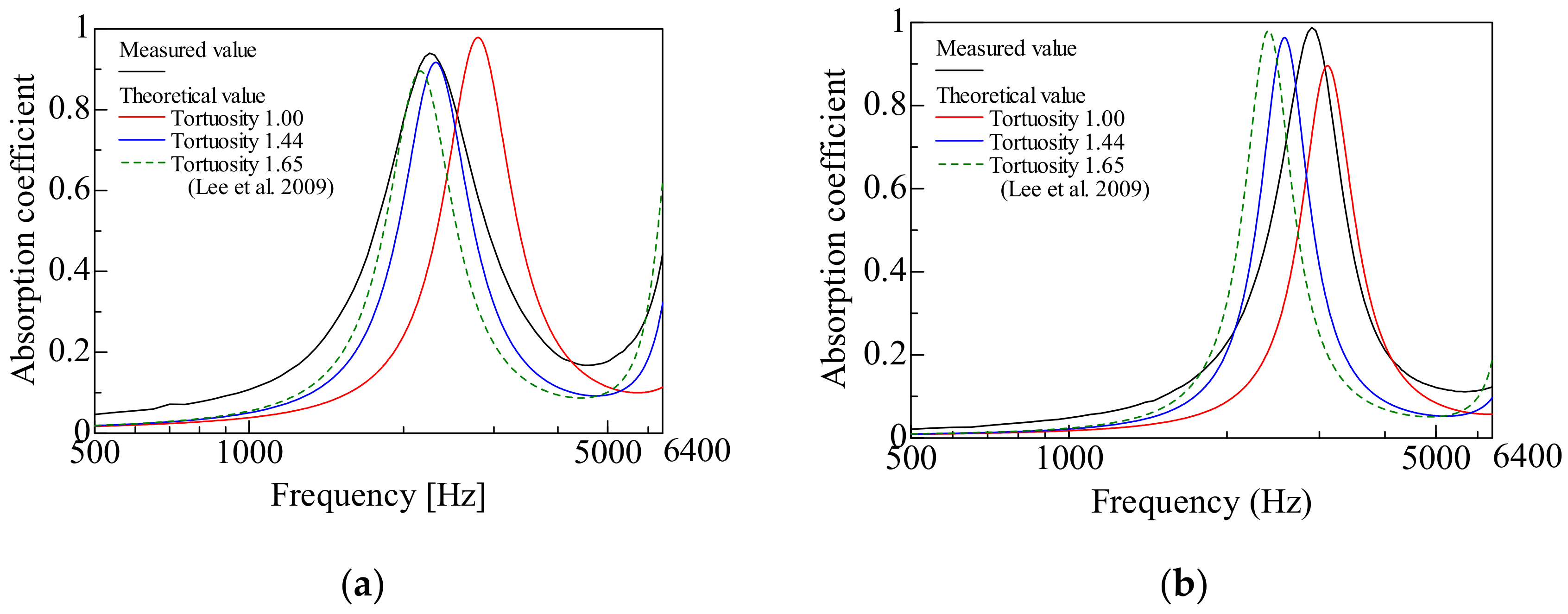
5. Comparison between Measured and Theoretical Values
6. Conclusions
- In both packing structures, the real area of the granular surface and the real volume of the clearance were obtained geometrically and analyzed theoretically.
- In both packing structures, the peak frequency tended to appear at a higher frequency than the measured value when the tortuosity was not considered.
- In the theoretical sound absorption, the peak value was higher when the tortuosity was considered compared to that without the consideration of the tortuosity (the peak frequency moved to a lower frequency). As a result, the theoretical value was becoming closer to the measured value.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Sandberg, U. Low noise road surfaces—A state-of-the-art review. J. Acoust. Soc. Jpn. 1999, 20, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Thompson, D.; Jeong, H.; Squicciarini, G. The effects of ballast on the sound radiation from railway track. J. Sound Vib. 2017, 339, 137–150. [Google Scholar] [CrossRef]
- Voronina, N.N.; Horoshenkov, K.V. A new empirical model for the acoustic properties of loose granular media. Appl. Acoust. 2003, 64, 415–432. [Google Scholar] [CrossRef]
- Gasser, S.; Paun, F.; Bréchet, Y. Absorptive properties of rigid porous media: Application to face centered cubic sphere packing. J. Acoust. Soc. Am. 2005, 117, 2090–2099. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-Y.; Leamy, M.J.; Nadler, J.H. Acoustic absorption calculation in irreducible porous media: A unified computational approach. J. Acoust. Soc. Am. 2009, 126, 1862–1870. [Google Scholar] [CrossRef] [PubMed]
- Dung, V.V.; Panneton, R.; Gagné, R. Prediction of effective properties and sound absorption of random close packings of monodisperse spherical particles: Multiscale approach. J. Acoust. Soc. Am. 2019, 145, 3606–3624. [Google Scholar] [CrossRef] [Green Version]
- Sakamoto, S.; Sakuma, Y.; Yanagimoto, K.; Watanabe, S. Basic Study for the Acoustic Characteristics of Granular Material (Normal Incidence Absorption Coefficient for Multilayer with Different Grain Diameters). J. Environ. Eng. 2012, 7, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Sakamoto, S.; Yamaguchi, K.; Ii, K.; Takakura, R.; Nakamura, Y.; Suzuki, R. Theoretical and experiment analysis on the sound absorption characteristics of a layer of fine lightweight powder. J. Acoust. Soc. Am. 2019, 146, 2253–2262. [Google Scholar] [CrossRef]
- Sakamoto, S.; Takakura, R.; Suzuki, R.; Katayama, I.; Saito, R.; Suzuki, K. Theoretical and Experimental Analyses of Acoustic Characteristics of Fine-grain Powder Considering Longitudinal Vibration and Boundary Layer Viscosity. J. Acoust. Soc. Am. 2021, 149, 1030–1040. [Google Scholar] [CrossRef]
- Sakamoto, S.; Ii, K.; Katayama, I.; Suzuki, K. Measurement and Theoretical Analysis of Sound Absorption of Simple Cubic and Hexagonal Lattice Granules. Noise Control Eng. J. 2021, 69, 401–410. [Google Scholar] [CrossRef]
- Allard, J.F.; Castagnede, B.; Henry, M. Evaluation of tortuosity in acoustic porous materials saturated by air. Rev. Sci. Instrum. 1994, 65, 754. [Google Scholar] [CrossRef] [Green Version]
- Tijdeman, H. On the propagation of sound waves in cylindrical tubes. J. Sound Vib. 1975, 39, 1–33. [Google Scholar] [CrossRef]
- Stinson, M.R. The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape. J. Acoust. Soc. Am. 1991, 89, 550–558. [Google Scholar] [CrossRef]
- Stinson, M.R.; Champou, Y. Propagation of sound and the assignment of shape factors in model porous materials having simple pore geometries. J. Acoust. Soc. Am. 1992, 91, 685–695. [Google Scholar] [CrossRef]
- Beltman, W.M.; van der Hoogt, P.J.M.; Spiering, R.M.E.J.; Tijdeman, H. Implementation and experimental validation of a new viscothermal acoustic finite element for acousto-elastic problems. J. Sound Vib. 1998, 216, 159–185. [Google Scholar] [CrossRef]
- Allard, J.F. Propagation of sound in Porous Media Modeling Sound Absorbing Materials. J. Acoust. Soc. Am. 1994, 95, 2785. [Google Scholar] [CrossRef] [Green Version]
- Tabana, E.; Khavanina, A.; Jafarib, A.J.; Faridanc, M.; Tabrizid, A.K. Experimental and mathematical survey of sound absorption performance of date palm fibers. Heliyon 2019, 5, e01977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duan, C.; Cui, G.; Xu, X.; Liu, P. Sound absorption characteristics of a high-temperature sintering porous ceramic material. Appl. Acoust. 2012, 73, 865–871. [Google Scholar] [CrossRef]
- Sakamoto, S.; Higuchi, K.; Saito, K.; Koseki, S. Theoretical analysis for sound-absorbing materials using layered narrow clearances between two planes. J. Adv. Mech. Des. Syst. Manuf. 2014, 8, 16. [Google Scholar] [CrossRef] [Green Version]






| Packing Structure | Diameter [mm] | Length [mm] | Aperture Ratio of Sample Holder | Filling Rate | Measured Tortuosity | Correspondence to Figure |
|---|---|---|---|---|---|---|
| Hexagonal close-packed | 4 | 27 | 0.57 | 0.74 | 1.44 | 1a |
| 8 | 27 | 0.67 | 0.74 | 1.44 | 1b | |
| Face-centered cubic | 4 | 22 | 0.58 | 0.74 | 1.43 | 1c |
| 8 | 21 | 0.85 | 0.74 | 1.43 | 1d |
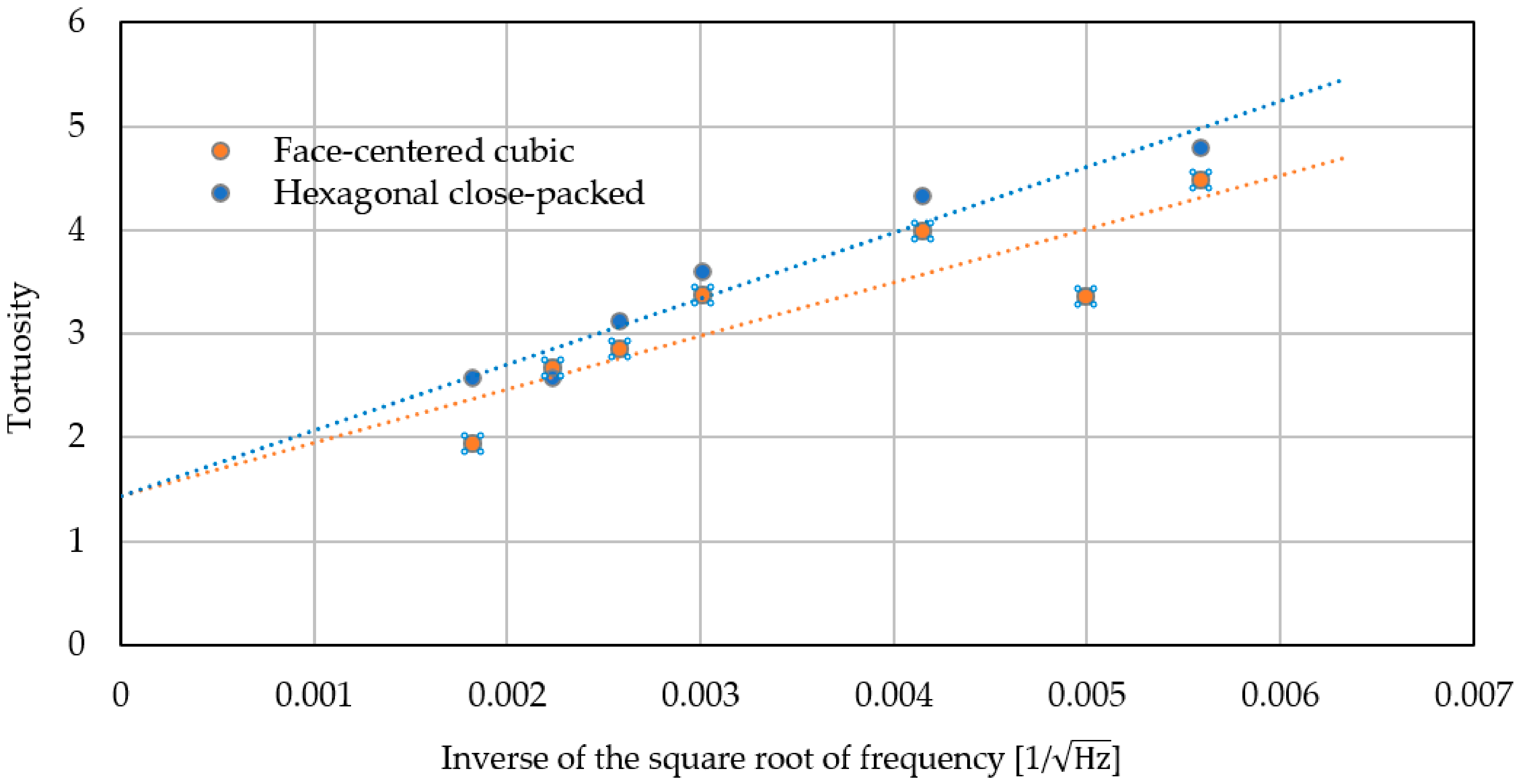
| Frequency [kHz] | Inverse of the Square Root of Frequency | Distance between Sensors [mm] | Transmission Time [ms] | Tortuosity | |
|---|---|---|---|---|---|
| Hexagonal Close-Packed | Face-Centered Cubic | ||||
| 32.7 | 0.00559 | 395 | 1.229 | 4.78 | 4.48 |
| 40 | 0.005 | 395 | - | - | 3.35 |
| 58 | 0.004152 | 395 | 1.199 | 4.31 | 3.98 |
| 110 | 0.003015 | 345 | 1.044 | 3.59 | 3.36 |
| 150 | 0.002582 | 204 | 0.626 | 3.11 | 2.84 |
| 200 | 0.002236 | 204 | 0.618 | 2.56 | 2.67 |
| 300 | 0.001826 | 204 | 0.615 | 2.56 | 1.93 |
| ∞ | 0 | - | - | 1.44 | 1.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of Tortuosity in Hexagonal Close-Packed and Face-Centered Cubic Lattices). Materials 2022, 15, 7393. https://doi.org/10.3390/ma15207393
Sakamoto S, Suzuki K, Toda K, Seino S. Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of Tortuosity in Hexagonal Close-Packed and Face-Centered Cubic Lattices). Materials. 2022; 15(20):7393. https://doi.org/10.3390/ma15207393
Chicago/Turabian StyleSakamoto, Shuichi, Kyosuke Suzuki, Kentaro Toda, and Shotaro Seino. 2022. "Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of Tortuosity in Hexagonal Close-Packed and Face-Centered Cubic Lattices)" Materials 15, no. 20: 7393. https://doi.org/10.3390/ma15207393
APA StyleSakamoto, S., Suzuki, K., Toda, K., & Seino, S. (2022). Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of Tortuosity in Hexagonal Close-Packed and Face-Centered Cubic Lattices). Materials, 15(20), 7393. https://doi.org/10.3390/ma15207393






