Pressure-Tuning Superconductivity in Noncentrosymmetric Topological Materials ZrRuAs
Abstract
:1. Introduction
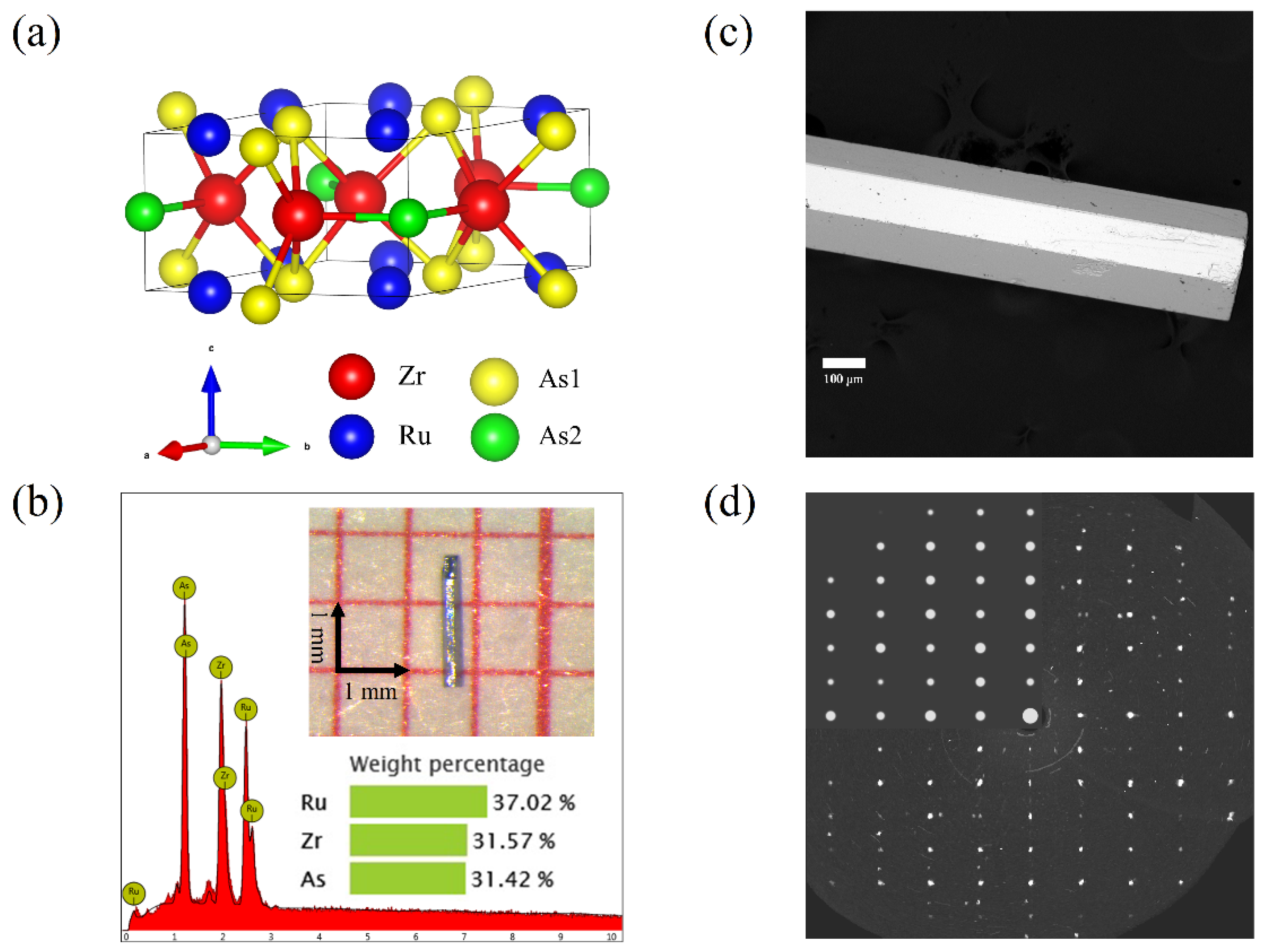
2. Experimental Detail
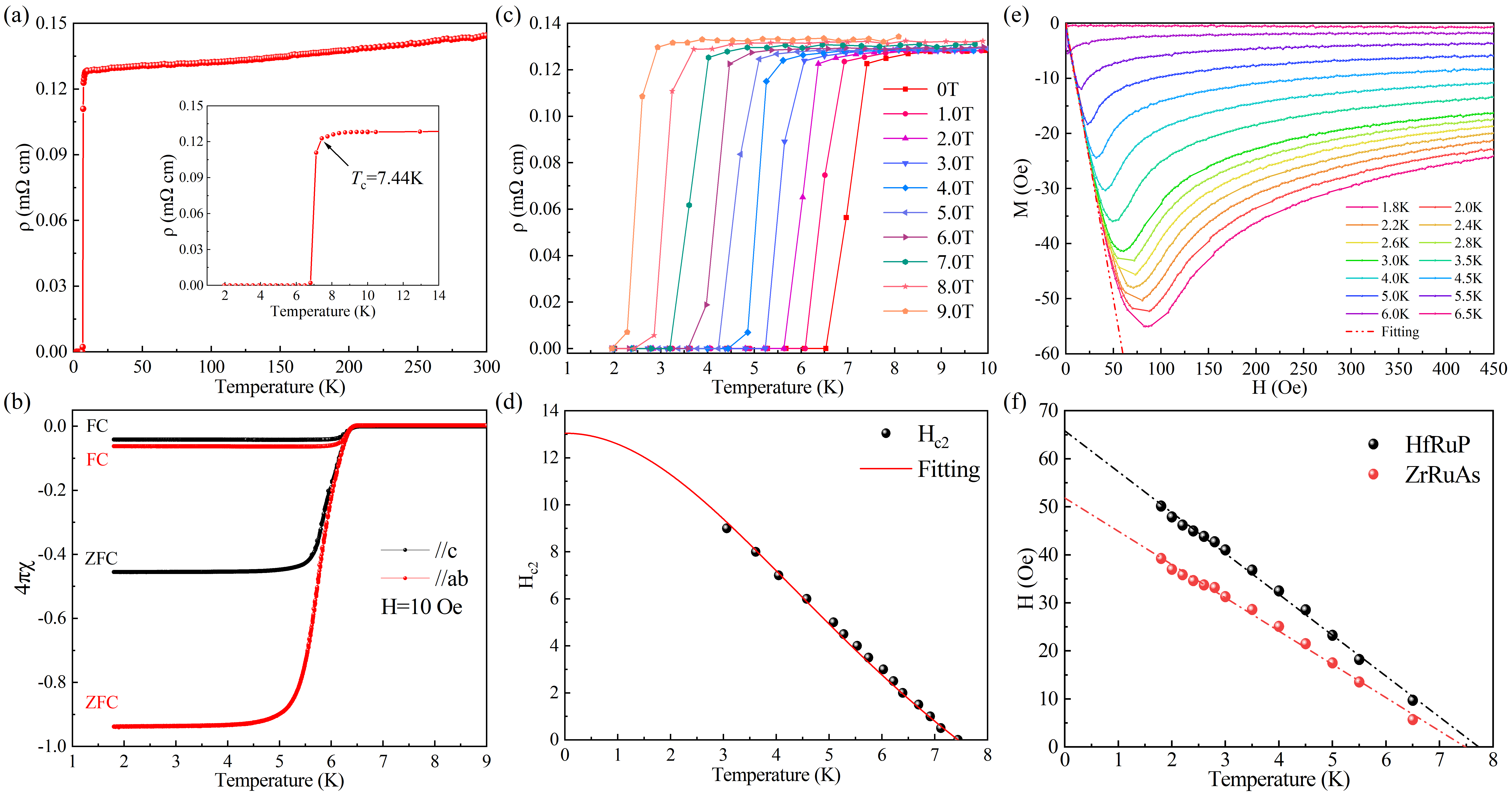
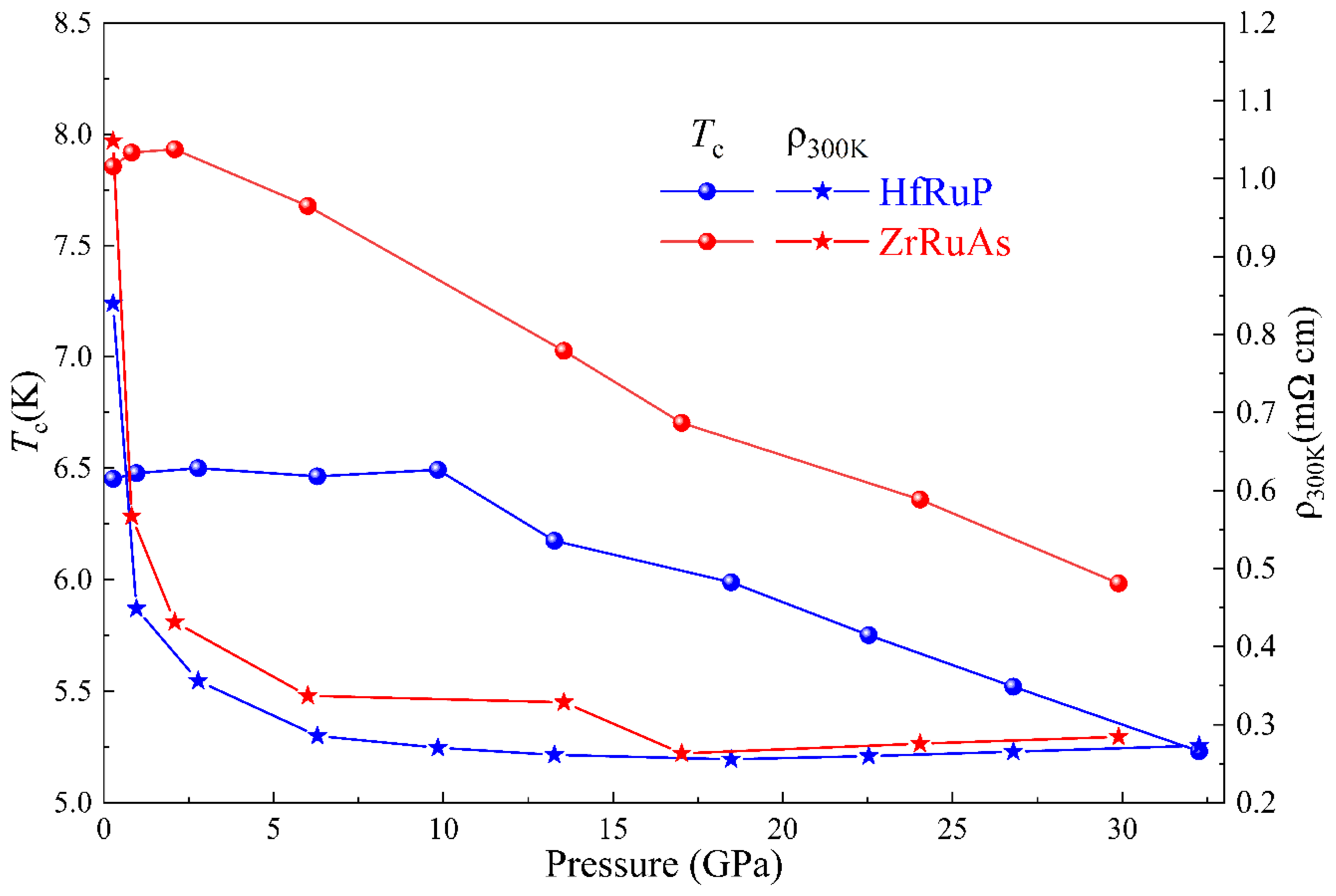
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef] [Green Version]
- Chiu, C.-K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Vanderbilt, D. Weyl semimetals from noncentrosymmetric topological insulators. Phys. Rev. B 2014, 90, 155316. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.X.; Wu, Z.; Wang, J.H.; Ye, Z.Y.; Gong, J.; Hou, X.Y.; Shan, L.; Li, A.; Liang, X.J.; Wu, X.X.; et al. Observation of a robust zero-energy bound state in iron-based superconductor Fe(Te,Se). Nat. Phys. 2015, 11, 543–546. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, P.; Xu, G.; Zeng, L.K.; Miao, H.; Xu, X.; Qian, T.; Weng, H.; Richard, P.; Fedorov, A.V.; et al. Topological nature of theFeSe0.5Te0.5superconductor. Phys. Rev. B 2015, 92, 115119. [Google Scholar] [CrossRef] [Green Version]
- Vancliff Johnson, W.J. Ternary Equiatomic Transition Metal Silicides and Germanides. J. Solid State Chem. 1972, 4, 123–130. [Google Scholar] [CrossRef]
- Qian, Y.; Nie, S.; Yi, C.; Kong, L.; Fang, C.; Qian, T.; Ding, H.; Shi, Y.; Wang, Z.; Weng, H.; et al. Topological electronic states in HfRuP family superconductors. Npj Comput. Mater. 2019, 5, 121. [Google Scholar] [CrossRef] [Green Version]
- Das, D.; Adroja, D.T.; Lees, M.R.; Taylor, R.W.; Bishnoi, Z.S.; Anand, V.K.; Bhattacharyya, A.; Guguchia, Z.; Baines, C.; Luetkens, H.; et al. Probing the superconducting gap structure in the noncentrosymmetric topological superconductor ZrRuAs. Phys. Rev. B 2021, 103, 144516. [Google Scholar] [CrossRef]
- Barz, H.; Ku, H.C.; Meisner, G.P.; Fisk, Z.; Matthias, B.T. Ternary transition metal phosphides: High-temperature superconductors. Proc. Natl. Acad. Sci. USA 1980, 77, 3. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, J.; Gong, C.; Wang, Q.; Gao, L.; Zhao, Y.; Tian, S.; Cao, W.; Li, C.; Lu, Z.-Y.; et al. Distinct superconducting behaviors of pressurized WB2 and ReB2 with different local B layers. Sci. China Phys. Mech. Astron. 2022, 65, 287412. [Google Scholar] [CrossRef]
- Cao, W.; Zhao, N.; Pei, C.; Wang, Q.; Zhang, Q.; Ying, T.; Zhao, Y.; Gao, L.; Li, C.; Yu, N.; et al. Pressure-induced superconductivity in the noncentrosymmetric Weyl semimetals LaAlX (X = Si,Ge). Phys. Rev. B 2022, 105, 174502. [Google Scholar] [CrossRef]
- Pei, C.; Ying, T.; Zhao, Y.; Gao, L.; Cao, W.; Li, C.; Hosono, H.; Qi, Y. Pressure-induced reemergence of superconductivity in BaIr2Ge7 and Ba3Ir4Ge16 with cage structures. Matter Radiat. Extrem. 2022, 7, 038404. [Google Scholar] [CrossRef]
- Pei, C.; Ying, T.; Zhang, Q.; Wu, X.; Yu, T.; Zhao, Y.; Gao, L.; Li, C.; Cao, W.; Zhang, Q.; et al. Caging-Pnictogen-Induced Superconductivity in Skutterudites IrX3 (X = As, P). J. Am. Chem. Soc. 2022, 144, 6208–6214. [Google Scholar] [CrossRef]
- Wang, Q.; Kong, P.; Shi, W.; Pei, C.; Wen, C.; Gao, L.; Zhao, Y.; Yin, Q.; Wu, Y.; Li, G.; et al. Charge Density Wave Orders and Enhanced Superconductivity under Pressure in the Kagome Metal CsV3 Sb5. Adv. Mater. 2021, 33, e2102813. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Gresch, D.; Autès, G.; Yazyev, O.V.; Troyer, M.; Vanderbilt, D.; Bernevig, B.A.; Soluyanov, A.A. Z2Pack: Numerical implementation of hybrid Wannier centers for identifying topological materials. Phys. Rev. B 2017, 95, 064302. [Google Scholar] [CrossRef] [Green Version]
- Bennemann, K.H.; Ketterson, J.B. Superconductivity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mao, H.K.; Chen, X.J.; Ding, Y.; Li, B.; Wang, L. Solids, liquids, and gases under high pressure. Rev. Mod. Phys. 2018, 90, 015007. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Dong, Z.-Y.; Hsieh, W.-P.; Goncharov, A.F.; Chen, X.-J. Thermal conductivity of materials under pressure. Nat. Rev. Phys. 2022, 4, 319–335. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef]
- Kong, P.; Minkov, V.S.; Kuzovnikov, M.A.; Drozdov, A.P.; Besedin, S.P.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S.; et al. Superconductivity up to 243 K in the yttrium-hydrogen system under high pressure. Nat. Commun. 2021, 12, 5075. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Wang, L.; Hu, Q.; Zhao, J.; Yan, S.; Yang, K.; Sinogeikin, S.; Gu, G.; Mao, H.K. Structural phase transitions in Bi2Se3 under high pressure. Sci. Rep. 2015, 5, 15939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moriwaki, T.; Akahama, Y.; Kawamura, H.; Nakano, S.; Takemura, K. Structural Phase Transition of Rutile-Type MgH2 at High Pressures. J. Phys. Soc. Jpn. 2006, 75, 074603. [Google Scholar] [CrossRef]
- Sato, M.; Fujimoto, S. Topological phases of noncentrosymmetric superconductors: Edge states, Majorana fermions, and non-Abelian statistics. Phys. Rev. B 2009, 79, 094504. [Google Scholar] [CrossRef] [Green Version]
- Fujimoto, S. Topological order and non-Abelian statistics in noncentrosymmetrics-wave superconductors. Phys. Rev. B 2008, 77, 220501. [Google Scholar] [CrossRef] [Green Version]
- Pei, C.; Jin, S.; Huang, P.; Vymazalova, A.; Gao, L.; Zhao, Y.; Cao, W.; Li, C.; Nemes-Incze, P.; Chen, Y.; et al. Pressure-induced superconductivity and structure phase transition in Pt2HgSe3. Npj Quantum Mater. 2021, 6, 98. [Google Scholar] [CrossRef]
- Meisner, G.P.; Ku, H.C.; Barz, H. Superconducting equiatomic ternary transition metal arsenides. Mater. Res. Bull. 1983, 18, 983–991. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Lin, H.; Liu, J.; Duan, W.; Bansil, A.; Fu, L. Topological crystalline insulators in the SnTe material class. Nat. Commun. 2012, 3, 982. [Google Scholar] [CrossRef]

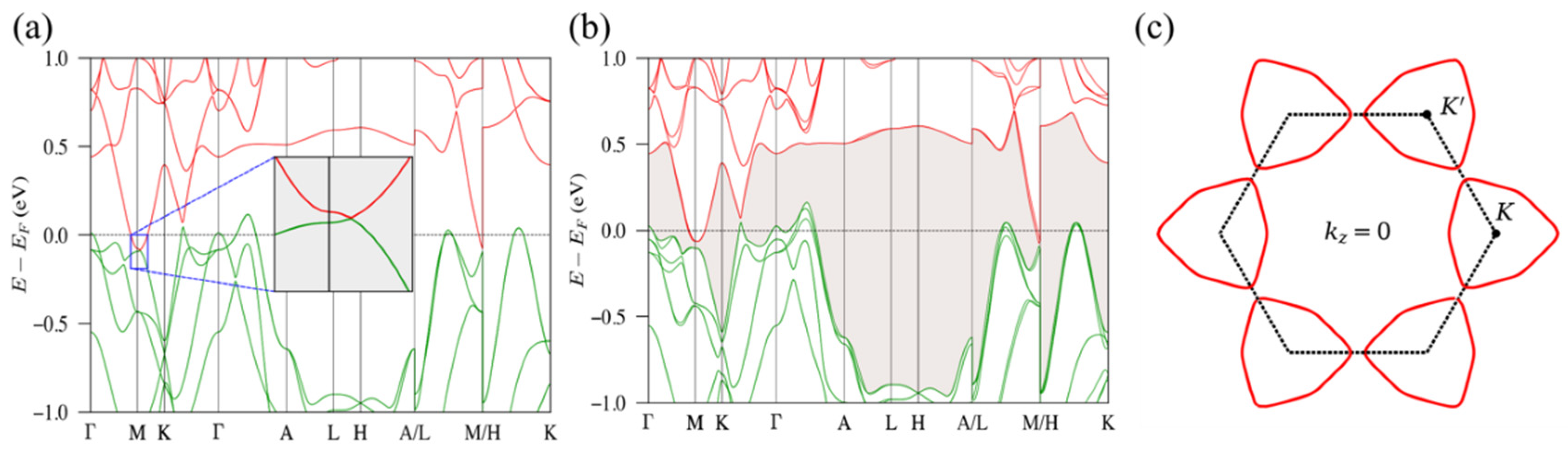
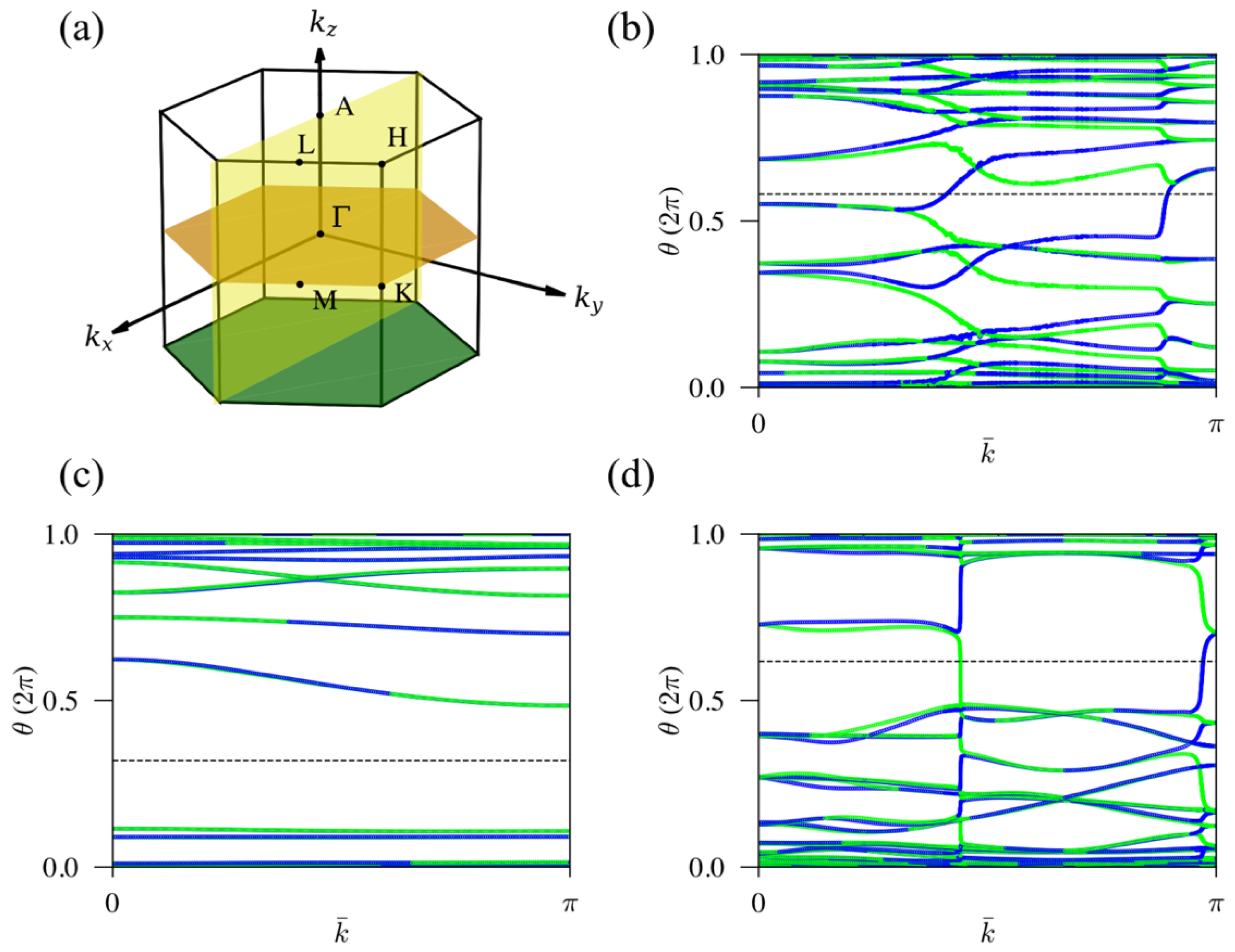
| Pressure (GPa) | 0.3 | 0.9 | 2.1 | 6.0 | 13.5 | 17.1 | 24.0 | 29.8 |
|---|---|---|---|---|---|---|---|---|
| CM (kz = 0) | 2 | −2 | 2 | −2 | 2 | 2 | 2 | 2 |
| CM (ky = 0) | 2 | −2 | −2 | 2 | 2 | −2 | −2 | −2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Su, Y.; Zhang, C.; Pei, C.; Cao, W.; Wang, Q.; Zhao, Y.; Gao, L.; Zhu, S.; Zhang, M.; et al. Pressure-Tuning Superconductivity in Noncentrosymmetric Topological Materials ZrRuAs. Materials 2022, 15, 7694. https://doi.org/10.3390/ma15217694
Li C, Su Y, Zhang C, Pei C, Cao W, Wang Q, Zhao Y, Gao L, Zhu S, Zhang M, et al. Pressure-Tuning Superconductivity in Noncentrosymmetric Topological Materials ZrRuAs. Materials. 2022; 15(21):7694. https://doi.org/10.3390/ma15217694
Chicago/Turabian StyleLi, Changhua, Yunlong Su, Cuiwei Zhang, Cuiying Pei, Weizheng Cao, Qi Wang, Yi Zhao, Lingling Gao, Shihao Zhu, Mingxin Zhang, and et al. 2022. "Pressure-Tuning Superconductivity in Noncentrosymmetric Topological Materials ZrRuAs" Materials 15, no. 21: 7694. https://doi.org/10.3390/ma15217694





