Cross-Sectional Profile Evolution of Cu-Ti Gradient Films on C17200 Cu by Vacuum Thermal Diffusion
Abstract
1. Introduction
2. Materials and Experiments
3. Modeling and Calculation
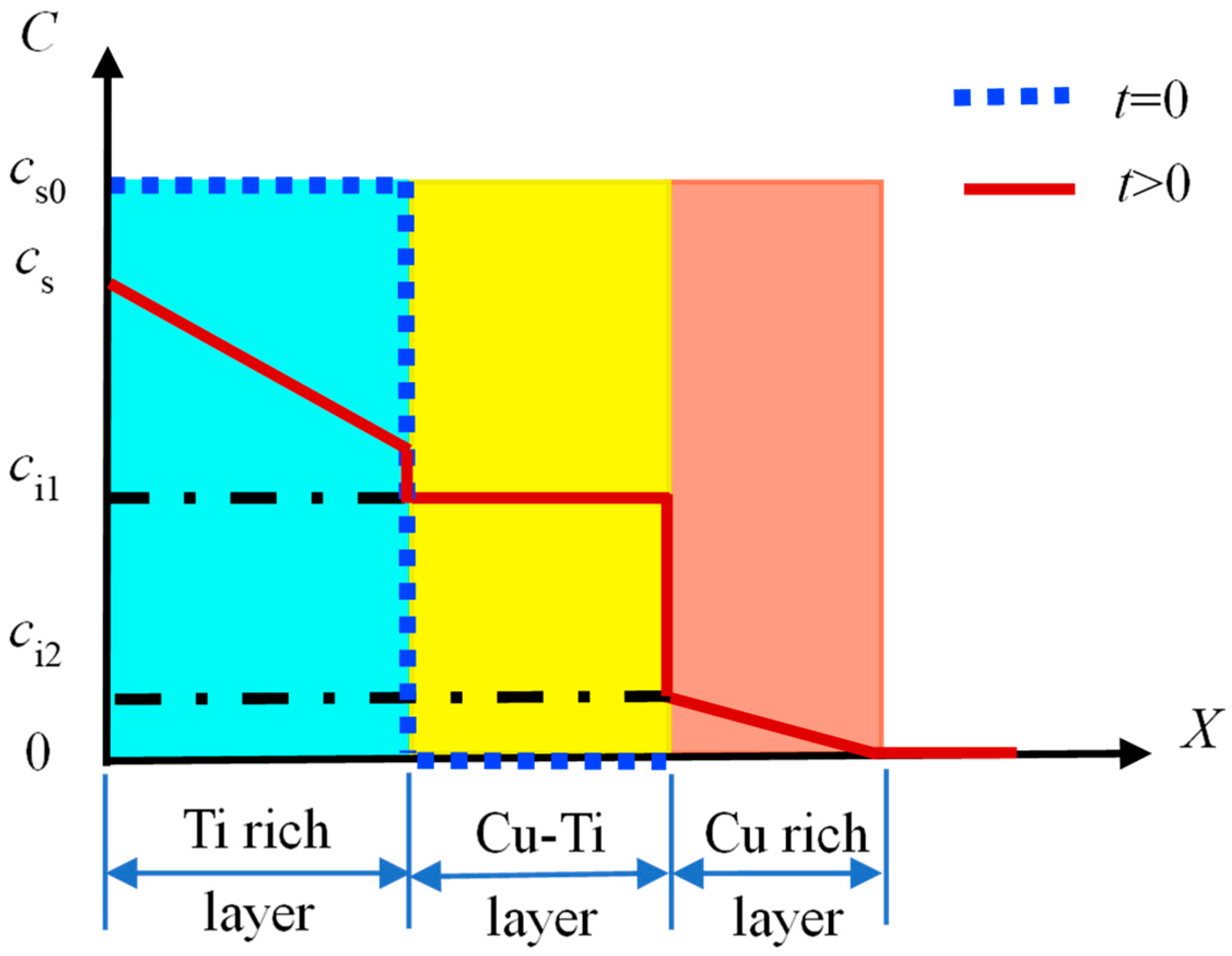
3.1. Assumption and Basic Theory
- (1)
- Only the diffusion of Ti elements is considered as the titanium atoms diffuse faster than copper atoms in this alloy [23], and the influence of alloying elements is neglected;
- (2)
- As the thickness of the multi-phase coating layer is much smaller than the sample during the Ti diffusion process, the process can be regarded as a diffusion problem in a one-dimensional and semi-infinite space;
- (3)
- The internal temperature of the sample is uniform and constant during the thermal diffusion process;
- (4)
- The Ti content in the Ti-rich layer changes linearly with time.
3.2. Mathematical Modeling and the Ti Atom Distribution in the Diffusion Process
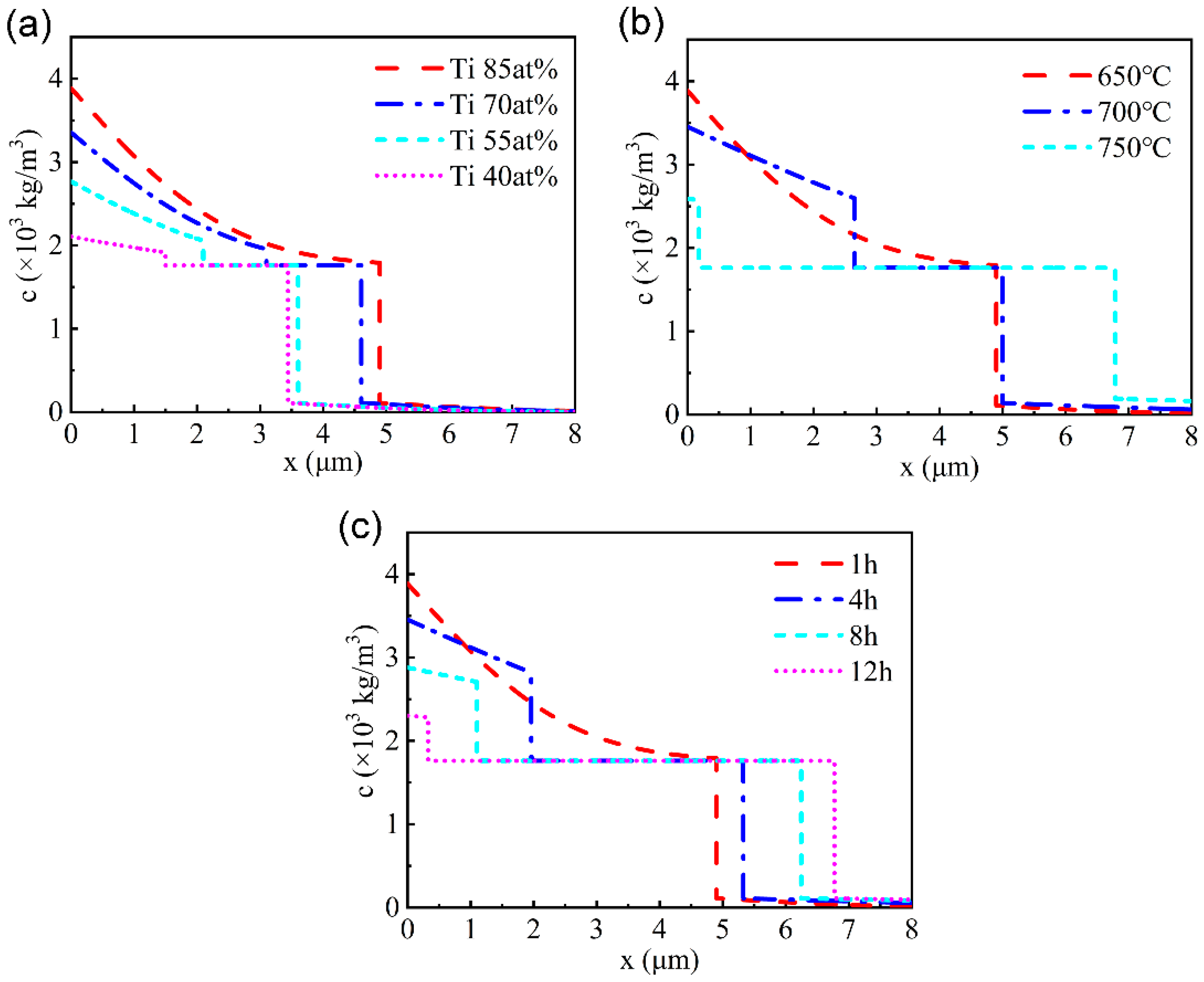
3.3. Simulation of Ti Concentration Distribution in the Modified Layer
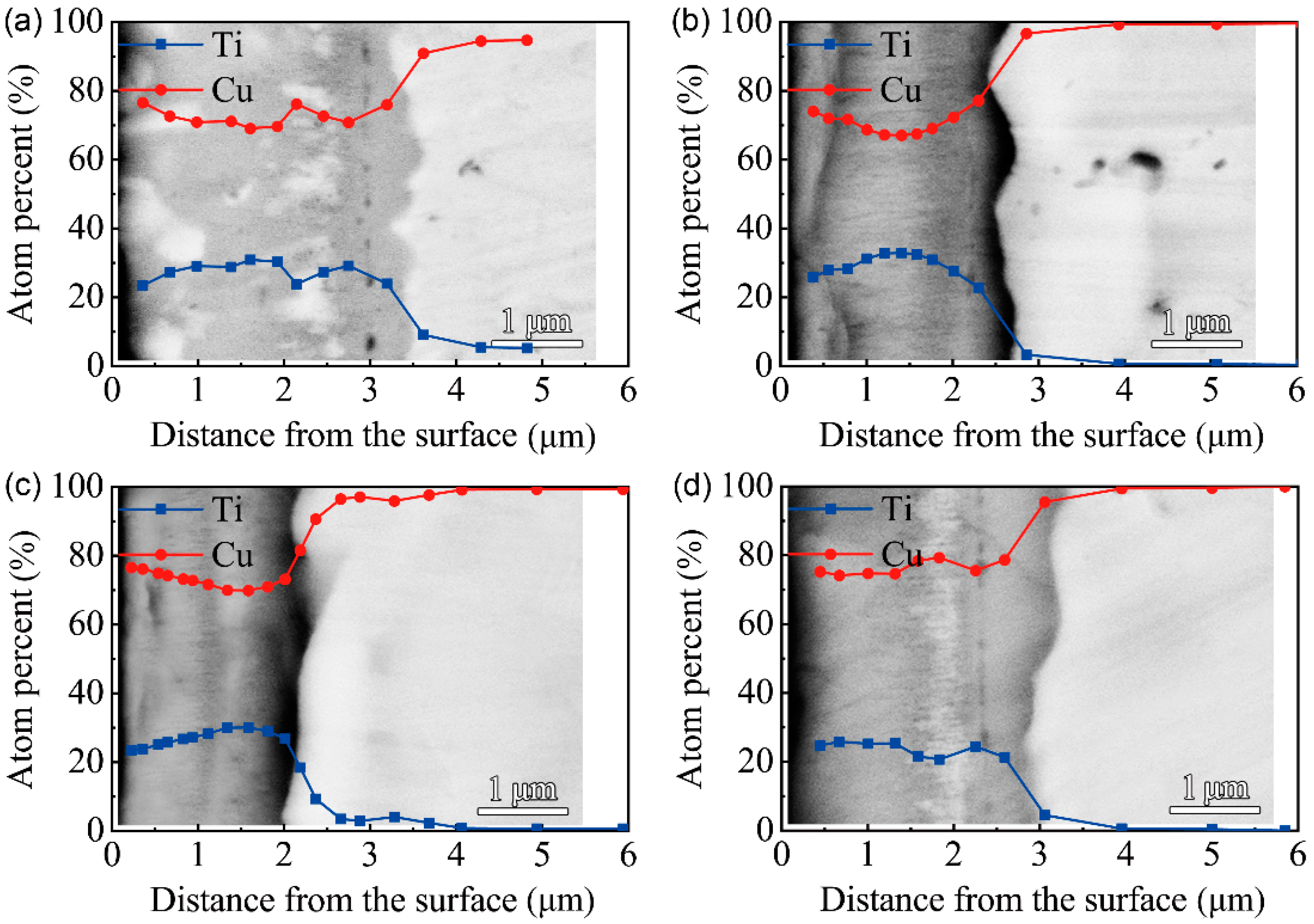
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Semboshi, S.; Al-Kassab, T.; Gemma, R.; Kirchheim, R. Microstructural evolution of Cu-1 at% Ti alloy aged in a hydrogen atmosphere and its relation with the electrical conductivity. Ultramicroscopy 2009, 109, 593–598. [Google Scholar] [CrossRef] [PubMed]
- Scardi, P.; Leoni, M.; Straffelini, G.; Giudici, G.D. Microstructure of Cu–Be alloy triboxidative wear debris. Acta Mater. 2007, 55, 2531–2538. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, F.Y.; Yan, M.F.; Zhang, M.L. Microstructure and mechanical properties of multiphase layer formed during thermo-diffusing of titanium into the surface of C17200 copper–beryllium alloy. Appl. Surf. Sci. 2014, 292, 225–230. [Google Scholar] [CrossRef]
- Liu, L.; Shen, H.H.; Liu, X.Z.; Guo, Q.; Meng, T.X.; Wang, Z.X.; Yang, H.J.; Liu, X.P. Wear resistance of TiN (Ti2N)/Ti composite layer formed on C17200 alloy by plasma surface Ti-alloying and nitriding. Appl. Surf. Sci. 2016, 388, 103–108. [Google Scholar] [CrossRef]
- Jiang, C.; Li, R.; Wang, X.; Shang, H.; Zhang, Y.; Liaw, P.K. Diffusion barrier performance of AlCrTaTiZr/AlCrTaTiZr-N high-entropy alloy films for Cu/Si connect System. Entropy 2020, 22, 234. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Prangnell, P.; Robson, J. Modeling of intermetallic compounds growth between dissimilar metals. Metall. Mater. Trans. A 2015, 46, 4106–4114. [Google Scholar] [CrossRef]
- Keddam, M.; Djeghlal, M.E.; Barrallier, L.; Salhi, E. Computer simulation of nitrided layers growth for pure iron. Comp. Mater. Sci. 2004, 29, 43–48. [Google Scholar] [CrossRef]
- Meinshausen, L.; Weide-Zaage, K.; Frémont, H. Dynamical IMC-growth calculation. Microelectron. Reliab. 2015, 55, 1832–1837. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, B.; Wei, Y.; Feng, G.; Deng, D. Microstructure and mechanical properties of vacuum diffusion bonded Ti2AlNb/Ti/TC4 joint. Crystals 2021, 11, 770. [Google Scholar] [CrossRef]
- Yan, M.F.; Zhu, Y.D.; Zhang, C.S.; Zhang, Y.X.; Wang, Y.X.; Yang, L. Microstructure and mechanical properties of copper–titanium–nitrogen multiphase layers produced by a duplex treatment on C17200 copper–beryllium alloy. Mater. Des. 2015, 84, 10–17. [Google Scholar] [CrossRef]
- Kim, Y.S.; Park, H.J.; Mun, S.C.; Jumaev, E.; Hong, S.H.; Song, G.; Kim, J.T.; Park, Y.K.; Kim, K.S.; Jeong, S.I.; et al. Investigation of structure and mechanical properties of TiZrHfNiCuCo high entropy alloy thin films synthesized by magnetron sputtering. J. Alloys Compd. 2019, 797, 834–841. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; He, X.; Li, M.; Huang, X.; Hang, R.; Tang, B. Wear and corrosion resistance of anti-bacterial Ti–Cu–N coatings on titanium implants. Appl. Surf. Sci. 2014, 317, 614–621. [Google Scholar] [CrossRef]
- Zhu, Y.D.; Yan, M.F.; Zhang, Y.X.; Chen, H.T.; Yang, Y. Microstructure formation and evolution mechanism of Cu-Ti coating during dual-magnetron sputtering and thermo plasma nitriding. Vacuum 2016, 134, 25–28. [Google Scholar] [CrossRef]
- Zhu, Y.D.; Yan, M.F.; Zhang, Y.X.; Zhang, C.S. Surface Modification of C17200 Copper-Beryllium Alloy by Plasma Nitriding of Cu-Ti Gradient Film. J. Mater. Eng. Perform. 2018, 27, 961–969. [Google Scholar] [CrossRef]
- Kuo, C.; Lin, Y.; Chan, A.; Chang, J. High temperature wear behavior of titanium nitride coating deposited using high power impulse magnetron sputtering. Coatings 2019, 9, 555. [Google Scholar] [CrossRef]
- Esmati, K.; Omidvar, H.; Jelokhani, J.; Naderi, M. Study on the microstructure and mechanical properties of diffusion brazing joint of C17200 Copper Beryllium alloy. Mater. Des. 2014, 53, 766–773. [Google Scholar] [CrossRef]
- Ghosh, G. First-principles calculations of structural energetics of Cu–TM (TM = Ti, Zr, Hf) intermetallics. Acta Mater. 2007, 55, 3347–3374. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, M.; Zhang, Q.; Wang, Q.; Zhuo, H. Effects of the prefabricated Cu-Ti film on the microstructure and mechanical properties of the multiphase coating by thermo plasma nitriding on C17200 Cu Alloy. Coatings 2019, 9, 694. [Google Scholar] [CrossRef]
- Qin, L.; Ma, D.; Li, Y.; Jing, P.; Huang, B.; Jing, F.; Xie, D.; Leng, Y.; Akhavan, B.; Huang, N. Ti–Cu coatings deposited by a combination of hipims and dc magnetron sputtering: The role of vacuum annealing on cu diffusion, microstructure, and corrosion resistance. Coatings 2020, 10, 1064. [Google Scholar] [CrossRef]
- Guo, C.; Zhou, F.; Chen, M.; Wang, J.; Zhu, S.; Wang, F. An in-situ formed ceramic/alloy/ceramic sandwich barrier to resist elements interdiffusion between NiCrAlY coating and a Ni-based superalloy. J. Mater. Sci. Technol. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Yan, M.; Yan, J.; Bell, T. Numerical simulation of nitrided layer growth and nitrogen distribution in ε-Fe2-3N, γ′-Fe4N and α-Fe during pulse plasma nitriding of pure iron. Model. Simul. Mater. Sci. Eng. 2000, 8, 491–496. [Google Scholar] [CrossRef]
- Yan, M.F.; Zhu, Y.D.; Zhang, Y.X.; Zhang, M.L. Combining thermo-diffusing titanium and plasma nitriding to modify C61900 Cu–Al alloy. Vacuum 2016, 126, 41–44. [Google Scholar] [CrossRef]
- Iijima, Y.; Hoshino, K.; Hirano, K. Diffusion of titanium in copper. Metall. Trans. A 1977, 8, 997–1001. [Google Scholar] [CrossRef]




| Be | Co | Ni | Fe | Si | Cu |
|---|---|---|---|---|---|
| 1.96 | 0.10 | 0.12 | 0.15 | 0.12 | Bal. |
| Process | Ti Target Power (W) | Ti Target Current (A) | Cu Target Power (W) | Cu Target Current (A) |
|---|---|---|---|---|
| F1 | 2500 | 7.00 | 100 | 0.33 |
| F2 | 2000 | 5.69 | 300 | 0.84 |
| F3 | 1000 | 3.02 | 450 | 1.18 |
| Total Ar Pressure (Torr) | Substrate Bias (V) | Sputtering Time (h) | Substrate-to-Target Distance (mm) | Workpiece Rotation Speed (r/min) | Vacuum Chamber Temperature (°C) |
|---|---|---|---|---|---|
| 3.7 × 10−2 | −70 | 3 | 120 | 5 | 20~150 |
| Materials | Coating Process | Film Composition | Film Thickness (μm) | |
|---|---|---|---|---|
| Cu (at.%) | Ti (at.%) | |||
| C17200 | F1 | 13 | 87 | 3.0 |
| F2 | 37 | 63 | 3.0 | |
| F3 | 67 | 33 | 2.5 | |
| Temperature (°C) | Duration (h) | Coating Process | Substrate Material |
|---|---|---|---|
| 650 | 1 | F1 F2 F3 | C17200 |
| 4 | |||
| 750 | 1 | F1 F2 F3 | C17200 |
| 4 |
| Ti content (at.%) | cs0 (×103 kg/m3) |
|---|---|
| 85 | 4.03 |
| 70 | 3.50 |
| 55 | 2.91 |
| 40 | 2.25 |
| Temperature (°C) | ci2 (×103 kg/m3) | D (×10−15 m2/s) |
|---|---|---|
| 650 | 0.11 | 0.56 |
| 700 | 0.14 | 2.08 |
| 750 | 0.19 | 6.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Li, Z.; Bi, H.; Shi, Q.; Han, Y.; Zhang, Q. Cross-Sectional Profile Evolution of Cu-Ti Gradient Films on C17200 Cu by Vacuum Thermal Diffusion. Materials 2022, 15, 8002. https://doi.org/10.3390/ma15228002
Zhu Y, Li Z, Bi H, Shi Q, Han Y, Zhang Q. Cross-Sectional Profile Evolution of Cu-Ti Gradient Films on C17200 Cu by Vacuum Thermal Diffusion. Materials. 2022; 15(22):8002. https://doi.org/10.3390/ma15228002
Chicago/Turabian StyleZhu, Yandan, Zecheng Li, Hongchao Bi, Qilong Shi, Yujun Han, and Quanli Zhang. 2022. "Cross-Sectional Profile Evolution of Cu-Ti Gradient Films on C17200 Cu by Vacuum Thermal Diffusion" Materials 15, no. 22: 8002. https://doi.org/10.3390/ma15228002
APA StyleZhu, Y., Li, Z., Bi, H., Shi, Q., Han, Y., & Zhang, Q. (2022). Cross-Sectional Profile Evolution of Cu-Ti Gradient Films on C17200 Cu by Vacuum Thermal Diffusion. Materials, 15(22), 8002. https://doi.org/10.3390/ma15228002






