Evaluation of Different Tools of Precision Finishing for Sun Gear with Inner-Outer Tooth Shapes
Abstract
1. Introduction
2. Precision Finishing Approach
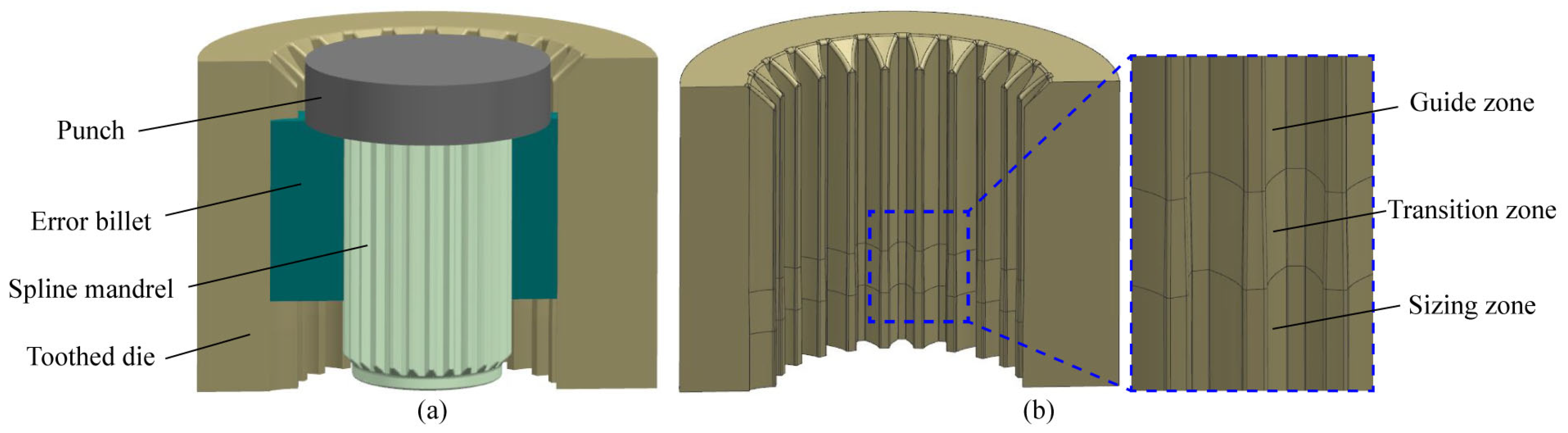
2.1. Cold Extruded Sun Gear
2.2. Precision Finishing Method Design
3. Simulation and Experiment Preparation
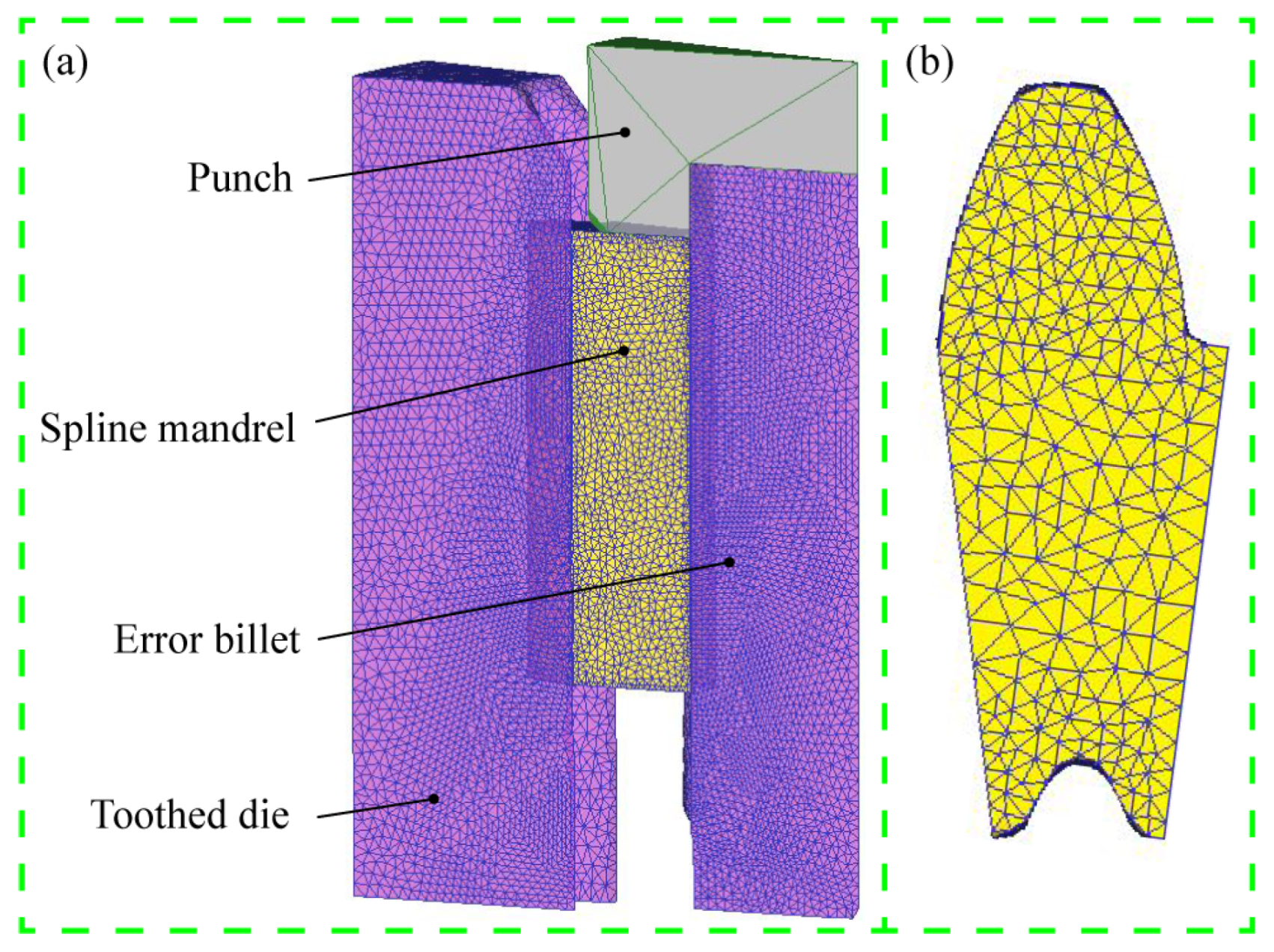
3.1. FE Modeling and Prediction Strategy
3.2. Experiment Preparation
4. Results and Discussion
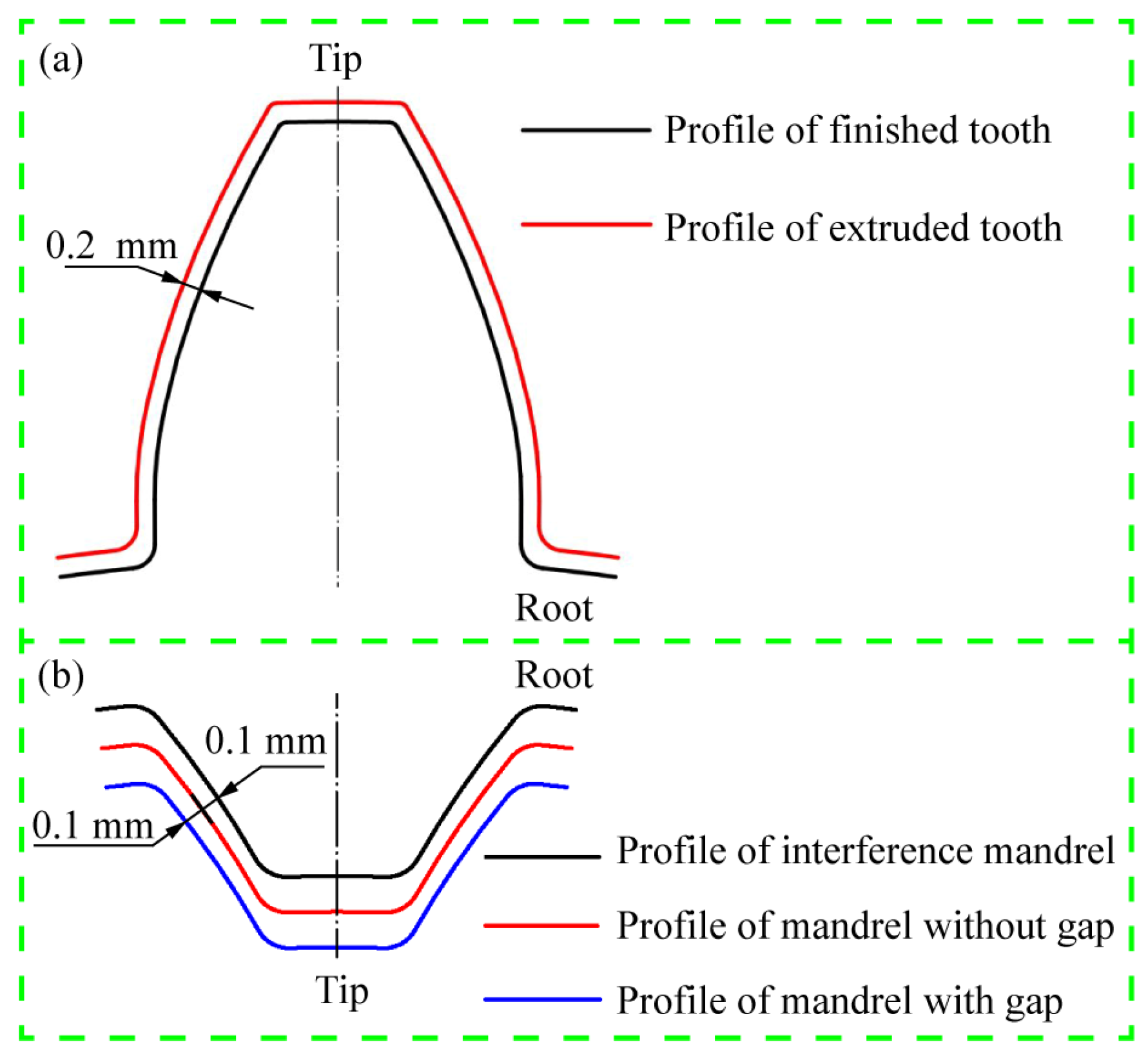
4.1. Tooth Deformation
4.2. Tool Stress
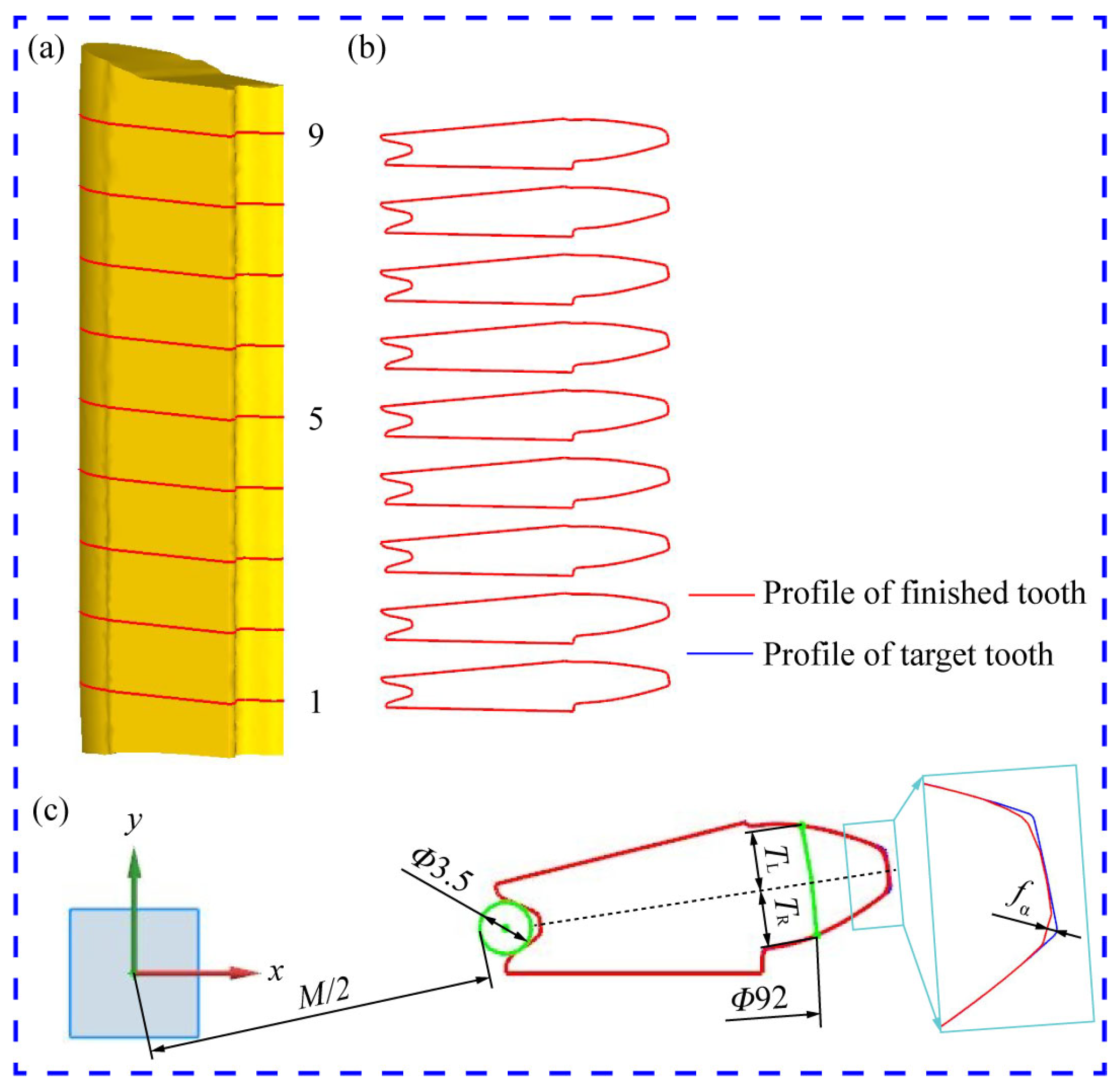
4.3. Tooth Accuracy
5. Conclusions
- (1)
- When the interference mandrel is used for the precision finishing process, the entire profiles of internal–external teeth will occur plastic deformation, and the finishing effect is better than mandrels both with gap and without gap. Therefore, the interference mandrel is recommended as the optimal reshaping tool to improve the tooth accuracy of cold extruded sun gear.
- (2)
- While the maximum compressive stress of the tools with the interference mandrel is larger than mandrels both with gap and without gap, the interference mandrel has a better restraint function on the billet, which indicates that this finishing tool can significantly improve the reshaping effect of internal–external gears.
- (3)
- The tooth accuracy class of the reshaped outer teeth in profile and helix were seventh and eighth, respectively, and the total M-value error of the inner teeth was decreased to 72.3 μm, indicating that the dimensional accuracy of the cold extruded teeth can be considerably improved by the precise finishing operation. The simulation results of dimensional errors were consistent with the experimental results, which verifies the dependability of the finite element prediction method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choia, J.C.; Choi, Y. Precision forging of spur gears with inside relief. Int. J. Mach. Tools Manuf. 1999, 39, 1575–1588. [Google Scholar] [CrossRef]
- Kanani, J.B.; Lalwani, D.I. An experimental and FEA investigation of near-net-shape cold forging of spur gear. Mater. Today Proc. 2021, 44, 92–98. [Google Scholar] [CrossRef]
- Cai, J.; Dean, T.A.; Hu, Z.M. Alternative die designs in net-shape forging of gears. J. Mater. Process. Technol. 2004, 150, 48–55. [Google Scholar] [CrossRef]
- Zuo, B.; Wang, B.-Y.; Li, Z.; Zheng, M.-N.; Zhu, X.-X. Design of relief-cavity in closed-precision forging of gears. J. Cent. South Univ. 2015, 22, 1287–1297. [Google Scholar] [CrossRef]
- Song, J.-H.; Im, Y.-T. The applicability of process design system for forward extrusion of spur gears. J. Mater. Process. Technol. 2007, 184, 411–419. [Google Scholar] [CrossRef]
- Jeong, M.-S.; Lee, S.-K.; Yun, J.-H.; Sung, J.H.; Kim, D.H.; Lee, S.; Choi, T.-H. Green manufacturing process for helical pinion gear using cold extrusion process. Int. J. Precis. Eng. Manuf. 2013, 14, 1007–1011. [Google Scholar] [CrossRef]
- Silveira, F.D.; Schaeffer, L. Evaluation of different levels of prestressing for cold forging tools by numerical simulation analysis. Int. J. Adv. Manuf. Technol. 2018, 98, 2487–2495. [Google Scholar] [CrossRef]
- Tiernan, P.; Hillery, M.T.; Draganescu, B.; Gheorghe, M. Modelling of cold extrusion with experimental verification. J. Mater. Process. Technol. 2005, 168, 360–366. [Google Scholar] [CrossRef]
- Hu, C.; Wang, K.; Liu, Q. Study on a new technological scheme for cold forging of spur gears. J. Mater. Process. Technol. 2007, 187–188, 600–603. [Google Scholar] [CrossRef]
- Gronostajski, Z.; Hawryluk, M. The main aspects of precision forging. Arch. Civ. Mech. Eng. 2008, 8, 39–55. [Google Scholar] [CrossRef]
- Stone, E.R.H.; Cai, J.; Hu, Z.M.; Dean, T.A. An exercise in cold ironing as the post-forging operation for net-shape manufacture. J. Mater. Process. Technol. 2003, 135, 278–283. [Google Scholar] [CrossRef]
- Li, Z.; Wang, B.; Ma, W.; Yang, L. Comparison of ironing finishing and compressing finishing as post-forging for net-shape manufacturing. Int. J. Adv. Manuf. Technol. 2016, 86, 3333–3343. [Google Scholar] [CrossRef]
- Behrens, B.A.; Doege, E. Cold Sizing of Cold- and Hot-Formed Gears. CIRP Ann. 2004, 53, 239–242. [Google Scholar] [CrossRef]
- Pfefferkorn, F.E.; Duffie, N.A.; Morrow, J.D.; Wang, Q. Effect of beam diameter on pulsed laser polishing of S7 tool steel. CIRP Ann. 2014, 63, 237–240. [Google Scholar] [CrossRef]
- Liu, G.H.; Zhong, Z.P.; Bian, Y.; Li, Q. Numerical Simulation on Precision Forging Process for Spur-Gear with Large Module. Adv. Mater. Res. 2012, 538–541, 927–931. [Google Scholar] [CrossRef]
- Ou, H.; Balendra, R. Die-elasticity for precision forging of aerofoil sections using finite element simulation. J. Mater. Process. Technol. 1998, 76, 56–61. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J.; Kwon, Y.; Ishikawa, T. Modeling approach to estimate the elastic characteristics of workpiece and shrink-fitted die for cold forging. J. Mater. Process. Technol. 2004, 147, 102–110. [Google Scholar] [CrossRef]
- Zhuang, W.; Han, X.; Hua, L.; Xu, M.; Chen, M. FE prediction method for tooth variation in hot forging of spur bevel gears. J. Manuf. Process. 2019, 38, 244–255. [Google Scholar] [CrossRef]
- Kang, J.H.; Lee, K.O.; Je, J.S.; Kang, S.S. Spur gear forging tool manufacturing method considering elastic deformation due to shrink fitting. J. Mater. Process. Technol. 2007, 187–188, 14–18. [Google Scholar] [CrossRef]
- Qin, Y.; Balendra, R. FE simulation of the influence of die-elasticity on component dimensions in forward extrusion. Int. J. Mach. Tools Manuf. 1997, 37, 183–192. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, J.; Qu, Z.; Wang, X.; Liang, Q.; Feng, W. A precision sizing method for cold extruded sun gear with internal-external tooth shapes. Int. J. Adv. Manuf. Technol. 2021, 115, 3331–3344. [Google Scholar] [CrossRef]
- Li, S.; Ji, H.; Wang, B.; Mu, Y. Numerical analysis and experimental validation of conjunction gear via hot forging-upsetting finishing-radial extrusion. Arch. Civ. Mech. Eng. 2019, 19, 391–404. [Google Scholar] [CrossRef]
- Nistor, L.; Neag, A.; Marian, I.; Frunza, D. Experimental and Numerical Simulation Study of Simultaneous Toothing of Spur Gears by Press-Rolling Process. J. Manuf. Sci. Eng. 2016, 138, 12. [Google Scholar] [CrossRef]
- Zuo, B.; Wang, B.; Li, Z.; Li, N.; Lin, J. An investigation of involute and lead deflection in hot precision forging of gears. Int. J. Adv. Manuf. Technol. 2016, 88, 3017–3030. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Q.; Zhou, J.; Feng, W.; Liang, Q. Design of precision finishing method for cold extruded sun gear with internal-external tooth shapes. Int. J. Adv. Manuf. Technol. 2021, 116, 3277–3293. [Google Scholar] [CrossRef]
- Liang, Q.; Zhou, J.; Zhu, S.; Xia, Z.; Liu, Z. The choice of cold precision sizing method for cold extrusion gear with big modulu. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 1995–2001. [Google Scholar]


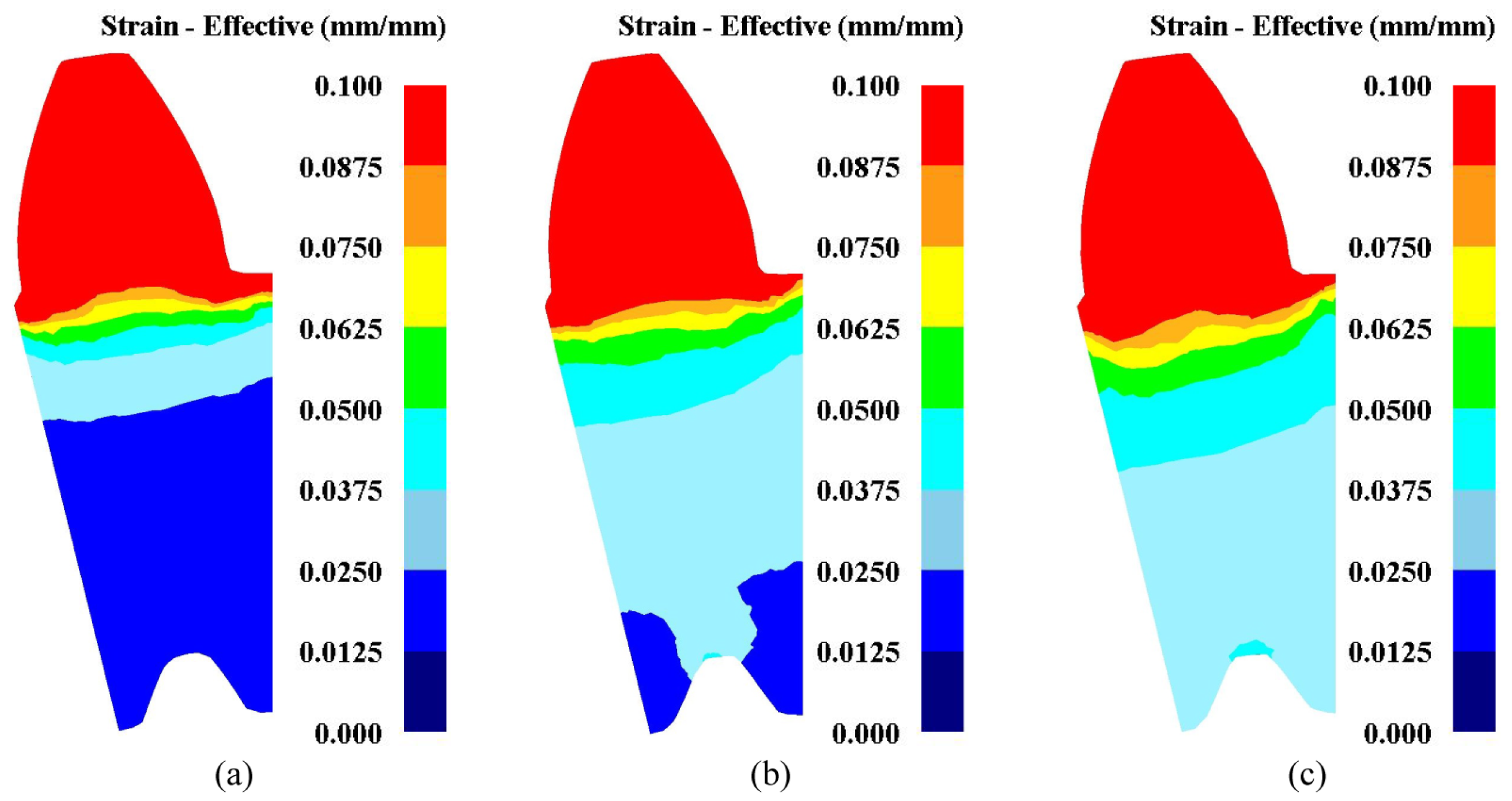
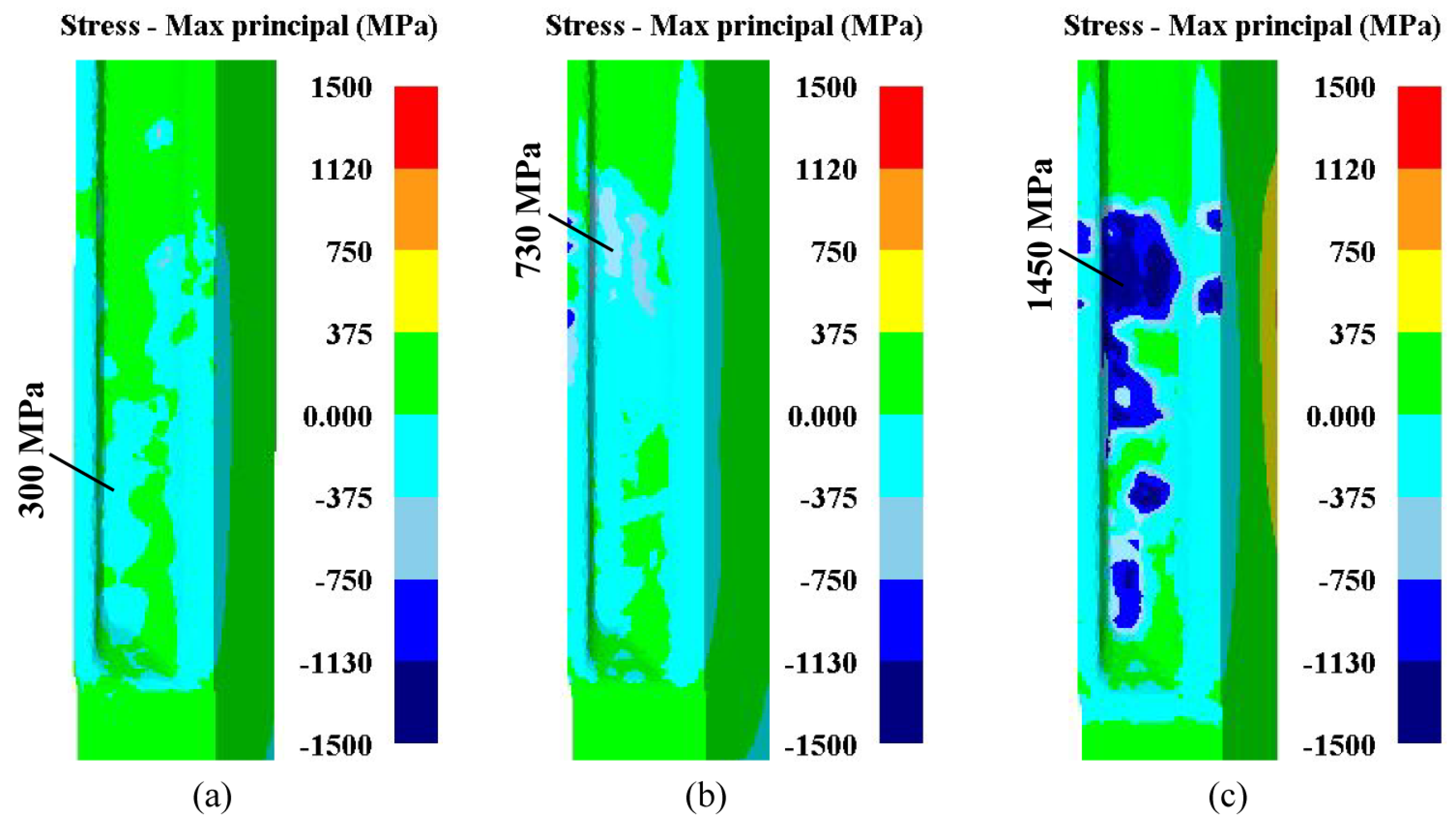

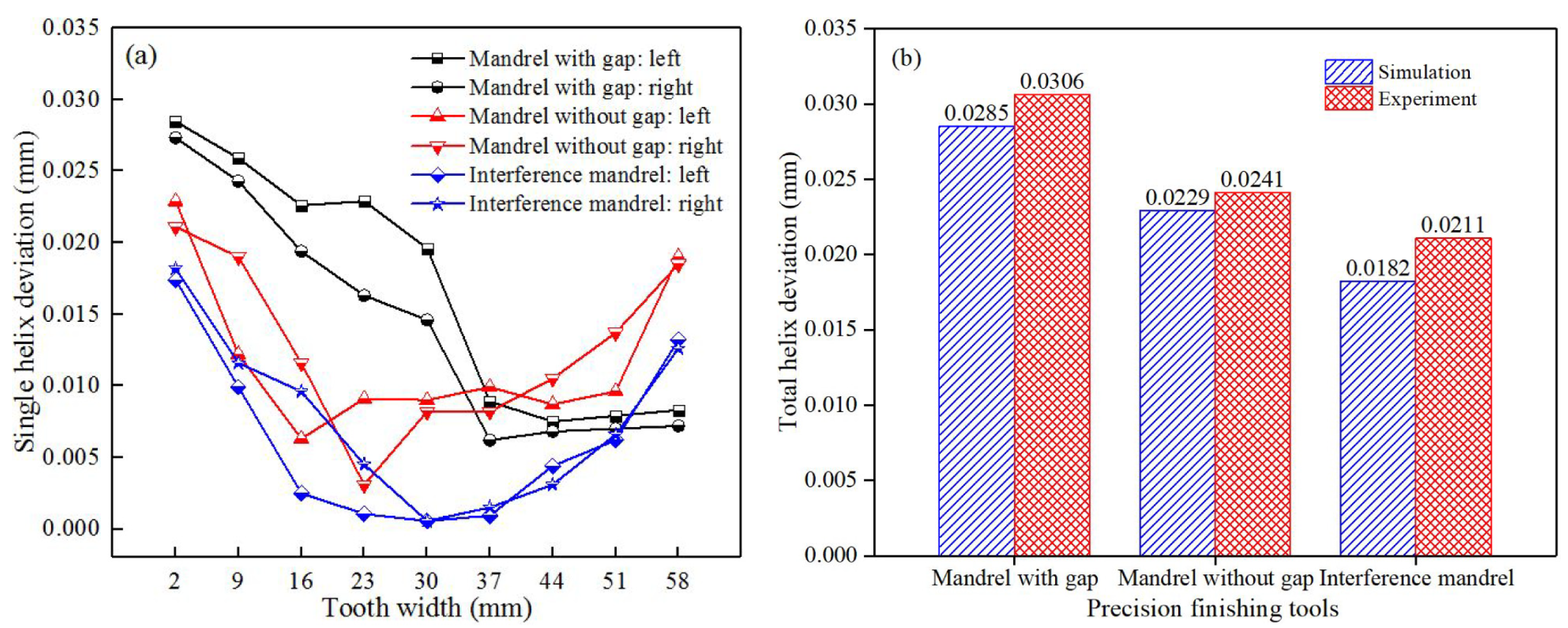
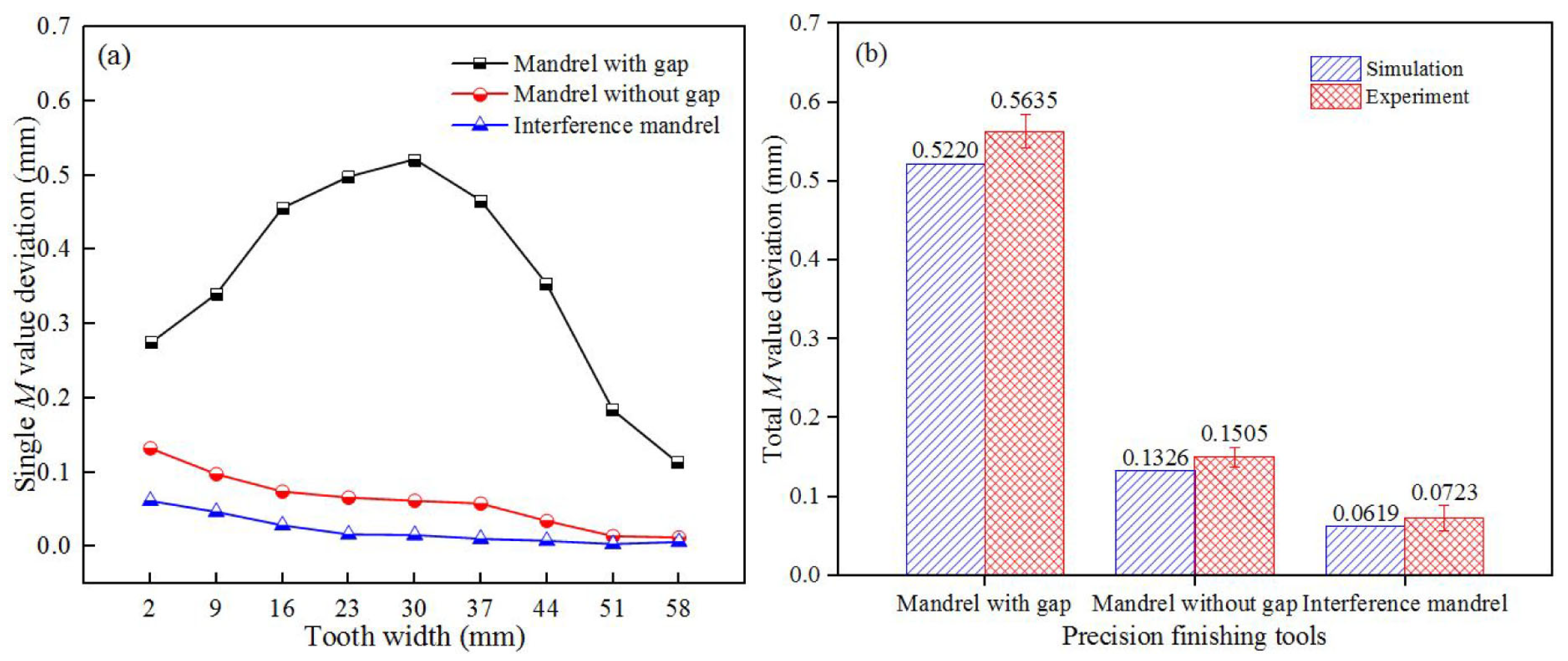

| Deviations | Values | Accuracy Class (ISO 1328) |
|---|---|---|
| FM | 276.4 μm | 100 μm |
| Fα | 30.2 μm | 9 class |
| Fβ | 55.9 μm | 10 class |
| Items | Values |
|---|---|
| Error billet material | SCM 420 |
| Finishing tools material | SKD11 |
| Error billet mesh number | 100,000 |
| Finishing tools mesh number | 100,000 |
| Mesh refined proportion of billet and tools | 0.1 |
| Mesh size of billet and tools | 1 |
| Finishing temperature (°C) | 20 |
| Pressing speed (mm/s) | 20 |
| Shear friction factor | 0.12 |
| Cr | Mn | C | Ni | Ti | Cu | S | Si | P | Fe |
|---|---|---|---|---|---|---|---|---|---|
| 1.20 | 0.90 | 0.18 | 0.18 | 0.08 | 0.22 | 0.02 | 0.26 | 0.023 | Bal. |
Curve of profile deviation  | 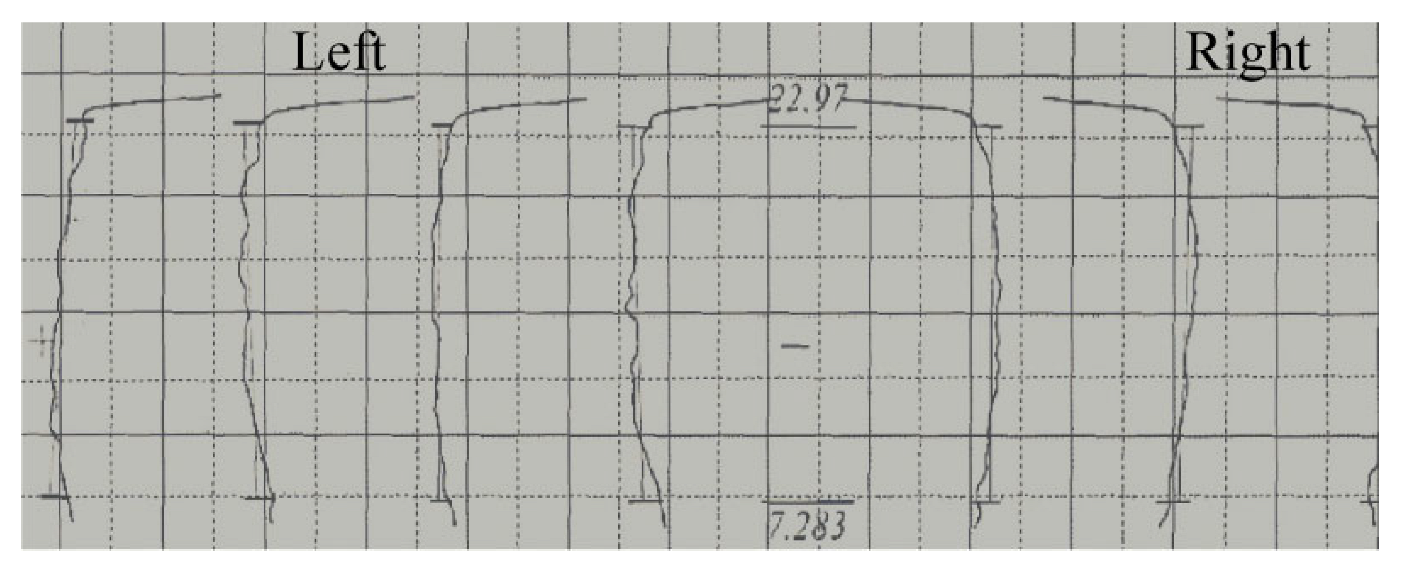 |
| Fα (ISO 1328) | 17.2 μm (7 class) |
Curve of helix deviation  | 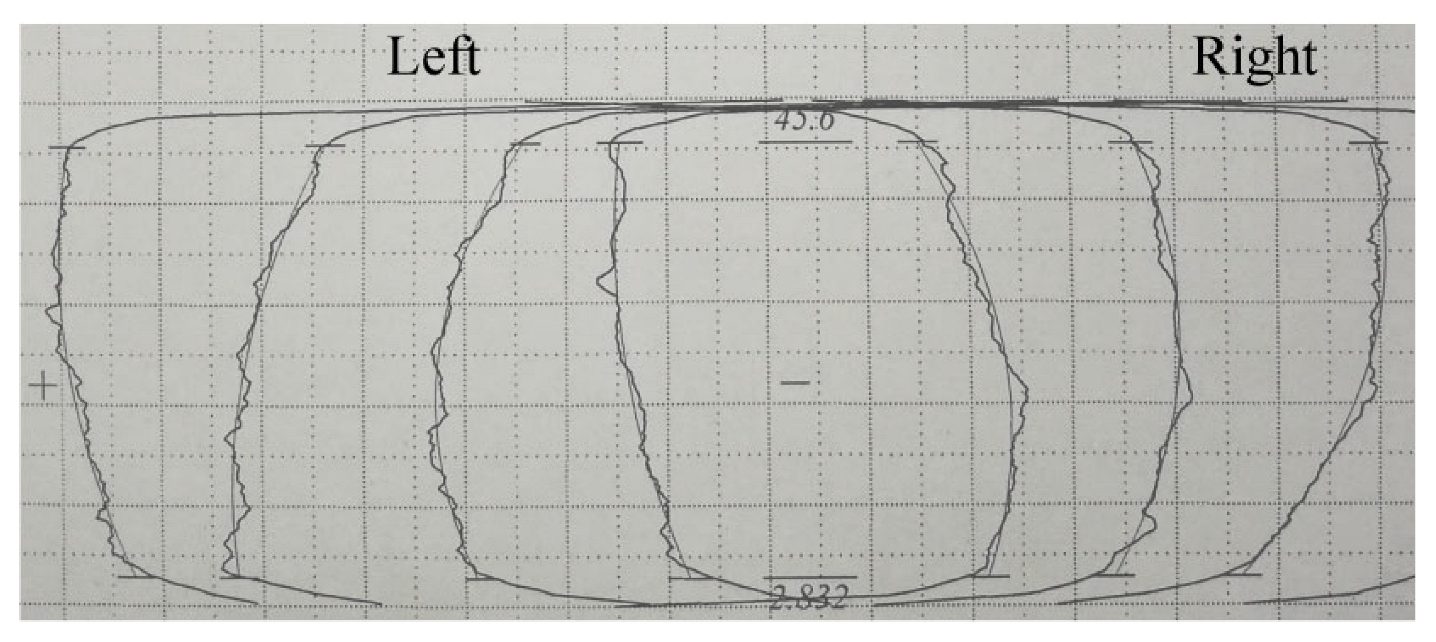 |
| Fβ (ISO 1328) | 21.1 μm (8 class) |
| FM (ISO 1328) | 72.3 μm (100 μm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Q.; Zhang, X.; Liu, Y.; Zhou, J.; Liu, Z. Evaluation of Different Tools of Precision Finishing for Sun Gear with Inner-Outer Tooth Shapes. Materials 2022, 15, 8081. https://doi.org/10.3390/ma15228081
Liang Q, Zhang X, Liu Y, Zhou J, Liu Z. Evaluation of Different Tools of Precision Finishing for Sun Gear with Inner-Outer Tooth Shapes. Materials. 2022; 15(22):8081. https://doi.org/10.3390/ma15228081
Chicago/Turabian StyleLiang, Qiang, Xianming Zhang, Yunqi Liu, Jie Zhou, and Zuofa Liu. 2022. "Evaluation of Different Tools of Precision Finishing for Sun Gear with Inner-Outer Tooth Shapes" Materials 15, no. 22: 8081. https://doi.org/10.3390/ma15228081
APA StyleLiang, Q., Zhang, X., Liu, Y., Zhou, J., & Liu, Z. (2022). Evaluation of Different Tools of Precision Finishing for Sun Gear with Inner-Outer Tooth Shapes. Materials, 15(22), 8081. https://doi.org/10.3390/ma15228081






