An Experimental and Numerical Study of the Influence of Temperature on Mode II Fracture of a T800/Epoxy Unidirectional Laminate
Abstract
1. Introduction
2. Delamination Tests on the ENF Specimen
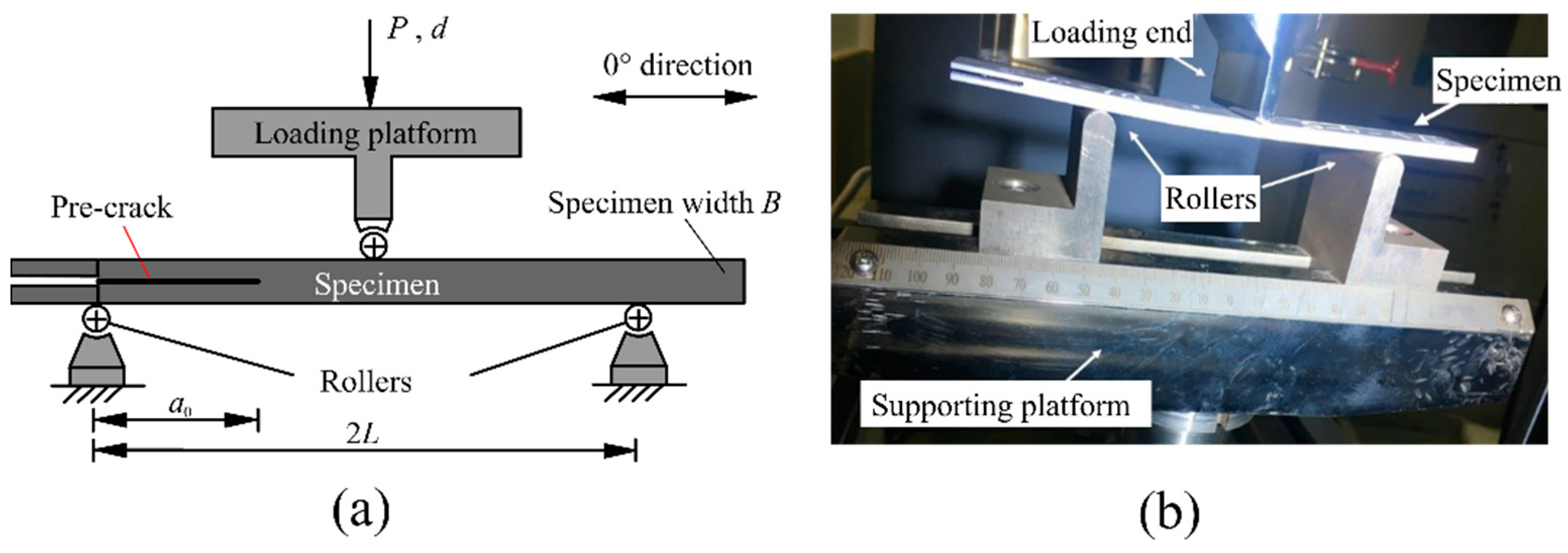
2.1. Specimen and Test Set-Up
2.2. Test Procedure
2.3. Date Reduction Method
2.3.1. ECM Method
2.3.2. SBT Method
2.3.3. CBTE
3. Test Results
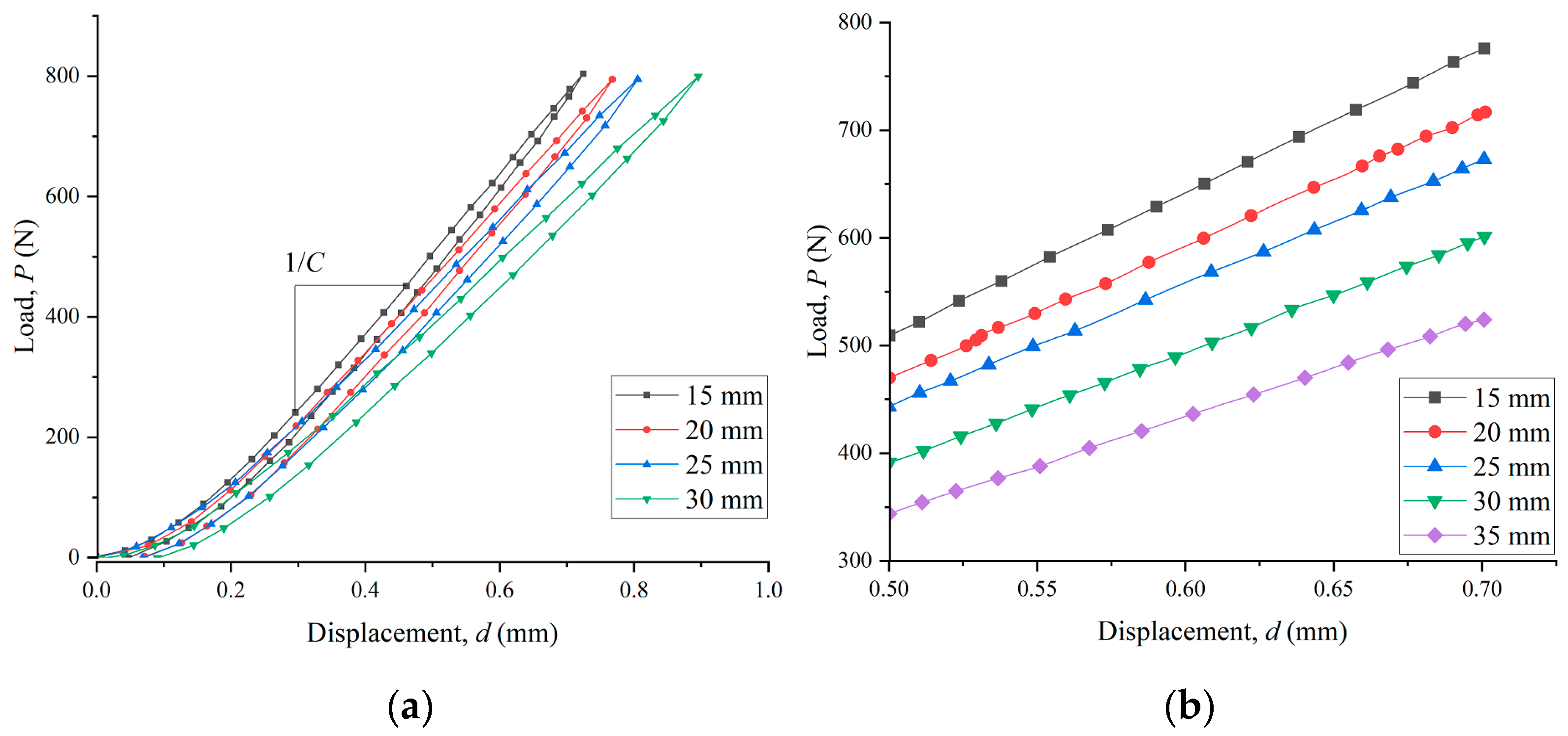
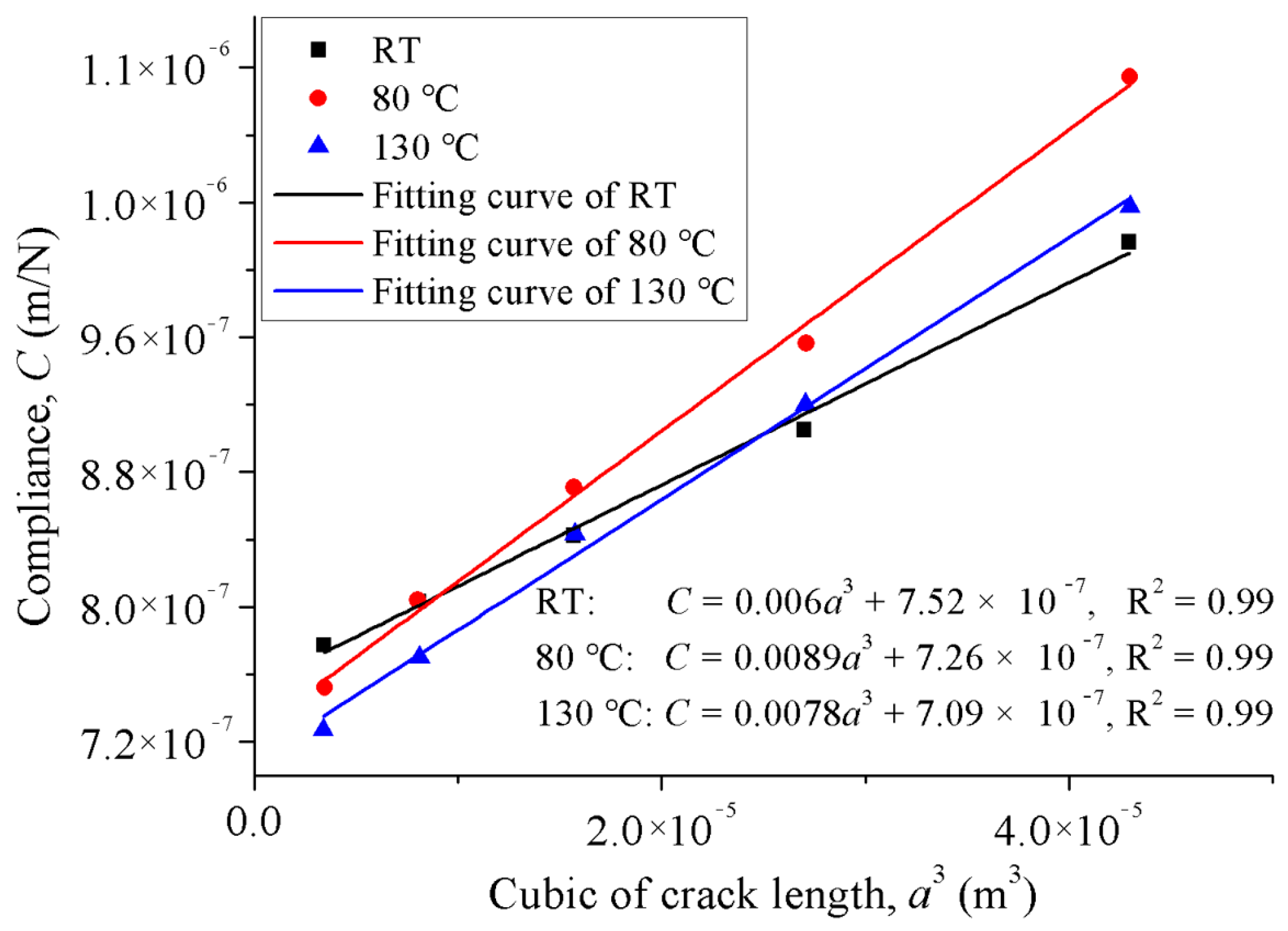
3.1. Compliance Calibration Results
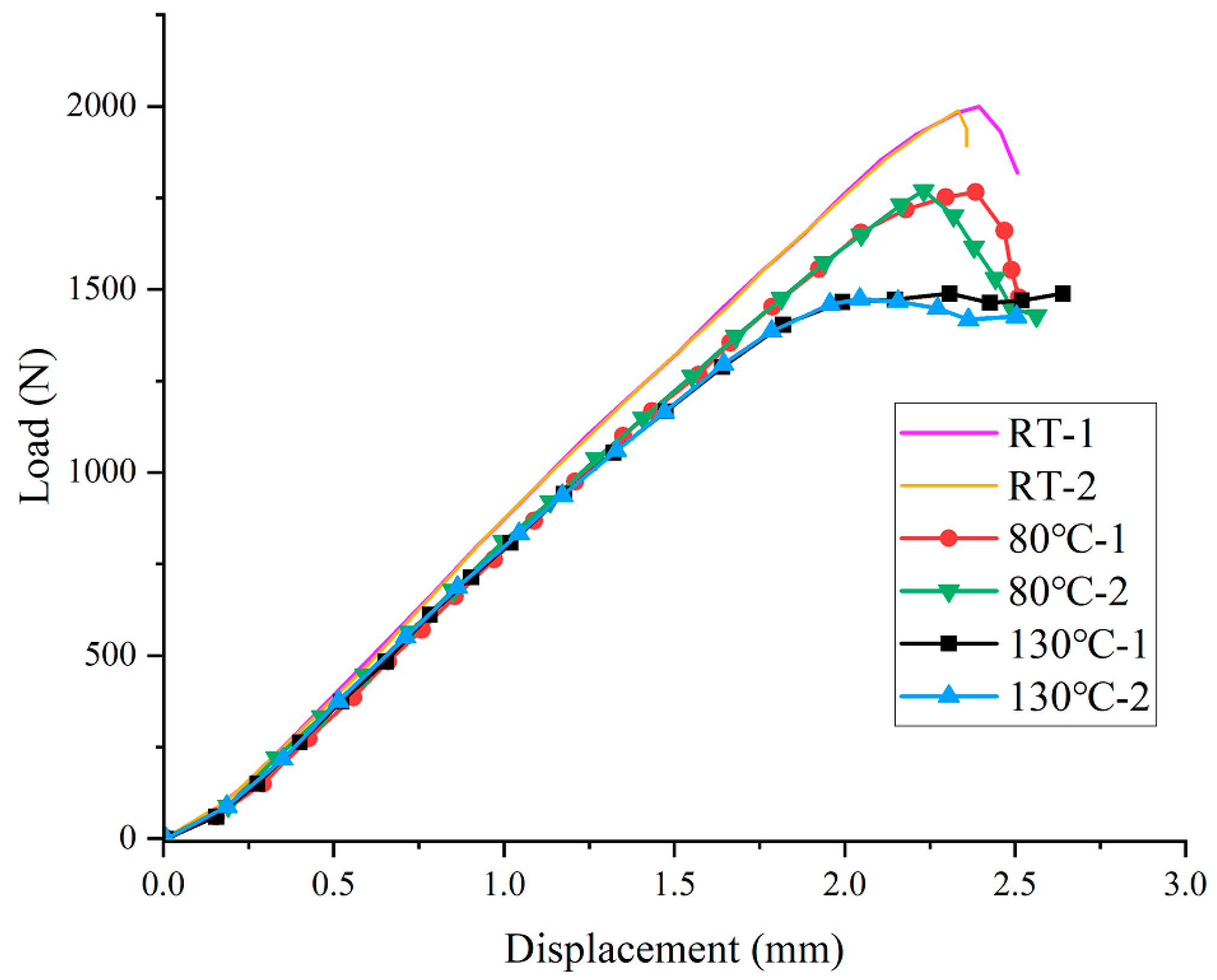
3.2. Load–Displacement Curve
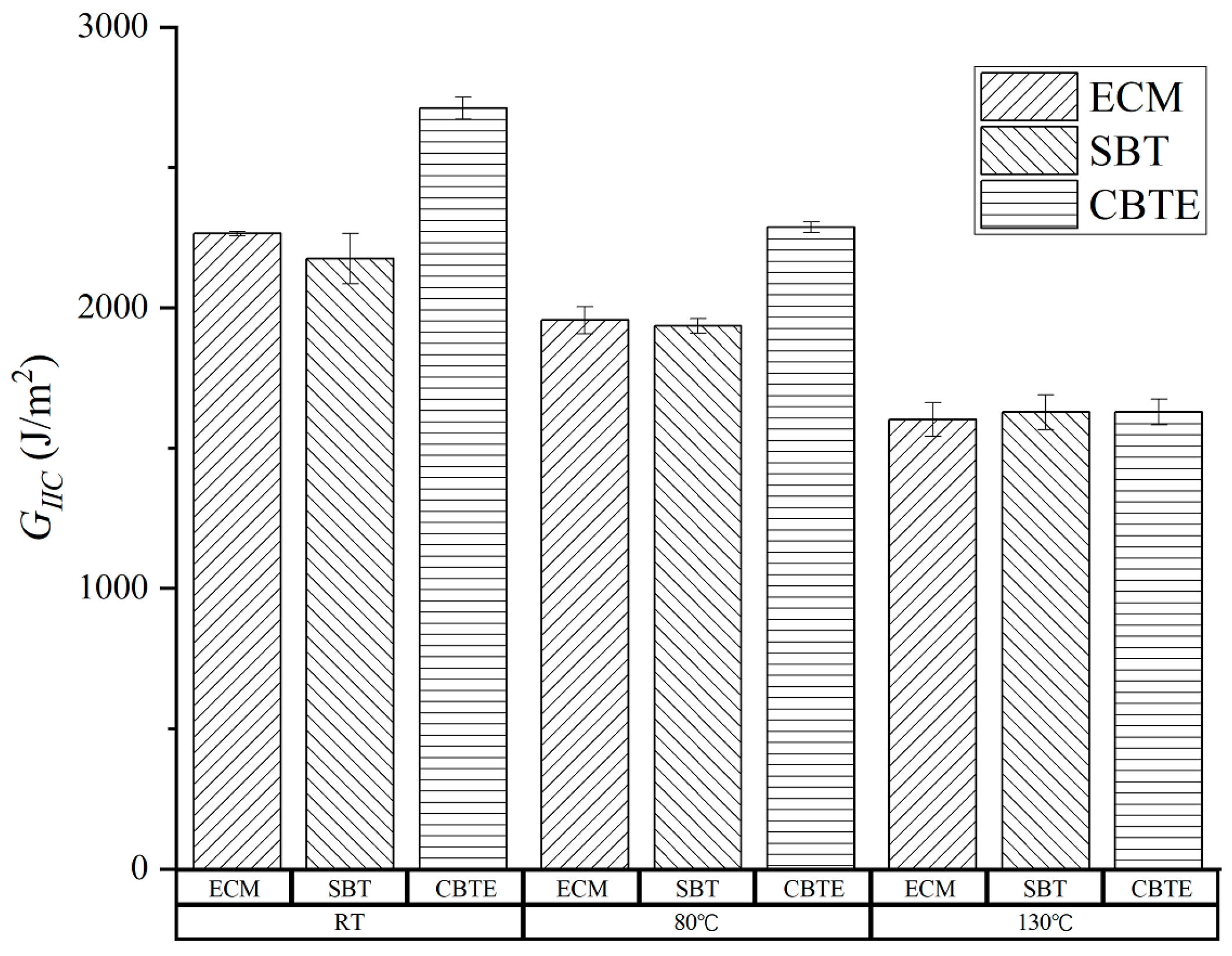
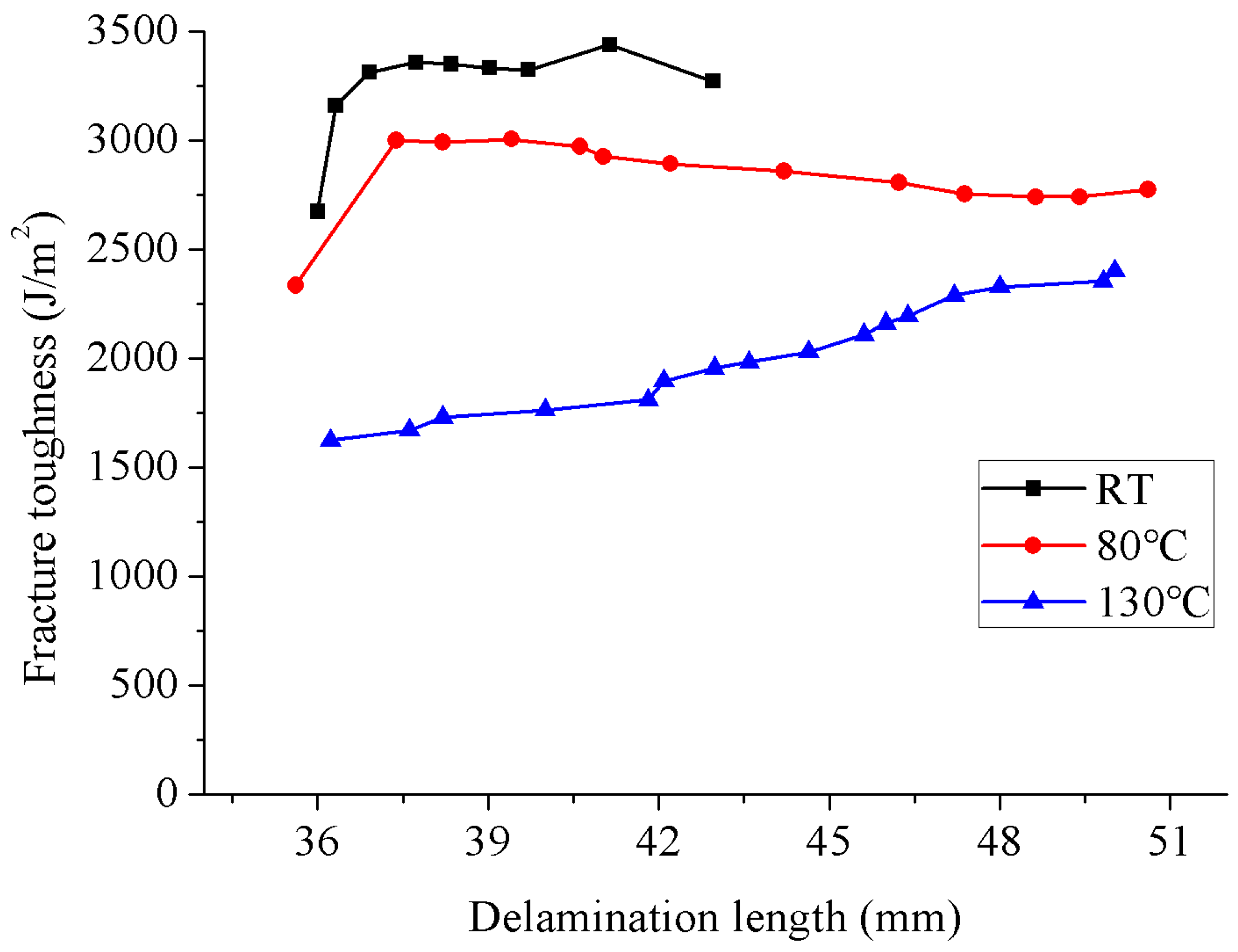
3.3. Fracture Toughness
3.4. Analysis on the Fracture Surface
4. Numerical Simulation for the Mode II Delamination in ENF Specimens
4.1. A model for the Thermal-Affected Material Properties
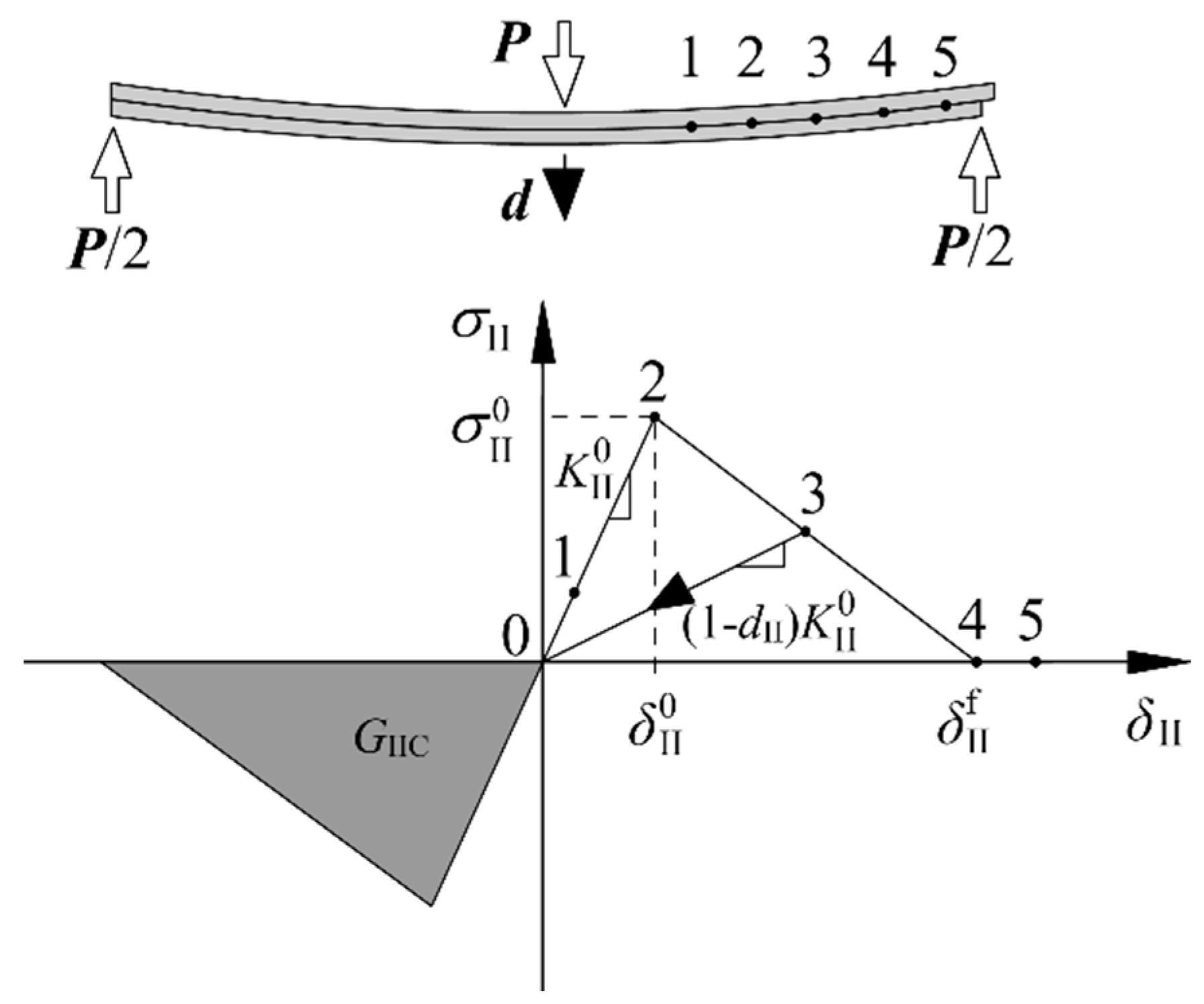
4.2. Cohesive Zone Model with a Bilinear Constitutive Law
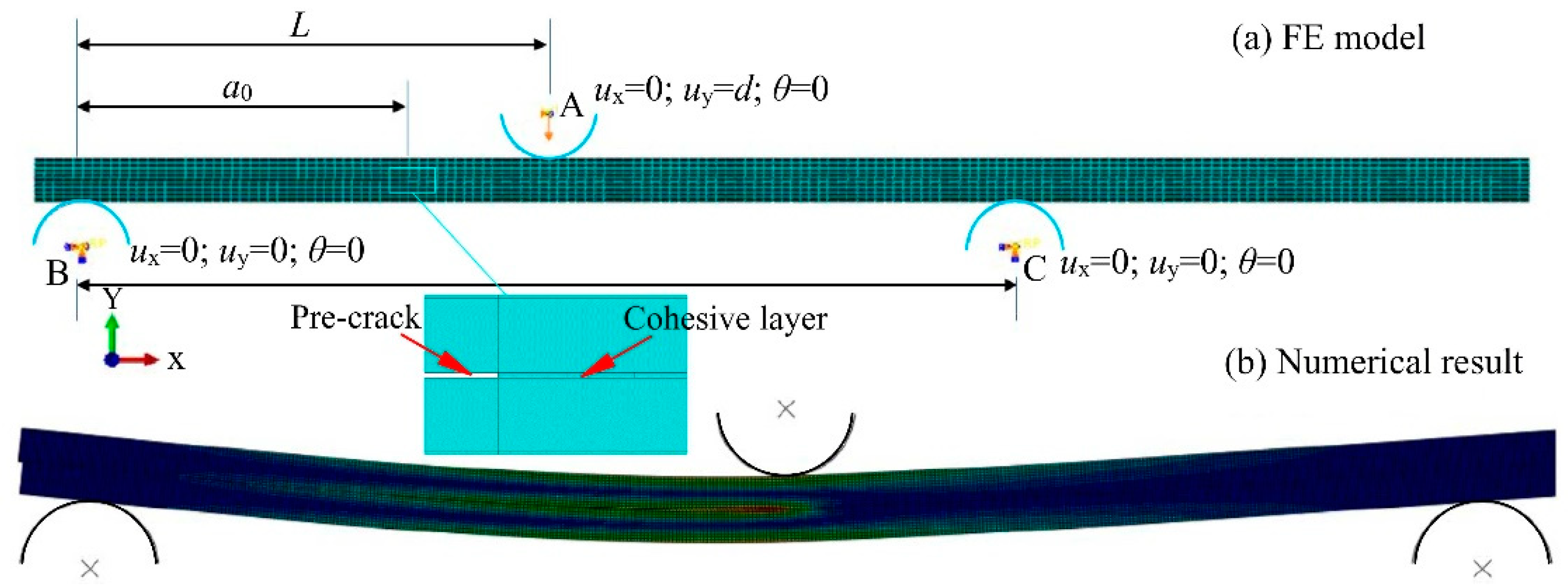
4.3. Numerical Model of the ENF Specimen
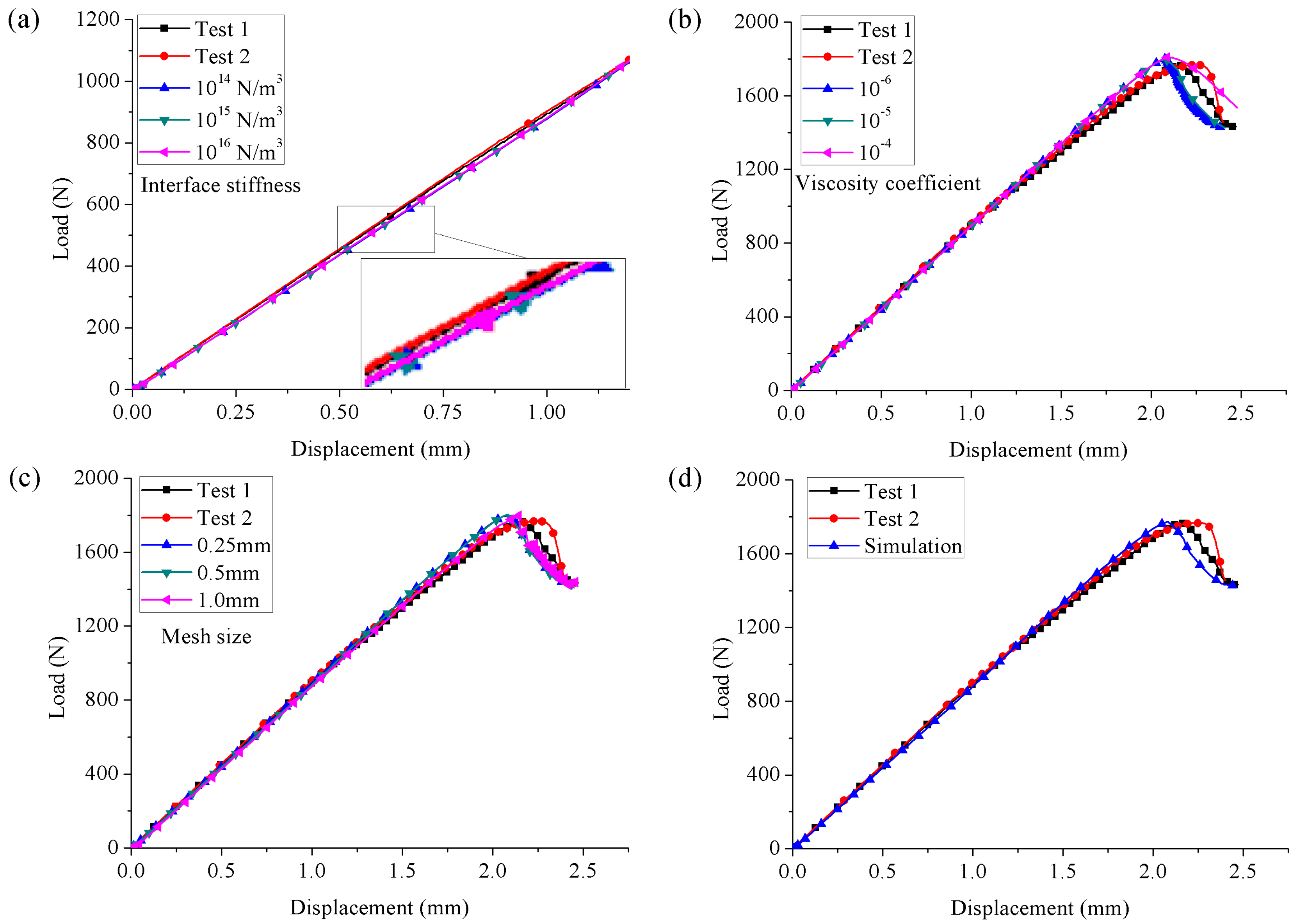
4.4. Simulated Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Gong, Y.; Gao, Y.; Hou, M.; Li, L. Failure analysis of hat-stringer-stiffened aircraft composite panels under four-point bending loading. Materials 2022, 15, 2430. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, Y.; Zhang, Q.; He, Y.; Liu, Z.; Hu, N. Fatigue behavior of 2.5D woven composites based on the first-order bending vibration tests. Compos. Struct. 2022, 284, 115218. [Google Scholar] [CrossRef]
- Li, X.; Gong, Y.; Jiang, L.; Zhao, Y.; Hu, N. A parametric study on the failure strength of multi-bolt composite repairs with different configurations. Theor. Appl. Fract. Mech. 2022, 121, 103459. [Google Scholar] [CrossRef]
- Li, B.; Gong, Y.; Xiao, H.; Gao, Y.; Liang, E. A two-dimensional model for pin-load distribution and failure analysis of composite bolted joints. Materials 2021, 14, 3646. [Google Scholar] [CrossRef]
- Hosseini, M.R.; Taheri-Behrooz, F.; Salamat-talab, M. Mode II interlaminar fracture toughness of woven E-glass/epoxy composites in the presence of mat interleaves. Int. J. Adhes. Adhes. 2020, 98, 102523. [Google Scholar] [CrossRef]
- Herráez, M.; Pichler, N.; Pappas, G.A.; Blondeau, C.; Botsis, J. Experiments and numerical modelling on angle-ply laminates under remote mode II loading. Compos. Part A Appl. Sci. Manuf. 2020, 134, 105886. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, X.; Li, W.; Zhao, L.; Tao, J.; Zhang, J.; Hu, N. Delamination in carbon fiber epoxy DCB laminates with different stacking sequences: R-curve behavior and bridging traction-separation relation. Compos. Struct. 2021, 262, 113605. [Google Scholar] [CrossRef]
- Gong, Y.; Tao, J.; Chen, X.; Zhao, J.; Hu, N. A semi-analytical method for determining mode-II fracture toughness and bridging law of composite laminates. Eng. Fract. Mech. 2022, 265, 108371. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, L.; Gong, Y.; Liu, H.; Zhao, J.; Ren, S. Failure prediction of marine non-planar composite π joints based on combined 2D material model and progressive damage method. Ocean Eng. 2021, 222, 108581. [Google Scholar] [CrossRef]
- Gong, Y.; Tian, D.; Cao, T.; Zhao, L.; Zhang, J.; Hu, N.; Zhang, C. An R-curve effect-included delamination growth criterion for mixed-mode I/II delamination predictions of composite laminates. Compos. Struct. 2022, 295, 115846. [Google Scholar] [CrossRef]
- Liu, C.; Gong, Y.; Gong, Y.; Li, W.; Liu, Z.; Hu, N. Mode II fatigue delamination behaviour of composite multidirectional laminates and the stress ratio effect. Eng. Fract. Mech. 2022, 264, 108321. [Google Scholar] [CrossRef]
- Abdel-Monsef, S.; Renart, J.; Carreras, L.; Maimí, P.; Turon, A. Effect of environmental conditioning on pure mode I fracture behaviour of adhesively bonded joints. Theor. Appl. Fract. Mech. 2020, 110, 102826. [Google Scholar] [CrossRef]
- Gong, Y.; Jiang, L.; Li, L.; Ren, S.; Zhao, Y.; Wang, Z.; Hu, N. Temperature effect on the static mode I delamination behavior of aerospace-grade composite laminates: Experimental and numerical study. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2827–2844. [Google Scholar] [CrossRef]
- Boni, L.; Fanteria, D.; Lazzeri, L.; Panettieri, E.; Mariani, U.; Rigamonti, M. Influence of environment conditioning on the interlaminar fracture toughness of a graphite/epoxy unidirectional material. Compos. Part B Eng. 2018, 153, 97–107. [Google Scholar] [CrossRef]
- Hashemi, S.; Kinloch, A.J.; Williams, J.G. The effects of geometry, rate and temperature on the mode I, mode II and mixed-mode I/II interlaminar fracture of carbon-fibre/poly (ether-ether ketone) composites. J. Compos. Mater. 1990, 24, 918–956. [Google Scholar] [CrossRef]
- Machado, J.J.M.; Marques, E.A.S.; Campilho, R.D.S.G.; da Silva, L.F.M. Mode II fracture toughness of CFRP as a function of temperature and strain rate. Compos. Part B Eng. 2017, 114, 311–318. [Google Scholar] [CrossRef]
- Chapman, T.; Smiley, A.; Pipes, R. Rate and temperature effects on mode II interlaminar fracture toughness in composite materials. Deformation and fracture of laminated composites. In Proceedings of the 6th International Conference on Composite Materials (ICCM-6), London, UK, 20–24 July 1987; pp. 3.295–3.304. [Google Scholar]
- Davies, P.; de Charentenay, F. Effect of temperature on the interlaminar fracture of tough composites. Deformation and fracture of laminated composites. In Proceedings of the 6th International Conference on Composite Materials (ICCM-6), London, UK, 20–24 July 1987; pp. 3.284–3.294. [Google Scholar]
- Russell, A.; Street, K. Moisture and Temperature effects on the Mixed-Mode Delamination Fracture of Unidirectional Graphite/Epoxy; Delamination and Debonding of Materials; ASTM International: West Conshohocken, PA, USA, 1985. [Google Scholar]
- Garg, A.C. Intralaminar and interlaminar fracture in graphite/epoxy laminates. Eng. Fract. Mech. 1986, 23, 719–733. [Google Scholar] [CrossRef]
- Kim, H.; Wang, W.; Takao, Y.; Ben, G. Effects of temperature on mode II fracture toughness of multidirectional CFRP laminates. Int. J. Mod. Phys. B 2003, 17, 1717–1723. [Google Scholar] [CrossRef]
- Asp, L.E. The effects of moisture and temperature on the interlaminar delamination toughness of a carbon/epoxy composite. Compos. Sci. Technol. 1998, 58, 967–977. [Google Scholar] [CrossRef]
- Sjögren, A.; Asp, L.E. Effects of temperature on delamination growth in a carbon/epoxy composite under fatigue loading. Int. J. Fatigue 2002, 24, 179–184. [Google Scholar] [CrossRef]
- Cowley, K.D.; Beaumont, P.W.R. The interlaminar and intralaminar fracture toughness of carbon-fibre/polymer composites: The effect of temperature. Compos. Sci. Technol. 1997, 57, 1433–1444. [Google Scholar] [CrossRef]
- Davidson, B.D.; Kumar, M.; Soffa, M.A. Influence of mode ratio and hygrothermal condition on the delamination toughness of a thermoplastic particulate interlayered carbon/epoxy composite. Compos. Part A Appl. Sci. Manuf. 2009, 40, 67–79. [Google Scholar] [CrossRef]
- Zulkifli, R.; Azhari, C.H. Mode II interlaminar fracture properties of treated silk fibre/ epoxy composites at low and high temperature range. Int. J. Eng. Technol. 2018, 7, 129–132. [Google Scholar] [CrossRef]
- Landry, B.; LaPlante, G.; LeBlanc, L.R. Environmental effects on mode II fatigue delamination growth in an aerospace grade carbon/epoxy composite. Compos. Part A Appl. Sci. Manuf. 2012, 43, 475–485. [Google Scholar] [CrossRef]
- D7905/D7905M-14; Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2014.
- Carlsson, L.A.; Gillespie, J.W.; Pipes, R.B. On the analysis and design of the end notched flexure (ENF) specimen for mode II testing. J. Compos. Mater. 1986, 20, 594–604. [Google Scholar] [CrossRef]
- Wilk, J. Applicability of mode II interlaminar fracture toughness testing methods for characterization of thermoplastic laminates with woven fabric reinforcements. Eng. Fract. Mech. 2019, 216, 106533. [Google Scholar] [CrossRef]
- ISO 15114; Fibre-Reinforced Plastic Composites-Determination of the Mode II Fracture Resistance for Unidirectionally Reinforced Materials Using the Calibrated End-Loaded Split (C-ELS) Test and an Effective Crack Length Approach. International Standards Organization: Geneva, Switzerland, 2014.
- Gong, Y.; Xia, K.; Wang, Y.; Zhao, L.; Zhang, J.; Hu, N. A semi-analytical model for the mode II fracture toughness of multidirectional composite laminates. Thin-Walled Struct. 2023, 182, 110235. [Google Scholar] [CrossRef]
- Blackman, B.; Brunner, A.J.; Williams, J.G. Mode II fracture testing of composites: A new look at an old problem. Eng. Fract. Mech. 2006, 73, 2443–2455. [Google Scholar] [CrossRef]
- Czabaj, M.W.; Davidson, B.D. Determination of the mode I, mode II, and mixed-mode I–II delamination toughness of a graphite/polyimide composite at room and elevated temperatures. J. Compos. Mater. 2015, 50, 2235–2253. [Google Scholar] [CrossRef]
- Zou, L.; Gong, Y.; Tian, D.; Zhao, L.; Zhang, J.; Hu, N. Effect of interface angle on mode I delamination damage behavior of multidirectional fully isotropic laminates with the same global stiffness. Thin-Walled Struct. 2023, 182, 110211. [Google Scholar] [CrossRef]
- Lee, S.M. Mode II delamination failure mechanisms of polymer matrix composites. J. Mater. Sci. 1997, 32, 1287–1295. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Zhang, J.; Gong, Y.; Lu, Z.; Hu, N.; Xu, J. An interface-dependent model of plateau fracture toughness in multidirectional CFRP laminates under mode I loading. Compos. Part B Eng. 2017, 131, 196–208. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Zhang, J.; Gong, Y.; Hu, N.; Li, N. XFEM-based model for simulating zigzag delamination growth in laminated composites under mode I loading. Compos. Struct. 2017, 160, 1155–1162. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, B.; Zhao, L.; Zhang, J.; Hu, N.; Zhang, C. R-curve behaviour of the mixed-mode I/II delamination in carbon/epoxy laminates with unidirectional and multidirectional interfaces. Compos. Struct. 2019, 223, 110949. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Wang, Y.; Hu, N. Delamination propagation criterion including the effect of fiber bridging for mixed-mode I/II delamination in CFRP multidirectional laminates. Compos. Sci. Technol. 2017, 151, 302–309. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N. An improved power law criterion for the delamination propagation with the effect of large-scale fiber bridging in composite multidirectional laminates. Compos. Struct. 2018, 184, 961–968. [Google Scholar] [CrossRef]
- Zhao, L.; Gong, Y.; Zhang, J.; Wang, Y.; Lu, Z.; Peng, L.; Hu, N. A novel interpretation of fatigue delamination growth behavior in CFRP multidirectional laminates. Compos. Sci. Technol. 2016, 133, 79–88. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N. A novel model for determining the fatigue delamination resistance in composite laminates from a viewpoint of energy. Compos. Sci. Technol. 2018, 167, 489–496. [Google Scholar] [CrossRef]
- Gong, Y.; Li, W.; Liu, H.; Yuan, S.; Wu, Z.; Zhang, C. A novel understanding of the normalized fatigue delamination model for composite multidirectional laminates. Compos. Struct. 2019, 229, 111395. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N.; Zhang, C. An insight into three approaches for determining fatigue delamination resistance in DCB tests on composite laminates. Compos. Part B-Eng. 2019, 176, 107206. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N. Crack closure in the fatigue delamination of composite multidirectional DCB laminates with large-scale fiber bridging. Compos. Struct. 2020, 244, 112220. [Google Scholar] [CrossRef]
- Kaw, A.K. Mechanics of Composite Materials, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Zhang, J.; Qi, D.; Zhou, L.; Zhao, L.; Hu, N. A progressive failure analysis model for composite structures in hygrothermal environments. Compos. Struct. 2015, 133, 331–342. [Google Scholar] [CrossRef]
- Benkhedda, A.; Tounsi, A.; Bedia, E.A.A. Effect of temperature and humidity on transient hygrothermal stresses during moisture desorption in laminated composite plates. Compos. Struct. 2008, 82, 629–635. [Google Scholar] [CrossRef]
- Shan, M.; Zhao, L.; Hong, H.; Liu, F.; Zhang, J. A progressive fatigue damage model for composite structures in hygrothermal environments. Int. J. Fatigue 2018, 111, 299–307. [Google Scholar] [CrossRef]
- Megueni, A.; Tounsi, A.; Bedia, E.A. Evolution of the stress intensity factor for patched crack with bonded hygrothermal aged composite repair. Mater. Design. 2007, 28, 287–293. [Google Scholar] [CrossRef]
- Chang, F.; Shahid, I.; Engdahl, R.A. Predicting Moduli and Strengths Reduction of Unidirectional Graphite/Epoxy Composites Due to Hygrothermal Effects. J. Reinf. Plast. Compos. 1989, 8, 106–132. [Google Scholar] [CrossRef]
- Christense, R.M. Tensor transformations and failure criteria for the analysis of fiber composite materials. J. Compos. Mater. 1988, 22, 874–897. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically-based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking: Part I: Development. Compos. Part A Appl. Sci. Manuf. 2006, 37, 63–73. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Belytschko, T.; Moës, N.; Usui, S.; Parimi, C. Arbitrary discontinuities in finite elements. Int. J. Numer. Meth. Eng. 2001, 50, 993–1013. [Google Scholar] [CrossRef]
- Abdullah, N.A.; Curiel-Sosa, J.L.; Taylor, Z.A.; Tafazzolimoghaddam, B.; Vicente, J.L.M.; Zhang, C. Transversal crack and delamination of laminates using XFEM. Compos. Struct. 2017, 173, 78–85. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, B.; Mukhopadhyay, S.; Hallett, S.R. Experimental study on delamination migration in multidirectional laminates under mode II static and fatigue loading, with comparison to mode I. Compos. Struct. 2018, 201, 683–698. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, B.; Hallett, S.R. Delamination migration in multidirectional composite laminates under mode I quasi-static and fatigue loading. Compos. Struct. 2018, 189, 160–176. [Google Scholar] [CrossRef]
- Hu, X.F.; Chen, B.Y.; Tirvaudey, M.; Tan, V.; Tay, T.E. Integrated XFEM-CE analysis of delamination migration in multi-directional composite laminates. Compos. Part A Appl. Sci. Manuf. 2016, 90, 161–173. [Google Scholar] [CrossRef]
- Thamburaja, P.; Sarah, K.; Srinivasa, A.; Reddy, J.N. Fracture of viscoelastic materials: FEM implementation of a non-local & rate form-based finite-deformation constitutive theory. Comput. Methods Appl. Mech. Eng. 2019, 354, 871–903. [Google Scholar]
- Sarah, K.; Thamburaja, P.; Srinivasa, A.; Reddy, J.N. Numerical simulations of damage and fracture in viscoelastic solids using a nonlocal fracture criterion. Mech. Adv. Mater. Struct. 2020, 27, 1085–1097. [Google Scholar] [CrossRef]
- Gong, Y.; Hou, Y.; Zhao, L.; Li, W.; Zhang, J.; Hu, N. A modified mode I cohesive zone model for the delamination growth in DCB laminates with the effect of fiber bridging. Int. J. Mech. Sci. 2020, 176, 105514. [Google Scholar] [CrossRef]
- Yin, S.; Gong, Y.; Li, W.; Zhao, L.; Zhang, J.; Hu, N. A novel four-linear cohesive law for the delamination simulation in composite DCB laminates. Compos. Part B Eng. 2020, 180, 107526. [Google Scholar] [CrossRef]
- Ye, J.; Gong, Y.; Tao, J.; Cao, T.; Zhao, L.; Zhang, J.; Hu, N. Efficiently determining the R-curve and bridging traction-separation relation of mode I delamination in a simple way. Compos. Struct. 2022, 288, 115388. [Google Scholar] [CrossRef]
- Cao, T.; Zhao, L.; Gong, Y.; Gong, X.; Zhang, J. An enhanced beam theory based semi-analytical method to determine the DCB mode I bridging-traction law. Compos. Struct. 2020, 245, 112306. [Google Scholar] [CrossRef]
- Cao, T.; Zhao, L.; Wang, L.; Wang, K.; Gong, Y.; Zhang, J. An efficient semi-analytical method to extract the mode II bridging-traction law in ENF tests directly from the experimental load displacement data. Compos. Struct. 2022, 285, 115229. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, X.; Tao, J.; Zhao, L.; Zhang, J.; Hu, N. A simple procedure for determining the mode I bridging stress of composite DCB laminates without measuring the crack opening displacement. Compos. Struct. 2020, 243, 112147. [Google Scholar] [CrossRef]
- Zhao, L.; Gong, Y.; Zhang, J.; Chen, Y.; Fei, B. Simulation of delamination growth in multidirectional laminates under mode I and mixed mode I/II loadings using cohesive elements. Compos. Struct. 2014, 116, 509–522. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, X.; Zou, L.; Li, X.; Zhao, L.; Zhang, J.; Hu, N. Experimental and numerical investigations on the mode I delamination growth behavior of laminated composites with different z-pin fiber reinforcements. Compos. Struct. 2022, 287, 115370. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modeer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]


| E1 (Gpa) | E2, E3 (Gpa) | G12, G13 (Gpa) | G23 (Gpa) | ν12, ν13 | ν23 |
| 163.5 | 9.0 | 4.14 | 3.08 | 0.32 | 0.46 |
| XT (MPa) | XC (MPa) | YT, ZT (MPa) | YC, ZC (MPa) | S12, S13 (MPa) | S23 (MPa) |
| 2992 | 1183 | 70.6 | 278 | 172 | 105 |
| Temperature | Method | Test 1 | Test 2 | Mean Value | S.D. | CoV (%) |
| RT | ECM | 2269.68 | 2259.09 | 2264.39 | 5.29 | 0.2 |
| SBT | 2237.93 | 2110.97 | 2174.45 | 63.48 | 2.9 | |
| CBTE | 2738.67 | 2684.17 | 2711.42 | 27.25 | 1.0 | |
| 80 °C | ECM | 1920.93 | 1989.62 | 1955.28 | 34.34 | 1.8 |
| SBT | 1916.81 | 1953.56 | 1935.19 | 18.38 | 0.9 | |
| CBTE | 2273.08 | 2300.07 | 2286.58 | 13.50 | 0.6 | |
| 130 °C | ECM | 1644.45 | 1558.94 | 1601.70 | 42.78 | 2.7 |
| SBT | 1584.24 | 1671.48 | 1627.86 | 43.63 | 2.7 | |
| CBTE | 1660.58 | 1595.40 | 1627.99 | 32.59 | 2.0 |
| Item | a | b | c | d | e |
| Value | 0.04 | 0.5 | 0.5 | 0.04 | 0.54 |
| Item | f | g | h | Tg/°C | Trm/°C |
| Value | 0.50 | 0.50 | 0.50 | 185 | 23 |
| Elastic property | 80 °C | 130 °C | Strength (MPa) | 80 °C | 130 °C |
| E1 (GPa) | 160.7 | 156.6 | XT | 2941 | 2866 |
| E2, E3 (GPa) | 7.245 | 5.24 | XC | 936 | 661 |
| G12, G13 (GPa) | 3.33 | 2.41 | YT, ZT | 56.8 | 41.2 |
| G23 (GPa) | 2.44 | 1.76 | YC, ZC | 224 | 162 |
| ν12, ν13 | 0.33 | 0.33 | S12, S13 | 138 | 100 |
| ν23 | 0.485 | 0.487 | S23 | 84 | 61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Jiang, L.; Li, L.; Zhao, J. An Experimental and Numerical Study of the Influence of Temperature on Mode II Fracture of a T800/Epoxy Unidirectional Laminate. Materials 2022, 15, 8108. https://doi.org/10.3390/ma15228108
Gong Y, Jiang L, Li L, Zhao J. An Experimental and Numerical Study of the Influence of Temperature on Mode II Fracture of a T800/Epoxy Unidirectional Laminate. Materials. 2022; 15(22):8108. https://doi.org/10.3390/ma15228108
Chicago/Turabian StyleGong, Yu, Linfei Jiang, Linkang Li, and Jian Zhao. 2022. "An Experimental and Numerical Study of the Influence of Temperature on Mode II Fracture of a T800/Epoxy Unidirectional Laminate" Materials 15, no. 22: 8108. https://doi.org/10.3390/ma15228108
APA StyleGong, Y., Jiang, L., Li, L., & Zhao, J. (2022). An Experimental and Numerical Study of the Influence of Temperature on Mode II Fracture of a T800/Epoxy Unidirectional Laminate. Materials, 15(22), 8108. https://doi.org/10.3390/ma15228108








