Kinetic Energy-Based Indicators to Compare Different Load Models of a Mobile Crane
Abstract
1. Introduction
2. Mathematical Models of the System
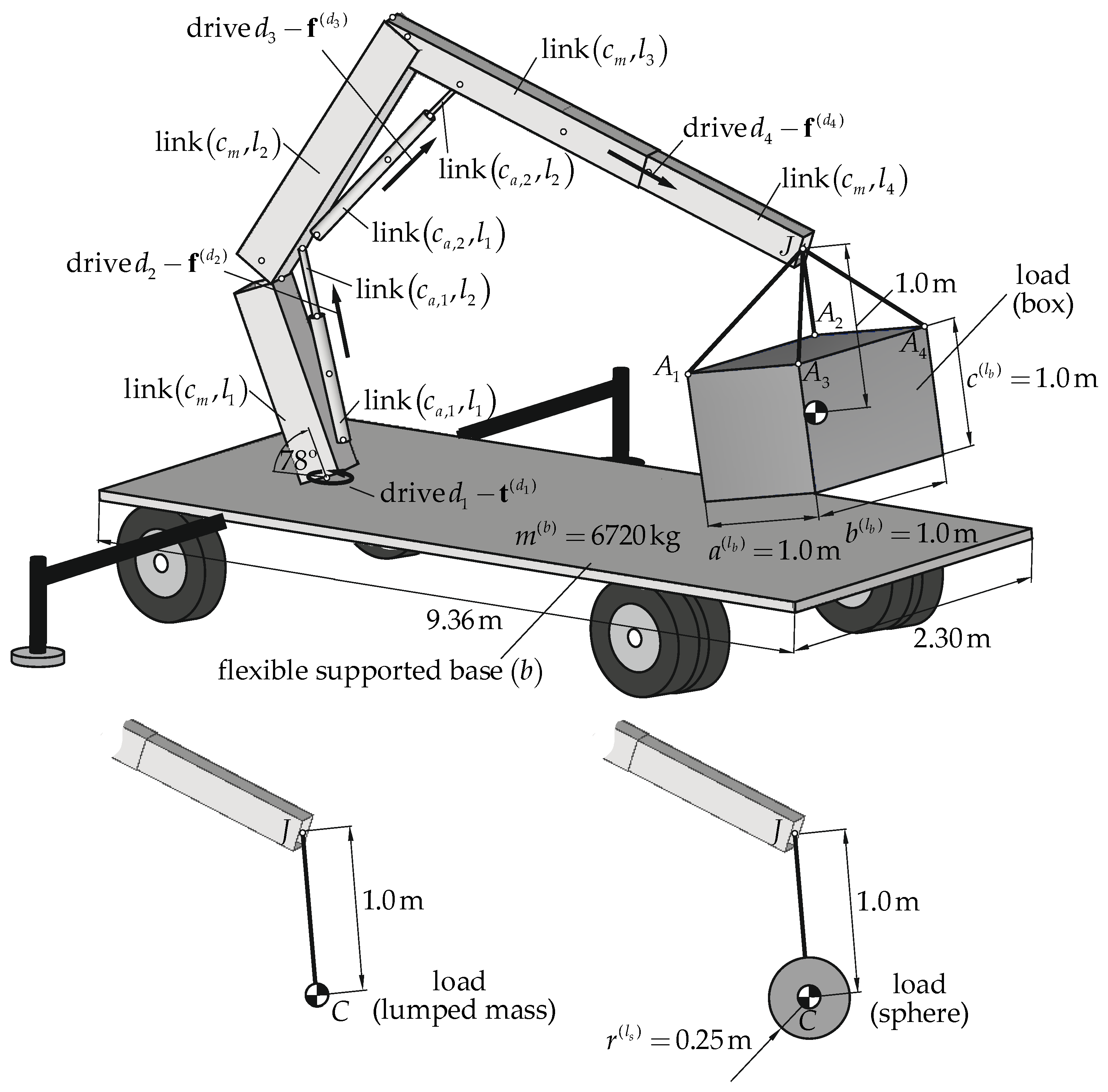
- Crane suspension subsystem. This system was modeled in the form of the flexible, supported base mounted on the ground by means of the system of wheels and outriggers. The wheels and outriggers systems were modeled using spring-damping elements.
- Supporting structure. This system contained the rotary column, two boom systems, and the telescopic boom section. It was modeled in the form of the open-loop kinematic chain (called the main chain—).
- Main load lifting subsystems. These systems refer to the hydraulic cylinders. They were modeled in the form of the closed-loop kinematic chain (called the auxiliary chains—).
- Load suspension subsystem. A carried load was modeled in three variants: as a lumped mass on one hook-sling (3 dofs), as a sphere on one hook-sling (6 dofs), and as a box on four hook-slings (6 dofs). The rope was modeled using spring-damping elements.
- are the vectors defining the motion of the crane and the load,
- is the vector describing the motion of the base, ,
- is the vector defining the motion of the supporting structure of the crane,
- ,
- and are the vectors describing the motions of the main load lifting systems (hydraulic cylinders). , , and
- are the mass matrices of the crane and load,
- are the constraint matrices related to the cut-joints and drives,
- is the vector of unknown reaction forces in the cut-joints,
- is the vector of the unknown driving torque and forces,
- are the vectors of the right side of the dynamics equations,
- ,
- are the vectors of the Coriolis, gyroscopic, and centrifugal forces,
- are the vectors of the gravity forces,
- is the vector of the spring and damping forces formulated to the wheels and outriggers,
- are the vectors of the spring and damping force(s) formulated to the rope(s),
- and are the vectors of the right side of the constraints.
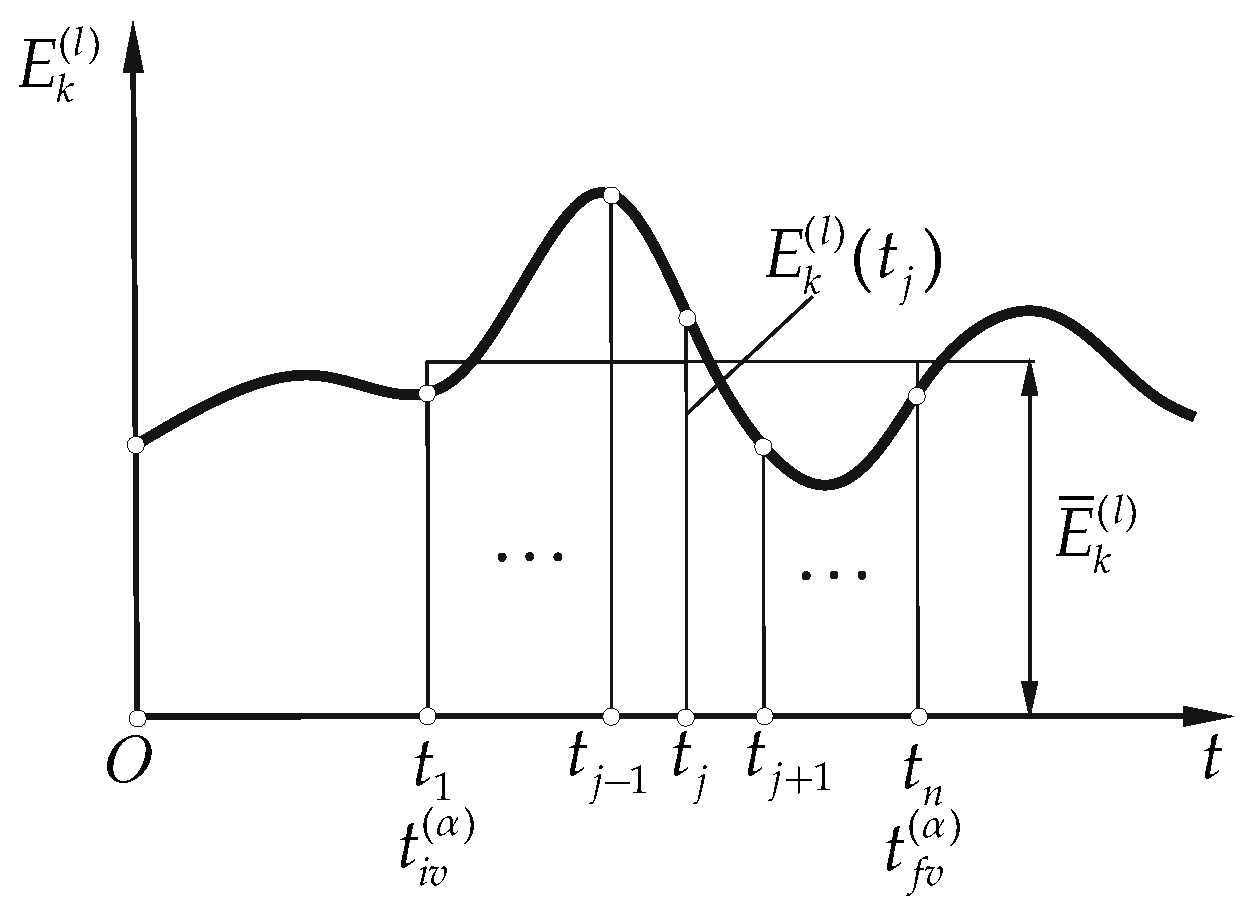
3. Numerical Results
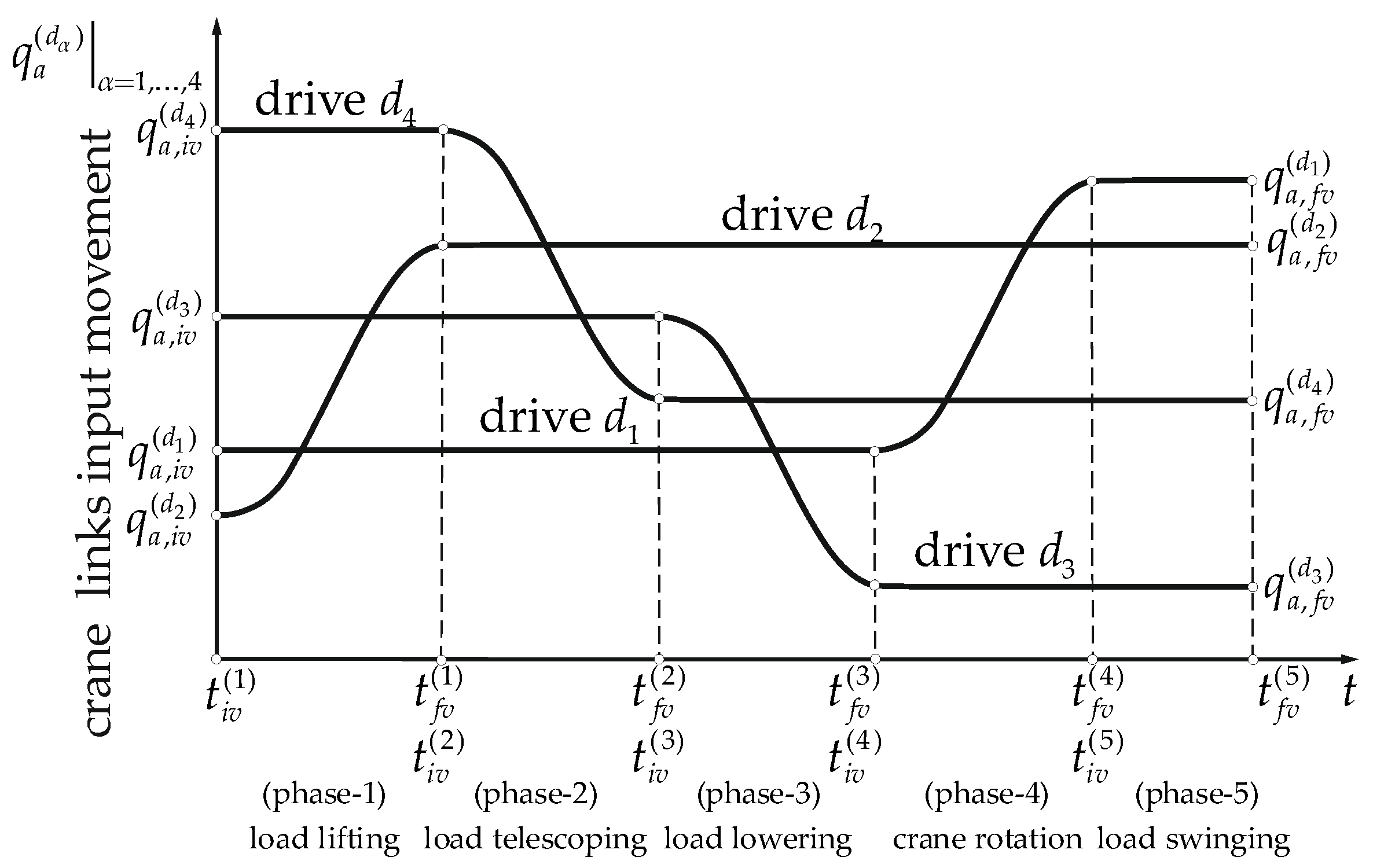
- load lifting—movement performed by drive for ;
- load telescoping—movement performed by drive for ;
- load lowering—movement performed by drive for ;
- crane rotation—movement performed by drive for ;
- load swinging—for .
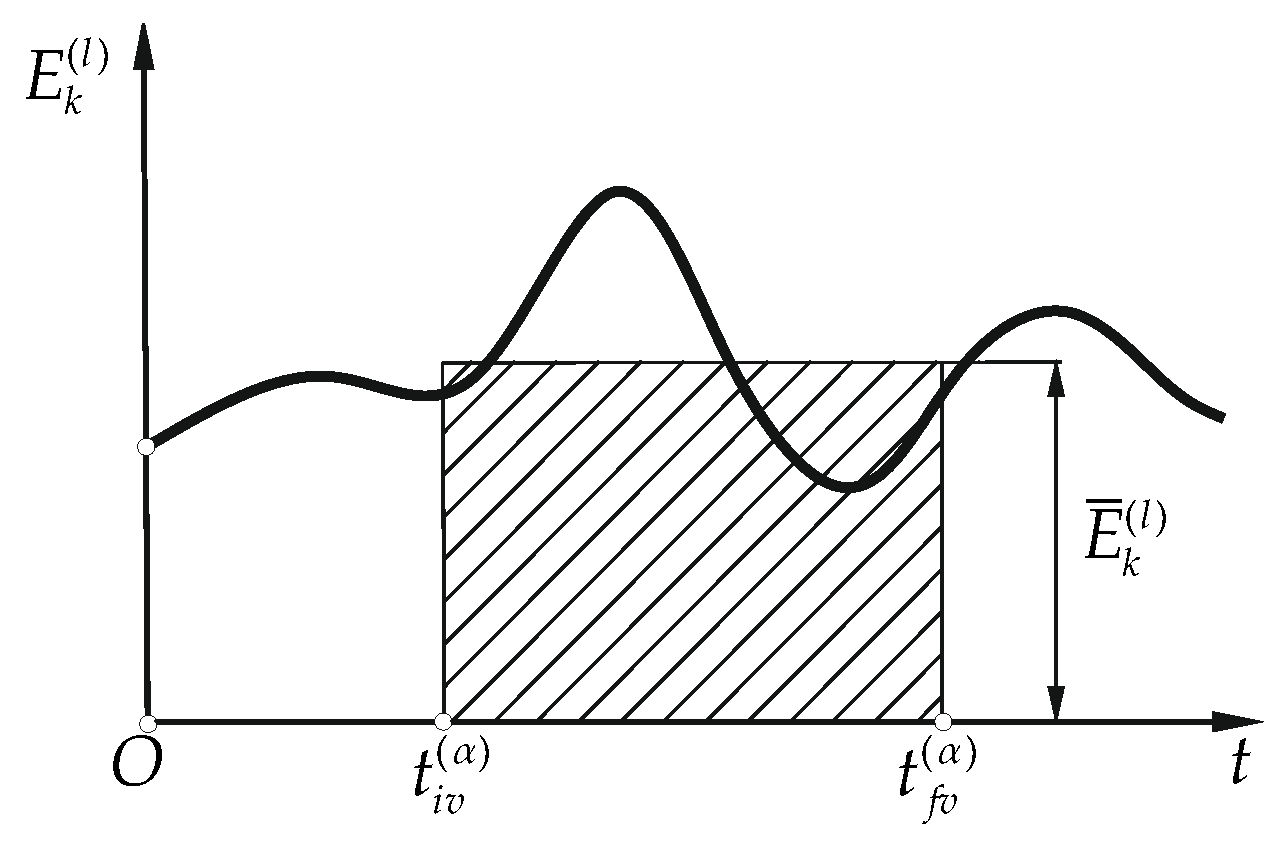
- is the mass of the load,
- is the transformation matrix describing the position and orientation of the load,
- is the pseudo-inertia matrix of the load [26],
- and is a trace of the matrix.
4. Discussion
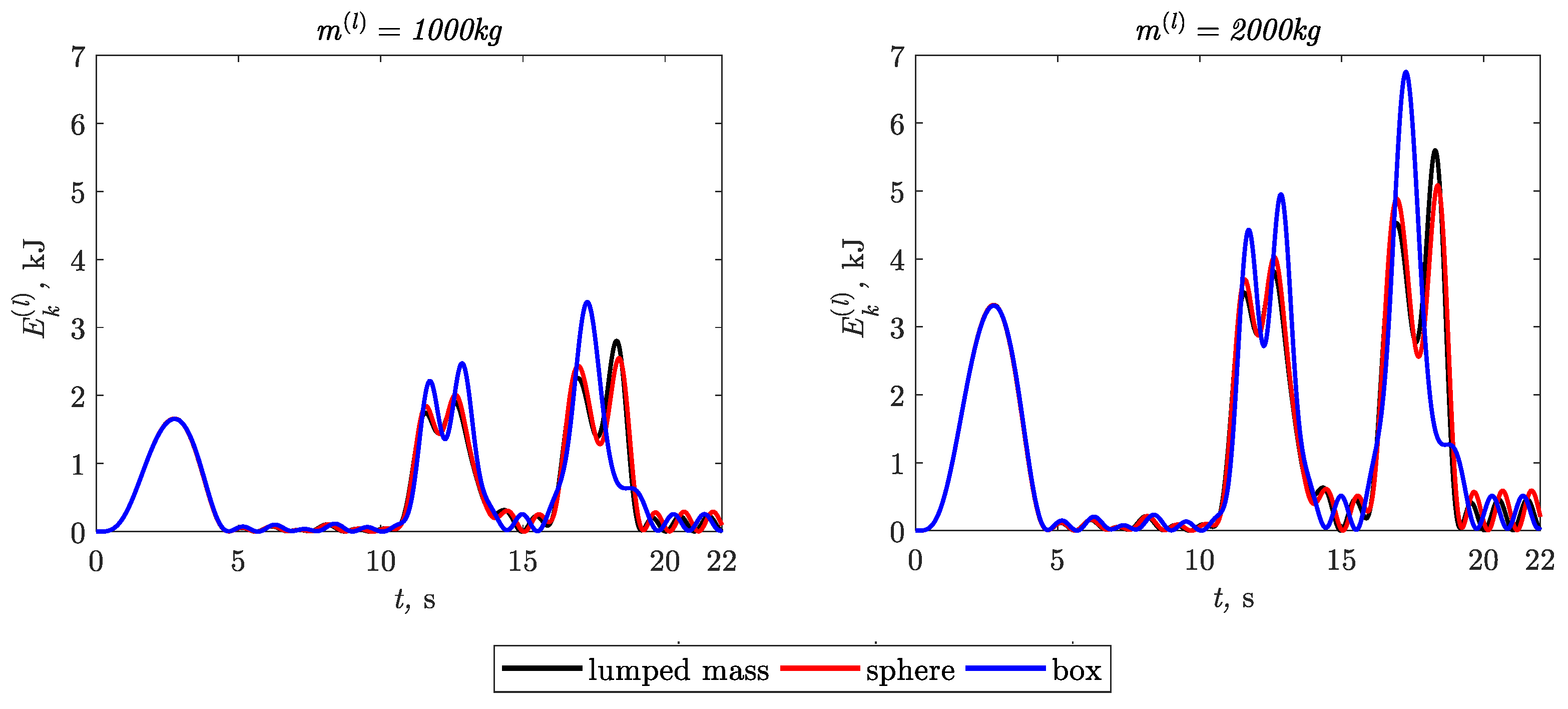
- The load modeling methods influence not only the maximum values but also the characters of the time courses of the kinetic energy in particular movement phases.
- The largest percentages of deviations in relation to the load reference model (load modeled as a lumped mass) are:
- −
- 22.3% in phase-5, when the load was modeled in the form of a sphere;
- −
- 23.0% in phase-3, when the load was modeled in the form of a box.
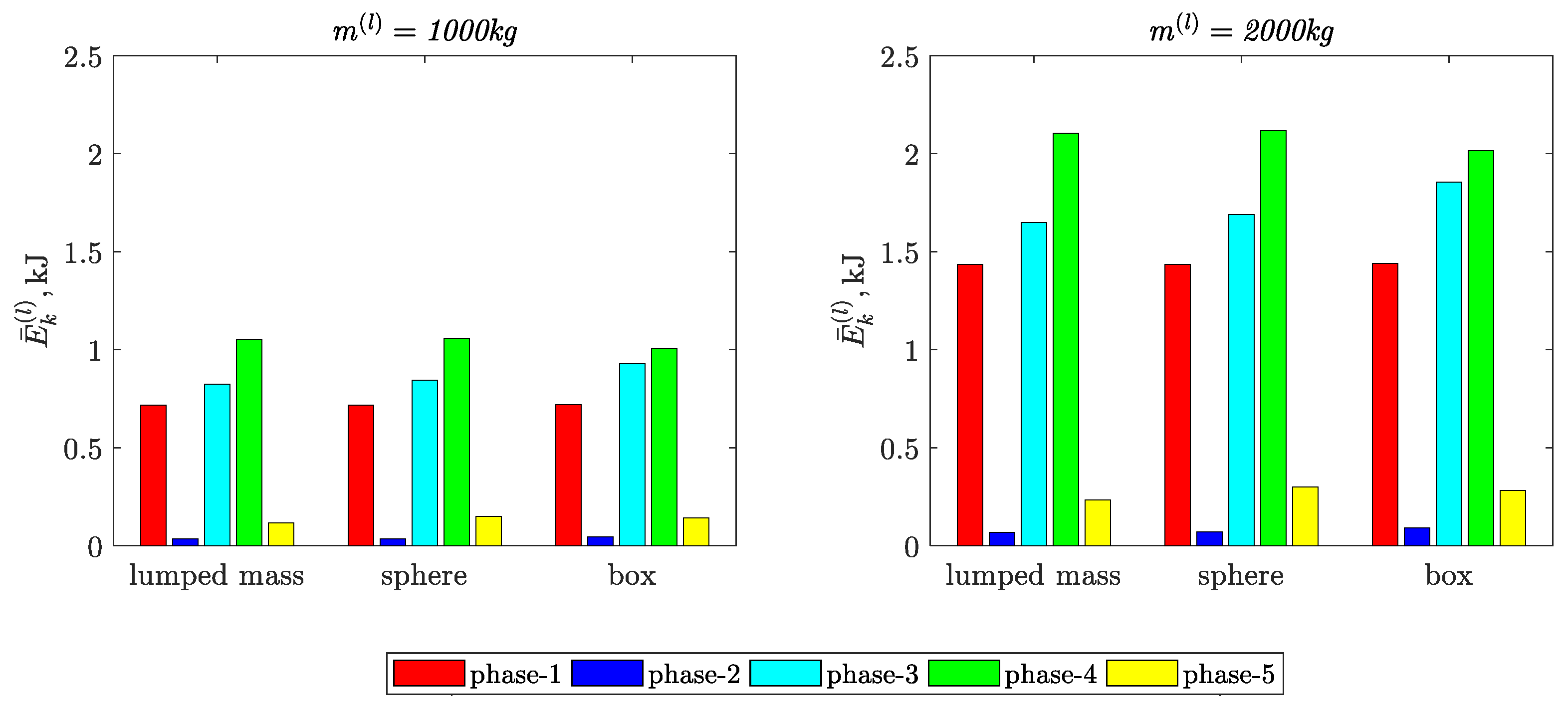
- The largest values of the relative percentage deviations of the kinetic energy integral mean values are:
- −
- 22.5% in phase-5, when the load was modeled in the form of a sphere;
- −
- 24.3% in phase-2, when the load was modeled in the form of a box.
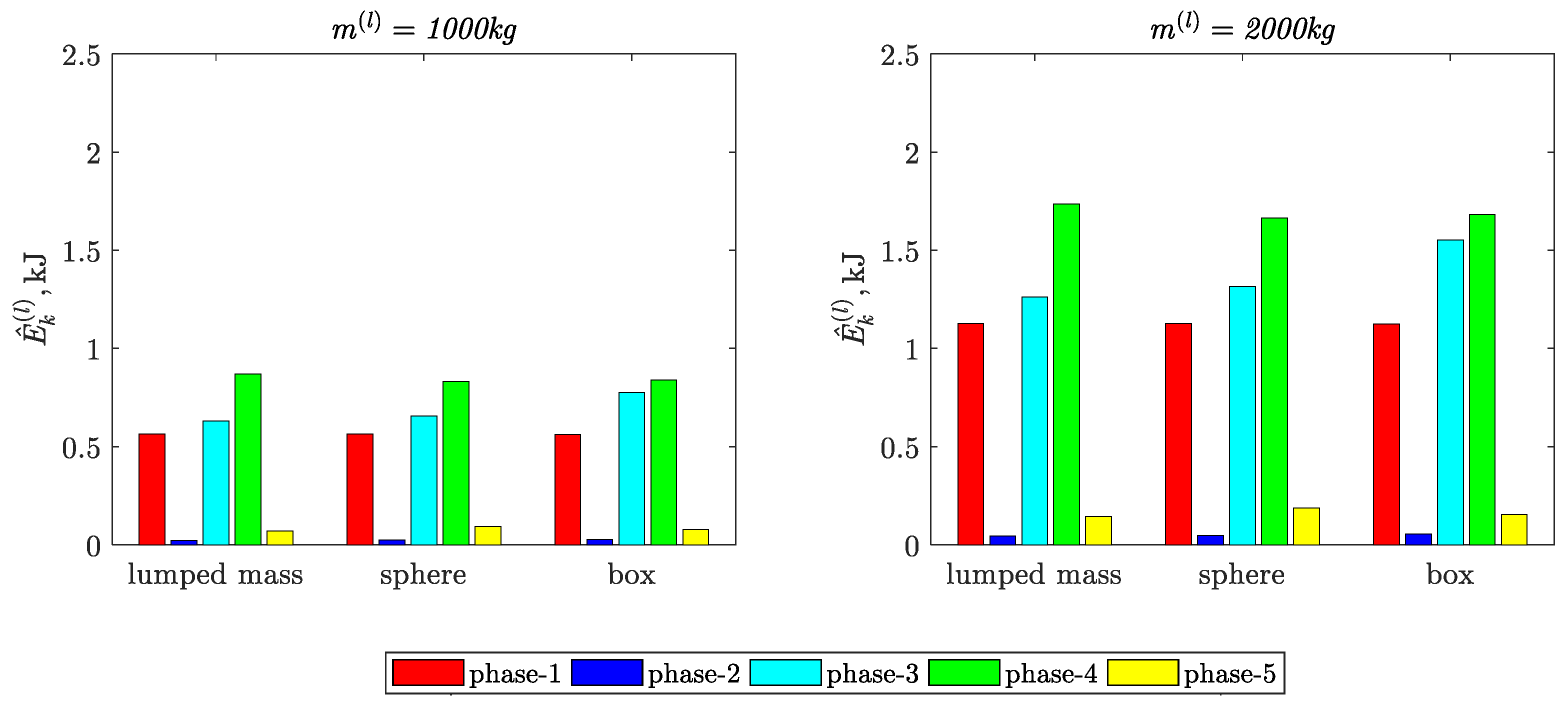
- The largest values of the relative percentage deviations of the kinetic energy arithmetic average deviation from the integral mean values are:
- −
- 23% in phase-5, when the load was modeled in the form of a sphere;
- −
- 18.9% in phase-3, when the load was modeled in the form of a box.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Ziyad, N.; Masoud, Z.N. Dynamics and Control of Cranes: A Review. J. Vib. Control. 2003, 9, 863–908. [Google Scholar] [CrossRef]
- Maczyński, A. Load positioning and minimization of load oscillations in rotary cranes. J. Theor. Appl. Mech. 2003, 41, 873–885. [Google Scholar]
- Maczyński, A.; Wojciech, S. Dynamics of a mobile crane and optimisation of the slewing motion of its upper structure. Int. J. Nonlinear Dyn. 2003, 32, 259–290. [Google Scholar] [CrossRef]
- Urbaś, A.; Augustynek, K. Mathematical model of a crane with taking into account friction phenomena in actuators. In Multibody Dynamics 2019, Proceedings of the 9th Eccomas Thematic Conference on Multibody Dynamics, Warsaw, Poland, 29 June–2 July; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 299–306. [Google Scholar]
- Amer, W.S. The dynamical motion of a gyroscope subjected to applied moments. Results Phys. 2019, 12, 1429–1435. [Google Scholar] [CrossRef]
- Amer, T.S.; Galal, A.A.; Abady, I.M.; Elkafly, H.F. The dynamical motion of a gyrostat for the irrational frequency case. Appl. Math. Model. 2021, 89, 1235–1267. [Google Scholar] [CrossRef]
- Cha, J.-H.; Roh, M.-I.; Lee, K.-Y. Dynamic response simulation of a heavy cargo suspended by a floating crane based on multibody system dynamics. Ocean. Eng. 2010, 37, 1273–1291. [Google Scholar] [CrossRef]
- Park, K.-P.; Cha, J.-H.; Lee, K.-Y. Dynamic factor analysis considering elastic boom effects in heavy lifting operations. Ocean. Eng. 2011, 38, 1100–1113. [Google Scholar] [CrossRef]
- Cibicik, A.; Egeland, O. Dynamic modelling and force analysis of a knuckle boom crane using screw theory. Mech. Mach. Theory 2018, 133, 179–194. [Google Scholar] [CrossRef]
- Cibicik, A.; Pedersen, E.; Egeland, O. Dynamics of luffing motion of a flexible knuckle boom crane actuated by hydraulic cylinders. Mech. Mach. Theory 2019, 143, 103616. [Google Scholar] [CrossRef]
- Cibicik, A.; Tysse, G.O.; Egeland, O. Determination of reaction forces of a deck crane in wave motion using screw theory. J. Offshore Mech. Arct. Eng. 2019, 141, 1–41. [Google Scholar] [CrossRef]
- Gao, T.; Huang, J.; Singhose, W. Eccentric-load dynamics and oscillation control of industrial cranes transporting heterogeneous loads. Mech. Mach. Theory 2022, 172, 104800. [Google Scholar] [CrossRef]
- Kacalak, W.; Budniak, Z.; Majewski, M. Stability assessment as a criterion of stabilization of the movement trajectory of mobile crane working elements. Int. J. Appl. Mech. Eng. 2018, 23, 65–77. [Google Scholar] [CrossRef]
- Kacalak, W.; Budniak, Z.; Majewski, M. Computer aided analysis of the mobile crane handling system using computational intelligence methods. Adv. Intell. Syst. Comput. 2018, 662, 250–261. [Google Scholar]
- Arena, A.; Casalotti, A.; Lacarbonara, W.; Cartmell, M.P. Dynamics of container cranes: Three-dimensional modeling, full-scale experiments, and identification. Int. J. Mech. Sci. 2015, 93, 8–21. [Google Scholar] [CrossRef]
- Cekus, D.; Kwiatoń, P. Effect of the rope system deformation on the working cycle of the mobile crane during interaction of wind pressure. Mech. Mach. Theory 2020, 153, 104011. [Google Scholar] [CrossRef]
- Cekus, D.; Kwiatoń, P. Method of determining the effective surface area of a rigid body under wind disturbances. Arch. Appl. Mech. 2021, 91, 1–14. [Google Scholar] [CrossRef]
- Cekus, D.; Kwiatoń, P.; Geisler, T. The dynamic analysis of load motion during the interaction of wind pressure. Meccanica 2021, 56, 785–796. [Google Scholar] [CrossRef]
- Posiadała, B.; Warys, P.; Cekus, D.; Tomala, M. The Dynamics of the forest crane during the load carrying. Int. J. Struct. Stab. Dyn. 2013, 13, 7. [Google Scholar] [CrossRef]
- La Hera, P.; Morales, D.O. Model-Based Development of Control Systems for Forestry Cranes. J. Control Sci. Eng. 2015, 2015, 256951. [Google Scholar] [CrossRef][Green Version]
- Urbaś, A.; Szczotka, M. The influence of the friction phenomenon on a forest crane operators level of discomfort. Maint. Reliab. 2019, 21, 197–210. [Google Scholar]
- Urbaś, A.; Augustynek, K.; Stadnicki, J. Kinetic energy based indicators to compare different load models of a mobile crane. In Proceedings of the Abstracts of 30th Conference Vibrations in Physical Systems–VIBSYS 2022, Poznań, Poland, 26–28 September 2022; pp. 84–85. [Google Scholar]
- Legnani, G.; Casalo, F.; Righettini, P.; Zappa, B. A homogeneous matrix approach to 3D kinematics and dynamics—I. Theory. Mech. Mach. Theory 1996, 31, 5. [Google Scholar] [CrossRef]
- Legnani, G.; Casalo, F.; Righettini, P.; Zappa, B. A homogeneous matrix approach to 3D kinematics and dynamics—II. Applications to chains of rigid bodies and serial manipulators. Mech. Mach. Theory 1996, 31, 5. [Google Scholar] [CrossRef]
- Urbaś, A.; Augustynek, K.; Martsenyuk, V. The influence of the load modeling methods on dynamics of a mobile crane. In Perspectives in Dynamical Systems II: Mathematical and Numerical Approaches; Springer Proceedings in Mathematics and Statistics: Berlin/Heidelberg, Germany, 2023; in print. [Google Scholar]
- Jurevič, E.I. (Ed.) Dynamics of Robot Control; Nauka: Moscow, Rusia, 1984. [Google Scholar]

| Link | Length, m | Cross-Section, mm |
|---|---|---|
| Phase-1 | Phase-2 | Phase-3 | Phase-4 | Phase-5 | ||
|---|---|---|---|---|---|---|
| 1000 kg | lumped mass | 1.661 | 0.106 | 1.907 | 2.805 | 0.227 |
| sphere | 1.660; (−0.04) | 0.108; (1.25) | 2.000; (5.13) | 2.550; (−10.01) | 0.292; (22.32) | |
| box | 1.656; (−0.31) | 0.117; (8.93) | 2.474; (22.93) | 3.373; (16.85) | 0.258; (11.89) | |
| 2000 kg | lumped mass | 3.323 | 0.213 | 3.819 | 5.599 | 0.458 |
| sphere | 3.322; (−0.04) | 0.216; (1.27) | 4.027; (5.18) | 5.084; (−10.14) | 0.590; (22.28) | |
| box | 3.312; (−0.33) | 0.234; (8.89) | 4.950; (22.85) | 6.752; (17.07) | 0.513; (10.61) | |
| Phase-1 | Phase-2 | Phase-3 | Phase-4 | Phase-5 | ||
|---|---|---|---|---|---|---|
| 1000 kg | lumped mass | 0.717 | 0.034 | 0.824 | 1.052 | 0.115 |
| sphere | 0.718; (0.06) | 0.035; (3.45) | 0.845; (2.41) | 1.058; (0.62) | 0.149; (22.50) | |
| box | 0.720; (0.43) | 0.045; (24.38) | 0.927; (11.09) | 1.008; (−4.35) | 0.142; (18.46) | |
| 2000 kg | lumped mass | 1.434 | 0.068 | 1.650 | 2.105 | 0.233 |
| sphere | 1.435; (0.06) | 0.071; (3.46) | 1.691; (2.41) | 2.117; (0.59) | 0.300; (22.39) | |
| box | 1.440; (0.42) | 0.090; (24.37) | 1.855; (11.04) | 2.016; (−4.38) | 0.282; (17.34) | |
| Phase-1 | Phase-2 | Phase-3 | Phase-4 | Phase-5 | ||
|---|---|---|---|---|---|---|
| 1000 kg | lumped mass | 0.563 | 0.023 | 0.630 | 0.869 | 0.071 |
| sphere | 0.563; (0) | 0.024; (3.62) | 0.657; (4.18) | 0.833; (−4.33) | 0.092; (23.04) | |
| box | 0.563; (−0.10) | 0.028; (17.41) | 0.776; (18.87) | 0.839; (−3.51) | 0.078; (8.54) | |
| 2000 kg | lumped mass | 1.127 | 0.046 | 1.261 | 1.736 | 0.144 |
| sphere | 1.127; (−0.01) | 0.048; (3.62) | 1.316; (4.18) | 1.664; (−4.35) | 0.187; (23.00) | |
| box | 1.126; (−0.10) | 0.056; (17.35) | 1.553; (18.79) | 1.682; (−3.21) | 0.155; (7.08) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urbaś, A.; Augustynek, K.; Stadnicki, J. Kinetic Energy-Based Indicators to Compare Different Load Models of a Mobile Crane. Materials 2022, 15, 8156. https://doi.org/10.3390/ma15228156
Urbaś A, Augustynek K, Stadnicki J. Kinetic Energy-Based Indicators to Compare Different Load Models of a Mobile Crane. Materials. 2022; 15(22):8156. https://doi.org/10.3390/ma15228156
Chicago/Turabian StyleUrbaś, Andrzej, Krzysztof Augustynek, and Jacek Stadnicki. 2022. "Kinetic Energy-Based Indicators to Compare Different Load Models of a Mobile Crane" Materials 15, no. 22: 8156. https://doi.org/10.3390/ma15228156
APA StyleUrbaś, A., Augustynek, K., & Stadnicki, J. (2022). Kinetic Energy-Based Indicators to Compare Different Load Models of a Mobile Crane. Materials, 15(22), 8156. https://doi.org/10.3390/ma15228156





