Analysis of Acousto-Optic Figure of Merit in KGW and KYW Crystals
Abstract
:1. Introduction
2. Materials and Methods
2.1. KREW Crystals’ Physical Properties
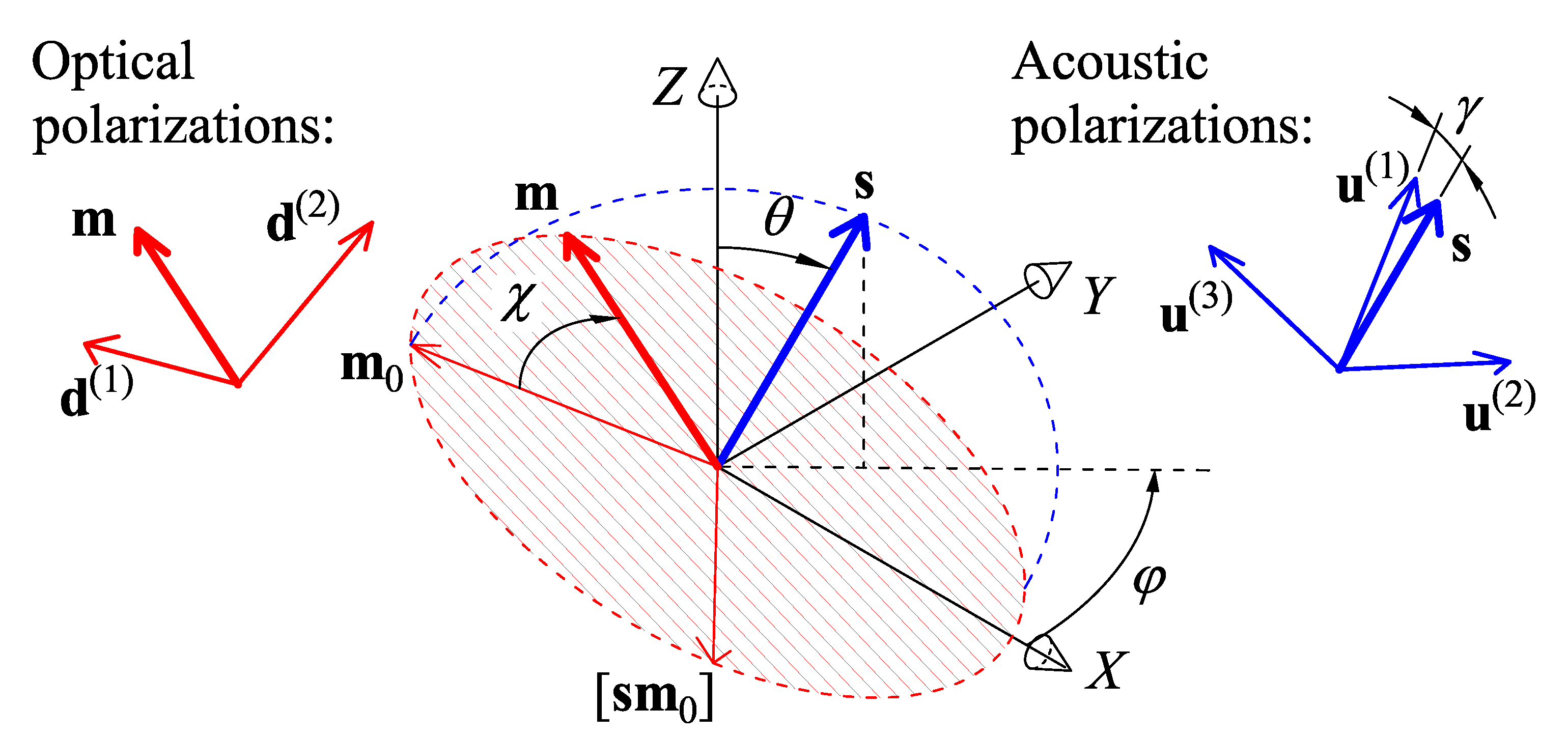
2.2. Acousto-Optic Figure of Merit
2.3. Software
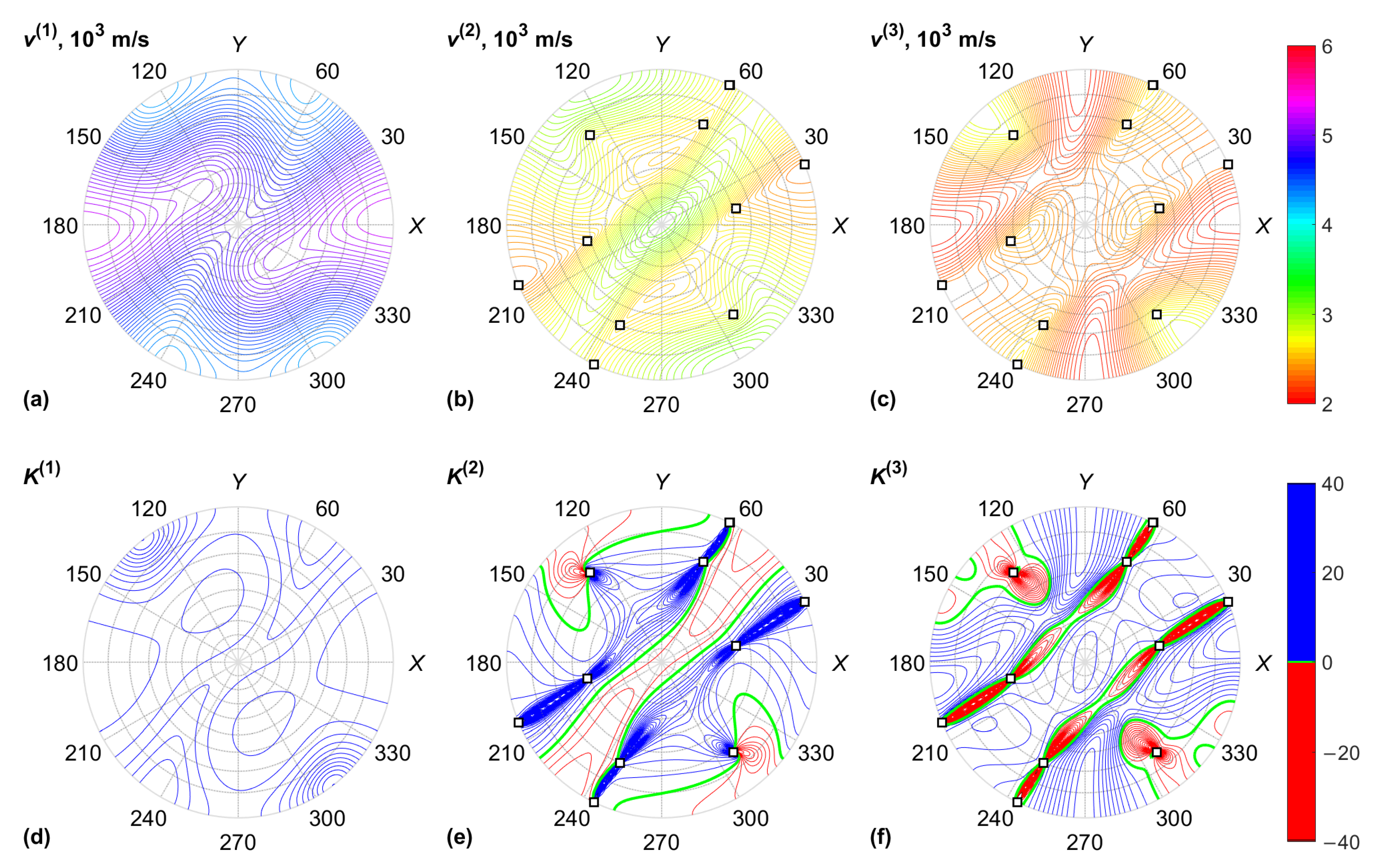
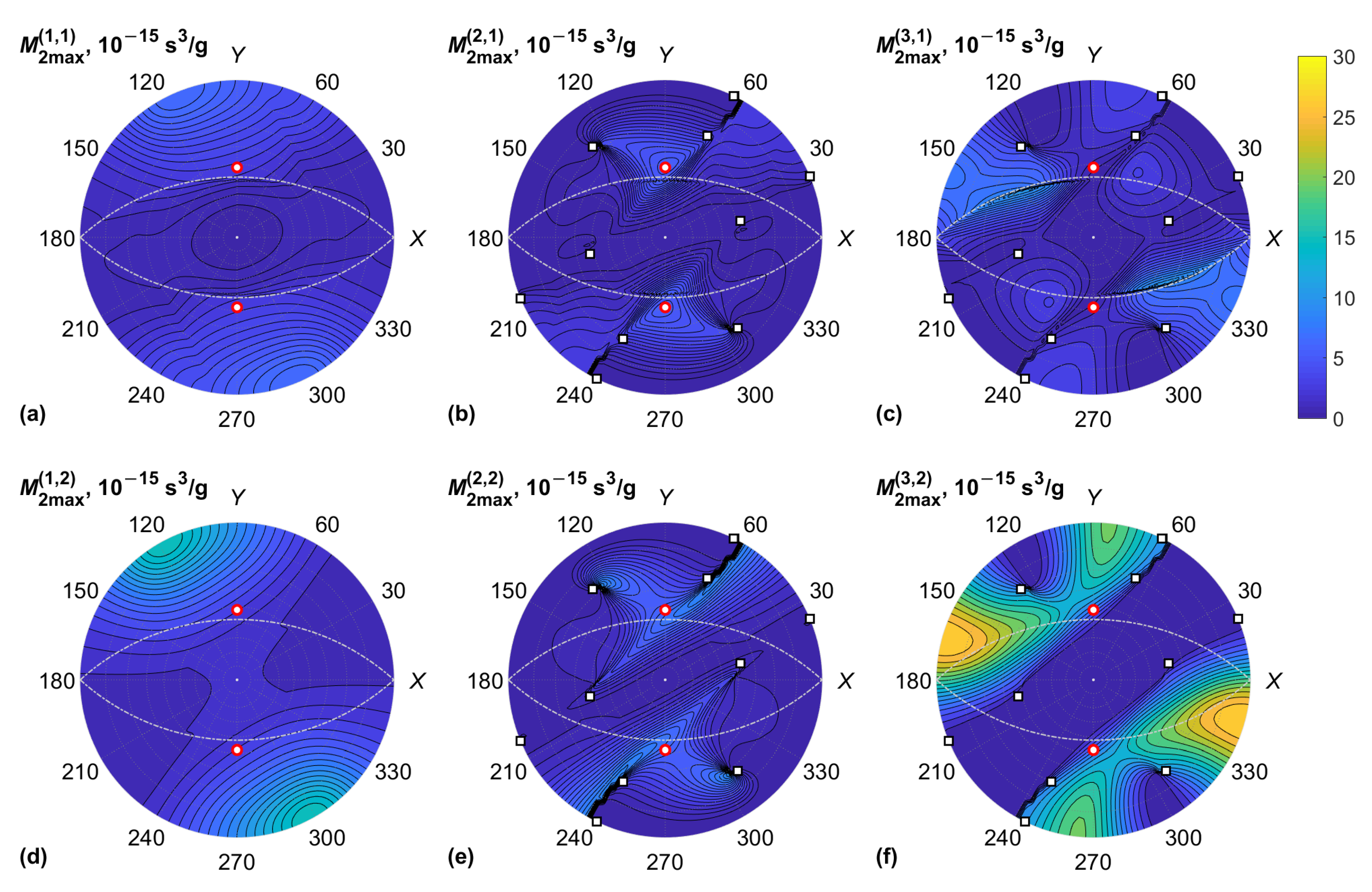
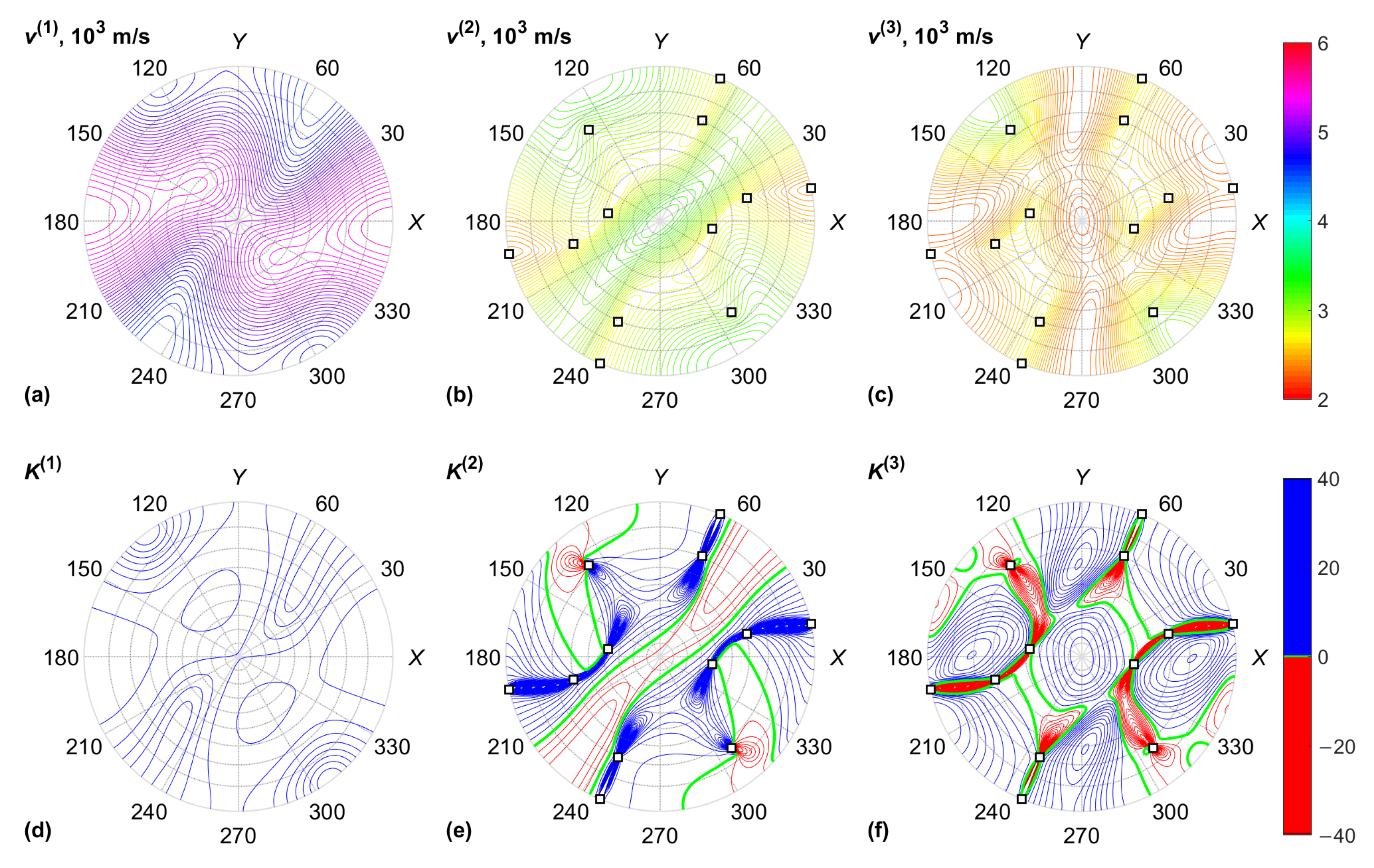
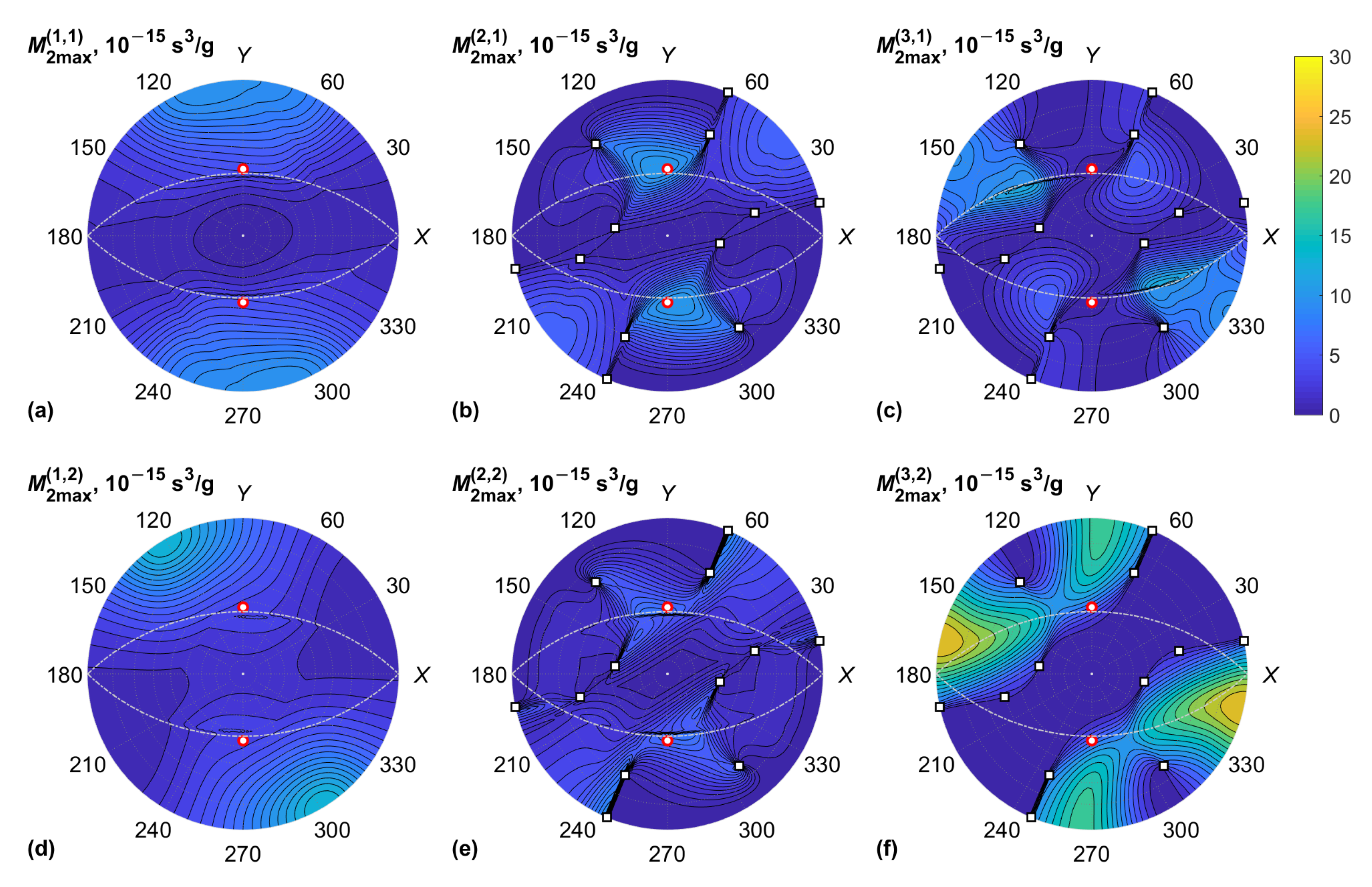
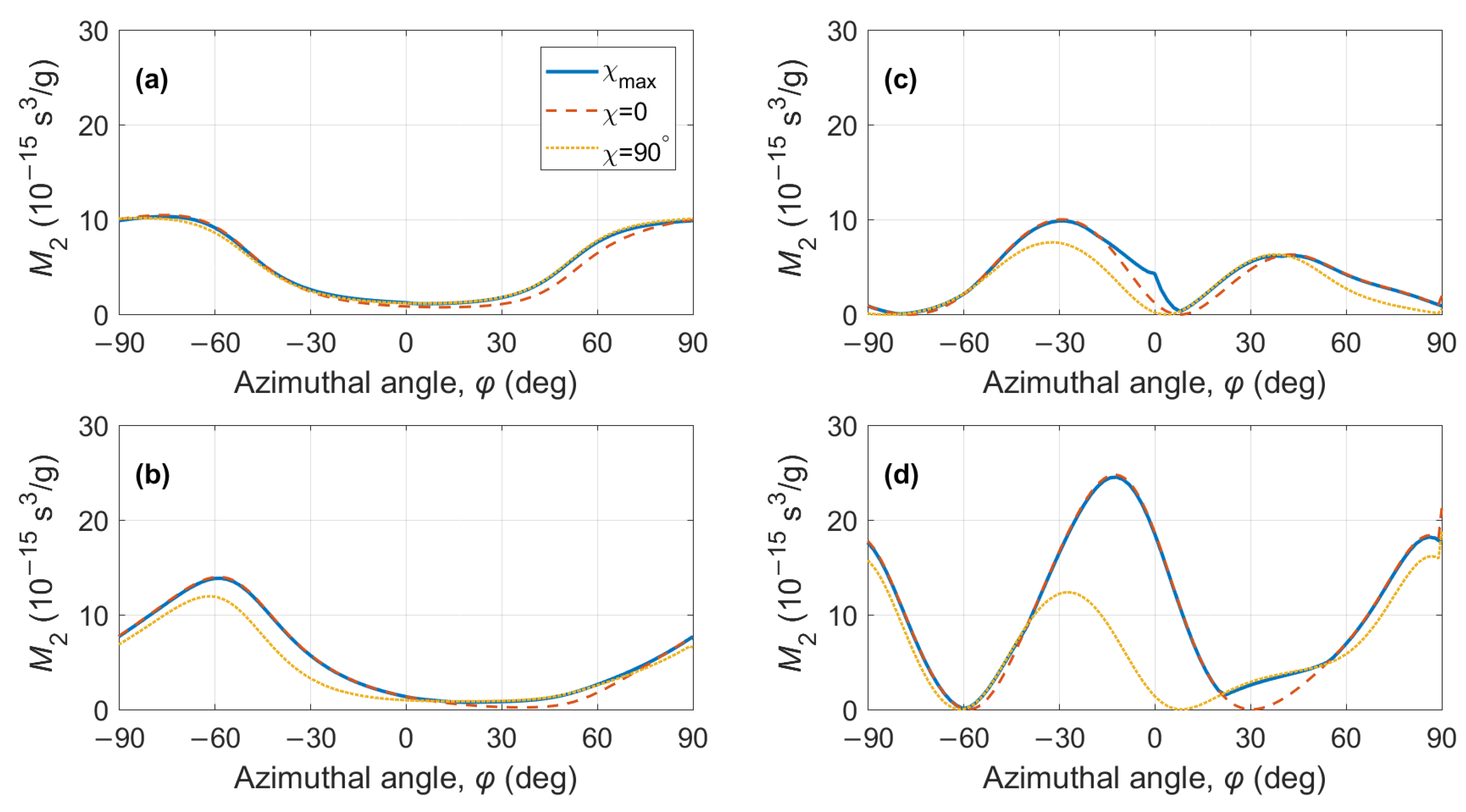
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AO | Acousto-optic |
| BAW | Bulk acoustic wave |
| IR | Infrared |
| KGW | KGd(WO), potassium gadolinium tungstate |
| KREW | Potassium rare-earth tungstate |
| KYW | KY(WO), potassium yttrium tungstate |
| QL | Quasi-longitudinal |
| QS | Quasi-shear |
Appendix A
Appendix A.1
Appendix A.2
References
- Belyi, V.N.; Khilo, N.A.; Kurilkina, S.N.; Kazak, N.S. Spin-to-orbital angular momentum conversion for Bessel beams propagating along the optical axes of homogeneous uniaxial and biaxial crystals. J. Opt. 2013, 15, 044018. [Google Scholar] [CrossRef]
- Mazur, M.M.; Velikovskiy, D.Y.; Mazur, L.I.; Pavluk, A.A.; Pozhar, V.E.; Pustovoit, V.I. Elastic and photo-elastic characteristics of laser crystals potassium rare-earth tungstates KRE(WO4)2, where RE = Y, Yb, Gd and Lu. Ultrasonics 2014, 54, 1311–1317. [Google Scholar] [CrossRef]
- Mazur, M.M.; Mazur, L.I.; Pozhar, V.E. Optimum configuration for acousto-optical modulator made of KGW. Phys. Proc. 2015, 70, 741–744. [Google Scholar] [CrossRef] [Green Version]
- Mazur, M.M.; Mazur, L.I.; Pozhar, V.E. Optimal configuration of an acoustooptic modulator based on a KY(WO4)(2) crystal. Tech. Phys. Lett. 2015, 41, 249–251. [Google Scholar] [CrossRef]
- Belyi, V.N.; Kulak, G.V.; Krokh, G.V.; Shakin, O.V. Collinear acousto-optical transformation of Bessel light beams in biaxial gyrotropic crystals. J. Appl. Spectrosc. 2016, 83, 283–287. [Google Scholar] [CrossRef]
- Mazur, M.M.; Mazur, L.I.; Pozhar, V.E. Specific directions of ultrasound propagation in double potassium tungstates for light modulation. Ultrasonics 2017, 73, 231–235. [Google Scholar] [CrossRef] [PubMed]
- Mazur, M.M.; Mazur, L.I.; Pozhar, V.E.; Shorin, V.N.; Konstantinov, Y.P. Acousto-optic modulators based on a KYW crystal. Quantum Electron. 2017, 47, 661–664. [Google Scholar] [CrossRef]
- Martynyuk-Lototska, I.; Trach, I.; Kokhan, O.; Vlokh, R. Efficient acousto-optic crystal, TlInS2: Acoustic and elastic anisotropy. Appl. Opt. 2017, 56, 3179–3184. [Google Scholar] [CrossRef]
- Wu, Q.; Gao, Z.; Tian, X.; Su, X.; Li, G.; Sun, Y.; Xia, S.; He, J.; Tao, X. Biaxial crystal β-BaTeMo2O9: Theoretical analysis and the feasibility as high-efficiency acousto-optic Q-switch. Opt. Express 2017, 25, 24893–24900. [Google Scholar] [CrossRef]
- Mytsyk, B.; Kryvyy, T.; Demyanyshyn, N.; Mys, O.; Martynyuk-Lototska, I.; Kokhan, O.; Vlokh, R. Piezo-, elasto- and acousto-optic properties of Tl3AsS4 crystals. Appl. Opt. 2018, 57, 3796–3801. [Google Scholar] [CrossRef]
- Milkov, M.G.; Voloshinov, V.B.; Isaenko, L.I.; Vedenyapin, V.N. An experimental study of ultra-wide-band and ultra-wide-aperture non-collinear acousto-optic diffraction in an optically biaxial potassium arsenate titanyl crystal. Moscow Univ. Phys. Bull. 2018, 72, 83–88. [Google Scholar] [CrossRef]
- Kupreychik, M.I.; Balakshy, V.I. Peculiarities of acousto-optic interaction in biaxial crystal of alpha-iodic acid. Appl. Opt. 2018, 57, 5549–5555. [Google Scholar] [CrossRef] [PubMed]
- Kupreychik, M.I.; Balakshy, V.I. Investigation of close to collinear anisotropic acousto-optic interaction in a biaxial crystal of alpha-iodic acid. In Proceedings of the Fourteenth School on Acousto-Optics and Applications; Grulkowski, I., Linde, B.B.J., Duocastella, M., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11210, p. 112100O. [Google Scholar] [CrossRef]
- Yushkov, K.B.; Chizhikov, A.I.; Naumenko, N.F.; Molchanov, V.Y.; Pavlyuk, A.A.; Makarevskaya, E.V.; Zakharov, N.G. KYW crystal as a new material for acousto-optical Q-switches. In Proceedings of the Components and Packaging for Laser Systems V; Glebov, A.L., Leisher, P.O., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 10899, p. 1089913. [Google Scholar] [CrossRef]
- Pushkin, A.V.; Mazur, M.M.; Sirotkin, A.A.; Firsov, V.V.; Potemkin, F.V. Powerful 3-μm lasers acousto-optically Q-switched with KYW and KGW crystals. Opt. Lett. 2019, 44, 4837–4840. [Google Scholar] [CrossRef] [PubMed]
- Porokhovnichenko, D.L.; Dyakonov, E.A.; Kuznetsov, S.V.; Voronov, V.V.; Fedorov, P.P.; Zaramenskikh, K.S.; Gasanov, A.A.; Zhukova, L.V.; Korsakov, A.S.; Salimgareev, D.D. Indium iodide single crystal: Breakthrough material for infrared acousto-optics. Opt. Lett. 2020, 45, 3435–3438. [Google Scholar] [CrossRef] [PubMed]
- Mazur, M.M.; Mazur, L.I.; Sirotkin, A.A.; Ryabinin, A.V.; Shorin, V.N. Acousto-optic modulators of high-power laser radiation on the basis of KGW and KYW crystals. Quantum Electron. 2020, 50, 957–961. [Google Scholar] [CrossRef]
- Chizhikov, A.I.; Molchanov, V.Y.; Naumenko, N.F.; Yushkov, K.B. Acousto-optic spatial light modulator (SLM) based on KYW crystal. In Proceedings of the Laser Beam Shaping XX; Dudley, A., Laskin, A.V., Eds.; SPIE: Bellingham, WA, USA, 2020; Volume 11486, p. 114860B. [Google Scholar] [CrossRef]
- Kupreychik, M.I.; Balakshy, V.I.; Pozhar, V.E. Wide-angle acousto-optic devices based on isotropic light scattering in biaxial crystals. J. Phys. Conf. Ser. 2021, 2091, 012010. [Google Scholar] [CrossRef]
- Yushkov, K.B. Noncritical acousto-optic Bragg phase matching: Analysis of orthorhombic and monoclinic crystal systems. Appl. Opt. 2021, 60, 7113–7121. [Google Scholar] [CrossRef]
- Yushkov, K.B.; Naumenko, N.F. Optical beam diffraction tensor in birefringent crystals. J. Opt. 2021, 60, 095602. [Google Scholar] [CrossRef]
- Chizhikov, A.I.; Naumenko, N.F.; Yushkov, K.B.; Molchanov, V.Y.; Pavlyuk, A.A. Acousto-optic modulation of light polarisation in monoclinic crystals. Quantum Electron. 2021, 51, 343–347. [Google Scholar] [CrossRef]
- Chizhikov, A.I.; Mukhin, A.V.; Egorov, N.A.; Gurov, V.V.; Molchanov, V.Y.; Naumenko, N.F.; Vorontsov, K.V.; Yushkov, K.B.; Zakharov, N.G. High-efficient KYW acousto-optic Q-switch for a Ho:YAG laser. Opt. Lett. 2022, 47, 1085–1088. [Google Scholar] [CrossRef]
- Kupreychik, M.I.; Yushkov, K.B. Topological evolution of acousto-optic transfer functions in biaxial crystals. J. Opt. Soc. Am. B Opt. Phys. 2022, 12. [Google Scholar] [CrossRef]
- Ristau, D. Laser-Induced Damage in Optical Materials; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Dieulesaint, E.; Royer, D. Ondes Élastiques Dans les Solides. Application au Traitment de signal; Mason: Paris, France, 1974. [Google Scholar]
- Goutzoulis, A.; Pape, D. Design and Fabrication of Acousto-Optic Devices; Marcel Dekker: New York, NY, USA, 1994; p. 497. [Google Scholar]
- Yushkov, K.; Naumenko, N. Acousto-Optic Figure of Merit of KREW Crystals;Version 1; Published on 24 October 24 2022. Available online: https://data.mendeley.com/datasets/cg38s35c8d/1 (accessed on 24 October 2022). [CrossRef]
- Naumenko, N.F.; Yushkov, K.B.; Molchanov, V.Y. Extreme acoustic anisotropy in crystals visualized by diffraction tensor. Eur. Phys. J. Plus 2021, 136, 95. [Google Scholar] [CrossRef]
- Loiko, P.; Segonds, P.; Inácio, P.L.; Peña, A.; Debray, J.; Rytz, D.; Filippov, V.; Yumashev, K.; Pujol, M.C.; Mateos, X.; et al. Refined orientation of the optical axes as a function of wavelength in three monoclinic double tungstate crystals KRE(WO4)2 (RE = Gd, Y or Lu). Opt. Mater. Express 2016, 6, 2984–2990. [Google Scholar] [CrossRef]
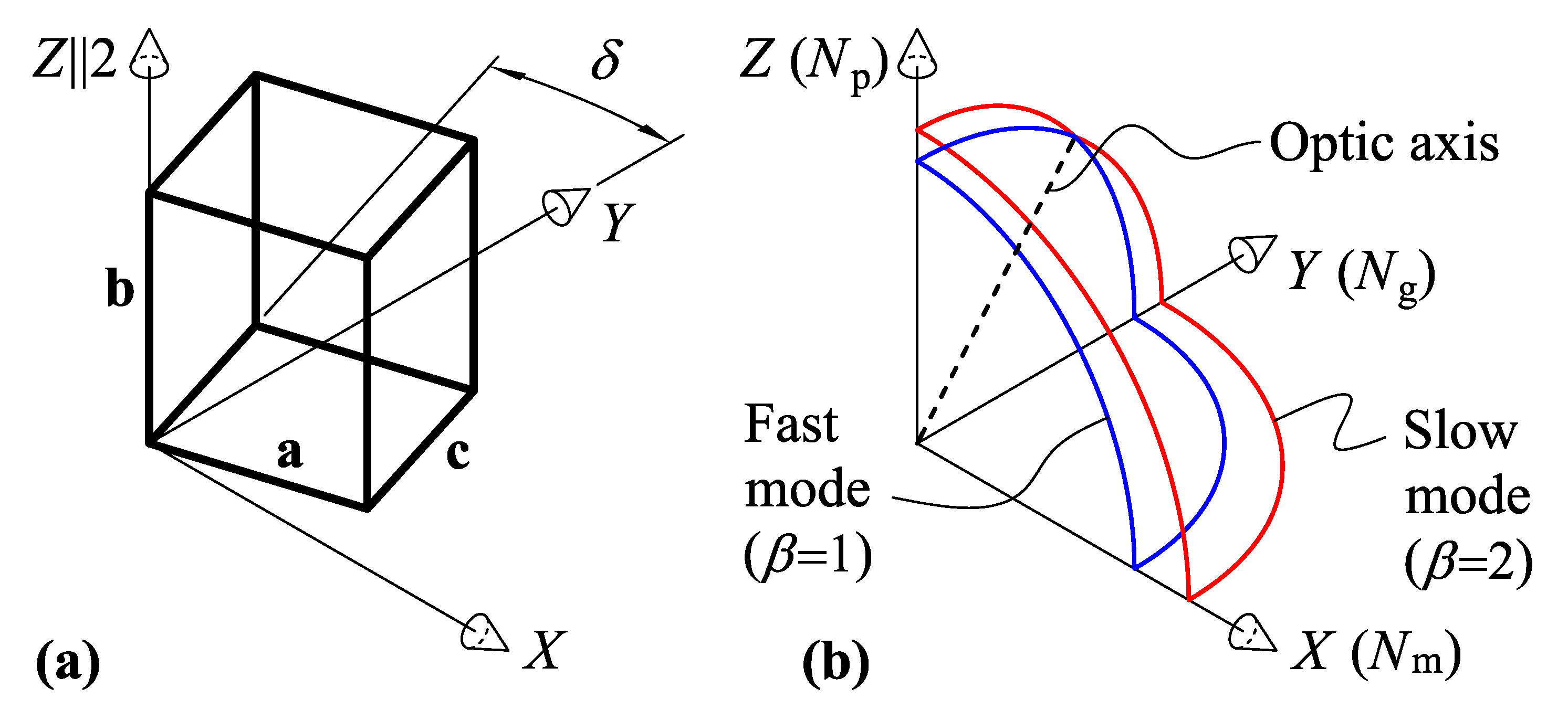

| Parameter | KGW Crystal | KYW Crystal | ||
|---|---|---|---|---|
| BAW mode, | 1 | 3 | 1 | 3 |
| Polarization type and angle, | QL () | QS () | QL () | QS () |
| Velocity, v ( m/s) | 4.33 | 2.22 | 4.73 | 2.38 |
| Azimuthal angle, | ||||
| Polar angle, | ||||
| Optical mode, | 2 | 2 | 2 | 2 |
| Rotation angle, | 0 | 0 | 0 | 0 |
| Figure of merit, ( s/g) | 15.8 | 27.8 | 13.8 | 24.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yushkov, K.B.; Naumenko, N.F.; Molchanov, V.Y. Analysis of Acousto-Optic Figure of Merit in KGW and KYW Crystals. Materials 2022, 15, 8183. https://doi.org/10.3390/ma15228183
Yushkov KB, Naumenko NF, Molchanov VY. Analysis of Acousto-Optic Figure of Merit in KGW and KYW Crystals. Materials. 2022; 15(22):8183. https://doi.org/10.3390/ma15228183
Chicago/Turabian StyleYushkov, Konstantin B., Natalya F. Naumenko, and Vladimir Ya. Molchanov. 2022. "Analysis of Acousto-Optic Figure of Merit in KGW and KYW Crystals" Materials 15, no. 22: 8183. https://doi.org/10.3390/ma15228183
APA StyleYushkov, K. B., Naumenko, N. F., & Molchanov, V. Y. (2022). Analysis of Acousto-Optic Figure of Merit in KGW and KYW Crystals. Materials, 15(22), 8183. https://doi.org/10.3390/ma15228183





