Study on the Magnetic Noise Characteristics of Amorphous and Nanocrystalline Inner Magnetic Shield Layers of SERF Co-Magnetometer
Abstract
1. Introduction
2. Magnetic Shield Noise Error Model Analysis
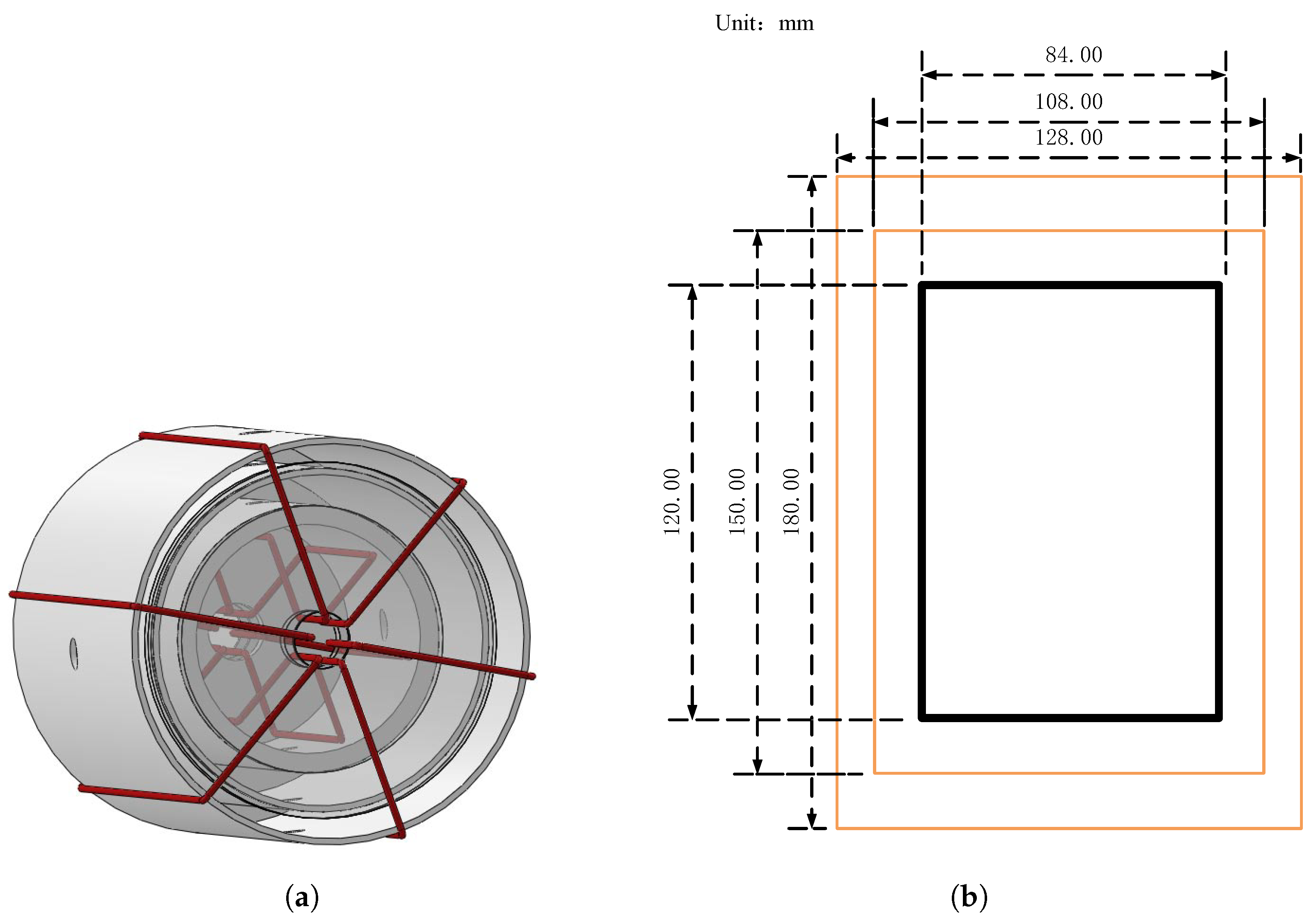
3. Experimental Setup
- 2-layer amorphous inner magnetic shield
- 4-layer amorphous inner magnetic shield
- 2-layer nanocrystalline inner magnetic shield
- 4-layer nanocrystalline inner magnetic shield
- 2-layer amorphous+aluminum inner magnetic shield
- 4-layer amorphous+aluminum inner magnetic shield
- 2-layer nanocrystalline+aluminum inner magnetic shield
- 4-layer nanocrystalline+aluminum inner magnetic shield
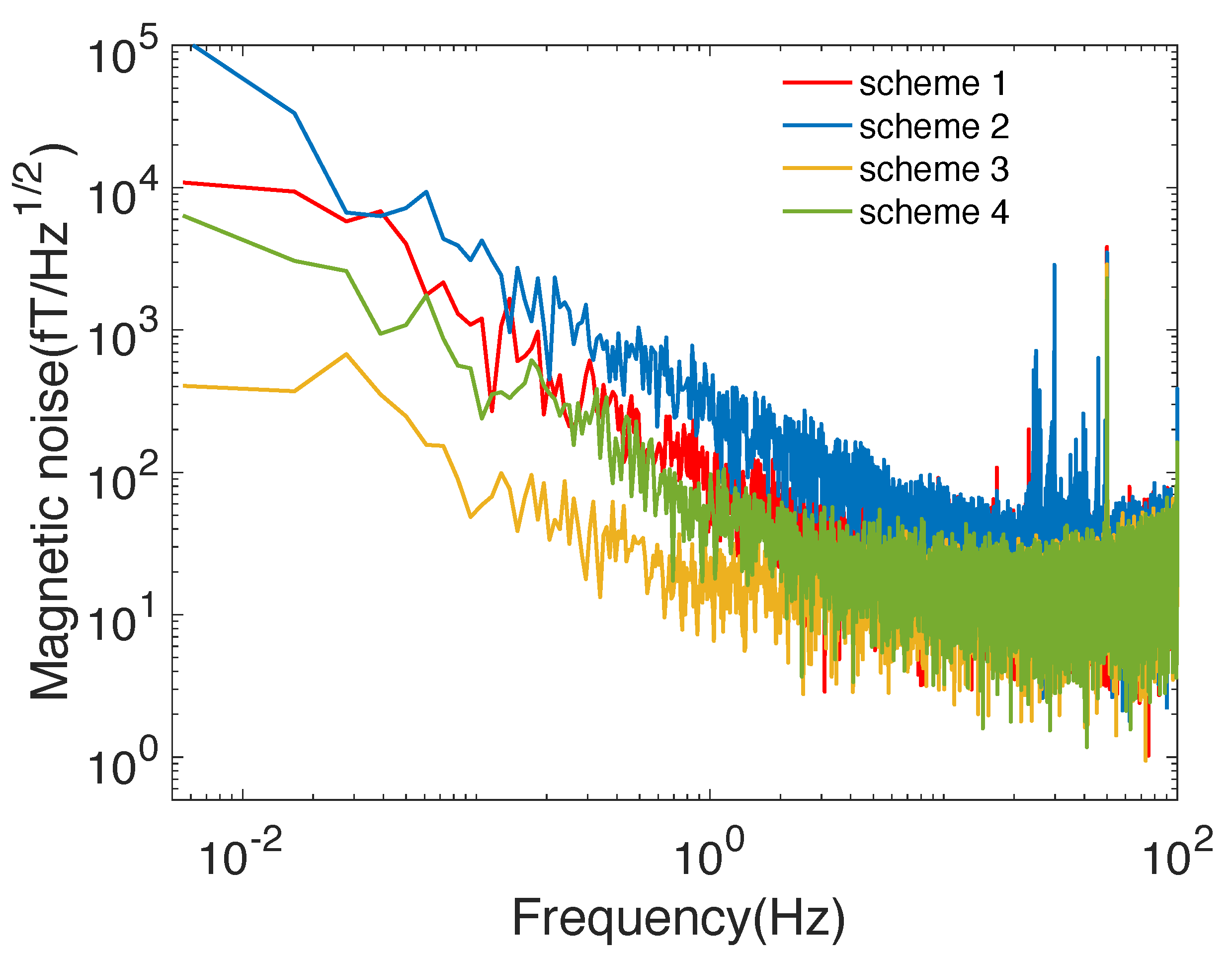
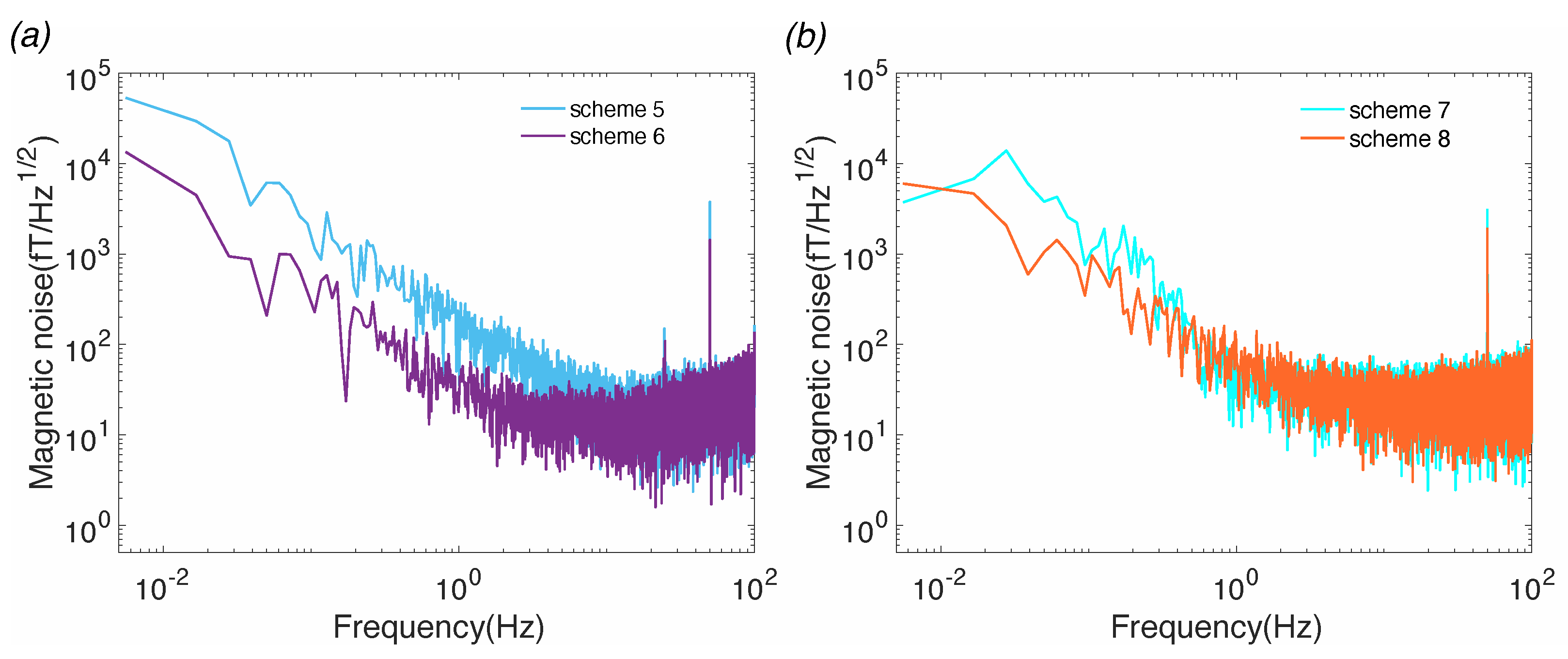
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flambaum, V.; Romalis, M.V. Limits on lorentz invariance violation from coulomb interactions in nuclei and atoms. Phys. Rev. Lett. 2017, 118, 142501. [Google Scholar] [CrossRef] [PubMed]
- Kosteleckỳ, V.A.; Russell, N. Data tables for lorentz and c p t violation. Rev. Mod. Phys. 2011, 83, 11. [Google Scholar] [CrossRef]
- Sheng, D.; Li, S.; Dural, N.; Romalis, M.V. Subfemtotesla scalar atomic magnetometry using multipass cells. Phys. Rev. Lett. 2013, 110, 160802. [Google Scholar] [CrossRef]
- Kominis, I.; Kornack, T.; Allred, J.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
- Kornack, T.; Ghosh, R.; Romalis, M.V. Nuclear spin gyroscope based on an atomic comagnetometer. Phys. Rev. Lett. 2005, 95, 230801. [Google Scholar] [CrossRef]
- Limes, M.; Sheng, D.; Romalis, M.V. He 3- xe 129 comagnetometery using rb 87 detection and decoupling. Phys. Rev. Lett. 2018, 120, 033401. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Liu, F.; Xing, L.; Liu, G. Suppression of the bias error induced by magnetic noise in a spin-exchange relaxation-free gyroscope. IEEE Sens. J. 2019, 19, 9712–9721. [Google Scholar] [CrossRef]
- Jiang, L.; Quan, W.; Liang, Y.; Liu, J.; Duan, L.; Fang, J. Effects of pump laser power density on the hybrid optically pumped comagnetometer for rotation sensing. Opt. Express 2019, 27, 420–430. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Liang, Y.; Li, G.; Cai, Z.; Wu, Z.; Quan, W. Dynamics of a spin-exchange relaxation-free comagnetometer for rotation sensing. Phys. Rev. Appl. 2022, 17, 014030. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, Z.; Xing, L.; Fan, W.; Ruan, J.; Pang, H. Suppression of non-uniform magnetic fields in magnetic shielding system for serf co-magnetometer. IEEE Trans. Instrum. Meas. 2022, 71, 9507008. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Zhang, W.; Xing, L.; Liu, G. Analysis on the magnetic field response for nuclear spin co-magnetometer operated in spin-exchange relaxation-free regime. IEEE Access 2019, 7, 28574–28580. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, W.; Fu, Y.; Pang, H.; Pei, H.; Quan, W. Suppression of low-frequency magnetic drift based on magnetic field sensitivity in k-rb-21 ne atomic spin comagnetometer. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar]
- Lee, S.-Y.; Lim, Y.-S.; Choi, I.-H.; Lee, D.-I.; Kim, S.-B. Effective combination of soft magnetic materials for magnetic shielding. IEEE Trans. Magn. 2012, 48, 4550–4553. [Google Scholar] [CrossRef]
- Lee, S.-K.; Romalis, M. Calculation of magnetic field noise from high-permeability magnetic shields and conducting objects with simple geometry. J. Appl. Phys. 2008, 103, 084904. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Grachev, A.A.; Odintsov, S.; Martyshkin, A.; Gubanov, V.A.; Sheshukova, S.E.; Nikitov, S.A. Neuromorphic calculations using lateral arrays of magnetic microstructures with broken translational symmetry. JETP Lett. 2018, 108, 312–317. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Bublikov, K.; Beginin, E.N.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Nonreciprocal propagation of hybrid electromagnetic waves in a layered ferrite–ferroelectric structure with a finite width. JETP Lett. 2015, 102, 142–147. [Google Scholar] [CrossRef]
- Li, J.; Quan, W.; Han, B.; Liu, F.; Xing, L.; Liu, G. Multilayer cylindrical magnetic shield for serf atomic co-magnetometer application. IEEE Sens. J. 2018, 19, 2916–2923. [Google Scholar] [CrossRef]
- He, K.; Wan, S.; Sheng, J.; Liu, D.; Wang, C.; Li, D.; Qin, L.; Luo, S.; Qin, J.; Gao, J.-H. A high-performance compact magnetic shield for optically pumped magnetometer-based magnetoencephalography. Rev. Sci. 2019, 90, 064102. [Google Scholar] [CrossRef]
- Freake, S.; Thorp, T. Shielding of low magnetic fields with multiple cylindrical shells. Rev. Sci. Instrum. 1971, 42, 1411–1413. [Google Scholar] [CrossRef]
- Altarev, I.; Bales, M.; Beck, D.; Chupp, T.; Fierlinger, K.; Fierlinger, P.; Kuchler, F.; Lins, T.; Marino, M.; Niessen, B.; et al. A large-scale magnetic shield with 106 damping at millihertz frequencies. J. Appl. Phys. 2015, 117, 183903. [Google Scholar] [CrossRef]
- Dang, H.; Maloof, A.C.; Romalis, M.V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Smiciklas, M.; Brown, J.; Cheuk, L.; Smullin, S.; Romalis, M.V. New test of local lorentz invariance using a ne 21- rb- k comagnetometer. Phys. Rev. Lett. 2011, 107, 171604. [Google Scholar] [CrossRef] [PubMed]
- Bevan, D.; Bulatowicz, M.; Clark, P.; Flicker, J.; Griffith, R.; Larsen, M.; Luengo-Kovac, M.; Pavell, J.; Rothballer, A.; Sakaida, D.; et al. Nuclear magnetic resonance gyroscope: Developing a primary rotation sensor. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018; pp. 1–2. [Google Scholar]
- Savukov, I.; Kim, Y.; Shah, V.; Boshier, M. High-sensitivity operation of single-beam optically pumped magnetometer in a khz frequency range. Meas. Sci. Technol. 2017, 28, 035104. [Google Scholar] [CrossRef]
- Lu, J.; Sun, C.; Ma, D.; Yang, K.; Zhao, J.; Han, B.; Quan, W.; Zhang, N.; Ding, M. Effect of gaps on magnetic noise of cylindrical ferrite shield. J. Phys. D Appl. Phys. 2021, 54, 255002. [Google Scholar] [CrossRef]
- Kornack, T.; Smullin, S.; Lee, S.-K.; Romalis, M. A low-noise ferrite magnetic shield. Appl. Phys. Lett. 2007, 90, 223501. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Liu, F.; Pang, H.; Xing, L.; Liu, G. Performance of low-noise ferrite shield in a k-rb-21 ne co-magnetometer. IEEE Sens. J. 2019, 20, 2543–2549. [Google Scholar] [CrossRef]
- Ma, D.; Lu, J.; Fang, X.; Yang, K.; Wang, K.; Zhang, N.; Han, B.; Ding, M. Parameter modeling analysis of a cylindrical ferrite magnetic shield to reduce magnetic noise. IEEE Trans. Ind. Electron. 2021, 69, 991–998. [Google Scholar] [CrossRef]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]
- Hasegawa, R. Advances in amorphous and nanocrystalline materials. J. Magn. Magn. Mater. 2012, 324, 3555–3557. [Google Scholar] [CrossRef]
- Fish, G.E. Soft magnetic materials. Proc. IEEE 1990, 78, 947–972. [Google Scholar] [CrossRef]
- Silveyra, J.M.; Ferrara, E.; Huber, D.L.; Monson, T.C. Soft magnetic materials for a sustainable and electrified world. Science 2018, 362, eaao0195. [Google Scholar] [CrossRef] [PubMed]
- DeVore, P.; Escontrias, D.; Koblesky, T.; Lin, C.; Liu, D.; Luk, K.B.; Ngan, J.; Peng, J.; Polly, C.; Roloff, J.; et al. Light-weight flexible magnetic shields for large-aperture photomultiplier tubes. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 737, 222–228. [Google Scholar] [CrossRef]
- Fu, Y.; Sun, J.; Ruan, J.; Quan, W. A nanocrystalline shield for high precision co-magnetometer operated in spin-exchange relaxation-free regime. Sens. Actuators A Phys. 2022, 339, 113487. [Google Scholar] [CrossRef]
- Kornack, T.; Romalis, M. Dynamics of two overlapping spin ensembles interacting by spin exchange. Phys. Rev. Lett. 2002, 89, 253002. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Quan, W.; Duan, L.; Lu, Y.; Jiang, L.; Fang, J. Spin-exchange collision mixing of the k and rb ac stark shifts. Phys. Rev. A 2016, 94, 052705. [Google Scholar] [CrossRef]


| (nT) | (nT) | (nT) | |
|---|---|---|---|
| without shielding | 9385 | 29,665 | 29,850 |
| Scheme 1 | 3 | 3.78 | 11.25 |
| Scheme 2 | 1.3 | 2.4 | 12.45 |
| Scheme 3 | 0.56 | 2.4 | 0.3 |
| Scheme 4 | 0.86 | 1.08 | 0.375 |
| Scheme 5 | 7.2 | 6.34 | 11.1 |
| Scheme 6 | 13.14 | 5.54 | 0.9 |
| Scheme 7 | 0.5 | 1.92 | 0.33 |
| Scheme 8 | 0.46 | 0.46 | 0.855 |
| 1 Hz fT/Hz | |
|---|---|
| Scheme 1 | 68.93 |
| Scheme 2 | 239.65 |
| Scheme 3 | 147.98 |
| Scheme 4 | 28.62 |
| Scheme 5 | 14.17 |
| Scheme 6 | 46.59 |
| Scheme 7 | 54.81 |
| Scheme 8 | 54.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gao, H.; Ma, L.; Quan, J.; Fan, W.; Xu, X.; Fu, Y.; Duan, L.; Quan, W. Study on the Magnetic Noise Characteristics of Amorphous and Nanocrystalline Inner Magnetic Shield Layers of SERF Co-Magnetometer. Materials 2022, 15, 8267. https://doi.org/10.3390/ma15228267
Liu Y, Gao H, Ma L, Quan J, Fan W, Xu X, Fu Y, Duan L, Quan W. Study on the Magnetic Noise Characteristics of Amorphous and Nanocrystalline Inner Magnetic Shield Layers of SERF Co-Magnetometer. Materials. 2022; 15(22):8267. https://doi.org/10.3390/ma15228267
Chicago/Turabian StyleLiu, Ye, Hang Gao, Longyan Ma, Jiale Quan, Wenfeng Fan, Xueping Xu, Yang Fu, Lihong Duan, and Wei Quan. 2022. "Study on the Magnetic Noise Characteristics of Amorphous and Nanocrystalline Inner Magnetic Shield Layers of SERF Co-Magnetometer" Materials 15, no. 22: 8267. https://doi.org/10.3390/ma15228267
APA StyleLiu, Y., Gao, H., Ma, L., Quan, J., Fan, W., Xu, X., Fu, Y., Duan, L., & Quan, W. (2022). Study on the Magnetic Noise Characteristics of Amorphous and Nanocrystalline Inner Magnetic Shield Layers of SERF Co-Magnetometer. Materials, 15(22), 8267. https://doi.org/10.3390/ma15228267







