A Novel Design Concept of Cemented Paste Backfill (CPB) Materials: Biobjective Optimization Approach by Applying an Evolved Random Forest Model
Abstract
:1. Introduction
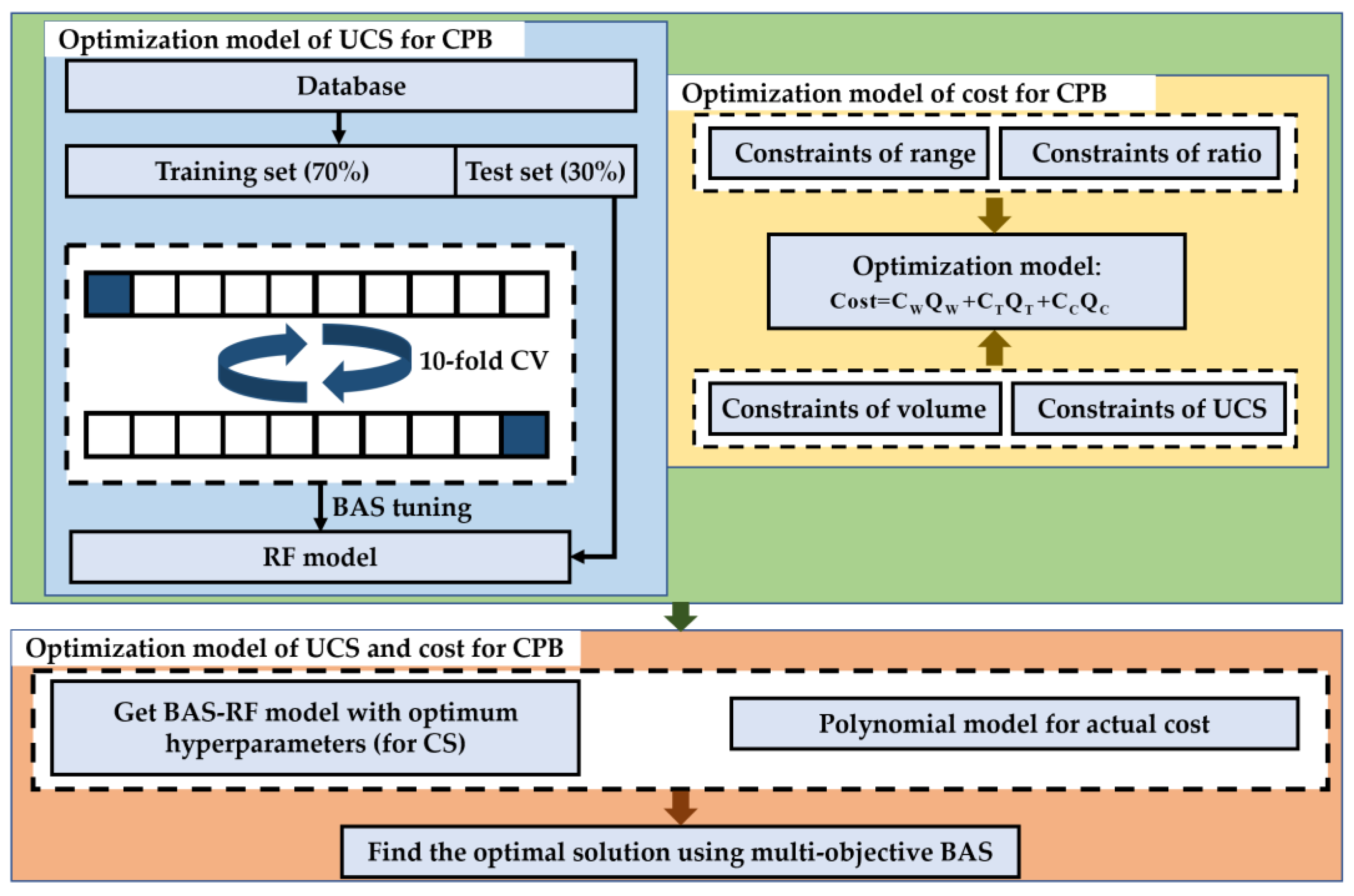
2. Methodology
2.1. Optimization of the UCS for CPB
Data Analysis
2.2. Optimization Model of UCS for CPB
2.2.1. Beetle Search Algorithm (BAS)
2.2.2. Random Forests (RF)
- (1)
- Data preprocessing. According to the requirements, the data set is divided into an input layer and an output layer. The employed dataset should be randomly divided into the training and testing parts according to the proportion.
- (2)
- Operation of the model. The RF model is established by using the training data set, and the model results are output.
- (3)
- Model evaluation. Select appropriate indexes and datasets to test the prediction effect of the established RF model on the UCS of CPB.
- (4)
- Repeat steps (2) and (3) until the best model parameters and results are found.
2.3. Optimization Model of Cost for CPB
- (1)
- Constraints of range
- (2)
- Constraints of the mixture proportion
- (3)
- Volume constraint
- (4)
- Constraints on the UCS of CPB
2.4. Biobjective Optimization Model Considering the UCS and Cost
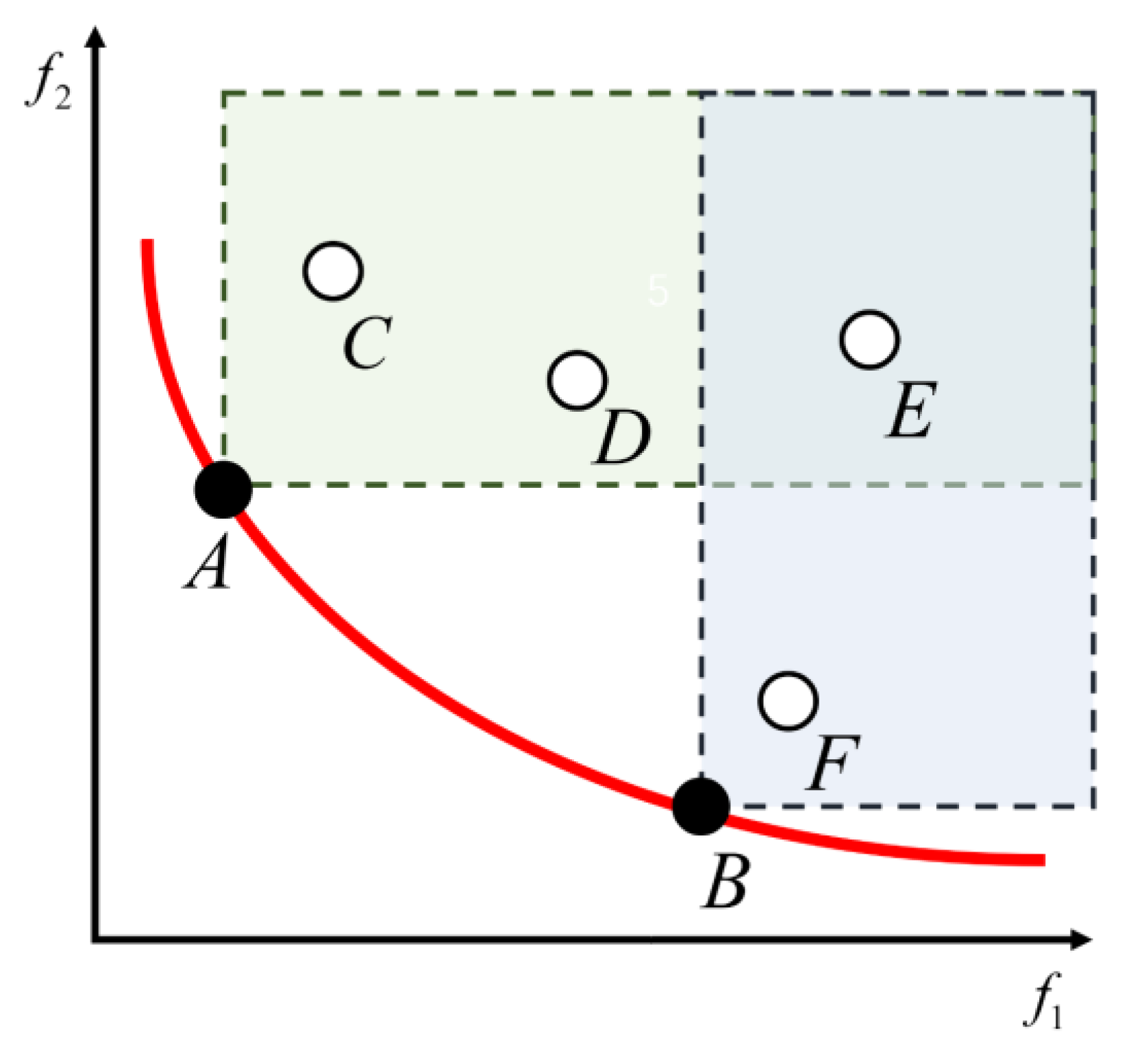
2.4.1. Biobjective Problem
2.4.2. Pareto Optimality
2.4.3. Weighted Sum Method
2.4.4. Decision-Making Method
3. Results and Discussion
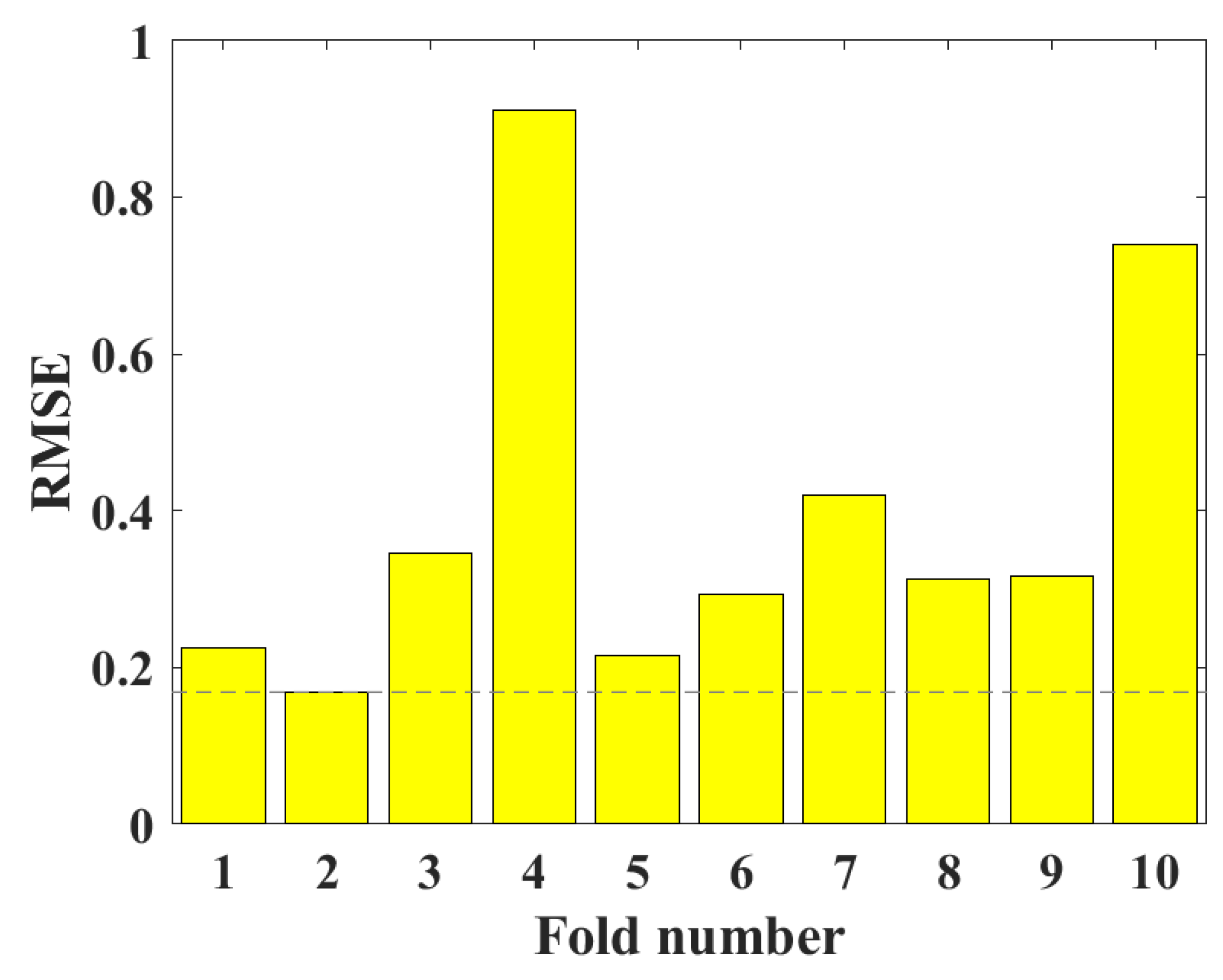
3.1. Hyperparameter Tuning
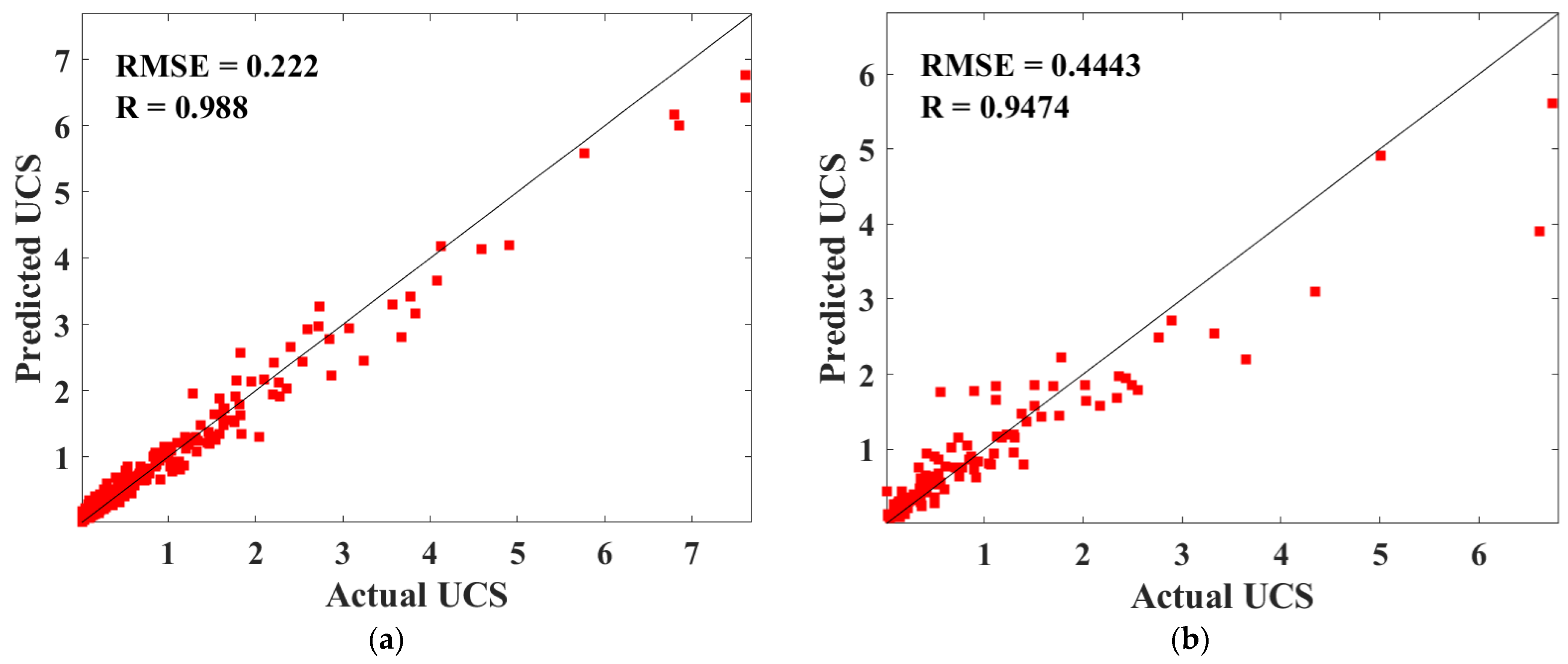
3.2. Evaluation of the Optimization Model of the UCS
3.3. Determination of the Effect of the Biobjective Optimization Model
4. Conclusions
- (1)
- BAS has good performance in RF hyperparameter tuning. The RMSE value of the UCS of CPB reaches the minimum value in the second iteration.
- (2)
- The BAS and RF hybrid machine learning model achieves high prediction accuracy on the training set (R = 0.988, RMSE = 0.222 MPa) and test set (R = 0.9474, RMSE = 0.443 MPa) for the UCS of CPB.
- (3)
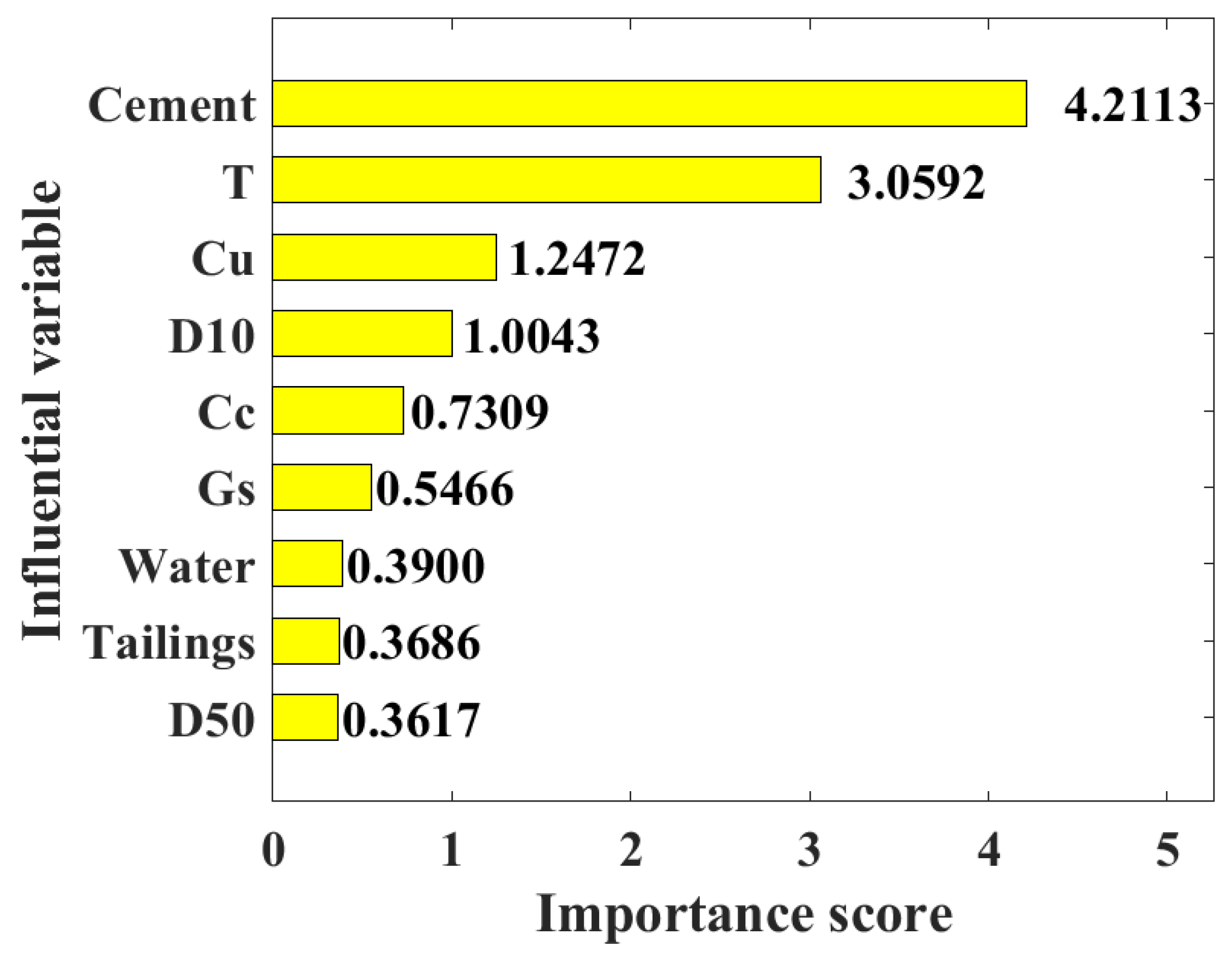
- The sensitivity of different input variables to the UCS of CPB from high to low is cement, T, Cu, D10, Cc, Gs, water, tailings, and D50.
- (4)
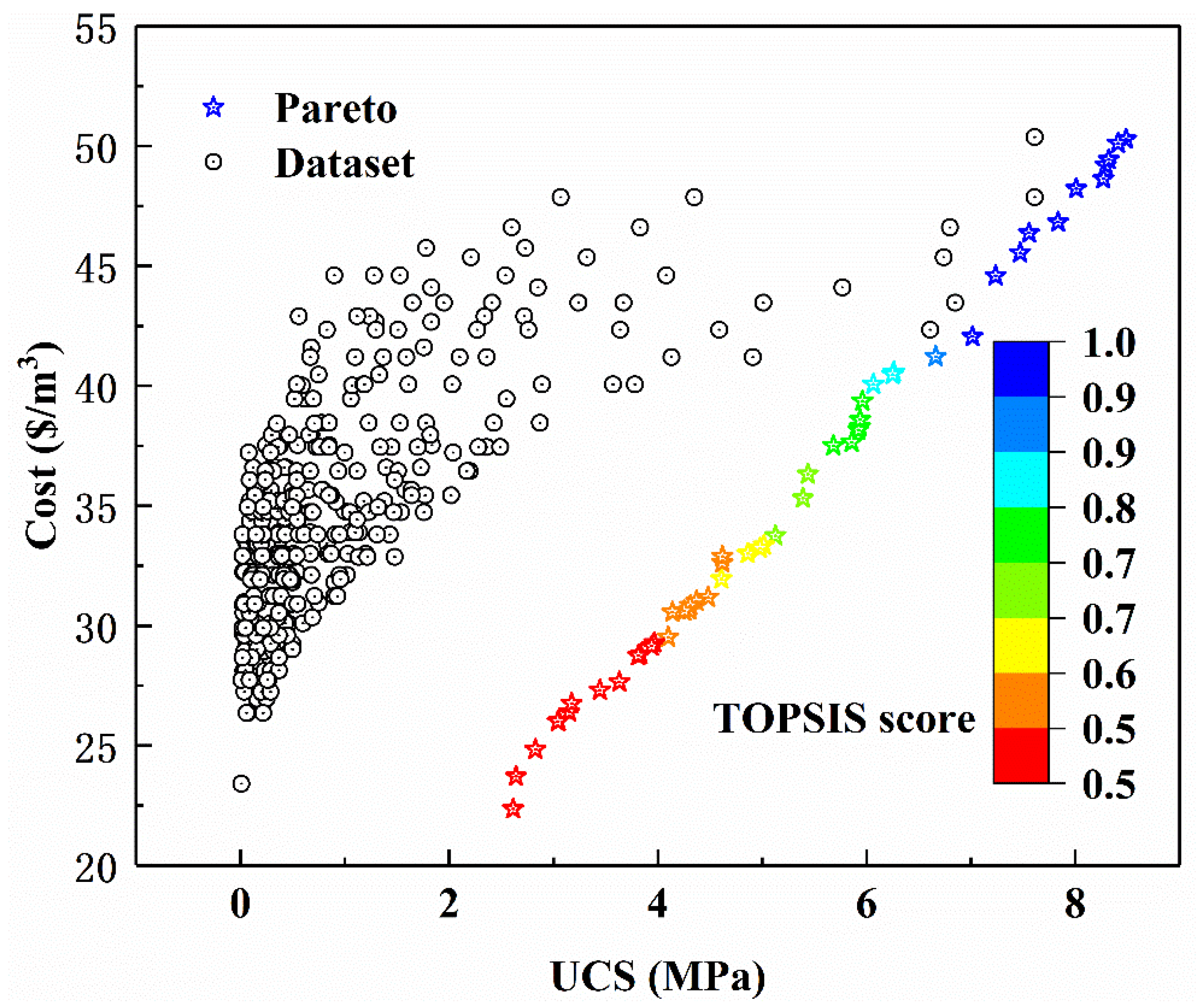
- The weighted sum method is used to transform the biobjective optimization problem of cost and UCS into a single objective optimization problem. Comparing the obtained Pareto front optimal solution set with the data set, it is found that under the same CPB cost, the Pareto front optimal solution set has a higher UCS, and under the same CPB UCS, the Pareto front optimal solution set has a lower cost. It is proved that the proposed biobjective optimization method is useful for the CPB optimization of the cost and UCS.
- (5)
- The TOPSIS method was used to rank the optimal solution of the Pareto front optimal solution. The UCS, cost, and values corresponding to input variables of the top 20 Pareto front optimal solutions are listed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, Q.; Guo, Y.; Dong, C.; Xu, J.; Lai, W.; Du, B. Mechanical properties of clay based cemented paste backfill for coal recovery from deep mines. Energies 2021, 14, 5764. [Google Scholar] [CrossRef]
- Cui, L.; Fall, M. Mathematical modelling of cemented tailings backfill: A review. Int. J. Min. Reclam. Environ. 2019, 33, 389–408. [Google Scholar] [CrossRef]
- Eker, H.; Bascetin, A. Influence of silica fume on mechanical property of cemented paste backfill. Construct. Build. Mater. 2022, 317, 126089. [Google Scholar] [CrossRef]
- Grabinsky, M.; Thompson, B.; Bawden, W. Evaluating cemented paste backfill plug strength and the potential for continuous pouring 1. In Proceedings of the 13th International Symposium on Mining with Backfill (MINEFILL), Katowice, Poland, 25–28 May 2021; pp. 127–139. [Google Scholar]
- He, W.; Zheng, C.; Li, S.; Shi, W.; Zhao, K. Strength development monitoring of cemented paste backfill using guided waves. Sensors 2021, 21, 8499. [Google Scholar] [CrossRef]
- Zhao, Y.; Taheri, A.; Karakus, M.; Chen, Z.; Deng, A. Effects of water content, water type and temperature on the rheological behaviour of slag-cement and fly ash-cement paste backfill. Int. J. Min. Sci. Technol. 2020, 30, 271–278. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, F.; Ren, Q.; Kuang, Y.; Zhou, T.; Luo, Z. Microscopic characterization and strength characteristics of cemented backfill under different humidity curing conditions. R. Soc. Open Sci. 2019, 6, 191227. [Google Scholar] [CrossRef] [Green Version]
- Ionescu, D.; Petrolito, J.; Dare, A.; Pentreath, Z.; Sonnberger, L.; Destech Publicat, I. Assessment of the effect of different cementing materials on the strength of cemented paste backfill. In Proceedings of the 3rd International Conference on Green Materials and Environmental Engineering (GMEE), Beijing, China, 22 October 2017; pp. 174–178. [Google Scholar]
- Jafari, M.; Shahsavari, M.; Grabinsky, M. Experimental study of the behavior of cemented paste backfill under high isotropic compression. J. Geotech. Geoenviron. Eng. 2020, 146, 06020019. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Yan, H.; Liu, H.; Zhu, C. Thermal enhancement of gangue-cemented paste backfill with graphite and silica sand: An experimental investigation. Environ. Sci. Pollut. Res. 2022, 29, 49050–49058. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Yan, H.; Zhou, N.; Li, M. Experimental investigation into the thermal conductivity of gangue-cemented paste backfill in mine application. J. Mater. Res. Technol. 2022, 16, 1792–1802. [Google Scholar] [CrossRef]
- Li, G.; Deng, G.-z.; Ma, J. Numerical modelling of the response of cemented paste backfill under the blasting of an adjacent ore stope. Construct. Build. Mater. 2022, 343, 128051. [Google Scholar] [CrossRef]
- Yu, X.; Tang, W.; Li, N.; Jiang, M.; Huang, J.; Wang, D. Refined decomposition: A new separation method for rap materials and its effect on aggregate properties. Construct. Build. Mater. 2022, 358, 129452. [Google Scholar] [CrossRef]
- Li, Z.; Shi, X.; Chen, X. Effect of rice straw on tensile properties of tailings cemented paste backfill. Appl. Sci. 2022, 12, 526. [Google Scholar] [CrossRef]
- Liu, H.-l.; Hou, C.; Li, L.; Du, J.-f.; Yan, B.-x. Experimental investigation on flow properties of cemented paste backfill through l-pipe and loop-pipe tests. J. Cent. South Univ. 2021, 28, 2830–2842. [Google Scholar] [CrossRef]
- Niu, H.; Hassani, F.P.; Kermani, M.F.; He, M. Rheological and mechanical properties of fibre-reinforced cemented paste and foam backfill. Int. J. Min. Reclam. Environ. 2021, 35, 488–505. [Google Scholar] [CrossRef]
- Tuylu, S. Effect of different particle size distribution of zeolite on the strength of cemented paste backfill. Int. J. Environ. Sci. Technol. 2022, 19, 131–140. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Wu, L.; Wu, A.; Ruan, Z.; Zhang, M.; Zhao, R. Effective reuse of red mud as supplementary material in cemented paste backfill: Durability and environmental impact. Construct. Build. Mater. 2022, 328, 127002. [Google Scholar] [CrossRef]
- Wu, W.; Xu, W.; Zuo, J. Effect of inclined interface angle on shear strength and deformation response of cemented paste backfill-rock under triaxial compression. Construct. Build. Mater. 2021, 279, 122478. [Google Scholar]
- Xu, S.; Suorineni, F.T.; Li, K.; Li, Y. Evaluation of the strength and ultrasonic properties of foam-cemented paste backfill. Int. J. Min. Reclam. Environ. 2017, 31, 544–557. [Google Scholar] [CrossRef]
- Huan, C.; Zhu, C.; Liu, L.; Wang, M.; Zhao, Y.; Zhang, B.; Zhang, X. Pore structure characteristics and its effect on mechanical performance of cemented paste backfill. Front. Mater. 2021, 8, 9947620. [Google Scholar] [CrossRef]
- Fu, J.-X.; Song, W.-D.; Tan, Y.-Y. Study on microstructural evolution and strength growth and fracture mechanism of cemented paste backfill. Adv. Mater. Sci. Eng. 2016, 2016, 9947620. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Han, J.; Li, Y.; Yilmaz, E.; Sun, Q.; Liu, J. Relationship between ultrasonic pulse velocity and uniaxial compressive strength for cemented paste backfill with alkali-activated slag. Nondestruct. Test. Eval. 2020, 35, 359–377. [Google Scholar] [CrossRef]
- Xu, W.; Tian, X.; Cao, P. Assessment of hydration process and mechanical properties of cemented paste backfill by electrical resistivity measurement. Nondestruct. Test. Eval. 2018, 33, 198–212. [Google Scholar] [CrossRef]
- Yu, Z.; Shi, X.-z.; Chen, X.; Zhou, J.; Qi, C.-c.; Chen, Q.-s.; Rao, D.-j. Artificial intelligence model for studying unconfined compressive performance of fiber-reinforced cemented paste backfill. Transact. Nonferrous Met. Soc. China 2021, 31, 1087–1102. [Google Scholar] [CrossRef]
- Ma, W.; Tian, Y.; Zhao, H.; Orton, S.L. Time-dependent behavior of reinforced concrete columns subjected to high sustained loads. J. Struct. Eng. 2022, 148, 04022161. [Google Scholar] [CrossRef]
- Huang, J.; Shiva Kumar, G.; Ren, J.; Zhang, J.; Sun, Y. Accurately predicting dynamic modulus of asphalt mixtures in low-temperature regions using hybrid artificial intelligence model. Construct. Build. Mater. 2021, 297, 123655. [Google Scholar] [CrossRef]
- Zhang, B.; Xin, J.; Liu, L.; Guo, L.; Song, K.-I. An experimental study on the microstructures of cemented paste backfill during its developing process. Adv. Civ. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Li, K.; Zhang, S.; Hu, Y.; Han, B. A modeling method for predicting the strength of cemented paste backfill based on a combination of aggregate gradation optimization and lstm. J. Renew. Mater. 2022, 10, 3539–3558. [Google Scholar] [CrossRef]
- Bian, J.; Fall, M.; Haruna, S. Sulfate-induced changes in rheological properties of fibre-reinforced cemented paste backfill. Mag. Concr. Res. 2021, 73, 574–583. [Google Scholar] [CrossRef]
- Jin, J.; Qin, Z.; Zuo, S.; Feng, J.; Sun, Q. The role of rheological additives on fresh and hardened properties of cemented paste backfill. Materials 2022, 15, 3006. [Google Scholar] [CrossRef]
- Chang, B.; Du, C.; Chu, X.; Zhang, L. Study on the optimization of filling ratio and strength variation characteristics of cemented backfills containing fly ash. Front. Mater. 2021, 8, 424. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Fu, J.; Song, W.; Zhang, Y. Effect of water saturation on mechanical characteristics and damage behavior of cemented paste backfill. J. Mater. Res. Technol. 2021, 15, 6624–6639. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X.; Dong, X.; Chen, Q.; Fourie, A.; Liu, E. Towards intelligent mining for backfill: A genetic programming-based method for strength forecasting of cemented paste backfill. Miner. Eng. 2019, 133, 69–79. [Google Scholar] [CrossRef]
- Mbonimpa, M.; Kwizera, P.; Belem, T. Mine backfilling in the permafrost, part II: Effect of declining curing temperature on the short-term unconfined compressive strength of cemented paste backfills. Minerals 2019, 9, 172. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yu, Z.; Wang, H. Experimental investigation on some performance of rubber fiber modified cemented paste backfill. Construct. Build. Mater. 2021, 271, 121586. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Li, X.; Qiao, Y.; Zhang, R.; Kumar, G.S. Investigating the effects of ensemble and weight optimization approaches on neural networks’ performance to estimate the dynamic modulus of asphalt concrete. Road Mater. Pavement Des. 2022, 23, 1–21. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Gao, Y.; Liu, H. Intelligently predict the rock joint shear strength using the support vector regression and firefly algorithm. Lithosphere 2021, 2021, 2467126. [Google Scholar] [CrossRef]
- Huang, J.; Xue, J. Optimization of svr functions for flyrock evaluation in mine blasting operations. Environ. Earth Sci. 2022, 81, 434. [Google Scholar] [CrossRef]
- Celestin, J.C.H.; Fall, M. Thermal conductivity of cemented paste backfill material and factors affecting it. Int. J. Min. Reclam. Environ. 2009, 23, 274–290. [Google Scholar] [CrossRef]
- Jiang, H.; Fall, M.; Cui, L. Freezing behaviour of cemented paste backfill material in column experiments. Construct. Build. Mater. 2017, 147, 837–846. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Li, L.; Fan, C.; He, Z.; Qian, Y. Utilization of low-alkalinity cementitious materials in cemented paste backfill of gold mine tailings. J. Renew. Mater. 2022, 10, 3439–3458. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, M.; Zhang, J.; Ren, J.; Vatin, N.I.; Sabri, M.M.S. Development of a new stacking model to evaluate the strength parameters of concrete samples in laboratory. Iran. J. Sci. Technol. Transact. Civ. Eng. 2022, 46, 4355–4370. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, M.; Zhang, J.; Ren, J.; Vatin, N.I.; Sabri, M.M.S. The use of ga and pso in evaluating the shear strength of steel fiber reinforced concrete beams. KSCE J. Civ. Eng. 2022, 26, 3918–3931. [Google Scholar] [CrossRef]
- Kou, B.; Ren, D.; Guo, S. Geometric parameter identification of medical robot based on improved beetle antennae search algorithm. Bioengineering 2022, 9, 58. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Zhang, F.; Ieee Comp, S.O.C. Beetle antennae search algorithm for community detection in complex network. In Proceedings of the 16th International Conference on Computational Intelligence and Security (CIS), Nanning, China, 27–30 November 2020; pp. 253–258. [Google Scholar]
- Zheng, Q.; Xiang, D.; Fang, J.; Wang, Y.; Zhang, H.; Hu, Z. Research on performance seeking control based on beetle antennae search algorithm. Meas. Control 2020, 53, 1440–1445. [Google Scholar] [CrossRef]
- Chen, D.; Lv, Z. Artificial intelligence enabled digital twins for training autonomous cars. Internet Things Cyber-Phys. Syst. 2022, 2, 31–41. [Google Scholar] [CrossRef]
- Chen, R.; Shen, H.; Lai, Y. A metaheuristic optimization algorithm for energy efficiency in digital twins. Internet Things Cyber-Phys. Syst. 2022, 2, 159–169. [Google Scholar] [CrossRef]

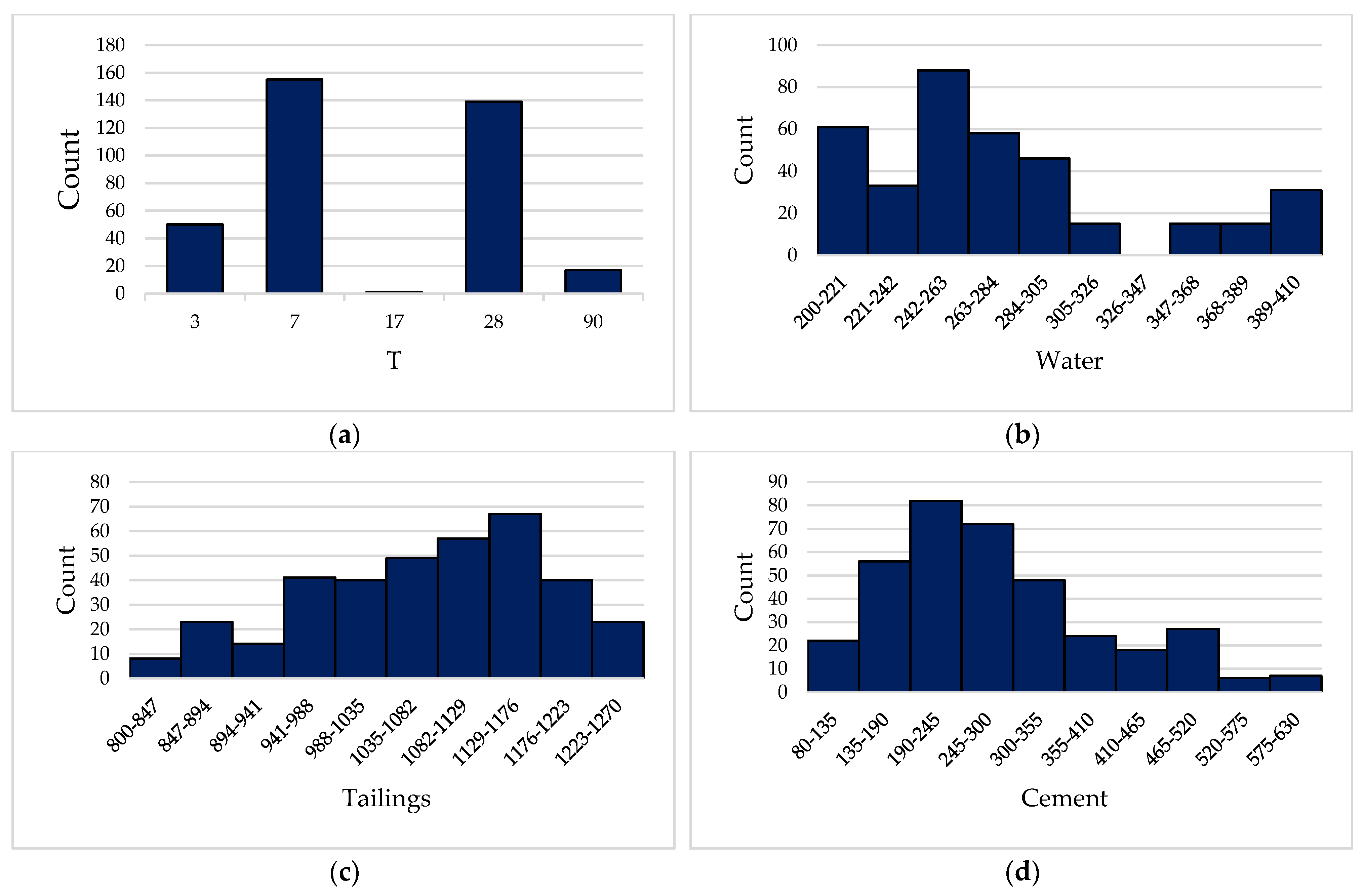


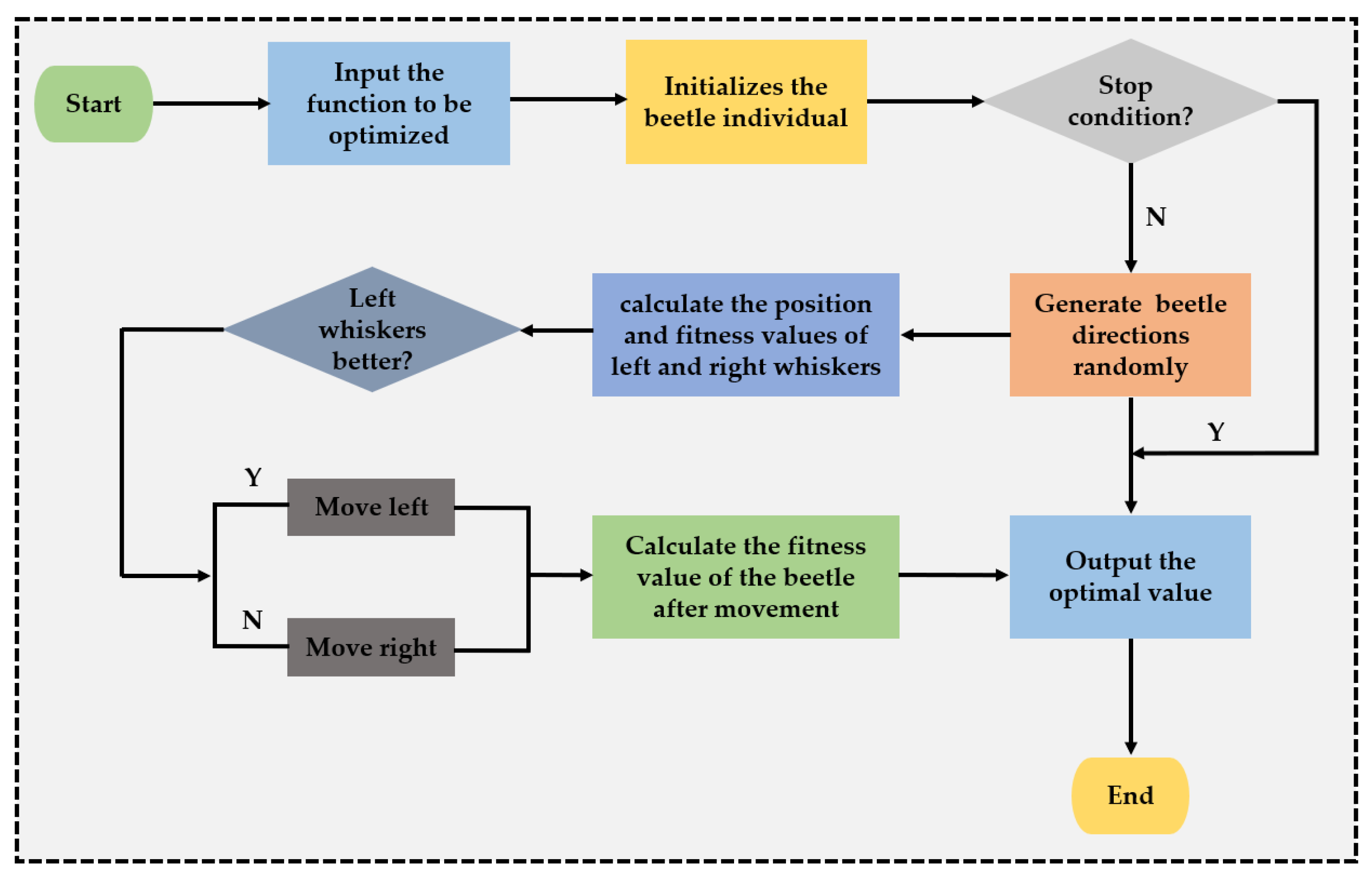
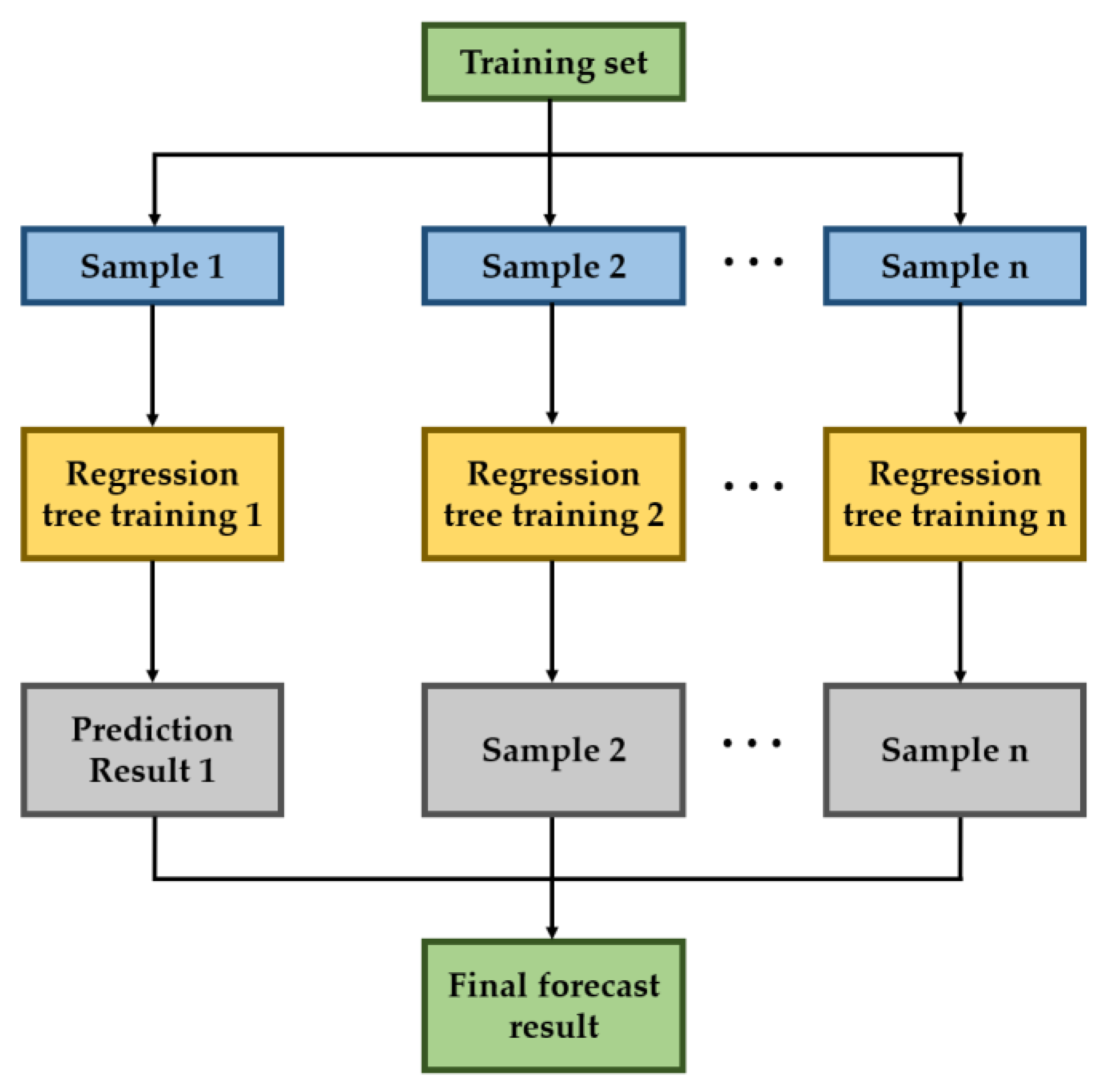
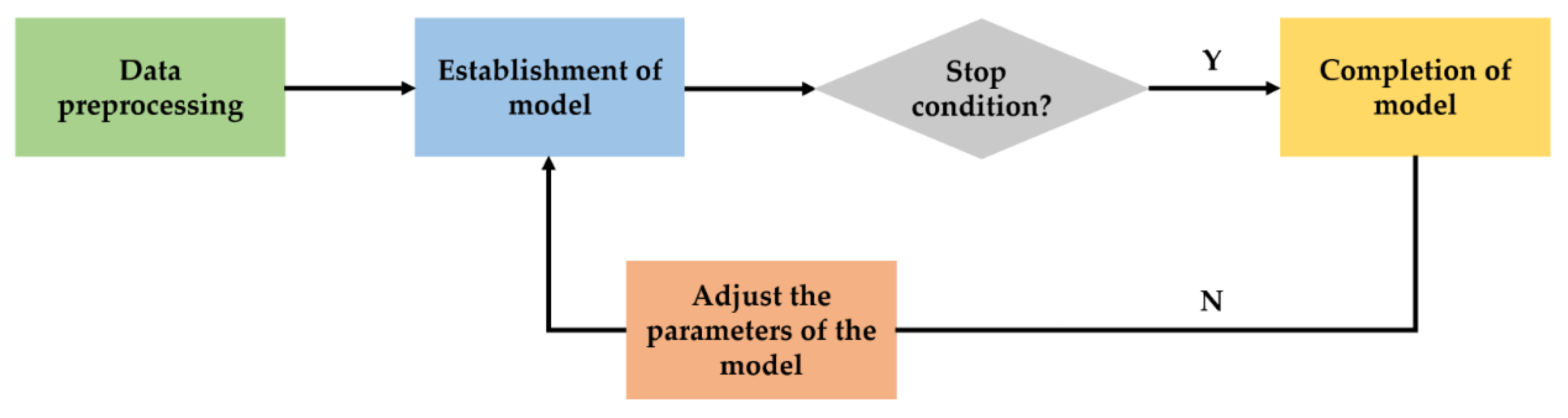


| Variables | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gs | 2.08 | 2.08 | 2.61 | 2.67 | 2.71 | 2.75 | 2.79 | 2.83 | 2.83 | 2.83 | 2.86 | 2.91 | 2.91 |
| D10 | 0.248 | 0.004 | 0.005 | 0.035 | 0.447 | 0.016 | 0.08 | 0.005 | 0.023 | 0.023 | 0.015 | 0.248 | 0.004 |
| D50 | 1.442 | 0.012 | 0.083 | 0.195 | 0.244 | 0.084 | 0.302 | 0.049 | 0.192 | 0.192 | 0.012 | 1.442 | 0.019 |
| Cu | 8.3 | 4.65 | 27.43 | 7.42 | 11.645 | 6.56 | 4.65 | 12.7 | 10.54 | 10.54 | 12.8 | 27.43 | 6.57 |
| Cc | 0.9 | 0.87 | 0.87 | 1.07 | 1.084 | 0.9 | 0.94 | 1.3 | 2.04 | 2.04 | 1.33 | 2.04 | 0.91 |
| No. | Gs (kg/m3) | D10 (kg/m3) | D50 (kg/m3) | Cu | Cc | T (Days) | Water (kg/m3) | Tailings (kg/m3) | Cement (kg/m3) | UCS (MPa) | Cost ($/m3) | TOPSIS Score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 7 | 200 | 1088 | 504 | 1.78 | 45.75 | 0.997 |
| 2 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 7 | 200 | 1133.33 | 420 | 1.3 | 42.66 | 0.994 |
| 3 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 7 | 200 | 1165.71 | 360 | 0.75 | 40.46 | 0.993 |
| 4 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 7 | 200 | 1208.89 | 280 | 0.38 | 37.53 | 0.989 |
| 5 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 7 | 200 | 1236.36 | 229.09 | 0.2 | 35.66 | 0.987 |
| 6 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 7 | 200 | 1255.38 | 193.85 | 0.18 | 34.36 | 0.982 |
| 7 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 28 | 200 | 1088 | 504 | 2.73 | 45.75 | 0.976 |
| 8 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 28 | 200 | 1133.33 | 420 | 1.83 | 42.66 | 0.968 |
| 9 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 28 | 200 | 1165.71 | 360 | 1.33 | 40.46 | 0.961 |
| 10 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 28 | 200 | 1208.89 | 280 | 0.85 | 37.53 | 0.943 |
| 11 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 28 | 200 | 1236.36 | 229.09 | 0.21 | 35.66 | 0.927 |
| 12 | 2.79 | 0.08 | 0.3 | 4.65 | 0.94 | 28 | 200 | 1255.38 | 193.85 | 0.2 | 34.36 | 0.903 |
| 13 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 3 | 200 | 1208.89 | 280 | 0.25 | 37.53 | 0.883 |
| 14 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 3 | 200 | 1236.36 | 229.09 | 0.14 | 35.66 | 0.857 |
| 15 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 3 | 200 | 1255.38 | 193.85 | 0.09 | 34.36 | 0.788 |
| 16 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 7 | 200 | 1208.89 | 280 | 0.55 | 37.53 | 0.783 |
| 17 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 7 | 200 | 1236.36 | 229.09 | 0.29 | 35.66 | 0.779 |
| 18 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 7 | 200 | 1255.38 | 193.85 | 0.21 | 34.36 | 0.768 |
| 19 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 28 | 200 | 1208.89 | 280 | 1.84 | 37.53 | 0.743 |
| 20 | 2.08 | 0.248 | 1.44 | 8.3 | 0.9 | 28 | 200 | 1236.36 | 229.09 | 0.58 | 35.66 | 0.721 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Cheng, Y.; Ma, M.; Li, F.; Song, Y.; Liu, L.; Wang, X.; Huang, J. A Novel Design Concept of Cemented Paste Backfill (CPB) Materials: Biobjective Optimization Approach by Applying an Evolved Random Forest Model. Materials 2022, 15, 8298. https://doi.org/10.3390/ma15238298
He Y, Cheng Y, Ma M, Li F, Song Y, Liu L, Wang X, Huang J. A Novel Design Concept of Cemented Paste Backfill (CPB) Materials: Biobjective Optimization Approach by Applying an Evolved Random Forest Model. Materials. 2022; 15(23):8298. https://doi.org/10.3390/ma15238298
Chicago/Turabian StyleHe, Yanjun, Yunhai Cheng, Mengxiang Ma, Fenghui Li, Yaxin Song, Long Liu, Xudong Wang, and Jiandong Huang. 2022. "A Novel Design Concept of Cemented Paste Backfill (CPB) Materials: Biobjective Optimization Approach by Applying an Evolved Random Forest Model" Materials 15, no. 23: 8298. https://doi.org/10.3390/ma15238298




