Figure 1.
(a) Minimum thickness of the simply supported slab and (b) minimum height of the supported beam.
Figure 1.
(a) Minimum thickness of the simply supported slab and (b) minimum height of the supported beam.
Figure 2.
(a) Minimum thickness of the fixed-ended supported slab and (b) of the fixed-ended slab.
Figure 2.
(a) Minimum thickness of the fixed-ended supported slab and (b) of the fixed-ended slab.
Figure 3.
Minimum thickness of the square flat slab.
Figure 3.
Minimum thickness of the square flat slab.
Figure 4.
Stress-strain curves for (
a) concrete and (
b) steel, both adapted from [
21].
Figure 4.
Stress-strain curves for (
a) concrete and (
b) steel, both adapted from [
21].
Figure 5.
(
a) Momentum-curvature curve of reinforced concrete, adapted from [
21], (
b) Illustrative graphic of creep, adapted from [
22]. (1) non-crack mode, (2) transition mode, (3) crack mode.
Figure 5.
(
a) Momentum-curvature curve of reinforced concrete, adapted from [
21], (
b) Illustrative graphic of creep, adapted from [
22]. (1) non-crack mode, (2) transition mode, (3) crack mode.
Figure 6.
(a) Simply supported beam with distributed load, (b) cross-section stress at the state I and (c) at state II.
Figure 6.
(a) Simply supported beam with distributed load, (b) cross-section stress at the state I and (c) at state II.
Figure 7.
(a) The simply supported slab and (b) supported fixed-ended slab.
Figure 7.
(a) The simply supported slab and (b) supported fixed-ended slab.
Figure 8.
(a) Fixed-ended slab and (b) flat slab.
Figure 8.
(a) Fixed-ended slab and (b) flat slab.
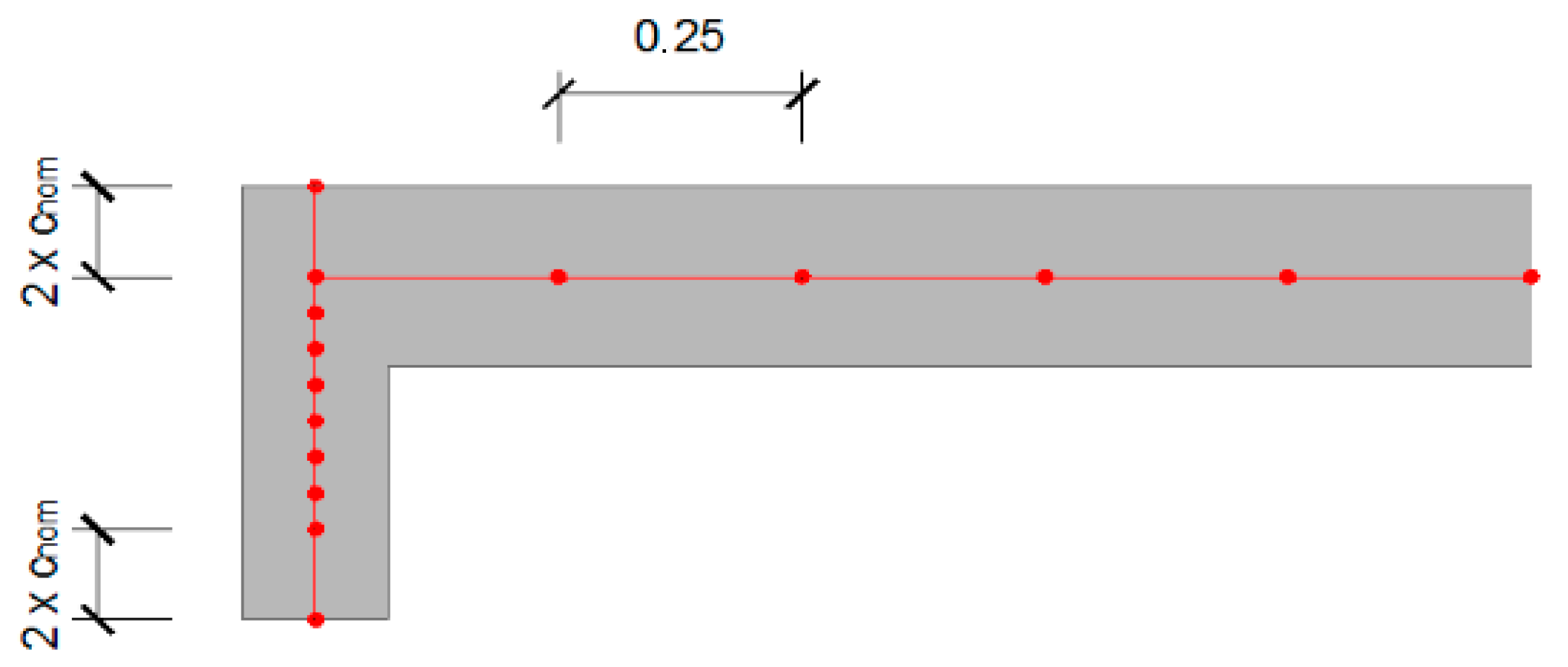
Figure 9.
Displacement compatibility at one point for a slab with one fixed-ended border.
Figure 9.
Displacement compatibility at one point for a slab with one fixed-ended border.
Figure 10.
k coefficient for (a) simply supported slab, (b) supported fixed-ended slab and (c) fixed-ended slab.
Figure 10.
k coefficient for (a) simply supported slab, (b) supported fixed-ended slab and (c) fixed-ended slab.
Figure 11.
Cross-section for (a) Reinforced concrete slab and (b) non-linear Shell element.
Figure 11.
Cross-section for (a) Reinforced concrete slab and (b) non-linear Shell element.
Figure 12.
Cross-section for (a) Reinforced concrete beam and (b) non-linear Shell element.
Figure 12.
Cross-section for (a) Reinforced concrete beam and (b) non-linear Shell element.
Figure 13.
Stress distribution in a cracked RC cross-section with 10 layers in SAP 2000.
Figure 13.
Stress distribution in a cracked RC cross-section with 10 layers in SAP 2000.
Figure 14.
Stress-strain curves for (a) LM; (b) 1NLM; (c) 2NLM and (d) steel used in SAP2000 (values in MPa and m/m).
Figure 14.
Stress-strain curves for (a) LM; (b) 1NLM; (c) 2NLM and (d) steel used in SAP2000 (values in MPa and m/m).
Figure 15.
Finite element meshes for (a) beam and (b) slab models.
Figure 15.
Finite element meshes for (a) beam and (b) slab models.
Figure 16.
Connection scheme for slab with the beam in the finite element model.
Figure 16.
Connection scheme for slab with the beam in the finite element model.
Figure 17.
Scheme for (a) simply supported slab; (b) fixed-ended supported slab; (c) fixed-ended slab and (d) flat slab.
Figure 17.
Scheme for (a) simply supported slab; (b) fixed-ended supported slab; (c) fixed-ended slab and (d) flat slab.
Figure 18.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for simply supported slab.
Figure 18.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for simply supported slab.
Figure 19.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for simply supported slab.
Figure 19.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for simply supported slab.
Figure 20.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for fixed-ended supported slab.
Figure 20.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for fixed-ended supported slab.
Figure 21.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for fixed-ended supported slab.
Figure 21.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for fixed-ended supported slab.
Figure 22.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for fixed-ended slab.
Figure 22.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for fixed-ended slab.
Figure 23.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for fixed-ended slab.
Figure 23.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for fixed-ended slab.
Figure 24.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for flat slab.
Figure 24.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for flat slab.
Figure 25.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for flat slab.
Figure 25.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for flat slab.
Figure 26.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for supported beam.
Figure 26.
Ratios values for (a) LM, (b) 1NLM and (c) 2NLM, for supported beam.
Figure 27.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for supported beam.
Figure 27.
Deformation values of 2NLM: (a) analytical and (b) numerical, with their limit values, for supported beam.
Figure 28.
Finite element mesh of the first case of study.
Figure 28.
Finite element mesh of the first case of study.
Figure 29.
Finite element mesh of the second case of study.
Figure 29.
Finite element mesh of the second case of study.
Figure 30.
Finite element mesh of the third case of study.
Figure 30.
Finite element mesh of the third case of study.
Table 1.
Ratio values (span/height) for indirect deformation control in REBAP.
Table 1.
Ratio values (span/height) for indirect deformation control in REBAP.
| Structural Element | l/h |
|---|
| Two-way reinforced simply supported slab | 34 |
| Two-way reinforced supported fixed-ended slab | 40 |
| Flat slab | 34 |
| Two-way reinforced fixed-ended slab | 48 |
| Simple beam | 16 |
| Two-way supported beam | 20 |
| Fixed-ended beam | 27 |
Table 2.
Concrete C30/37 properties.
Table 2.
Concrete C30/37 properties.
| fck (MPa) | fctm (MPa) | Ec,m (MPa) |
|---|
| 30.0 | 2.9 | 33.0 |
Table 3.
Steel A500NR properties.
Table 3.
Steel A500NR properties.
Table 4.
Data to calculate beam height to verify indirect deformation, according to EC2.
Table 4.
Data to calculate beam height to verify indirect deformation, according to EC2.
| l [m] | K | ρ | ρ’ | ρ0 | fck (MPa) |
|---|
| 3.8 | 1.3 | 0.015 | 0 | 0.0055 | 30.0 |
Table 5.
Beams dimension for first case of study (h, b, As, As’ values in m and cm2).
Table 5.
Beams dimension for first case of study (h, b, As, As’ values in m and cm2).
| EC2 | h | b | As | As’ | REBAP | h | b | As | As’ |
|---|
| V1 | 0.34 | 0.15 | 6.53 | 6.53 | V1 | 0.26 | 0.15 | 4.73 | 4.73 |
| V2 | 0.44 | 0.18 | 8.78 | 8.78 | V2 | 0.35 | 0.15 | 6.75 | 6.75 |
| V3 | 0.38 | 015 | 7.43 | 7.43 | V3 | 0.30 | 0.15 | 5.63 | 5.63 |
Table 6.
Slab dimension for first case of study (e, As, As’ values in m and cm2/m).
Table 6.
Slab dimension for first case of study (e, As, As’ values in m and cm2/m).
| Slab | e | As | As’ |
|---|
| EC2 | 0.23 | 4.73 | 4.73 |
| REBAP | 0.20 | 8.50 | 8.50 |
Table 7.
Deformation ratios from LM, 1NLM and 2NLM for the first case of study.
Table 7.
Deformation ratios from LM, 1NLM and 2NLM for the first case of study.
| Linear Model | 1° Non-Linear Model | 2° Non-Linear Model |
|---|
| | EC2 | REBAP | EC2 | REBAP | EC2 | REBAP |
| Comb. | APC | FC | APC | FC | APC | FC | APC | FC | APC | FC | APC | FC |
| Beam | 0.93 | 0.92 | 1.04 | 1.04 | 1.27 | 1.25 | 1.77 | 1.76 | 0.81 | 0.79 | 0.81 | 0.81 |
| Slab | 0.79 | 0.76 | 0.63 | 0.63 | 0.57 | 0.56 | 0.54 | 0.53 | 0.49 | 0.50 | 0.46 | 0.41 |
Table 8.
Deformation and limit values of the 2NLM for the first case of study (values in mm).
Table 8.
Deformation and limit values of the 2NLM for the first case of study (values in mm).
| Comb. | APC | FC | | APC | FC |
|---|
| EC2 | δAnaly | δNum | δlimit | δAnaly | δNum | δlimit | REBAP | δAnaly | δNum | δlimit | δAnaly | δNum | δlimit |
| Beam | 5.39 | 4.34 | 24 | 5.69 | 4.51 | 15 | Beam | 8.46 | 6.88 | 24 | 8.83 | 7.16 | 15 |
| Slab | 6.52 | 3.21 | 24 | 6.80 | 3.42 | 15 | Slab | 9.19 | 4.27 | 24 | 10.89 | 4.46 | 15 |
Table 9.
Slab dimension for second case of study (e, As, As’ values in m and cm2/m).
Table 9.
Slab dimension for second case of study (e, As, As’ values in m and cm2/m).
| Slab | e | As | As’ |
|---|
| EC2 | 0.28 | 12.5 | 12.5 |
| REBAP | 0.20 | 10.0 | 10.0 |
Table 10.
Deformation ratios from LM, 1NLM and 2NLM for the second case of study of L3.
Table 10.
Deformation ratios from LM, 1NLM and 2NLM for the second case of study of L3.
| L3 | Linear Model | 1° Non-Linear Model | 2° Non-Linear Model |
|---|
| Combination | APC | FC | APC | FC | APC | FC |
| EC2 | 1.2 | 1.2 | 0.86 | 0.86 | 0.66 | 0.66 |
| REBAP | 0.9 | 0.9 | 0.75 | 0.76 | 0.4 | 0.4 |
Table 11.
Deformation and limit values of the 2NLM for the second case of study (values in mm).
Table 11.
Deformation and limit values of the 2NLM for the second case of study (values in mm).
| Comb. | APC | FC |
|---|
| | δAnaly | δNum | δlimit | δAnaly | δNum | δlimit |
| EC2 | 5.6 | 3.71 | 19.2 | 5.8 | 3.83 | 12 |
| REBAP | 20.7 | 8.31 | 19.2 | 21.5 | 8.66 | 12 |
Table 12.
Slab dimension for third case of study (e, As, As’ values in m and cm2/m).
Table 12.
Slab dimension for third case of study (e, As, As’ values in m and cm2/m).
| Slab | e | As | As’ |
|---|
| EC2 | 0.27 | 12.0 | 12.0 |
| REBAP | 0.19 | 8.0 | 8.0 |
Table 13.
Deformation ratios from LM, 1NLM and 2NLM for the third case of study of L3.
Table 13.
Deformation ratios from LM, 1NLM and 2NLM for the third case of study of L3.
| L4 | Linear Model | 1° Non-Linear Model | 2° Non-Linear Model |
|---|
| Combination | APC | FC | APC | FC | APC | FC |
| EC2 | 1.4 | 1.3 | 0.64 | 0.63 | 0.41 | 0.41 |
| REBAP | 0.8 | 0.8 | 0.46 | 0.47 | 0.24 | 0.24 |
Table 14.
Deformation and limit values of the 2NLM for the third case of study (values in mm).
Table 14.
Deformation and limit values of the 2NLM for the third case of study (values in mm).
| Comb. | APC | FC |
|---|
| | δAnaly | δNum | δlimit | δAnaly | δNum | δlimit |
| EC2 | 5.15 | 2.11 | 22 | 5.4 | 2.2 | 14 |
| REBAP | 20.57 | 4.91 | 22 | 21.7 | 5.3 | 14 |