Turbulent CFD Simulation of Two Rotor-Stator Agitators for High Homogeneity and Liquid Level Stability in Stirred Tank
Abstract
1. Introduction
2. Numerical Modeling
2.1. The Governing Equations
2.2. Simulation Setup
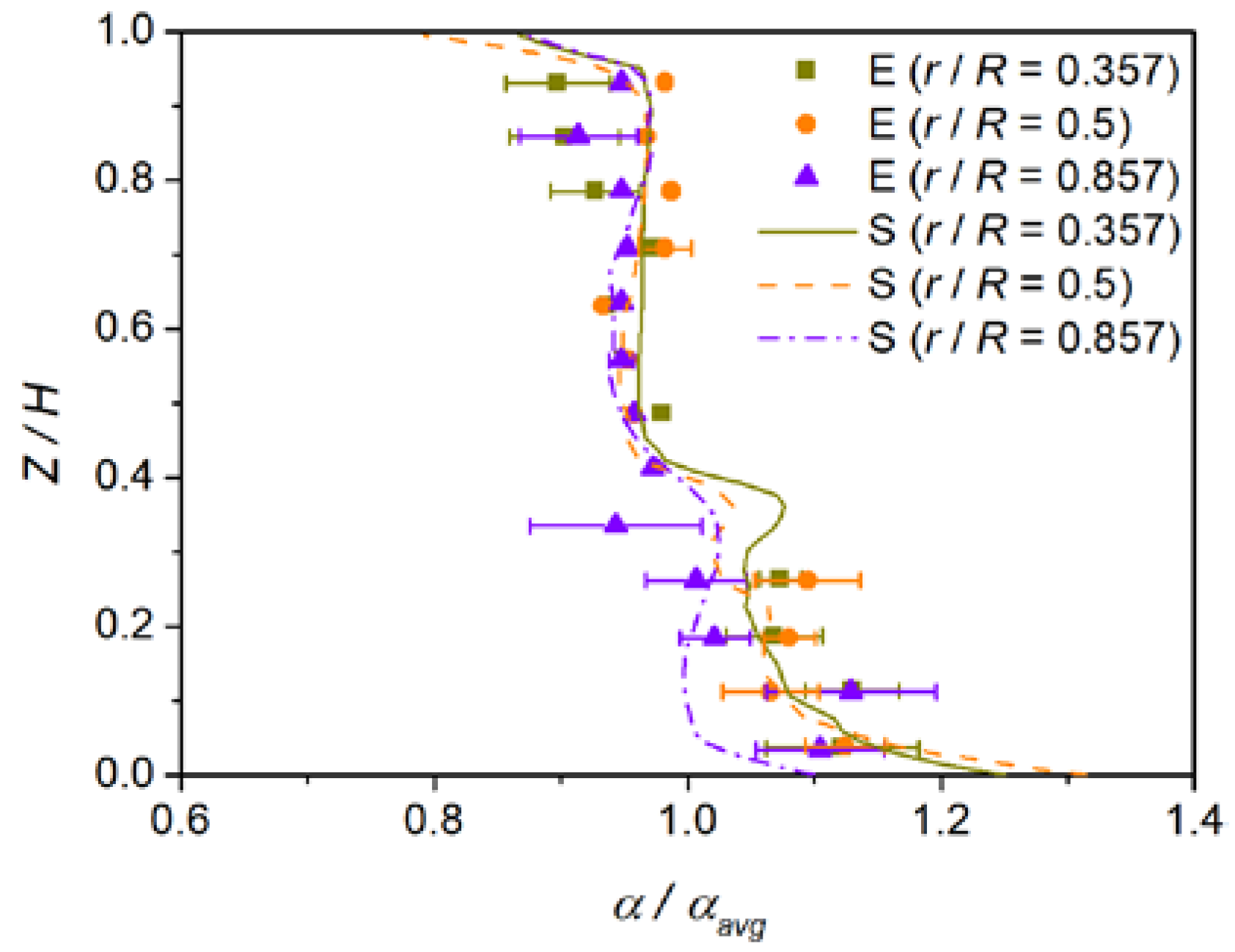
2.3. Model Validation
3. Results and Discussion
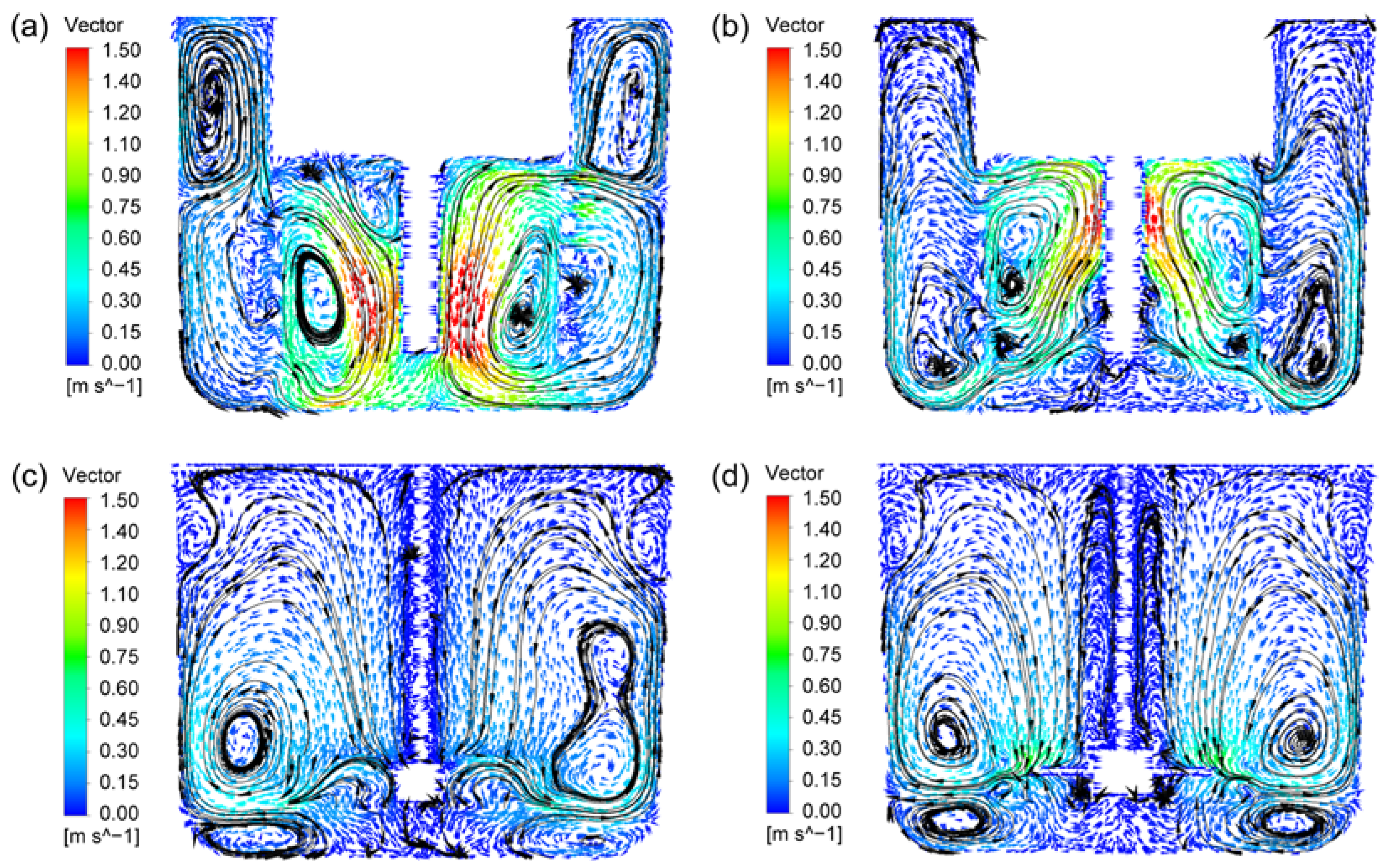
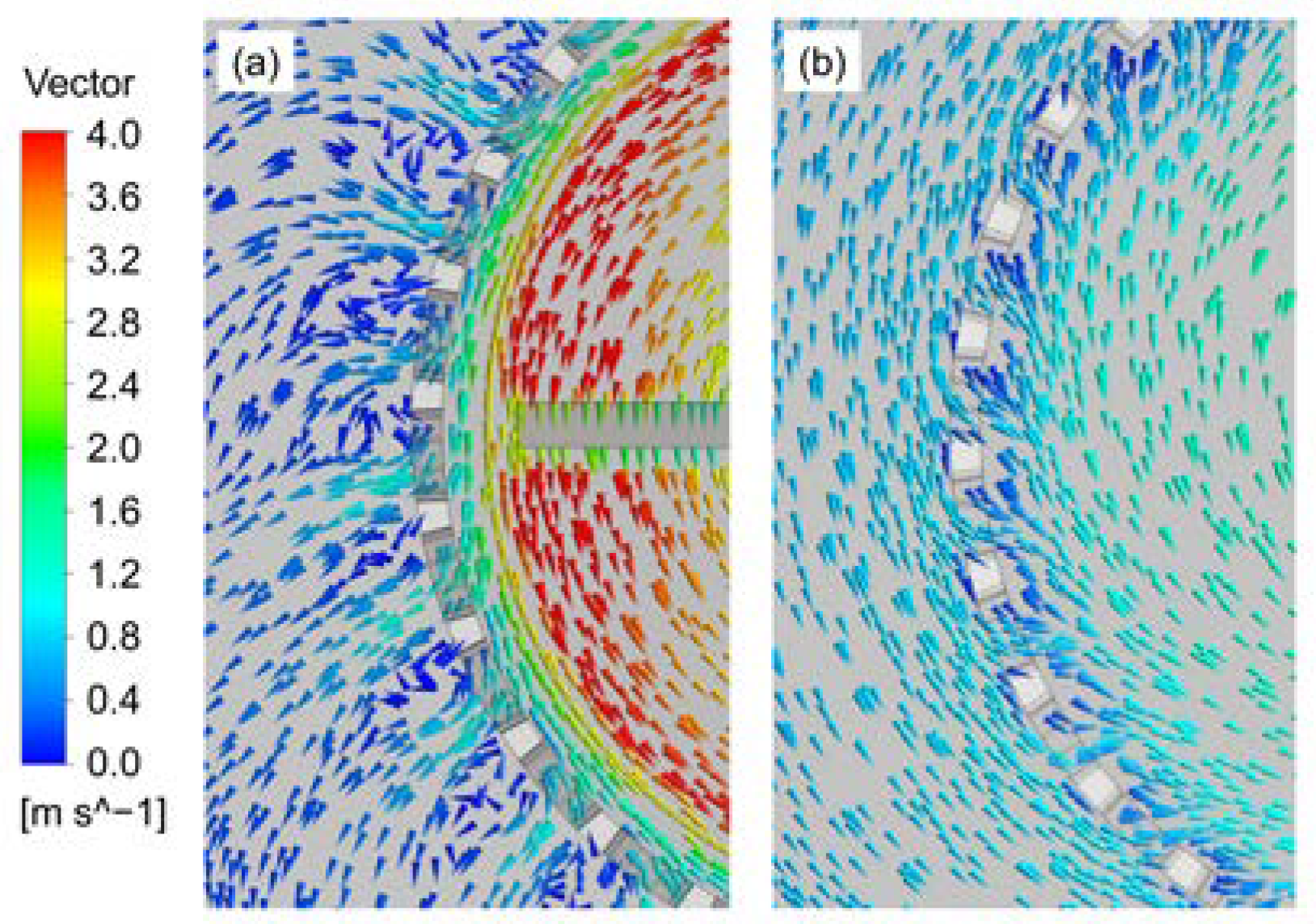
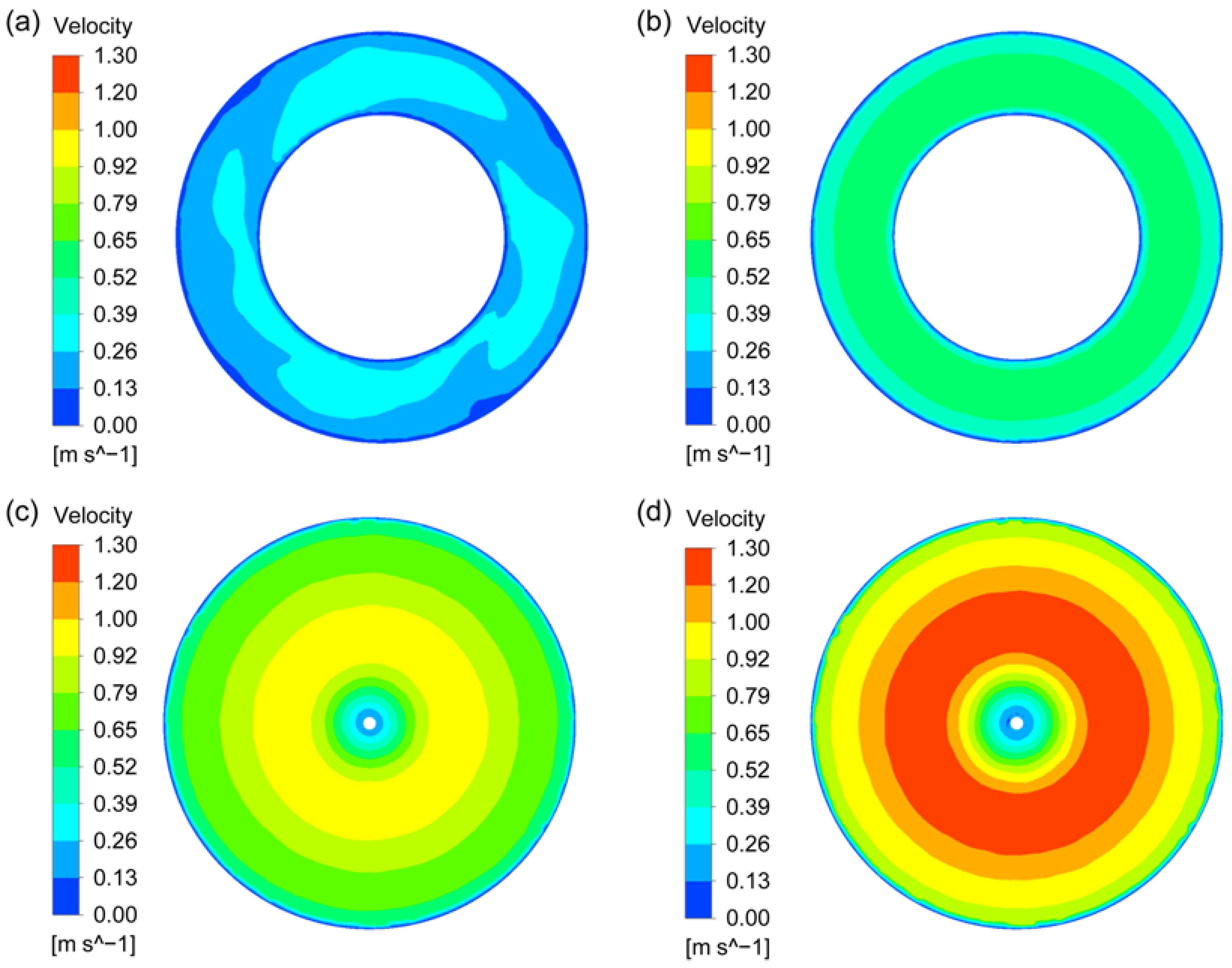
3.1. Flow Fields
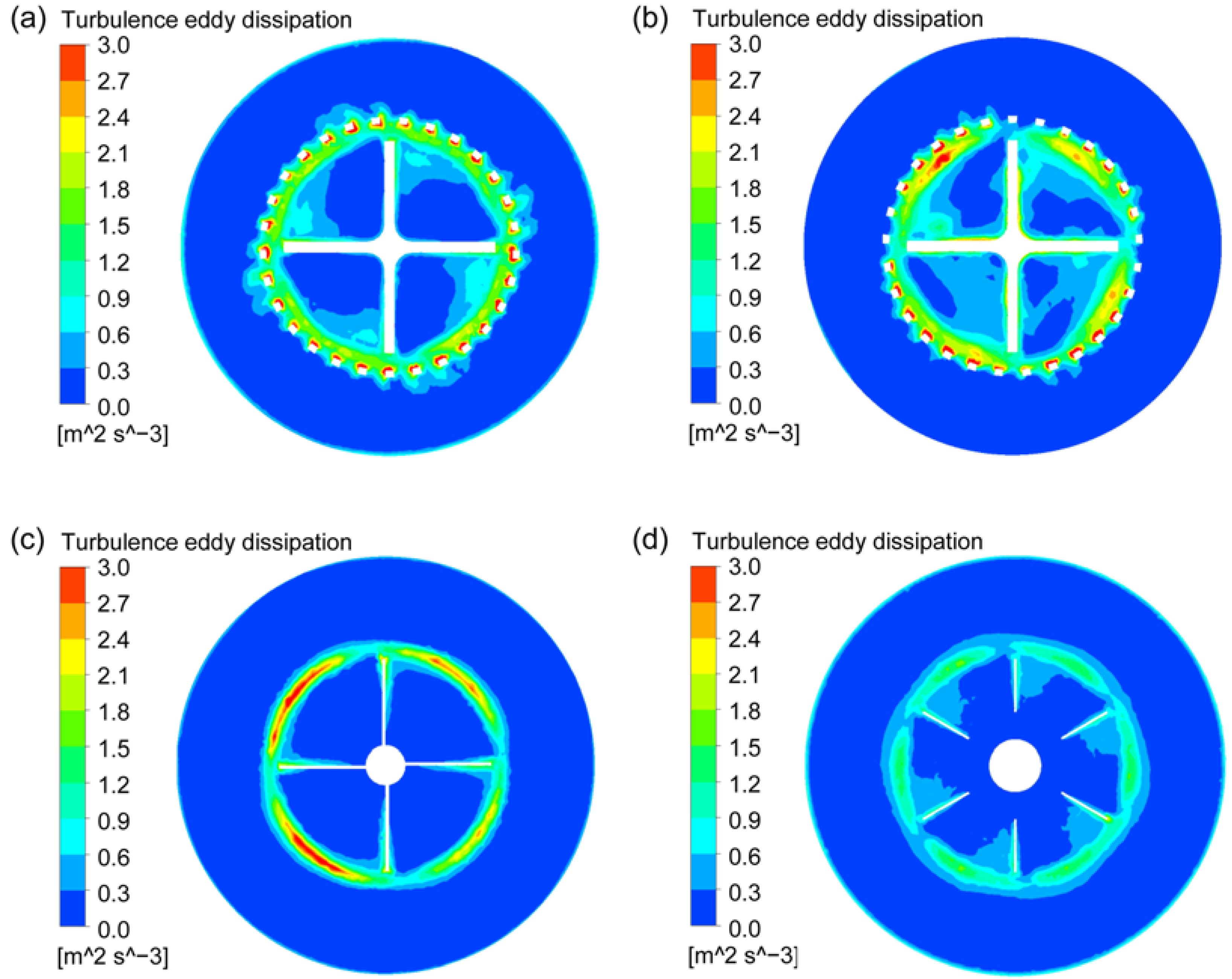
3.2. Turbulent Energy Dissipation
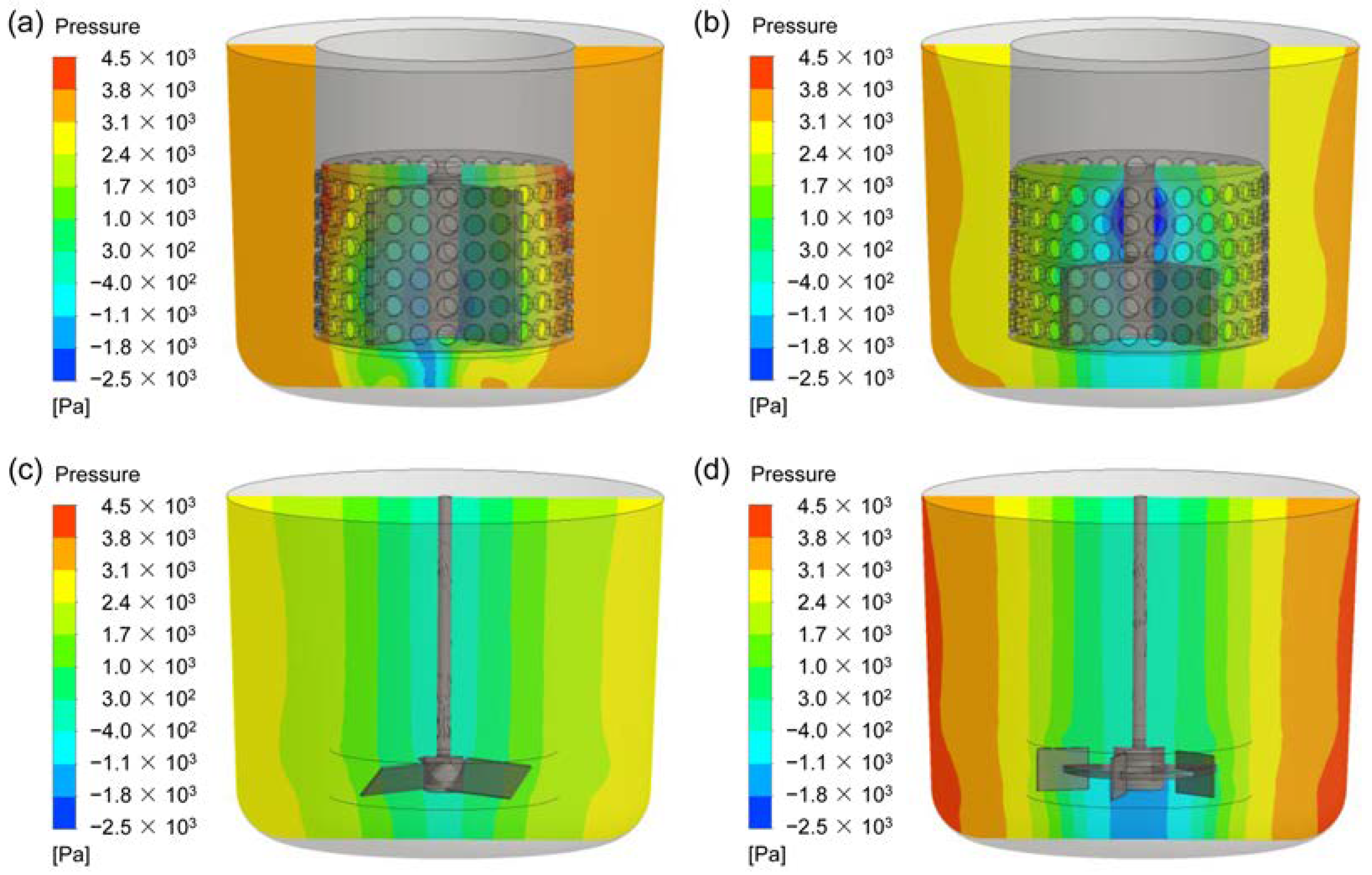
3.3. Pressure Fields
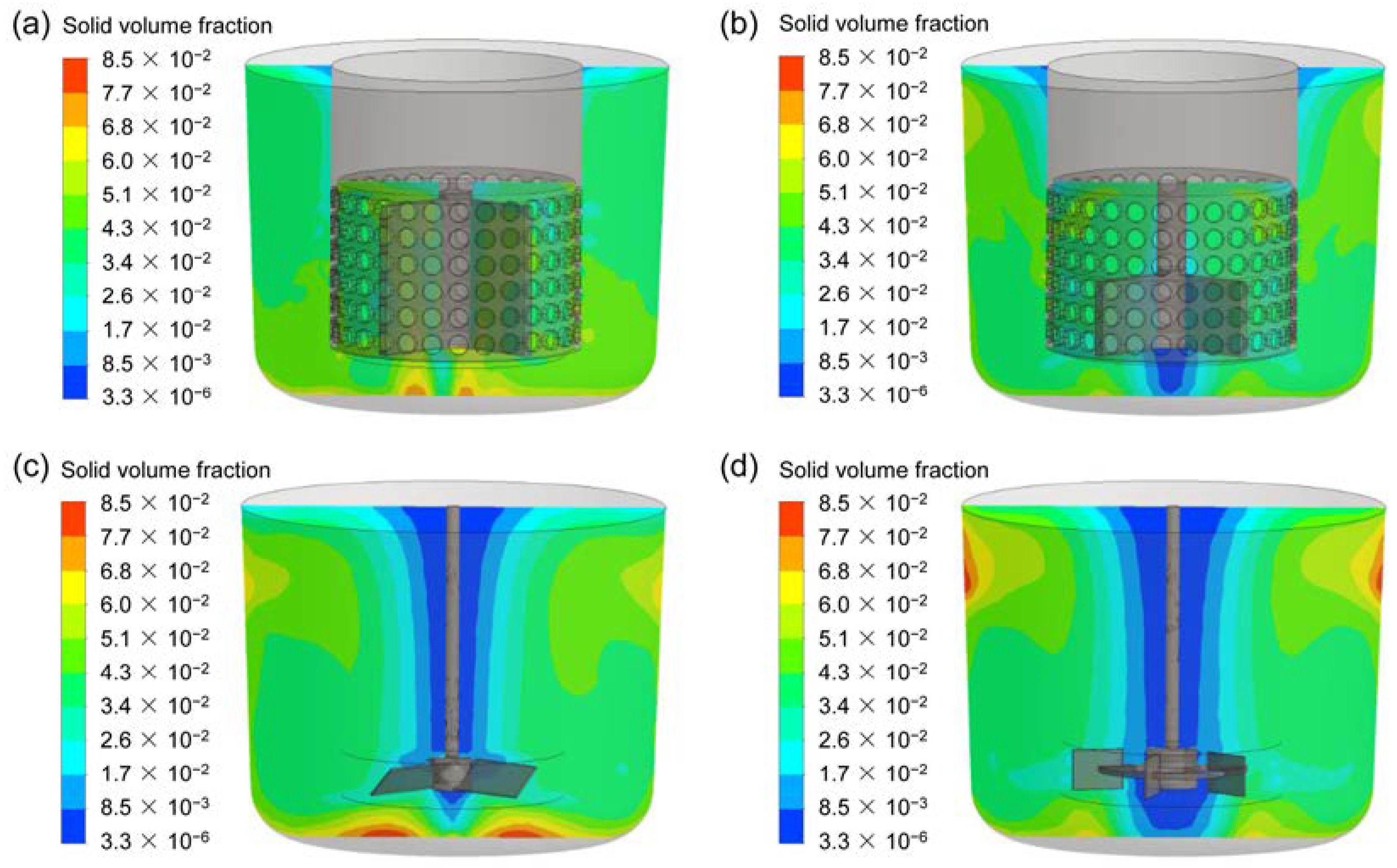
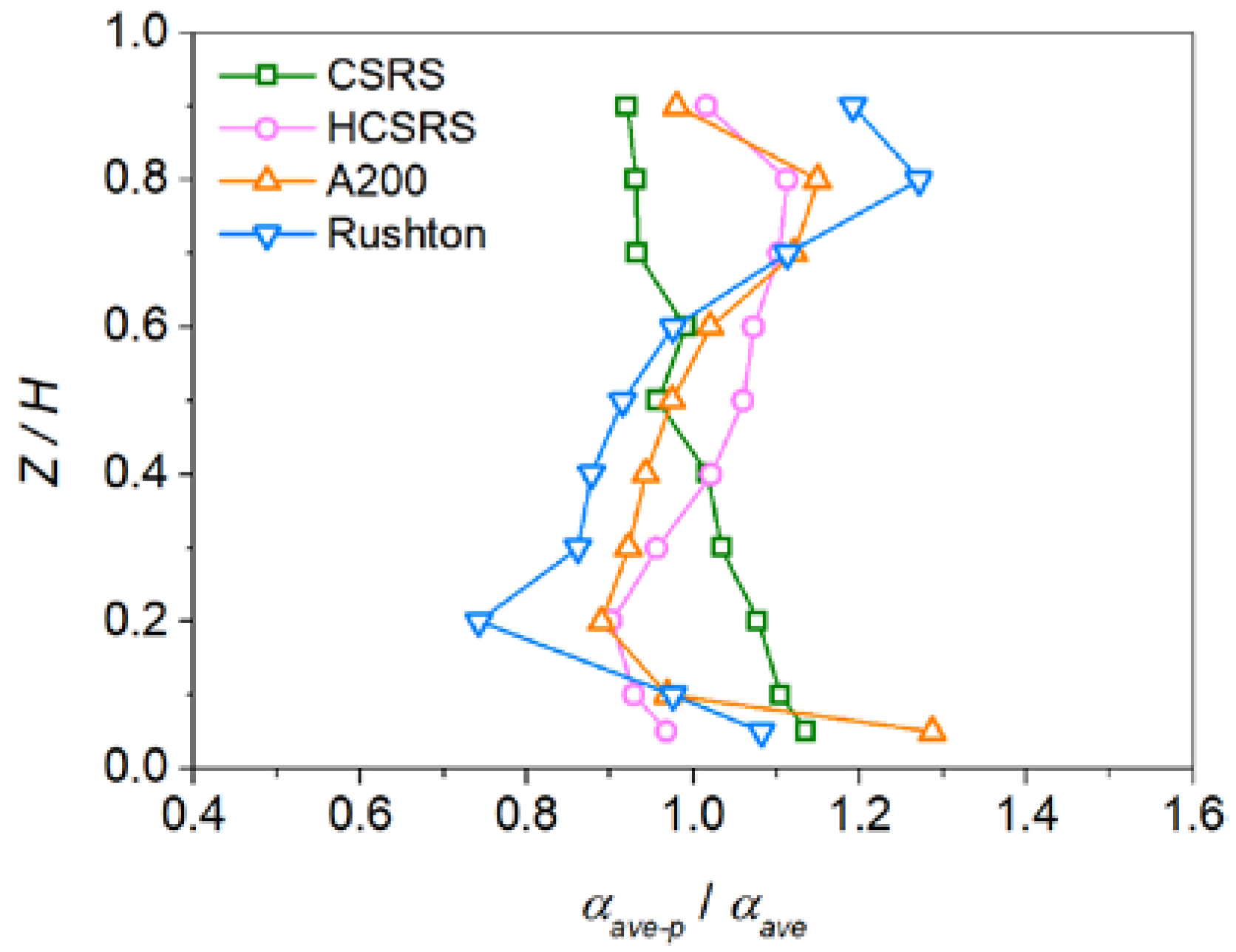
3.4. Solid Particle Distribution
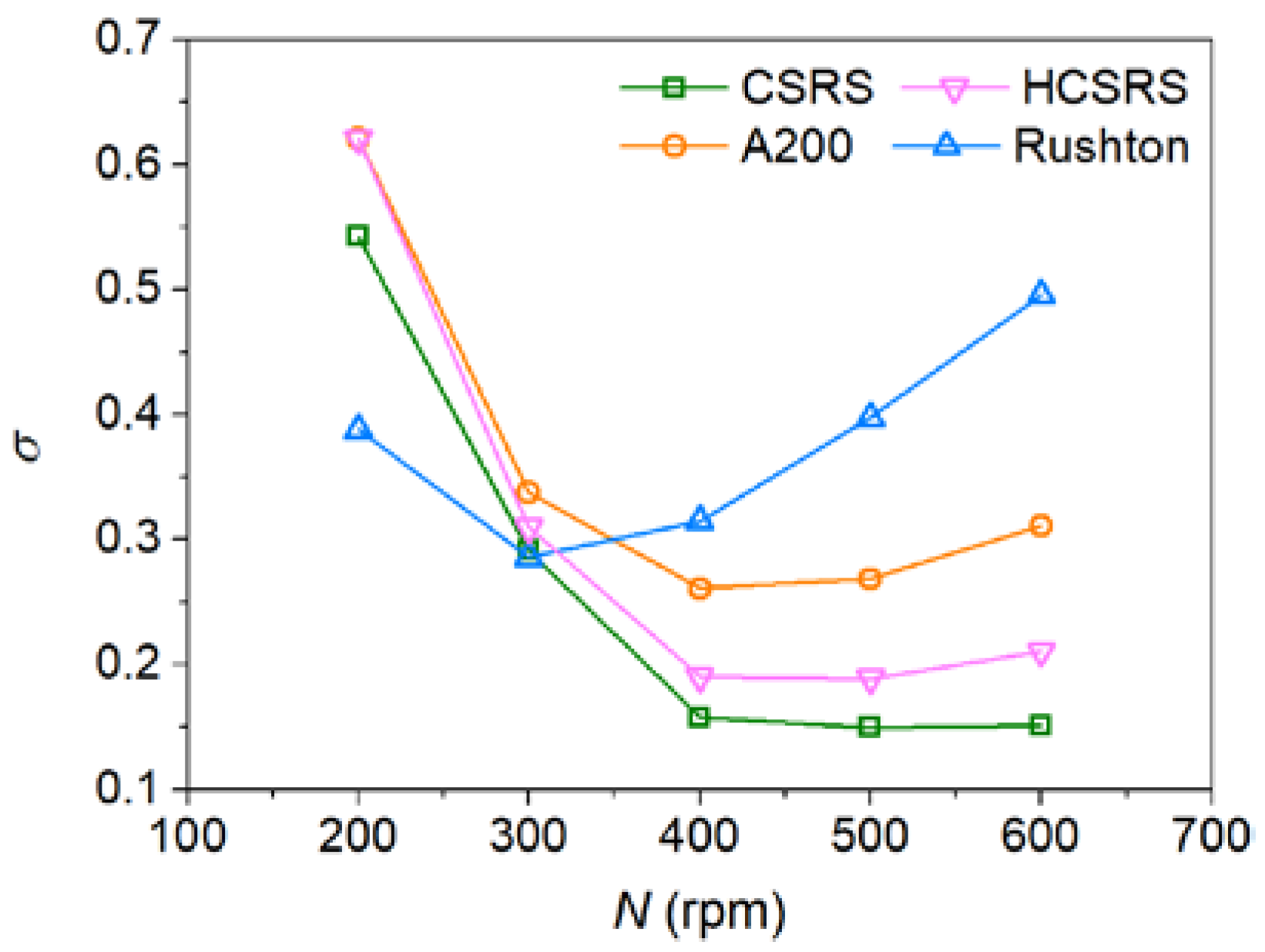
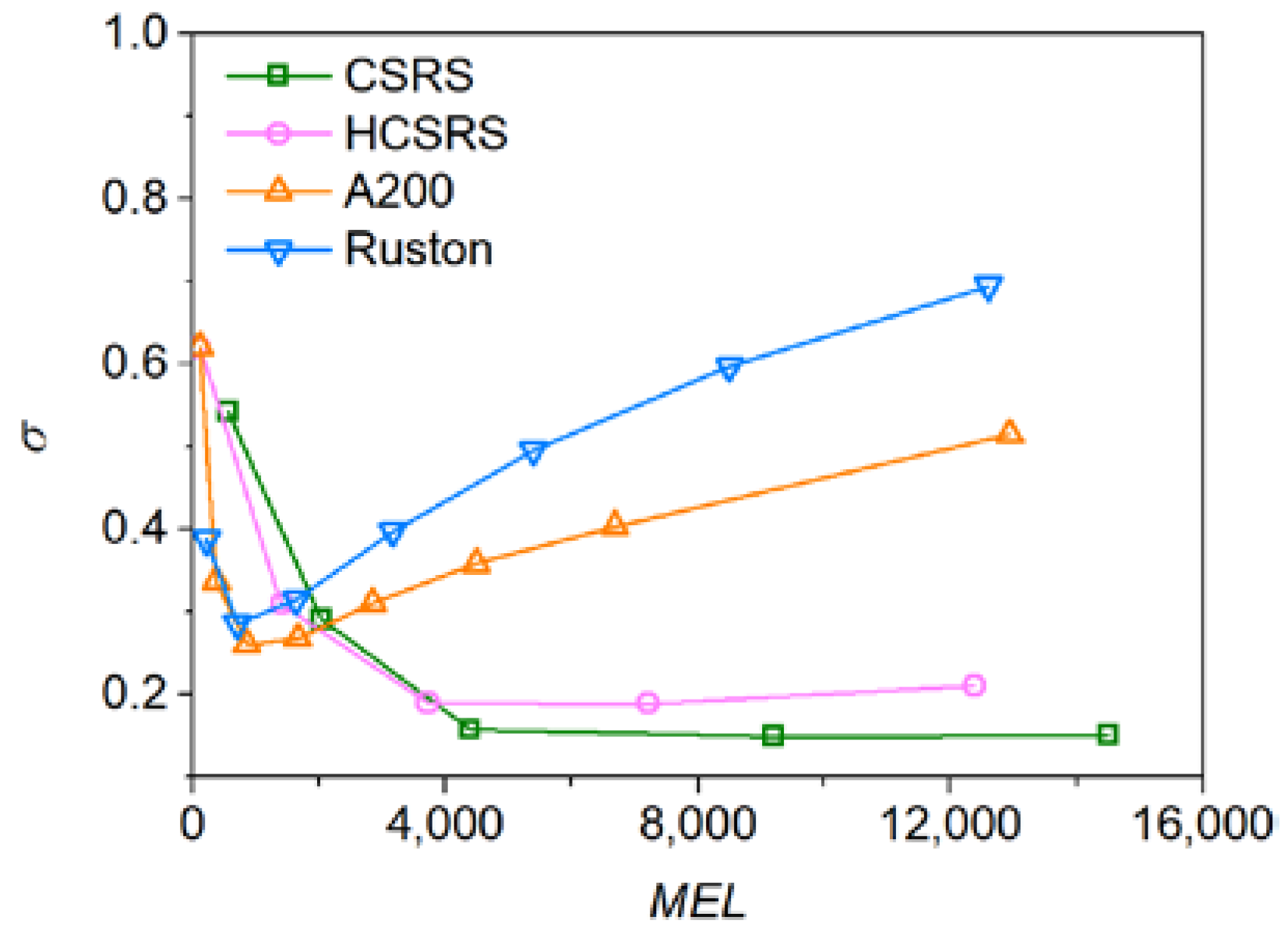
3.5. Effect of Stirring Speed
3.6. Evaluation of Power Consumption and Surface Stability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Huang, Y.; Song, B.; Kainer, K.U.; Dieringa, H. Enhancing the creep resistance of AlN/Al nanoparticles reinforced Mg-2.85Nd-0.92Gd-0.41Zr-0.29Zn alloy by a high shear dispersion technique. Mater. Sci. Eng. A 2019, 755, 18–27. [Google Scholar] [CrossRef]
- Paul, E.L.; Atiemo-obeng, V.A.; Kresta, S.M. Handbook of Industrial Mixing: Science and Practice; John Wiley & Sons, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Kumaresan, T.; Joshi, J.B. Effect of impeller design on the flow pattern and mixing in stirred tanks. Chem. Eng. J. 2006, 115, 173–193. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int. J. Heat Mass Transf. 2014, 78, 741–754. [Google Scholar] [CrossRef]
- Mak, A.T.-C. Solid-Liquid Mixing in Mechanically Agitated Vessels; University of London: London, UK, 1992. [Google Scholar]
- Frijlink, J.J.; Bakker, A.; Smith, J.M. Suspension of solid particles with gassed impellers. Chem. Eng. Sci. 1990, 45, 1703–1718. [Google Scholar] [CrossRef]
- Ayranci, I.; Kresta, S.M. Design rules for suspending concentrated mixtures of solids in stirred tanks. Chem. Eng. Res. Des. 2011, 89, 1961–1971. [Google Scholar] [CrossRef]
- Devarajulu, C.; Loganathan, M. Effect of impeller clearance and liquid level on critical impeller speed in an agitated vessel using different axial and radial impellers. J. Appl. Fluid Mech. 2016, 9, 2753–2761. [Google Scholar] [CrossRef]
- Hosseini, S.; Patel, D.; Ein-Mozaffari, F.; Mehrvar, M. Study of solid-liquid mixing in agitated tanks through electrical resistance tomography. Chem. Eng. Sci. 2010, 65, 1374–1384. [Google Scholar] [CrossRef]
- Kazemzadeh, A.; Ein-Mozaffari, F.; Lohi, A. Effect of impeller type on mixing of highly concentrated slurries of large particles. Particuology 2020, 50, 88–99. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Z.; Bao, Y. Effects of the blade shape on the trailing vortices in liquid flow generated by disc turbines. Chin. J. Chem. Eng. 2011, 19, 232–242. [Google Scholar] [CrossRef]
- Ankamma Rao, D.; Sivashanmugam, P. Experimental and CFD simulation studies on power consumption in mixing using energy saving turbine agitator. J. Ind. Eng. Chem. 2010, 16, 157–161. [Google Scholar] [CrossRef]
- Mishra, P.; Ein-Mozaffari, F. Using tomograms to assess the local solid concentrations in a slurry reactor equipped with a Maxblend impeller. Powder Technol. 2016, 301, 701–712. [Google Scholar] [CrossRef]
- Mishra, P.; Ein-Mozaffari, F. Using computational fluid dynamics to analyze the performance of the Maxblend impeller in solid-liquid mixing operations. Int. J. Multiph. Flow 2017, 91, 194–207. [Google Scholar] [CrossRef]
- Gu, D.; Liu, Z.; Qiu, F.; Li, J.; Tao, C.; Wang, Y. Design of impeller blades for efficient homogeneity of solid-liquid suspension in a stirred tank reactor. Adv. Powder Technol. 2017, 28, 2514–2523. [Google Scholar] [CrossRef]
- Başbuğ, S.; Papadakis, G.; Vassilicos, J.C. Reduced power consumption in stirred vessels by means of fractal impellers. AIChE J. 2018, 64, 1485–1499. [Google Scholar] [CrossRef]
- Gu, D.; Cheng, C.; Liu, Z.; Wang, Y. Numerical simulation of solid-liquid mixing characteristics in a stirred tank with fractal impellers. Adv. Powder Technol. 2019, 30, 2126–2138. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Mao, Z.S.; Yang, C. Enhanced micromixing of non-Newtonian fluids by a novel zigzag punched impeller. Ind. Eng. Chem. Res. 2019, 58, 6822–6829. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, Z.; Yang, Q.; Zhou, S.; Xia, D. Study of novel punched-bionic impellers for high efficiency and homogeneity in pcm mixing and other solid-liquid stirs. Appl. Sci. 2021, 11, 9883. [Google Scholar] [CrossRef]
- Padron, G.; Eagles, W.; Özcan-Taskin, G.; McLeod, G.; Xie, L. Effect of particle properties on the break up of nanoparticle clusters using an in-line rotor-stator. J. Dispers. Sci. Technol. 2008, 29, 580–586. [Google Scholar] [CrossRef]
- Özcan-Taşkin, N.G.; Padron, G.; Voelkel, A. Effect of particle type on the mechanisms of break up of nanoscale particle clusters. Chem. Eng. Res. Des. 2009, 87, 468–473. [Google Scholar] [CrossRef]
- Bałdyga, J.; Orciuch, W.; Makowski, Ł.; Malski-Brodzicki, M.; Malik, K. Break up of nano-particle clusters in high-shear devices. Chem. Eng. Process. Process Intensif. 2007, 46, 851–861. [Google Scholar] [CrossRef]
- Bałdyga, J.; Orciuch, W.; Makowski, Ł.; Malik, K.; Özcan-Taşkin, G.; Eagles, W.; Padron, G. Dispersion of nanoparticle clusters in a rotor-stator mixer. Ind. Eng. Chem. Res. 2008, 47, 3652–3663. [Google Scholar] [CrossRef]
- Hall, S.; Cooke, M.; El-Hamouz, A.; Kowalski, A.J. Droplet break-up by in-line Silverson rotor-stator mixer. Chem. Eng. Sci. 2011, 66, 2068–2079. [Google Scholar] [CrossRef]
- Qin, C.; Chen, C.; Xiao, Q.; Yang, N.; Yuan, C.; Kunkelmann, C.; Cetinkaya, M.; Mülheims, K. CFD-PBM simulation of droplets size distribution in rotor-stator mixing devices. Chem. Eng. Sci. 2016, 155, 16–26. [Google Scholar] [CrossRef]
- James, J.; Cooke, M.; Kowalski, A.; Rodgers, T.L. Scale-up of batch rotor-stator mixers. Part 2—Mixing and emulsification. Chem. Eng. Res. Des. 2017, 124, 321–329. [Google Scholar] [CrossRef]
- Gallassi, M.; Gonçalves, G.F.N.; Botti, T.C.; Moura, M.J.B.; Carneiro, J.N.E.; Carvalho, M.S. Numerical and experimental evaluation of droplet breakage of O/W emulsions in rotor-stator mixers. Chem. Eng. Sci. 2019, 204, 270–286. [Google Scholar] [CrossRef]
- Rueger, P.E.; Calabrese, R.V. Dispersion of water into oil in a rotor-stator mixer. Part 1: Drop breakup in dilute systems. Chem. Eng. Res. Des. 2013, 91, 2122–2133. [Google Scholar] [CrossRef]
- Rueger, P.E.; Calabrese, R.V. Dispersion of water into oil in a rotor-stator mixer. Part 2: Effect of phase fraction. Chem. Eng. Res. Des. 2013, 91, 2134–2141. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Li, X.; Zhang, Y. Experimental investigation and CFD simulation of liquid-solid-solid dispersion in a stirred reactor. Chem. Eng. Sci. 2010, 65, 5559–5572. [Google Scholar] [CrossRef]
- Fathi Roudsari, S.; Dhib, R.; Ein-Mozaffari, F. Using a novel CFD model to assess the effect of mixing parameters on emulsion polymerization. Macromol. React. Eng. 2016, 10, 108–122. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Brucato, A.; Ciofalo, M. Influence of drag and turbulence modelling on CFD predictions of solid liquid suspensions in stirred vessels. Chem. Eng. Res. Des. 2014, 92, 1045–1063. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B.N.; Mathpati, C.S.; Patwardhan, A.W.; Ranade, V.V. CFD simulation of stirred tanks: Comparison of turbulence models. Part I: Radial flow impellers. Can. J. Chem. Eng. 2011, 89, 23–82. [Google Scholar] [CrossRef]
- Wadnerkar, D.; Utikar, R.P.; Tade, M.O.; Pareek, V.K. CFD simulation of solid-liquid stirred tanks. Adv. Powder Technol. 2012, 23, 445–453. [Google Scholar] [CrossRef]
- Hosseini, S.; Patel, D.; Ein-Mozaffari, F.; Mehrvar, M. Study of solid-liquid mixing in agitated tanks through computational fluid dynamics modeling. Ind. Eng. Chem. Res. 2010, 49, 4426–4435. [Google Scholar] [CrossRef]
- Derksen, J.J. Numerical simulation of solids suspension in a stirred tank. AIChE J. 2003, 49, 2700–2714. [Google Scholar] [CrossRef]
- Wadnerkar, D.; Tade, M.O.; Pareek, V.K.; Utikar, R.P. CFD simulation of solid–liquid stirred tanks for low to dense solid loading systems. Particuology 2016, 29, 16–33. [Google Scholar] [CrossRef]
- Qi, N.; Zhang, H.; Zhang, K.; Xu, G.; Yang, Y. CFD simulation of particle suspension in a stirred tank. Particuology 2013, 11, 317–326. [Google Scholar] [CrossRef]
- Tamburini, A.; Cipollina, A.; Micale, G.; Brucato, A.; Ciofalo, M. CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: Prediction of solid particle distribution. Chem. Eng. J. 2013, 223, 875–890. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Decker, S. State of the art and future trends in CFD simulation of stirred vessel hydrodynamics. Chem. Eng. Technol. 2004, 27, 215–224. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiple Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar] [CrossRef]
- Khopkar, A.R.; Kasat, G.R.; Pandit, A.B.; Ranade, V.V. Computational fluid dynamics simulation of the solid suspension in a stirred slurry reactor. Ind. Eng. Chem. Res. 2006, 45, 4416–4428. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, G.; Siddhu, M.A.H.; Masroor, A.; Ali, M.F.; Abdeltawab, A.A.; Chen, X. Effect of impeller on sinking and floating behavior of suspending particle materials in stirred tank: A computational fluid dynamics and factorial design study. Adv. Powder Technol. 2017, 28, 1159–1169. [Google Scholar] [CrossRef]
- Siddqui, M.I.H.; Jha, P.K. Assessment of turbulence models for prediction of intermixed amount with free surface variation using coupled level set volume of fluid method. ISIJ Int. 2014, 54, 2578–2587. [Google Scholar] [CrossRef]
- Murthy, B.N.; Ghadge, R.S.; Joshi, J.B. CFD simulations of gas-liquid-solid stirred reactor: Prediction of critical impeller speed for solid suspension. Chem. Eng. Sci. 2007, 62, 7184–7195. [Google Scholar] [CrossRef]
- Vojir, D.J.; Michaelides, E.E. Effect of the history term on the motion of rigid spheres in a viscous fluid. Int. J. Multiph. Flow 1994, 20, 547–556. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Ochieng, A.; Lewis, A.E. CFD simulation of solids off-bottom suspension and cloud height. Hydrometallurgy 2006, 82, 1–12. [Google Scholar] [CrossRef]
- Bohnet, M.; Niesmak, G. Distribution of solids in stirred suspension. Ger. Chem. Eng. 1980, 3, 57–65. [Google Scholar] [CrossRef]






| Geometric Parameter (mm) | Values |
|---|---|
| Diameter of top of stirring tank | 253 |
| Diameter below stirring tank | 240 |
| Stirring tank height | 200 |
| Height of hole area | 100 |
| Total height of stator | 170 |
| Hole center spacing of stator | 16 |
| Hole diameter of stator | 12 |
| Inner diameter of stator | 142 |
| Outer diameter of stator | 150 |
| Variable | Values |
|---|---|
| Agitator type | CSRS, HCSRS, A200, Rushton |
| Stirring speed (rpm) | 200, 300, 400, 500, 600 |
| Particle size (μm) | 100 |
| Solids weight fraction (wt.%) | 10 |
| Grain density (kg/m3) | 4506 |
| Liquid density (kg/m3) | 1650 |
| Liquid viscosity (Pa*s) | 0.00139 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Zheng, K.; He, J.; Xiong, Y.; Tian, Z.; Lin, Y.; Long, D. Turbulent CFD Simulation of Two Rotor-Stator Agitators for High Homogeneity and Liquid Level Stability in Stirred Tank. Materials 2022, 15, 8563. https://doi.org/10.3390/ma15238563
Yin C, Zheng K, He J, Xiong Y, Tian Z, Lin Y, Long D. Turbulent CFD Simulation of Two Rotor-Stator Agitators for High Homogeneity and Liquid Level Stability in Stirred Tank. Materials. 2022; 15(23):8563. https://doi.org/10.3390/ma15238563
Chicago/Turabian StyleYin, Cuicui, Kaihong Zheng, Jiazhen He, Yongnan Xiong, Zhuo Tian, Yingfei Lin, and Danfeng Long. 2022. "Turbulent CFD Simulation of Two Rotor-Stator Agitators for High Homogeneity and Liquid Level Stability in Stirred Tank" Materials 15, no. 23: 8563. https://doi.org/10.3390/ma15238563
APA StyleYin, C., Zheng, K., He, J., Xiong, Y., Tian, Z., Lin, Y., & Long, D. (2022). Turbulent CFD Simulation of Two Rotor-Stator Agitators for High Homogeneity and Liquid Level Stability in Stirred Tank. Materials, 15(23), 8563. https://doi.org/10.3390/ma15238563





