Analysis and Measurement of Differential-Mode Magnetic Noise in Mn-Zn Soft Ferrite Shield for Ultra-Sensitive Sensors
Abstract
:1. Introduction
2. Methods
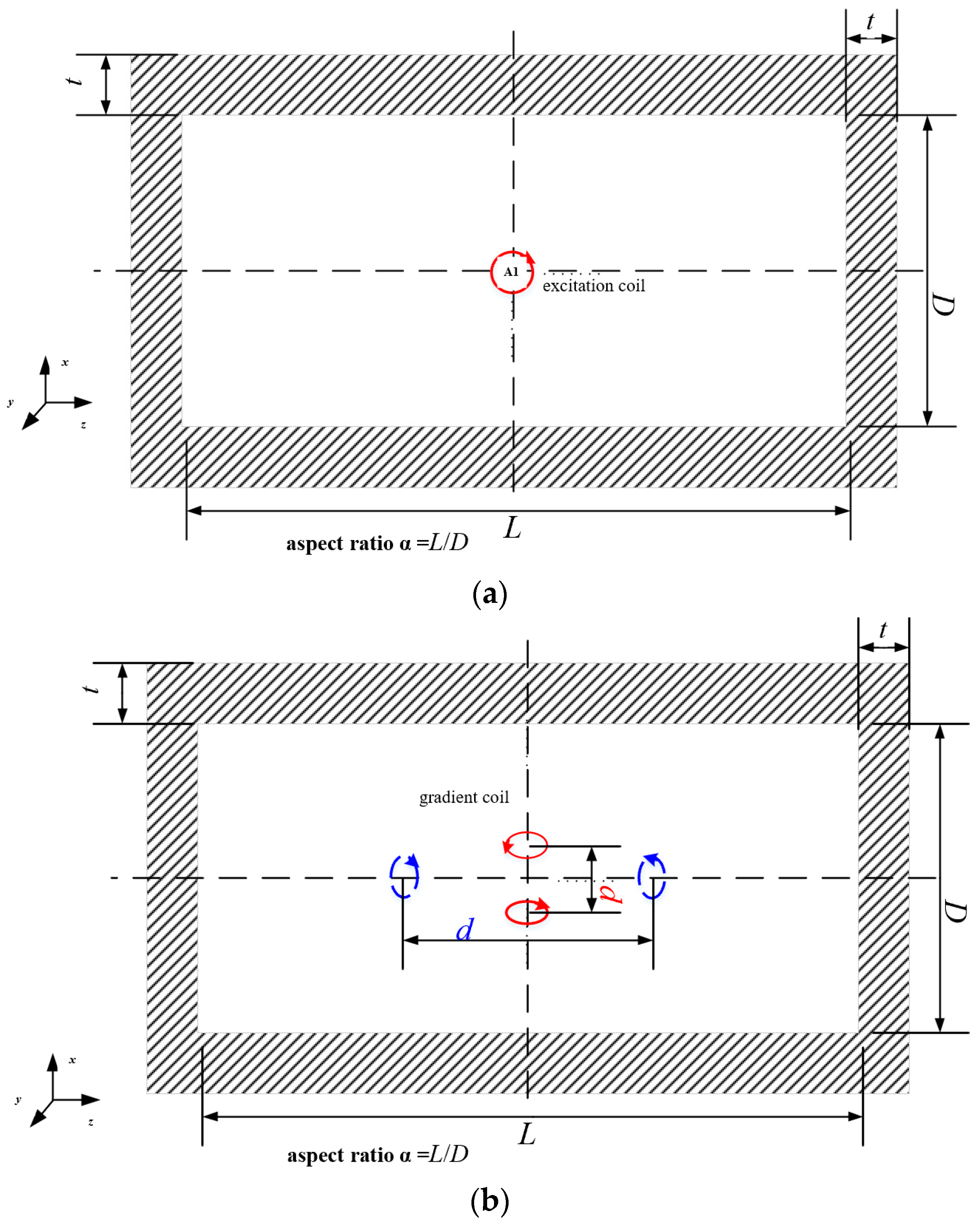
2.1. Magnetic Field Response and Differential Measurement Model
2.2. Analysis of Differential Reduction Capability
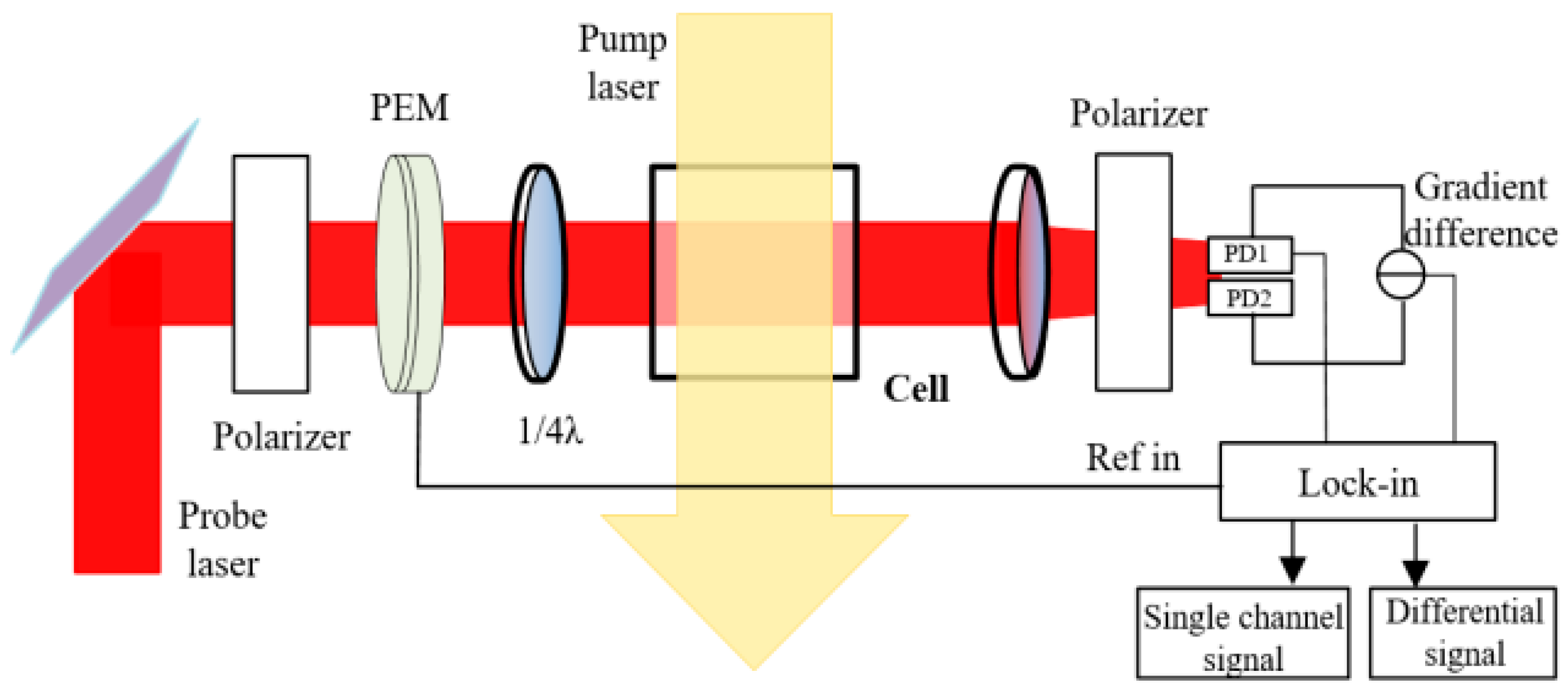
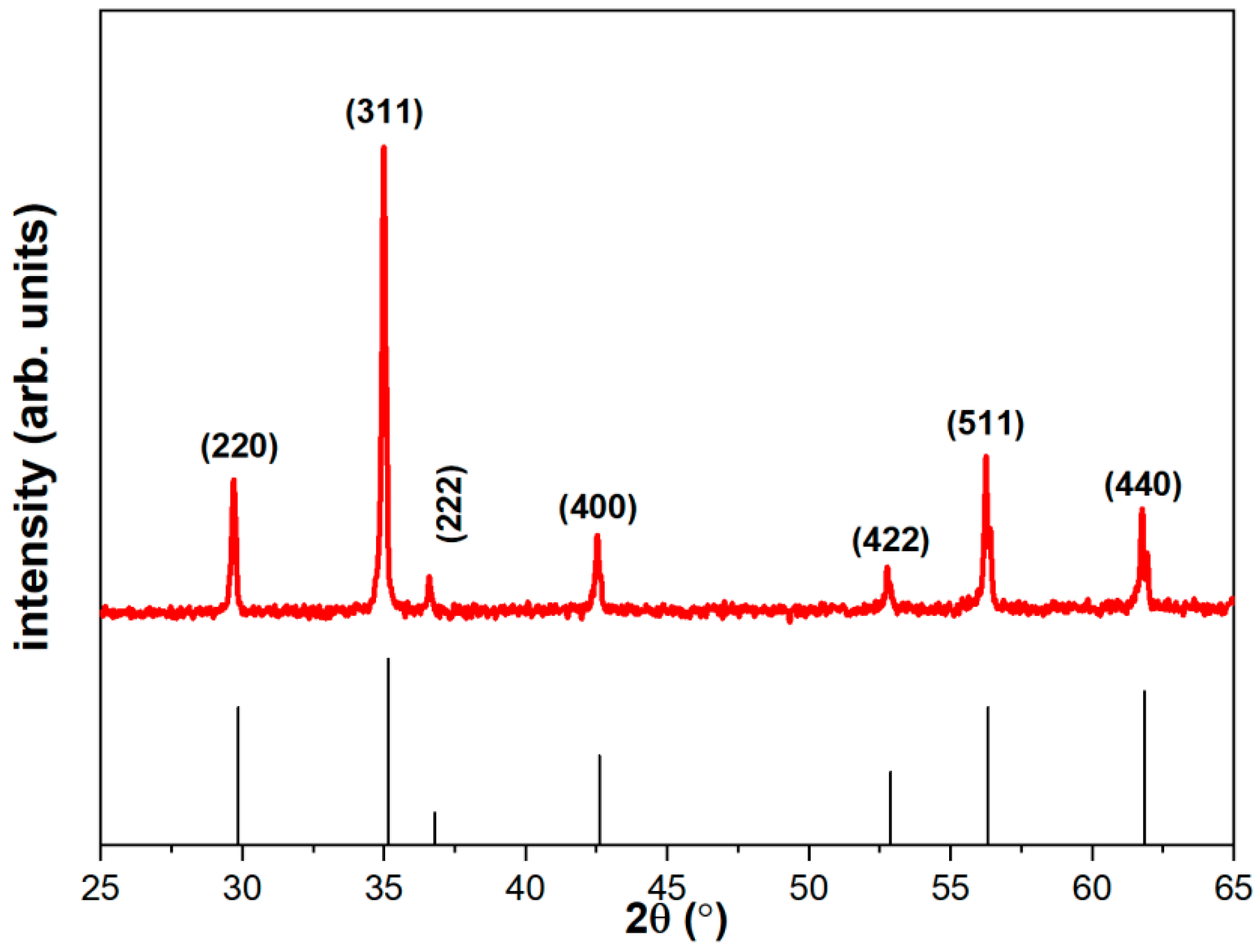
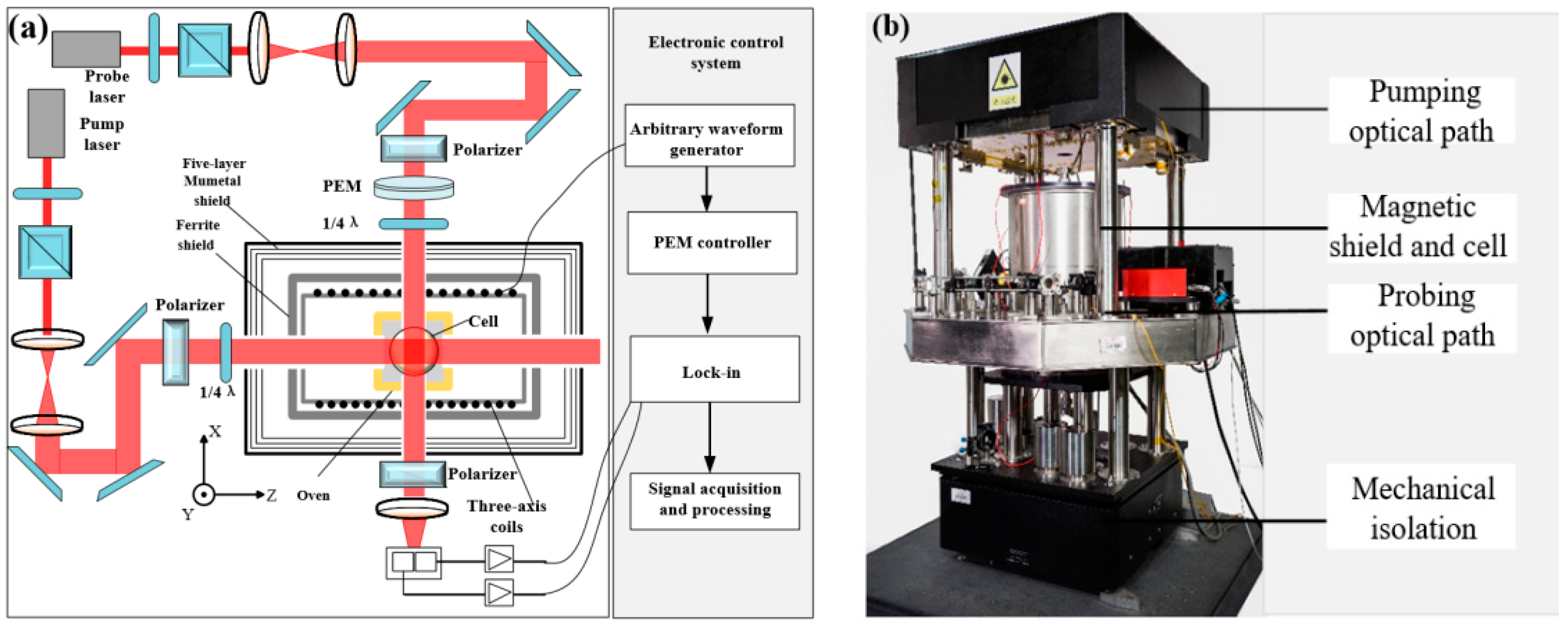
3. Experimental Setup and Results
3.1. Magnetic Field Response and Differential Measurement Model
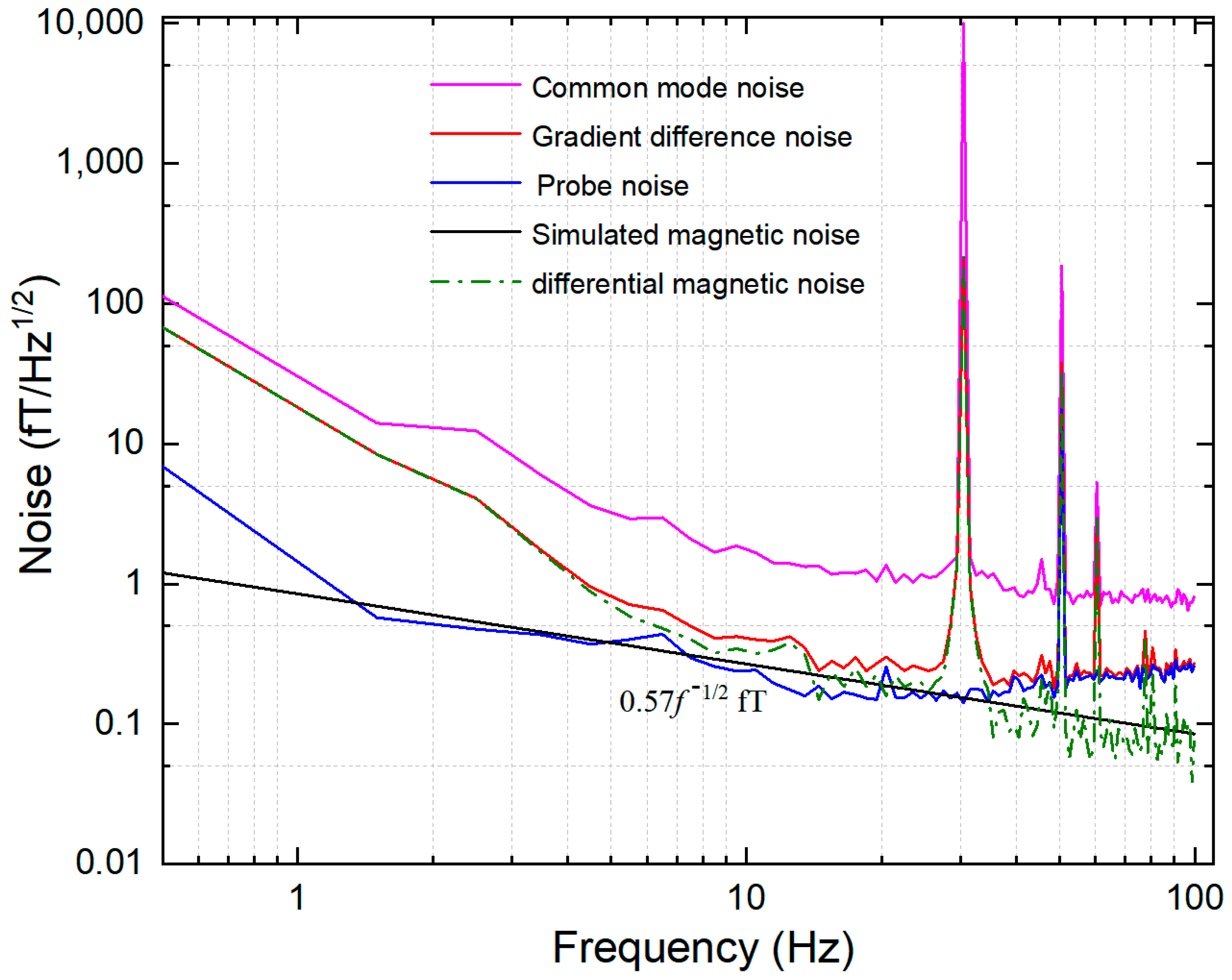
3.2. Magnetic Noise Measurement
4. Noise Reduction Capability of Differential Measurement
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Begus, S.; Xia, H.; Lee, S.; Jazbinsek, V.; Trontelj, Z.; Romalis, M.V. Multi-channel atomic magnetometer for magnetoencephalography: A configuration study. NeuroImage 2014, 89, 143–151. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Wan, S.; Sheng, J.; Liu, D.; Gao, J.H. A high-performance compact magnetic shield for optically pumped magnetometer-based magnetoencephalography. Rev. Sci. Instrum. 2019, 90, 064102. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhao, L.; Zhang, N.; Yu, M.; Ma, Y.; Han, X.; Zhao, M.; Lin, Q.; Yang, P.; Jiang, Z. Single beam Cs-Ne SERF atomic magnetometer with the laser power differential method. Opt. Express 2022, 30, 16541–16552. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Kimball, D.; Sushkov, A.O.; Aybas, D.; Blanchard, J.W.; Centers, G.; Kelley, S.; Wickenbrock, A.; Fang, J.; Budker, D. Application of spin-exchange relaxation-free magnetometry to the cosmic axion spin precession experiment. Phys. Dark Universe 2017, 19, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Niu, Y.; Ye, C. Optically pumped magnetometer with dynamic common mode magnetic field compensation. Sens. Actuator A Phys. 2021, 332, 113195. [Google Scholar]
- Satpute, N.; Dhoka, P.; Iwaniec, M.; Jabade, S.; Karande, P. Manufacturing of Pure Iron by Cold Rolling and Investigation for Application in Magnetic Flux Shielding. Materials 2022, 15, 2630. [Google Scholar] [CrossRef]
- Mateos, I.; Patton, B.; Zhivun, E.; Budker, D.; Wurm, D.; Ramos-Castro, J. Noise characterization of an atomic magnetometer at sub-millihertz frequencies. Sens. Actuator A Phys. 2015, 224, 147–155. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Zhao, L.; Chen, Y.; Luo, G.; Yu, M.; Wang, Y.; Guo, J.; Yang, P.; Lin, Q.; Jiang, Z. The micro-fabrication and performance analysis of non-magnetic heating chip for miniaturized SERF atomic magnetometer. J. Magn. Magn. Mater. 2022, 557, 169495. [Google Scholar] [CrossRef]
- Pan, D.; Lin, S.; Li, L.; Li, J.; Jin, Y.; Sun, Z.; Liu, T. Research on the design method of uniform magnetic field coil based on the MSR. IEEE Trans. Ind. Electron. 2020, 67, 1348–1356. [Google Scholar] [CrossRef]
- Fang, X.; Wei, K.; Zhao, T.; Zhai, Y.; Ma, D.; Xing, B.; Liu, Y.; Xiao, Z. High spatial resolution multi-channel optically pumped atomic magnetometer based on a spatial light modulator. Opt. Express 2020, 28, 26447–26460. [Google Scholar] [CrossRef] [PubMed]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Lu, J.; Fang, X.; Yang, K.; Wang, K.; Zhang, N.; Han, B.; Ding, M. Parameter modeling analysis of a cylindrical ferrite magnetic shield to reduce magnetic noise. IEEE Trans. Ind. Electron. 2022, 45, 991–998. [Google Scholar] [CrossRef]
- Lee, S.K.; Romalis, M.V. Calculation of magnetic field noise from high-permeability magnetic shields and conducting objects with simple geometry. J. Appl. Phys. 2008, 103, 084904. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.; Quan, W.; Liu, F.; Pang, H.; Xing, L.; Liu, G. Performance of low-noise ferrite shield in a K-Rb-Ne21 co-magnetometer. IEEE Sens. J. 2019, 20, 2543–2549. [Google Scholar] [CrossRef]
- Ma, D.; Lu, J.; Fang, X.; Dou, Y.; Wang, K.; Gao, Y.; Li, S.; Han, B. A novel low-noise Mu-metal magnetic shield with winding shape. Sens. Actuator A Phys. 2022, 346, 113884. [Google Scholar] [CrossRef]
- Wang, M.; Feng, J.; Shi, Y.; Shen, M. Demagnetization weakening and magnetic field concentration with ferrite core characterization for efficient wireless power transfer. IEEE Trans. Ind. Electron. 2019, 66, 1842–1851. [Google Scholar] [CrossRef]
- Kornack, T.W.; Smullin, S.J.; Lee, S.K.; Romalis, M.V. A low-noise ferrite magnetic shield. J. Appl. Phys. 2007, 90, 223501. [Google Scholar] [CrossRef] [Green Version]
- Savukov, I.; Kim, Y.J. Investigation of magnetic noise from conductive shields in the 10–300 kHz frequency range. J. Appl. Phys. 2020, 128, 234501. [Google Scholar] [CrossRef]
- Ichihara, S.; Mizutani, N.; Ito, Y.; Kobayashi, T. Differential measurement With the Balanced Response of Optically Pumped Atomic Magnetometers. IEEE Trans. Magn. 2016, 52, 1–9. [Google Scholar] [CrossRef]
- Kamada, K.; Ito, Y.; Ichihara, S.; Mizutani, N.; Kobayashi, T. Noise reduction and signal-to-noise ratio improvement of atomic magnetometers with optical gradiometer configurations. Opt. Express 2015, 23, 6976–6987. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Huang, S.; Xu, F.; Hu, Z.; Lin, Q. Multi-channel spin exchange relaxation free magnetometer towards two-dimensional vector, magnetoencephalography. Opt. Express 2019, 27, 597–607. [Google Scholar] [CrossRef] [PubMed]
- Wakai, R.T. The atomic magnetometer: A new era in biomagnetism. AIP Conf. Proc. 2014, 1626, 46–54. [Google Scholar]
- Nenonen, J.; Montonen, J.; Katila, T. Thermal noise in biomagnetic measurements. Rev. Sci. Instrum. 1996, 67, 2397–2405. [Google Scholar] [CrossRef]
- Sandin, H.J.; Volegov, P.L.; Espy, M.A.; Matlashov, A.N.; Savukov, I.M.; Schultz, L.J. Noise modeling from conductive shields using Kirchhoff equations. IEEE Trans. Appl. Supercon. 2010, 21, 489–492. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Ma, D.; Yang, K.; Quan, W.; Zhao, J.; Xing, B.; Han, B.; Ding, M. Study of Magnetic Noise of a Multi-Annular Ferrite Shield. IEEE Access 2020, 8, 40918–40924. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1996, 29, 255. [Google Scholar] [CrossRef] [Green Version]
- Ito, Y.; Sato, D.; Kamada, K.; Kobayashi, T. Measurements of Magnetic Field Distributions With an Optically Pumped K-Rb Hybrid Atomic Magnetometer. IEEE Trans. Magn. 2014, 50, 4006903. [Google Scholar] [CrossRef]
- Budker, D.; Romalis, M. Optical Magnetometry. Nat. Phys. 2007, 3, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Smythe, W.R. Static and Dynamic Electricity; McGraw-Hill: New York, NY, USA, 1968; pp. 188–190. [Google Scholar]
- Ionel, D.M.; Popescu, M.; McGilp, M.I.; Miller, T.J.E.; Dellinger, S.J.; Heideman, R.J. Computation of core losses in electrical machines using improved models for laminated steel. IEEE Trans. Ind. Electron. 2007, 43, 1554–1564. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Lu, J.; Xiujie, F.; Wang, K.; Jing, W.; Zhang, N.; Chen, H.; Ding, M.; Han, B. Analysis of coil constant of triaxial uniform coils in Mn–Zn ferrite magnetic shields. J. Phys. D Appl. Phys. 2021, 54, 275001. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Liu, F.; Xing, L.; Liu, G. Suppression of the Bias Error Induced by Magnetic Noise in a Spin-Exchange Relaxation-Free Gyroscope. IEEE Sens. J. 2019, 19, 9712–9721. [Google Scholar] [CrossRef]



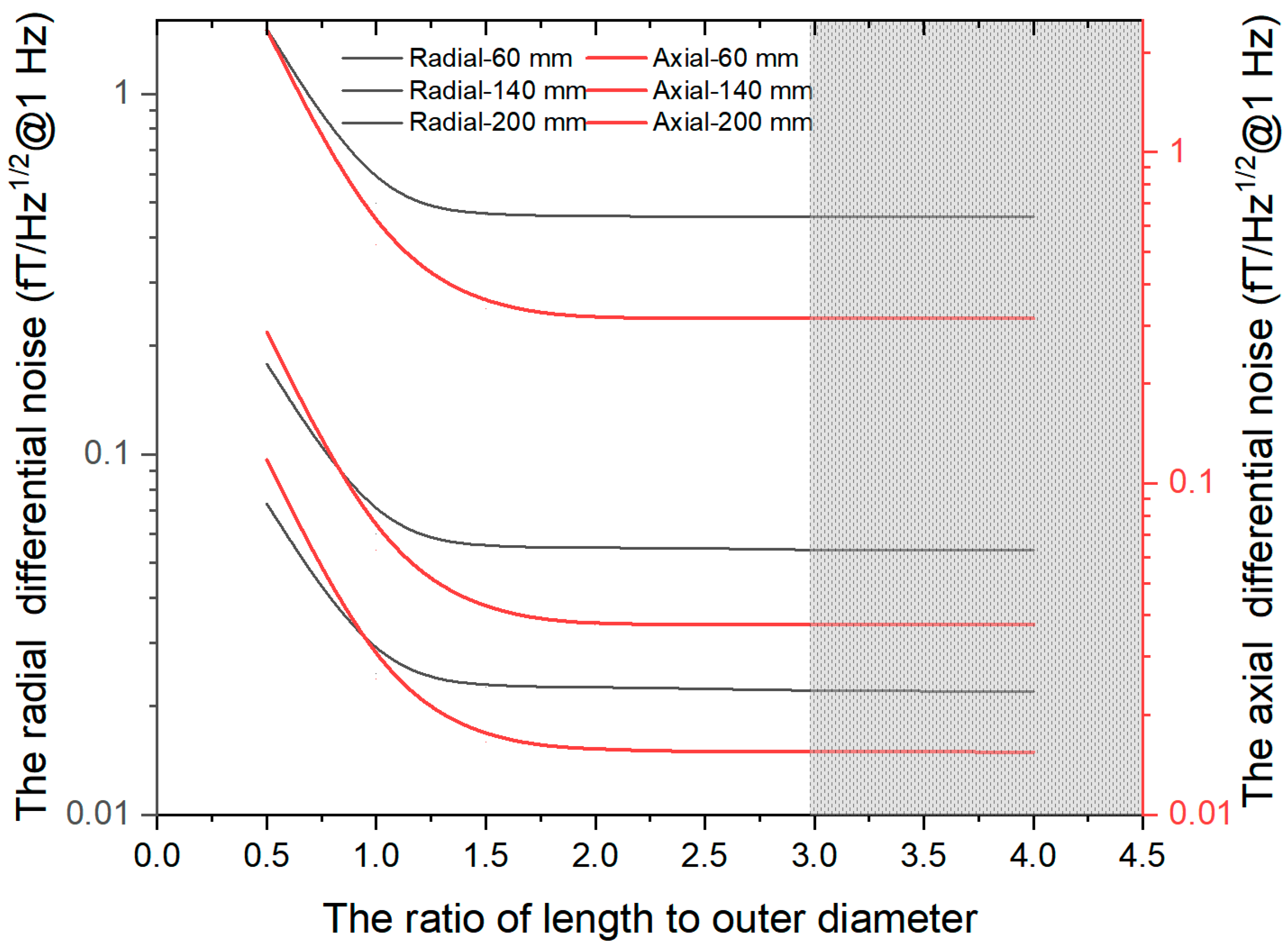
| Magnetic Noise (fT/Hz1/2@1 Hz) Diameter | D = 60 mm | D = 140 mm | D = 200 mm | |
|---|---|---|---|---|
| Radial magnetic noise | 7.67 | 2.16 | 1.26 | |
| Axial magnetic noise | 5.66 | 1.59 | 0.94 | |
| d = 0.5 mm | Radial DM noise | 0.50 | 0.06 | 0.03 |
| Axial DM noise | 0.35 | 0.04 | 0.02 | |
| Radial reduction capability | 15.24 | 35.73 | 50.30 | |
| Axial reduction capability | 16.27 | 38.89 | 55.32 | |
| d = 1.5 mm | Radial DM noise | 0.96 | 0.12 | 0.07 |
| Axial DM noise | 0.66 | 0.08 | 0.03 | |
| Radial reduction capability | 7.97 | 18.73 | 17.83 | |
| Axial reduction capability | 8.52 | 20.23 | 29.06 | |
| d = 2 mm | Radial DM noise | 1.83 | 0.22 | 0.09 |
| Axial DM noise | 1.23 | 0.15 | 0.06 | |
| Radial reduction capability | 4.19 | 9.78 | 13.87 | |
| Axial reduction capability | 1.35 | 10.49 | 15.11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; Fang, X.; Lu, J.; Wang, K.; Sun, B.; Gao, Y.; Xu, X.; Han, B. Analysis and Measurement of Differential-Mode Magnetic Noise in Mn-Zn Soft Ferrite Shield for Ultra-Sensitive Sensors. Materials 2022, 15, 8704. https://doi.org/10.3390/ma15238704
Ma D, Fang X, Lu J, Wang K, Sun B, Gao Y, Xu X, Han B. Analysis and Measurement of Differential-Mode Magnetic Noise in Mn-Zn Soft Ferrite Shield for Ultra-Sensitive Sensors. Materials. 2022; 15(23):8704. https://doi.org/10.3390/ma15238704
Chicago/Turabian StyleMa, Danyue, Xiujie Fang, Jixi Lu, Kun Wang, Bowen Sun, Yanan Gao, Xueping Xu, and Bangcheng Han. 2022. "Analysis and Measurement of Differential-Mode Magnetic Noise in Mn-Zn Soft Ferrite Shield for Ultra-Sensitive Sensors" Materials 15, no. 23: 8704. https://doi.org/10.3390/ma15238704





