Numerical Analysis of Dynamic Properties of an Auxetic Structure with Rotating Squares with Holes
Abstract
1. Introduction
- (1)
- re-entrant type (2D re-entrant, 2D re-entrant triangular, 3D re-entrant, double arrowhead);
- (2)
- rotating polygons (squares, rectangles, rhombi, parallelograms, triangles, tetrahedral);
- (3)
- chiral type (chiral circular, rotachiral, 3D chiral, anti-chiral);
- (4)
- perforated sheets (perpendicularly oriented cuts, randomly oriented cuts, diamond perforations, star perforations, 2D sheet containing holes);
- (5)
- crumpled sheets (aluminum thin foils, graphene sheet);
- (6)
- other (nodule fibril model, hexatruss, egg rack structure, missing rib, generalized tethered nodule, entangled single wire auxetic, grooved block of metal, hard discs).
2. Mathematical Model-Governing Equation
2.1. Linear Elasticity Equations
- plane stress—the load acts in a plane, and the thickness of the structure is constant and appropriately small in relation to other dimensions of the structure (appropriate thinness);
- plane strain—a constant load acts along the entire length of the structure (large enough), and its cross-section is constant over the entire length of its thickness.
2.2. Effective Mechanical Properties of the Structure
2.3. Dynamic Properties of the Structure
3. Models and Methods
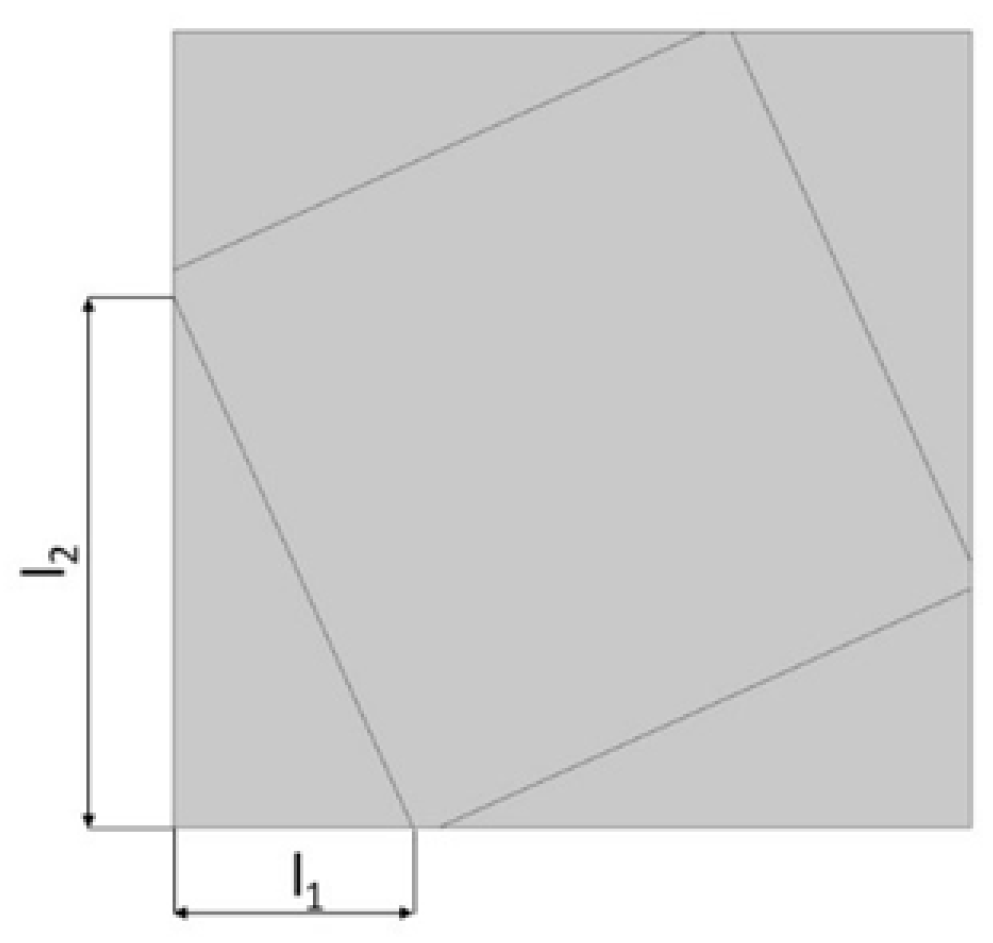
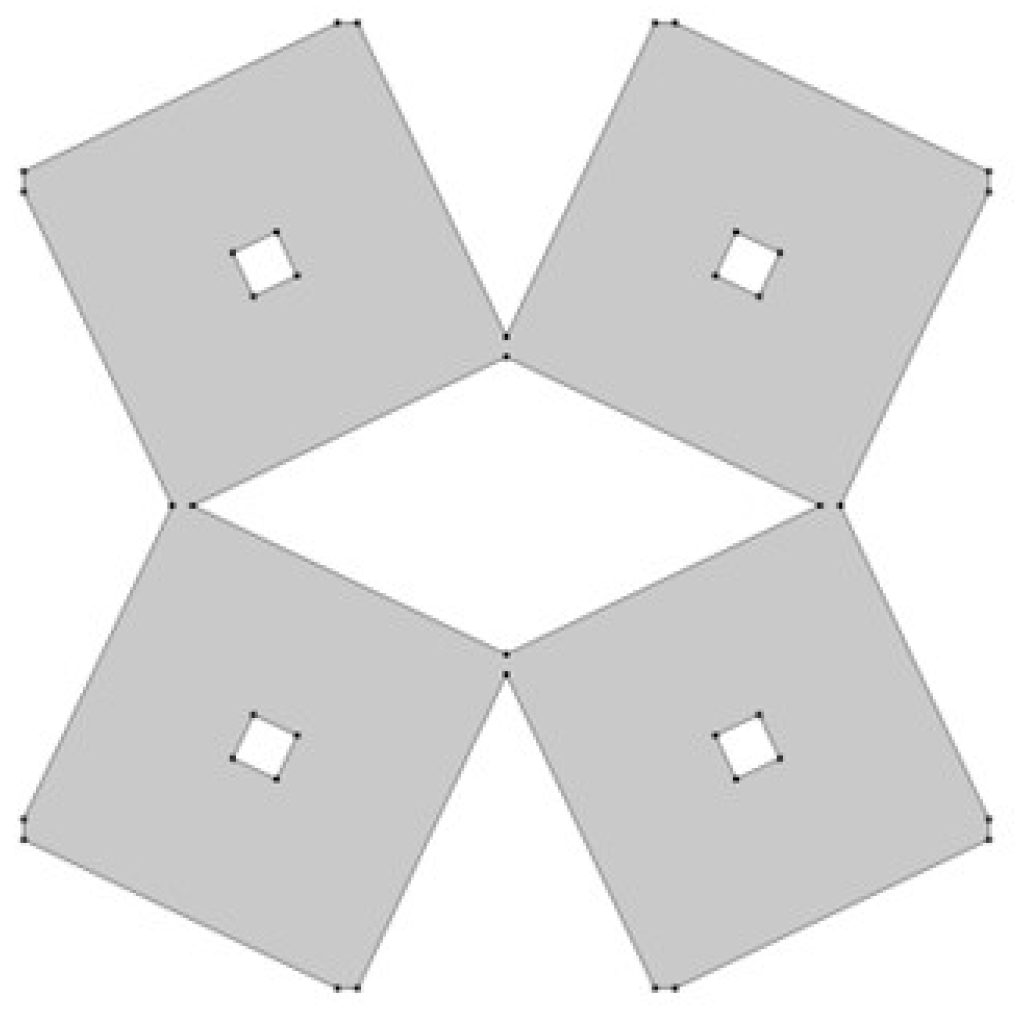
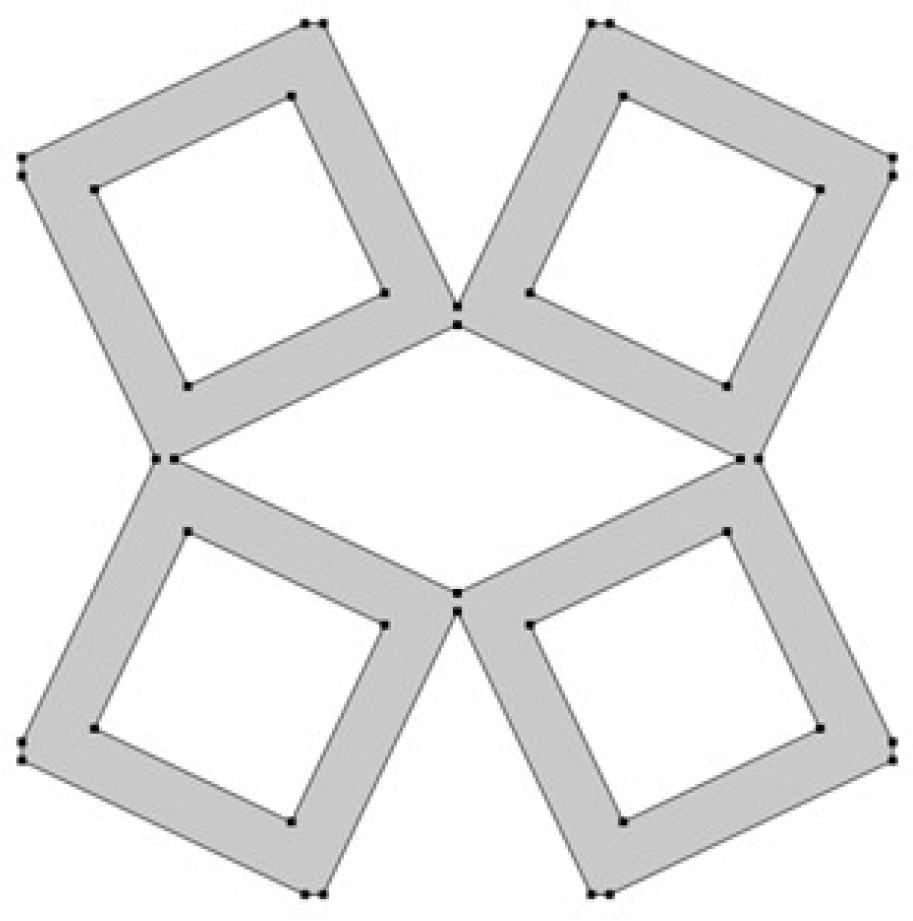
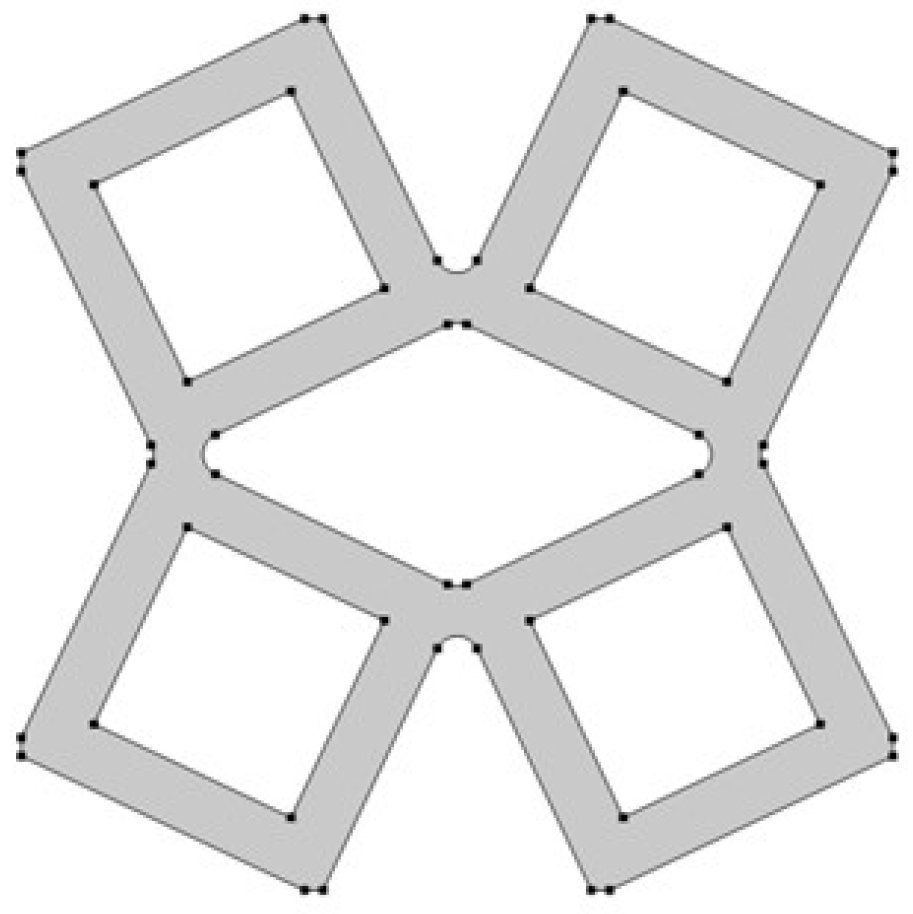
3.1. Geometrical Model
- right boundary (RB): and ;
- left boundary (LB): and ;
- bottom boundary (BB): and ;
- top boundary (TB): and .
3.2. Finite Element Model
- boundary (RB): free BC;
- boundary (LB): roller (symmetry) BC: , where is the normal unit vector to the boundary;
- boundary (BB): roller (symmetry) BC:,
- boundary (TB): prescribed displacement: ; or
- boundary (TB): applied force: , and , where is the length of boundary TB.
- boundary (RB): free BC;
- boundary (LB): free BC;
- boundary (TB): free BC;
- boundary (BB): harmonic excitation prescribed displacement BC: ; or
- boundary (BB): harmonic excitation force BC:, and .
4. Numerical Results
4.1. Effective Mechanical Properties of the Analyzed Structure
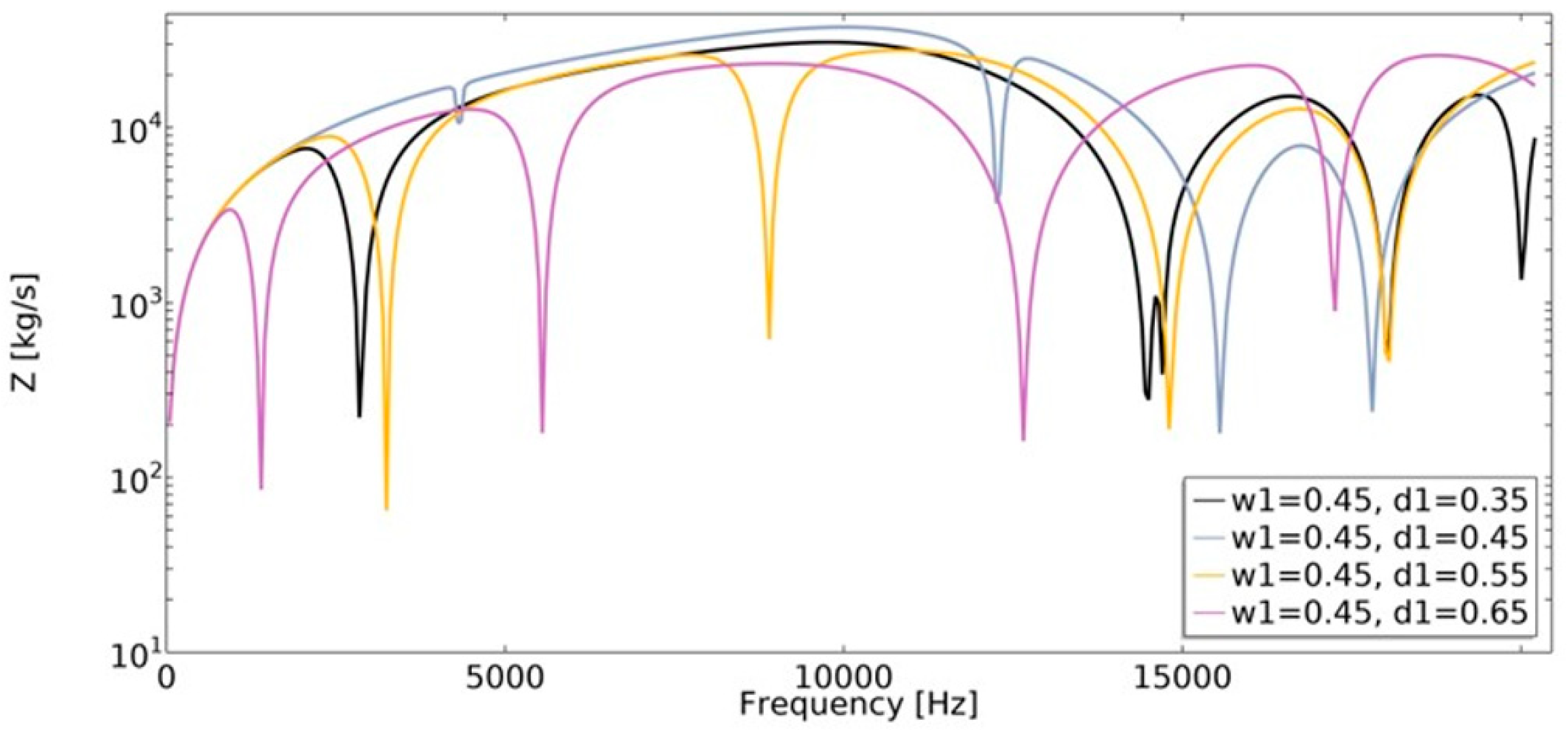
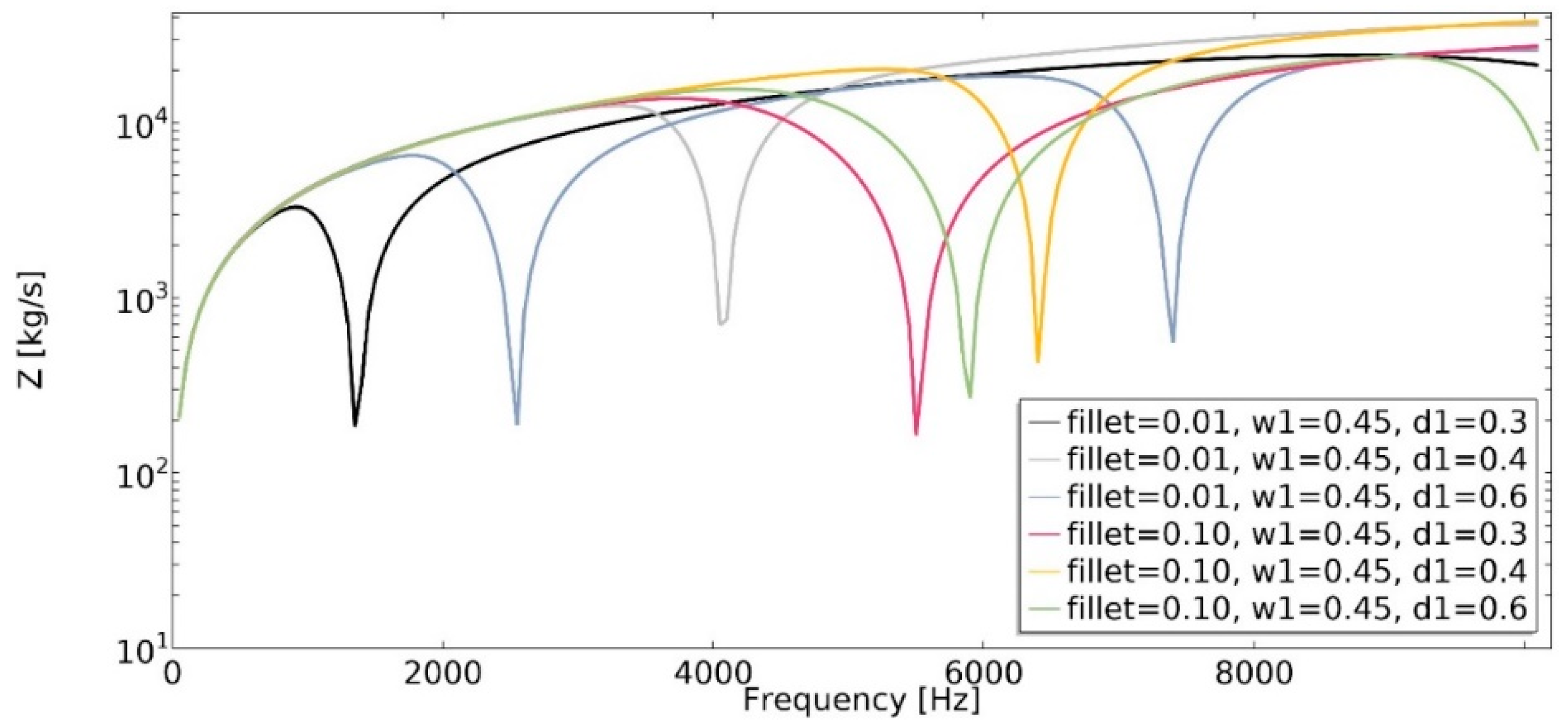
4.2. Mechanical Impedance
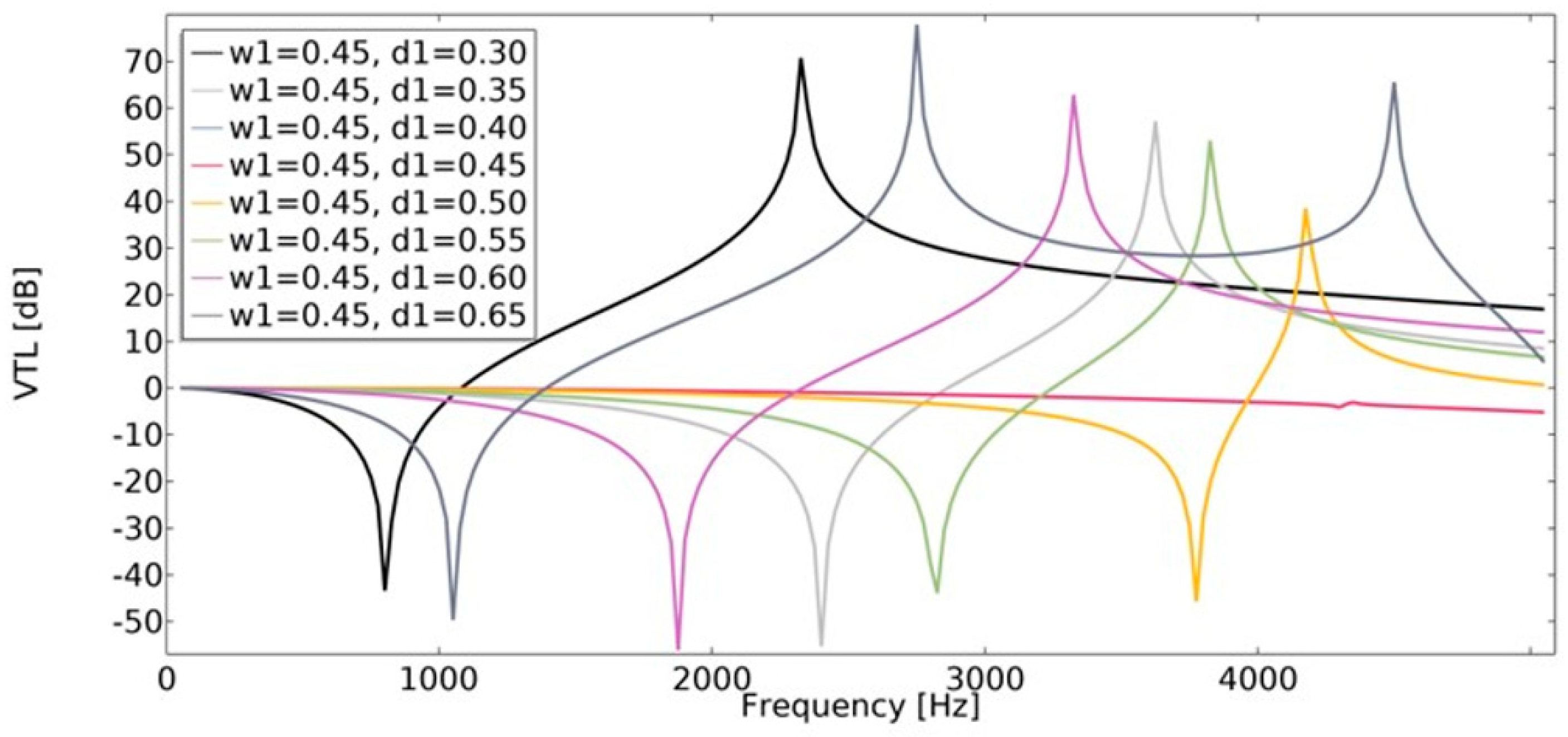
4.3. Vibration Transmission Loss (VTL)
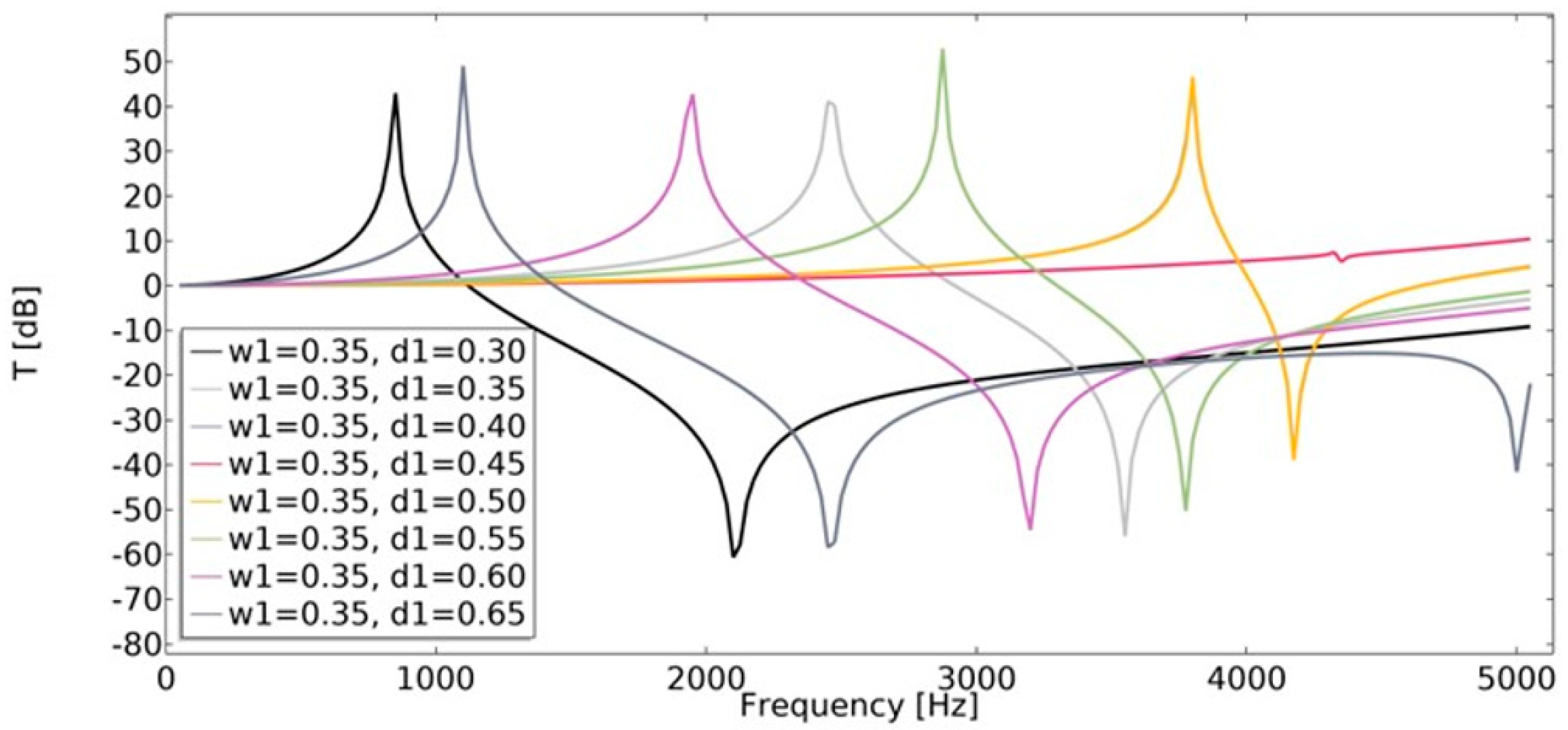
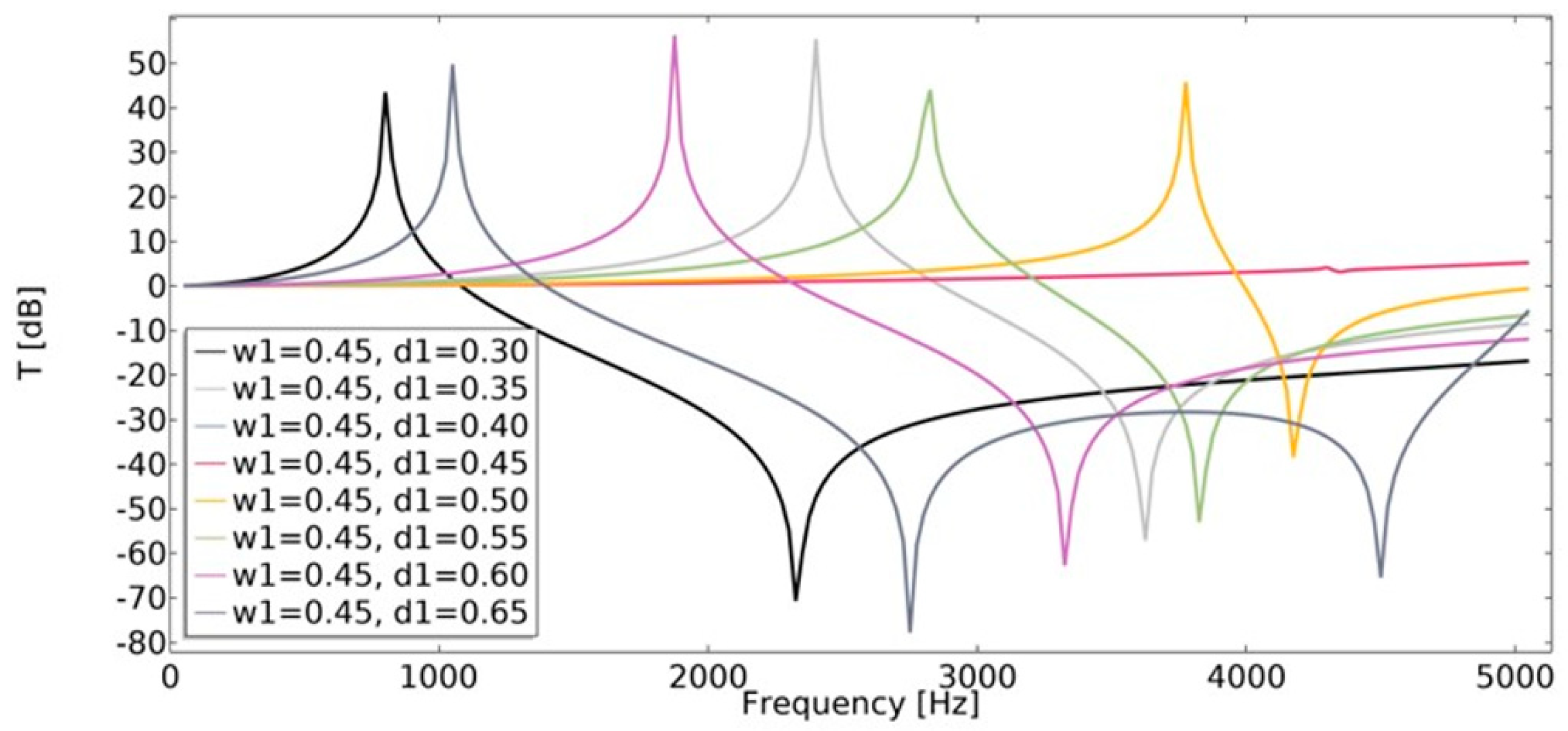
4.4. Transmissibility
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lakes; Roderic, S. Composites and Metamaterials; University of Wisconsin-Madison: Madison, WI, USA; World Scientific: Hackensack, NJ, USA, 2020. [Google Scholar]
- Lim, T.C. Auxetic Materials and Structures; Springer Science+Business Media: Singapore, 2015. [Google Scholar]
- Greaves, G.N. Poisson’s ratio over two centuries: Challenging hypotheses. Notes Rec. R. Soc. J. Hist. Sci. 2012, 67, 37–58. [Google Scholar] [CrossRef] [PubMed]
- Marqués, R.; Martín, F.; Sorolla, M. Metamaterials with Negative Parameters; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Lim, T.-C. Mechanics of Metamaterials with Negative Parameters; Springer Nature Singapore Pte Ltd.: Singapore, 2020. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014, 2014, 753496. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Auxetic Cellular Materials—A Review. Stroj. Vestn.-J. Mech. Eng. 2016, 62, 485–493. [Google Scholar] [CrossRef]
- Saxena, K.K.; Das, R.; Calius, E. Three Decades of Auxetics Research − Materials with Negative Poisson’s Ratio: A Review. Adv. Eng. Mater. 2016, 18, 1847–1870. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef]
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Re-view of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Kelkar, P.U.; Kim, H.S.; Cho, K.-H.; Kwak, J.Y.; Kang, C.-Y.; Song, H.-C. Cellular Auxetic Structures for Mechanical Metamaterials: A Review. Sensors 2020, 20, 3132. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Attard, D.; Grima, J.N.; Evans, K.E. Auxetic Behavior and Other Negative Thermomechanical Properties from Rotating Rigid Units. Phys. Status Solidi RRL 2022, 16, 2100322. [Google Scholar] [CrossRef]
- Bilski, M.; Pigłowski, P.; Wojciechowski, K. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. [Google Scholar] [CrossRef]
- Bilski, M.; Wojciechowski, K.W.; Strek, T.; Kedziora, P.; Grima-Cornish, J.N.; Dudek, M.R. Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties. Materials 2021, 14, 7837. [Google Scholar] [CrossRef] [PubMed]
- Novak, N.; Starčevič, L.; Vesenjak, M.; Ren, Z. Blast response study of the sandwich composite panels with 3D chiral auxetic core. Compos. Struct. 2018, 210, 167–178. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Kennedy, G.; Thadhani, N.; Ren, Z. Response of Chiral Auxetic Composite Sandwich Panel to Fragment Simulating Projectile Impact. Phys. Status Solidi 2019, 257, 1900099. [Google Scholar] [CrossRef]
- Novak, N.; Nowak, M.; Vesenjak, M.; Ren, Z. Structural Optimization of the Novel 3D Graded Axisymmetric Chiral Auxetic Structure. Phys. Status Solidi 2022, 2200409. [Google Scholar] [CrossRef]
- Lim, T.C. A perfect 2D auxetic sliding mechanism based on an Islamic geometric pattern. Eng. Res. Express 2021, 3, 015025. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Nienartowicz, M. Dynamic response of sandwich panels with auxetic cores. Phys. Status Solidi 2015, 252, 1540–1550. [Google Scholar] [CrossRef]
- Strek, T.; Matuszewska, A.; Jopek, H. Finite Element Analysis of the Influence of the Covering Auxetic Layer of Plate on the Contact Pressure. Phys. Status Solidi 2017, 254, 1700103. [Google Scholar] [CrossRef]
- Strek, T.; Michalski, J.; Jopek, H. Computational analysis of the mechanical impedance of the sandwich beam with auxetic metal foam core. Phys. Status Solidi B 2019, 256, 1800423. [Google Scholar] [CrossRef]
- Shepherd, T.; Winwood, K.; Venkatraman, P.; Alderson, A.; Allen, T. Validation of a Finite Element Modeling Process for Auxetic Structures under Impact. Phys. Status Solidi B 2020, 257, 1900197. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Thermal and structural dependence of auxetic properties of composite materials. Phys. Status Solidi 2015, 252, 1551–1558. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Thermoauxetic Behavior of Composite Structures. Materials 2018, 11, 294. [Google Scholar] [CrossRef] [PubMed]
- Michalski, J.; Strek, T. Fatigue Life of Auxetic Re-entrant Honeycomb Structure. In Advances in Manufacturing II. Lecture Notes in Mechanical Engineering; Gapiński, B., Szostak, M., Ivanov, V., Eds.; Springer: Cham, Switzerland, 2019; pp. 50–60. [Google Scholar]
- Michalski, J.; Strek, T. Blast resistance of sandwich plate with auxetic anti-tetrachiral core. Vib. Phys. Syst. 2020, 31, 2020317. [Google Scholar]
- Michalski, J.; Strek, T. Response of a Sandwich Plate with Auxetic Anti-tetrachiral Core to Puncture. In Advances in Manufacturing III. MANUFACTURING 2022. Lecture Notes in Mechanical Engineering; Gapiński, B., Ciszak, O., Ivanov, V., Eds.; Springer: Cham, Switzerland, 2022; pp. 1–18. [Google Scholar]
- Burlaga, B.; Strek, T. The vibrations induced by fluid flow in plates with different Poisson’s ratios. Vib. Phys. Syst. 2020, 31, 2020301. [Google Scholar]
- Zhang, Q.; Yu, X.; Scarpa, F.; Barton, D.; Zhu, Y.; Lang, Z.; Zhang, D. A dynamic poroelastic model for auxetic polyurethane foams involving viscoelasticity and pneumatic damping effects in the linear regime. Mech. Syst. Signal Process. 2022, 179, 109375. [Google Scholar] [CrossRef]
- Lim, T.C. Analogies across auxetic models based on deformation mechanism. Phys. Status Solidi RRL 2017, 11, 1600440. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Negative Poisson’s Ratios From Rotating Rectangles. Comput. Methods Sci. Technol. 2004, 10, 137–145. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating rigid units. Phys. Stat. Sol. 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Grima, J.N.; Zammit, V.; Gatt, R.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating semi-rigid units. Phys. Status Solidi B 2007, 244, 866–882. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.S.; Gatt, R.; Attard, D. On the auxetic properties of rotating rhombi and parallelograms: A preliminary investigation. Phys. Status Solidi B 2008, 245, 521–529. [Google Scholar] [CrossRef]
- Dubrovski, P.D.; Novak, N.; Borovinšek, M.; Vesenjak, M.; Ren, Z. In-Plane Deformation Behavior and the Open Area of Rotating Squares in an Auxetic Compound Fabric. Polymers 2022, 14, 571. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; Ren, X.; Zhang, Y.; Zhang, X.Y.; Zhang, X.G.; Luo, C.; Xie, Y.M. Lightweight auxetic metamaterials: Design and characteristic study. Compos. Struct. 2022, 293, 115706. [Google Scholar] [CrossRef]
- Strek, T.; Kedziora, P.; Maruszewski, B.; Pozniak, A.; Tretiakov, K.V.; Wojciechowski, K.W. Finite element analysis of auxetic obstacle deformation and fluid flow in a channel. J. Non-Cryst. Solids 2009, 355, 1387–1392. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Meireles, J.; Puga, H. Auxetic Materials—A Review. Mater. Sci.-Pol. 2013, 31, 561–571. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Duncan, O. Auxetic Foams for Sports Applications. Ph.D. Thesis, Sheffield Hallam University, Sheffield, UK, 2019. [Google Scholar]
- Proffit, M.; Kennedy, J. Dynamic response of auxetic structures. Vibroengineering PROCEDIA 2020, 31, 1–6. [Google Scholar] [CrossRef]
- Fuguang, R.; Wang, L.; Liu, H. Low frequency and broadband vibration attenuation of a novel lightweight bidirectional re-entrant lattice metamaterial. Mater. Lett. 2021, 299, 130133. [Google Scholar]
- Tao, Z.; Ren, X.; Zhao, A.G.; Sun, L.; Zhang, Y.; Jiang, W.; Han, D.; Zhang, X.Y.; Xie, Y.M. A novel auxetic acoustic metamaterial plate with tunable bandgap. Int. J. Mech. Sci. 2022, 226, 107414. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Z.; Bi, Q. Multistability and fast-slow analysis for van der Pol–Duffing oscillator with varying exponential delay feedback factor. Appl. Math. Model. 2018, 57, 448–458. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Z.; Han, X. Periodic or chaotic bursting dynamics via delayed pitchfork bifurcation in a slow-varying controlled system. Commun Nonlinear Sci. Numer. Simulat. 2018, 56, 380–391. [Google Scholar] [CrossRef]
- Bhullar, S.K.; Mawanane Hewage, A.T.; Alderson, A.; Alderson, K.; Jun, M.B.G. Influence of Negative Poisson’s Ratio on Stent Applications. Adv. Mater. 2013, 2, 42–47. [Google Scholar] [CrossRef]
- Bhullar, S.K.; Ko, J.; Ahmed, F.; Ju, M.B.G. Design and Fabrication of Stent with Negative Poisson’s Ratio. World Academy of Science. Engineering and Technology. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 462–468. [Google Scholar]
- Gatt, R.; Mizzi, L.; Azzopardi, J.I.; Azzopardi, K.M.; Attard, D.; Casha, A.; Grima, J.N. Hierarchical Auxetic Mechanical Metamaterials. Sci. Rep. 2015, 5, 8395. [Google Scholar] [CrossRef] [PubMed]
- Khoshgoftar, M.J.; Barkhordari, A.; Limuti, M.; Buccino, F.; Vergani, L.; Mirzaali, M.J. Bending analysis of sandwich panel composite with a re-entrant lattice core using zig-zag theory. Sci. Rep. 2022, 12, 15796. [Google Scholar] [CrossRef]
- Documentation of COMSOL Multiphysics Software. In Structural Mechanics Module User’s Guide; COMSOL: Stockholm, Sweden, 2015.
- Bower, A.F. Applied Mechanics of Solids; Taylor and Francis Group, LLC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Zi-Xing, L.; Qiang, L.; Zhen-Yu, Y. Predictions of Young’s modulus and negative Poisson’s ratio of auxetic foams. Phys. Status Solidi B 2011, 248, 167–174. [Google Scholar]
- On, F.J. Mechanical Impedance Analysis For Lumped Parameter Multi-Degree of Freedom. In Multi-Dimensional Systems; NASA: Washington, DC, USA, 1967. [Google Scholar]
- Gatti, P.L.; Ferrari, V. Applied Structural and Mechanical Vibrations; CRC Press Taylor & Francis Group: New York, NY, USA, 2014. [Google Scholar]
- Song, Y.; Sun, X. Modeling and Dynamics of a MDOF Isolation System. Appl. Sci. 2017, 7, 393. [Google Scholar] [CrossRef]
- Thamburaj, P.; Sun, J.Q. Effect of Material and Geometry on the Sound and Vibration Transmission across a Sandwich Beam. J. Vib. Acoust. 2001, 123, 205–212. [Google Scholar] [CrossRef]
- Idczak, E.; Stręk, T. Computational Modelling of Vibrations Transmission Loss of Auxetic Lattice Structure. Vib. Phys. Syst. 2016, 27, 123–128. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000; Volumes 1–3. [Google Scholar]







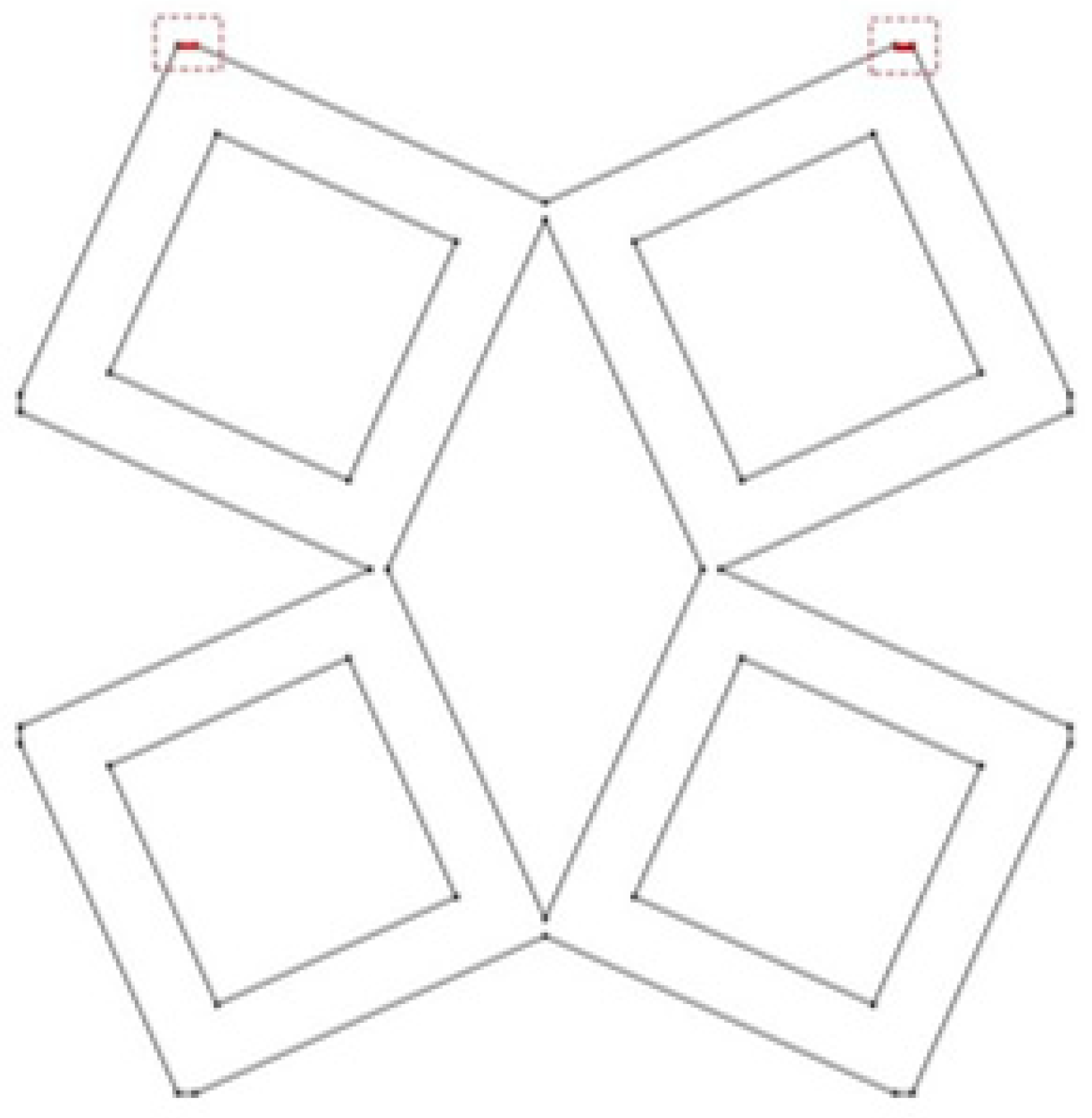


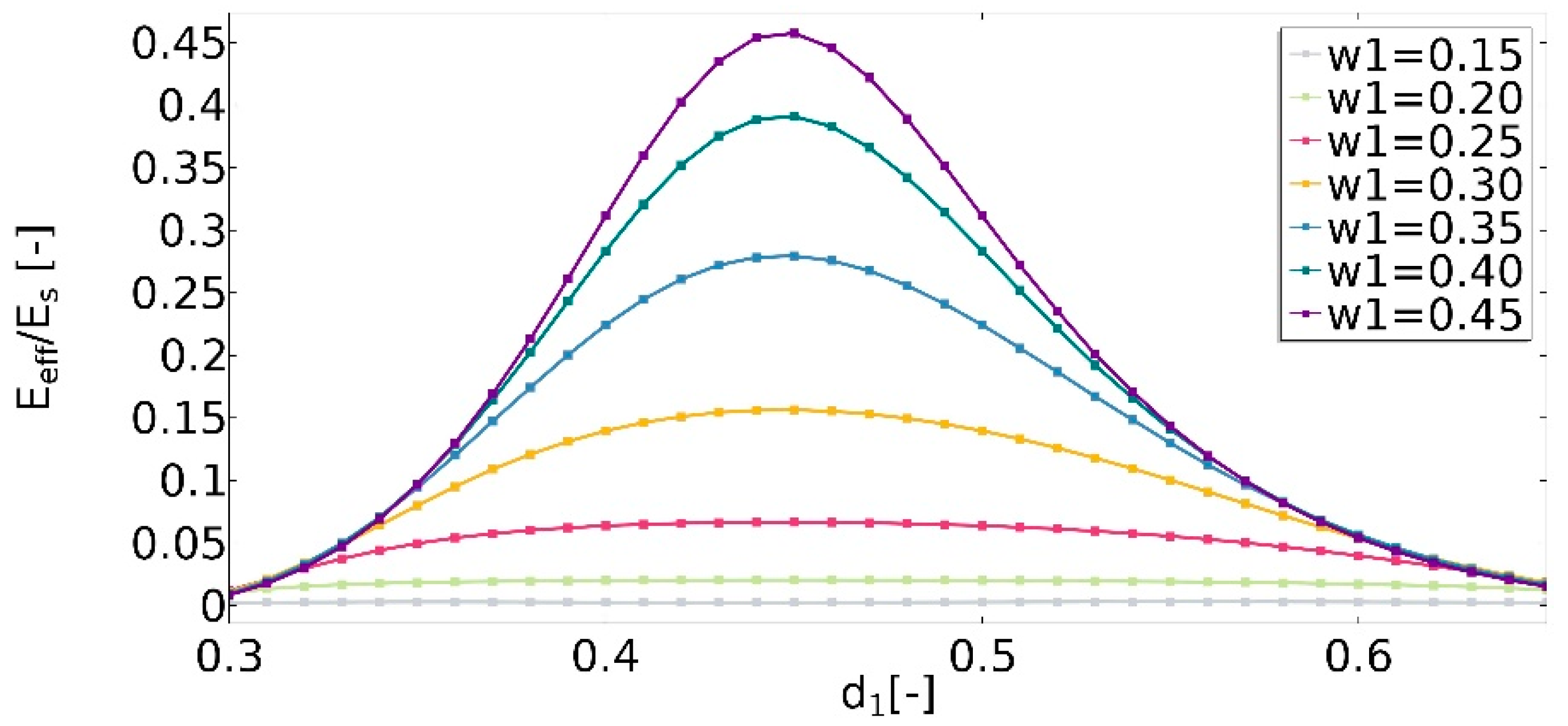
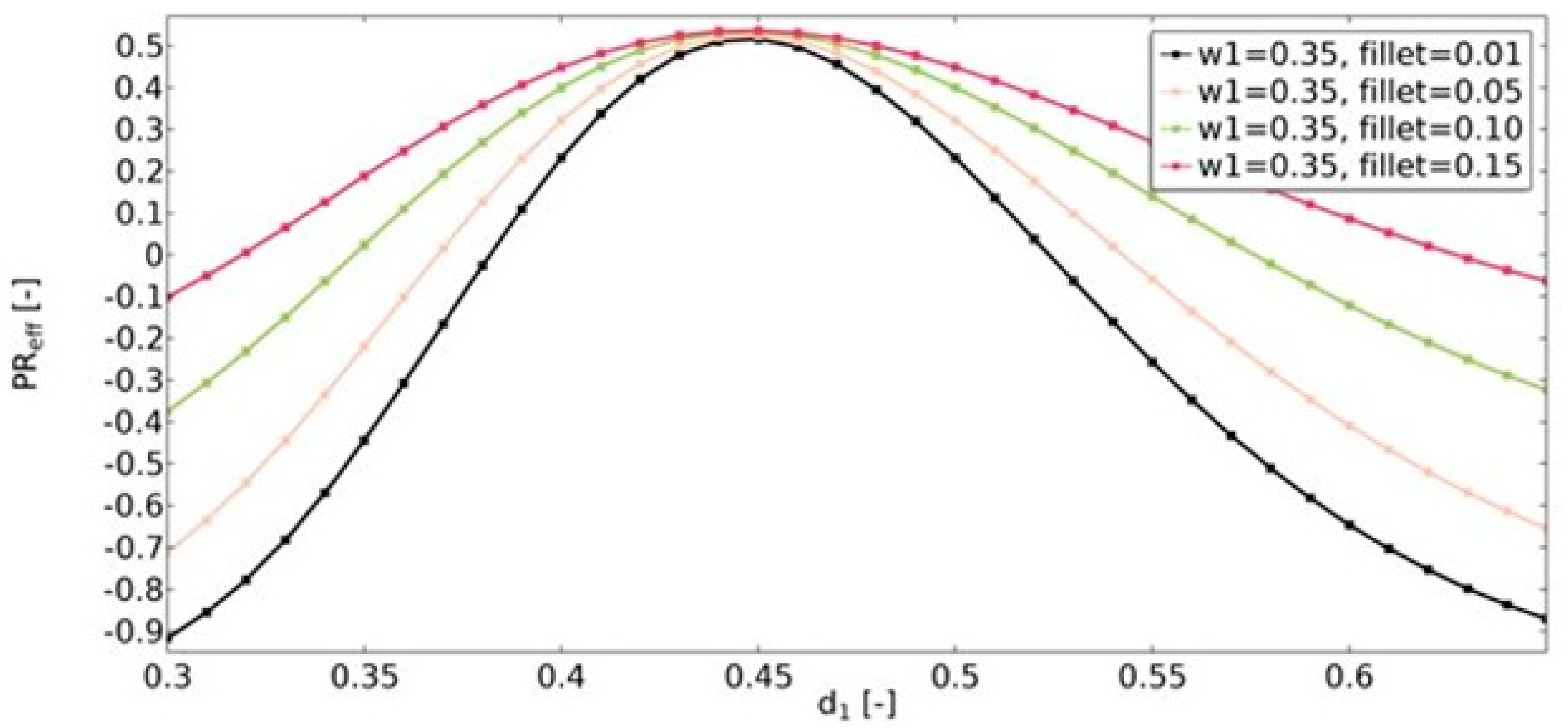

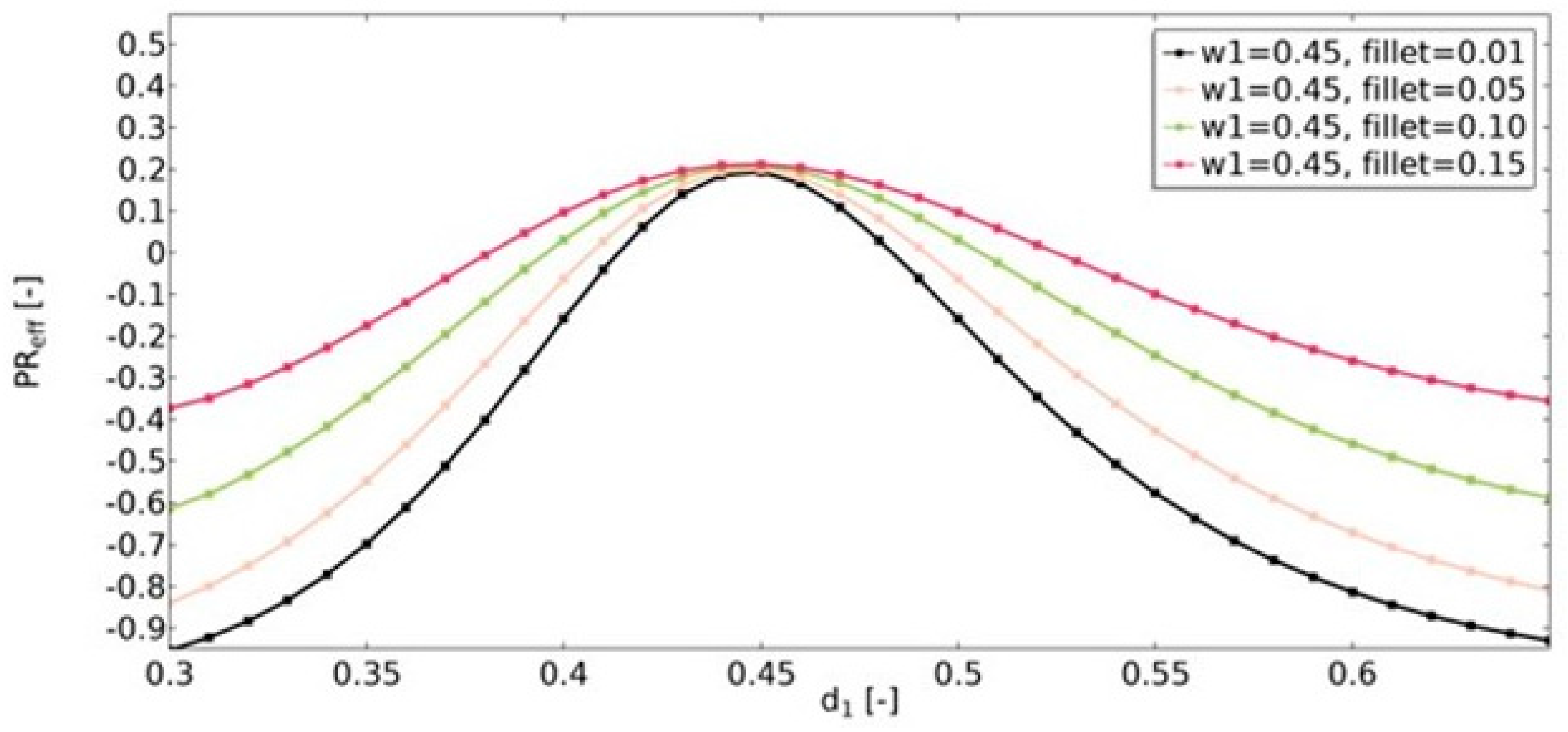


| Property | Value [unit] |
|---|---|
| Density | |
| Young’s modulus | 200e9 [Pa] |
| Poisson’s ratio | 0.30 [-] |
| Isotropic loss factor | 0.0024 [-] |
| Parameter | Range of Parameter Values [-] |
|---|---|
| d1 | 0.30–0.65 |
| w1 | 0.15–0.45 |
| fillet | 0.00–0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mrozek, A.; Strek, T. Numerical Analysis of Dynamic Properties of an Auxetic Structure with Rotating Squares with Holes. Materials 2022, 15, 8712. https://doi.org/10.3390/ma15248712
Mrozek A, Strek T. Numerical Analysis of Dynamic Properties of an Auxetic Structure with Rotating Squares with Holes. Materials. 2022; 15(24):8712. https://doi.org/10.3390/ma15248712
Chicago/Turabian StyleMrozek, Agata, and Tomasz Strek. 2022. "Numerical Analysis of Dynamic Properties of an Auxetic Structure with Rotating Squares with Holes" Materials 15, no. 24: 8712. https://doi.org/10.3390/ma15248712
APA StyleMrozek, A., & Strek, T. (2022). Numerical Analysis of Dynamic Properties of an Auxetic Structure with Rotating Squares with Holes. Materials, 15(24), 8712. https://doi.org/10.3390/ma15248712







