Compression Strength of PLA Bolts Produced via FDM
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
| Property | Testing Method | Value |
|---|---|---|
| Specific Density | ISO 1183 | 1.24 g/cm3 |
| Tensile Strength (Yield) | ISO 527 | 50 MPa |
| Tensile Strength (Break) | ISO 527 | 53 MPa |
| Tensile Modulus | ISO 527 | 3500 MPa |
| Elongation (Yield) | ISO 527 | 6% |
| Flexural Strength | ISO 178 | 81 MPa |
| Flexural Modulus | ISO 178 | 3800 MPa |
| Izod Impact Strength (Notched, 23 °C) | ISO 180 | 2 kJ/m2 |
| Diameter (mm) | Pitch (mm) | Pitch Diameter (mm) | Minor Diameter (mm) | Infill Diameter (mm) | Nut Height (mm) | Diameter of the Hole in the Nut (mm) |
|---|---|---|---|---|---|---|
| 42 | 1.5 | 41.026 | 36.479 | 34.679 | 34 | 40.376 |
| 3 | 40.051 | 38.319 | 36.519 | 34 | 38.752 | |
| 4.5 | 39.077 | 39.479 | 37.679 | 34 | 37.129 | |
| 48 | 2 | 46.701 | 45.546 | 43.746 | 38 | 45.835 |
| 3 | 46.051 | 44.319 | 42.519 | 38 | 44.752 | |
| 5 | 44.752 | 41.866 | 40.066 | 38 | 42.587 | |
| 56 | 2 | 54.701 | 53.546 | 51.746 | 45 | 53.835 |
| 4 | 53.402 | 51.093 | 49.293 | 45 | 51.67 | |
| 5.5 | 52.428 | 49.252 | 47.452 | 45 | 50.046 | |
| 60 | 2 | 58.701 | 57.546 | 55.746 | 48 | 57.835 |
| 4 * | 57.402 * | 55.093 * | 53.293 * | 48 * | 55.67 * | |
| 5.5 | 56.428 | 53.252 | 51.452 | 48 | 54.046 | |
| 64 | 2 | 62.701 | 61.546 | 59.746 | 51 | 61.835 |
| 4 | 61.402 | 59.093 | 57.293 | 51 | 59.67 | |
| 6 | 60.103 | 56.639 | 54.839 | 51 | 57.505 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Layer height | 0.15 mm | Fill printing speed | 70 mm/s |
| First layer height | 0.2 mm | Exterior wall printing speed | 45 mm/s |
| Layer width | 0.45 mm | Outer layers printing speed | 45 mm/s |
| First layer width | 0.45 mm | Travel speed without printing | 80 mm/s |
| Number of layers in the wall | 4 | Top and bottom layer printing speed | 32.5 mm/s |
| Distance between lines | 0.2 mm | Number of slower layers | 2 |
| Bottom and top thickness | 0.8 mm | Acceleration of printing | 1500 mm/s2 |
| Number of top layers | 3 | Acceleration of travel speed without printing | 2000 mm/s2 |
| Number of bottom layers | 5 | Retraction | Yes |
| Infill ratio of the rod core | 35% | Retraction distance | 3 mm |
| Filling shape | Tringle pattern | Retraction speed | 25 mm/s |
| Printing temperature | 208 °C | Retraction acceleration | 25 mm/s2 |
| First layer printing temperature | 208 °C | Retraction for minimal movement | 0.9 mm |
| Initial printing temperature | 198 °C | Applicable for | All layers |
| Worktable temperature | 60 °C | Cooling fan efficiency grade | 100% |
| Printing speed | 65 mm/s | Initial height without maximum cooling | 5 mm |
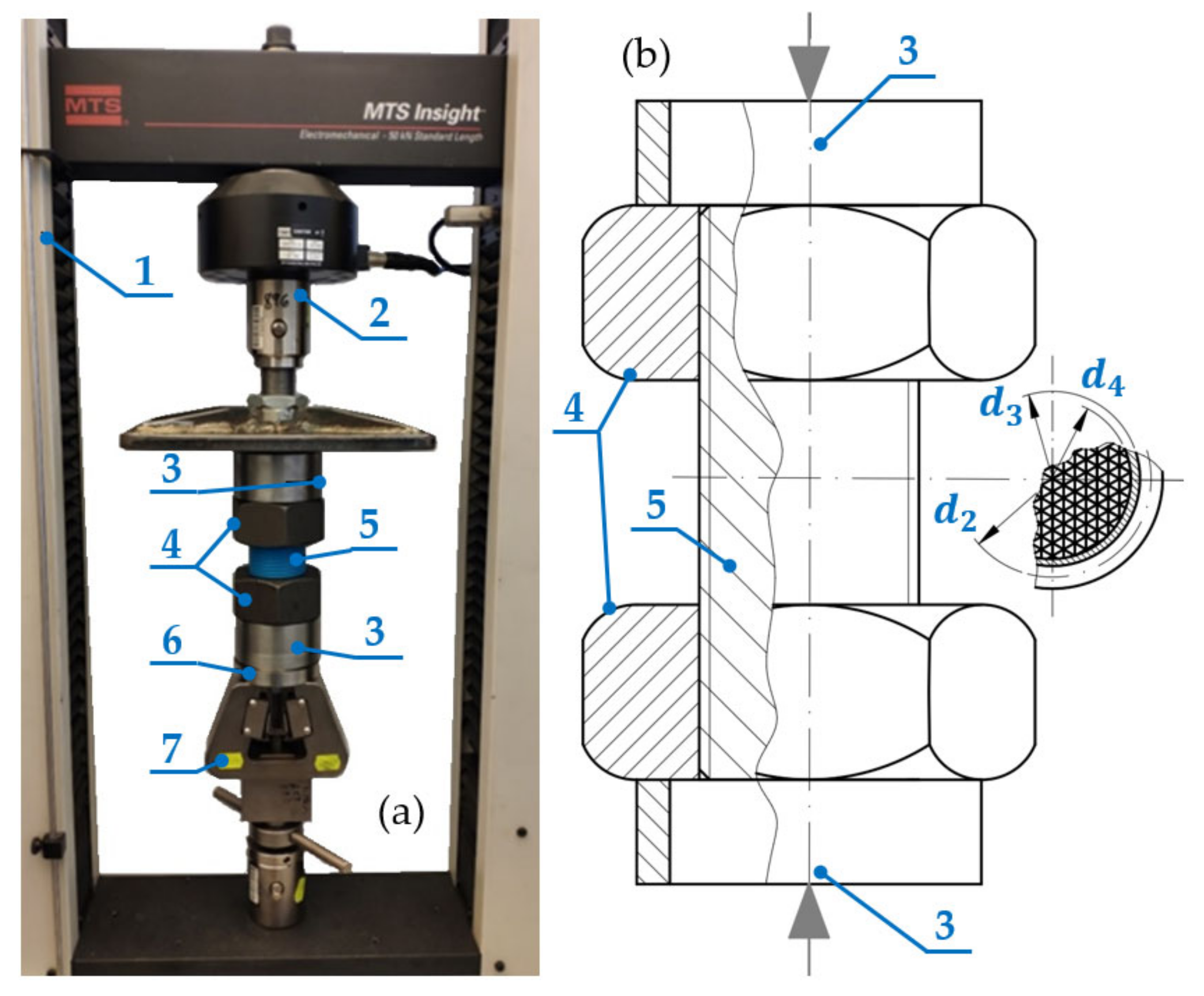
2.2. Methodology of Static Tests
2.3. Methodology of Cyclic Tests
3. Results and Discussion
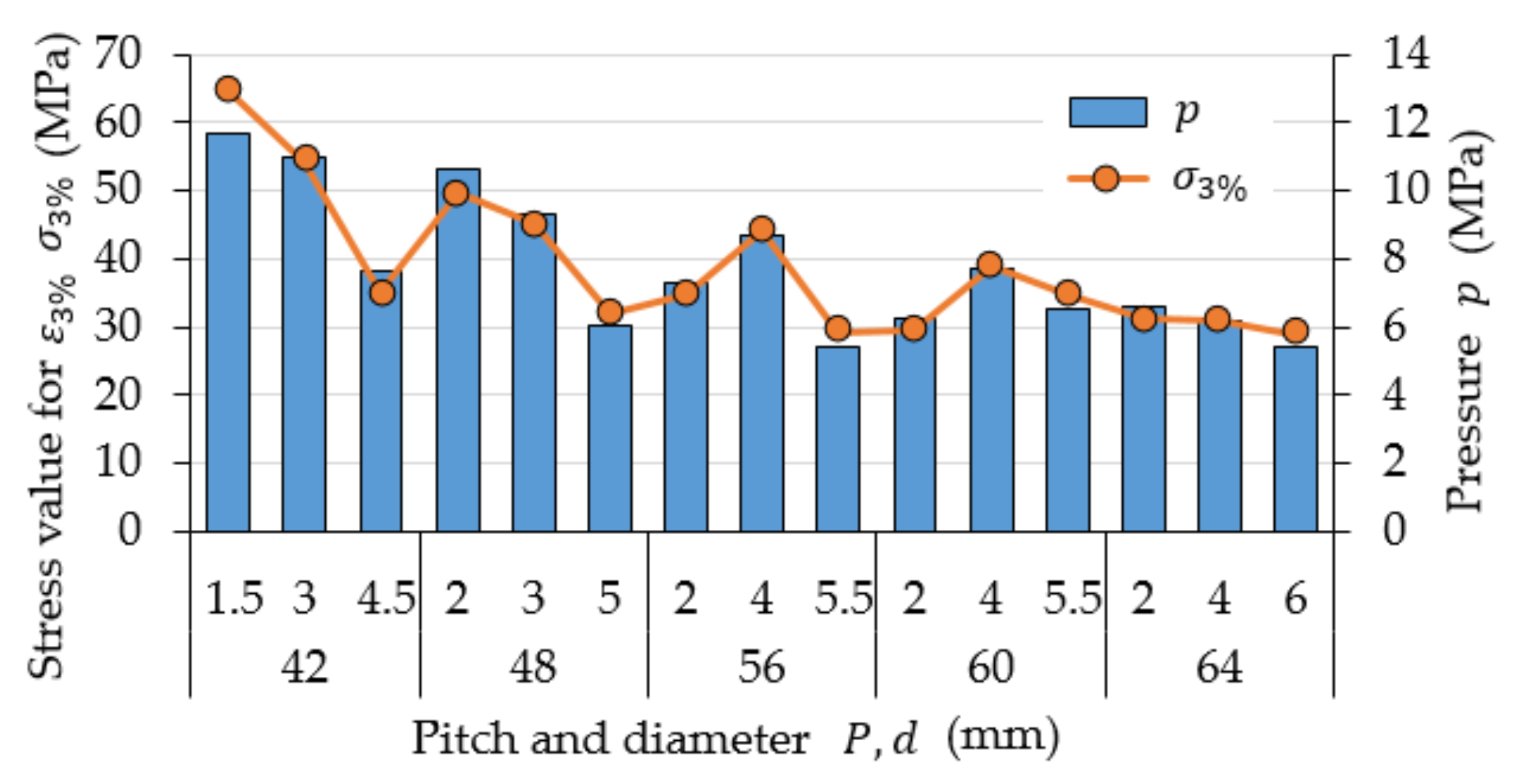
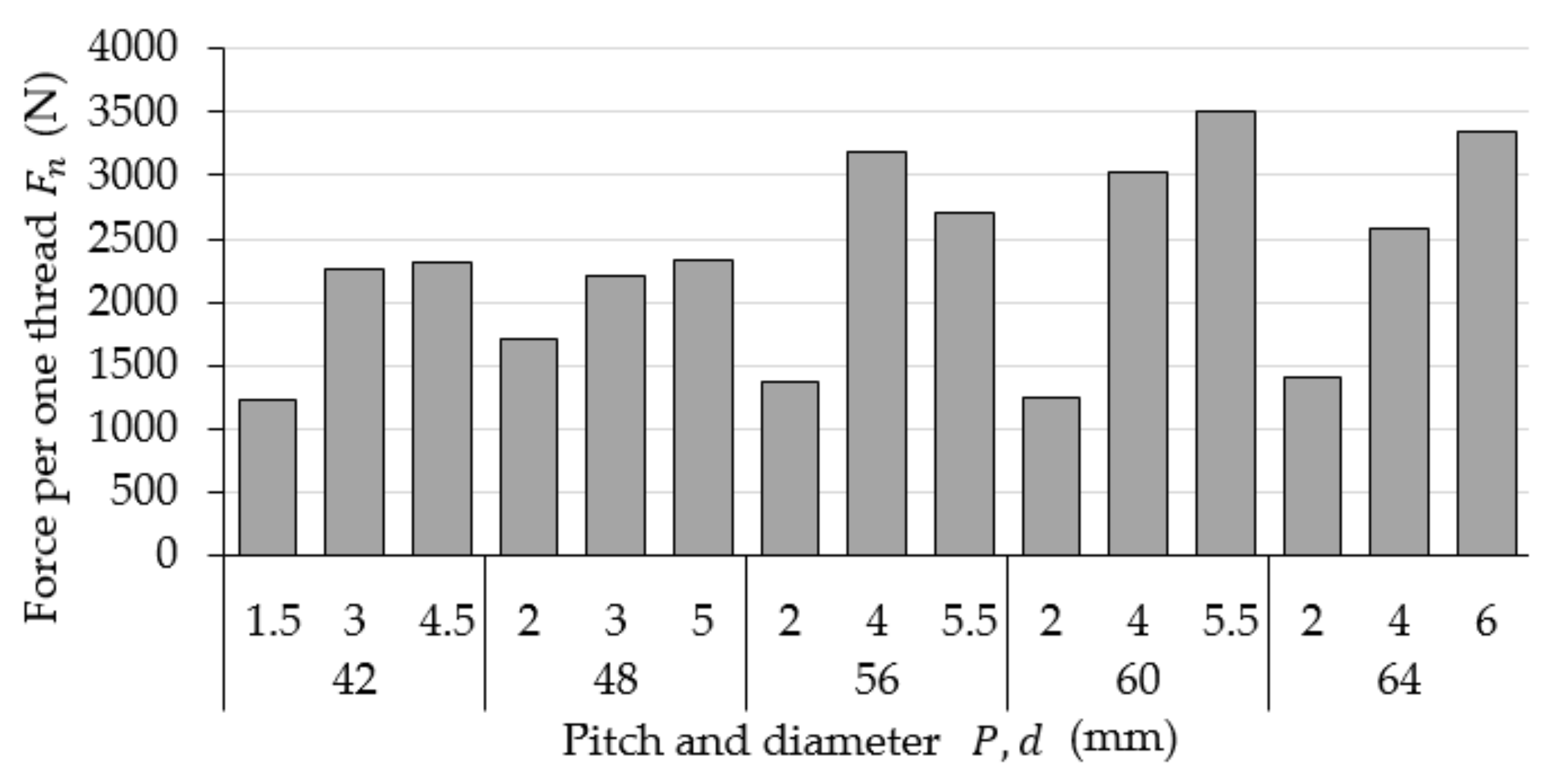
3.1. Results of Static Tests
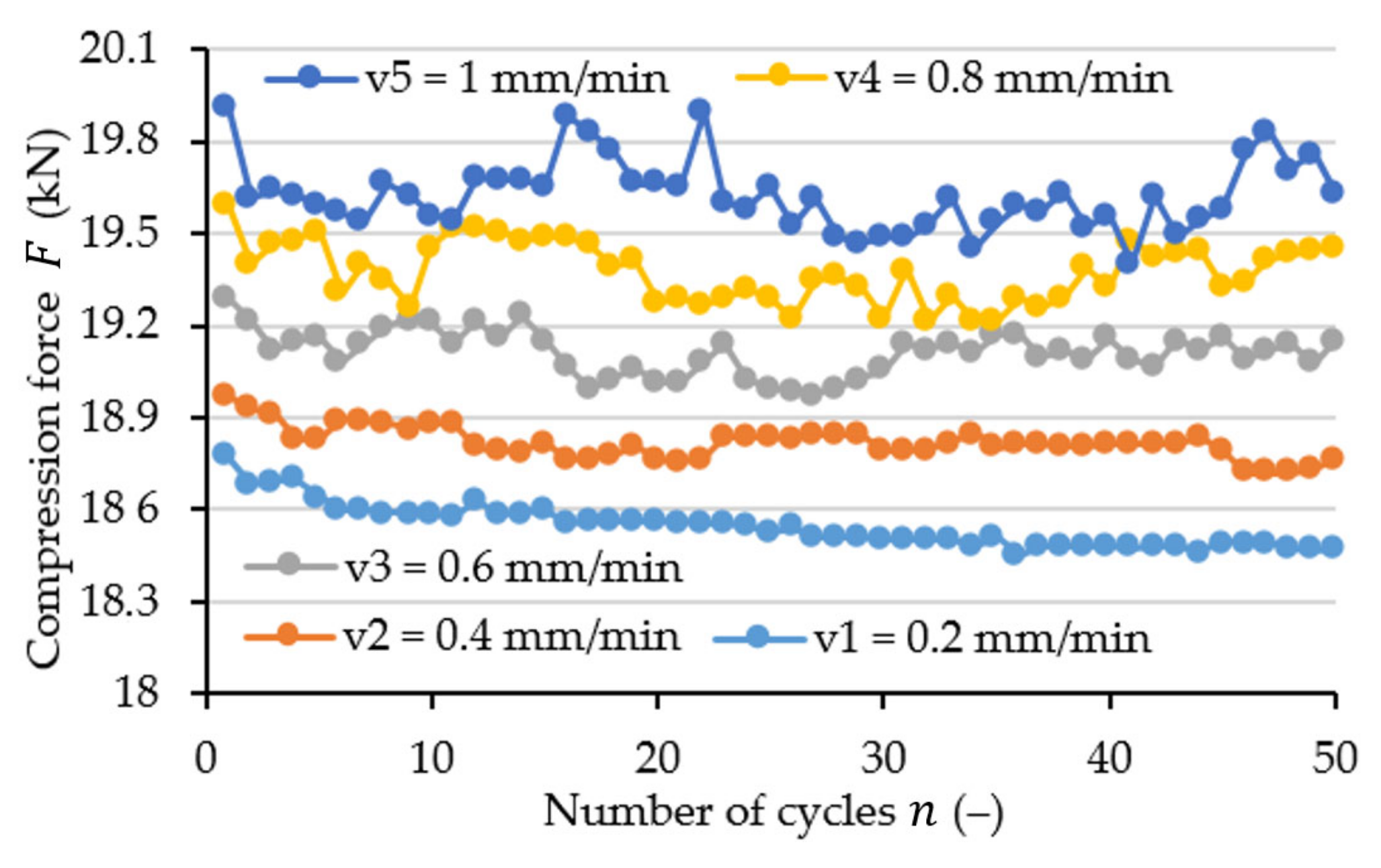
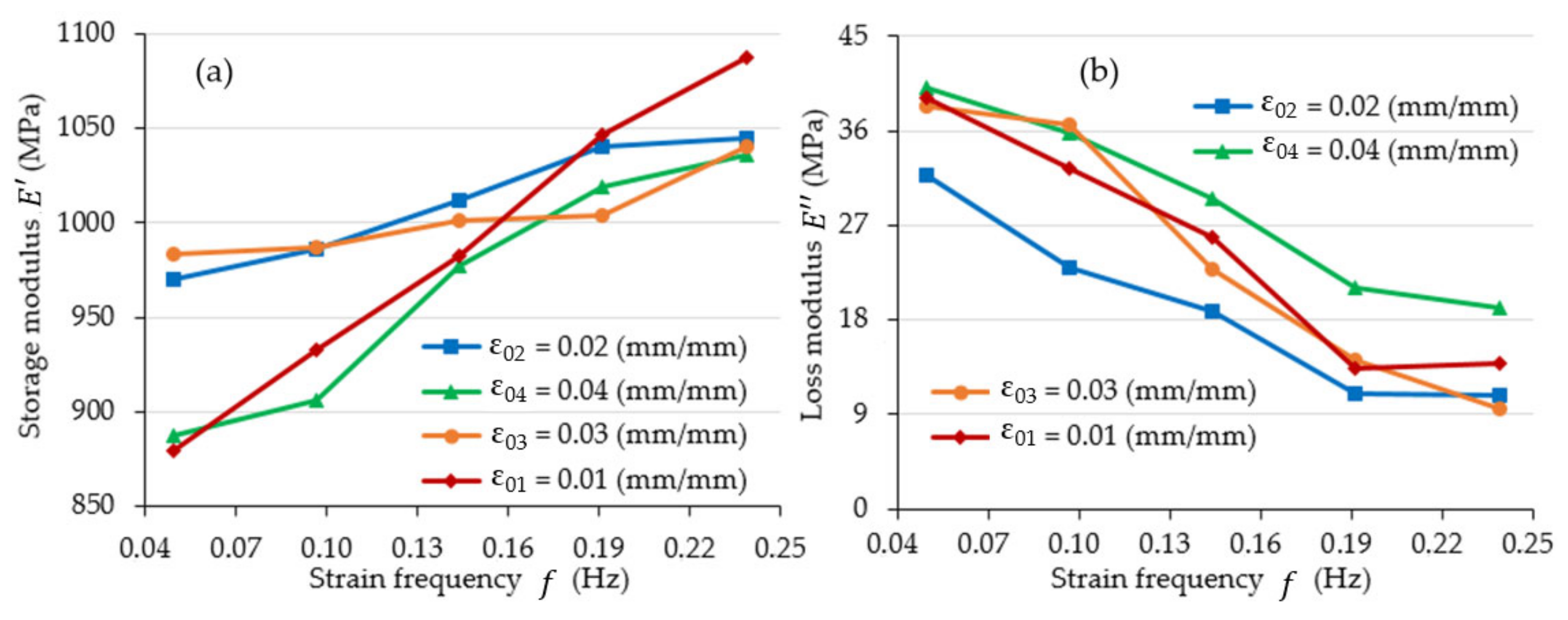
3.2. Results of Cyclic Tests
4. Conclusions
- During the performed static compression tests, approximately 11% of all tested samples were damaged. Both fracture failure (1 case) and ductile failure (all other cases) of the samples was observed. Thus, even in uniform conditions of production of threaded elements using the FDM method, it is difficult to explicitly predict the nature of failure or the value of the breaking stress. It is thus advisable to consider the value of safety coefficient when implementing bolt connections made of PLA.
- The mean compression modulus value for all measurements was 917.79 ± 184.99 MPa. The large value of standard deviation further supports the conclusion of the difficulty of precisely predicting the strength parameters of a printed thread element.
- The defined values of the compression modulus differ from those specified in the literature by 2–2.5 times. The differences mentioned above were probably caused by the implementation of a threaded rod infill ratio of 35%.
- The values of the storage modulus defined in cyclic tests increase , while the values of the loss modulus decrease when the value of the strain frequency increases.
- Simultaneously, ascertaining the nature of the variations in storage modulus values in the function of the strain amplitude was not possible on the basis of the determined values. This issue remains open and requires further testing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Diameter (mm) | Pitch (mm) | Stress Value (MPa) | Pressure (MPa) | Compression Modulus (MPa) | Standard Deviation for Compression Modulus (MPa) | Force per One Thread (N) |
|---|---|---|---|---|---|---|
| 42 | 1.5 | 64.6 | 11.7 | 938.6 | 125.1 | 1228.2 |
| 3 | 54.2 | 11.0 | 953.9 | 91.4 | 2260.9 | |
| 4.5 | 35.0 | 7.6 | 645.4 | 29.4 | 2311.4 | |
| 48 | 2 | 49.6 | 10.7 | 946.3 | 25.5 | 1702.5 |
| 3 | 45.1 | 9.3 | 1036.3 | 22.4 | 2207.3 | |
| 5 | 31.9 | 6.1 | 1074.8 | 96.4 | 2335.7 | |
| 56 | 2 | 34.7 | 7.3 | 668.6 | 53.8 | 1364.7 |
| 4 | 44.2 | 8.7 | 970.2 | 27.2 | 3178.7 | |
| 5.5 | 29.3 | 5.5 | 964.5 | 51.2 | 2705.5 | |
| 60 | 2 | 29.6 | 6.3 | 795.3 | 34.9 | 1252.7 |
| 4 | 38.9 | 7.7 | 899.6 | 34.9 | 3024.9 | |
| 5.5 | 34.9 | 6.6 | 1172.1 | 114.5 | 3498.2 | |
| 64 | 2 | 31.1 | 6.6 | 1257.5 | 34.3 | 1406.4 |
| 4 | 30.9 | 6.2 | 770.8 | 9.3 | 2587.6 | |
| 6 | 29.0 | 5.4 | 673.1 | 23.8 | 3353.4 |
| Strain Amplitude (mm/mm) | Frequency (Hz) | Storage Modulus (MPa) | Loss Modulus (MPa) | Loss Angle (Rad) |
|---|---|---|---|---|
| 0.011 | 0.049 | 879.3 | 39.1 | 0.044 |
| 0.097 | 932.4 | 32.4 | 0.035 | |
| 0.144 | 982.5 | 25.8 | 0.026 | |
| 0.191 | 1046.8 | 13.4 | 0.013 | |
| 0.239 | 1087.7 | 13.8 | 0.013 | |
| 0.021 | 0.049 | 969.6 | 31.8 | 0.033 |
| 0.097 | 986.1 | 23.0 | 0.023 | |
| 0.144 | 1012.0 | 18.8 | 0.019 | |
| 0.191 | 1040.2 | 11.0 | 0.011 | |
| 0.239 | 1044.5 | 10.8 | 0.010 | |
| 0.030 | 0.049 | 983.7 | 38.4 | 0.039 |
| 0.097 | 987.0 | 36.6 | 0.037 | |
| 0.144 | 1001.5 | 22.8 | 0.023 | |
| 0.191 | 1004.1 | 14.2 | 0.014 | |
| 0.239 | 1040.4 | 9.5 | 0.009 | |
| 0.040 | 0.049 | 887.5 | 40.2 | 0.045 |
| 0.097 | 906.0 | 35.7 | 0.039 | |
| 0.144 | 977.1 | 29.5 | 0.030 | |
| 0.191 | 1019.2 | 21.1 | 0.021 | |
| 0.239 | 1036.3 | 19.2 | 0.019 |
References
- Wi, J.-H.; Lee, K.-H.; Lee, C.-H. Self-loosening of 3D printed bolted joints for engineering applications. MATEC Web Conf. 2018, 185, 00029. [Google Scholar] [CrossRef] [Green Version]
- Chand, R.; Sharma, V.S.; Trehan, R.; Gupta, M.K. A physical investigation of dimensional and mechanical characteristics of 3D printed nut and bolt for industrial applications. Rapid Prototyp. J. 2022, 28, 953–966. [Google Scholar] [CrossRef]
- Feng, X.; Xue, F. Characterization of 3D printed bolts based on digital image correlation and infrared thermography. Mater. Des. 2020, 191, 108641. [Google Scholar] [CrossRef]
- Feng, X. Tentative Experiment on 3D Printed Coal Mine Bolt. In Proceedings of the 5th ISRM Young Scholars’ Symposium on Rock Mechanics and International Symposium on Rock Engineering for Innovative Future, Okinawa, Japan, 1–4 December 2019. [Google Scholar]
- Ranjan, N. Dimensional and roughness analysis of ABS polymer-based 3D printed nuts and bolts. Mater. Today Proc. 2022, 48, 1604–1608. [Google Scholar] [CrossRef]
- Harshitha, V.; Rao, S.S. Design and analysis of ISO standard bolt and nut in FDM 3D printer using PLA and ABS materials. Mater. Today Proc. 2019, 19, 583–588. [Google Scholar] [CrossRef]
- Kumar, C.L.; Prasad, V.V.S.H.; Vanaja, T. Experimental Validation of 3-D Printed Bolts. Int. J. Mod. Eng. Res. 2017, 7, 1–12. [Google Scholar]
- Eraliev, O.; Lee, K.-H.; Lee, C.-H. Self-Loosening of a 3D-printed bolt by Using Three Different Materials under Cyclical Temperature Changes. Appl. Sci. 2022, 12, 3001. [Google Scholar] [CrossRef]
- Narayanan, G.; Vernekar, V.N.; Kuyinu, E.L.; Laurencin, C.T. Poly (lactic acid)-based biomaterials for orthopaedic regenerative engineering. Adv. Drug Deliv. Rev. 2016, 107, 247–276. [Google Scholar] [CrossRef] [Green Version]
- DeStefano, V.; Khan, S.; Tabada, A. Applications of PLA in modern medicine. Eng. Regen. 2020, 1, 76–87. [Google Scholar] [CrossRef]
- Wang, H.T.; Chiang, P.C.; Tzeng, J.J.; Wu, T.L.; Pan, Y.H.; Chang, W.J.; Huang, H.M. In vitro biocompatibility, radiopacity, and physical property tests of nano-Fe3O4 incorporated poly-L-lactide bone screws. Polymers 2017, 9, 191. [Google Scholar] [CrossRef] [Green Version]
- Sundar, R.; Mathivani, K.; Muruga, D.B. Fabrication and Analysis of PLA based Nuts, Bolts and Study (3d printing). Int. Res. J. Eng. Technol. 2019, 6, 2355–2359. [Google Scholar]
- Kasa, S.N.; Omar, M.F.; Abdullah, M.M.A.B.; Ismail, I.N.; Ting, S.S.; Vac, S.C.; Vizureanu, P. Effect of Unmodified and Modified Nanocrystalline Cellulose Reinforced Polylactic Acid (PLA) Polymer Prepared by Solvent Casting Method Morphology, Mechanical and Thermal Properties. Mater. Plast. 2017, 54, 91–97. [Google Scholar] [CrossRef]
- EN 4014; Hexagon Head Bolts—Product Grades A and B. International Organization for Standardization: Geneva, Switzerland, 2011.
- Fuß, F.; Rieckert, M.; Steinhauer, S.; Liesegangb, M.; Thielea, G. 3D-printed equipment to decouple (powder) X-ray diffraction sample preparation and measurement. J. Appl. Cryst. 2022, 55, 686–692. [Google Scholar] [CrossRef] [PubMed]
- Pearce, J.; Wittbrodt, B.T. The effects of PLA color on material properties of 3-D printed components. Addit. Manuf. 2015, 8, 110–116. [Google Scholar] [CrossRef] [Green Version]
- EN 4032; Hexagon Regular Nuts (Style 1)—Product Grades A and B. International Organization for Standardization: Geneva, Switzerland, 2012.
- Pernet, B.; Nagel, J.K.; Zhang, H. Compressive Strength Assessment of 3D Printing Infill Patterns. Procedia CIRP 2022, 105, 682–687. [Google Scholar] [CrossRef]
- Parab, S.; Zaveri, N. Investigating the Influence of Infill Pattern on the Compressive Strength of Fused Deposition Modelled PLA Parts. In Proceedings of International Conference on Intelligent Manufacturing and Automation; Vasudevan, H., Kottur, V., Raina, A., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Available online: https://zadar.pl/userdata/public/assets/karty-filamentow/easy-pla-tds.pdf (accessed on 28 November 2022).
- EN 604:2002; Plastics—Determination of Compressive Properties. International Organization for Standardization: Geneva, Switzerland, 2002.
- Vukasovic, T.; Vivanco, J.F.; Celentano, D.; García-Herrera, C. Characterization of the mechanical response of thermoplastic parts fabricated with 3D printing. Int. J. Adv. Manuf. Technol. 2019, 104, 4207–4218. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. An Experimental Comparison for Compression of PLA Specimens Printed in In-Plane and Out-of-Plane Directions. Am. J. Appl. Sci. 2020, 13, 563–583. [Google Scholar] [CrossRef]
- Mercado-Colmenero, J.M.; Rubio-Paramio, M.A.; la Rubia-Garcia, M.D.; Lozano-Arjona, D.; Martin-Doñate, C. A numerical and experimental study of the compression uniaxial properties of PLA manufactured with FDM technology based on product specifications. Int. J. Adv. Manuf. Technol. 2019, 103, 1893–1909. [Google Scholar] [CrossRef]
- Torre, R.; Brischetto, S.; Rocco Dipietro, I. Buckling developed in 3D printed PLA cuboidal samples under compression: Analytical, numerical and experimental investigations. Addit. Manuf. 2021, 38, 101790. [Google Scholar] [CrossRef]
- Ma, Q.; Rejab, M.; Kumar, A.P.; Fu, H.; Kumar, N.M.; Tang, J. Effect of infill pattern, density and material type of 3D printed cubic structure under quasi-static loading. Int. J. Mark. Res. 2021, 235, 435–438. [Google Scholar] [CrossRef]
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 9781420053128. [Google Scholar]
- Barczewski, M.; Mysiukiewicz, O. Rheological and Processing Properties of Poly(lactic acid) Composites Filled with Ground Chestnut Shell. Polymer 2018, 42, 267–274. [Google Scholar] [CrossRef]
- Kamal, M.R.; Khoskava, V. Effect of cellulose nanocrystals (CNC) on rheological and mechanical properties and crystallization behavior of PLA/CNC nanocomposites. Carbohydr. Polym. 2015, 123, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Salehiyan, R.; Kyu, H. Effect of organoclay on non-linear rheological properties of poly(lactic acid)/poly(caprolactone) blends. Korean J. Chem. Eng. 2013, 30, 1013–1022. [Google Scholar] [CrossRef]
- Lee, S.; Kim, M.; Song, H.Y.; Hyun, K. Characterization of the Effect of Clay on Morphological Evaluations of PLA/Biodegradable Polymer Blends by FT-Rheology. Macromolecules 2019, 52, 7904–7919. [Google Scholar] [CrossRef]
- Pérez-Fonseca, A.A.; Ramírez-Herrera, V.O.; Fuentes-Talavera, F.J.; Rodrigue, D.; Silva-Guzmán, J.A.; Robledo-Ortíz, J.R. Crystallinity And Impact Strength Improvement Of Wood-Polylactic Acid Biocomposites Produced By Rotational And Compression Molding. Maderas Cienc. Tecnol. 2021, 23. [Google Scholar] [CrossRef]
- Huda, M.S.; Drzal, L.T.; Mohanty, A.K.; Misra, M. Chopped glass and recycled newspaper as reinforcement fibers in injection molded poly(lactic acid) (PLA) composites: A comparative study. Compos. Sci. Technol. 2006, 66, 1813–1824. [Google Scholar] [CrossRef]
- Jaszkiewicz, A.; Bledzki, A.K.; Meljon, A. Dynamic Mechanical Thermal Analysis of Biocomposites Basedon PLA and PHBV—A Comparative Study to PP Counterparts. J. Appl. Polym. Sci. 2013, 130, 3175–3183. [Google Scholar] [CrossRef]
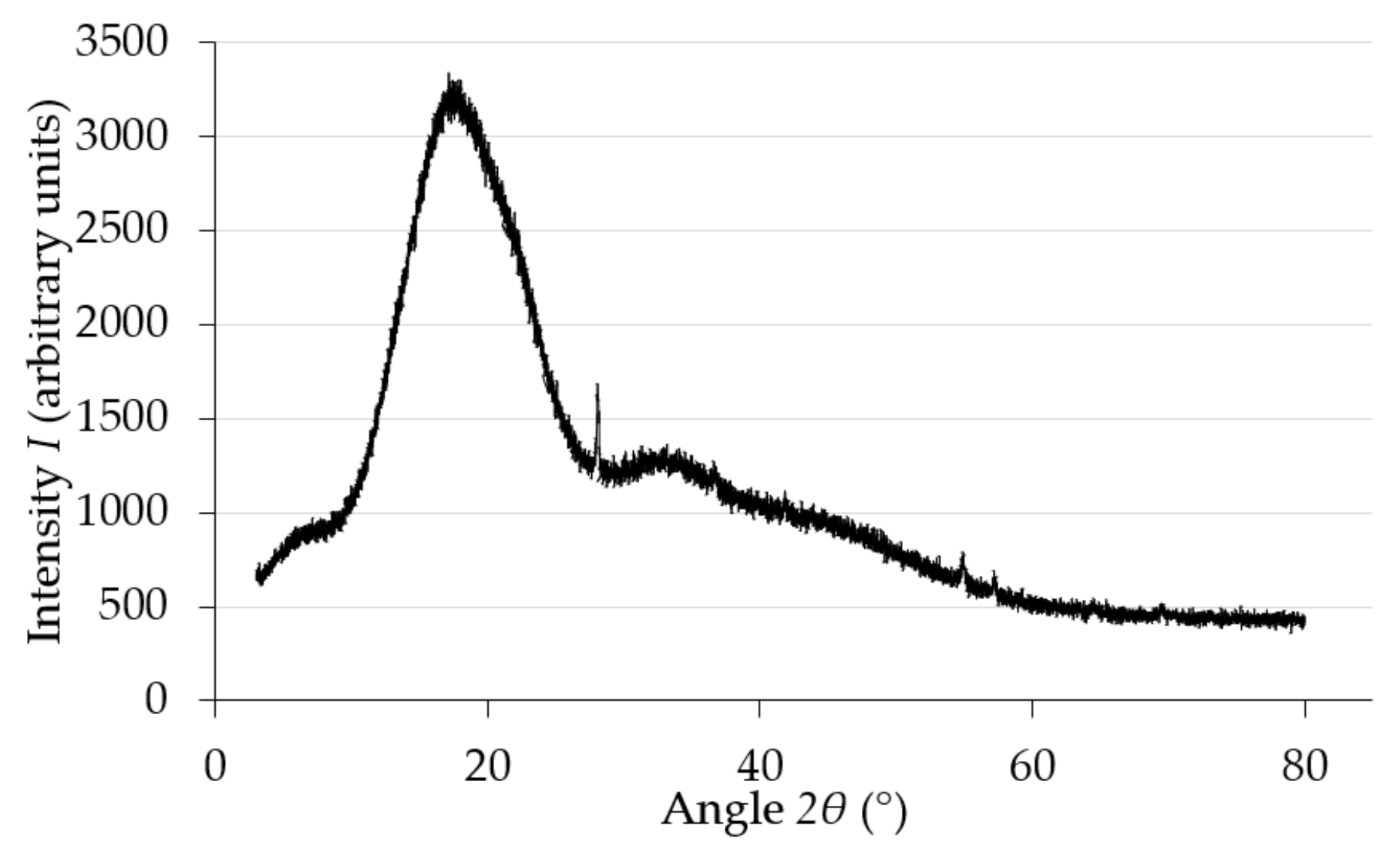




| Strain Amplitude | Value (mm/mm) | Strain Frequency | Value (Hz) |
|---|---|---|---|
| 0.01 | 0.049 | ||
| 0.02 | 0.097 | ||
| 0.03 | 0.144 | ||
| 0.04 | 0.191 | ||
| 0.239 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kukla, M.; Sieracki, I.; Maliga, W.; Górecki, J. Compression Strength of PLA Bolts Produced via FDM. Materials 2022, 15, 8740. https://doi.org/10.3390/ma15248740
Kukla M, Sieracki I, Maliga W, Górecki J. Compression Strength of PLA Bolts Produced via FDM. Materials. 2022; 15(24):8740. https://doi.org/10.3390/ma15248740
Chicago/Turabian StyleKukla, Mateusz, Igor Sieracki, Wojciech Maliga, and Jan Górecki. 2022. "Compression Strength of PLA Bolts Produced via FDM" Materials 15, no. 24: 8740. https://doi.org/10.3390/ma15248740
APA StyleKukla, M., Sieracki, I., Maliga, W., & Górecki, J. (2022). Compression Strength of PLA Bolts Produced via FDM. Materials, 15(24), 8740. https://doi.org/10.3390/ma15248740








