Programmable Thermo-Responsive Self-Morphing Structures Design and Performance
Abstract
:1. Introduction
2. State-of-the-Art Review
3. Experimental Setup
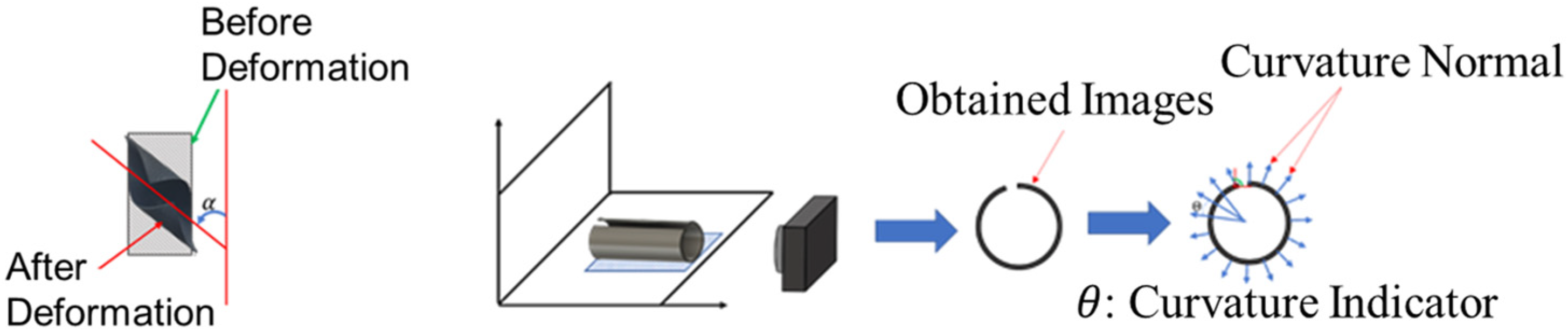
Morphing Performance Measurements
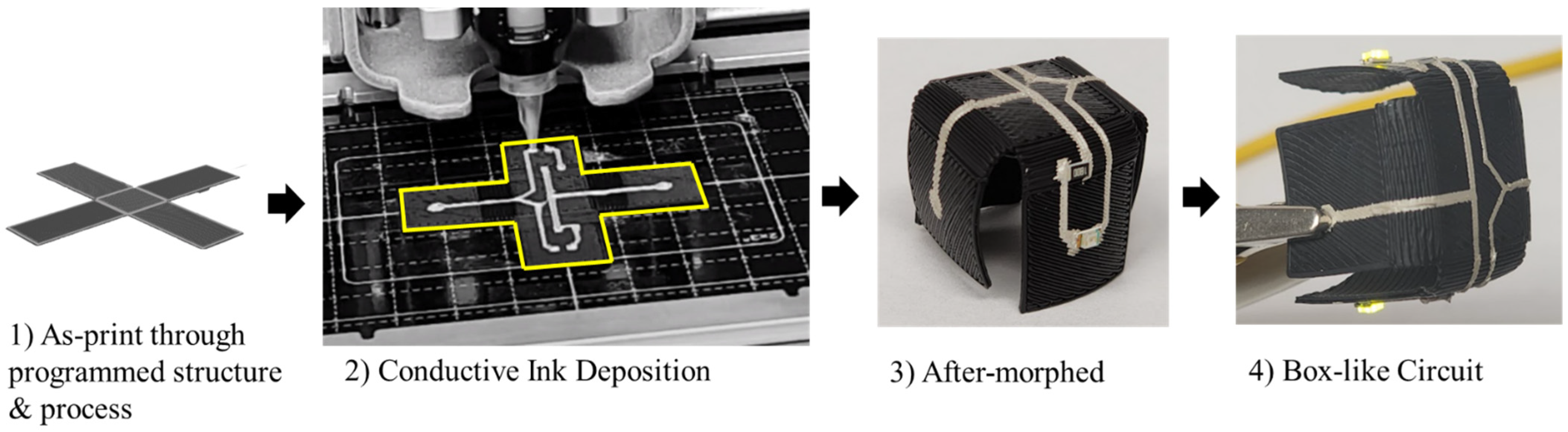
4. Methodology
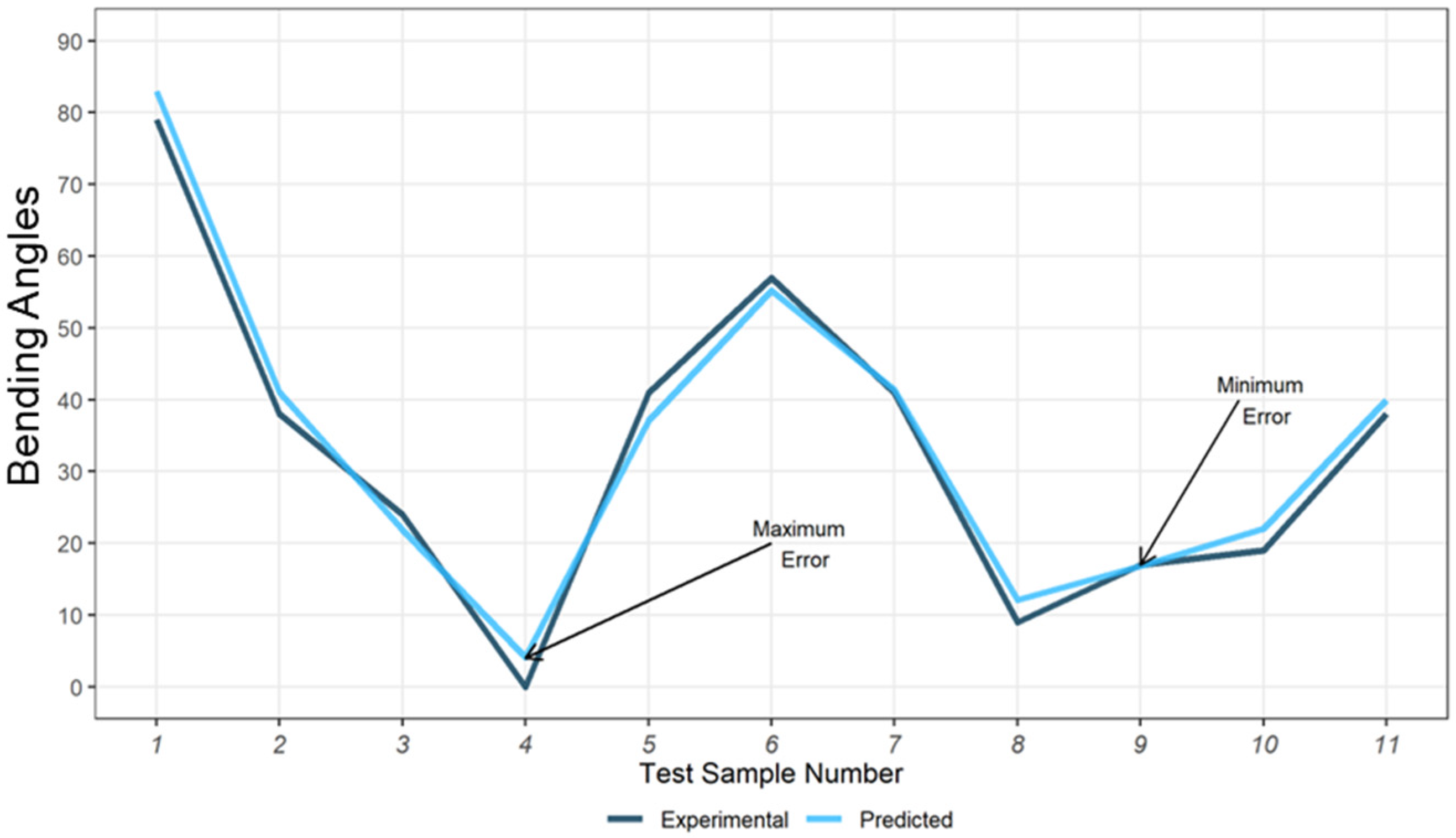
5. Results
- Integrate the morphing physics with the performance quantitatively;
- Multi-functional/degrees of morphing demeanor can be performed through single-material FDM process;
- Reverse design of the 3D-printed structure and appropriate process condition can be obtained when the desired after-morphing complex shapes are provided.
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, X.; Joshi, S. Process planning for five-axis support free additive manufacturing. Addit. Manuf. 2020, 36, 101569. [Google Scholar] [CrossRef]
- Xiao, X.; Joshi, S. Decomposition and Sequencing for a 5-Axis Hybrid Manufacturing Process. In Proceedings of the ASME 2020 15th International Manufacturing Science and Engineering Conference, Virtual, 3 September 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84256, p. V001T01A049. [Google Scholar]
- Xiao, X.; Xiao, H. Autonomous robotic feature-based freeform fabrication approach. Materials 2021, 15, 247. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Weeger, O.; Qi, H.J.; Dunn, M.L. 4D rods: 3D structures via programmable 1D composite rods. Mater. Des. 2018, 137, 256–265. [Google Scholar] [CrossRef]
- Rafiee, M.; Farahani, R.D.; Therriault, D. Multi-material 3D and 4D printing: A survey. Adv. Sci. 2020, 7, 1902307. [Google Scholar] [CrossRef] [PubMed]
- van Manen, T.; Dehabadi, V.M.; Saldívar, M.C.; Mirzaali, M.J.; Zadpoor, A.A. Theoretical stiffness limits of 4D printed self-folding metamaterials. Commun. Mater. 2022, 3, 1–12. [Google Scholar] [CrossRef]
- Zou, S.; Pang, L.; Xu, C.; Xiao, X. Effect of Process Parameters on Distortions Based on the Quantitative Model in the SLM Process. Appl. Sci. 2022, 12, 1567. [Google Scholar] [CrossRef]
- Xiao, X.; Roh, B.M.; Zhu, F. Strength enhancement in fused filament fabrication via the isotropy toolpath. Appl. Sci. 2021, 11, 6100. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, K.; Hu, G. Smart three-dimensional lightweight structure triggered from a thin composite sheet via 3D printing technique. Sci. Rep. 2016, 6, 2431. [Google Scholar] [CrossRef] [Green Version]
- Kačergis, L.; Mitkus, R.; Sinapius, M. Influence of fused deposition modeling process parameters on the transformation of 4D printed morphing structures. Smart Mater. Struct. 2019, 28, 105042. [Google Scholar] [CrossRef]
- Tomec, D.K.; Straže, A.; Haider, A.; Kariž, M. Hygromorphic Response Dynamics of 3D-Printed Wood-PLA Composite Bilayer Actuators. Polymers 2021, 13, 3209. [Google Scholar] [CrossRef]
- van Manen, T.; Janbaz, S.; Zadpoor, A.A. Programming the shape-shifting of flat soft matter. Mater. Today 2018, 21, 144–163. [Google Scholar] [CrossRef]
- Zheng, S.Y.; Shen, Y.; Zhu, F.; Yin, J.; Qian, J.; Fu, J.; Wu, Z.L.; Zheng, Q. Programmed Deformations of 3D-Printed Tough Physical Hydrogels with High Response Speed and Large Output Force. Adv. Funct. Mater. 2018, 28, 1803366. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.R.; Liao, W.H. Adaptive metamaterials by functionally graded 4D printing. Mater. Des. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Bodaghi, M.; Liao, W.H. 4D printed tunable mechanical metamaterials with shape memory operations. Smart Mater. Struct. 2019, 28, 045019. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, X. An accurate finite element approach for programming 4D-printed self-morphing structures produced by fused deposition modeling. Mech. Mater. 2020, 151, 103628. [Google Scholar] [CrossRef]
- Bouaziz, R.; Roger, F.; Prashantha, K. Thermo-mechanical modeling of semi-crystalline thermoplastic shape memory polymer under large strain. Smart Mater. Struct. 2017, 26, 055009. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, H.; Qian, K.; Yang, H.; McGehee, M.; Gu, J.; Luo, D.; Yao, L.; Zhang, Y.J. Material characterization and precise finite element analysis of fiber reinforced thermoplastic composites for 4D printing. Comput.-Aided Des. 2020, 122, 102817. [Google Scholar] [CrossRef]
- Noroozi, R.; Bodaghi, M.; Jafari, H.; Zolfagharian, A.; Fotouhi, M. Shape-Adaptive Metastructures with Variable Bandgap Regions by 4D Printing. Polymers 2020, 12, 519. [Google Scholar] [CrossRef] [Green Version]
- Ang, K.J.; Riley, K.S.; Faber, J.; Arrieta, A.F. Switchable Bistability in 3D Printed Shells with Bio-Inspired Architectures and Spatially Distributed Pre-Stress. 2018. Available online: https://proceedings.asmedigitalcollection.asme.org (accessed on 1 December 2022).
- Zeng, S.; Gao, Y.; Feng, Y.; Zheng, H.; Qiu, H.; Tan, J. Programming the deformation of a temperature-driven bilayer structure in 4D printing. Smart Mater. Struct. 2019, 28, 105031. [Google Scholar] [CrossRef]
- Choi, W.; Kim, T.Y.; Lee, Y.G. Rolling of 3D Printed Dual-Layer Beam into a Cylinder by Ethanol Absorption. Macromol. Mater. Eng. 2018, 303, 1700675. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Song, Z.; Ren, L.; Liu, Q.; Ren, L. Programming Multistage Shape Memory and Variable Recovery Force with 4D Printing Parameters. Adv. Mater. Technol. 2019, 4, 1900535. [Google Scholar] [CrossRef]
- Alshebly, Y.S.; Mustapha, K.B.; Zolfagharian, A.; Bodaghi, M.; Mohamed Ali, M.S.; Almurib, H.A.; Nafea, M. Bioinspired Pattern-Driven Single-Material 4D Printing for Self-Morphing Actuators. Sustainability 2022, 14, 10141. [Google Scholar] [CrossRef]
- Rajkumar, A.R.; Shanmugam, K. Additive manufacturing-enabled shape transformations via FFF 4D printing. J. Mater. Res. 2018, 33, 4362–4376. [Google Scholar] [CrossRef]
- Goo, B.; Hong, C.H.; Park, K. 4D printing using anisotropic thermal deformation of 3D-printed thermoplastic parts. Mater. Des. 2020, 188, 108485. [Google Scholar] [CrossRef]
- Nezhad, I.S.; Golzar, M.; Behravesh, A.h.; Zare, S. Comprehensive study on shape shifting behaviors in FDM-based 4D printing of bilayer structures. Int. J. Adv. Manuf. Technol. 2022, 120, 959–974. [Google Scholar] [CrossRef]
- Song, J.; Feng, Y.; Wang, Y.; Zeng, S.; Hong, Z.; Qiu, H.; Tan, J. Complicated deformation simulating on temperature-driven 4D printed bilayer structures based on reduced bilayer plate model. Appl. Math. Mech. 2021, 42, 1619–1632. [Google Scholar] [CrossRef]
- Wu, H.C.; Chen, T.C.T. Quality control issues in 3D-printing manufacturing: A review. Rapid Prototyp. J. 2018, 24, 607–614. [Google Scholar] [CrossRef]
- Livolsi, F.; May, T.; Caputo, D.; Fouladi, K.; Eslami, B. Multiscale Study on Effect of Humidity on Shape Memory Polymers Used in Three-Dimensional Printing. ASME J. Manuf. Sci. Eng. 2021, 143, 091010. [Google Scholar] [CrossRef]
- Jackson, B.; Fouladi, K.; Eslami, B. Multi-Parameter Optimization of 3D Printing Condition for Enhanced Quality and Strength. Polymers 2022, 14, 1586. [Google Scholar] [CrossRef]
- Xiao, X.; Roh, B.M.; Hamilton, C. Porosity management and control in powder bed fusion process through process-quality interactions. CIRP J. Manuf. Sci. Technol. 2022, 38, 120–128. [Google Scholar] [CrossRef]
- Xiao, X.; Waddell, C.; Hamilton, C.; Xiao, H. Quality Prediction and Control in Wire Arc Additive Manufacturing via Novel Machine Learning Framework. Micromachines 2022, 13, 137. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, S.; Liu, H.; Wang, L.; Xiao, X. Effects of Hatch Distance on the Microstructure and Mechanical Anisotropy of 316 L Stainless Steel Fabricated by Laser Powder Bed Fusion. J. Mater. Eng. Perform. 2022, 1–11. [Google Scholar] [CrossRef]
- Roh, B.M.; Kumara, S.R.; Yang, H.; Simpson, T.W.; Witherell, P.; Jones, A.T.; Lu, Y. Ontology Network-Based In-Situ Sensor Selection for Quality Management in Metal Additive Manufacturing. J. Comput. Inf. Sci. Eng. 2022, 22, 060905. [Google Scholar] [CrossRef]
- Roh, B.M.; Kumara, S.R.; Witherell, P.; Simpson, T.W. Ontology-based process map for metal additive manufacturing. J. Mater. Eng. Perform. 2021, 30, 8784–8797. [Google Scholar] [CrossRef]
- Roh, B.M.; Kumara, S.R.; Yang, H.; Simpson, T.W.; Witherell, P.; Lu, Y. In-Situ Observation Selection for Quality Management in Metal Additive Manufacturing. In Proceedings of the ASME 2021 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85376, p. V002T02A069. [Google Scholar]
- Roh, B.M.; Yang, H.; Simpson, T.W.; Jones, A.T.; Witherell, P. A Hierarchical V-Network Framework for Part Qualification in Metal Additive Manufacturing. In Proceedings of the 2022 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 25–27 July 2022; University of Texas at Austin: Austin, TX, USA, 2022. [Google Scholar]
- Xiao, X.; Chu, B.; Zhang, Z. Quality Quantification and Control via Novel Self-Growing Process-Quality Model of Parts Fabricated by LPBF Process. Materials 2022, 15, 8520. [Google Scholar] [CrossRef]
- Seeger, M. Gaussian processes for machine learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Wilamowski, B.M. Levenberg–marquardt training. In Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, F.; Luo, F.; Huang, Y.; Cao, X.; Yuan, C. 4D Printing Via Multispeed Fused Deposition Modeling. Adv. Mater. Technol. 2022, 2201383. [Google Scholar] [CrossRef]
- Aberoumand, M.; Soltanmohammadi, K.; Soleyman, E.; Rahmatabadi, D.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Baghani, M. A comprehensive experimental investigation on 4D printing of PET-G under bending. J. Mater. Res. Technol. 2022, 18, 2552–2569. [Google Scholar] [CrossRef]




| Properties | Values |
|---|---|
| Density | 125 g/cm3 |
| Thermal Expansion Coefficient | 68 µm/m-K |
| Ultimate Tensile Strength | 58 MPa |
| Glass Transition Temperature | 78 °C |
| Parameters | Range |
|---|---|
| Path-layering Orientation | (0, 15, 30, 45, 60, 75, 90) |
| Layer Thickness | (0.1, 0.2, 0.3, 0.4) |
| Speed | (20, 25, 30, 40) |
| Sample Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Thickness | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.4 | 0.4 | 0.3 | 0.4 | 0.3 | 0.3 |
| Print Angle | 45 | 0 | 10 | 65 | 35 | 80 | 25 | 25 | 10 | 35 | 5 | |
| Print Speed | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | |
| Layer 2 | Thickness | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Print Angle | 10 | 45 | 65 | 85 | 50 | 35 | 40 | 70 | 65 | 60 | 40 | |
| Print Speed | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | |
| Sample Number | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Layer 1 | Thickness | 0.4 | 0.4 | 0.3 | 0.3 | 0.3 |
| Print Angle | 25 | 10 | 25 | 35 | 5 | |
| Print Speed | 25 | 25 | 25 | 25 | 25 | |
| Layer 2 | Layer Thickness | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Print Angle | 40 | 65 | 70 | 60 | 40 | |
| Print Speed | 27.5 | 27.5 | 27.5 | 27.5 | 27.5 | |
| Measured Curvature | 6.91 | 12.97 | 6.82 | 6.74 | 5.35 | |
| Predicted Curvature | 7.35 | 11.81 | 6.81 | 5.96 | 5.71 | |
| Deviation % | 6.32 | 8.94 | 0.15 | 11.61 | 6.8 | |
| Single-Fold Petals | Two-Fold Petals | Twisted Flower | Double-Sided Fold | Flat Structure | |
|---|---|---|---|---|---|
| Desired shape |  |  |  |  |  |
| 3D Printable Data (Blue – Supports; Red – 3D Model) |  |  |  |  |  |
| 4D Print Design |  |  |  |  |  |
| 4D Print Process |  |  |  | 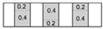 |  |
 |  | 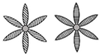 | 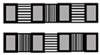 |  | |
| After-Morphed |  |  |  |  |  |
| Print Time (min) | Material Usage (g) | |||
|---|---|---|---|---|
| Two-Fold Petals | 3D | 44.00 | 28,514.40 | 3.00 |
| 4D | 10.00 | 6000.00 | 1.00 | |
| %Red | −77.27% | −78.96% | −66.67% | |
| Double Sided Fold | 3D | 77.00 | 37,135.60 | 6.00 |
| 4D | 8.00 | 1200.00 | 1.00 | |
| %Red | −89.61% | −96.77% | −83.33% | |
| Single Fold Petals | 3D | 73.00 | 27,922.50 | 6.00 |
| 4D | 10.00 | 4399.44 | 1.00 | |
| %Red | −86.30% | −84.24% | −83.33% | |
| Twisted Flower | 3D | 57.00 | 70,599.29 | 4.00 |
| 4D | 10.00 | 4399.44 | 1.00 | |
| %Red | −82.46% | −93.77% | −75.00% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandeya, S.P.; Zou, S.; Roh, B.-M.; Xiao, X. Programmable Thermo-Responsive Self-Morphing Structures Design and Performance. Materials 2022, 15, 8775. https://doi.org/10.3390/ma15248775
Pandeya SP, Zou S, Roh B-M, Xiao X. Programmable Thermo-Responsive Self-Morphing Structures Design and Performance. Materials. 2022; 15(24):8775. https://doi.org/10.3390/ma15248775
Chicago/Turabian StylePandeya, Surya Prakash, Sheng Zou, Byeong-Min Roh, and Xinyi Xiao. 2022. "Programmable Thermo-Responsive Self-Morphing Structures Design and Performance" Materials 15, no. 24: 8775. https://doi.org/10.3390/ma15248775
APA StylePandeya, S. P., Zou, S., Roh, B.-M., & Xiao, X. (2022). Programmable Thermo-Responsive Self-Morphing Structures Design and Performance. Materials, 15(24), 8775. https://doi.org/10.3390/ma15248775









