Mixed Mode Fracture Investigation of Rock Specimens Containing Sharp V-Notches
Abstract
:1. Introduction
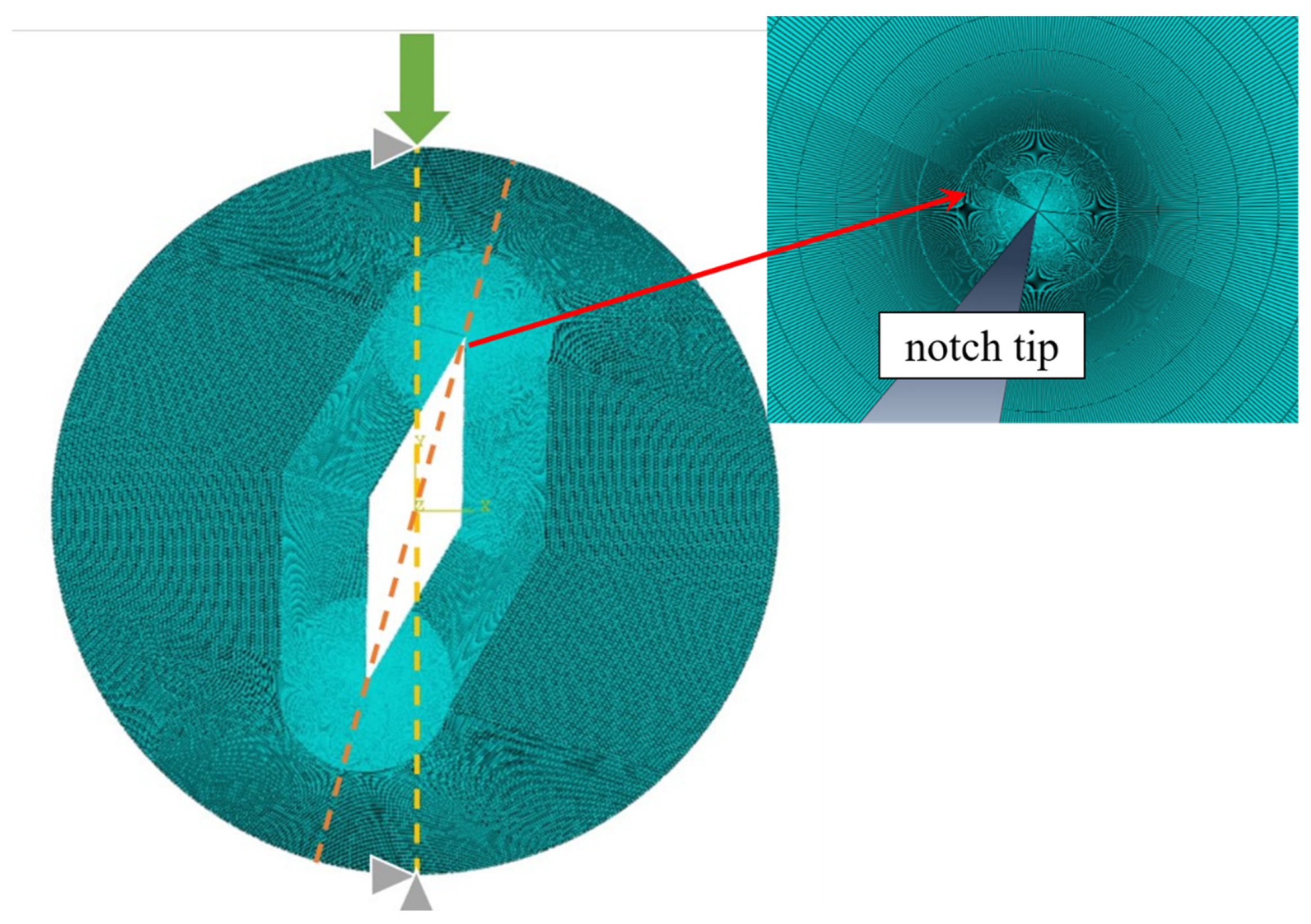
2. Materials and Methods
2.1. Material, Tests and Experimental Results
2.2. Analytical Approach: Mixed-Mode Fracture Criterion
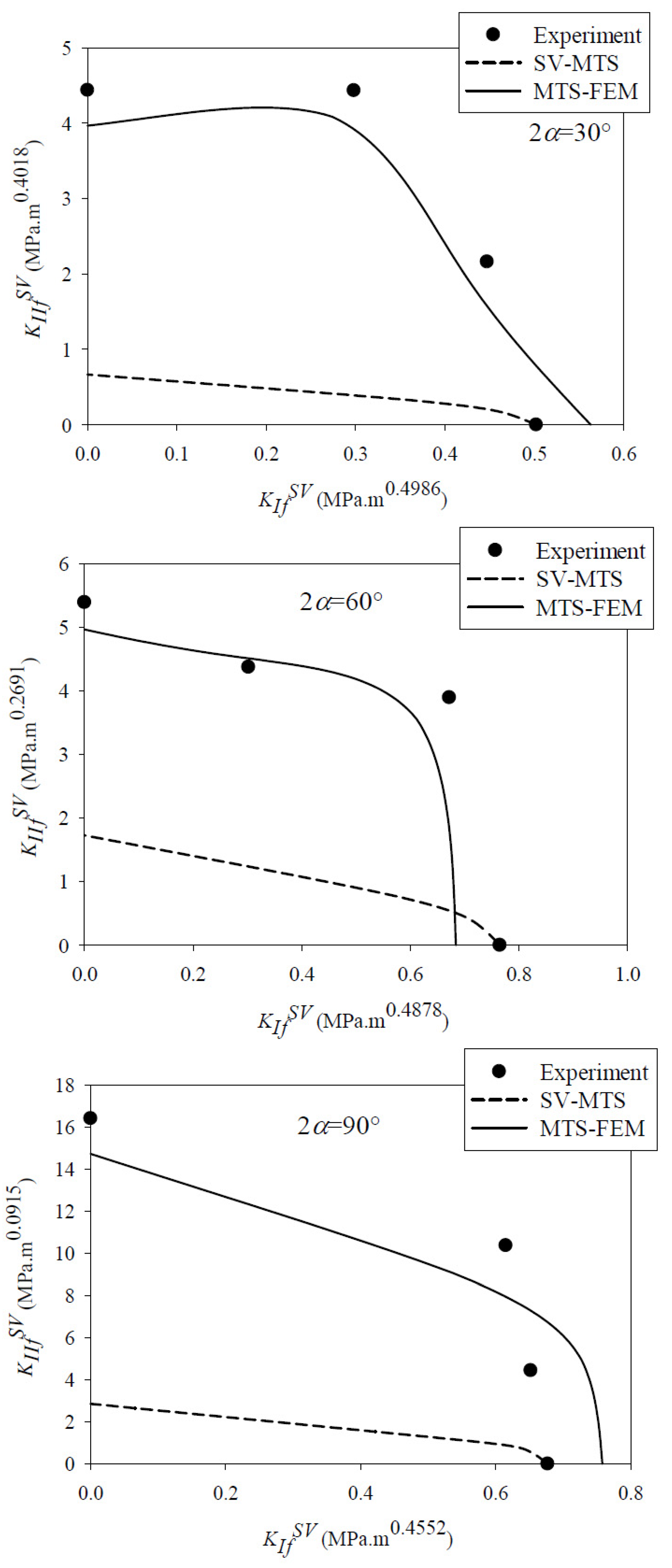
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| d | Notch length in SVNBD specimens |
| D | Diameter of the circular specimens |
| ft | Tensile strength |
| KIc | Fracture toughness |
| KISV, KIISV | Sharp V-notch stress intensity factor under mode I and mode II |
| KIfSV, KIIfSV | Critical values of KISV and KIISV, respectively |
| KI* | Dimensionless parameters for stress terms in cracked conditions |
| P | Applied load |
| Pf | Fracture load |
| rc,V | Critical distance for sharp V-notch |
| t | Specimen thickness |
| YIV, YIIV | Dimensionless parameters for stress terms in notched conditions |
| α | Half of the notch opening angle |
| β | Loading angle for Brazilian disk specimen |
| βII | Loading angle corresponding to pure mode II loading |
| λi | Eigenvalues |
| σrθ | In-plane shear stress |
| σθθ | Tangential stress |
| σθθc | Critical value of σθθ |
| θ0 | Notch bifurcation angle |
| θ0I | Notch bifurcation angle for pure mode I |
| θ0II | Notch bifurcation angle for pure mode II |
| ω | Notch solid angle |
| BD | Brazilian disk |
| CBD | Cracked Brazilian disk specimen |
| MTS | Maximum tangential stress criterion |
| MTS-FEM | Modified MTS criterion based on the finite element method |
| SVNBD | Sharp V-notched Brazilian disk |
| SV-MTS | MTS criterion for sharp V-notch |
References
- Lazzarin, P.; Berto, F.; Radaj, D. Fatigue-relevant stress field parameters of welded lap joints: Pointed slit tip compared with keyhole notch. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 713–735. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Sih, G.C. Strain-energy-density factor applied to mixed mode crack problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Yosibash, Z.; Bussiba, A.; Gilad, I. Failure criteria for brittle elastic materials. Int. J. Fract. 2004, 125, 307–333. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R. A criterion for brittle fracture in U-notched components under mixed mode loading. Eng. Fract. Mech. 2009, 76, 1883–1896. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R. Brittle fracture in rounded-tip V-shaped notches. Mater. Des. 2010, 31, 60–67. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R. Tensile fracture in notched polycrystalline graphite specimens. Carbon 2010, 48, 2255–2265. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R.; Azizi, P. Experimental and theoretical assessment of brittle fracture in engineering components containing a sharp V-notch. Exp. Mech. 2011, 51, 919–932. [Google Scholar] [CrossRef]
- Seweryn, A.; Łukaszewicz, A. Verification of brittle fracture criteria for elements with V-shaped notches. Eng. Fract. Mech. 2002, 69, 1487–1510. [Google Scholar] [CrossRef]
- Kim, J.K.; Cho, S.B. A unified brittle fracture criterion for structures with sharp V-notches under mixed mode loading. J. Mech. Sci. Technol. 2008, 22, 1269–1278. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Berto, F.; Lazzarin, P. Mixed mode brittle fracture of sharp and blunt V-notches in polycrystalline graphite. Carbon 2011, 49, 2465–2474. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Nejati, M. Experimental evaluation of stress field around the sharp notches using photoelasticity. Mater. Des. 2011, 32, 561–569. [Google Scholar] [CrossRef]
- Bahrami, B.; Ayatollahi, M.R.; Torabi, A.R. Application of digital image correlation method for determination of mixed mode stress intensity factors in sharp notches. Opt. Lasers Eng. 2020, 124, 105830. [Google Scholar] [CrossRef]
- Pranjol, P.; Murthy, K.S.R.K.; Chakraborty, D. A strain gage technique for mode I notch stress intensity factor of sharp V-notched configurations. Theor. Appl. Fract. Mech. 2018, 94, 57–70. [Google Scholar]
- Ayatollahi, M.R.; Nejati, M. Determination of NSIFs and coefficients of higher order terms for sharp notches using finite element method. Int. J. Mech. Sci. 2011, 53, 164–177. [Google Scholar] [CrossRef]
- Treifi, M.; Olutunde Oyadiji, S.; Tsang, D.K.L. Computation of the stress intensity factors of sharp notched plates by the fractal-like finite element method. Int. J. Numer. Methods Eng. 2009, 77, 558–580. [Google Scholar] [CrossRef]
- Williams, M.L. Stress singularities resulting from various boundary conditions in angular corners of plates in extension. J. Appl. Mech. 1952, 19, 526–528. [Google Scholar] [CrossRef]
- Justo, J.; Castro, J.; Cicero, S. Energy-based approach for fracture assessment of several rocks containing U-shaped notches through the application of the SED criterion. Int. J. Rock Mech. Min. Sci. 2018, 110, 306–315. [Google Scholar] [CrossRef]
- Justo, J.; Castro, J.; Cicero, S. Notch effect and fracture load predictions of rock beams at different temperatures using the Theory of Critical Distances. Int. J. Rock Mech. Min. Sci. 2020, 125, 104161. [Google Scholar] [CrossRef]
- Justo, J.; Castro, J.; Cicero, S.; Sánchez-Carro, M.A.; Husillos, R. Notch effect on the fracture of several rocks: Application of the Theory of Critical Distances. Theor. Appl. Fract. Mech. 2017, 90, 251–258. [Google Scholar] [CrossRef] [Green Version]
- Ghadirian, H.R.; Akbardoost, J.; Zhaleh, A.R. Fracture analysis of rock specimens weakened by rounded-V and U-shaped notches under pure mode I loading. Int. J. Rock Mech. Min. Sci. 2019, 123, 104103. [Google Scholar] [CrossRef]
- Sangsefidi, M.; Akbardoost, J.; Mesbah, M. Experimental and theoretical fracture assessment of rock-type U-notched specimens under mixed mode I/II loading. Eng. Fract. Mech. 2020, 230, 106990. [Google Scholar] [CrossRef]
- Torabi, A.R.; Taherkhani, M. Extensive data of notch shape factors for V-notched Brazilian disc specimen under mixed mode loading. Mater. Sci. Eng. A 2011, 528, 8599–8609. [Google Scholar] [CrossRef]
- ISRM. Suggested methods for determining tensile strength of rock materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 99–103. [Google Scholar] [CrossRef]
- Akbardoost, J.; Ayatollahi, M.R. Experimental analysis of mixed mode crack propagation in brittle rocks: The effect of non-singular terms. Eng. Fract. Mech. 2014, 129, 77–89. [Google Scholar] [CrossRef]
- Filippi, S.; Lazzarin, P.; Tovo, R. Developments of some explicit formulas useful to describe elastic stress fields ahead of notches in plates. Int. J. Solids Struct. 2002, 39, 4543–4565. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Pugno, N.; Sapora, A.; Taylor, D. A finite fracture mechanics approach to structures with sharp V-notches. Eng. Fract. Mech. 2008, 75, 1736–1752. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Ayatollahi, M.R.; Smith, D.J.; Pavier, M.J. Geometry and size effects on fracture trajectory in a limestone rock under mixed mode loading. Eng. Fract. Mech. 2010, 77, 2200–2212. [Google Scholar] [CrossRef]
- Awaji, H.; Sato, S. Combined mode fracture toughness measurement by the disc test. J. Eng. Mater. Technol. Trans. ASME 1978, 100, 175–182. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M. Fracture toughness study for a brittle rock subjected to mixed mode I/II loading. Int. J. Rock Mech. Min. Sci. 2007, 44, 617–624. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Sistaninia, M. Mode II fracture study of rocks using Brazilian disk specimens. Int. J. Rock Mech. Min. Sci. 2011, 48, 819–826. [Google Scholar] [CrossRef]
- Mirsayar, M.M. Mixed mode fracture analysis using extended maximum tangential strain criterion. Mater. Des. 2015, 86, 941–947. [Google Scholar] [CrossRef]
- Mirsayar, M.M. T-strain effects in kinked interfacial fracture of bonded composites. Theor. Appl. Fract. Mech. 2019, 104, 102381. [Google Scholar] [CrossRef]
- Smith, D.J.; Ayatollahi, M.R.; Pavier, M.J. The role of T-stress in brittle fracture for linear elastic materials under mixed-mode loading. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 137–150. [Google Scholar] [CrossRef]
- Aslani, M.; Akbardoost, J.; Berto, F. A stress-based approach for considering the size effect on the mixed mode fracture behavior of rock. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022, 236, 10841–10851. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Torabi, A.R.; Bahrami, B. On the necessity of using critical distance model in mixed mode brittle fracture prediction of V-notched Brazilian disk specimens under negative mode I conditions. Theor. Appl. Fract. Mech. 2016, 84, 38–48. [Google Scholar] [CrossRef]
- Sangsefidi, M.; Akbardoost, J.; Zhaleh, A.R. Assessment of mode I fracture of rock-type sharp V-notched samples considering the size effect. Theor. Appl. Fract. Mech. 2021, 116, 103136. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Ferro, G. Size effects on nominal tensile strength of concrete structures: Multifractality of material ligaments and dimensional transition from order to disorder. Mater. Struct. 1995, 28, 311–317. [Google Scholar] [CrossRef]
- Fett, T. Influence of a finite notch root radius on fracture toughness. J. Eur. Ceram. Soc. 2005, 25, 543–54740. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C. Notch depth and root radius effects on quasi-brittle fracture of materials related to grain size. Ceram. Int. 2022, 48, 23706–23712. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Zhang, X. Notch radius effect on fracture toughness of ceramics pertinent to grain size. J. Eur. Ceram. Soc. 2020, 40, 4217–4223. [Google Scholar] [CrossRef]
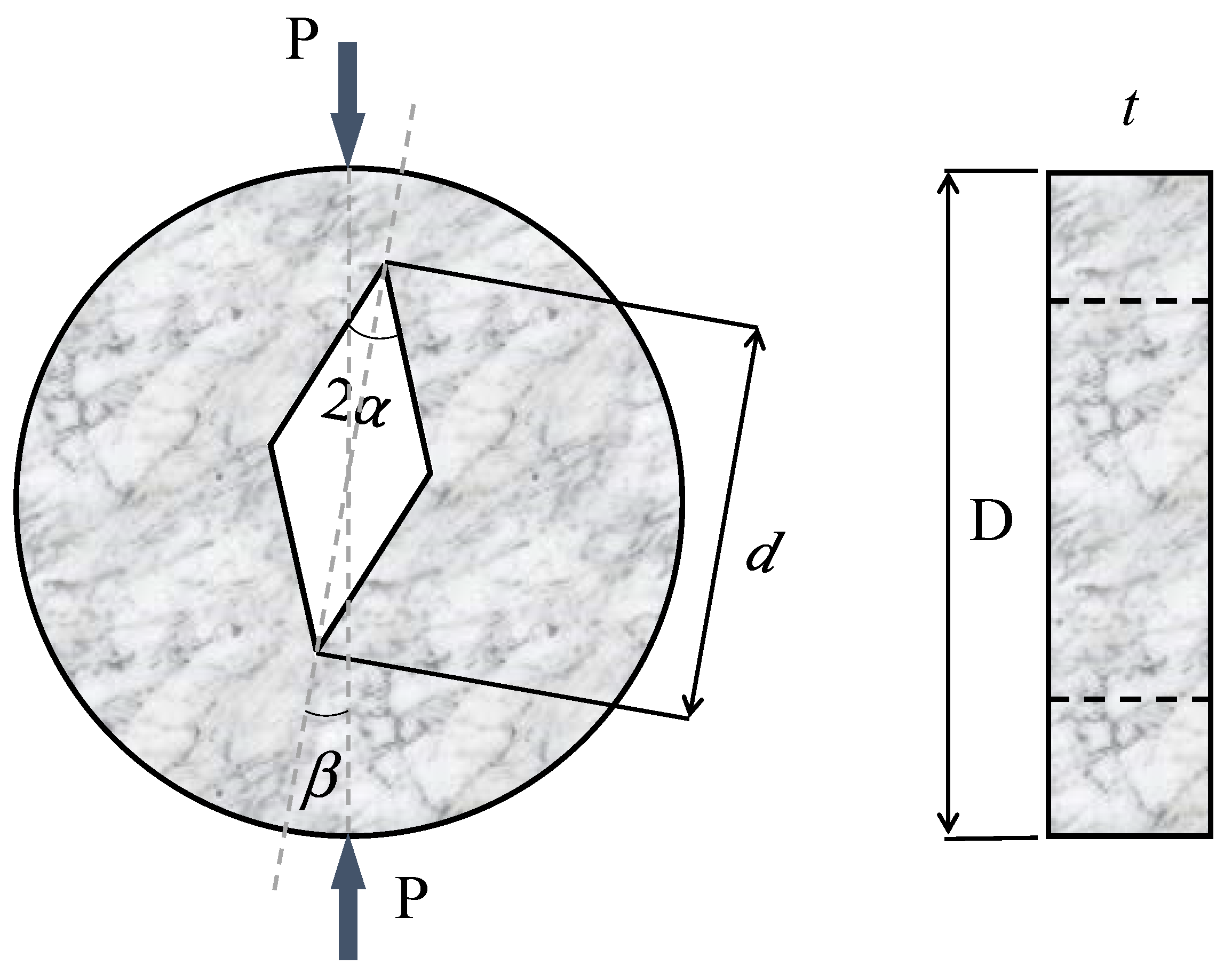



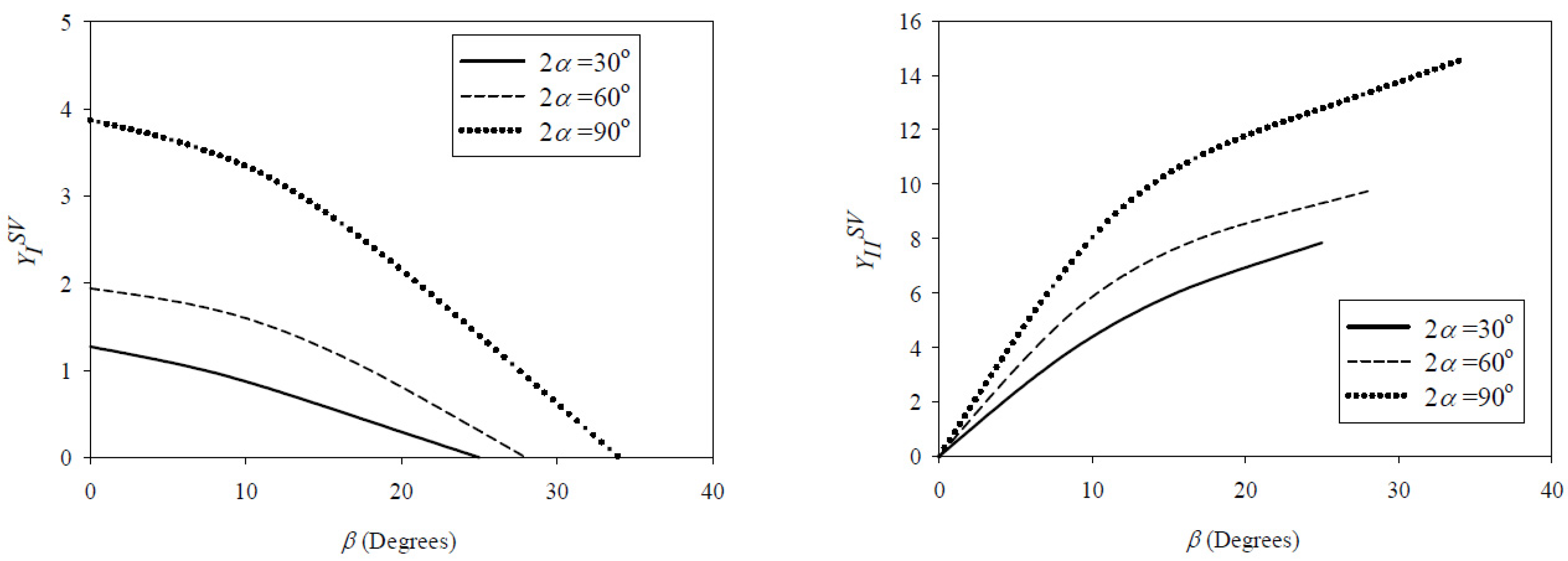
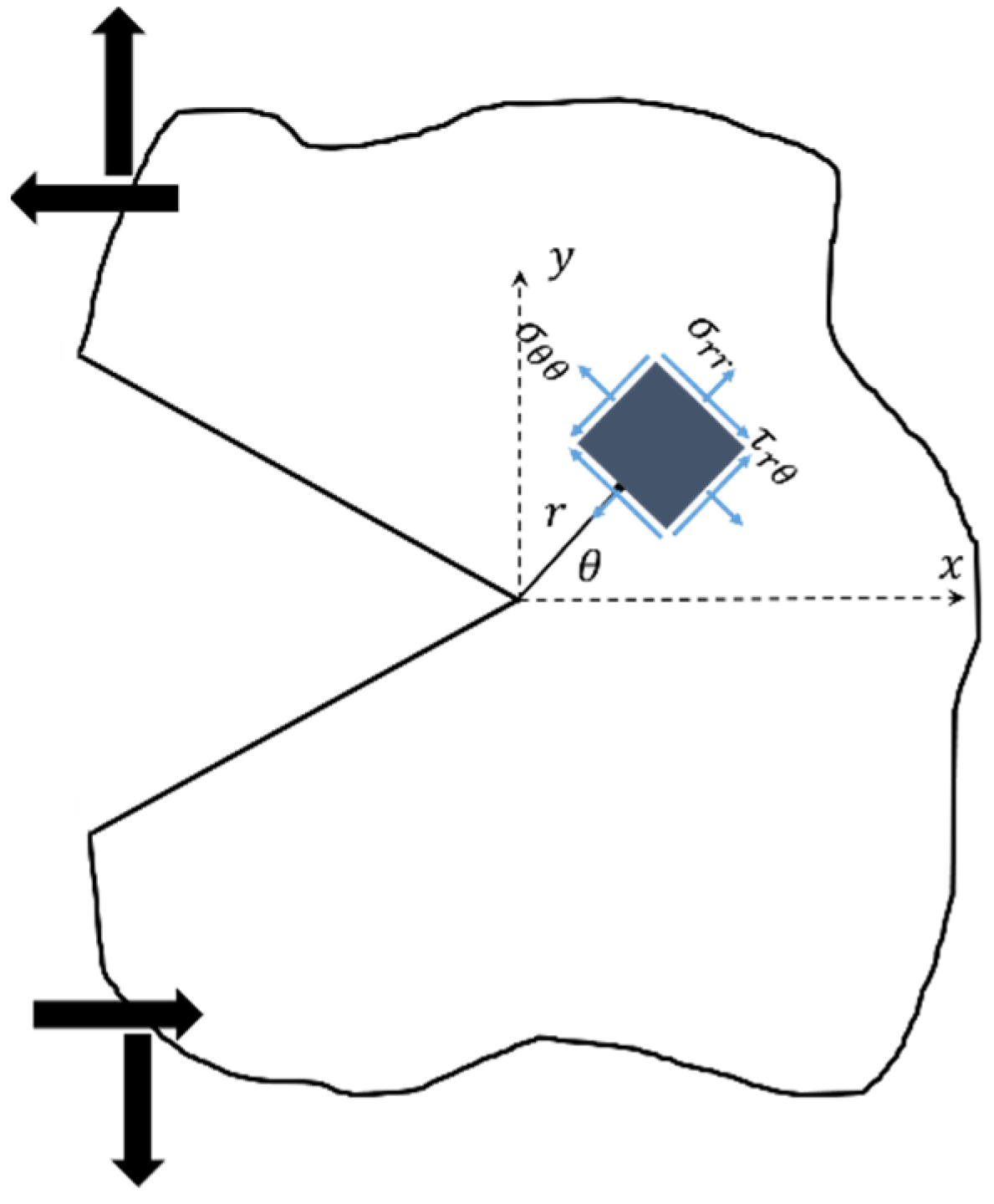
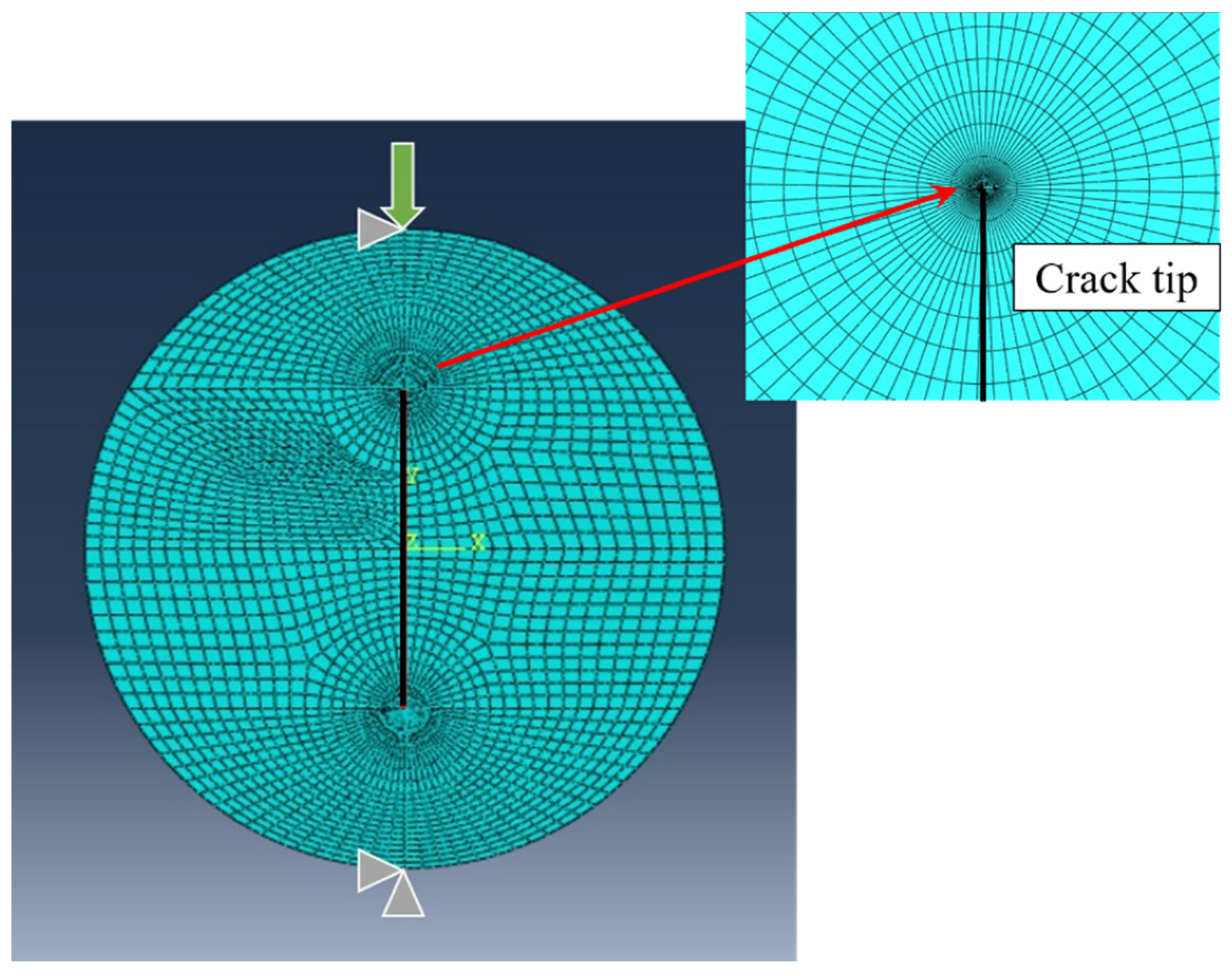

| D (mm) | t (mm) | d (mm) | 2α (°) | β (°) | Pf Avg. (N) | Standard Deviation SD (N) |
|---|---|---|---|---|---|---|
| 150 | 29.4 | 75 | 30 | 0 | 6335.7 | 646.9 |
| 150 | 32 | 75 | 30 | 8 | 8081.3 | 1725.0 |
| 150 | 27.7 | 75 | 30 | 16 | 8572.4 | 1692.7 |
| 150 | 30.4 | 75 | 30 | 25 | 7263.7 | 1307.7 |
| 150 | 31.4 | 75 | 60 | 0 | 6599.7 | 857.7 |
| 150 | 33.3 | 75 | 60 | 9 | 7096.3 | 1228.3 |
| 150 | 35.5 | 75 | 60 | 18 | 5732.4 | 1307.0 |
| 150 | 34.4 | 75 | 60 | 28 | 5743.8 | 2612.6 |
| 150 | 33.9 | 75 | 90 | 0 | 2903.5 | 274.7 |
| 150 | 34.5 | 75 | 90 | 11 | 3421.2 | 706.3 |
| 150 | 32.8 | 75 | 90 | 22 | 5283.6 | 638.7 |
| 150 | 34.6 | 75 | 90 | 34 | 7396.1 | 813.4 |
| Avg. (N) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 0 | 6335.7 | 0.5014 | 0.5982 | 1.27 | 0 | 0.502 (MPa·m0.4986) | 0 (MPa·m0.4018) |
| 8 | 8081.3 | 0.5014 | 0.5982 | 0.97 | 3.65 | 0.447 (MPa·m0.4986) | 2.163 (MPa·m0.4018) | |
| 16 | 8572.4 | 0.5014 | 0.5982 | 0.53 | 6.13 | 0.298 (MPa·m0.4986) | 4.436 (MPa·m0.4018) | |
| 25 | 7263.7 | 0.5014 | 0.5982 | 0 | 7.85 | 0 (MPa·m0.4986) | 4.44 (MPa·m0.4018) | |
| 60 | 0 | 6599.7 | 0.5122 | 0.7309 | 1.94 | 0 | 0.765 (MPa·m0.4878) | 0 (MPa·m0.2691) |
| 9 | 7096.3 | 0.5122 | 0.7309 | 1.65 | 5.43 | 0.672 (MPa·m0.4878) | 3.895 (MPa·m0.2691) | |
| 18 | 5732.4 | 0.5122 | 0.7309 | 1 | 8.21 | 0.302 (MPa·m0.4878) | 4.374 (MPa·m0.2691) | |
| 28 | 5743.8 | 0.5122 | 0.7309 | 0 | 9.75 | 0 (MPa·m0.4878) | 5.391 (MPa·m0.2691) | |
| 90 | 0 | 2903.5 | 0.5448 | 0.9085 | 3.87 | 0 | 0.677 (MPa·m0.4552) | 0 (MPa·m0.0915) |
| 11 | 3421.2 | 0.5448 | 0.9085 | 3.26 | 8.65 | 0.652 (MPa·m0.4552) | 4.436 (MPa·m0.0915) | |
| 22 | 5283.6 | 0.5448 | 0.9085 | 1.86 | 12.21 | 0.615 (MPa·m0.4552) | 10.365 (MPa·m0.0915) | |
| 34 | 7396.1 | 0.5448 | 0.9085 | 0 | 14.56 | 0 (MPa·m0.4552) | 16.402 (MPa·m0.0915) |
| Pf (N) | Dicrepancy (%) | |||||
|---|---|---|---|---|---|---|
| Experiment | SV-MTS | MTS-FEM | SV-MTS | MTS-FEM | ||
| 30° | 0 | 6335.7 | 6335.7 | 7103.3 | 0.0 | 12.1 |
| 8 | 8081.3 | 3311.1 | 7566.9 | 59.0 | 6.4 | |
| 16 | 8572.4 | 1401.7 | 7847.2 | 83.6 | 8.5 | |
| 25 | 7263.7 | 1117.8 | 6532.1 | 84.6 | 10.1 | |
| Mean discrepancy (%) | 56.3 | 9.25 | ||||
| 60 | 0 | 6599.7 | 6599.7 | 5879.6 | 0.0 | 10.9 |
| 9 | 7096.3 | 3668.5 | 6557.8 | 48.3 | 7.5 | |
| 18 | 5732.4 | 2325 | 5858.8 | 59.4 | 2.2 | |
| 28 | 5743.8 | 1813.1 | 5271.3 | 68.4 | 8.2 | |
| Mean discrepancy (%) | 45.2 | 7.2 | ||||
| 90 | 0 | 2903.5 | 2903.5 | 3243.9 | 0.0 | 11.7 |
| 11 | 3421.2 | 2023.3 | 3787.2 | 40.9 | 10.7 | |
| 22 | 5283.6 | 1378 | 4624.2 | 73.9 | 12.5 | |
| 34 | 7396.1 | 1266.2 | 6645.7 | 82.9 | 10.2 | |
| Mean discrepancy (%) | 49.4 | 11.2 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arabnia, A.; Akbardoost, J.; Cicero, S.; Torabi, A.R. Mixed Mode Fracture Investigation of Rock Specimens Containing Sharp V-Notches. Materials 2022, 15, 8779. https://doi.org/10.3390/ma15248779
Arabnia A, Akbardoost J, Cicero S, Torabi AR. Mixed Mode Fracture Investigation of Rock Specimens Containing Sharp V-Notches. Materials. 2022; 15(24):8779. https://doi.org/10.3390/ma15248779
Chicago/Turabian StyleArabnia, Ali, Javad Akbardoost, Sergio Cicero, and Ali Reza Torabi. 2022. "Mixed Mode Fracture Investigation of Rock Specimens Containing Sharp V-Notches" Materials 15, no. 24: 8779. https://doi.org/10.3390/ma15248779
APA StyleArabnia, A., Akbardoost, J., Cicero, S., & Torabi, A. R. (2022). Mixed Mode Fracture Investigation of Rock Specimens Containing Sharp V-Notches. Materials, 15(24), 8779. https://doi.org/10.3390/ma15248779







