Identification of Hyperelastic Material Parameters of Elastomers by Reverse Engineering Approach
Abstract
:1. Introduction
2. Experimental Study
2.1. Samples Configurations
2.1.1. Component Test Configurations
2.1.2. Coupon Test Configurations for Validation Study
2.2. Experimental Setup
2.2.1. Experimental Component Testing for Material Predictions and Validation Study
2.2.2. Experimental Coupon Testing for The Validation Study
3. Numerical Modelling
3.1. Traditional Approach to Determining Hyperelastic Material Parameter
3.2. ANN Approach to Determine Hyperelastic Material Parameter
3.2.1. Data Derivation
3.2.2. ANN Model Development
4. Results
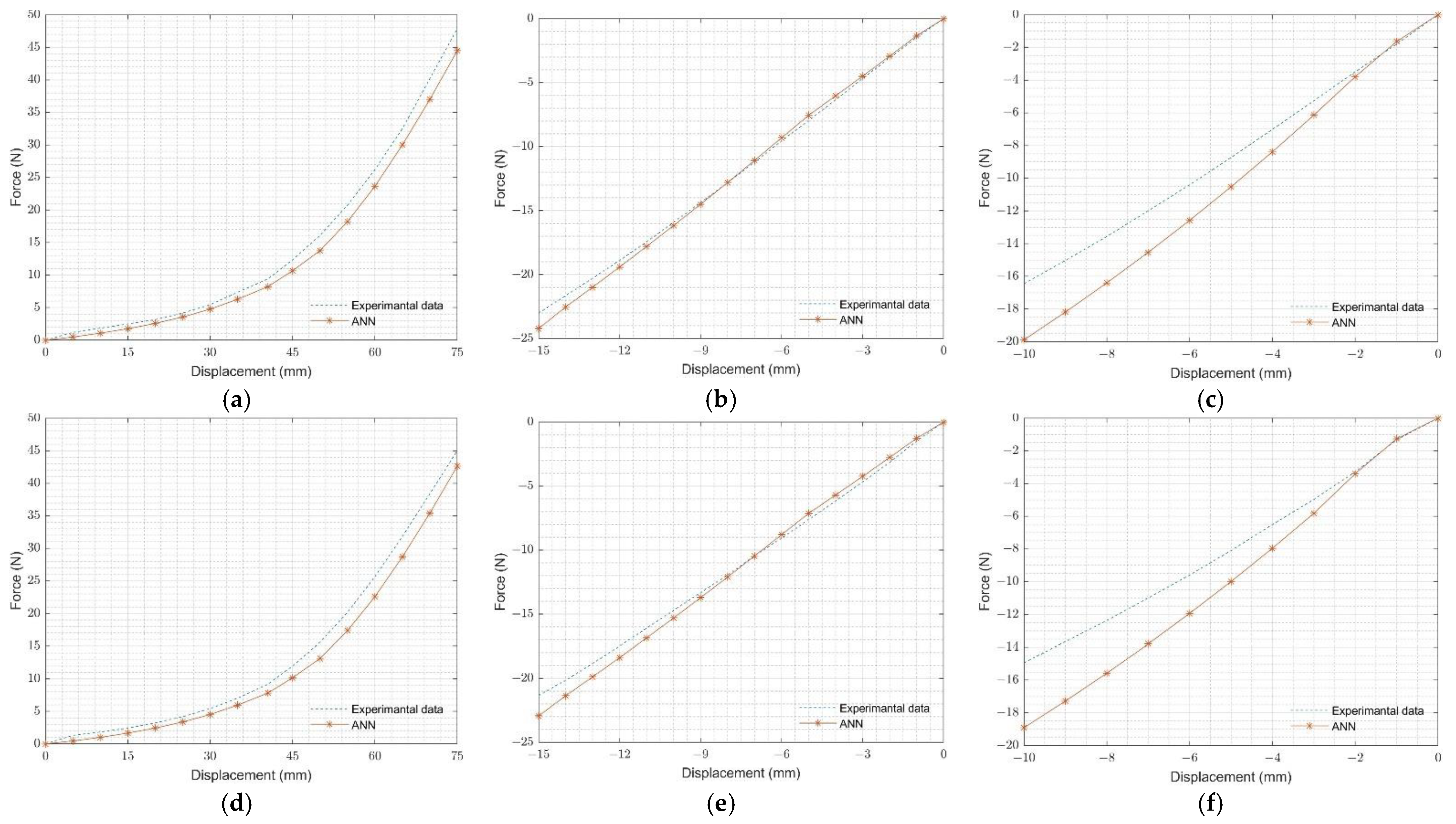
4.1. ANN Material Predictions
4.2. Testing of Ogden-2 Hyperelastic Material Parameters
4.3. Validation of Ogden-2 Hyperelastic Material Parameters
4.3.1. Validation of Component Test: O-Ring Multi-Contact
4.3.2. Validation of Coupon Test
4.4. Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, H.; Wan, Z.; Chen, X.; Wan, J.; Luo, L.; Zhang, H.; Shu, S.; Tu, Z. Temperature and humidity effect on aging of silicone rubbers as sealing materials for proton exchange membrane fuel cell applications. Appl. Therm. Eng. 2016, 104, 472–478. [Google Scholar] [CrossRef]
- Roland, C.M. Mechanical Behavior of Rubber at High Strain Rates. Rubber Chem. Technol. 2006, 79, 429–459. [Google Scholar] [CrossRef]
- Aleksey, D. Drozdov Viscoelastic Structures; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lakes, R. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gkouti, E.; Yenigun, B.; Czekanski, A. Transient Effects of Applying and Removing Strain on the Mechanical Behavior of Rubber. Materials 2020, 13, 4333. [Google Scholar] [CrossRef]
- Chaudhry, M.S.; Czekanski, A. Evaluating FDM Process Parameter Sensitive Mechanical Performance of Elastomers at Various Strain Rates of Loading. Materials 2020, 13, 3202. [Google Scholar] [CrossRef]
- Gkouti, E.; Yenigun, B.; Jankowski, K.; Czekanski, A. Experimental Study of Mullins Effect In Natural Rubber for Different Stretch Conditions. In Proceedings of the ASME Design Engineering Technical Conference, Virtual Conference, 17–19 August 2020; Volume 2. [Google Scholar]
- Iguez-Macedo, S.; Lostado-Lorza, R.; Escribano-García, R.; Ángeles, M. Finite Element Model Updating Combined with Multi-Response Optimization for Hyperelastic 4 Materials Characterization 5. Materials 2019, 12, 1019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef] [Green Version]
- Rivlin, R.S.; Saunders, D.W. Large elastic deformations of isotropic materials VII. Experiments on the deformation of rubber. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1951, 243, 251–288. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Hart-Smith, L.J. Elasticity parameters for finite deformations of rubber-like materials. Z. Für Angew. Math. Und Phys. ZAMP 1966, 17, 608–626. [Google Scholar] [CrossRef]
- Schweickert, E.; Mihai, L.A.; Martin, R.J.; Neff, P. A note on non-homogeneous deformations with homogeneous Cauchy stress for a strictly rank-one convex energy in isotropic hyperelasticity. Int. J. Non-linear Mech. 2019, 119, 103282. [Google Scholar] [CrossRef]
- Bergstrom, J.S. Mechanics of Solid Polymers Theory and Computational Modeling, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Liao, B.; Sun, B.; Yan, M.; Ren, Y.; Zhang, W.; Zhou, K. Time-Variant Reliability Analysis for Rubber O-Ring Seal Considering Both Material Degradation and Random Load. Materials 2017, 10, 1211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koeller, R.C. A Theory Relating Creep and Relaxation for Linear Materials With Memory. J. Appl. Mech. Trans. ASME 2010, 77, 031008. [Google Scholar] [CrossRef]
- Luo, R.; Lv, H.; Liu, H. Development of Prony series models based on continuous relaxation spectrums for relaxation moduli determined using creep tests. Constr. Build. Mater. 2018, 168, 758–770. [Google Scholar] [CrossRef]
- Przybylo, P.A.; Arruda, E.M. Experimental Investigations and Numerical Modeling of Incompressible Elastomers during Non-Homogeneous Deformations. Rubber Chem. Technol. 1998, 71, 730–749. [Google Scholar] [CrossRef]
- Boyce, M.C.; Arruda, E.M. Constitutive Models of Rubber Elasticity: A Review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Dassault Systèmes Abaqus 6.14 Online Documentation. Available online: http://130.149.89.49:2080/v6.14/books/usb/default.htm (accessed on 15 November 2022).
- Destrade, M.; Saccomandi, G.; Sgura, I. Methodical fitting for mathematical models of rubber-like materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160811. [Google Scholar] [CrossRef] [Green Version]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 2nd ed.; Oxford University Press: Oxford, UK, 1958. [Google Scholar]
- Barghamadi, M.; Ghoreishy, M.H.R.; Karrabi, M.; Mohammadian-Gezaz, S. Modeling of nonlinear hyper-viscoelastic and stress softening behaviors of acrylonitrile butadiene rubber/polyvinyl chloride nanocomposites reinforced by nanoclay and graphene. Polym. Compos. 2020, 42, 583–596. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. New numerical stress solutions to calibrate hyper-visco-pseudo-elastic material models effectively. Mater. Des. 2020, 194, 108861. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Guan, F.; Han, X.; Cao, L.; Shan, K. Identification of the visco-hyperelastic properties of brain white matter based on the combination of inverse method and experiment. Med. Biol. Eng. Comput. 2019, 57, 1109–1120. [Google Scholar] [CrossRef]
- Hou, J.; Lu, X.; Zhang, K.; Jing, Y.; Zhang, Z.; You, J.; Li, Q. Parameters Identification of Rubber-like Hyperelastic Material Based on General Regression Neural Network. Materials 2022, 15, 3776. [Google Scholar] [CrossRef]
- Ghoreishy, M.H.R.; Abbassi-Sourki, F. Nonlinear stress relaxation of filled rubber compounds: A new theoretical model and experimental investigation. J. Appl. Polym. Sci. 2020, 138, 49884. [Google Scholar] [CrossRef]
- Qi, Z.; Hu, N.; Li, G.; Zeng, D.; Su, X. Constitutive modeling for the elastic-viscoplastic behavior of high density polyethylene under cyclic loading. Int. J. Plast. 2018, 113, 125–144. [Google Scholar] [CrossRef]
- Kocáb, J.; Kottner, R.; Kossa, A. Characterization of a cork-rubber composite using advanced material models. Mater. Today: Proc. 2019, 12, 340–345. [Google Scholar] [CrossRef]
- Karim, M.R.; Zhang, Z.; Zhu, Y. Prediction of Nonlinear Viscoelastic Recovery of Thermoplastic Polymers Using Abaqus Parallel Rheological Framework (PRF) Model. In In Proceedings of the Science in the Age of Experience 2016, Boston, MA, USA, 23–27 May 2016. [Google Scholar]
- Ghoreishy, M.H.R.; Sourki, F.A. Development of a new combined numerical/experimental approach for the modeling of the nonlinear hyper-viscoelastic behavior of highly carbon black filled rubber compound. Polym. Test. 2018, 70, 135–143. [Google Scholar] [CrossRef]
- Wang, Y.; Marshall, K.L.; Baba, Y.; Lumpkin, E.A.; Gerling, G.J. Compressive Viscoelasticity of Freshly Excised Mouse Skin Is Dependent on Specimen Thickness, Strain Level and Rate. PLoS ONE 2015, 10, e0120897. [Google Scholar] [CrossRef]
- Tho, K.K.; Swaddiwudhipong, S.; Liu, Z.; Hua, J. Artificial neural network model for material characterization by indentation. Model. Simul. Mater. Sci. Eng. 2004, 12, 1055–1062. [Google Scholar] [CrossRef]
- Promma, N.; Raka, B.; Grédiac, M.; Toussaint, E.; Le Cam, J.-B.; Balandraud, X.; Hild, F. Application of the virtual fields method to mechanical characterization of elastomeric materials. Int. J. Solids Struct. 2009, 46, 698–715. [Google Scholar] [CrossRef]
- Román, A.J.; Qin, S.; Rodríguez, J.C.; González, L.D.; Zavala, V.M.; Osswald, T.A. Natural Rubber Blend Optimization via Data-Driven Modeling: The Implementation for Reverse Engineering. Polymers 2022, 14, 2262. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Hou, X.; Xiang, Q.; Xiao, F. Viscosity Prediction of Rubberized Asphalt–Rejuvenated Recycled Asphalt Pavement Binders Using Artificial Neural Network Approach. J. Mater. Civ. Eng. 2021, 33, 04021071. [Google Scholar] [CrossRef]
- Yenigun, B.; Kilickap, E. Prediction of the Tensile Load of Drilled CFRP by Artificial Neural Network. Appl. Sci. 2018, 8, 549. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, H.; Wang, Y.; Jiang, T.; Jiang, H. Predicting Nonlinear and Anisotropic Mechanics of Metal Rubber Using a Combination of Constitutive Modeling, Machine Learning, and Finite Element Analysis. Materials 2021, 14, 5200. [Google Scholar] [CrossRef] [PubMed]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties fromspherical indentation data using neural networks. Part i:the case of pure kinematic hardening in plasticity laws. J. Mech. Phys. Solids 1999, 47, 1569–1588. [Google Scholar] [CrossRef]
- Tyulyukovskiy, E.; Huber, N. Identification of viscoplastic material parameters from spherical indentation data: Part I. Neural networks. J. Mater. Res. 2006, 21, 664–676. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. A neural network tool for identifying the material parameters of a finite deformation viscoplasticity model with static recovery. Comput. Methods Appl. Mech. Eng. 2001, 191, 353–384. [Google Scholar] [CrossRef]
- Muliana, A.; Haj-Ali, R.M.; Steward, R.; Saxena, A. Artificial neural network and finite element modeling of nanoindentation tests. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2002, 33, 1939–1947. [Google Scholar] [CrossRef]
- Iliescu, D.; Gehin, D.; Gutierrez, M.; Girot, F. Modeling and tool wear in drilling of CFRP. Int. J. Mach. Tools Manuf. 2010, 50, 204–213. [Google Scholar] [CrossRef]
- Li, H.; Rong, L.; Zong, C.; Zhang, G. A numerical study on forced convective heat transfer of a chicken (model) in horizontal airflow. Biosyst. Eng. 2016, 150, 151–159. [Google Scholar] [CrossRef]
- Lee, H.; Huen, W.Y.; Vimonsatit, V.; Mendis, P. An Investigation of Nanomechanical Properties of Materials using Nanoindentation and Artificial Neural Network. Sci. Rep. 2019, 9, 13189. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Dao, M.; Kumar, P.; Ramamurty, U.; Karniadakis, G.E.; Suresh, S. Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proc. Natl. Acad. Sci. USA 2020, 117, 7052–7062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pham, T.T.; Woo, C.; Choi, S.; Min, J.; Beomkeun, K. Development of Hyperelastic Model for Butadiene Rubber Using a Neural Network. Elastomers Compos. 2021, 56, 79–84. [Google Scholar] [CrossRef]
- Pierron, F.; Grédiac, M. The Virtual Fields Method; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Grédiac, M.; Pierron, F. Applying the Virtual Fields Method to the identification of elasto-plastic constitutive parameters. Int. J. Plast. 2006, 22, 602–627. [Google Scholar] [CrossRef]
- Bastos, G.; Sales, L.; Di Cesare, N.; Tayeb, A.; Le Cam, J.-B. Inverse-Pagerank-particle swarm optimisation for inverse identification of hyperelastic models: A feasibility study. J. Rubber Res. 2021, 24, 447–460. [Google Scholar] [CrossRef]
- Tayeb, A.; Le Cam, J.B.; Grédiac, M.; Toussaint, E.; Robin, E.; Balandraud, X.; Canévet, F. Identifying hyperelastic constitutive parameters with sensitivity-based virtual fields. Strain 2021, 57, 12397. [Google Scholar] [CrossRef]
- Johlitz, M.; Diebels, S. Characterisation of a polymer using biaxial tension tests. Part I: Hyperelasticity. Arch. Appl. Mech. 2010, 81, 1333–1349. [Google Scholar] [CrossRef]
- Yenigun, B.; Gkouti, E.; Czekanski, A.; Barbaraci, G.; Jankowski, K. Comparison of Elasto-Mechanical Behavior of Rubbers. In Proceedings of the CSME, Sherbrooke, QC, Canada, 2–4 May 2020. [Google Scholar] [CrossRef]
- Esmail, J.F.; Mohamedmeki, M.Z.; Ajeel, A.E. Using the uniaxial tension test to satisfy the hyperelastic material simulation in ABAQUS. IOP Conf. Series: Mater. Sci. Eng. 2020, 888, 2065. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.B.; Lee, J.; Cho, S.; Park, H.; Yeom, S.; Park, S.H. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012, 13, 759–764. [Google Scholar] [CrossRef]
- WELSIM-Finite Element Analysis Solutions No Title. Available online: https://getwelsim.medium.com/ogden-hyperelastic-model-for-nonlinear-finite-element-analysis-df9518de3b48# (accessed on 24 May 2022).
- Liu, Y.; Qian, L.; Zou, J.; Xia, C.; Lian, Z. Study on failure mechanism and sealing performance optimization of compression packer. Eng. Fail. Anal. 2022, 136, 106176. [Google Scholar] [CrossRef]
- Deladi, E.; de Rooij, M.; Schipper, D. Modelling of static friction in rubber–metal contact. Tribol. Int. 2007, 40, 588–594. [Google Scholar] [CrossRef]
- Gómez, M.C.; Gallardo-Hernández, E.; Torres, M.V.; Bautista, A.P. Rubber steel friction in contaminated contacts. Wear 2013, 302, 1421–1425. [Google Scholar] [CrossRef]
- Rosa, A.G.D.A.; Ii, I.; Moreto, J.A.; Manfrinato, M.D.; Rossino, L.S. Study on friction and wear behavior of SAE 1045 steel, reinforced nylon 6.6 and NBR rubber used in clutch disks. Mater. Res. 2014, 17, 1397–1403. [Google Scholar] [CrossRef]








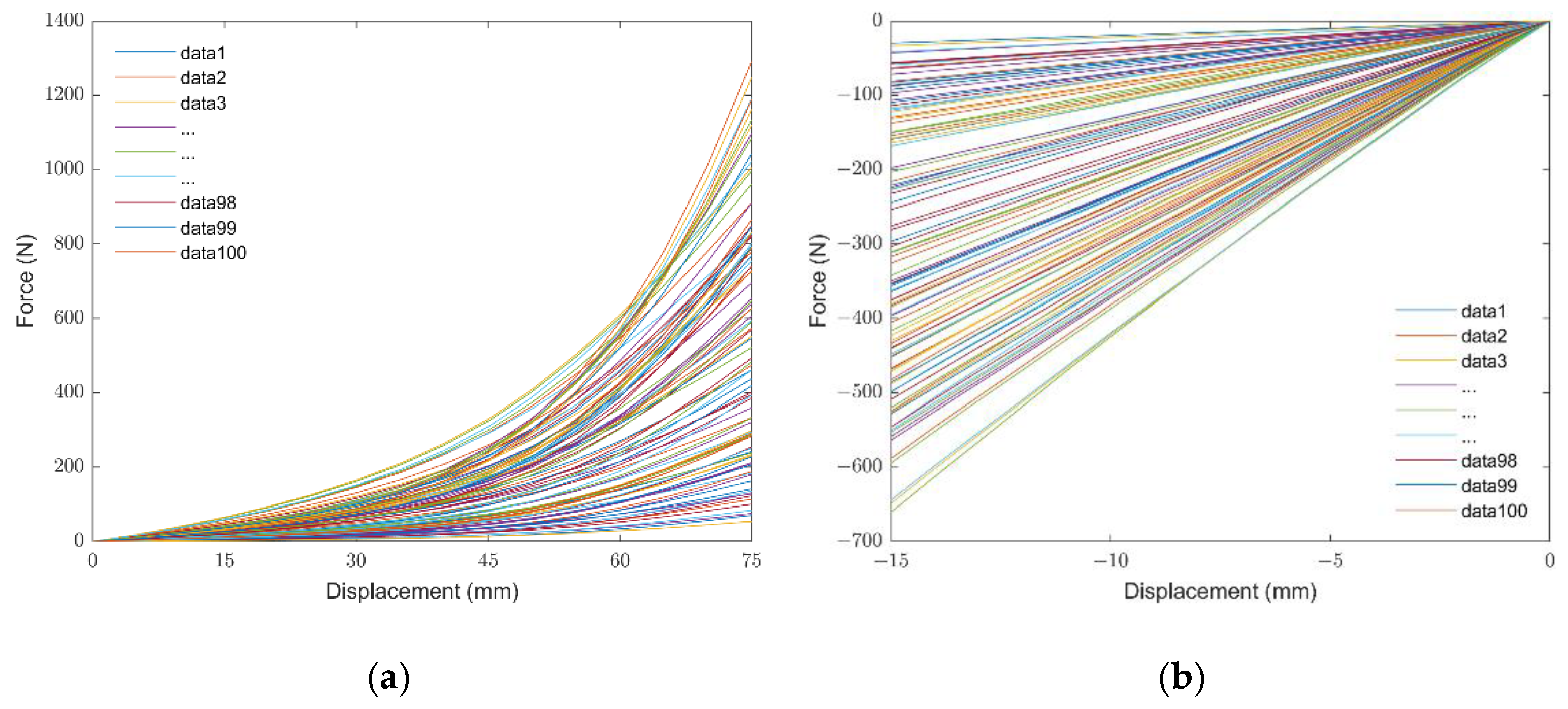
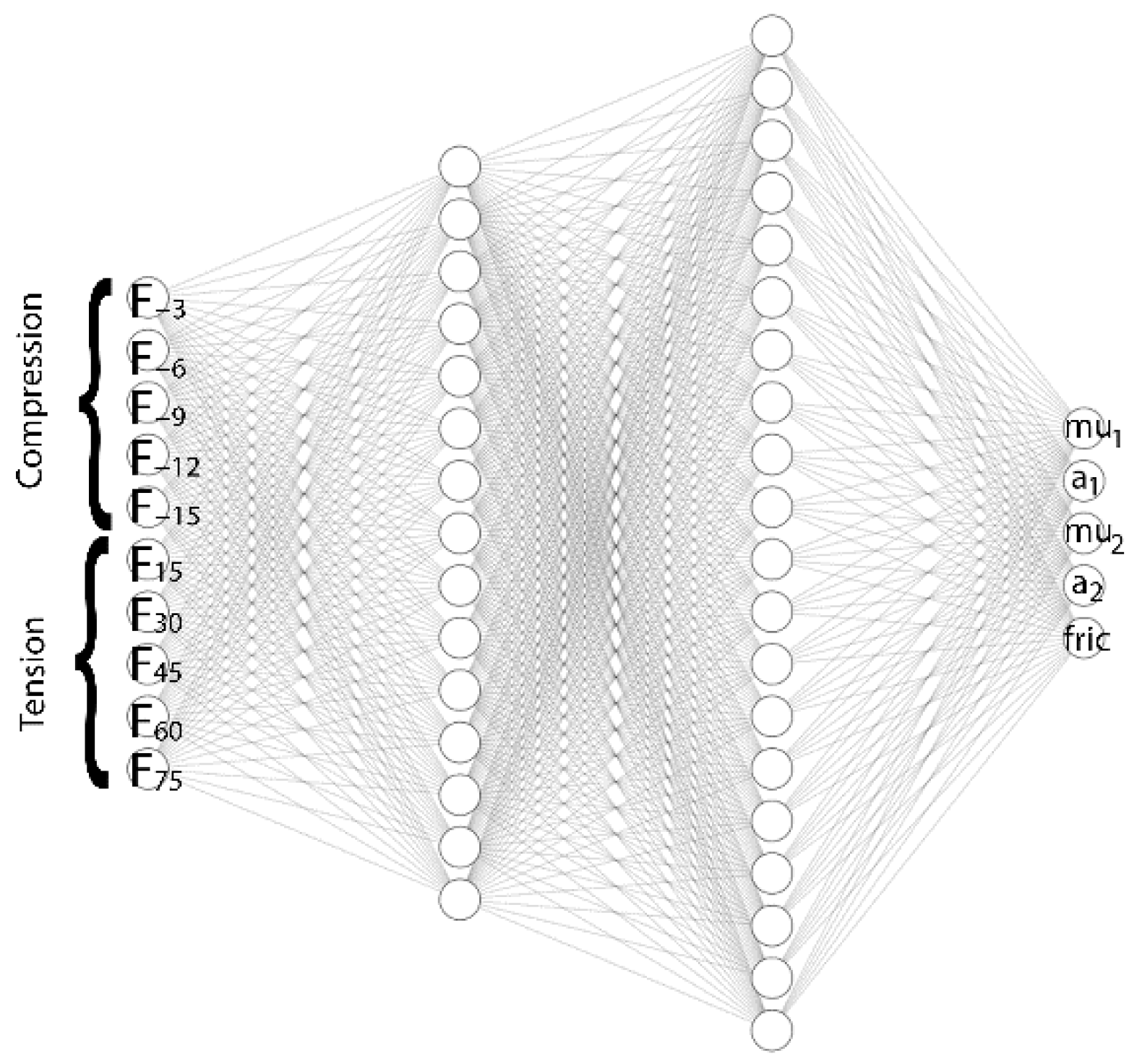
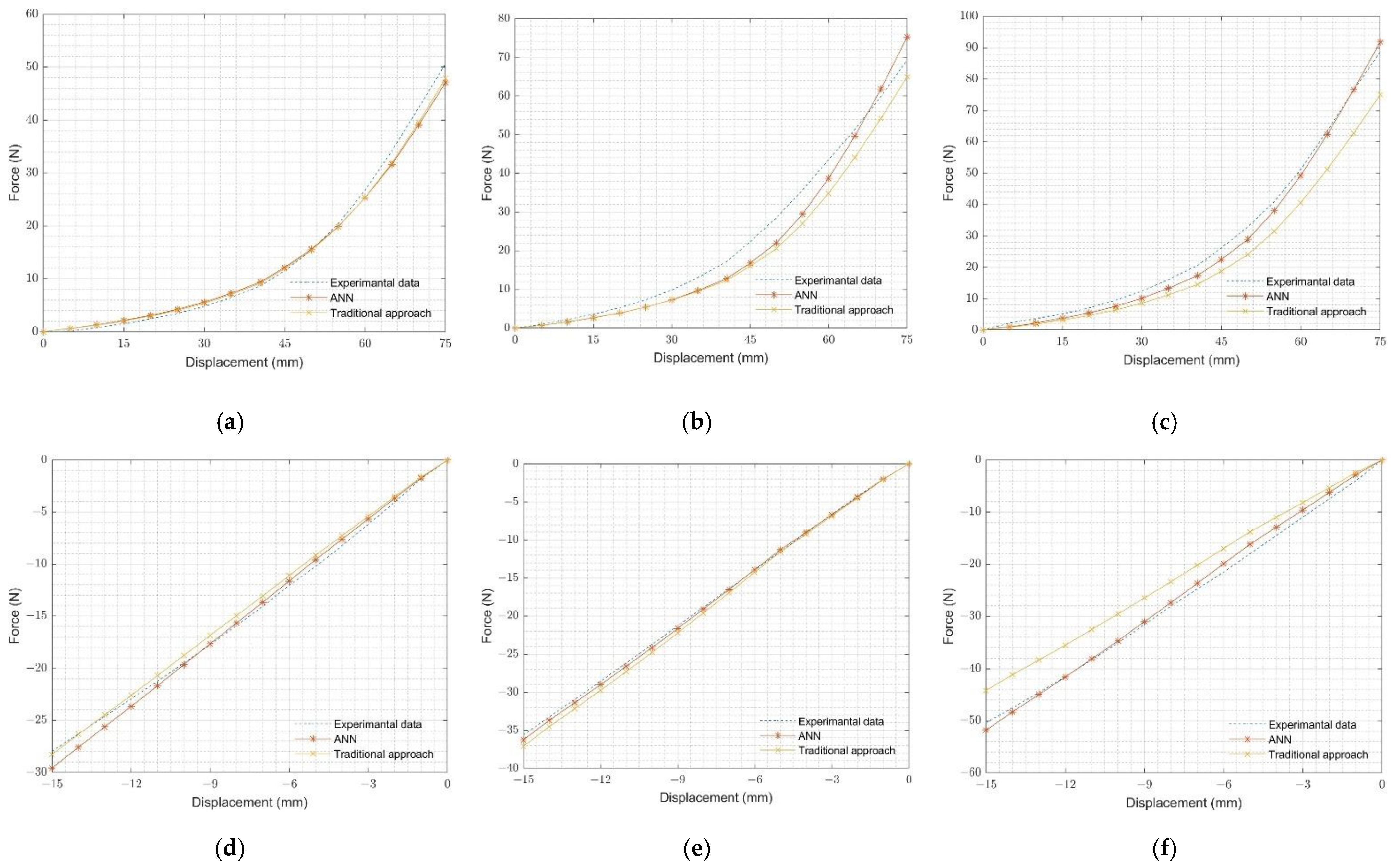
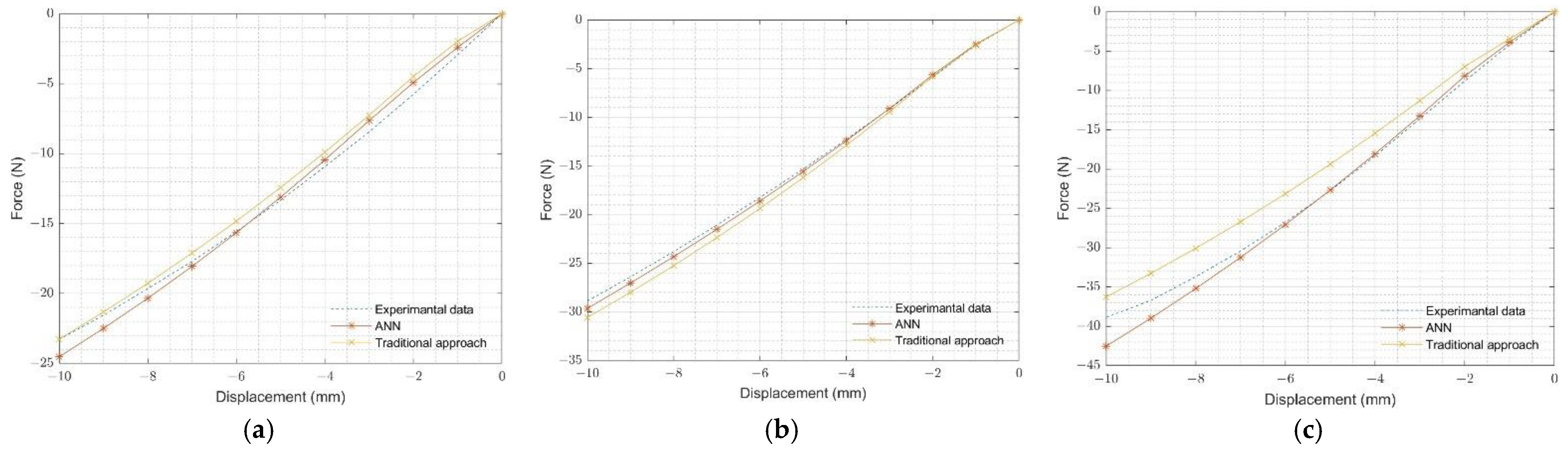

| Data Number | Alpha1 | Mu1 | Alpha2 | Mu2 | Friction |
|---|---|---|---|---|---|
| 1 | 1.5540 | 2.1625 | 2.9479 | −4.1510 | 1.8134 |
| 2 | 1.5422 | 4.3829 | 5.8699 | −5.9271 | 0.0443 |
| 3 | 1.4168 | 3.5313 | 4.7432 | −6.0336 | 1.1834 |
| . | . | . | . | . | . |
| . | . | . | . | . | . |
| . | . | . | . | . | . |
| 50 | 0.814 | 5.747 | 7.757 | −6.404 | 0.889 |
| 51 | 0.553 | 9.692 | 4.545 | 4.358 | 0.950 |
| . | . | . | . | . | . |
| . | . | . | . | . | . |
| . | . | . | . | . | . |
| 99 | 0.9865 | 8.1362 | 7.2496 | 1.5037 | 1.0994 |
| 100 | 0.2656 | 5.5092 | 4.5852 | 2.8785 | 1.0216 |
| Parameter | Value |
|---|---|
| Input layer size | 10 |
| Hidden layer1 size | 15 |
| Hidden layer2 size | 20 |
| Output layer size | 5 |
| Activation function | tansig |
| Backpropagation algorithm | Levenberg–Marquardt |
| Data ratio | %70 training, %15 validation, %15 testing |
| Parameters | Natural Rubber | Silicone Rubber | Neoprene Rubber | |||
|---|---|---|---|---|---|---|
| Traditional | ANN | Traditional | ANN | Traditional | ANN | |
| alpha1 | 0.2526 | 0.2422 | 0.6793 | 0.3701 | 0.0292 | 0.2427 |
| mu1 | 3.8250 | 4.9068 | 1.1441 | 2.0343 | 1.4824 | 3.6534 |
| alpha2 | 0.4098 | 0.4102 | 0.1117 | 0.5590 | 0.4833 | 0.2913 |
| mu2 | −0.3865 | 4.8452 | 1.1440 | 2.0467 | 1.4970 | 0.6877 |
| friction | - | 0.7465 | - | 0.8534 | - | 0.7538 |
| Parameters | ANN 50 °C | ANN 80 °C |
|---|---|---|
| alpha1 | 0.2913 | 0.2940 |
| mu1 | 3.5942 | 3.7996 |
| alpha2 | 0.1430 | 0.1159 |
| mu2 | −0.0340 | −0.4132 |
| friction | 0.7513 | 0.8013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yenigun, B.; Gkouti, E.; Barbaraci, G.; Czekanski, A. Identification of Hyperelastic Material Parameters of Elastomers by Reverse Engineering Approach. Materials 2022, 15, 8810. https://doi.org/10.3390/ma15248810
Yenigun B, Gkouti E, Barbaraci G, Czekanski A. Identification of Hyperelastic Material Parameters of Elastomers by Reverse Engineering Approach. Materials. 2022; 15(24):8810. https://doi.org/10.3390/ma15248810
Chicago/Turabian StyleYenigun, Burak, Elli Gkouti, Gabriele Barbaraci, and Aleksander Czekanski. 2022. "Identification of Hyperelastic Material Parameters of Elastomers by Reverse Engineering Approach" Materials 15, no. 24: 8810. https://doi.org/10.3390/ma15248810
APA StyleYenigun, B., Gkouti, E., Barbaraci, G., & Czekanski, A. (2022). Identification of Hyperelastic Material Parameters of Elastomers by Reverse Engineering Approach. Materials, 15(24), 8810. https://doi.org/10.3390/ma15248810






