1. Introduction
Laser beam machining (LBM) is a widely used energy-based non-contact advanced machining process which may be applied to a wide variety of materials. The performance of cutting quality can be improved considerably via an appropriate selection of a laser and operating parameters. Dubey and Yadava reviewed many studies focusing on the development and application of laser beam cutting technology [
1].
Nd: YAG laser has less reflection on metal surfaces because of its shorter wavelength, and its high absorptivity enables it to process more reflective materials with relatively less laser energy. However, pulsed Nd: YAG laser produces high laser beam intensity, low mean beam power, narrow heat-affected zone (HAZ), and small recast layer in cutting applications with a high peak power or a shorter interaction time [
2,
3].
Grey relational analysis (GRA) is an important technique for making predictions and decisions effectively in various manufacturing and product processing areas. Anup Malik et al. [
4] used GRA to optimize the input process parameters of the laser-assisted jet electrochemical machining (LA-JECM) and improve machining performance. Taguchi’s method-based design of experiment with L
16 (4
4) orthogonal array was employed in the experiments. The optimal parametric combination for multi-response optimization was identified based on the collective implementation of the Taguchi methodology and GRA during the micro-drilling of Inconel-718. Thus, LA-JECM was developed and used in subsequent experimental investigation [
4].
In laser material processing (LMP), the heat-affected zone (HAZ) of the material occurs when it is subjected to long-duration or high-energy laser exposure. This, in turn, affects the quality of drilling when the laser processing time is insufficient. However, a longer processing time results in a large HAZ and other effects [
5]. When the laser energy is too high (e.g., when it starts burning black spots on the material), an acrylic (PMMA) [
6] plate target can expand rapidly and undergo undesirable modifications, such as crazing. The parameters associated with laser processing, their effects on the HAZ, surface roughness and the depth, width, and shape of the drilled hole have been investigated [
5].
Since laser beam machining (LBM) had no effects on tool wear and cutting force or vibrations during cutting, laser beam drilling has been proposed as an alternative to improving traditional drilling [
7]. In one study, variance analysis was used to investigate the impact of scanning speed and frequency on macro-geometric parameters, surface quality, and defects (tapers and heat-affected zones). Moreover, to identify drilling wall problems, stereoscopic optical microscopes (SOMs) and scanning electron microscopes (SEMs) were used. This experimental method revealed the conditions to minimize deviations, defects, and damage in hole drilling [
7].
The theory of roundness is an important concept in many engineering fields. The relevant roundness parameters are defined in the ISO 12181-1 [
8] and used as standard filters in the ISO 12181-2 [
9]. When determining a roundness profile for the cross-sections of large flexible rotors, such as paper machine rolls, several conditions can restrict the available roundness measurement methods. Rotors may be too large to be placed onto precision spindles, and, under rotation, the cross-sections’ center point movement can be unpredictable and unrepeatable [
9]. When using a multi-probe roundness measurement frame position, the resulting error may cause the angle of the entire probe to deviate from the target angle. In fact, the angle of the probe can be accurately determined by its cross-correlation after being placed in the measurement frame [
10]. Determining the center point coordinates and the roundness error is essentially a problem with three degrees of freedom. Thus, they have to be measured by at least three probes to become independent. Measurement with one probe is sufficient only when the measurements are performed on a precision spindle with a roundness measuring instrument or in a coordinate measuring machine [
11].
K. Pratap Singh et al. [
12] conducted L
9 orthogonal array-based experiments. Since then, hole circularity and taper angle have been measured for L
9 with different combinations of input laser drilling parameters. Furthermore, the Taguchi optimization technique has been implemented for hole circularity and taper angle, and the non-uniform dimensioning hole has been employed due to the converging-diverging nature of the laser beam. Hence, a lower value of the taper angle gives better hole circularity [
12].
Pan LK et al. [
13] demonstrated that a hybrid approach combining the Taguchi method and principal component analysis can be applied to laser beam cutting to optimize input parameters and their influence on multiple quality characteristics. Among them, the GRA proposed by Deng [
14] in 1989 is one of the foremost techniques applied when the nature of information is incomplete and uncertain. As implied by its name, GRA can effectively optimize complex interrelationships. It has been widely used in evaluating available information and complex projects [
13].
Li et al. [
15] employed Taguchi’s method and applied a complicated score transformation to transfer six cutting-quality characteristics of each experiment into a single cutting-quality score. However, the transferred equations could not easily indicate the importance of each required quality in the experiments. Therefore, Tsai et al. [
16] employed a Taguchi’s method-based GRA approach to directly integrate six laser-cutting quality characteristics of each experiment into a grey relational grade (GRG). The actual cutting results could be immediately known by the obtained grades [
16].
Kumar Singh Yadav et al. [
17] presented an experimental study and a machining parameter design of electro-discharge diamond grinding (EDDG). The EDDG setup was designed and fabricated, and the experiments were conducted on high-speed steel (HSS) workpieces under varying currents, pulse-on time, duty factor, and wheel speed. The settings of the machining parameters were determined using the Taguchi experimental design method [
17].
Das et al. [
18] proposed a Taguchi-Based grey relational analytical method to determine the optimal processing parameters of Ti6Al4V. The machining forces, including longitudinal force (F
x), radial force (F
y), tangential force (F
z), surface roughness, and material removal rate (MRR), were measured during the facing operation. The effects of three process parameters, including cutting speed, tool feed, and cutting depth, were studied on the matching responses. The orthogonal design of the experiment (Taguchi L
9) was adopted to execute the process parameters at each level. The GRA optimization approach was applied to validate the process output parameters. It was found that the hardness of Ti6Al4V MMC was 59.4 HRA and the composition of the material remained the same after the milling operation [
18].
C. Sarala Rubi et al. [
19] investigated the effects of machining parameters during the drilling of LM 6/B4C composite materials. The optimization process aimed to attain the lowest thrust force (TF), surface roughness (SR), and burr height (BH). The feed rate (F), the spindle speed (S), the drill material (D), and the reinforcing percentage (R) were determined. Finally, the predicted GRG was 0.846, whereas the experimental GRG was 0.865, with a 2.2% error indicating that the optimization process was valid [
19].
Due to the localized and non-contact process, the use of lasers for cutting material can result in precise cuts with a small heat-affected zone (HAZ). One study used GRA to determine a single optimized set of cutting parameters for three different thermoplastics. The optimized processing parameters were found at low laser power (200 W), high cutting speed (0.4 m/min), and low compressed air pressure (2.5 bar) [
20].
Prasanth Achuthamenon Sylajakumari et al. [
21] studied the optimization of wear parameters using the Taguchi method with grey relational analysis and their effect on dry sliding wear performance of AA6063/SiC co-continuous composite. A Taguchi L
9 orthogonal array was designed, and nine experimental runs were performed based on the planned experiments. The confirmation experiments conducted using the optimal parameters indicated an improvement in quality [
21].
A new optimization strategy was used to investigate the effects of processing parameters and cryogenic treatment on cutting force and surface roughness in the milling of Ti6AI4V alloy, and it was proposed to simultaneously optimize the response parameters by EKİCİ, E. et al. The effects of cutting speed, feed rate, and the treatments applied to the tools were evaluated using the Taguchi method and grey relational analysis. The control factors in the experiments performed under dry cutting conditions were based on two different cutting speeds and three different feed rates and tool properties. It was observed that the cutting force values decreased with increased cutting speed and significantly increased parallel to the feed rate. In terms of surface roughness, they were observed to change based on the cutting parameters. The optimal machining conditions were determined as A1B3C2 after the grey relational analysis was performed on both responses [
22].
GRA-based Taguchi methods for the optimization of submerged arc welding (SAW) process parameters in hardfacing were adopted to solve the SAW process with multiple weld qualities in one study. A grey relational analysis was used for the multiple characteristic optimization. Then, the optimal process parameters were determined [
23].
The research by Md. Nahid Pervez et al. [
24] investigated the influence and optimization of the factors for a non-formaldehyde resin finishing process on cotton fabric using a Taguchi-based grey relational analysis. An L
27 orthogonal array was selected for five parameters with three levels by applying Taguchi’s design of experiments. The Taguchi technique was coupled with a grey relational analysis to obtain a GRG for evaluating multiple responses. The results showed an improved thermal stability and confirmed the presence of well-deposited resin on the optimized fabric surface [
24].
Wanqin Zhao et al. [
25] compared the results of micro-deep hole drilling by picosecond ultra-short pulse laser in four metals, including copper, aluminum alloy, titanium alloy, and nickel alloy. Destructive testing was performed to measure the depth, shape, and side-wall morphology of the micro-deep holes. The diameters and depths of the micro-deep holes in the four metals ablated using the same processing parameters were compared. The influence mechanisms, especially the side-wall morphology, such as the thresholds, conical emission, self-cleaning effect, physical properties of metals, energy transmission, plasma effect, and thermochemical reaction, were discussed. [
25].
In the studies by Pu et al. [
26], the effects and optimization of laser power, spindle speed, feed rate, and cutting depth on surface roughness and work hardening of LAM Si3N4 were systematically studied by using grey relational analysis coupled with the Taguchi method. The results showed that the combination of machining parameters determined the material removal mode at the material removal location, and this then affected the surface quality [
26].
An analysis of the GRG in one study indicates that the parameter significance and the optimal parameter combination for a laser-cutting process can be identified. The analytical results from two confirmation experiments using the optimal parameters confirmed that the laser-cutting technology could be effectively applied to cut substrates into special shapes [
27].
Laser drilling has swiftly become an economical and well-regulated substitute for conventional hole drilling methods. The circularity of drilled holes at the entry and exit and the taper are very important attributes that influence the quality of a drilled hole by a laser beam. For this reason, an experimentation based on central composite design was performed on austenitic stainless steel to examine the effect of laser parameters, such as lamp current, pulse frequency, gas pressure, and pulse width, on the quality of drilled holes [
28].
The experimental parameters and their levels were tested in the study by Gonfa et al. [
29] at three different stirring speeds (350, 450, and 550 rpm), three different stirring times (5, 10, and 15 min), three different weight percentages of SiC (0, 5, 10 wt.%) and three different weight percentages of MoS2 (0, 2, 4 wt.%). Nine samples were fabricated by stir casting using the Taguchi method L
9 orthogonal arrays. Composite hardness, tensile strength, and wear rate were investigated using Taguchi’s signal-to-noise ratio as a single response characteristic, and hybrid Taguchi–grey relational analysis (HTGRA) was used to study and analyze them as a multi-response characteristic. The results revealed that the addition of SiC in the composite produced better hardness, tensile strength, and wear rate [
29]. Tsai et al. presented Optimization of laser-cutting parameters for QFN packages by utilizing artificial neural networks and genetic algorithm [
30]. A more detailed cutting quality can be predicted by using the proposed method.
Laser material processing (LMP) is used to replace traditional material processing techniques, such as material cutting, thin plate drilling, and surface processing. The early laser plasma is used as a cleaning material and the Raman spectroscopy is used for material identification. Laser plasma is produced when a high-energy laser beam meets matter, leading to a rapid increase in the temperature of the material. The energy of a pulsed laser can be varied to alter the cavity gap created by the laser plasma. The working distance is set to a value to obtain a negative drill-hole divergence angle. The characteristics of the laser plasma can be varied by changing the laser energy, thereby broadening its potential applications. A 3-mm-thick, optical-grade acrylic (PMMA) plate was drilled using a neodymium-doped yttrium aluminum garnet (Nd: YAG) pulse laser in one study, and the plasma effect between the focusing position offset and taper were investigated [
5]. In this study, the Nd: YAG pulse laser, including a self-designed optical alignment system, was used for drilling an acrylic (PMMA) plate of high optical density grade. The highlight of the current work is described below. The laser plasma generated by the Nd: YAG pulse laser can produce a cavity gap located on the focusing position of the acrylic (PMMA) plate so that the taper angle and the divergence angle can be easily distinguished. Nine sets of experiments were performed by using the Taguchi method with orthogonal arrays in L
9(3
4). The experimental results with multiple quality characteristics are measured and used to optimize the control factors by using GRA with equal weighting factors of four qualities to find the best quality processing parameters.
2. Materials and Laboratory Tools
In this study, we used an acrylic or poly (methyl methacrylate) PMMA plate (Model P5P05) with Laser Safe Flat Window and Visible Light Transmission (VLT) by LASERVISION [
6], which is an optical grade safety window 7+ with high optical density (OD) and a thickness of 3 mm. The PMMA plate is lightweight, easy to fabricate, and has high chemical stability and mechanical strength [
6].
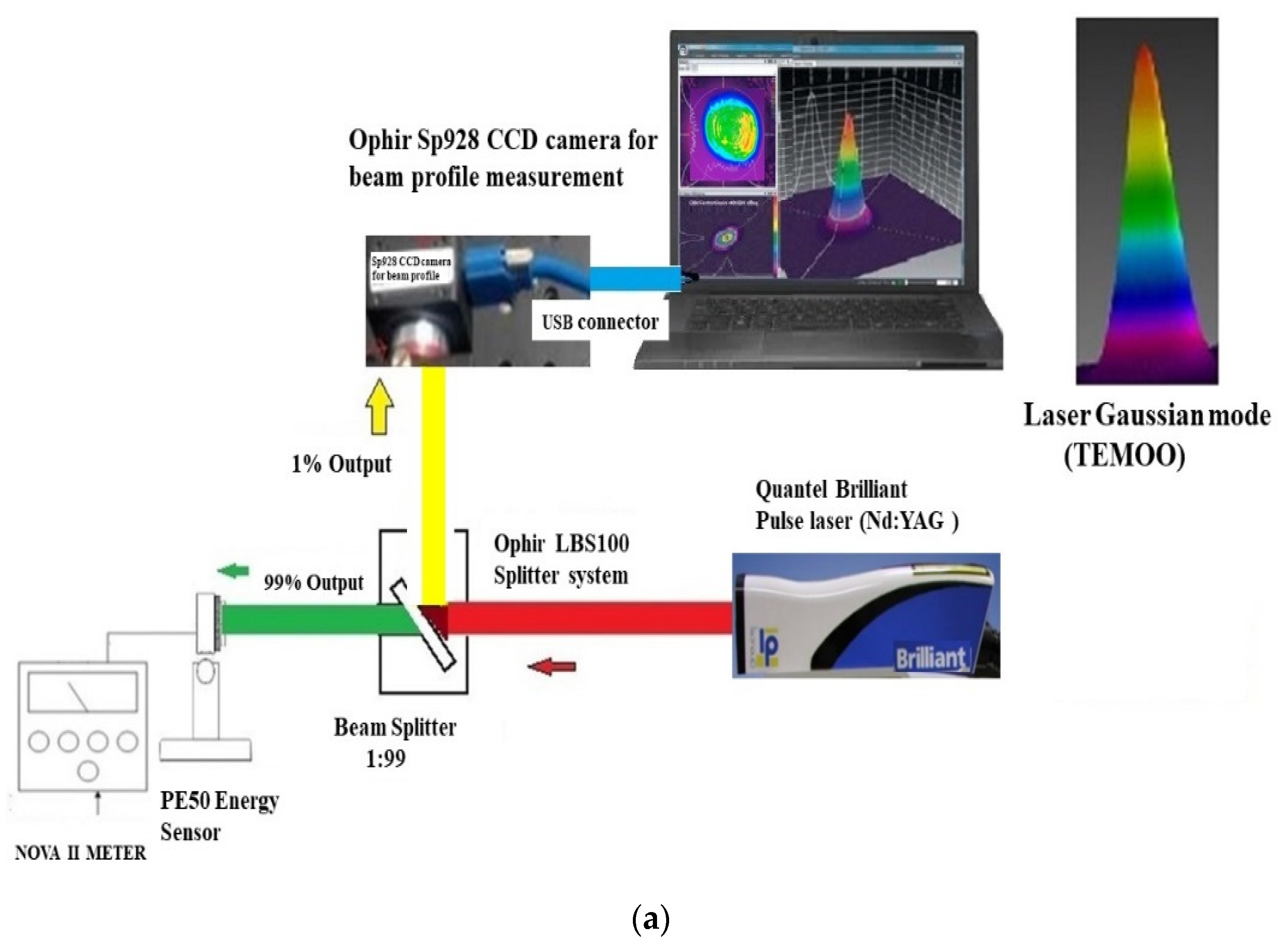
A Nd: YAG pulse laser (Quantel Brilliant [
31]), which has a maximum energy of 360 mJ per pulse, was designed to drill the PMMA plate. The used beam splitter (Ophir LBS-100) has a ratio of 1%:99% [
32]. About 99% of the laser energy is split for the laser energy measurement by an energy sensor (Ophir PE50BB-DIF [
32]) and a display meter (Ophir NOVAII) [
32]. The other 1% of the laser energy is used for the beam profile measurement using a CCD (Ophir SP928 [
32]), which is connected to a computer through a USB interface, as shown in
Figure 1a. The laser beam profile with an approximate Gaussian mode (TEM 00 mode) was confirmed using the Ophir BeamGage software [
33].
To avoid measurement uncertainty due to unstable power, a laser power meter was used to measure power stability in which the laser power was set at 1.053 W and measured for one hour. As shown in
Table 1, the result shows a stability of 5.6%, making it an effective method. The comprehensive specifications of the used Nd: YAG laser are shown in
Table 1.
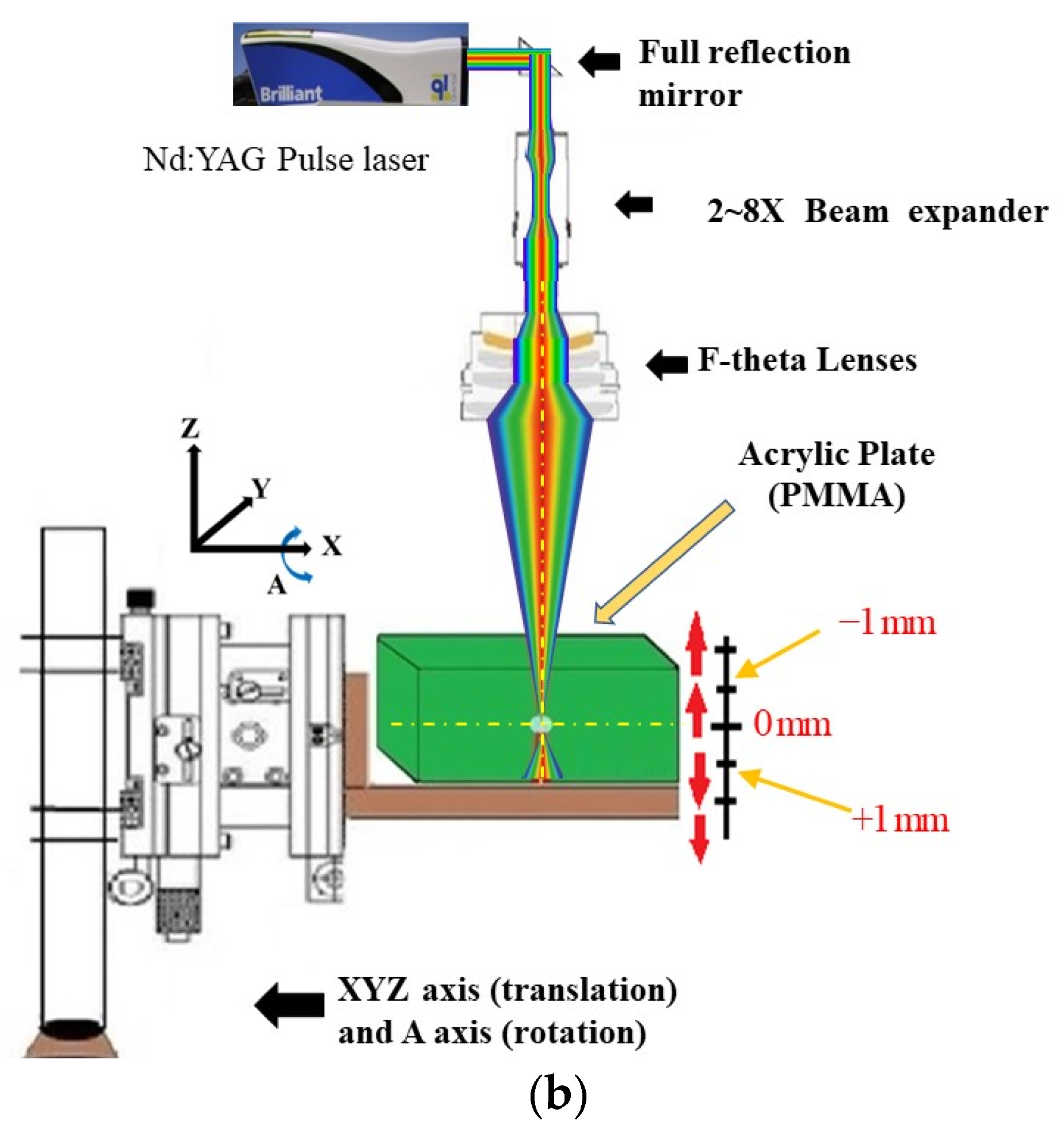
The laser’s light source is a high-energy pulse laser (145.0 mJ/pulse, generating 3000 pulses in 7 min). The energy density per pulse produced is 522.98 J/cm
2. In the system setup, a beam expander (LINOS Model: 4401-256-000-20 [
34]) and an F-theta lens (LINOS Model: 4401-508-000-26 [
35]) are combined to adjust the laser beam shape with a spot size of a 0.2 mm diameter, as shown in
Figure 1b. It is necessary to make sure that the incident beam is focused on the center of the F-theta lenses. A motorized XYZ and rotation stage is used to carry the drilled PMMA plate. Finally, the focusing position of the laser beam is located at the center of the PMMA plate with thickness of 3 mm. During the experiment, the Z-axis can be adjusted forwardly and backwardly to obtain and focus offset. The schematic of the laser beam alignment and focusing position adjustment is shown in
Figure 1b.
The Taguchi method with orthogonal arrays and GRA were employed to find the controlled parameters for the best drilling quality. The main four control factors discussed in this study are laser pulse energy (A), focusing position offset (B), drilling time (C), and repetition rate (D). Each factor has three levels (Level 1, Level 2, and Level 3), which are shown in
Table 2. Factor A (laser energy) has three levels: 75, 110, and 145 (mJ/pulse). Factor B (focusing position offset) may be (−1 mm), (0 mm), or (+1 mm) from the center of the PMMA plate. Factor C (drilling time) may be set as 3 min, 5 min, and 7 min. Factor D (repetition rate) may be set as 1.8 kHz, 3.0 kHz, and 4.2 kHz. The definition of the terms and measurement methods will be described in the next section. These control factors of the orthogonal arrays were used to optimize performance characteristics related to laser drilling on the PMMA plate, which included roundness, hillock width, taper, and HAZ qualities.
It has been shown that limiting laser energy to between 75 and 145 mJ/pulse can avoid the phenomenon of excessive HAZ caused by high energy and low drilling quality caused by low energy. The focusing position offset between +1 and −1 mm is suitable for observing taper and can narrow the range in factor design [
5].
When applying the Taguchi-based experiment design of L
9 (3
4), there are nine experiments (runs) to be conducted with the parameters shown in
Table 3. After the experiments have been conducted, the obtained experimental results with multiple quality characteristics are used to optimize the control factors by using GRA with equal weighting of the four qualities.