Evaluation of the Fracture Toughness KIc for Selected Magnetron Sputtering Coatings by Using the Laugier Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Samples
2.2. Mechanical Properties of Prepared Samples
2.3. The Fracture Toughness by the Laugier Model
3. Results
3.1. The TiBW and TiBCr Coatings Characterization
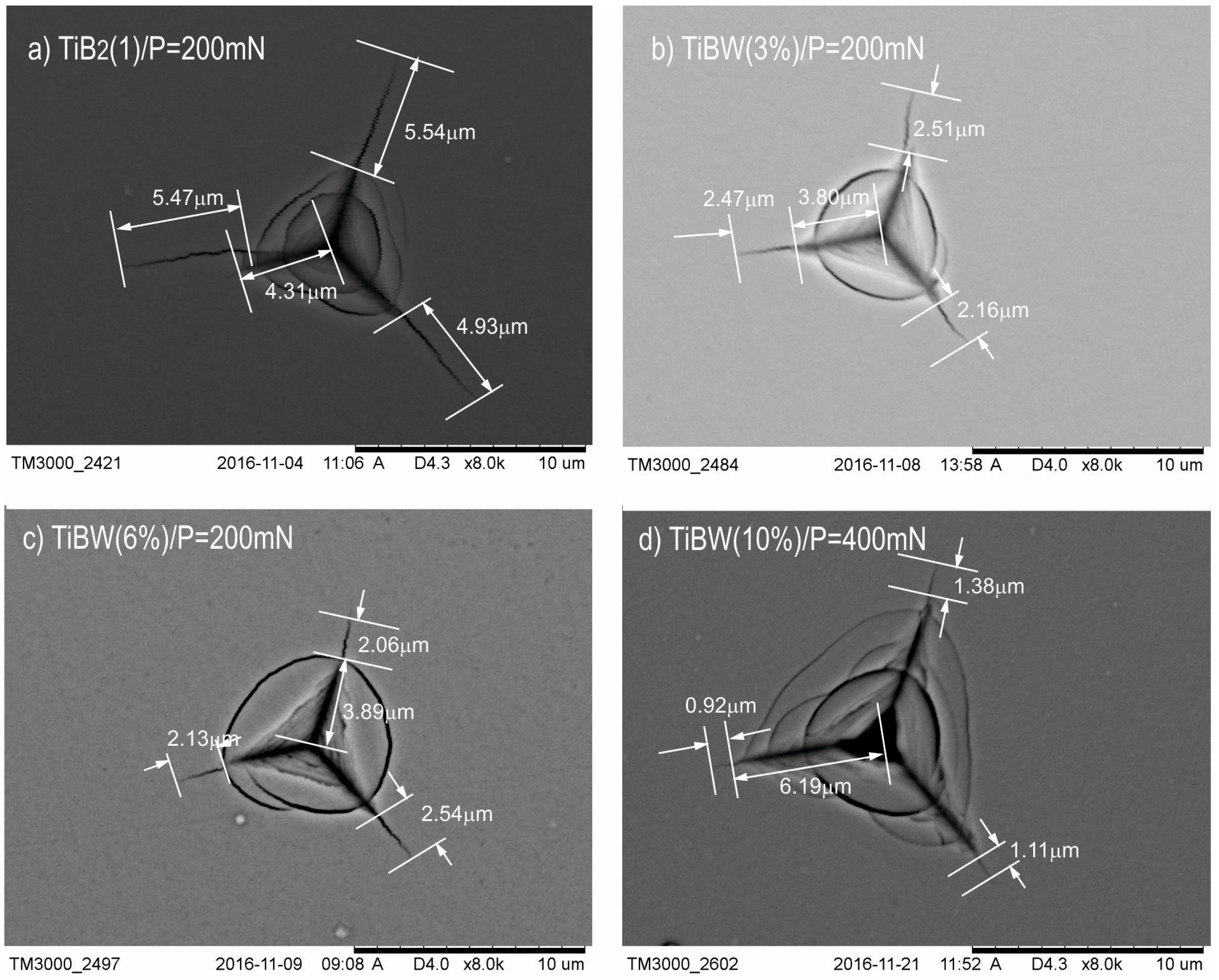
3.2. Determination of the Fracture Toughness KIc for Series of TiBW Coatings
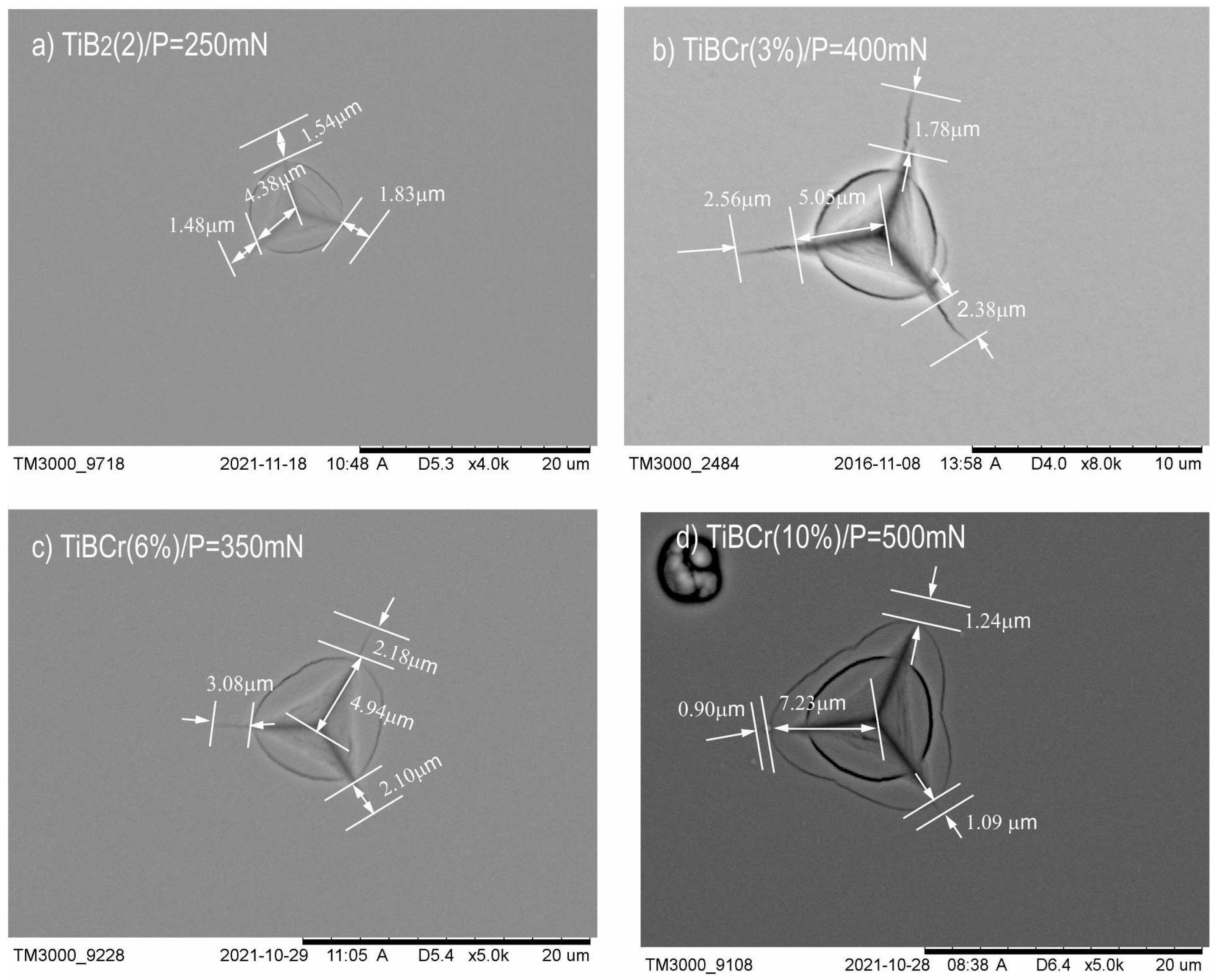
3.3. Determination of the Fracture Toughness KIc for Series of TiBCr Coatings
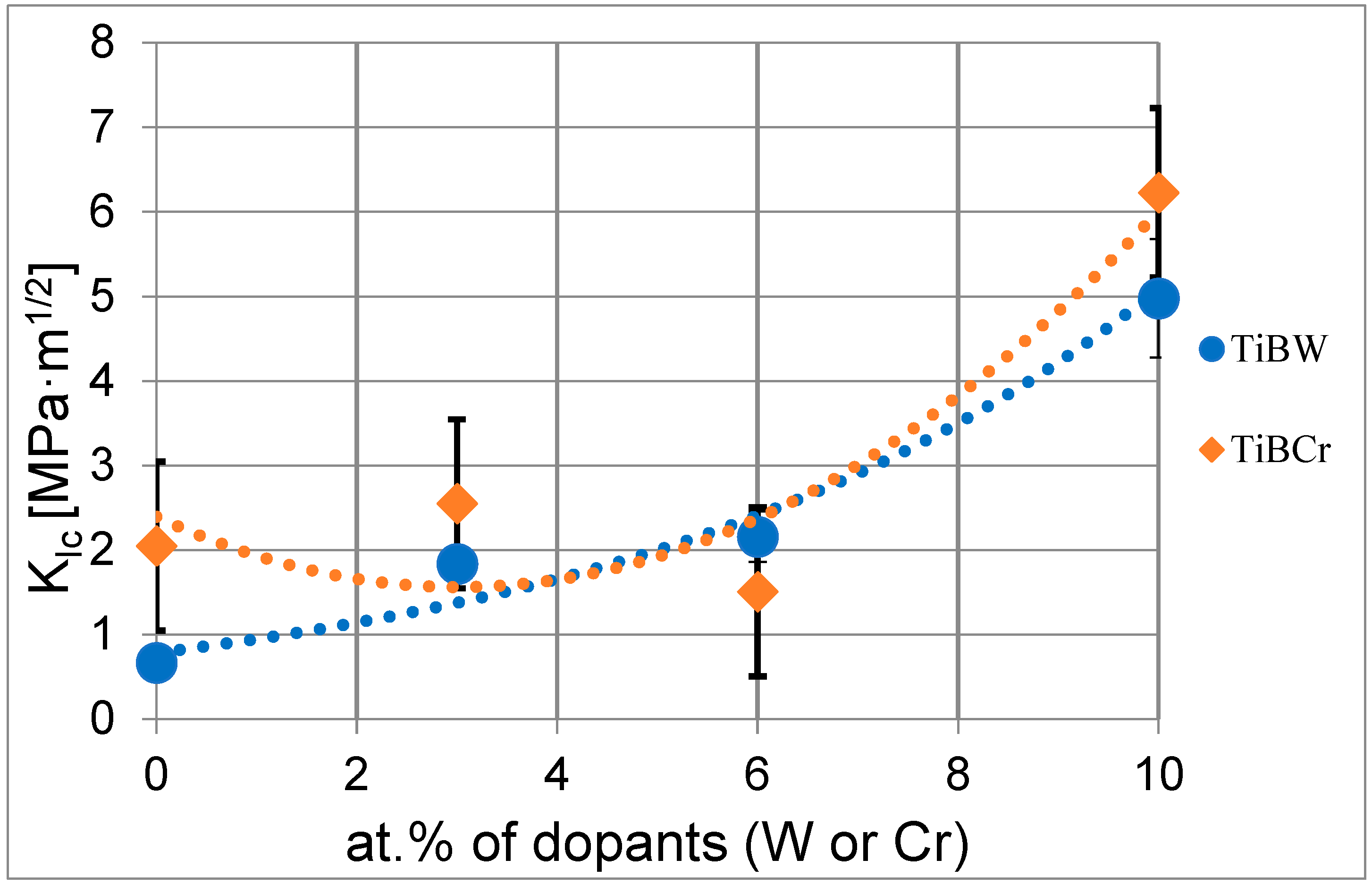
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leonardi, A.; Furgiuele, F.; Wood, J.K.R.; Syngellakis, S. Numerical analysis of brittle materials fractured by sharp indenters. Eng. Fract. Mech. 2010, 77, 264–276. [Google Scholar] [CrossRef]
- PN-EN ISO 12737(2001); Metallic materials—Determination of plane-strain fracture toughness. Polski Komitet Normalizacyjny: Warszawa, Poland, 2001.
- Zhu, X.-K.; Joyce, J.A. Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Malzbender, J.; den Toonder, J.M.J.; Balenende, A.R.; de With, G.M. Measuring mechanical properties of coatings: A methodology applied to nanoparticle-filled sol-gel coatings on glass. Mater. Sci. Eng. R Rep. 2002, 40, 47–103. [Google Scholar] [CrossRef]
- Casellas, D.; Caro, J.; Molas, S.; Prado, J.M.; Vallis, I. Fracture toughness of carbides in tool steels evaluated by nanoindentatiom. Acta Mater. 2007, 55, 4277–4286. [Google Scholar] [CrossRef]
- Evans, A.G.; Charles, E.A. Fracture toughness determinations by indentation. J. Am. Ceram. Soc. 1976, 59, 371–372. [Google Scholar] [CrossRef]
- Lawn, B.R.; Evans, A.G.; Marshall, D.B. Elastic/plastic indentation damage in ceramics: The median/radial crack system. J. Am. Ceram. Soc. 1980, 63, 574–581. [Google Scholar] [CrossRef]
- Chen, J.; Bull, S.J. Indentation fracture and toughness assessment for thin optical coatings on glass. J. Phys. D Appl. Phys. 2007, 40, 5401. [Google Scholar] [CrossRef]
- Harding, D.S.; Oliver, W.C.; Pharr, G.M. Cracking during nanoindenatation and its use in the measurement of fracture toughness. Mat. Res. Soc. Symp. Proceed. 1995, 356, 663. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.; Pharr, G.M. Influence of indenter angle on cracking in Si and Ge during nanoindentation. Acta Mater. 2008, 56, 4458–4469. [Google Scholar] [CrossRef]
- Morris, D.J.; Cook, R.F. In situ cube-corner indentation of soda-lime glass and fused silica. J. Am. Ceram. Soc. 2008, 87, 1494–1501. [Google Scholar] [CrossRef]
- Schiffmann, K.I. Determination of fracture toughness of bulk materials and thin films by nanoindentation: Comparison of different models. Philos. Mag. 2011, 91, 1163–1178. [Google Scholar] [CrossRef]
- Jungk, J.M.; Boyce, B.L.; Buchheit, T.E.; Friedman, T.A.; Yang, D.; Gerberich, W.W. Indentation fracture toughness and acoustic energy release in tetrahedral amorphous carbon diamond-like thin films. Acta Mater. 2006, 54, 4043–4052. [Google Scholar] [CrossRef]
- Anstis, G.R.; Chantikul, P.; Lawn, B.R.; Marshall, D.B. A critical evaluation of Indentation Techniques for Measuring Fracture Toughness: I, Direct Crack Measurement. J. Am. Ceram. Soc. 1981, 64, 539–543. [Google Scholar] [CrossRef]
- Palmqvist, S. The work for the formation of a crack during Vickers indentation as a measure of the toughness of hard metals. Arch. Einsenhuttenwes 1962, 33, 629–634. [Google Scholar] [CrossRef]
- Nihara, K. A fracture mechanics analysis of indentation-induced Palmquist crack in ceramics. J. Mater. Sci. Lett. 1983, 2, 221–223. [Google Scholar] [CrossRef]
- Laugier, M.T. New formula for indentation toughness in ceramics. J. Mater. Sci. Lett. 1987, 6, 355–356. [Google Scholar] [CrossRef]
- Dukino, R.D.; Swain, M.V. Comparative measurement of indentation fracture toughness with Berkovich and Vickers indenters. J. Am. Ceram. Soc. 1992, 75, 3299–3304. [Google Scholar] [CrossRef]
- Ouchterlony, F. Stress intensity factors for the expansion loaded star crack. Eng. Fract. Mech. 1976, 8, 447–448. [Google Scholar] [CrossRef] [Green Version]
- Smolik, J.; Kacprzyńska-Gołacka, J.; Sowa, S.; Piasek, A. The Analysis of Resistance to Brittle Cracking of Tungsten Doped TiB2 Coatings Obtained by Magnetron Sputtering. Coatings 2020, 10, 807. [Google Scholar] [CrossRef]
- Chudzik-Poliszak, E.; Cieniek, Ł.; Moskalewicz, T.; Kowalski, K.; Kopia, A.; Smolik, J. Influence of W Addition on Microstructure and Resistance to Brittle Cracking of TiB2 Coatings Deposited by DCMS. Materials 2021, 14, 4664. [Google Scholar] [CrossRef] [PubMed]
- Sowa, S.; Smolik, J.; Kacprzyńska-Gołacka, J.; Piasek, A. The analysis of different fracture toughness models for PVD coatings. In Proceedings of the 31st International Conference on Metallurgy and Materials, Brno, Czech Republic, 18–19 May 2022; pp. 555–560. [Google Scholar] [CrossRef]
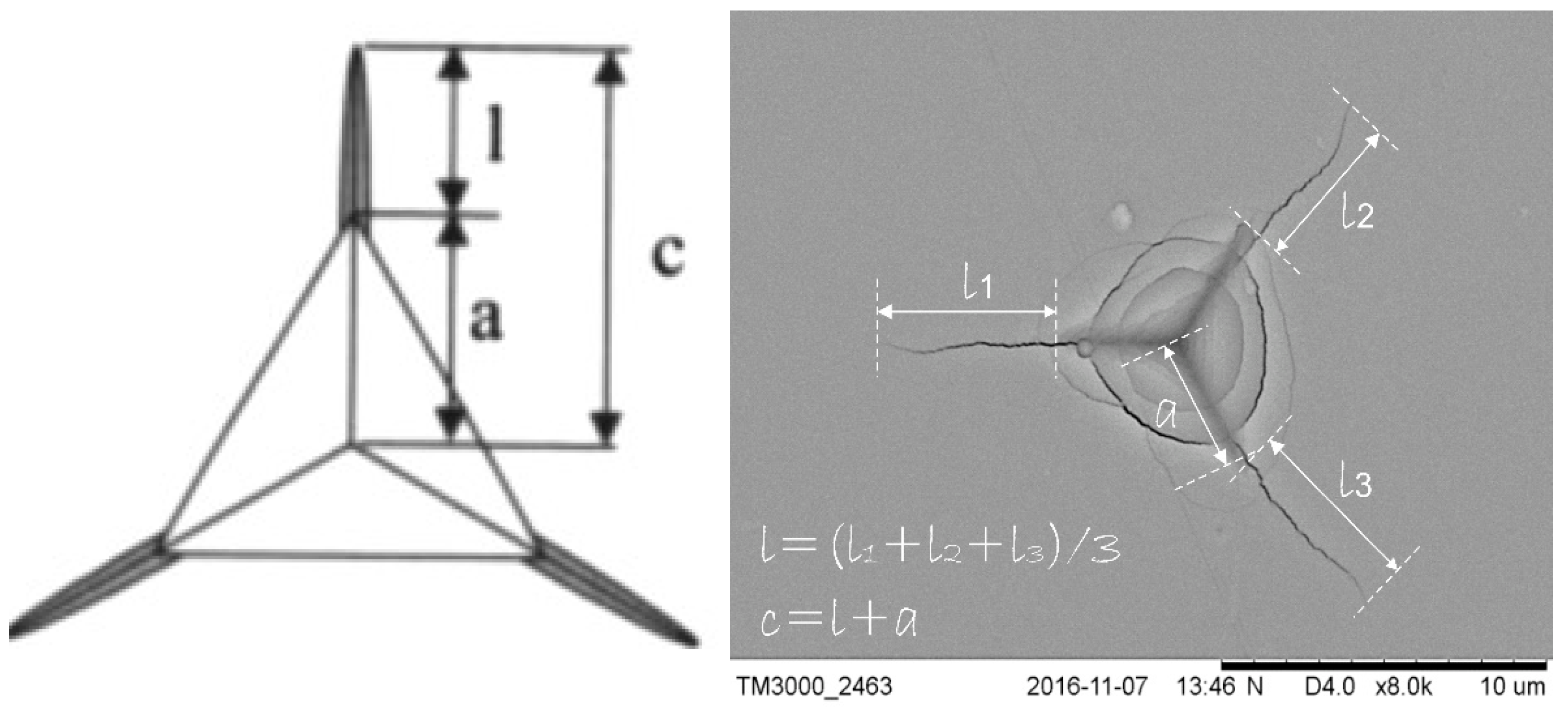




| Coatings | Atmosphere | Pressure (Pa) | UBias (V) | Power of Magnetron TiB2/W or Cr |
|---|---|---|---|---|
| TiB2 (1) | Ar 100% | 0.5 | −50 | 1000/0 |
| TiBW (3%) | −50 | 1000/25 | ||
| TiBW (6%) | −50 | 1000/50 | ||
| TiBW (10%) | −50 | 1000/75 | ||
| TiB2 (2) | −100 | 2000/0 | ||
| TiBCr (3%) | −100 | 2000/70 | ||
| TiBCr (6%) | −100 | 2000/100 | ||
| TiBCr (10%) | −100 | 2000/165 |
| Coatings | Thickness (µm) | Critical Load Pcritical (mN) | Hardness H (GPa) | Young’s Modulus E (GPa) | Plasticity Index H/E | Resistance to the Plastic Deformation H3/E2 | a (μm) | l (μm) | KIc (MPa·m1/2) |
|---|---|---|---|---|---|---|---|---|---|
| TiB2 (1) | 1.00 | 200 | 34.5 ± 2 | 405 ± 5 | 0.075 | 0.239 | 4.20 ± 0.3 | 5.32 ± 0.3 | 0.67 ± 0.1 |
| TiBW (3%) | 1.10 | 200 | 35.5 ± 2 | 415 ± 10 | 0.085 | 0.259 | 3.34 ± 0.2 | 2.12 ± 0.3 | 1.58 ± 0.2 |
| TiBW (6%) | 1.20 | 200 | 37.0 ± 2 | 425 ± 7 | 0.087 | 0.280 | 3.45 ± 0.3 | 2.10 ± 0.4 | 1.78 ± 0.3 |
| TiBW (10%) | 1.30 | 400 | 38.0 ± 3 | 435 ± 5 | 0.087 | 0.289 | 6.20 ± 0.2 | 1.20 ± 0.4 | 4.69 ± 0.7 |
| Coatings | Thickness (µm) | Critical Load Pcritical (mN) | Hardness H (GPa) | Young’s Modulus E (GPa) | Plasticity Index H/E | Resistance to the Plastic Deformation H3/E2 | a (μm) | l (μm) | KIc (MPa·m1/2) |
|---|---|---|---|---|---|---|---|---|---|
| TiB2 (2) | 1.60 | 250 | 34.5 ± 2 | 410 ± 5 | 0.084 | 0.244 | 4.18 ± 0.3 | 1.83 ± 0.4 | 2.05 ± 0.3 |
| TiBCr (3%) | 1.73 | 400 | 33.3 ± 2 | 393 ± 9 | 0.085 | 0.239 | 6.13 ± 0.6 | 1.92 ± 0.6 | 2.55 ± 0.8 |
| TiBCr (6%) | 1.73 | 350 | 32.5 ± 1 | 388 ± 8 | 0.084 | 0.228 | 5.41 ± 0.4 | 3.04 ± 0.7 | 1.60 ± 0.4 |
| TiBCr (10%) | 1.79 | 500 | 30.3 ± 2 | 383 ± 9 | 0.079 | 0.190 | 7.01 ± 0.3 | 0.71 ± 0.7 | 6.23 ± 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smolik, J.; Sowa, S.; Kacprzyńska-Gołacka, J.; Piasek, A. Evaluation of the Fracture Toughness KIc for Selected Magnetron Sputtering Coatings by Using the Laugier Model. Materials 2022, 15, 9061. https://doi.org/10.3390/ma15249061
Smolik J, Sowa S, Kacprzyńska-Gołacka J, Piasek A. Evaluation of the Fracture Toughness KIc for Selected Magnetron Sputtering Coatings by Using the Laugier Model. Materials. 2022; 15(24):9061. https://doi.org/10.3390/ma15249061
Chicago/Turabian StyleSmolik, Jerzy, Sylwia Sowa, Joanna Kacprzyńska-Gołacka, and Artur Piasek. 2022. "Evaluation of the Fracture Toughness KIc for Selected Magnetron Sputtering Coatings by Using the Laugier Model" Materials 15, no. 24: 9061. https://doi.org/10.3390/ma15249061
APA StyleSmolik, J., Sowa, S., Kacprzyńska-Gołacka, J., & Piasek, A. (2022). Evaluation of the Fracture Toughness KIc for Selected Magnetron Sputtering Coatings by Using the Laugier Model. Materials, 15(24), 9061. https://doi.org/10.3390/ma15249061








