Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety
Abstract
:1. Introduction
2. Materials and Methods
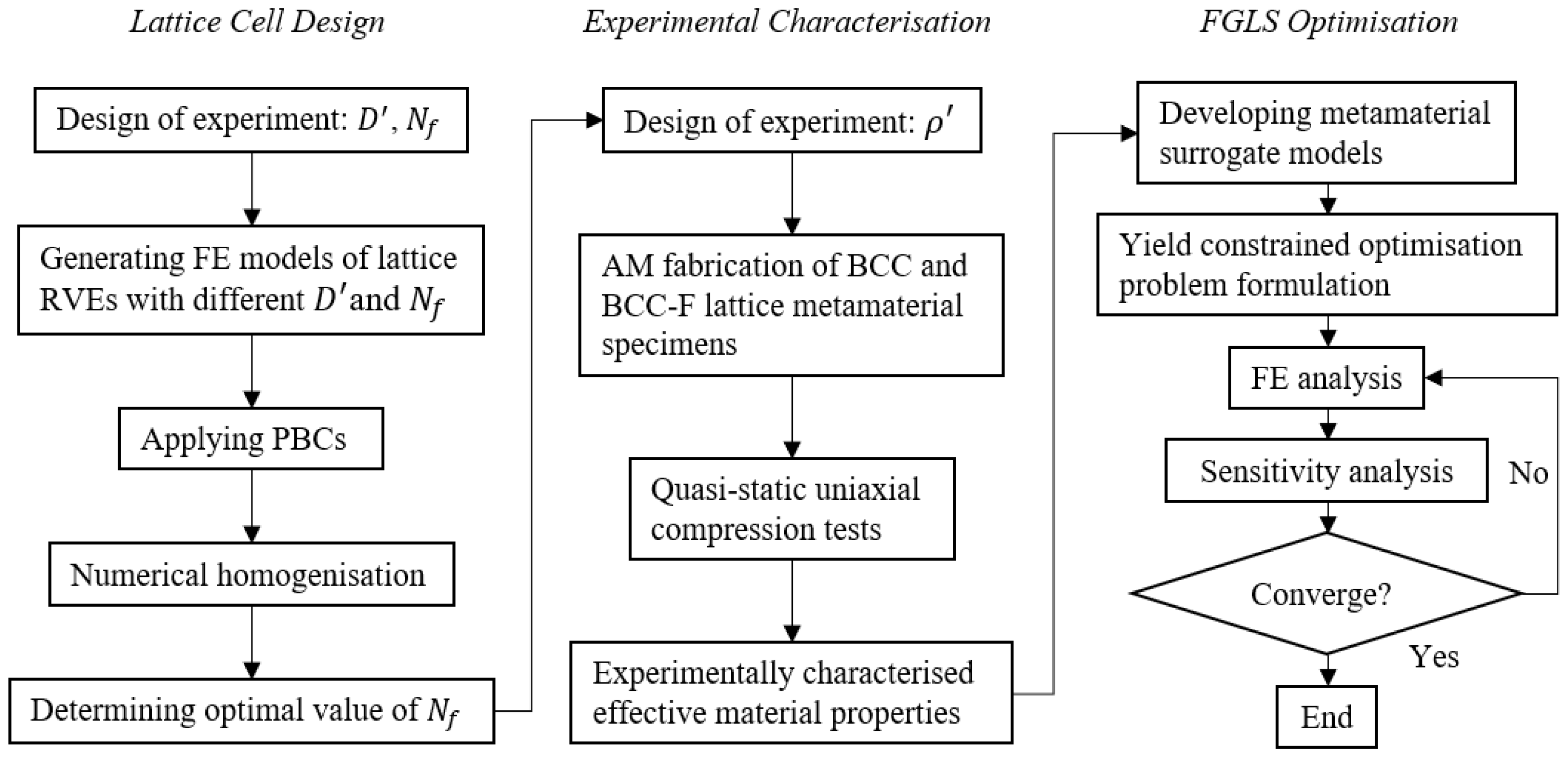
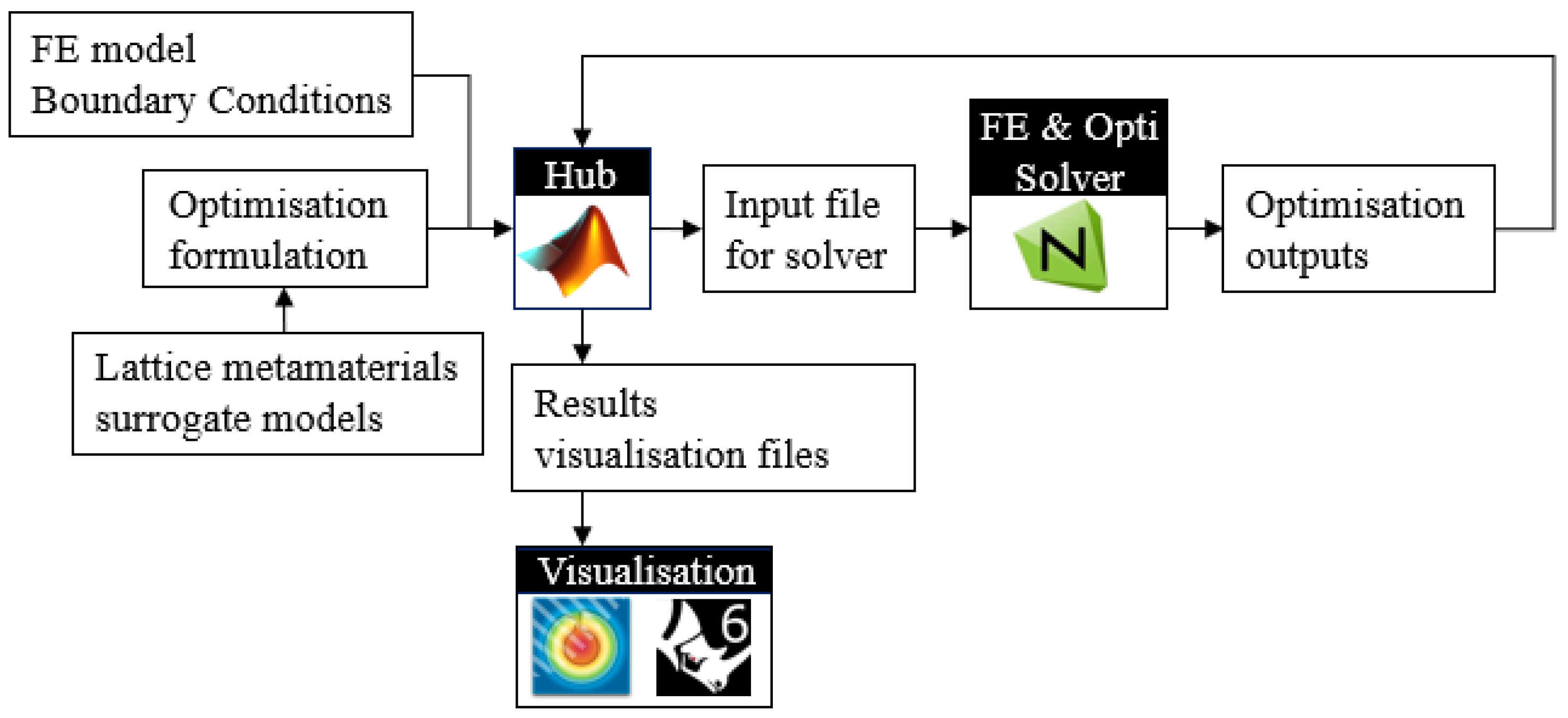
2.1. Overview of Workflow and Methodologies
2.2. Unit Cell Design for Lattice Metamaterials
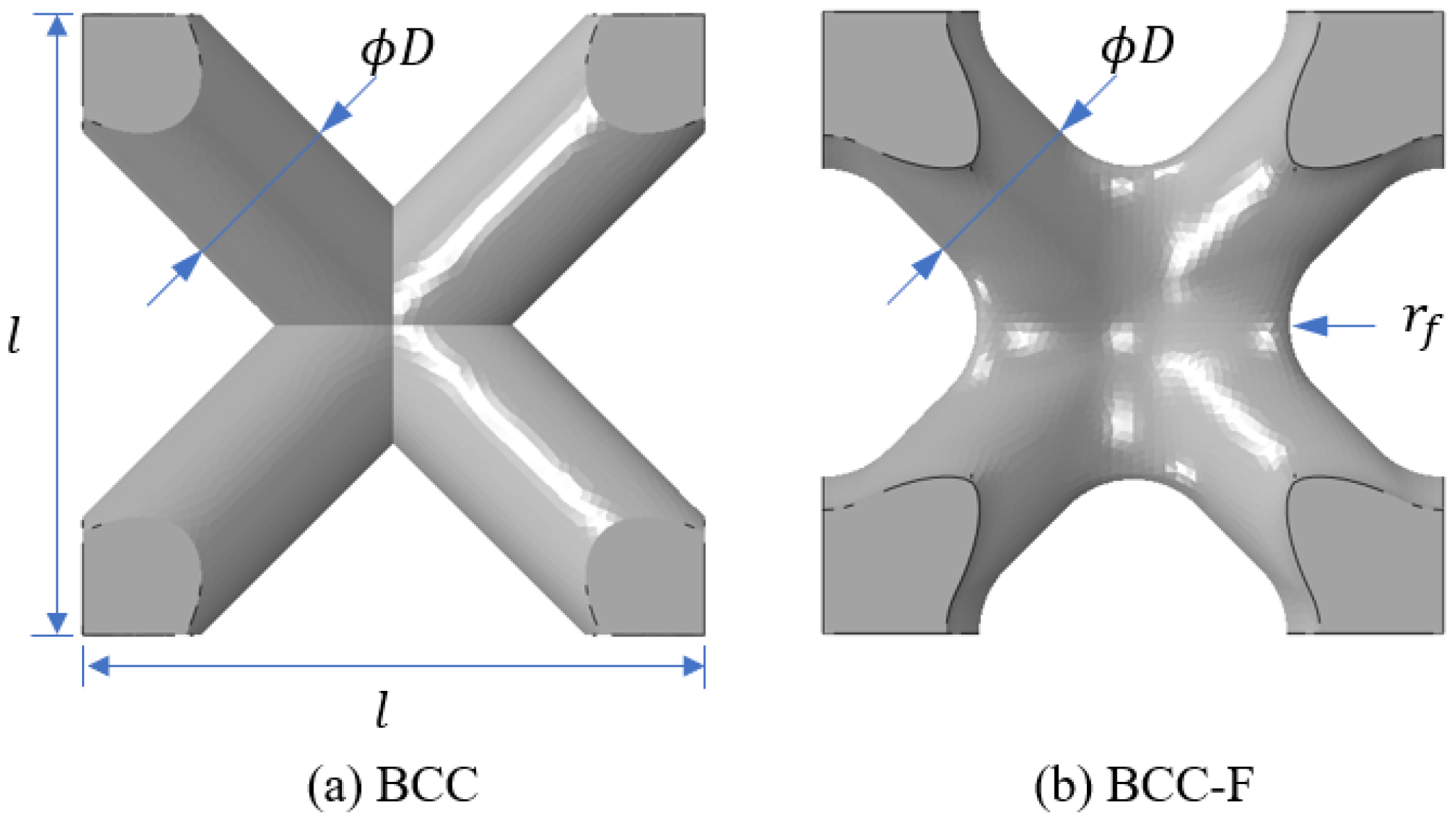
2.2.1. Design of BCC Type Lattice Unit Cells
2.2.2. Numerical Characterisation of Lattice Metamaterials and Parametric Study on the Fillet Design
2.3. Experimental Characterisation of BCC and BCC-F Lattice Metamaterials
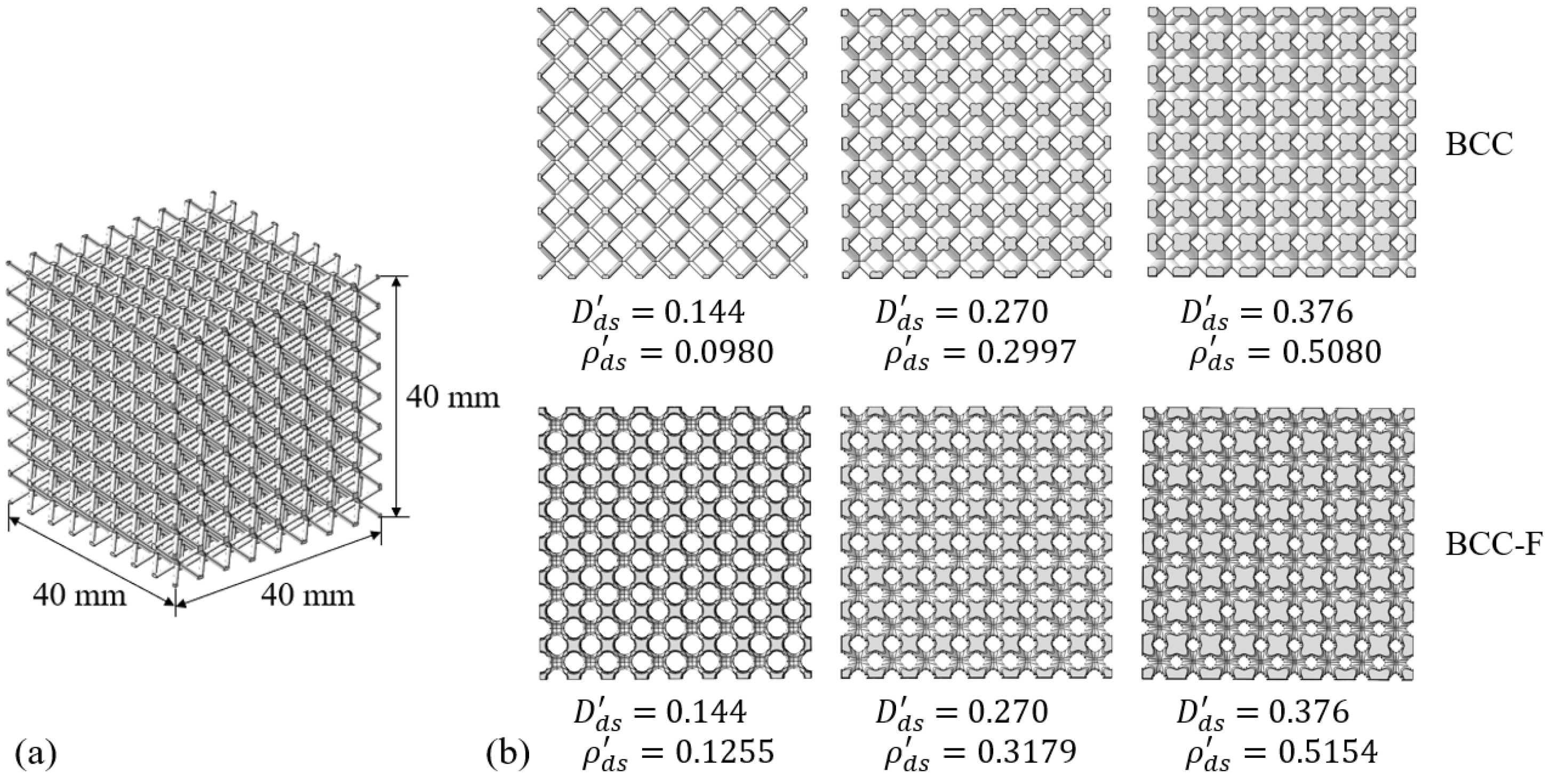
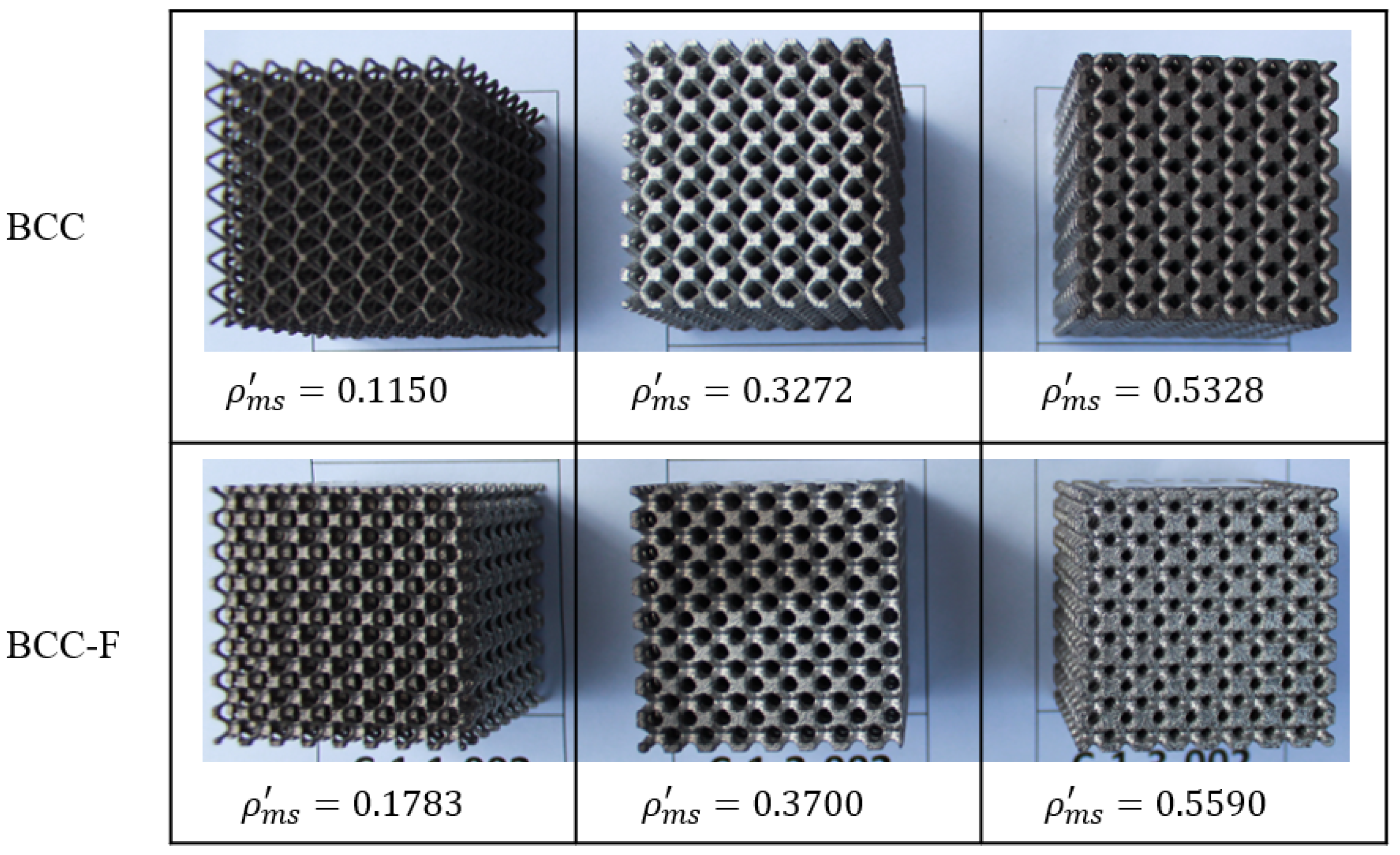
2.3.1. Design and Fabrication of the BCC and BCC-F Lattice Specimens
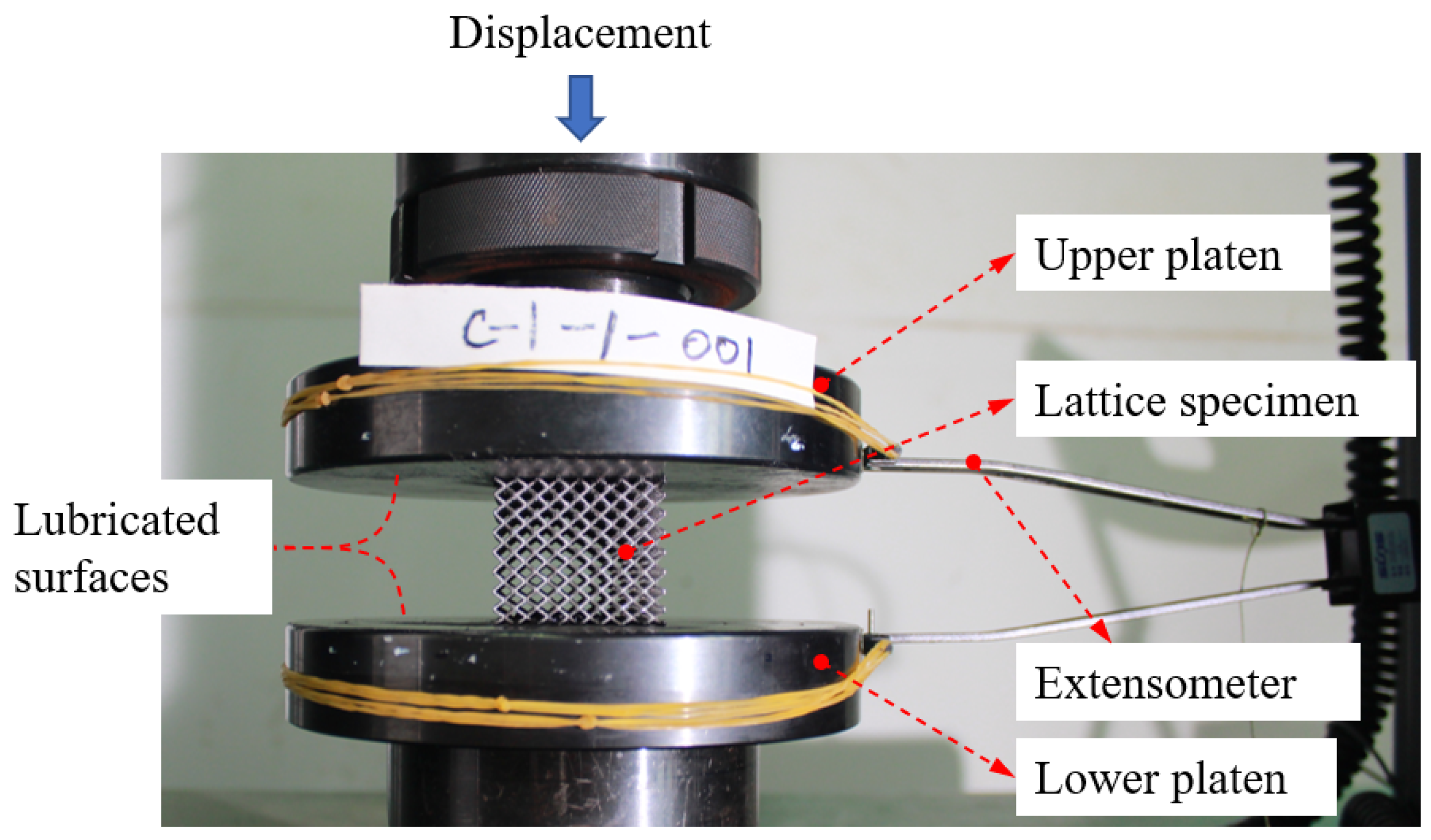
2.3.2. Experimental Setup and Procedure of Uniaxial Compression Tests
3. Results and Discussion
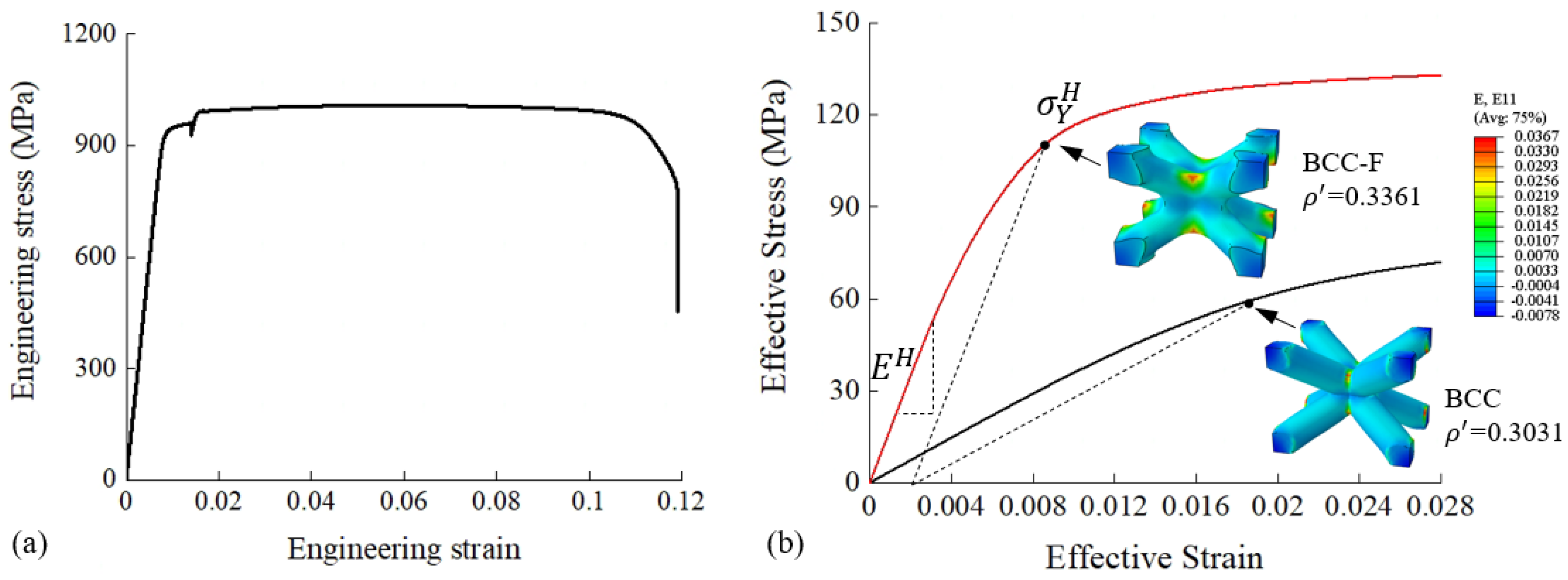
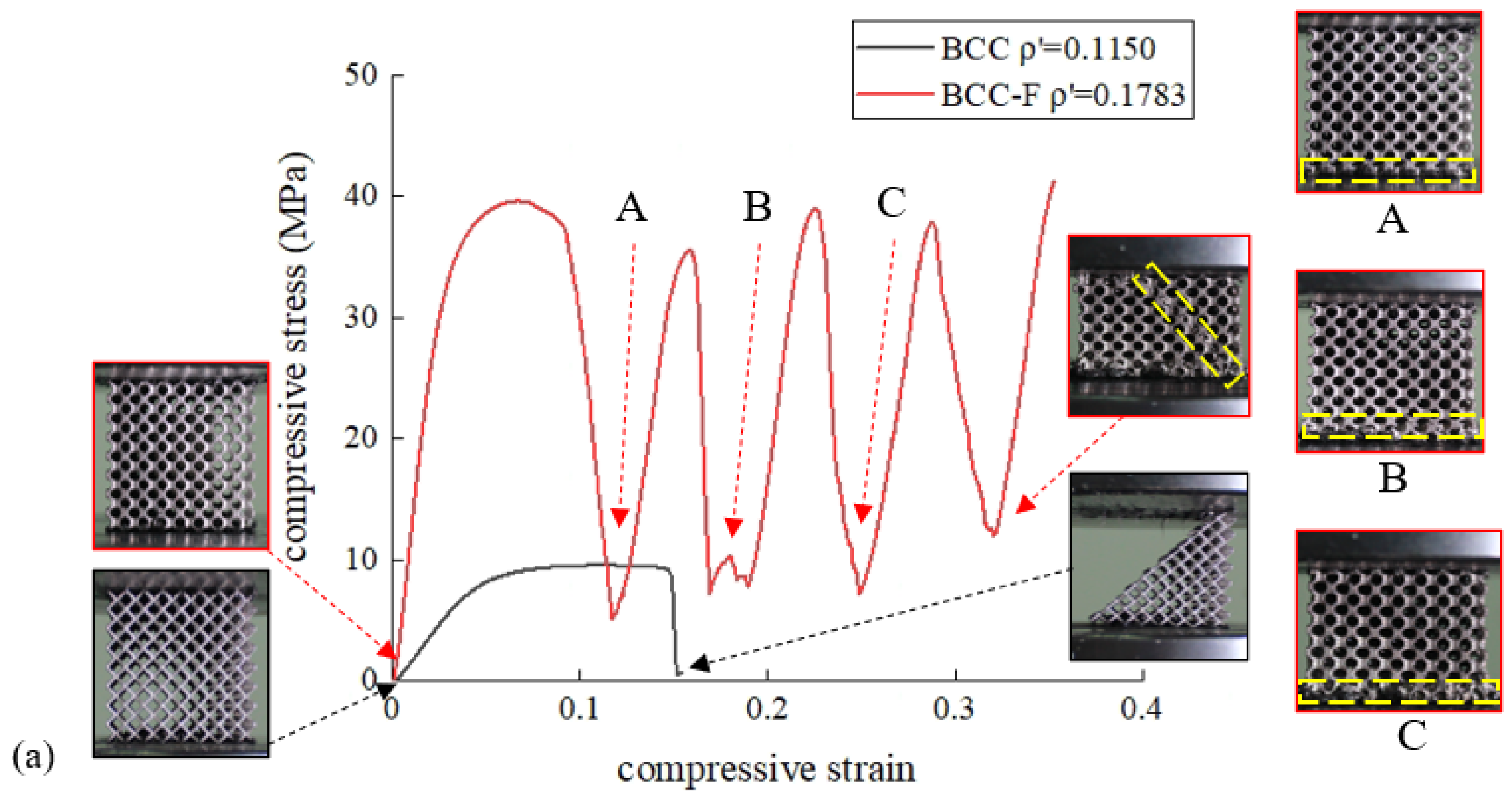
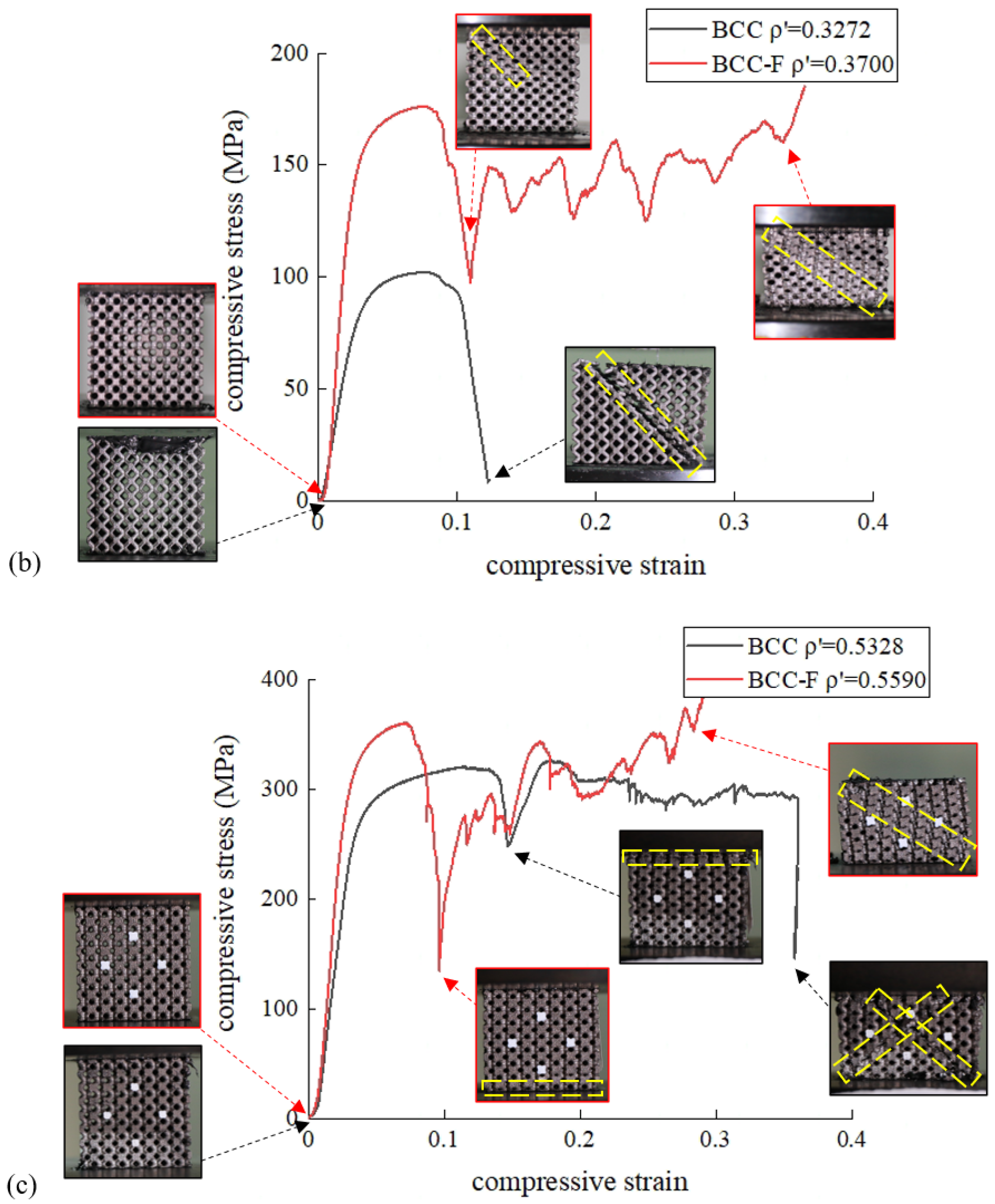
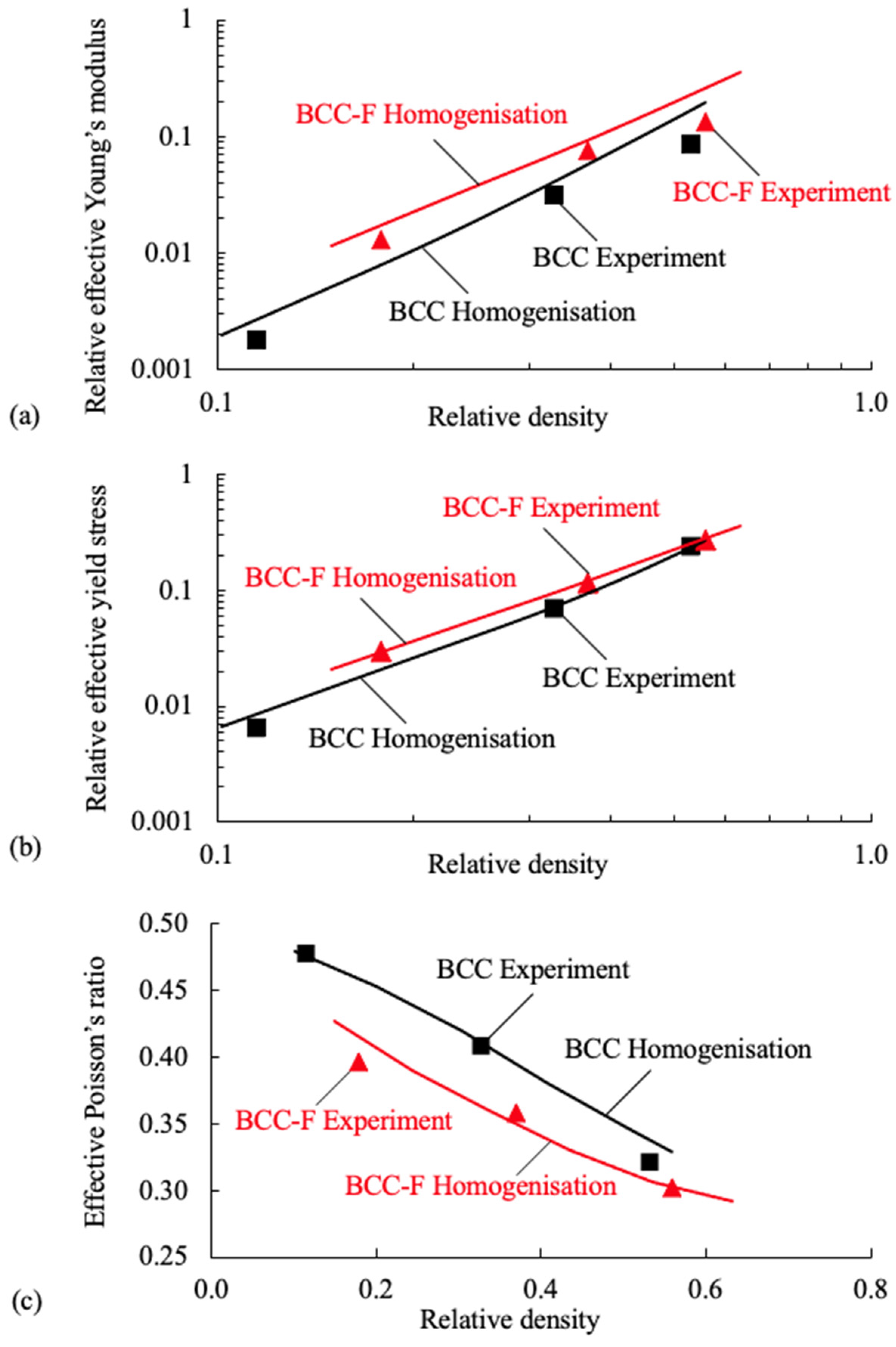
3.1. Experimental Results and Discussion of The Compression Tests
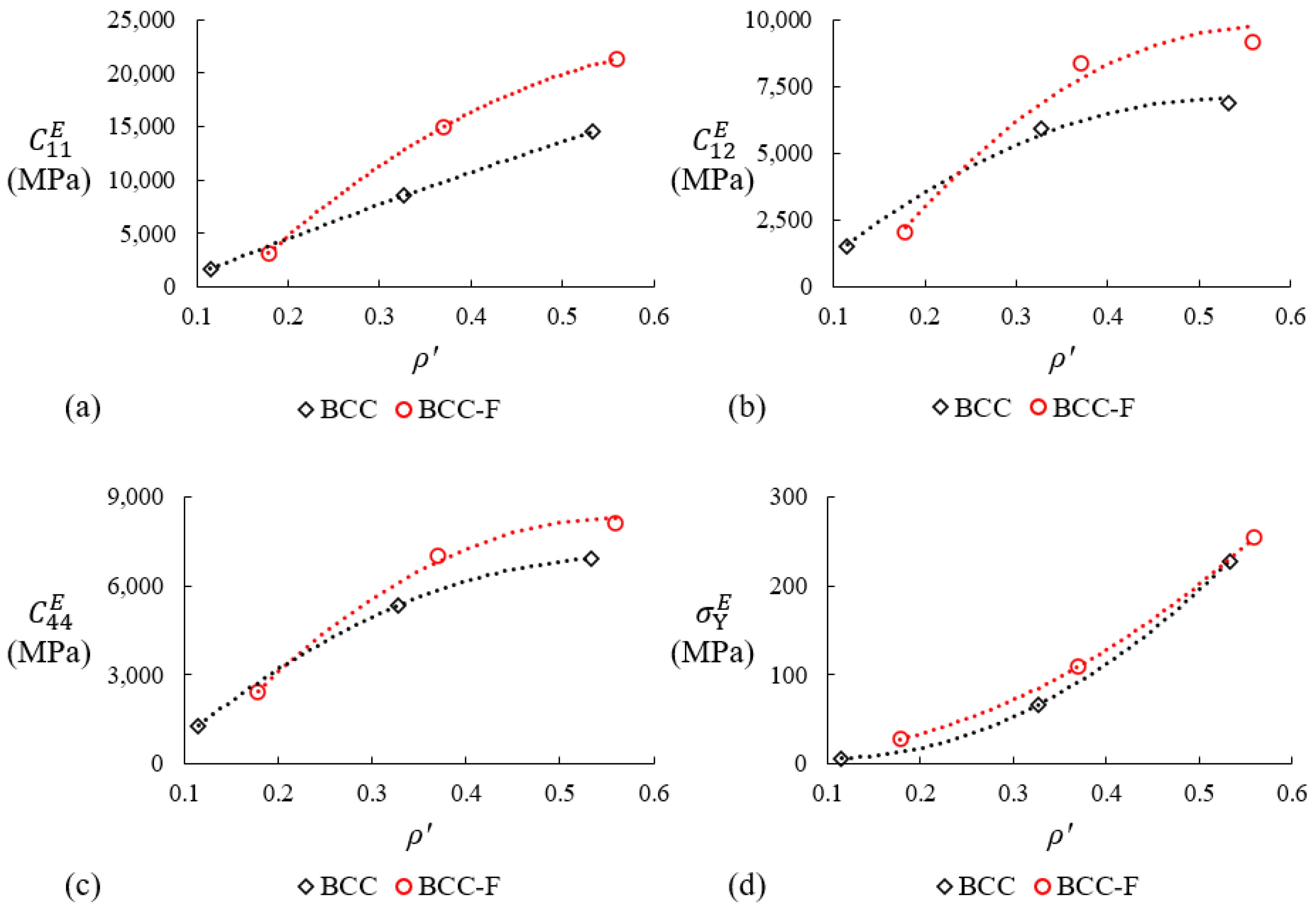
3.2. Evaluation of Effective Properties
3.3. Development of a Yield Constrained Optimisation Framework for Functionally Graded Lattice Structural Designs
3.3.1. Development of Surrogate Models of BCC and BCC-F Lattices
3.3.2. Optimisation Problem Formulation
3.3.3. Implementation of Optimisation
3.4. Optimisation Case Study
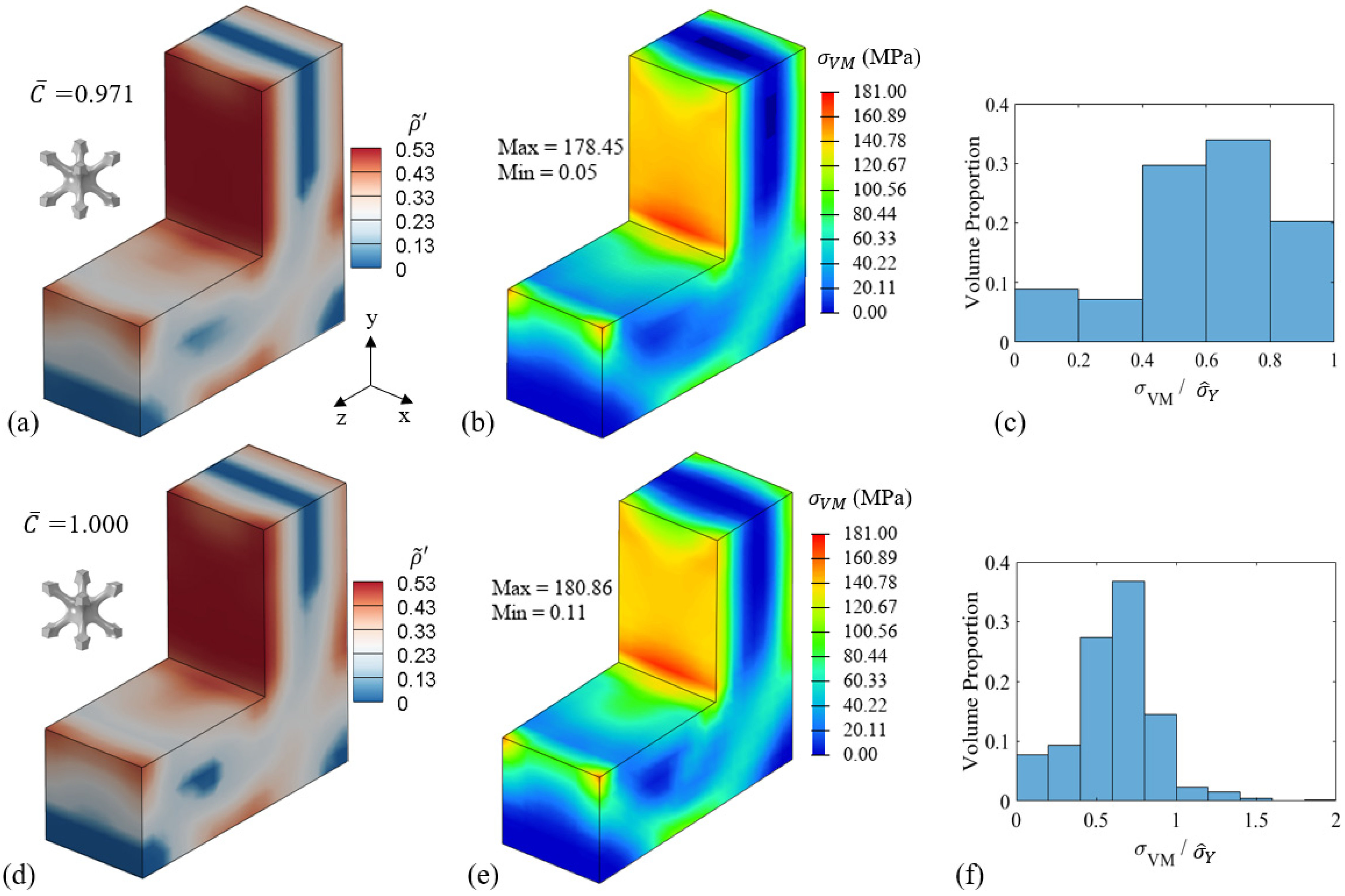
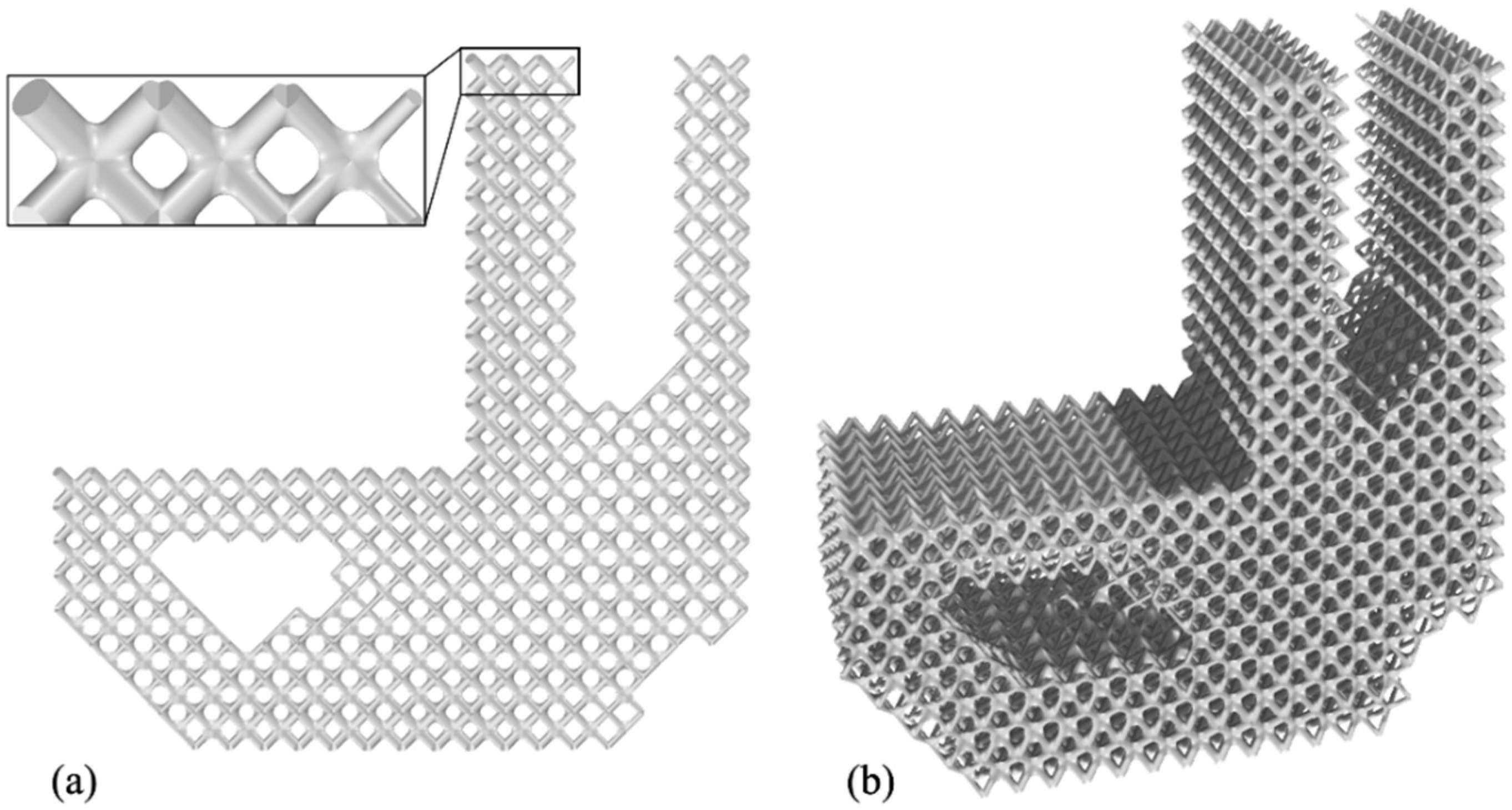
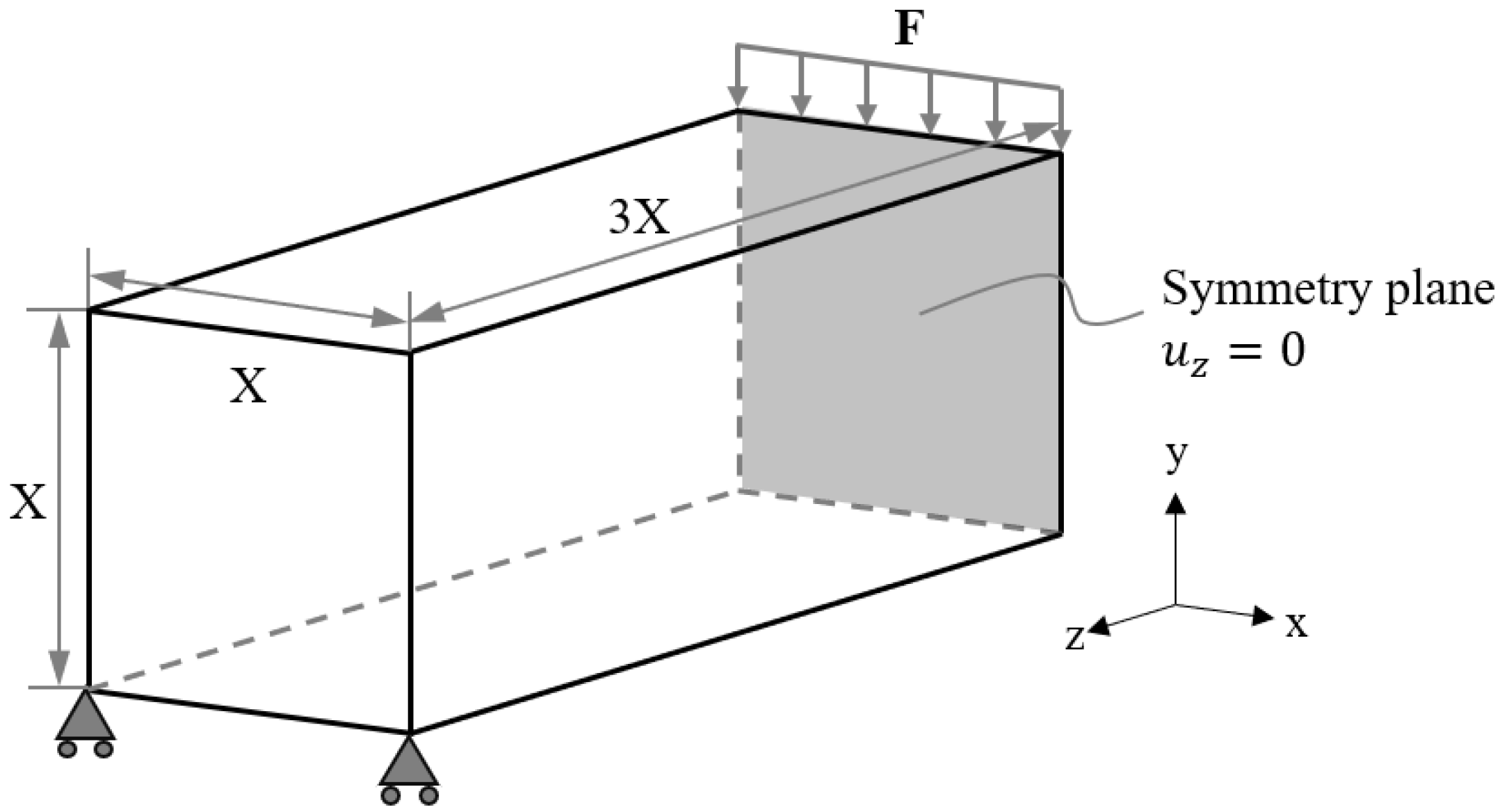
3.4.1. L-Shaped Beam Case Study with Optimisation Problem
3.4.2. MBB Beam Case Study with Optimisation Problem
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef]
- Huang, P.; Chang, W.S.; Ansell, M.P.; Chew, Y.M.J.; Shea, A. Density distribution profile for internodes and nodes of Phyllostachys edulis (Moso bamboo) by computer tomography scanning. Constr. Build. Mater. 2015, 93, 197–204. [Google Scholar] [CrossRef]
- Audibert, C.; Chaves-Jacob, J.; Linares, J.M.; Lopez, Q.A. Bio-inspired method based on bone architecture to optimize the structure of mechanical workspieces. Mater. Des. 2018, 160, 708–717. [Google Scholar] [CrossRef]
- Boyle, C.; Kim, I.Y. Three-dimensional micro-level computational study of Wolff’s law via trabecular bone remodeling in the human proximal femur using design space topology optimization. J. Biomech. 2011, 44, 935–942. [Google Scholar] [CrossRef] [PubMed]
- Alkebsi, E.A.A.; Ameddah, H.; Outtas, T.; Almutawakel, A. Design of graded lattice structures in turbine blades using topology optimization. Int. J. Comput. Integr. Manuf. 2021, 34, 370–384. [Google Scholar] [CrossRef]
- Gok, M.G. Creation and finite-element analysis of multi-lattice structure design in hip stem implant to reduce the stress-shielding effect. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 429–439. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Effect of density and unit cell size grading on the stiffness and energy absorption of short fibre-reinforced functionally graded lattice structures. Addit. Manuf. 2020, 33, 101171. [Google Scholar] [CrossRef]
- Uribe-Lam, E.; Treviño-Quintanilla, C.D.; Cuan-Urquizo, E.; Olvera-Silva, O. Use of additive manufacturing for the fabrication of cellular and lattice materials: A review. Mater. Manuf. Process. 2021, 36, 257–280. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Li, D.; Zhao, Y.F. Design and optimization of solid lattice hybrid structures fabricated by additive manufacturing. Addit. Manuf. 2020, 33, 101116. [Google Scholar] [CrossRef]
- Xu, W.; Brandt, M.; Sun, S.; Elambasseril, J.; Liu, Q.; Latham, K.; Xia, K.; Qian, M. Additive manufacturing of strong and ductile Ti-6Al-4V by selective laser melting via in situ martensite decomposition. Acta Mater. 2015, 85, 74–84. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Vayre, B.; Vignat, F.; Villeneuve, F. Metallic additive manufacturing: State-of-the-art review and prospects. Mech. Ind. 2012, 13, 89–96. [Google Scholar] [CrossRef]
- Crupi, V.; Kara, E.; Epasto, G.; Guglielmino, E.; Aykul, H. Static behavior of lattice structures produced via direct metal laser sintering technology. Mater. Des. 2017, 135, 246–256. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.N.; Leong, K.F.; Wei, J. Compressive properties of Ti-6Al-4V lattice structures fabricated by selective laser melting: Design, orientation and density. Addit. Manuf. 2017, 16, 213–224. [Google Scholar] [CrossRef]
- Alsalla, H.; Hao, L.; Smith, C. Fracture toughness and tensile strength of 316L stainless steel cellular lattice structures manufactured using the selective laser melting technique. Mater. Sci. Eng. A 2016, 669, 1–6. [Google Scholar] [CrossRef]
- Yang, L.; Han, C.; Wu, H.; Hao, L.; Wei, Q.; Yan, C.; Shi, Y. Insights into unit cell size effect on mechanical responses and energy absorption capability of titanium graded porous structures manufactured by laser powder bed fusion. J. Mech. Behav. Biomed. Mater. 2020, 109, 103843. [Google Scholar] [CrossRef]
- Teimouri, M.; Asgari, M. Mechanical performance of additively manufactured uniform and graded porous structures based on topology-optimized unit cells. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 235, 26. [Google Scholar] [CrossRef]
- Pham, M.S.; Liu, C.; Todd, I.; Lertthanasarn, J. Damage-tolerant architected materials inspired by crystal microstructure. Nature 2019, 565, 305–311. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Zheng, J.; Xin, L.; Xiong, Y.; Wu, X.; Hu, M.; Li, K.; Sun, Y. Quasi-Static compressive responses and fatigue behaviour of Ti-6Al-4 V graded lattice structures fabricated by laser powder bed fusion. Mater. Des. 2021, 210, 110110. [Google Scholar] [CrossRef]
- Takezawa, A.; Zhang, X.; Kitamura, M. Optimization of an additively manufactured functionally graded lattice structure with liquid cooling considering structural performances. Int. J. Heat Mass Transf. 2019, 143, 118564. [Google Scholar] [CrossRef]
- Simsek, U.; Gayir, C.E.; Kiziltas, G.; Sendur, P. An integrated homogenization–based topology optimization via RBF mapping strategies for additively manufactured FGLS and its application to bandgap structures. Int. J. Adv. Manuf. Technol. 2020, 111, 1361–1374. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Duysinx, P.; Bendsøe, M.P. Topology optimization of continuum structures with local stress constraints. Int. J. Numer. Methods Eng. 1998, 43, 1453–1478. [Google Scholar] [CrossRef]
- Han, Y.; Xu, B.; Wang, Q.; Liu, Y.; Duan, Z. Topology optimization of material nonlinear continuum structures under stress constraints. Comput. Methods Appl. Mech. Eng. 2021, 378, 113731. [Google Scholar] [CrossRef]
- da Silva, G.A.; Aage, N.; Beck, A.T.; Sigmund, O. Three-dimensional manufacturing tolerant topology optimization with hundreds of millions of local stress constraints. Int. J. Numer. Methods Eng. 2021, 122, 548–578. [Google Scholar] [CrossRef]
- Fernandes, R.R.; Tamijani, A.Y. Design optimization of lattice structures with stress constraints. Mater. Des. 2021, 210, 110026. [Google Scholar] [CrossRef]
- Yu, H.; Huang, J.; Zou, B.; Shao, W.; Liu, J. Stress-constrained shell-lattice infill structural optimisation for additive manufacturing. Virtual Phys. Prototyp. 2020, 15, 35–48. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Sharpe, C.; Seepersad, C.C. Stress-Constrained design of functionally graded lattice structures with spline-Based dimensionality reduction. J. Mech. Des. Trans. ASME 2020, 142, 091702. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—Homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Thillaithevan, D.; Bruce, P.; Santer, M. Stress-constrained optimization using graded lattice microstructures. Struct. Multidiscip. Optim. 2021, 63, 721–740. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef] [Green Version]
- Producers, B.R.; Bureau, N. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Bai, J.; To, A.C. Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints. Comput. Methods Appl. Mech. Eng. 2019, 344, 334–359. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for periodic RVE homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Tang, Y.; Xiong, Y.; Park, S.; Boddeti, G.N.; Rosen, D. Generation of Lattice Structures with Convolution Surface. In Proceedings of the 16th annual International CAD Conference, Singapore, 24–26 June 2019; pp. 69–74. [Google Scholar]
- Sing, S.L.; Yeong, W.Y.; Wiria, F.E.; Tay, B.Y. Characterization of Titanium Lattice Structures Fabricated by Selective Laser Melting Using an Adapted Compressive Test Method. Exp. Mech. 2016, 56, 735–748. [Google Scholar] [CrossRef]
- Campoli, G.; Borleffs, M.S.; Amin Yavari, S.; Wauthle, R.; Weinans, H.; Zadpoor, A.A. Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing. Mater. Des. 2013, 49, 957–965. [Google Scholar] [CrossRef]
- ISO 13314:2011; Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals. International Organization for Standardization: Geneva, Switzerland, 2011.
- Onal, E.; Frith, J.E.; Jurg, M.; Wu, X.; Molotnikov, A. Mechanical properties and in vitro behavior of additively manufactured and functionally graded Ti6Al4V porous scaffolds. Metals 2018, 8, 200. [Google Scholar] [CrossRef]
- Collet, M.; Noël, L.; Bruggi, M.; Duysinx, P. Topology optimization for microstructural design under stress constraints. Struct. Multidiscip. Optim. 2018, 58, 2677–2695. [Google Scholar] [CrossRef] [Green Version]
- Holmberg, E.; Torstenfelt, B.; Klarbring, A. Stress constrained topology optimization. Struct. Multidiscip. Optim. 2013, 48, 33–47. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.; James, K.A.; Martins, J.R.R.A. Stress-constrained topology optimization with design-dependent loading. Struct. Multidiscip. Optim. 2012, 46, 647–661. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- SIEMENS. Design Sensitivity and Optimization User’s Guide; Siemens PLM: Plano, TX, USA, 2018. [Google Scholar]
- Xu, K.; Wang, G.; Wang, L.; Yun, F.; Sun, W.; Wang, X.; Chen, X. Parameter analysis and optimization of annular jet pump based on Kriging model. Appl. Sci. 2020, 10, 7860. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, L.; Wang, X.; Li, N. Optimisation of three-dimensional hierarchical structures with tailored lattice metamaterial anisotropy. Mater. Des. 2021, 210, 110083. [Google Scholar] [CrossRef]





| Abbreviation | Description |
|---|---|
| FGLS | Functionally graded lattice structures |
| BCC | Body-centred cubic |
| BCC-F | Filleted body-centred cubic |
| AM | Additive manufacturing |
| SLM | Selective laser melting |
| DMLS | Direct metal laser sintering |
| PC | Primitive cubic |
| FE | Finite element |
| RVE | Representative volume element |
| PBC | Periodic boundary condition |
| SLM Processing Parameters | Values |
|---|---|
| Material | Ti6Al4V |
| Powder grade | Gd5 |
| Spherical particle size (μm) | 15–53 |
| Laser power (W) | 320 |
| Laser scanning speed (mm/s) | 1200 |
| Hatch spacing (mm) | 0.14 |
| Layer thickness (mm) | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Wang, X.; Sun, L.; Hu, Q.; Li, N. Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety. Materials 2022, 15, 9072. https://doi.org/10.3390/ma15249072
Zhu L, Wang X, Sun L, Hu Q, Li N. Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety. Materials. 2022; 15(24):9072. https://doi.org/10.3390/ma15249072
Chicago/Turabian StyleZhu, Lei, Xiaoyang Wang, Liao Sun, Quandong Hu, and Nan Li. 2022. "Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety" Materials 15, no. 24: 9072. https://doi.org/10.3390/ma15249072
APA StyleZhu, L., Wang, X., Sun, L., Hu, Q., & Li, N. (2022). Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety. Materials, 15(24), 9072. https://doi.org/10.3390/ma15249072







