First Principle Study of MgSnLa Compounds in Mg-3Sn-1Mn-1La Alloy Processed by Rheo-Rolling
Abstract
:1. Introduction
2. Computational and Experimental Procedure
3. Results and Discussion
4. Conclusions
- (1)
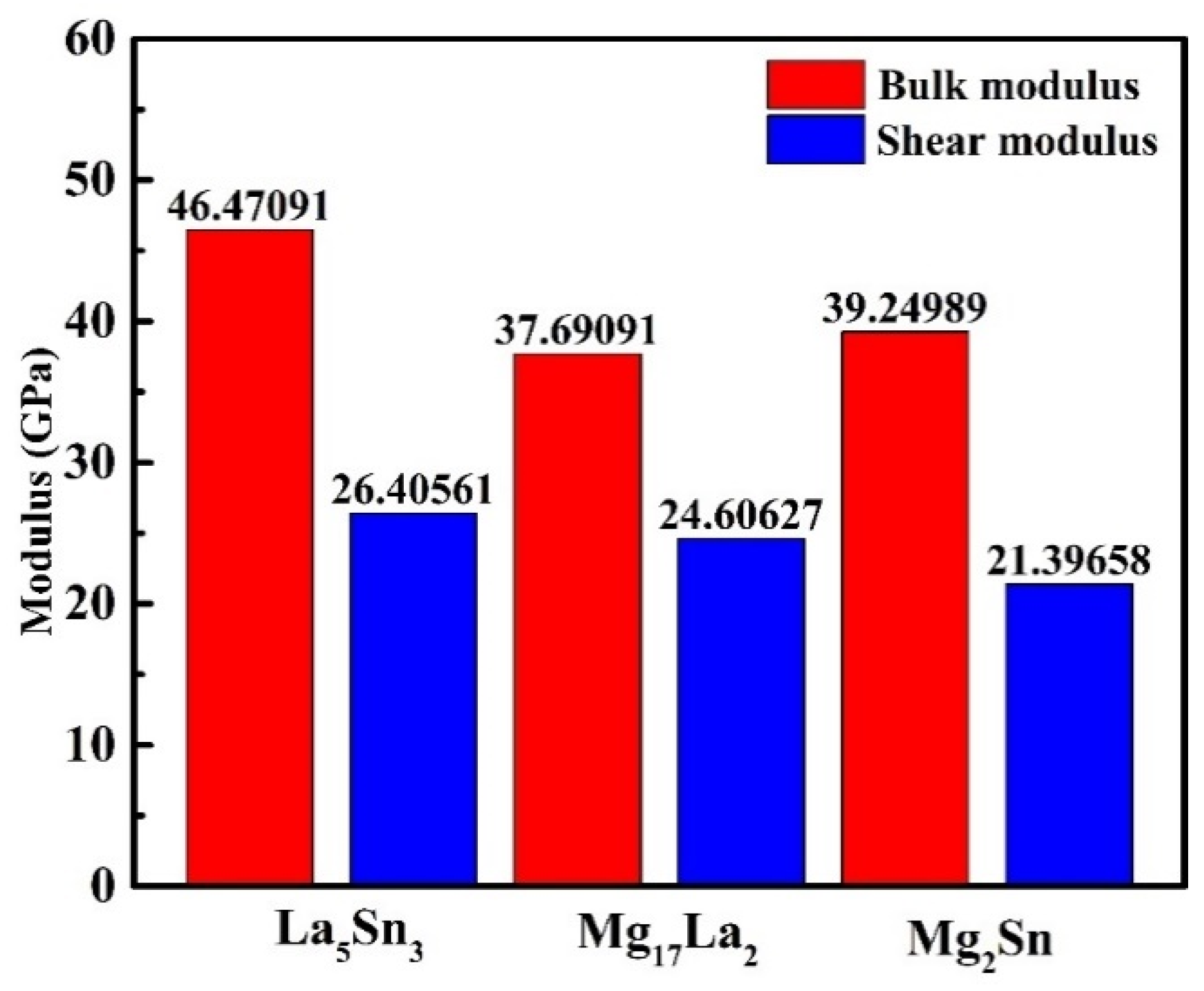
- According to the calculation results, MgSnLa compounds (La5Sn3, Mg17La2 and Mg2Sn) all show certain metallicity, and La5Sn3 has better mechanical properties (higher bulk modulus and shear modulus) than the other two phases.
- (2)
- For the binding energy, it can be concluded that La5Sn3 is the most stable, followed by Mg17La2 and finally Mg2Sn.
- (3)
- The structural stability of the MgSnLa compounds increases with the increase in temperature.
- (4)
- As the temperature increases, the free energy of Mg17La2 is most sensitive to temperature changes, and the downward trend is the largest, followed by La5Sn3, and Mg2Sn is the least sensitive.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Jin, L.; Li, W.; Song, Y.; Hao, L. Microstructure and mechanical properties of as aged Mg–3Sn–1Al and Mg–3Sn–2Zn–1Al alloy. Mater. Sci.Technol. 2015, 31, 73–78. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.H.; Yang, X.M.; Hou, H. Mechanical and Thermodynamic Properties of Mg17La2, La5Si4 and La5Sn3 Phases in Mg-Sn-Mn (Si)-La Alloy from First-Principles Calculations. Sci. Adv. Mater. 2020, 12, 1649–1655. [Google Scholar]
- Luo, J.; Chen, R.S.; Han, E.H. Effects of Gd on the Microstructure and Mechanical Properties of Mg-3Sn Alloys. Mater. Sci. Forum 2013, 747–748, 245–250. [Google Scholar] [CrossRef]
- Radha, R.; Sreekanth, D. Mechanical and corrosion behaviour of hydroxyapatite reinforced Mg-Sn alloy composite by squeeze casting for biomedical applications. J. Magnes. Alloy 2020, 8, 452–460. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Chen, X.H.; Pan, F.S.; Gao, S.Y.; Zhao, D.; Liu, X.F. Effect of Sn content on strain hardening behavior of as-extruded Mg-Sn alloys. Mater. Sci. Eng. A 2018, 713, 244–252. [Google Scholar] [CrossRef]
- Wei, S.H.; Chen, Y.G.; Tang, Y.B.; Zhang, X.P.; Liu, M.; Xiao, S.F.; Zhao, Y.H. Compressive creep behavior of Mg–Sn–La alloys. Mater. Sci. Eng. A 2009, 508, 59–63. [Google Scholar] [CrossRef]
- Liu, H.M.; Chen, Y.G.; Tang, Y.B.; Huang, D.M.; Niu, G. The microstructure and mechanical properties of permanent-mould cast Mg–5wt%Sn–(0–2.6)wt%Di alloys. Mater. Sci. Eng. A 2006, 437, 348–355. [Google Scholar] [CrossRef]
- Pan, F.S.; Yang, M.B. Preliminary investigations about effects of Zr, Sc and Ce additions on as-cast microstructure and mechanical properties of Mg–3Sn–1Mn (wt.%) magnesium alloy. Mater. Sci. Eng. A 2011, 528, 4973–4981. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, Y.G.; Xiao, S.F.; Zhang, X.P.; Tang, Y.B.; Wei, S.H.; Zhao, Y.H. Study on microstructure and mechanical properties of as-cast Mg-Sn-Nd alloys. J. Rare Earths 2010, 28, 790–793. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Guan, R.G.; Shen, Y.F.; Bai, P.K. Grain refinement mechanism of Mg-3Sn-1Mn-1La alloy during accumulative hot rolling. J. Mater. Sci. Technol. 2021, 91, 251–261. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Bai, P.K.; Guan, R.G.; Murugadoss, V.; Liu, H.; Wang, X.J.; Guo, Z.H. Microstructural evolution and mechanical strengthening mechanism of Mg-3Sn-1Mn-1La alloy after heat treatments. Mater. Sci. Eng. A 2018, 734, 200–209. [Google Scholar] [CrossRef]
- Evdokimenko, V.I.; Kripyakevich, P.I. Über die Löslichkeit von Lanthan in Aluminium, Magnesium und den homogenen Legierungen des Magnesiums und Aluminiums. Z. Electrochem. Angew. Phys. Chem. 1940, 46, 357–364. [Google Scholar]
- Franceschi, E.A. Dimorphism of La5Sn3, Ce5Sn3 and Pr5Sn3 compounds. J. Less Common Met. 1979, 66, 175–181. [Google Scholar] [CrossRef]
- Guan, R.G.; Shen, Y.F.; Zhao, Z.Y.; Misra, R.D.K. Nanoscale precipitates strengthened lanthanum-bearing Mg-3Sn-1Mn alloys through continuous rheo-rolling. Sci. Rep. 2016, 6, 23154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guan, R.G.; Zhao, Z.Y.; Zhang, H.; Lian, C.; Lee, C.S.; Liu, C.M. Microstructure evolution and properties of Mg–3Sn–1Mn (wt%) alloy strip processed by semisolid rheo-rolling. J. Mater. Process. Technol. 2012, 212, 1430–1436. [Google Scholar] [CrossRef]
- Zheng, B.; Zhao, L.; Hu, X.B.; Dong, S.J.; Li, H. First-principles studies of Mg17Al12,Mg2Al3,Mg2Sn,MgZn2,Mg2Ni and Al3Ni phases. Phys. B 2019, 560, 255–260. [Google Scholar] [CrossRef]
- Wu, H.Y.; Dong, Y.P.; Li, X.W.; Li, Y.L.; Yan, M. First principle calculations and low cost SLM processing of Ti–TiB composite materials. Mater. Sci. Eng. A 2021, 803, 140711. [Google Scholar] [CrossRef]
- Martin, A.C.; Oliveira, J.P.; Fink, C. Elemental effects on weld cracking susceptibility in AlxCoCrCuyFeNi high-entropy alloy. Metall. Mater. Trans. A 2020, 51, 778–787. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Shen, J.; Zeng, Z.; Park, J.M.; Choi, Y.T.; Schell, N.; Maawad, E.; Zhou, N.; Kim, H.S. Dissimilar laser welding of a CoCrFeMnNi high entropy alloy to 316 stainless steel. Scr. Mater. 2022, 206, 114219. [Google Scholar] [CrossRef]
- Shao, H.B.; Huang, Y.C.; Liu, Y.; Ren, X.W.; Xiao, Z.B. Structural stabilities and thermal properties of η′-Mg2Zn5-xAl2+x and η-MgZn2 phase in Al–Zn–Mg alloy: First-principles calculation and quasi-harmonic Debye approximation. J. Mater. Res. Technol. 2021, 10, 840–852. [Google Scholar]
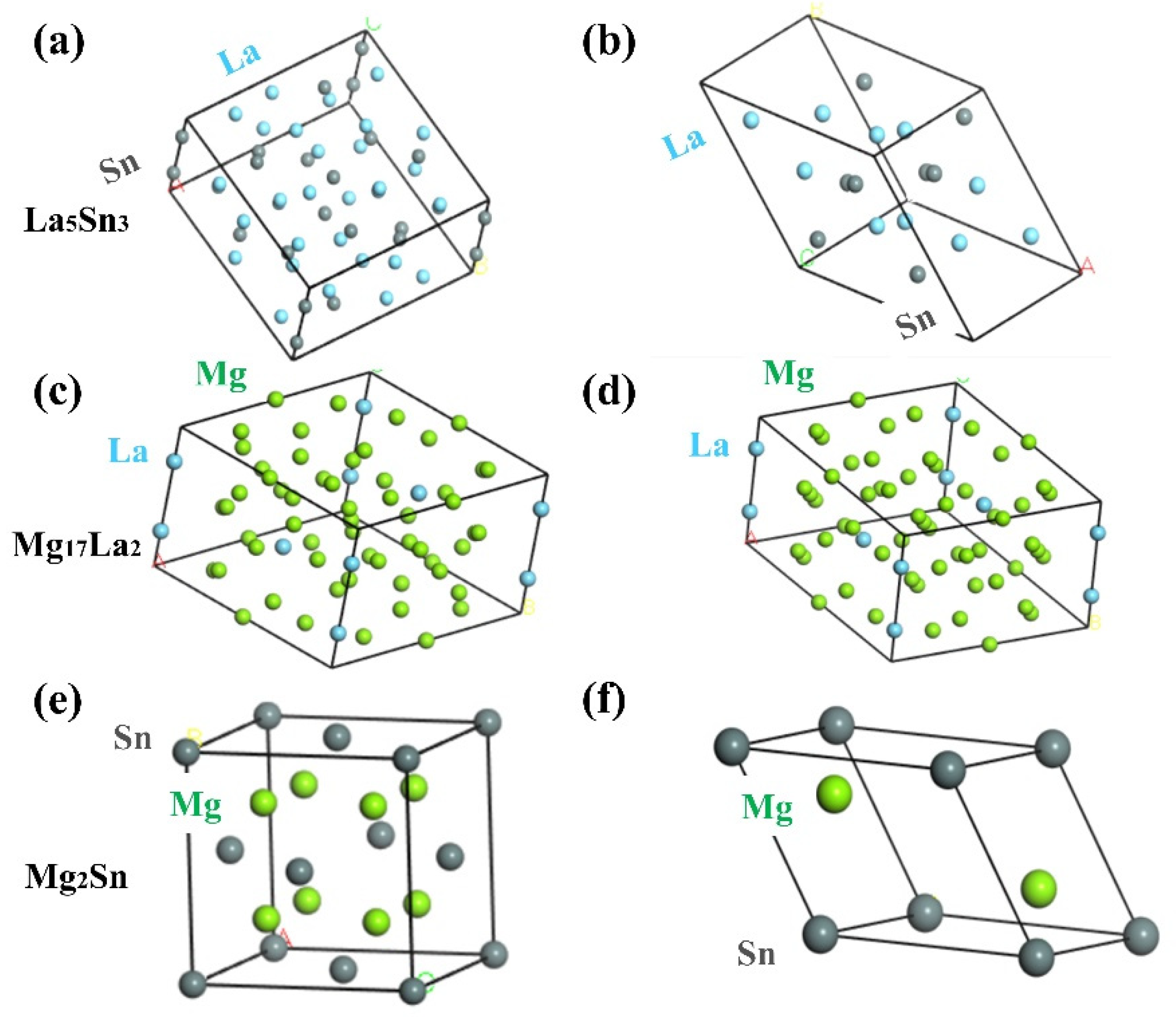




| Phases | La5Sn3 | Mg17La2 | Mg2Sn |
|---|---|---|---|
| Space group | 14/MCM (140) | P63/MMC (194) | FM-3M (225) |
| Lattice constants | a = b = 12.749 Å, c = 6.343 Å | a = b = 10.35 Å, c = 10.28 Å | a = b = c = 6.81 Å |
| Atomic coordinates | La (0, 0.5, 0.25), Sn (0, 0, 0.25) | La (0, 0, 0.25), Mg (0.333, 0.666, 0.11) | Mg (0.25, 0.25, 0.25), Sn (0, 0, 0) |
| Phases | Optimal State | a (Å) | b (Å) | c (Å) | α | β | γ |
|---|---|---|---|---|---|---|---|
| La5Sn3 | before optimization | 12.749 | 12.749 | 6.343 | 90° | 90° | 90° |
| after optimization | 9.687 | 9.687 | 9.687 | 96.31° | 96.31° | 141.3° | |
| Mg17La2 | before optimization | 10.35 | 10.35 | 10.28 | 90° | 90° | 120° |
| after optimization | 10.43 | 10.43 | 10.16 | 90° | 90° | 120° | |
| Mg2Sn | before optimization | 6.81 | 6.81 | 6.81 | 90° | 90° | 90° |
| after optimization | 4.83 | 4.83 | 4.83 | 60° | 60° | 60° |
| Phases | C11 | C12 | C13 | C33 | C44 | C66 |
|---|---|---|---|---|---|---|
| La5Sn3 | 92.47 | 33.56 | 25.13 | 70.99 | 22.09 | 32.36 |
| Mg17La2 | 69.98 | 21.21 | 19.12 | 80.78 | 22.73 | - |
| Mg2Sn | 58.45 | 29.65 | - | - | 27.91 | - |
| Phases | E/(eV/Atom) | H/(eV/Atom) |
|---|---|---|
| La5Sn3 | 5.33 | −1.03 |
| Mg17La2 | 2.48 | −0.65 |
| Mg2Sn | 0.17 | −6.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-H.; Zhao, Z.-Y. First Principle Study of MgSnLa Compounds in Mg-3Sn-1Mn-1La Alloy Processed by Rheo-Rolling. Materials 2022, 15, 1361. https://doi.org/10.3390/ma15041361
Wang J-H, Zhao Z-Y. First Principle Study of MgSnLa Compounds in Mg-3Sn-1Mn-1La Alloy Processed by Rheo-Rolling. Materials. 2022; 15(4):1361. https://doi.org/10.3390/ma15041361
Chicago/Turabian StyleWang, Jian-Hong, and Zhan-Yong Zhao. 2022. "First Principle Study of MgSnLa Compounds in Mg-3Sn-1Mn-1La Alloy Processed by Rheo-Rolling" Materials 15, no. 4: 1361. https://doi.org/10.3390/ma15041361
APA StyleWang, J.-H., & Zhao, Z.-Y. (2022). First Principle Study of MgSnLa Compounds in Mg-3Sn-1Mn-1La Alloy Processed by Rheo-Rolling. Materials, 15(4), 1361. https://doi.org/10.3390/ma15041361







