Modeling the Simultaneous Effects of Particle Size and Porosity in Simulating Geo-Materials
Abstract
:1. Introduction
2. Joint Particle Model and Joint Particle Size
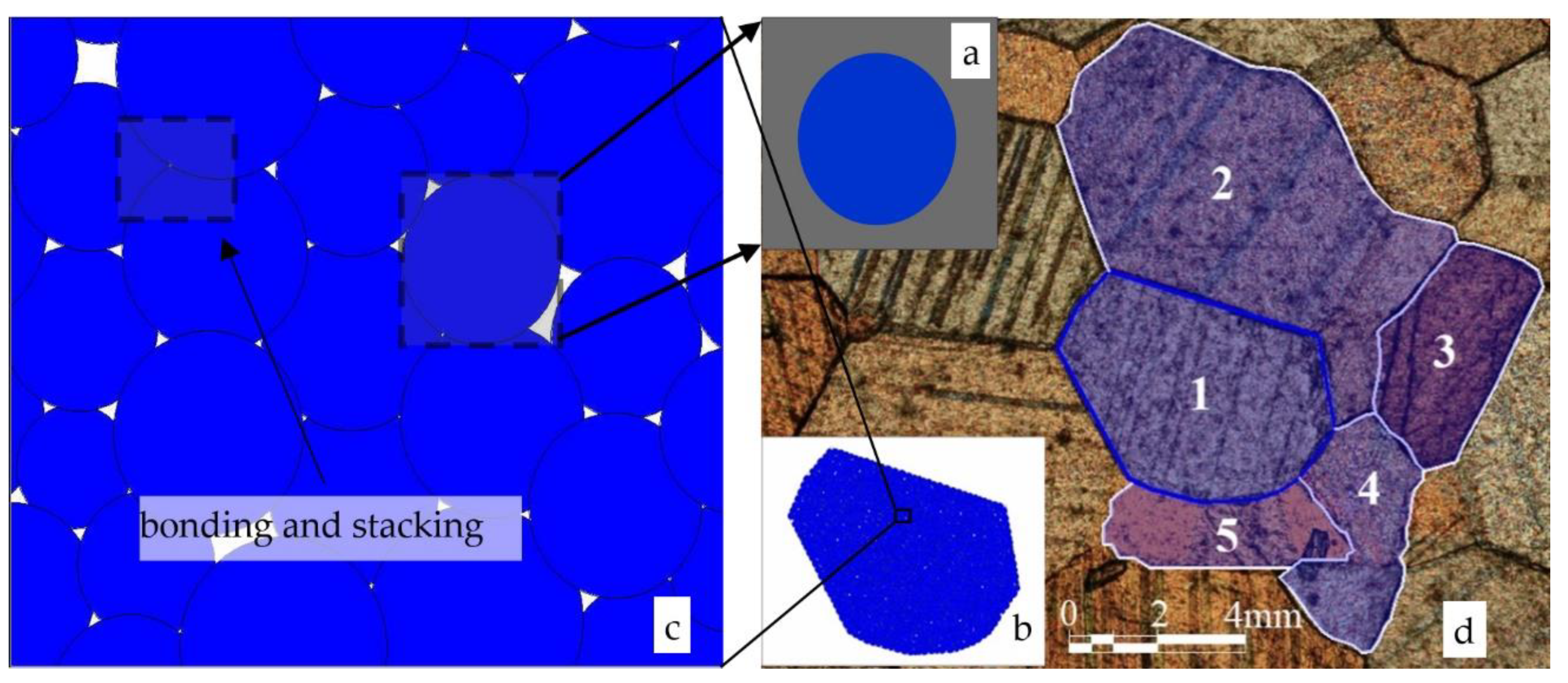
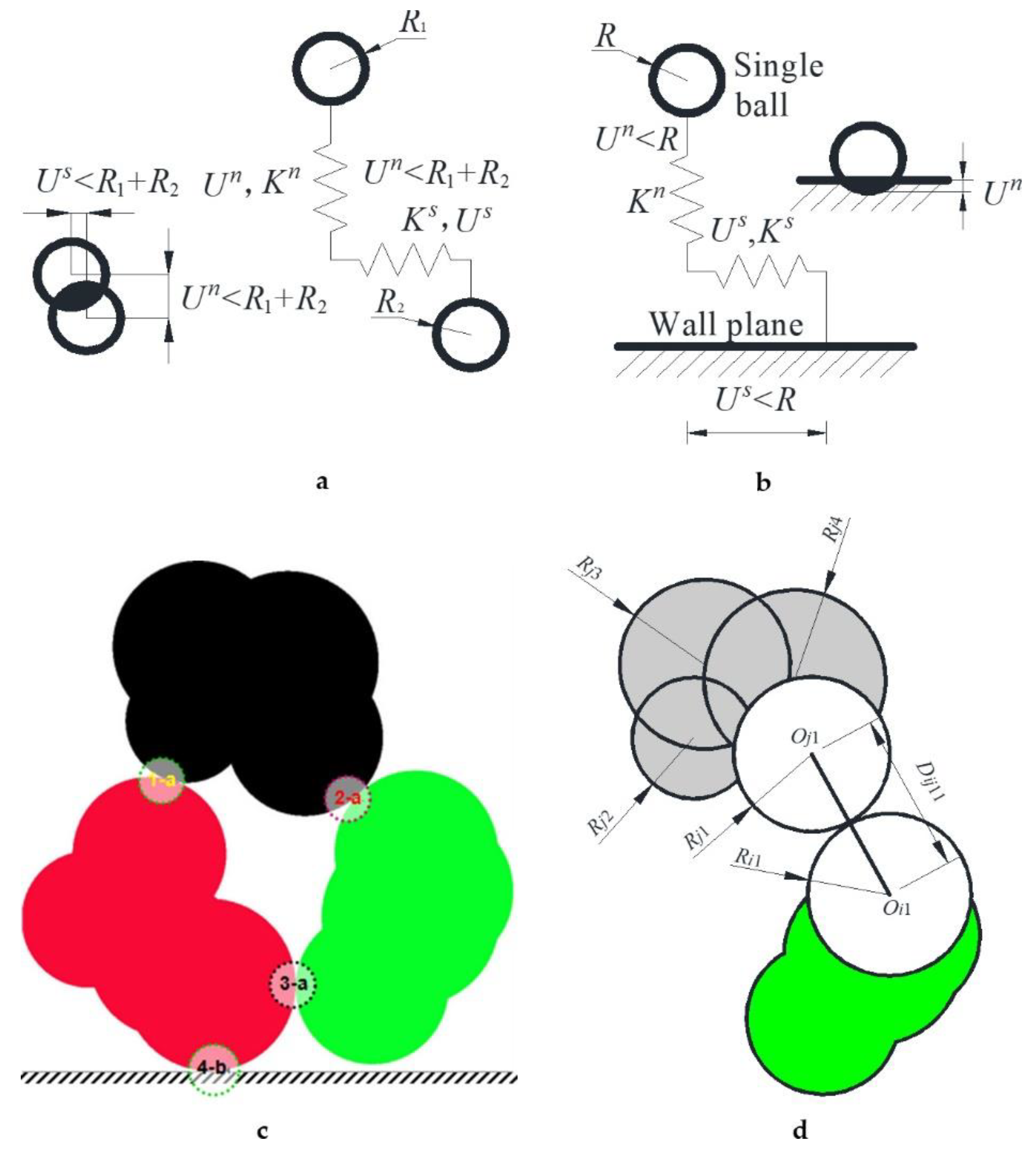
2.1. Joint Model for Soils
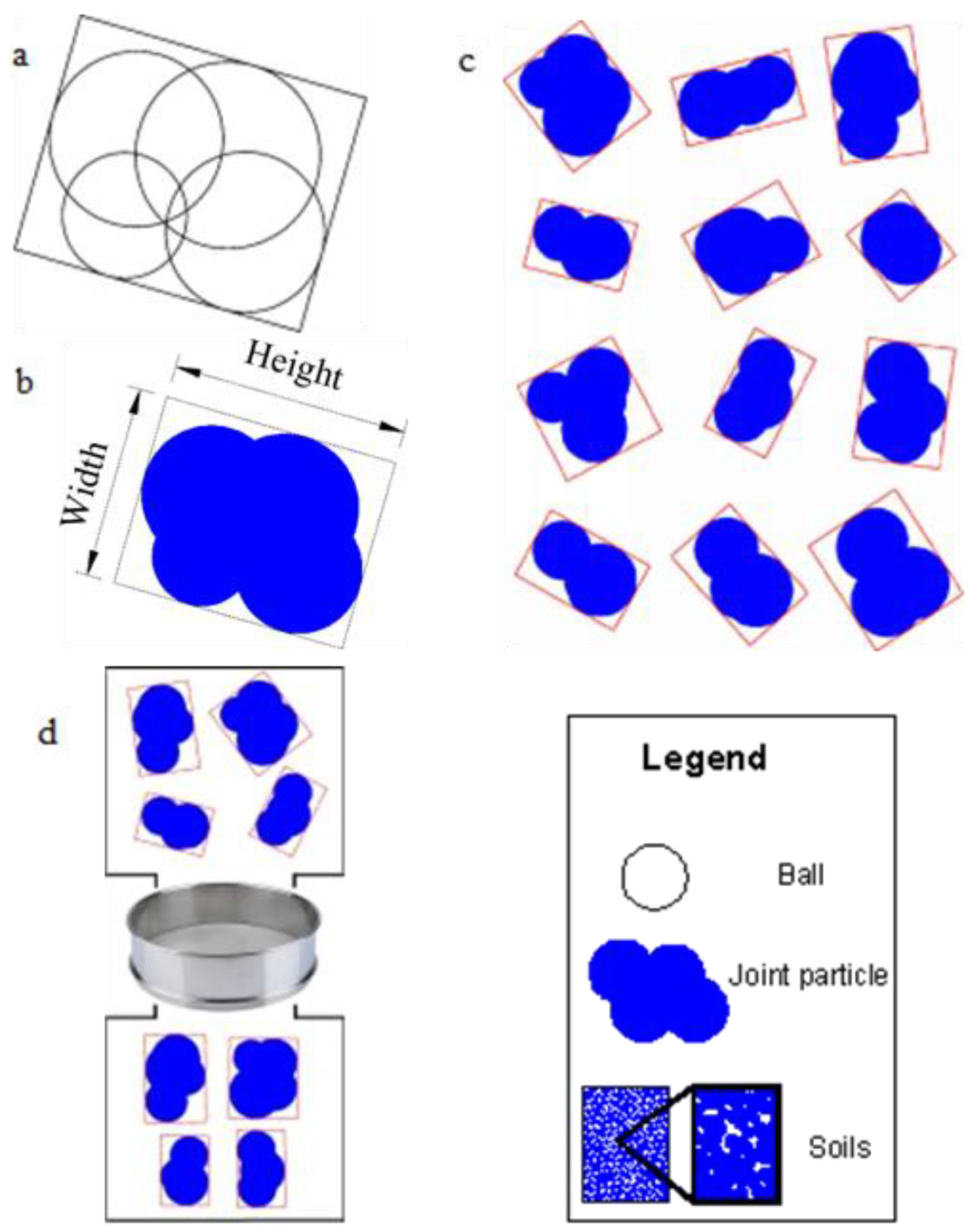
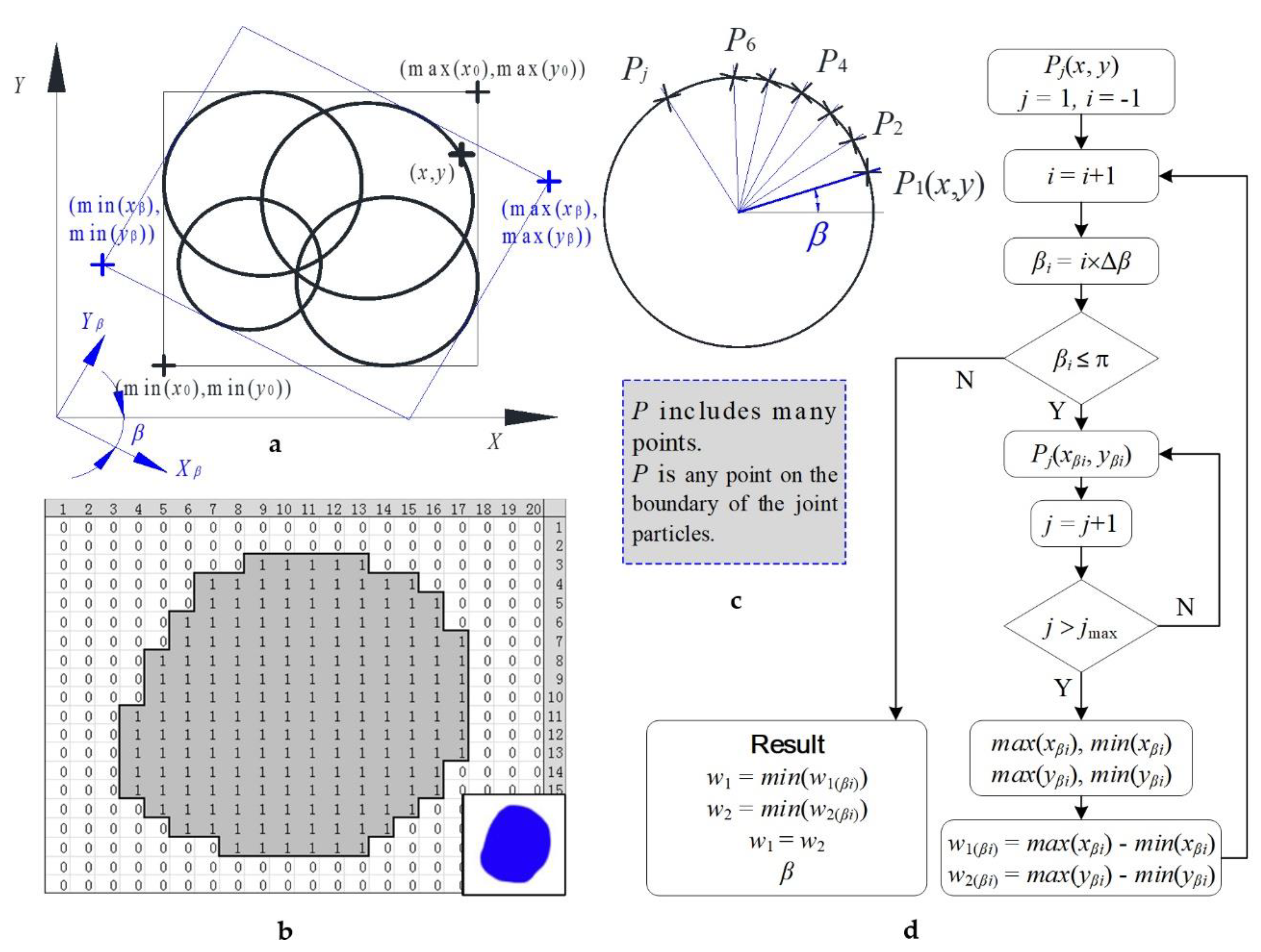
2.2. Joint Particle Size: Rotation Calculation Model
2.3. Porosity Estimation of Overlapping Particles: Pixel Counting Method
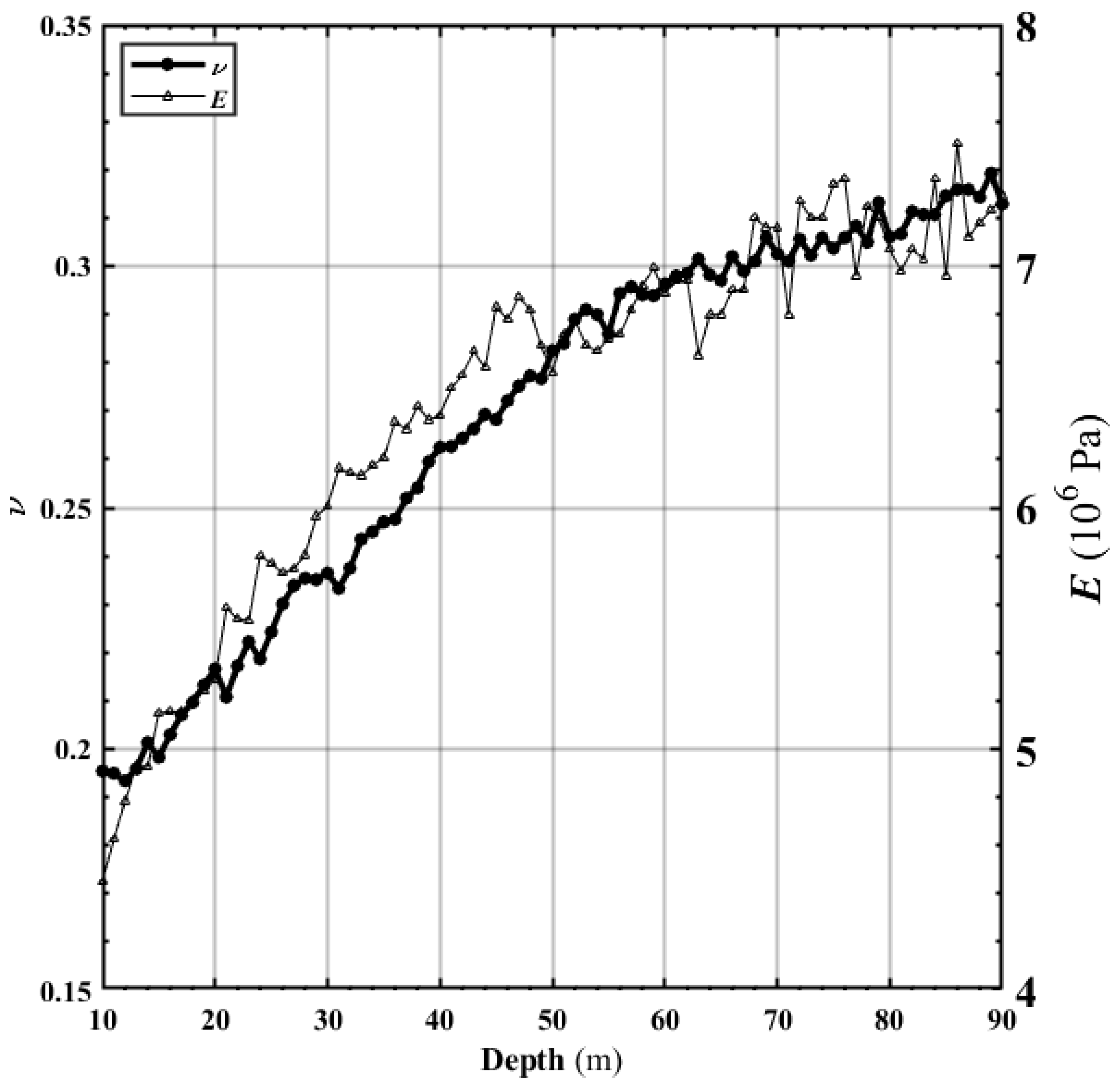
2.4. Elastic Modulus and Poisson’s Ratio
3. Example
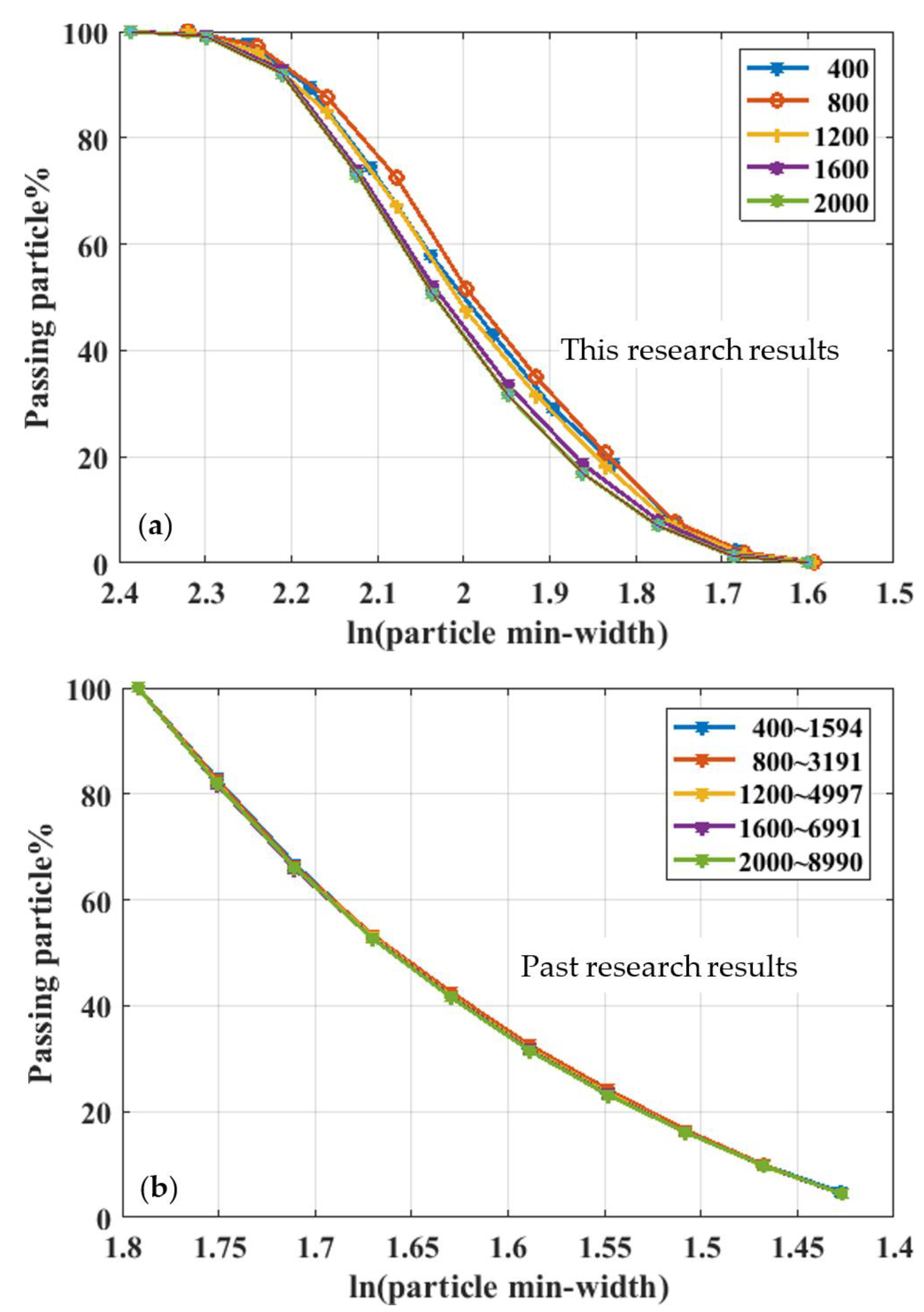
3.1. Joint Particle Size
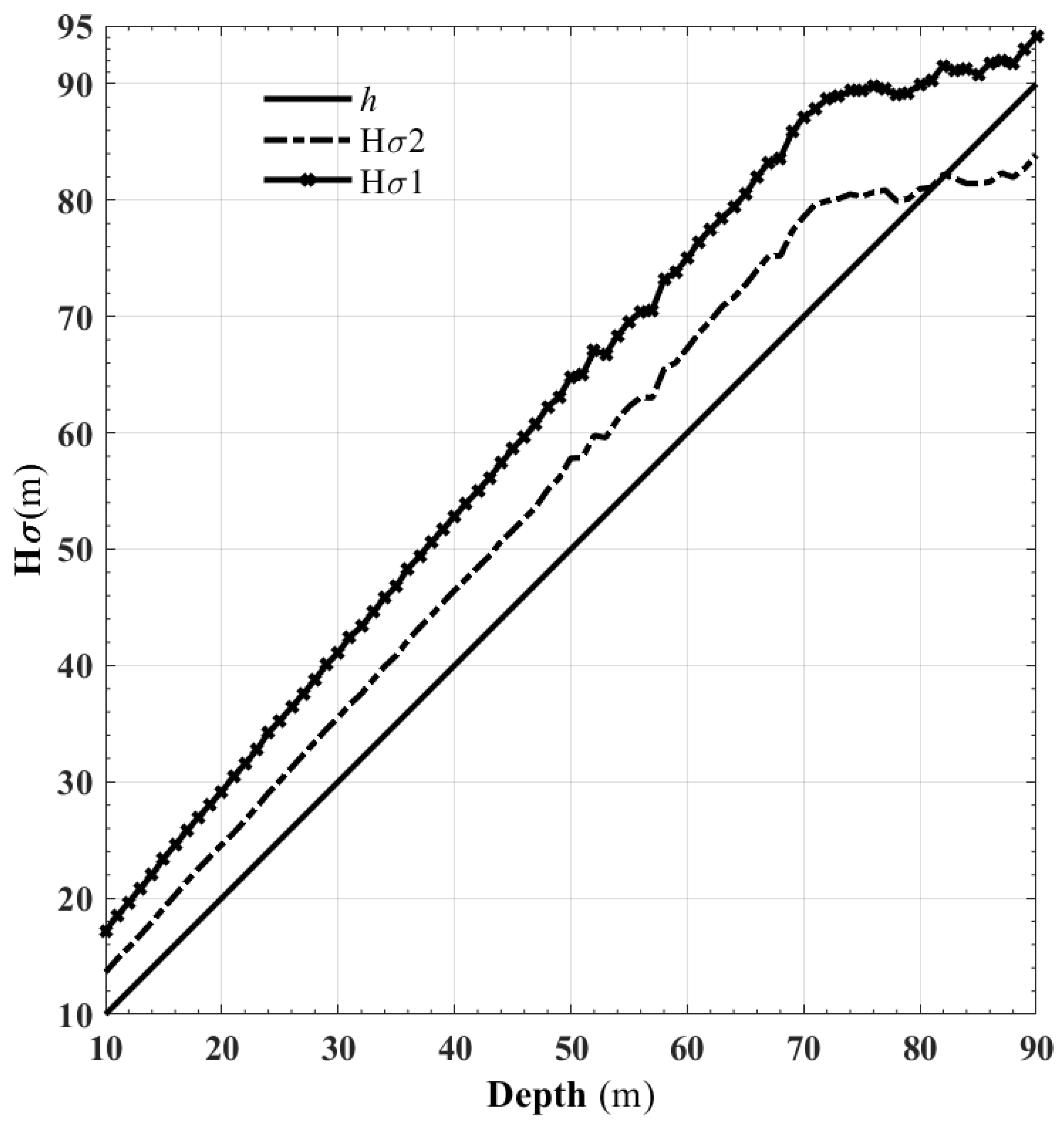
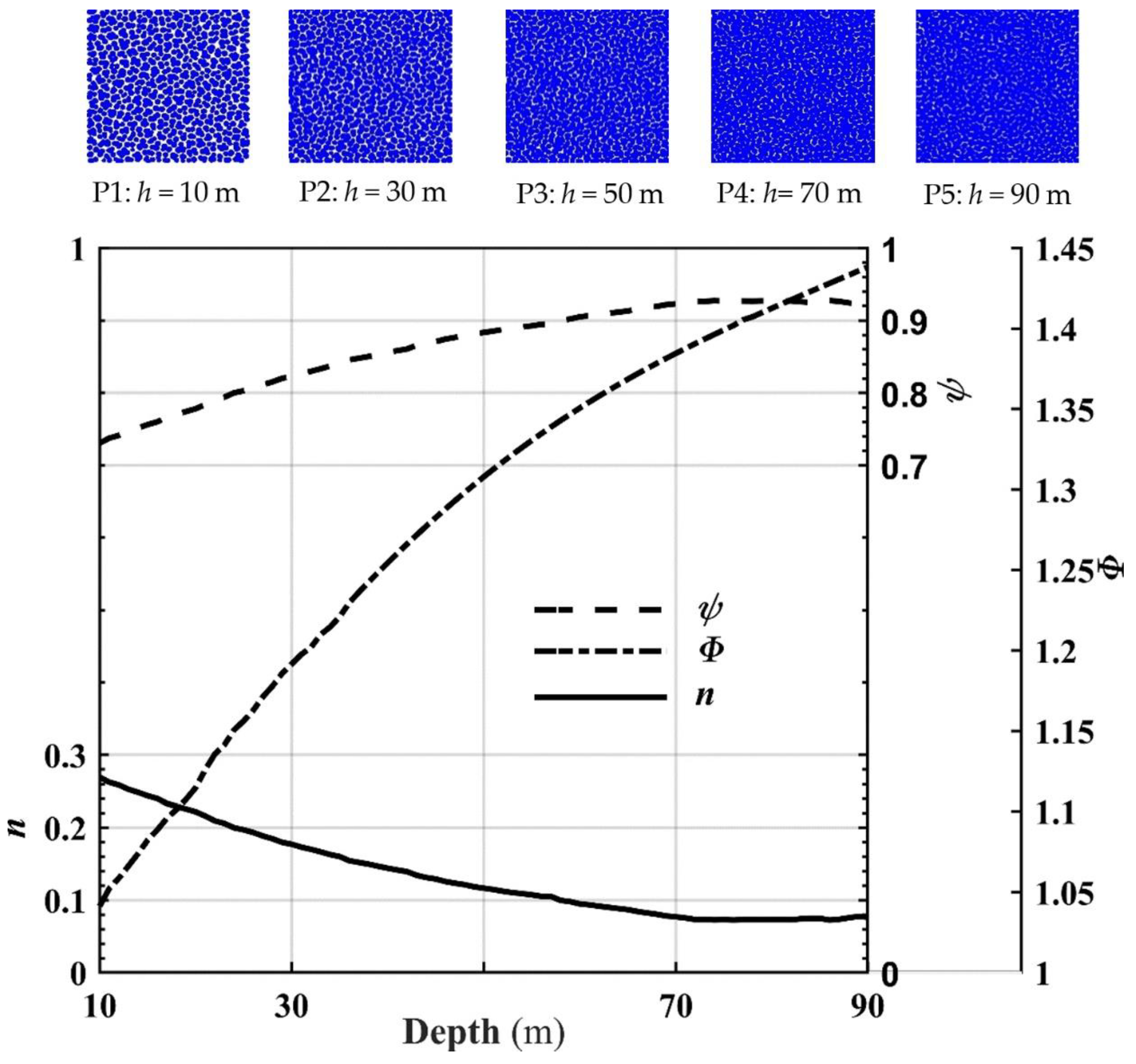
3.2. Particle Gradation and Porosity under Pressure
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Mangione, A.; Lewis, H.; Geiger, S.; Wood, R.; Beavington-Penney, S.; McQuilken, J.; Cortes, J. Combining basin modeling with high-resolution heat-flux simulations to investigate the key drivers for burial dolomitization in an offshore carbonate reservoir. Petrol. Geosci. 2018, 24, 112–130. [Google Scholar] [CrossRef] [Green Version]
- Bakhshi, E.; Rasouli, V.; Ghorbani, A.; Marji, M.F.; Damjanac, B.; Wan, X. Lattice Numerical Simulations of Lab-Scale Hydraulic Fracture and Natural Interface Interaction. Rock Mech. Rock Eng. 2019, 52, 1315–1337. [Google Scholar] [CrossRef]
- Müller, C.; Frühwirt, T.; Haase, D.; Schlegel, R.; Konietzky, H. Modeling deformation and damage of rock salt using the discrete element method. Int. J. Rock Mech. Min. Sci. 2018, 103, 230–241. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Mode For Granular Assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Sun, J. Hard particle force in a soft fracture. Sci. Rep. 2019, 9, 10. [Google Scholar] [CrossRef]
- Sun, J. Mechanical analysis about hard particles moving in a soft tube fracture. Fresenius Environ. Bull. 2019, 28, 2314–2320. [Google Scholar]
- Borykov, T.; Mege, D.; Mangeney, A.; Richard, P.; Gurgurewicz, J.; Lucas, A. Empirical investigation of friction weakening of terrestrial and Martian landslides using discrete element models. Landslides 2019, 16, 1121–1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehrpay, S.; Wang, Z.; Ueda, T. Development and application of a new discrete element into simulation of nonlinear behavior of concrete. Struct. Concr. 2020, 21, 548–569. [Google Scholar] [CrossRef]
- Sarfarazi, V.; Haeri, H.; Marji, M.F.; Zhu, Z.M. Fracture Mechanism of Brazilian Discs with Multiple Parallel Notches Using PFC2D. Period. Polytech.-Civ. Eng. 2017, 61, 653–663. [Google Scholar] [CrossRef] [Green Version]
- Sun, J. Ground sediment transport model and numerical simulation. Pol. J. Environ. Stud. 2016, 25, 1691–1697. [Google Scholar] [CrossRef]
- Haeri, H.; Sarfarazi, V.; Marji, M.F. Numerical simulation of the effect of confining pressure and tunnel depth on the vertical settlement using particle flow code (with direct tensile strength calibration in PFC Modeling). Smart Struct. Syst. 2020, 25, 433–446. [Google Scholar] [CrossRef]
- Sun, J. Permeability of Particle Soils Under Soil Pressure. Transp. Porous Media 2018, 123, 257–270. [Google Scholar] [CrossRef]
- Sinha, S.; Abousleiman, R.; Walton, G. Effect of Damping Mode in Laboratory and Field-Scale Universal Distinct Element Code (UDEC) Models. Rock Mech. Rock Eng. 2021, 1–17. [Google Scholar] [CrossRef]
- Mamot, P.; Weber, S.; Eppinger, S.; Krautblatter, M. A temperature-dependent mechanical model to assess the stability of degrading permafrost rock slopes. Earth Surf. Dyn. 2021, 9, 1125–1151. [Google Scholar] [CrossRef]
- Maljaei, S.R.; Katebi, H.; Mahdi, M.; Javadi, A.A. Modeling of Uplift Resistance of Buried Pipeline by Geogrid and Grid-Anchor System. J. Pipel. Syst. Eng. Pract. 2022, 13, 11. [Google Scholar] [CrossRef]
- Nadimi, S.; Forbes, B.; Moore, J.; McLennan, J.D. Effect of natural fractures on determining closure pressure. J. Pet. Explor. Prod. Technol. 2020, 10, 711–728. [Google Scholar] [CrossRef] [Green Version]
- Duan, K.; Kwok, C.Y. Evolution of stress-induced borehole breakout in inherently anisotropic rock: Insights from discrete element modeling. J. Geophys. Res.-Sol. Earth 2016, 121, 2361–2381. [Google Scholar] [CrossRef] [Green Version]
- Ndimande, C.B.; Cleary, P.W.; Mainza, A.N.; Sinnott, M.D. Using two-way coupled DEM-SPH to model an industrial scale Stirred Media Detritor. Miner. Eng. 2019, 137, 259–276. [Google Scholar] [CrossRef]
- Liu, L.Y.; Han, L.Z.; Shi, X.; Tan, W.; Cao, W.F.; Zhu, G.R. Hydrodynamic separation by changing equilibrium positions in contraction-expansion array channels. Microfluid. Nanofluidics 2019, 23, 12. [Google Scholar] [CrossRef]
- Chiu, C.C.; Wang, T.T.; Weng, M.C.; Huang, T.H. Modeling the anisotropic behavior of jointed rock mass using a modified smooth-joint model. Int. J. Rock Mech. Min. Sci. 2013, 62, 14–22. [Google Scholar] [CrossRef]
- Li, G.; Wang, B.B.; Wu, H.J.; DiMarco, S.F. Impact of bubble size on the integral characteristics of bubble plumes in quiescent and unstratified water. Int. J. Multiph. Flow 2020, 125, 10. [Google Scholar] [CrossRef]
- Wang, B.B.; Lai, C.C.K.; Socolofsky, S.A. Mean velocity, spreading and entrainment characteristics of weak bubble plumes in unstratified and stationary water. J. Fluid Mech. 2019, 874, 102–130. [Google Scholar] [CrossRef]
- Jiang, M.J.; Yan, H.B.; Zhu, H.H.; Utili, S. Modeling shear behavior and strain localization in cemented sands by two-dimensional distinct element method analyses. Comput. Geotech. 2011, 38, 14–29. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Malama, B.; Wang, J. Physical and particle flow modeling of jointed rock block behavior under uniaxial loading. Int. J. Rock Mech. Min. Sci. 2001, 38, 641–657. [Google Scholar] [CrossRef]
- Lian, C.; Yan, Z.; Beecham, S. Numerical simulation of the mechanical behaviour of porous concrete. Eng. Comput. 2011, 28, 984–1002. [Google Scholar] [CrossRef]
- Das, B.M. Advanced Soil Mechanics, 3rd ed.; Taylor & Francis: New York, NY, USA, 2008. [Google Scholar]
- Aysen, A. Problem Solving in Soil Mechanics; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Sun, J.; Wang, G. Transport model of underground sediment in soils. Sci. World J. 2013, 367918. [Google Scholar] [CrossRef]
- Sun, J.; Wang, G. Research on underground water pollution caused by geological fault through radioactive stratum. J. Radioanal. Nucl. Chem. 2013, 297, 27–32. [Google Scholar]
- Ajamzadeh, M.R.; Sarfarazi, V.; Haeri, H.; Dehghani, H. The effect of micro parameters of PFC software on the model calibration. Smart Struct. Syst. 2018, 22, 643–662. [Google Scholar] [CrossRef]
- Group, I.C. PFC2D (Particle Flow Code in 2 Dimensions) Fish in PFC2D; Itasca Consulting Group Press: Minneapolis, MN, USA, 2008; Available online: https://www.itascacg.com/ (accessed on 1 November 2008).
- Sun, J. Joint particles model database for discrete element numerical simulation. Int. J. Ground Sediment Water 2022, 16, 973–976. [Google Scholar]
- Committee, E.G.H.C. Engineering Geology Handbook; China Architecture and Building Press: Beijing, China, 2007. [Google Scholar]
- Mercerat, E.; Souley, M.; Driad, L.; Bernard, P. Induced seismicity in a salt mine environment evaluated by a coupled continuum-discrete modelling. Symp. Post Min. 2005, ineris-00972514. Available online: https://hal-ineris.archives-ouvertes.fr/ineris-00972514 (accessed on 17 January 2022).
- Monkul, M.M.; Etminan, E.; Senol, A. Influence of coefficient of uniformity and base sand gradation on static liquefaction of loose sands with silt. Soil Dyn. Earthq. Eng. 2016, 89, 185–197. [Google Scholar] [CrossRef]
- Keaton, J.R. Coefficient of Uniformity. In Encyclopedia of Engineering Geology; Bobrowsky, P.T., Marker, B., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.K.; Neekhra, S.; Zollinger, D.G. Preliminary Characterization of Aggregate Coefficient of Thermal Expansion and Gradation for Paving Concrete; Technical Report 0-1700-5; Texas Transportation Institute: College Station, TX, USA, 2007. [Google Scholar]
- Hanmaiahgari, P.R.; Gompa, N.R.; Pal, D.; Pu, J.H. Numerical modeling of the Sakuma Dam reservoir sedimentation. Nat. Hazards 2018, 91, 1075–1096. [Google Scholar] [CrossRef] [Green Version]
- Martineau, B. Formulation of a general gradation curve and its transformation to equivalent sigmoid form to represent grain size distribution. Road Mater. Pavement Des. 2017, 18, 199–207. [Google Scholar] [CrossRef]
- Armstrong, P.A.; Allis, R.G.; Funnell, R.H.; Chapman, D.S. Late Neogene exhumation patterns in Taranaki Basin (New Zealand): Evidence from offset porosity-depth trends. J. Geophys. Res.-Sol. Earth 1998, 103, 30269–30282. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Teng, J.W.; Wang, Q.S.; Lu, Q.T.; Si, X.; Xu, T.; Badal, J.; Yan, J.Y.; Hao, Z.B. A gravity study along a profile across the Sichuan Basin, the Qinling Mountains and the Ordos Basin (central China): Density, isostasy and dynamics. J. Asian Earth Sci. 2017, 147, 310–321. [Google Scholar] [CrossRef]
- Ramm, M.; Bjorlykke, K. Porosity depth trends in reservoir sandstones—Assessing the quantitative effects of varying pore-pressure, temperature history and mineralogy, Norwegian shelf data. Clay Miner. 1994, 29, 475–490. [Google Scholar] [CrossRef]
- Ramm, M. Porosity-depth trends in reservoir sandstones: Theoretical models related to Jurassic sandstones offshore Norway. Mar. Petrol. Geol. 1992, 9, 553–567. [Google Scholar] [CrossRef]
- Bahrani, N.; Kaiser, P.K. Numerical investigation of the influence of specimen size on the unconfined strength of defected rocks. Comput. Geotech. 2016, 77, 56–67. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhou, G.Q.; Liu, J. DEM Research on Influence Factors of Particle Crushing of Sand; Int Industrial Electronic Center: Sham Shui Po, Hong Kong, 2011; pp. 166–171. [Google Scholar]
- Jia, X.; Jia, X.; Chai, H.; Chai, H.; Yan, Z.; Yan, Z.; Zheng, Y.; Zheng, Y. PFC2D simulation research on vibrating compaction test of soil and rock aggregate mixture. In Proceedings of the Bearing Capacity of Roads, Railways and Airfields. 8th International Conference (BCR2A’09), Champaign, IL, USA, 29 June–2 July 2009. [Google Scholar]
- Meng, Y.W.; Jia, X.M.; Chai, H.J. PFC3D Simulation Research on Vibrating Compaction Test of Soil and Rock Aggregate Mixture; CRC Press-Taylor & Francis Group: Boca Raton, FL, USA, 2011; pp. 565–569. [Google Scholar]
- Shen, S.H.; Yu, H.A. Characterize packing of aggregate particles for paving materials: Particle size impact. Constr. Build. Mater. 2011, 25, 1362–1368. [Google Scholar] [CrossRef]
- Sun, J. Survey and research frame for ground sediment. Environ. Sci. Pollut. Res. 2016, 23, 18960–18965. [Google Scholar] [CrossRef] [Green Version]
- Tellez, J.; Cordoba, D. Crustal shear-wave velocity and Poisson’s ratio distribution in northwest Spain. J. Geodyn. 1998, 25, 35–45. [Google Scholar] [CrossRef]
- Heap, M.J.; Baud, P.; Meredith, P.G.; Vinciguerra, S.; Reuschle, T. The permeability and elastic moduli of tuff from Campi Flegrei, Italy: Implications for ground deformation modelling. Solid Earth 2014, 5, 25–44. [Google Scholar] [CrossRef] [Green Version]

| Number of Particles | Combined Particles | Single Ball | Error | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D10 | D30 | D60 | Cc | Cu | D10 | D30 | D60 | Cc | Cu | |Ccc-Ccs|/Ccc % | |Cuc-Cus|/Cuc % | |
| 400 | 5.87 | 6.692 | 7.744 | 0.985 | 1.319 | 4.342 | 4.842 | 5.427 | 0.995 | 1.250 | 1.016 | 5.245 |
| 800 | 5.881 | 6.605 | 7.605 | 0.975 | 1.293 | 4.340 | 4.840 | 5.430 | 0.994 | 1.251 | 1.951 | 3.243 |
| 1200 | 5.934 | 6.731 | 7.758 | 0.984 | 1.307 | 4.349 | 4.854 | 5.435 | 0.997 | 1.250 | 1.322 | 4.375 |
| 1600 | 6.009 | 6.885 | 7.904 | 0.998 | 1.315 | 4.344 | 4.864 | 5.441 | 1.001 | 1.252 | 0.301 | 4.766 |
| 2000 | 6.082 | 6.961 | 7.943 | 1.003 | 1.306 | 4.344 | 4.864 | 5.435 | 1.002 | 1.251 | 0.100 | 4.206 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Huang, Y. Modeling the Simultaneous Effects of Particle Size and Porosity in Simulating Geo-Materials. Materials 2022, 15, 1576. https://doi.org/10.3390/ma15041576
Sun J, Huang Y. Modeling the Simultaneous Effects of Particle Size and Porosity in Simulating Geo-Materials. Materials. 2022; 15(4):1576. https://doi.org/10.3390/ma15041576
Chicago/Turabian StyleSun, Jichao, and Yuefei Huang. 2022. "Modeling the Simultaneous Effects of Particle Size and Porosity in Simulating Geo-Materials" Materials 15, no. 4: 1576. https://doi.org/10.3390/ma15041576
APA StyleSun, J., & Huang, Y. (2022). Modeling the Simultaneous Effects of Particle Size and Porosity in Simulating Geo-Materials. Materials, 15(4), 1576. https://doi.org/10.3390/ma15041576






