RC Medium-Rise Building Damage Sensitivity with SSI Effect
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rocking and Structural Frequencies of Medium-Rise Reinforced Concrete Buildings
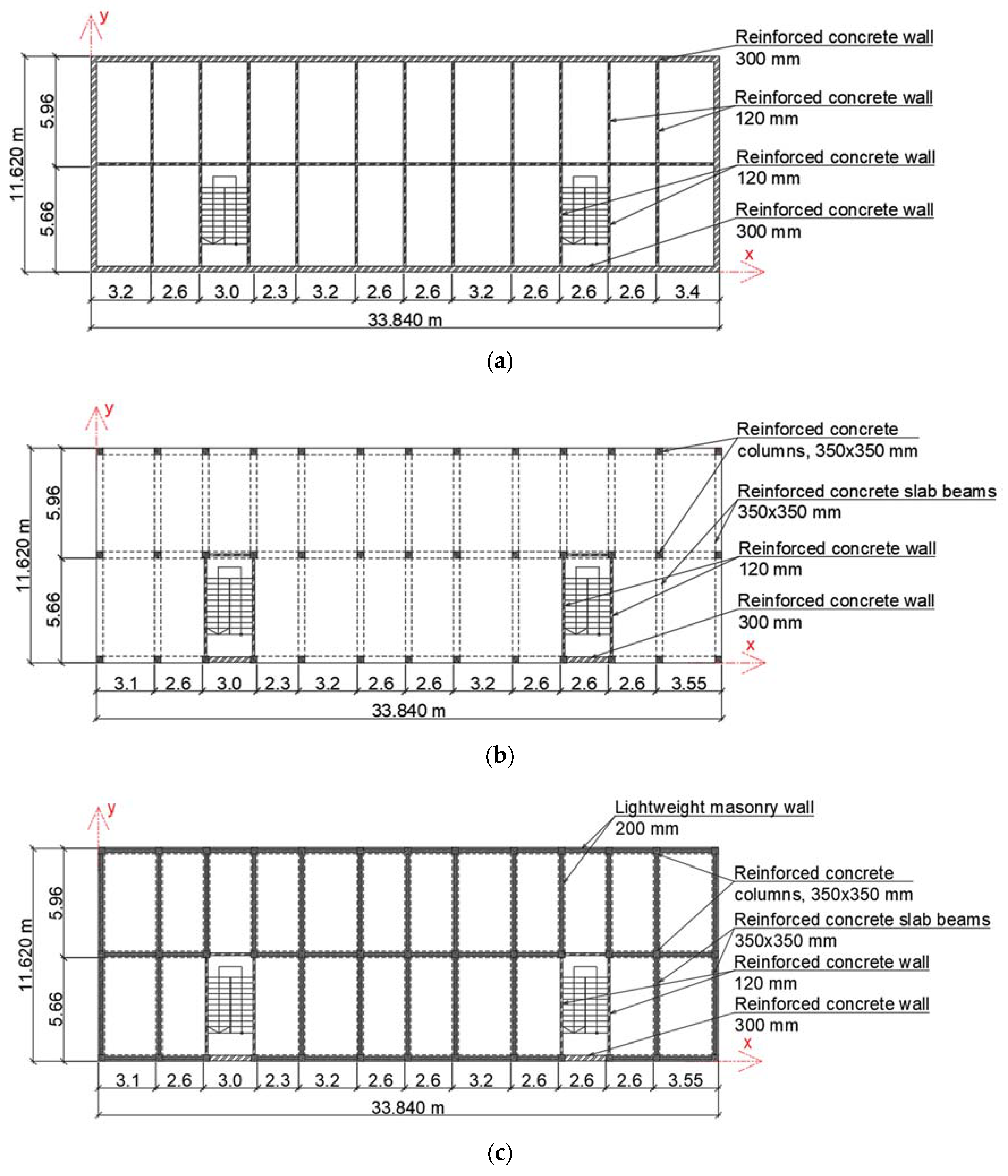
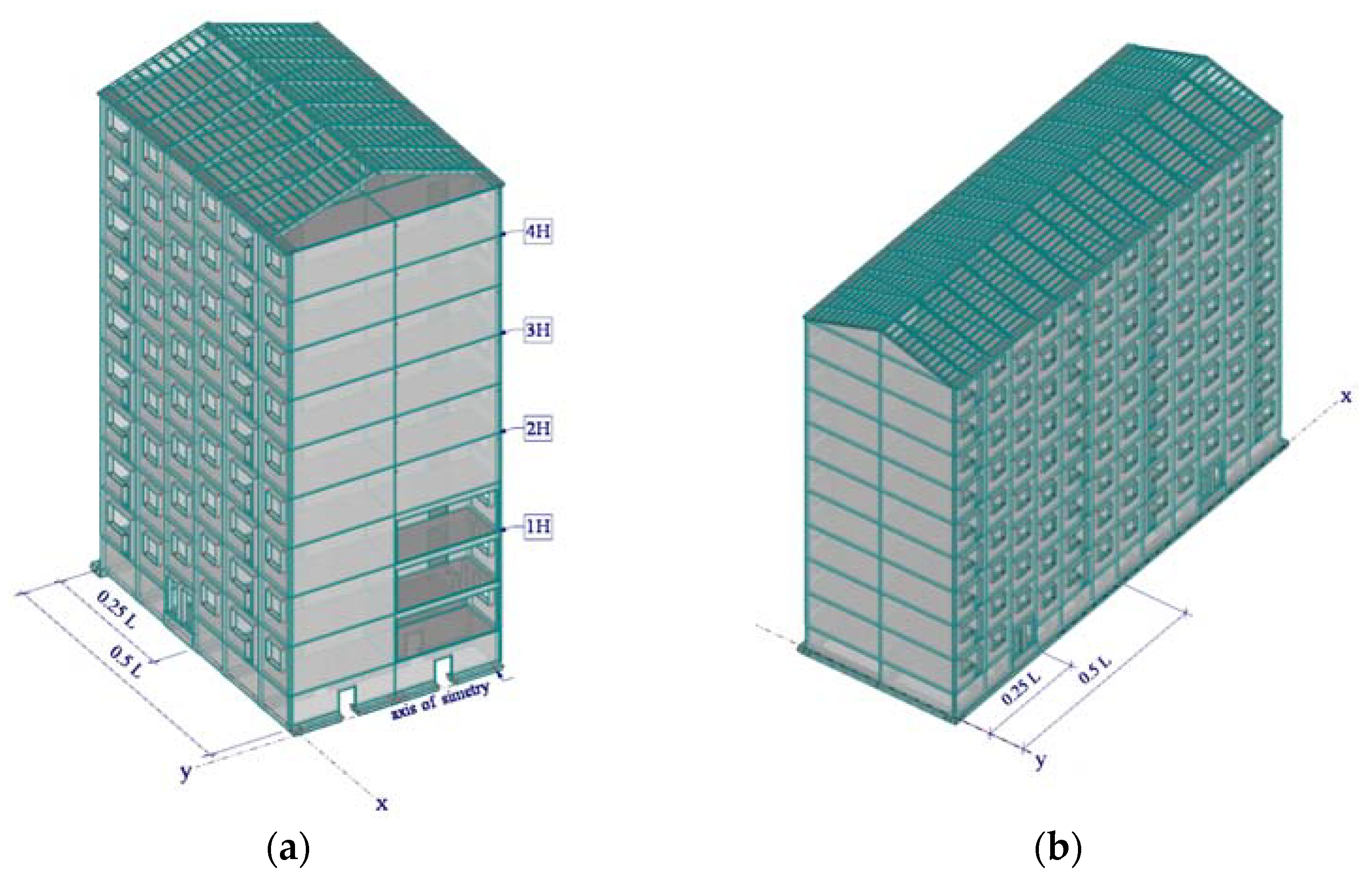
2.2. Data for the Numerical Study
- cellular structure, reinforced concrete (RC) building (reference model #1);
- frame structure, RC building (reference model #2);
- frame structure with masonry infill walls, RC building (reference model #3).
3. Results
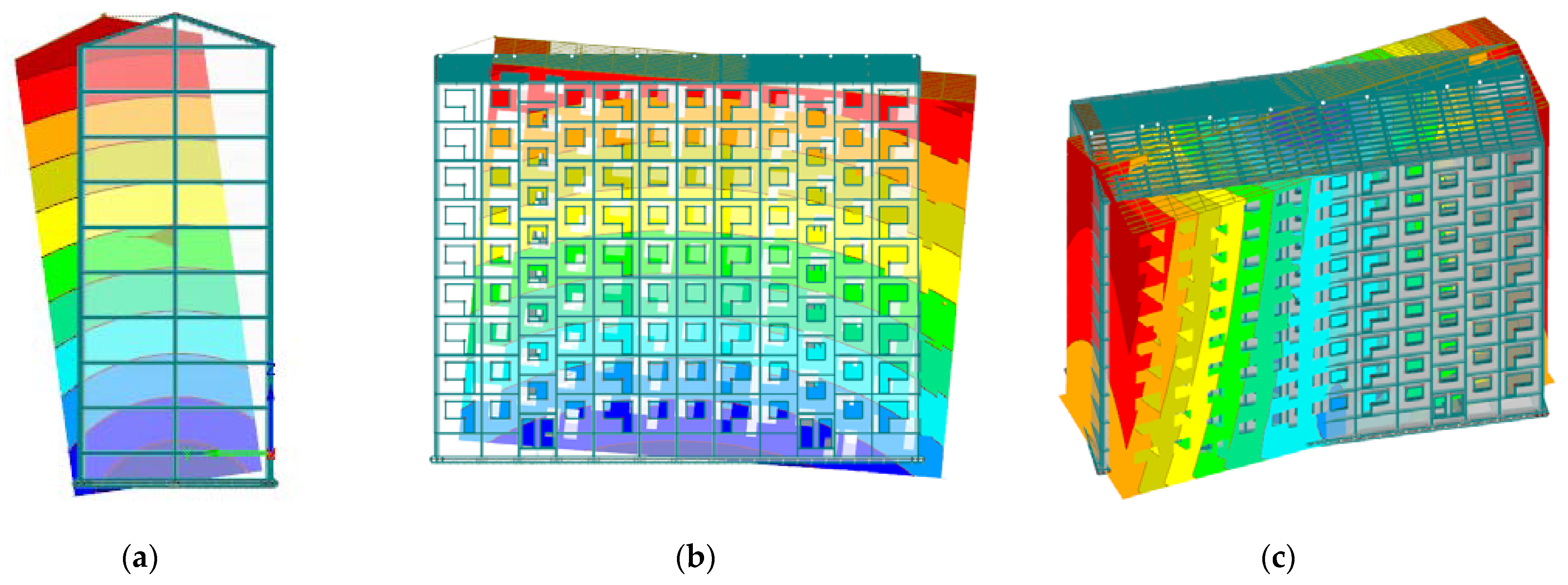
3.1. Modal Components of Medium-Rise RC Buildings
3.2. Effect of Structural Changes on the Natural Frequencies of RC Building
4. Discussion
5. Conclusions
- -
- For structural damage monitoring purposes of stiff medium-rise buildings (cellular type or moment-frame with infills), structural frequency (fixed base model) should be used instead of fundamental frequency (which includes the SSI effect); practically, this can be done by firstly identifying rocking frequency and fundamental frequency before calculating structural frequency;
- -
- Statistical significance levels for structural frequency changes should be adopted at no more than 0.1% for such rigid buildings when aiming for damage detection in vertical loadbearing building elements. This requires experimental modal identification procedures performed with less than 0.1% uncertainty.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Cha, Y.-J.; Kim, Y.; You, T. Advanced Sensing and Structural Health Monitoring. J. Sens. 2018, 2018, 7286069. [Google Scholar] [CrossRef] [Green Version]
- Bies, D.A. Engineering Noise Control; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2010, 10, 83–111. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L. Frequency domain decomposition revisited. In Proceedings of the IOMAC 2009—3rd International Operational Modal Analysis Conference, Portonovo, Italy, 4–6 May 2009; pp. 615–626. [Google Scholar]
- Amador, S.; Lysgaard, P.; Amador, S.D.R.; Brincker, R. Vibration-Based Damage Detection Using Input-Output and Output-Only Environmental Models: A Comparison. Available online: https://www.researchgate.net/publication/339310311 (accessed on 12 December 2021).
- Sentosa, B.-O.-B.; Bui, Q.-B.; Ple, O.; Plassiard, J.-P.; Perrotin, P. Assessing Damage to Beam–Column Connections in Reinforced Concrete Structures from Vibrational Measurement Results. Struct. Eng. Int. 2019, 29, 396–403. [Google Scholar] [CrossRef]
- Xu, G.Y.; Zhu, W.D.; Emory, B.H. Experimental and numerical investigation of structural damage detection using changes in natural frequencies. J. Vib. Acoust. Trans. ASME 2007, 129, 686–700. [Google Scholar] [CrossRef]
- Ruggieri, S.; Fiore, A.; Uva, G. A New Approach to Predict the Fundamental Period of Vibration for Newly-designed Reinforced Concrete Buildings. J. Earthq. Eng. 2021, 1–26. [Google Scholar] [CrossRef]
- NEHRP Consultants Joint Venture. Soil-Structure Interaction for Building Structures. Nist Gcr 2012, 12, 917–921. [Google Scholar]
- Gravett, D.Z.; Mourlas, C.; Taljaard, V.-L.; Bakas, N.; Markou, G.; Papadrakakis, M. New fundamental period formulae for soil-reinforced concrete structures interaction using machine learning algorithms and ANNs. Soil Dyn. Earthq. Eng. 2021, 144, 106656. [Google Scholar] [CrossRef]
- Kabtamu, H.G.; Peng, G.; Chen, D. Dynamic Analysis of Soil Structure Interaction Effect on Multi Story RC Frame. Open J. Civ. Eng. 2018, 08, 426–446. [Google Scholar] [CrossRef] [Green Version]
- Ratnika, L.; Gaile, L.; Vatin, N. Impact of Groundwater Level Change on Natural Frequencies of RC Buildings. Buildings 2021, 11, 265. [Google Scholar] [CrossRef]
- Chopra, A.K.; Yim, S.C. Simplified Earthquake Analysis of Structures with Foundation Uplift. J. Struct. Eng. 1985, 111, 906–930. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Todorovska, M.I.; Manić, M.I.; Bulajić, B.Đ. Threshold changes in building frequencies of vibration associated with structural damage–study of full-scale observations in the Borik-2 Building in Former Yugoslavia. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Hans, S.; Boutin, C. Dynamics of discrete framed structures: A unified homogenized description. J. Mech. Mater. Struct. 2008, 3, 1709–1739. [Google Scholar] [CrossRef] [Green Version]
- Acikgoz, S.; DeJong, M.J. Analytical modelling of multi-mass flexible rocking structures. Earthq. Eng. Struct. Dyn. 2016, 45, 2103–2122. [Google Scholar] [CrossRef]
- Ivanović, S.; Trifunac, M.; Novikova, E.; Gladkov, A.; Todorovska, M. Ambient vibration tests of a seven-story reinforced concrete building in Van Nuys, California, damaged by the 1994 Northridge earthquake. Soil Dyn. Earthq. Eng. 2000, 19, 391–411. [Google Scholar] [CrossRef]
- Gallipoli, M.R.; Mucciarelli, M.; Šket-Motnikar, B.; Zupanćić, P.; Gosar, A.; Prevolnik, S.; Herak, M.; Stipčević, J.; Herak, D.; Milutinović, Z.; et al. Empirical estimates of dynamic parameters on a large set of European buildings. Bull. Earthq. Eng. 2009, 8, 593–607. [Google Scholar] [CrossRef]
- Oliveira, C.S.; Navarro, M. Fundamental periods of vibration of RC buildings in Portugal from in-situ experimental and numerical techniques. Bull. Earthq. Eng. 2010, 8, 609–642. [Google Scholar] [CrossRef]
- Goel, R.K.; Chopra, A.K. Period Formulas for Moment-Resisting Frame Buildings. J. Struct. Eng. 1997, 123, 1454–1461. [Google Scholar] [CrossRef] [Green Version]
- Gaile, L.; Sliseris, J.; Ratnika, L. Towards SHM of medium-rise buildings in non-seismic areas. In Proceedings of the 10th International Conference on Structural Health Monitoring of Untelligent Infrastructure, SHMII 10, Porto, Portugal, 30 June–2 July 2021; pp. 1–8. [Google Scholar]
- Psycharis, I.N. Dynamics of flexible systems with partial lift-off. Earthq. Eng. Struct. Dyn. 1983, 11, 501–521. [Google Scholar] [CrossRef]
- Palmeri, A.; Makris, N. Response analysis of rigid structures rocking on viscoelastic foundation. Earthq. Eng. Struct. Dyn. 2008, 37, 1039–1063. [Google Scholar] [CrossRef]
- Di Trapani, F.; Bertagnoli, G.; Ferrotto, M.F.; Gino, D. Empirical Equations for the Direct Definition of Stress–Strain Laws for Fiber-Section-Based Macromodeling of Infilled Frames. J. Eng. Mech. 2018, 144, 04018101. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Englewood Cliffs: Prentice Hall, NJ, USA, 1996; p. 1037. [Google Scholar]
- Knappett, J.; Craig, R.F. Craig’s Soil Mechanics; CRC Press: London, UK, 2019. [Google Scholar] [CrossRef]
- Akehashi, H.; Kojima, K.; Fujita, K.; Takewaki, I. Critical Response of Nonlinear Base-Isolated Building Considering Soil-Structure Interaction Under Double Impulse as Substitute for Near-Fault Ground Motion. Front. Built Environ. 2018, 4, 34. [Google Scholar] [CrossRef]
- Gueguen, P.; Bard, P.Y. Soil-structure and soil-structure-soil interaction: Experimental evidence at the Volvi test site. J. Earthq. Eng. 2005, 9, 657–693. [Google Scholar] [CrossRef]
- Hashemi, B.H.; Legzian, G.; Hosseini, M. A study on the behavior of structures based on the rocking motion of rigid cores involving pre-compressed springs and viscous dampers. J. Vibroeng. 2019, 21, 2180–2195. [Google Scholar] [CrossRef]
- Nozari, A.; Behmanesh, I.; Yousefianmoghadam, S.; Moaveni, B.; Stavridis, A. Effects of variability in ambient vibration data on model updating and damage identification of a 10-story building. Eng. Struct. 2017, 151, 540–553. [Google Scholar] [CrossRef]

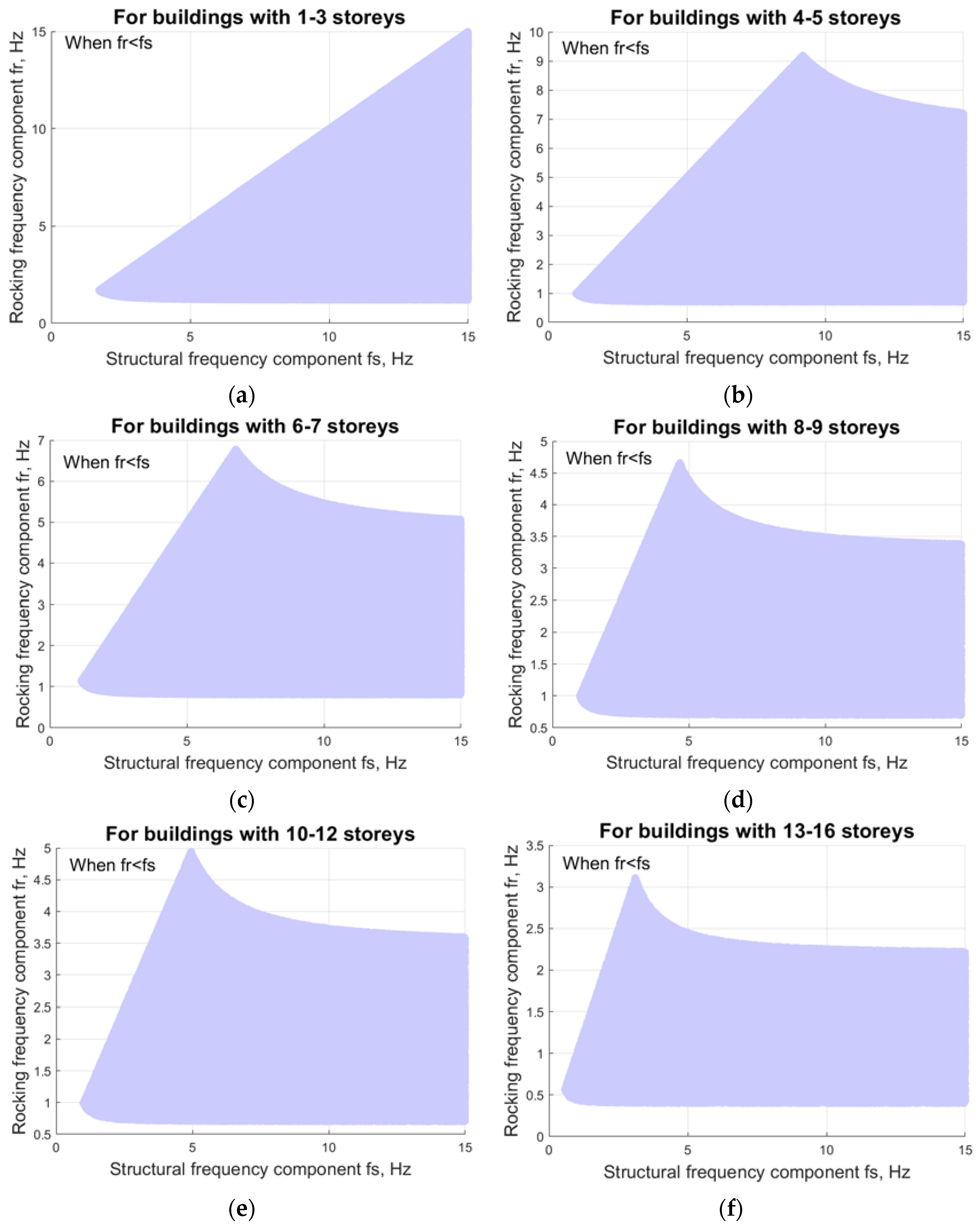




| Number of Stories (Number of Assessed Buildings) | Typical Fundamental Frequency Range, Hz | Mean (Standard Deviation), Hz |
|---|---|---|
| 1–3 (63) | 1.2–12.5 | 6.1 (2.8) |
| 4–5 (108) | 0.7–6.5 | 3.8 (1.2) |
| 6–7 (91) | 0.8–4.8 | 2.8 (0.8) |
| 8–9 (71) | 0.7–3.3 | 2.1 (0.6) |
| 10–12 (86) | 0.7–3.5 | 1.9 (0.6) |
| 13–16 (53) | 0.4–2.2 | 1.3 (0.4) |
| Type of Element | Model #1 | Model #2 | Model #3 |
|---|---|---|---|
| Main vertical elements | Shear walls with thickness 120 mm | Columns 350 × 350 | Columns 350 × 350 |
| Floor slabs | 100 mm | 100 mm | 100 mm |
| Roof slab | 100 mm | 100 mm | 100 mm |
| Infill walls | - | - | Lightweight masonry wall 200 mm |
| Foundation | Strip foundation 800 × 400 (h) mm | Strip foundation 800 × 400 (h) mm | Strip foundation 800 × 400 (h) mm |
| Global stiffness (direction x) | 1,617,143 kN/m | 27,610 kN/m | 1,415,000 kN/m |
| Global stiffness (direction y) | 1,197,857 kN/m | 27,180 kN/m | 1,081,935 kN/m |
| Total mass of building 1 | 8,386,020.66 kg | 3,741,773.96 kg | 8,308,993.32 kg |
| Soil Description | Soil Layer Parameters | |||||
|---|---|---|---|---|---|---|
| Specific Weight | Modulus of Elasticity, MN/m2 | Poisson’s Ratio ν | Thickness, m | Ordinate from Ground Level, m | ||
| Unsaturated Weight γ, kN/m3 | Saturated Weight γsat, kN/m3 | |||||
| Sand, closely graded | 17.0 | 19.0 | 30.0 | 0.30 | 0.80 | 0.80 |
| Sand | 19.0 | 21.0 | 30.0 | 0.30 | 3.0 | 3.80 |
| Dusty sand | 18.0 | 20.3 | 18.0 | 0.30 | 4.0 | 7.80 |
| Sand, gravelly sand | 18.0 | 20.0 | 20.0 | 0.30 | 8.20 | 16.0 |
| Soil Description | Soil Layer Parameters | |||||
|---|---|---|---|---|---|---|
| Specific Weight | Modulus of Elasticity, MN/m2 | Poisson’s Ratio ν | Thickness, m | Ordinate from Ground Level, m | ||
| Unsaturated Weight γ, kN/m3 | Saturated Weight γsat, kN/m3 | |||||
| Sand, closely graded | 17.0 | 19.0 | 30.0 | 0.30 | 0.80 | 0.80 |
| Sand | 19.0 | 21.0 | 30.0 | 0.30 | 3.0 | 3.80 |
| Clay, low plasticity | 19.0 | 19.5 | 2.50 | 0.42 | 4.50 | 8.30 |
| Sand–clay mixture | 18.0 | 19.0 | 10.0 | 0.35 | 7.70 | 16.0 |
| Soil Description | Soil Layer Parameters | |||||
|---|---|---|---|---|---|---|
| Specific Weight | Modulus of Elasticity, MN/m2 | Poisson’s Ratio ν | Thickness, m | Ordinate from Ground Level, m | ||
| Unsaturated Weight γ, kN/m3 | Saturated Weight γsat, kN/m3 | |||||
| Sand, closely graded | 17.0 | 19.0 | 30.0 | 0.30 | 0.80 | 0.80 |
| Sand | 19.0 | 21.0 | 30.0 | 0.30 | 3.0 | 3.80 |
| Peat | 10.40 | 10.40 | 1.0 | 0.40 | 0.80 | 4.60 |
| Dusty sand | 18.0 | 20.3 | 18.0 | 0.30 | 3.7 | 8.30 |
| Sand, gravelly sand | 18.0 | 20.0 | 20.0 | 0.30 | 7.7 | 16.0 |
| Type of Soil | Para-Meter 2 | Mode # of Model #1 | Mode # of Model #2 | Mode # of Model #3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lateral | Longitudinal | Torsional | Lateral | Longitudinal | Torsional | Lateral | Longitudinal | Torsional | ||
| I | f1 | 1.255 | 1.973 | 2.171 | 0.518 | 0.630 | 0.702 | 1.215 | 1.897 | 2.128 |
| fs | 5.339 | 6.800 | 7.481 | 0.854 | 0.903 | 1.077 | 4.965 | 5.844 | 6.392 | |
| fr | 1.291 | 2.062 | 2.269 | 0.652 | 0.879 | 0.926 | 1.253 | 2.006 | 2.257 | |
| fs/f1 | 4.25 | 3.45 | 3.45 | 1.65 | 1.43 3 | 1.53 | 4.09 | 3.08 | 3.00 | |
| II | f1 | 0.867 | 1.628 | 2.164 | 0.433 | 0.603 | 0.670 | 0.838 | 1.573 | 2.113 |
| fs | 5.339 | 6.800 | 7.481 | 0.854 | 0.903 | 1.077 | 4.965 | 5.844 | 6.392 | |
| fr | 0.879 | 1.677 | 2.261 | 0.518 | 0.810 | 0.856 | 0.850 | 1.633 | 2.239 | |
| fs/f1 | 6.16 | 4.18 | 3.46 | 1.97 | 1.50 | 1.61 | 5.92 | 3.72 | 3.03 | |
| III | f1 | 1.025 | 1.796 | 2.166 | 0.476 | 0.615 | 0.684 | 0.993 | 1.73 | 2.118 |
| fs | 5.339 | 6.800 | 7.481 | 0.854 | 0.903 | 1.077 | 4.965 | 5.844 | 6.392 | |
| fr | 1.044 | 1.862 | 2.263 | 0.573 | 0.840 | 0.886 | 1.013 | 1.811 | 2.245 | |
| fs/f1 | 5.21 | 3.79 | 3.45 | 1.79 | 1.47 | 1.57 | 5.00 | 3.38 | 3.02 | |
| Type of Soil | Parameter 1 | Mode # of Model #1 | Mode # of Model #2 | Mode # of Model #3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lateral | Longitudinal | Torsional | Lateral | Longitudinal | Torsional | Lateral | Longitudinal | Torsional | ||
| I | fr | 1.291 | 2.062 | 2.269 | 0.652 | 0.879 | 0.926 | 1.253 | 2.006 | 2.257 |
| Δfr | - | - | - | - | - | - | - | - | - | |
| II | fr | 0.879 | 1.677 | 2.261 | 0.518 | 0.810 | 0.856 | 0.850 | 1.633 | 2.239 |
| Δfr | 46.87% | 22.96% | 0.35% | 25.87% | 8.52% | 8.18% | 47.4% | 22.84% | 0.80% | |
| III | fr | 1.044 | 1.862 | 2.263 | 0.573 | 0.840 | 0.886 | 1.013 | 1.811 | 2.245 |
| Δfr | 23.66% | 10.74% | 0.27% | 13.79% | 4.64% | 4.52% | 23.69% | 10.76% | 0.55% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaile, L.; Ratnika, L.; Pakrastins, L. RC Medium-Rise Building Damage Sensitivity with SSI Effect. Materials 2022, 15, 1653. https://doi.org/10.3390/ma15051653
Gaile L, Ratnika L, Pakrastins L. RC Medium-Rise Building Damage Sensitivity with SSI Effect. Materials. 2022; 15(5):1653. https://doi.org/10.3390/ma15051653
Chicago/Turabian StyleGaile, Liga, Lasma Ratnika, and Leonids Pakrastins. 2022. "RC Medium-Rise Building Damage Sensitivity with SSI Effect" Materials 15, no. 5: 1653. https://doi.org/10.3390/ma15051653
APA StyleGaile, L., Ratnika, L., & Pakrastins, L. (2022). RC Medium-Rise Building Damage Sensitivity with SSI Effect. Materials, 15(5), 1653. https://doi.org/10.3390/ma15051653







